The Functions of Sleep

1.   Introduction

Recently, the theory of nonlinear systems with time-delay has been a hot topic, due to its wide application in practical problems, such as physical engineering, biological systems and economic processes. Among these, the Lyapunov-Krasovskii methodology plays a crucial role in dealing with time-delay systems. Based on the above method, Pepe ^[1] addressed the input state stability of nonlinear systems with time-delay. Zhang ^[2] designed a stabilized controller for time-delay feed-forward nonlinear systems to achieve system stability. In order to address the stabilization problem of high-order nonlinear systems with time-delay, some researchers try to find new ways to design corresponding controllers. Yang and Sun ^[3] investigated the state feedback stabilization problem of controlled systems with high-order or/and time-delay via the homogeneous domination idea. With the help of the saturation function technique, homogeneous domination idea and Lyapunov approach, Song ^[4] studied the stabilization problem of high order feed-forward time-delay nonlinear systems. In addition to the above works, many results in ^{[5,6,7,8,9,10]} have established and improved the concept framework of nonlinear systems with time-delay.

Ever since the stochastic stability theory was founded and enriched by Deng and Zhu ^[11,12], great progress has been made on the global stabilization of stochastic nonlinear systems ^{[13,14,15,16]}. Subsequently, Florchinger ^[17] extended the theory of control with the Lyapunov-Krasovskii functional. With the stochastic stability theory in mind, it is still important and meaningful to address high-order stochastic nonlinear systems with time-delay. Zha ^[18] investigated the issue of output feedback stabilization. Liu ^[19] studied the output feedback stabilization problem for time-delay stochastic feed-forward systems. By using a power integrator approach, the work in ^{[20,21,22,23]} also considered the state-feedback stabilization problems. However, the state feedback stabilization problem for stochastic high-order and low-order nonlinear systems with time-delay has not been well addressed, which leads us to take the interesting problem into account.

How to deal with the state feedback stabilization problem for high-order and low-order nonlinear systems with time-delay? By using a power integrator approach, Liu & Sun ^[24] constructed a time-delay independent controller for the aforementioned systems to relax the growth condition and the power order limitations. However, to the best of our knowledge, research on the corresponding stochastic version is limited with scarcely a few convincing results. The main difficulties are explained from two aspects. On one hand, the $ It\hat{o} $ formula brings the gradient terms and the Hessian terms in the Lyapunov analysis. On the other hand, the particularity of its structure has made many traditional methods inapplicable. Therefore, we need to give a new way to consider stochastic nonlinear systems. Inspired by a large number of results in ^{[25,26,27,28,29]}, stochastic high-order and low-order nonlinear systems with time-delay will be considered as follows:

where $ x(t) = [x_{1}(t), \ldots, x_{n}(t)]^{T} \in R^{n} $ is state, and $ u(t)\in R $ is input; the nonnegative real number $ \tau $ is the time-delay of the states. $ \omega(t) = [\omega_{1}(t), \ldots, \omega_{r}(t)]^{T} $. The high-order can be revealed by $ p_{i}\in R ^{ > 1}_{odd} = :\{\frac{p}{q}|p\geq q > 0 $ $ and\; p, q\; are\; odd \; integers\} $. The drift terms $ f_{i}: R ^{i}\times R ^{i}\times R_{+}\longrightarrow R $ and the diffusion terms $ g_{i}: R^{i}\times R ^{i}\times R_{+}\longrightarrow R ^{r}, \; i = 1, \ldots, n $ are considered as locally Lipschitz with $ f_{i}(0, 0, t) = 0 $ and $ g_{i}(0, 0, t) = 0 $.

The contributions are highlighted in the following:

$ (i) $ Systems considered are more general. Systems in ^[24] only solve the control issues for deterministic cases. It is more complex to consider the stochastic disturbance. By using the homogeneous domination idea, one can give a novel perspective to generalize the control strategy for deterministic systems to the corresponding stochastic cases.

$ (ii) $ The result extends the works ^[30,31,32] by relaxing the growth condition and the power order limitations. The low order of the nonlinear terms is successfully relaxed to the high-order and low-order of the nonlinear terms. Based on the above situations, we use a proper Lyapunov-Krasovskii functional to handle the stabilization problem under the weaker assumptions.

Notations: $ R_{+} $$\triangleq \{x|x\geq0, x\in R\},$$ \; R^{n} $$ \triangleq \{x^{n}|x\geq0\} $. For a given vector/matrix $ D $, $ D^{T} $ denotes its transpose, $ Tr\{D\} $ is the trace when $ D $ is square, and the Euclidean norm of a vector $ |D| $. $ \mathcal{C}^{i} $ is composed of continuous and $ i $th partial derivable functions. $ \mathcal{K} $ is composed of continuous functions and strictly increasing; $ \mathcal{K}_{\infty} $ is composed of functions with $ \mathcal{K} $. One sometimes denotes $ X(t) $ by $ X $ to simplify the procedure.

2.   Problem statement and preliminaries

2.1.   Problem statement

Now, the time-delay stochastic nonlinear systems are addressed as follows:

$ \{x(s) $$:-d\leq s\leq0\}$$ = z $$\in \mathcal{C}^{b}_{\mathcal{F}_{0}}$$ ([-d, 0];R^{n}) $ is an initial data, and $ \omega(t) $ denotes a Brownian motion with dimension $ r $ defined on a complete probability space $ (\Omega, \mathcal{F}, \{\mathcal{F} _{t}\}_{t \geq 0}, P) $.

The following assumptions are needed:

Assumption 1. For $ i = 1, \ldots, n $, there exist two constants $ a_{1} > 0 $ and $ a_{2} > 0 $ such that

in which $ \theta $$ = \frac{m}{n}\geq0 $, $ n $ is an odd integer, $ m $ is an even integer, and $ r_{i}'s $ have the following definitions:

Remark 1. Assumption 1 encompasses and extends high-order and/or low-order results. We discuss this point from two cases.

Case I: Condition (2.2), when $ \tau = 0 $ it reduces to high-order growth condition with $ \theta \geq 0, $

and low-order growth condition with $ \theta = 0 $,

We further discuss its significance from value ranges of both low-order and high-order. From $ \theta \in (- \frac{1}{p_{j}\ldots p_{i-1}}, 0] $, it is easy to see that $ 0 < \frac{r_{i}+\theta}{r_{j}} \leq\frac{1}{p_{j}\ldots p_{i-1}} $, which implies that both low-order and high-order in Assumption 1 can take any value in $ (0, \frac{1}{p_{j}\ldots p_{i-1}}], [\frac{1}{p_{j}\ldots p_{i-1}}, +\infty) $, respectively.

Case II: When $ \tau\neq 0 $, several new results ^{[18,19,20,21,22]} have been achieved on feedback stabilization of high-order nonlinear time-delay systems. The nonlinearities in ^{[18,19,20,21,22]} only have high-order terms. The nonlinearities in ^[24] include linear and nonlinear parts, and their nonlinear parts only allow low-order $ \frac{1}{p_{j}\ldots p_{i-1}} $ and high-order $ \frac{r_{i}+\theta}{r_{j}} $ with $ \theta\geq0 $.

While in this paper, (2.2) not only includes time-delays but relaxes the intervals of low-order and high-order.

Remark 2. When $ p_{i} = 1, i = 1, 2, \ldots, n-1 $, and $ \tau = 0 $, equation (1) reduces to the well-known form, for which the feedback control problem has been well developed in recent years^[16,24,26].

Proposition 1. For $ r_{1}, \ldots, r_{n} $ and $ \sigma = p_{1}\ldots p_{n}r_{n+1} $ having the following properties:

● $ r_{k}\in R^{\geq1}_{odd}, \; \frac{\sigma}{r_{k}}\in R^{\geq1}_{odd}, \; \sigma \in R^{\geq1}_{odd}, \; \frac{\sigma}{r_{k}p_{k-1}\;\ldots\; p_{1}}\in R^{\geq1}_{odd} $.

● $ \sigma \geq max_{1\leq k\leq n}\{r_{k}+\theta\} $.

● There hold

● For $ i = 1, \ldots, k-1 $, one has

Remark 3. It is not difficult to see that system (1.1) is a class of high-order and low-order stochastic nonlinear systems with time-delay satisfying Assumption 1. Compared with ^[30], it is significant to point out that system (1.1) addressed here is more general. The systems can be composed by time-delay and the coupling of the high-order and low-order terms. Moreover, if $ g = 0 $, Assumption 1 will generate the same assumption as in ^[24]. When $ p_{i} > 3 $, the state feedback stabilization problem under constraint $ p_{i} = p $ can give similar results as ^[19]. Under Assumption 1 with $ \tau = 0 $, we can obtain the same results with ^[30], if there are no low-order nonlinearities.

Remark 4. For the case of $ \tau = 0 $ in system (1.1), with the help of adding a power integrator, fruitful results have been achieved over the past years. However, for the case of $ \tau\neq0 $, some essential difficulties will inevitably be encountered in constructing the desired controller. For instance, the time-delay effect will make the common assumption on the high-order system nonlinearities infeasible, and what conditions should be placed to the nonlinearities remains unanswered. Second, due to the higher power, time-delay and assumptions on the nonlinearities, it is more complicated to find a Lyapunov-Krasovskii functional which can be behaved well in theoretical analysis.

2.2.   Useful definitions and lemmas

For ease of the controller design, some helpful definitions are presented.

Definition 1. ^[19] Consider the stochastic system $ dx(t) = f(x, t)dt+g(x, t)d\omega $. For any given $ C^{2} $ function $ V(x, t) $, the differential operator $ \mathcal{L} $ is defined as follows:

where $ \frac{1}{2}Tr\{g^{T}\frac{\partial^{2}V}{\partial^{2}t}g\} $ is called the Hessian term of $ \mathcal{L} $.

Definition 2. ^[25] There exists coordinate $ (x_{1}, \ldots, x_{n})\in R^{n}, \; h_{i} > 0, \; i = 1, \ldots, n $, for arbitrarily $ \varepsilon > 0 $.

$ \bullet $ The dilation $ \Delta_{\varepsilon}(x) = (\varepsilon^{h_{1}} x_{1}, \ldots, \varepsilon^{h_{n}}x_{n}), $ and $ h_{i} $ is referred to as the weights. And one defines dilation weight as $ \triangle = (h_{1}, \ldots, h_{n}) $.

$ \bullet $ A function $ U\in \mathcal{C}(R^{n}, R) $ is considered as homogeneous of degree $ \mu $, if $ \mu \in R $, then $ U(\Delta_{\varepsilon}(x)) = \varepsilon^{\mu}U(x_{1}, \ldots, x_{n}), $ for arbitrarily $ x\in R^{n}\setminus\{0\} $.

$ \bullet $ A vector field $ f_{i} \in \mathcal{C}(R^{n}, R) $ is considered as homogeneous of degree $ \mu $, if $ \mu \in R $, then $ f_{i}(\Delta_{\varepsilon}(x)) = \varepsilon^{\mu+h_{i}}f_{i}(x) $, for arbitrarily $ x\in R^{n}\setminus\{0\}, $ $ i = 1, \ldots, n $.

$ \bullet $ A homogeneous $ \gamma $-norm is considered as $ \|x\|_{\triangle, \gamma} = (\sum_{i = 1}^{n}|x_{i}|^{\frac{\gamma}{h_{i}}})^{\frac{1}{\gamma}} $, for any $ x\in R^{n} $, where $ \gamma\geq1 $. We use $ \|x\|_{\triangle} $ or $ \|x\|_{\triangle, 2} $ to a exhibit 2-norm.

With the above definitions, we give some lemmas which will be crucial for controller design.

Lemma 1. ^[13] For $ m \in R^{\geq1}_{odd} $, $ \forall a\in R\; and\; \forall b \in R $, there hold

Lemma 2. ^[13] For given $ a, b\geq0 $ and a given positive function $ f(x, y) $, there exists a positive function $ g(x, y) $, such that

Lemma 3. ^[13] For a continuous function $ g $, if it is monotone, and $ g(s) = 0 $, then

Lemma 4. ^[19] Given $ \tau_{i}\in R, \; i = 1, \ldots, n $ satisfying $ 0\leq\tau_{1}\leq\ldots\leq\tau_{n} $ and for given nonnegative functions $ a_{i}(x, y), \; i = 1, \ldots, n, $ there holds

3.   Design procedures

3.1.   Control design procedures

Consider the stochastic high-order and low-order nonlinear systems with time-delay as follows:

Step 0: To begin with, introducing the complete form of the controller,

The purpose of this work is to construct a state controller to render system $ (1.1) $ globally asymptotically stable in probability. To achieve this goal, propositions are presented as follows.

Proposition 2. For $ c_{1} > 0 $, $ c_{2} > 0 $, $ i = 1, \dots, n $, there hold

Step 1. First, we will construct a Lyapunov-candidate-function $ V_{1} = \int_{0}^{x_{1}} s^{3}ds+\int_{0}^{x_{1}} s^{\frac{4\sigma-r_{2}p_{1}}{r_{1}}} ds+n\int _{t-\tau}^{t} ({z_{1}^{4}(l)+z_{1}^{\frac{4\sigma}{r_{1}}}(l))dl} $. Along the solution of (3.1), one has

where $ \Psi_{1} = \frac{1}{2}Tr\{g_{1}^{T}\frac{\partial ^{2}V_{1}}{\partial x_{1}^{2}}g_{1}\} $, which leads to

With Proposition 2, Lemma 1 and Lemma 2 in mind, one has

with the help of Lemma 4, we can see it satisfies $ |z_{1}|^{\frac{r_{2}p_{1}}{r_{1}}}z_{1}^{3}\leq|z_{1}|^{\frac{r_{2}+\theta+3r_{1}}{r_{1}}}\leq|z_{1}|^{4+\theta}\leq z_{1}^{4}+z_{1}^{\frac{4\sigma}{r_{1}}} $ when $ 4\leq 4+\theta\leq\frac{2r_{2}p_{1}}{\sigma}+3\leq\frac{4\sigma}{r_{1}} $. Similarly, one can obtain

where $ \beta_{1} = 4c_{1}+2c_{1}^{2}+\frac{4\sigma-r_{2}p_{1}}{\sigma}(\frac{2r_{2}p_{1}}{\sigma})^{\frac{r_{2}p_{1}}{4\sigma-r_{2}p_{1}}}c_{1}^{{\frac{2\sigma}{4\sigma-r_{2}p_{1}}}} $. Now, one designs the virtual controller $ \alpha_{1} $ as

where $ \varrho_{1} > 1 $ is a positive constant. Noticing that

and using (4.1) and (3.7) with (3.4) after complex calculations, one finally obtains

To complete the induction, at the $ k $th step, we now define

Lyapunov function $ V_{k} = V_{k-1}+W_{Lk}+W_{Hk}+W_{Dk} $ is $ C^{2} $, proper and positive definite. Moreover, for $ i = 1, \ldots, k-1 $, $ W_{Lk}(\cdot), \; W_{Hk}(\cdot), \; W_{Dk}(\cdot) $ satisfy

Step k (k = 2, 3, …, n): As in step k-1, there exists Lyapunov-candidate-function $ V_{k-1} $, implying

where $ \Psi_{k-1} $$ = $ $ \frac{1}{2}Tr\{\bar{\psi}_{k-1}^{T} $ $ \frac{\partial ^{2}V_{k-1}}{\partial \bar{x}_{k-1}^{2}} $ $ \bar{\psi}_{k-1}\} $, $ \bar{\psi}_{k-1} $ $ = $ $ (g_{1} $, $ \ldots $, $ g_{k-1}). $ Hence, one will consider $ V_{k} = V_{k-1}+W_{Lk}+{W_{Hk}+W_{Dk}} $ and define an appropriate virtual controller $ \alpha_{k} $. Similar to step $ 1 $, one can obtain

where $ \Psi_{k} = \frac{1}{2}Tr\{\bar{\psi}_{k}^{T} \frac{\partial ^{2}V_{k}}{\partial \bar{x}_{k}^{2}} \bar{\psi}_{k}\} $, $ \bar{\psi}_{k} = (g_{1}, \ldots, g_{k}). $ Obviously, the virtual controller $ \alpha_{k} $ is used to eliminate the last three terms of (3.12). In light of (3.2) and Lemma 1, it yields that

In the case of $ 4\sigma-\theta\leq4\sigma $, by Lemma 2, one obtains that

where $ \beta_{k1} $ denotes a positive constant. On the basis of Proposition 2 and Lemma 3, one has

where $ \beta_{k2} $ denotes a positive constant. In the sequel, one estimates the last term. With the help (3.2), Lemmas 2 and 4, it is not hard to achieve

Similarly, one can obtain

On the basis of the previous inequality, one has

in which $ d_{ki} $ denotes a positive constant. Define $ \beta_{k} = \beta_{k1}+\beta_{k2}+\beta_{k3} $ with $ \beta_{k3} = \sum_{i = 1}^{k-1}d_{ki} $ and choose the virtual controller $ \alpha_{k} $ as

By Lemma 2, one can arrive at

Substituting (3.13)–(3.18) into (3.12) yields

It is shown that the above formula holds for $ k = n $ with virtual controllers (3.18). Similarly, we choose $ V_{n}(x) = \sum_{i = 1}^{n}(W_{Li}(\cdot)+W_{Hi}(\cdot)+W_{Di}(\cdot)) $. There is an actual control law

such that

Until now, the recursive design has been completed. Under the new coordinates

where $ k_{1} = 0 $, $ k_{i} = \frac{k_{i-1}+1}{p_{i-1}} $, $ i = 2, \;\ldots\;, n $ and $ L > 1 $ is a constructed constant, system $ (1.1) $ can be rewritten in the form

By (3.18) and (3.20), the system $ (3.1) $ can be integrated into the complex format

where $ \xi $$= (\xi_{1}, \;\ldots\;, \xi_{n})^{T} $, $ R(\xi)$$ = (\xi_{2}^{p} $, $ \;\ldots\;, \xi_{n}^{p} $, $ \nu^{p})^{T} $, $ T(t, \xi $, $ \xi(t-\tau)) $$= (f_{1} $, $ \frac{f_{2}}{L^{k_{2}}}, \;\ldots\; $, $ \frac{f_{n}}{L^{k_{n}}})^{T} $, $ \psi(t, \xi, \xi(t-\tau))$$ = (g_{1} $, $ \frac{g_{2}}{L^{k_{2}}}, \;\ldots\; $, $ \frac{g_{n}}{L^{k_{n}}}) $. Introducing the dilation weight $ \triangle $$ = (r_{1}, r_{2}, \;\ldots\;, r_{n}) $, one gets

where $ s $ is defined as $ s = r_{i}\zeta $. With the help of the above formula and Definition 2, it can be concluded that $ V_{n}(\xi) $ is homogeneous of degree $ 4\sigma-\theta $.

3.2.   Stability analysis

The main result of this manuscript will be stated as follows.

Theorem 1. Suppose Assumptions 1 apply to stochastic system $ (1) $, under the state feedback controller $ u^{p} = L^{k_{n}+1}\nu^{p} $ and (3.20), then:

$ (i) $ There exists a unique solution on $ [-d, \infty) $;

$ (ii) $ The equilibrium at the origin is globally asymptotically stable in probability.

Proof. Four steps are used to verify Theorem 1.

Step 1: By the definition of $ \varrho > 0 $, we know that $ {p_{1}\;\ldots\; p_{j-1}-1} > 1 $, which implies that $ 4-\frac{1}{p_{1}\;\ldots\; p_{k-1}-1} > 2 $, $ \frac{4\sigma-r_{k+1}\;p_{k}}{r_{k}p_{k-1}\;\ldots\; p_{1}} > 2 $. Therefore, $ \frac{\partial\alpha_{i}^{p_{1}\;\ldots\; p_{i}}(t)}{\partial x_{j}(t)} $ is continuous, and $ u^{p_{n}} = L^{k_{n+1}}\nu^{p_{n}} $ is $ \mathcal{C} $. As is known to all, the function is $ \mathcal{C} $. The closed-loop system satisfies the locally Lipschitz condition based on $ f_{i} $ and $ g_{i} $ being locally Lipschitz.

Step 2: Consider the Lyapunov-candidate-function:

where $ h_{1} $ and $ h_{2} $ are positive parameters. It is straightforward to prove that $ V(\xi) $ is $ \mathcal{C}^{2} $ on $ \xi $. Since $ V_{n}(\xi) $ is continuous, positive definite and radially unbounded, from Lemma 1, one can have

where $ \alpha_{20} $ and $ \alpha_{21} $ are $ \mathcal{K}_{\infty} $ functions. With the help of the homogeneous theory, one finally has

in which $ \bar{c}_{0} > 0 $, $ \underline{c}_{0} > 0 $, and $ U(\xi) $ denotes a positive definite function of the $ 4\sigma $ homogeneous degree. Hence, one has the formula

(3.29) leads to

where $ \eta = s+t $, $ \tilde{c} > 0 $, $ c > 0 $ and $ \alpha _{22} $ is a class $ \mathcal{K}_{\infty} $ function. Since

Defining $ \beta_{2} = \alpha_{21}+\alpha_{22} $, by (3.26)-(3.30), one gets

Step 3: With the help of Lemma 1 and (3.20), $ c_{01} $ is a positive constant, and one has

By Proposition 2 and $ L > 1 $, one can have

in which $ \bar{\delta}_{1}, \delta_{1} > 0 $. With the help of Lemmas 1, 2 and (3.32), one can obtain

where $ c_{02}, $ $ \bar{c}_{02}, $ $ \tilde{c}_{02} $ and $ \bar{\gamma_{0}} = \min\limits_{1\leq i\leq n}{\gamma_{i1}} $ are positive constants. Similar to (3.32), we use $ \delta_{2} $ and $ \gamma_{i2} < 1/2 $ to show that

Using Lemma 1, Lemma 3, Lemma 4 and (3.34), one obtains

in which $ \tilde{\gamma}_{0} = \min\limits_{1\leq i, j\leq n}\{\gamma_{i2}+\gamma_{j2}\} > 0 $, $ c_{03} > 0, $ $ \bar{c}_{03} > 0 $ and $ \tilde{c}_{03} > 0 $ are constants. Based on $ L > 1 $, we have

By Definition 1, (3.26), (3.31), (3.33) and (3.34), one has

which satisfies $ \gamma_{0} $$= min$$ \{\bar{\gamma}_{0} $, $ \tilde{\gamma}_{0}\} < 1 $. Because $ c_{01} $ is a constant independent of $ c_{02}, \; c_{03} $, we choose $ L > L^{\ast} $$= \max$$ \{(\frac{c_{02}+c_{03}+\frac{h_{1}+h_{2}}{1-\gamma}}{c_{1}})^{\frac{1}{\gamma_{0}}}, 1\} $, and there exists a constant $ B = c_{01}-(c_{02}+c_{03}+\frac{h_{1}+h_{2}}{1-\gamma})L^{-\gamma_{0}} > 0 $, such that

With the help of the above formula and (3.28), one obtains

Briefly, following Steps $ 1 $–$ 3 $, the system has a unique solution on $ [-d, \infty] $, and $ \xi(t) = 0 $ is globally asymptotically stable in probability.

Step 4: Because (3.20) is an equivalent transformation, the system composed by $ (1) $ and $ u^{p} = L^{k_{n+1}}v^{p} $ is similar to the systems (3.20) and (3.22).

Remark 5. Compared with ^[24], we construct a state-feedback controller independent of time delays for the stochastic nonlinear system. Compared with ^[30], we use the methods of adding a power integrator to relax the nonlinear growth condition to cover both high-order and low-order nonlinearities. Not only does it not need to know anything information about the unknown function, but also it can reduce burdensome computations.

Remark 6. The homogeneous domination method is used for the first time to solve the stabilization problem of stochastic high-order and low-order nonlinear system (1.1) with time-delay.

Remark 7. In this paper, it is hard to adopt a Lyapunov-Krasovskii functional. In order to solve the above the problem, a suitable Lyapunov-candidate-function is designed to guarantee good system performance, and stabilization analysis is proposed to save better resources

Remark 8. The construction of the controller effectively keeps away from the zero-division problem of $ \frac{\partial^{2}\xi_{i}^{\ast\mu/r_{i}}}{\partial\xi^{2}_{j}} $. It need be noted that the non-zero-division problem and the locally Lipschitz condition (see Step 1 in the proof of Theorem $ 1 $) should to be guaranteed simultaneously, which will increase more difficulties.

4.   Simulation example

Consider the following stochastic high-order and low-order nonlinear systems with time-delay:

One can see that Assumption 1 is satisfied with $ p_{1} = p_{2} = 3, \tau = 1, C = 1, r_{1} = 1, \theta = \frac{2}{5} $. One can easily get

In this simulation, we choose $ V_{1}(z_{1}) = \frac{1}{5}z_{1}^{5}+\frac{1}{10}z_{1}^{10}+2\int_{t-1}^{t}(z_{1}^{4}+z_{1}^{\frac{4\sigma}{r_{1}}})dl $. Several calculations lead to

where $ \alpha^{p_{1}} = -(2n+\beta_{1})(z_{1}^{3}+z_{1}^{\frac{7}{5}}) $. By choosing $ V_{2}(\overline{\eta}_{2}) = V_{1}(\eta_{1})+W_{L2}+W_{H2}+W_{D2} $, a direct calculation leads to

From the previous manipulations, one obtains the following actual controller

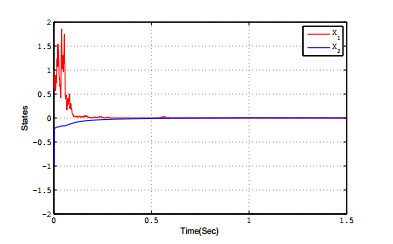
The initial condition can be given as $ \xi_{0}(\theta)\equiv[1, -1]^{T} $. Figure 1 illustrates that the globally asymptotically stable in probability has been achieved and the responses of (4.7) is given in Figure 2.

5.   Conclusions

In this technical note, we investigate the state feedback stabilization problem of stochastic high-order and low-order nonlinear systems with time-delay successfully. According to the homogeneous domination method and the design of integral Lyapunov functions, the control strategy is achieved with the controller design. The above results indicate that the closed-loop system is globally asymptotically stable in probability. There still remain problems to be investigated, such as how to take into account output feedback control and how to extend our results under weaker conditions.

Acknowledgments

This work is supported by National Natural Science Foundation of China under Grant 62173208, Taishan Scholar Project of Shandong Province of China under Grant tsqn202103061, Shandong Qingchuang Science and Technology Program of Universities under Grant 2019KJN036.

Conflict of interest

The authors declare no conflicts of interest.