L^p-analysis of one-dimensional repulsive Hamiltonian with a class of perturbations

Abbreviations

1.   Introduction

In practice, descriptions of the system and its components from different reliability assessments may be based on many sources of information. Some might be unbiased measurements based on existing statistical models or relative frequencies. Others could come from engineers' or specialists' views on the underlying problem. The opinion of engineers can be crucial, especially for real-world reliability problems where they may be the only source of information. Natural language statements can be used to communicate reliability assessments, as these expressions are often better suited to convey reliability information than numerical expressions. This demonstrates the importance of quantifying reliability assessment tools.

The phenomenon of aging is one of the most remarkable features of reliability. The mathematical theory of aging provides important measures for the quantification of aging concepts in reliability analysis. "No aging" means that the age of a component does not influence how its remaining lifetime is distributed. "Positive aging" is the process by which the remaining life of a component decreases with age in the probable sense of the word. Reliability engineers often deal with such situations as parts deteriorate over time due to increasing wear. However, the remaining lifetime is affected by "negative aging". Reliability growth phenomena can occur in certain cases when a system is regularly tested and improved, even if this happens less frequently. Aging concepts explain how a system or component gets better or worse with age. The aging characteristics of many classes of life distributions are defined or classified in the literature. The aging characteristics of the distribution function of a non-negative random variable (rv), which symbolizes the lifetime of a reliability system, are often very important for defining the best operating strategies associated with the underlying lifetime event.

Aging classes of life distributions are a subset of the bigger class of non-parametric families of life distributions, which has been studied in the context of reliability theory and survival analysis in the literature. The assumption that a distribution function gives rise to an aging property causes it to belong to a particular family, which can sometimes be supported by a physical understanding of the failure mechanism since the families are characterized by attributes that have physically relevant interpretations. For these non-parametric families, numerous statistical techniques can be viewed as a middle ground between parametric and conventional distribution-free analysis. Life distributions describe the time until an event occurs, such as failure in a system. Common life distributions include exponential, Weibull, and their generalizations. Each has specific characteristics that can be leveraged in reliability analysis. (see, e.g., Barlow and Proschan ^[4] and Marshall and Olkin ^[24]).

The preservation properties of classes of life distributions under coherent systems are important for reliability theory and systems engineering. We illustrate here a breakdown of their importance and usefulness. Coherent systems are constructed in such a way that their reliability can be analyzed through their components. These systems can be series, parallel, or more complex configurations. The overall reliability of a coherent system is determined by the reliability of its components and their arrangement. Preservation properties refer to the characteristics of certain life distributions that are preserved when applied to coherent systems. For example, several classes of lifetime distributions have the property that if individual components have a certain reliability, the coherent system will also have similar reliability properties. Understanding how lifetime distributions behave in coherent systems allows engineers and reliability analysts to predict the performance of complex systems based on the properties of simpler components. In the design domain of an optimization problem, if designers know which classes of lifetime distributions preserve certain properties, they can select components that ensure the desired reliability level of the system. In risk management, preservation properties help assess risks associated with system failures, enabling better decision-making regarding maintenance and component selection. In various areas of engineering such as aerospace, automotive, and electronics, where a system failure can have catastrophic consequences, understanding these properties is critical to ensuring safety and reliability. In healthcare, where medical devices and treatments are used, maintaining certain life distribution properties can provide insight into patient outcomes and device longevity. In finance, understanding the preservation of life distributions for risk assessment models can help in evaluating the longevity of financial products or investments. In general, the preservation properties of classes of life distributions under coherent systems are crucial for effective reliability analysis and system design. They provide the fundamental knowledge needed to ensure that systems operate reliably over time, which is essential in various industries where performance and safety are paramount. Understanding these concepts enables better decision-making and optimization in complex systems.

The $(n-k+1)$-out-of-$n$ structures are considered as an important class of coherent systems in the context of reliability. An $(n-k+1)$-out-of-$n$ structure is a structure of order $n$ that functions if and only if at least $n-k+1$ components function, where $1\leq k \leq n$. These structures are important because, as Barlow and Proschan ^[3] have shown, the $(n-k+1)$-out-of-$n$ structure has the steepest reliability functions among all monotone structures of order $n$. Moreover, these types of systems are very useful from a mathematical point of view, since quantitative results are easy to obtain. Two important special cases of $(n-k+1)$-out-of-$n$ systems are parallel systems and series systems corresponding to $k = n$ and $k = 1$, respectively. The $(n-k+1)$-out-of-$n$ system structure is a very popular type of redundancy in fault-tolerant systems. It is widely used in both industrial and military systems. Fault-tolerant systems include the multi-display system in a cockpit, the multi-motor system in an airplane, and the multi-pump system in a hydraulic control system.

The problem of obtaining the class of lifetime distribution of systems with the $(n-k+1)$-out-of-$n$ structure has been a key subject in the reliability field. To be more specific, it may be of some interest to determine, for each class of life distributions, whether the $(n-k+1)$-out-of-$n$ structure yields a system's life distribution within the same class. In the literature, this kind of problem is referred to as preservation properties of reliability (or aging) class of life distributions under the structure of $(n-k+1)$-out-of-$n$ systems. Barlow and Proschan ^[4] showed that the increasing failure rate (IFR) and the increasing failure rate in average (IFRA) classes are preserved under a system of independent components with the $(n-k+1)$-out-of-$n$ structure where component lifetimes are identically distributed. The preservation property of different classes of life distributions in various cases where the component lifetimes are possibly dependent has also been studied in the literature. The readers are referred to Samaniego ^[32], Navarro et al. ^[26], Navarro ^[27], Buono et al. ^[9], Lindqvist et al. ^[22], Lindqvist and Samaniego ^[23], and Izadkhah et al. ^[14] for recent developments on the area.

Barlow and Proschan ^[4] considered the problem of stochastic partial orderings of distributions within a class so that, roughly speaking, within the IFR class, the distributions are ordered according to the degree of IFR-ness, and similarly for other classes of life distributions. The objective of the current study is to concentrate on two classes of life distributions that induce the concept of aging speed. We obtain preservation properties of these classes under the formation of $(n-k+1)$-out-of-$n$ systems with independent and identically distributed (i.i.d.) component lifetimes. Our results showed that if the distribution of lifetime components of a $(n-k+1)$-out-of-$n$ system possesses some kind of decreasing aging rate over time, then the distribution of the lifetime of the system will also induce the same property.

The rest of the paper is organized as follows. In Section 2, we provide basic definitions used throughout the paper. In Section 3, we consider two classes of life distributions, namely decreasing (increasing) relative failure rate and decreasing (increasing) failure rate relative to average failure rate, and focus on some of their reliability properties. In Section 4, the preservation property of the decreasing relative failure rate class under the structure of $(n-k+1)$-out-of-$n$ systems is discussed. In Section 5, we get the preservation of decreasing failure rate relative to the average failure rate class under the formation of $(n-k+1)$-out-of-$n$ systems. In Section 6, illustrative conclusions of the paper are given and some remarks for future studies are appended.

2.   Preliminaries

Let $X$ be a non-negative rv that represents the lifetime of an item. We assume that $X$ has cumulative distribution function (cdf) $F_X$, probability density function (pdf) $f_X$, and survival function (sf) $\bar{F}_{X}\equiv 1-F_X$. The hazard rate (hr) function (or failure rate function) of $X$, as an instantaneous measure of risk or failure, is defined as

which is well-defined for all $t\geq 0,$ for which $\bar{F}_X(t) > 0$. The average failure rate of $X$ is then given by

The functions $h_X(t)$ and $H_X(t)$, as two useful reliability quantities, have been used repeatedly in reliability studies and survival analyses for various purposes, from statistical inference procedures to advanced stochastic analyses. Most of the important aging classes of lifetime distributions are constructed using the failure rate or/and the failure rate average due to their monotonicity properties as well as their non-monotonic behavior (see, for instance, Proschan ^[29], Lai and Xie ^[19], Finkelstein ^[12], Bhattacharyya et al. ^[6], and Kayid ^[17].

Jiang et al. ^[15] have pointed out that an unimodal failure rate can be effectively viewed as approximately decreasing, approximately increasing, or approximately constant. Clearly, such representation is qualitative. In their paper, a quantitative measure, called the aging intensity (AI) function, defined as the ratio of the failure rate $h_X(t)$ to the average failure rate $H_X(t)$, was studied. The AI function is defined as

Nanda et al. ^[25] explored the different properties of the AI function in several reliability problems. The closure properties of the aging classes defined in terms of AI function under different reliability operations such as the formation of $k$-out-of-$n$ system, and increasing transformations, were also presented. Bhattacharjee et al. ^[5] derived the AI function and also discussed its properties for various Weibull models. The aging properties of a system are quantitatively analyzed by the AI function. Regarding the AI function, Bhattacharjee et al. ^[5] investigated some system characteristics and the behavior of some generalized Weibull models. According to Bhattacharjee et al. ^[5], the AI function plays a significant and completely unique role in the reliability consideration when researching the aging behavior of systems. For some recent works on the study of the AI function, we refer the readers to Sunoj and Rasin ^[34], Szymkowiak ^[35], Szymkowiak ^[36], Szymkowiak ^[37], and Bhattacharjee et al. ^[7].

Here, we provide some elementary materials and definitions that are needed during our investigation. $X$ describes the lifetime of a device or a system of components. We suppose that $X$ has cdf $F_X$, sf $\bar{F}_{X}$, and pdf $f_X$ whenever it exists. Two partial stochastic orders are used in this paper, and they are defined as follows (cf. Shaked and Shanthikumar ^[33]).

Definition 2.1. Let $X$ and $Y$ represent two random lifetimes, where $X$ and $Y$ have sfs $\bar{F}_X$ and $\bar{F}_Y,$ and pdfs $f_X$ and $f_Y,$ respectively. Then, it is said that $X$ is smaller than $Y$ in the

(i) usual stochastic order (written as $X\leq_{st} Y$) if $\bar{F}_X(t)\leq \bar{F}_Y(t),$ for all $t\geq 0$, or equivalently, for all increasing functions $\phi$, it holds that $E[\phi(X)]\leq E[\phi(Y)]$.

(ii) likelihood ratio order (written as $X\leq_{lr} Y$) if $\frac{f_Y(t)}{f_X(t)}$ is increasing in $t\in S_X \cup S_Y$, where $S_X\equiv \{t\geq 0: f_X(t) > 0\}$ and $S_Y\equiv \{t\geq 0: f_Y(t) > 0\}$ are the supports of $X$ and $Y$, respectively.

It is well-known in the literature that $X\leq_{lr}Y \; \Rightarrow \; X\leq_{st}Y$ (see, e.g., Shaked and Shanthikumar ^[33]).

The following definition presents some aging classes of life distributions.

Definition 2.2. (Lai and Xie ^[19]). It is said that $X$ possesses

(i) increasing [resp. decreasing] failure rate behaviour, denoted by $X\in IFR$ (resp. $X\in DFR$) when $h_X(t)$ is non-decreasing [resp. non-increasing] in $t > 0$.

(ii) increasing [resp. decreasing] failure rate in average property, denoted by $X\in IFRA$ (resp. $X\in DFRA$), when $H_X(t) = \frac{1}{t}\int_0^{t} h_X(x)dx$ is non-decreasing [resp. non-increasing] in $t > 0$.

It is known that $X\in IFR$ implies that $X\in IFRA$ and, moreover, $X\in DFR$ concludes that $X\in DFRA$ (cf. Lai and Xie ^[19]).

The following technical definition can be found in Karlin ^[16].

Definition 2.3. Let $K(x, y)$ be a non-negative bivariate function. It is said that $K(\cdot, \cdot)$ is a totally positive of order 2 (abbreviated as $TP_2$) function in $(x, y)\in \mathcal{B}_1 \times \mathcal{B}_2$ where $\mathcal{B}_1$ and $\mathcal{B}_2$ are considered as two arbitrary subsets of the real line, whenever

If the inequality's direction in (2.1) is reversed, then $K(x, y)$ is called a reverse regular of order 2 (abbreviated as $RR_2$) function in $(x, y)\in \mathcal{B}_1 \times \mathcal{B}_2$.

3.   Two relative aging classes of life distributions

This section provides the definitions, descriptions, and preliminary properties of some classes of life distributions that consider the relative aging phenomenon. The concept of relative aging has been used to define an order relation between two lifetime distributions to induce that one-lifetime unit ages faster than the other lifetime unit. The concept of relative aging can also be extended to describe the aging behavior of a single lifetime unit. For instance, when it is said that a unit with random lifetime $X$ has an IFR distribution, it is evident that its hr function, $h_X(t)$, is increasing in $t\geq 0$; however, the speed of aging and that how fast the hr function increases as time traverses $[0, +\infty)$ is not considered. Despite that, the hr function may increase (or decrease) at an increasing rate or it may increase (or decrease) at a decreasing rate. This is another important aspect of a life distribution that is a fresh feature needing to be quantified. The following definition is essential to our development.

In this manuscript, we will only consider nonnegative random variables that denote the life length of a lifetime unit (e.g., a life span). The random variables are assumed to have absolutely continuous distribution functions.

We first provide the definitions of some classes of life distributions before going into their details. As two devices or life spans have a lifetime distribution which has increasing hazard rate functions, one may ask whether one of them ages faster than the other. The following definition introduces two three notions of aging for a lifetime device concerning its hr function.

Definition 3.1. Let $X$ be a non-negative rv representing the lifetime of a device. Let $X$ have hr function $h_X$. Then, it is said that $X$ has

(i) increasing (decreasing) relative failure rate property [denoted by $X\in IRFR$ ($X\in DRFR$)], whenever '$\frac{h_X(t)}{h_X(\alpha t)}$ is increasing (decreasing) in $t\geq 0$', for all $\alpha \in (0, 1)$.

(ii) increasing (decreasing) failure rate relative to average failure rate property [denoted as $X\in IFR/A$ ($X\in DFR/A$)], whenever '$\frac{th_X(t)}{\int_{0}^{t} h_X(x)dx}$ is increasing (decreasing) in $t\geq 0$' (Righter et al. ^[30]).

(iii) $X$ has initially increasing [resp. decreasing] failure rate (written as $X\in Initially$-$IFR$ [resp. $X\in Initially$-$DFR$]) whenever there exists an $\tau > 0$, such that $h_X(t)$ increases in $t\in (0, \tau]$.

Keep in mind that if $X$ is $IFR$, then $h_X(\alpha t) \leq h_X(t),$ for all $t\geq 0,$ and for all $\alpha \in [0, 1].$ We know that if $X$ is $IFR$, the hr function $h_X(t)$ progressively increases as $t$ increases and traverses $[0, +\infty)$. Nevertheless, it is not clear how fast the hr function increases in different time intervals. In this context, if $X$ is $IRFR$, the amount of increase of $\log(h_X(t))$ as the time goes from $\alpha t$ (for each $\alpha \in [0, 1]$) toward $t$ increases with $t$, i.e., the difference $\log(h_X(t))$-$\log(h_{X}(\alpha t)$ increases with $t$, for all $\alpha \in [0, 1].$ This means that the speed of aging increases with time. Likewise, the two classes $Initially$-$IFR$ and $Initially$-$DFR$ encompass many parametric families of distributions (see, e.g., Kelly et al. ^[18]). There are many parametric distributions that have not monotone hr functions. Despite that, their hr function may have the initially-increasing or initially-decreasing properties.

Remark 3.1. It is worth pointing out that sufficient conditions for $X\in IRFR$ and $X\in DRFR$ can be established. Let $\lambda(t, s)$ be a bivariate function on $R_{+}^{2} = [0, \infty)\times[0, \infty)$. If $\lambda(t, s)$ is $TP_2$ [or $RR_2$] in $(t, s) \in R_{+}^{2}$, then $X\in IRFR$ [or $X\in DRFR$]. If $\frac{\partial}{\partial t}\log(\lambda(t, s))$ and $\frac{\partial}{\partial s}\log(\lambda(t, s))$ exist and are continuous, Theorem 7.1 in Holland and Wang ^[13] shows that $\lambda(t, s)$ is $TP_2$ [or $RR_2$] in $(t, s) \in R_{+}^{2}$ if and only if $\frac{\partial^2}{\partial t \partial s} \log(\lambda(t, s)) \geq 0$ [or $\leq 0$] for all $(t, s) \in R_{+}^{2}$.

In general, the $IFR$ and $DFR$ classes are neither implied by nor do they imply the $IRFR$ and $DRFR$ classes. The following counterexample presents a situation where $X\in IFR$ but $X \not\in IRFR$.

Counterexample 3.1. Suppose that $X$ has an Erlang distribution with pdf $f_X(t) = 4te^{-2t}, t\geq 0$ which has hr function $h_X(t) = \frac{4t}{1+2t}$. This hr function is increasing, thus $X\in IFR$. On the other hand, for all $t\geq 0$ and for every $\alpha \in [0, 1]$, one has $\frac{\partial}{\partial t}\frac{h_X(\alpha t)}{h_X(t)} = \frac{2\alpha (1-\alpha)}{(1+2\alpha t)^2}$ which is non-negative for all $t\geq 0$ and for any $\alpha \in [0, 1]$. Therefore, $\frac{h_X(\alpha t)}{h_X(t)}$ is increasing in $t\geq 0$. Hence, according to Definition 3.1(i), one concludes that $X\in DRFR$. Thus, in general $DRFR \nsubseteq DFR.$

However, we establish two propositions that provide some mild conditions under which $X\in IRFR$ [resp. $X\in DRFR$] implies that $X\in IFR$ [resp. $X\in DFR$].

Proposition 3.1. Suppose $f_X(t)$ is right-continuous at $t = 0$ such that $0 < \lim_{x\rightarrow 0^{+}}f_X(x) < \infty$ and $\bar{F}_X(0) = 1$. Then:

(i) $X\in IRFR$ implies that $X\in IFR$.

(ii) $X\in DRFR$ implies that $X\in DFR$.

Proof. We only prove part (ⅰ), as the proof for part (ⅱ) is similar. Since $X \in IRFR$, by Definition 3.1, $\frac{h_{X}(\alpha t)}{h_X(t)}$ is non-increasing for $t \geq 0$. Therefore, for any $t_1 \leq t_2 \in [0, \infty)$, we have

So, it implies that

Thus, we have shown that for all $t_1 \leq t_2 \in [0, \infty),$ it follows that $h_X(t_1) \leq h_X(t_2),$ establishing that $X$ is IFR. Hence, the proof of part (ⅰ) is completed. □

It is remarkable here that in Example 3.1, $\lim_{x\rightarrow 0^{+}}f_X(x) = 0,$ $X\in DRFR$ but $X\not\in DFR$, which shows that the condition $0 < \lim_{x\rightarrow 0^{+}}f_X(x) < \infty$ in Proposition 3.1 cannot be dropped.

In the following proposition, we prove that the $IRFR$ and $DRFR$ properties of a lifetime distribution translate the initially-increasing and initially-decreasing (i.e., $Initially$-$IFR$ and $Initially$-$IFR$) properties of the hr function of the lifetime distribution to the entirely-increasing and entirely-decreasing (i.e., $IFR$ and $DFR$) properties of the hr function.

Proposition 3.2. The following implications hold:

(i) Let $X\in IRFR$. Then, $X\in Initially-IFR$ yields $X\in IFR$.

(ii) Let $X\in DRFR$. Then, $X\in Initially-DFR$ yields $X\in DFR$.

Proof. We prove the result of assertion (ⅰ). The proof of assertion (ⅱ) is analogous. Since $X \in Initially-IFR$, thus for every $t_1^{\star} \leq t_2^{\star} \in (0, \tau]$, one has $h_X(t_1^{\star}) \leq h_X(t_2^{\star}) \leq h_X(\tau)$. On the other hand, since $X\in IRFR$, thus for all $t_1 \leq t_2 \in (0, \infty)$,

We need to demonstrate that for all $t_1 \leq t_2 \in (\tau, +\infty),$ it holds that $h_X(\tau) \leq h_X(t_1) \leq h_X(t_2)$. To this end, let us fix $t_1 \leq t_2 \in (\tau, +\infty),$ and select an $\alpha > 0$ such that $\alpha \leq \min (\frac{\tau}{t_1}, \frac{\tau}{t_2})$. Now, observe that $\alpha t_1 \leq \alpha t_2 \in (0, \tau].$ Since $X\in Initially$-$IFR$, thus, $h_X(\alpha t_{1}) \leq h_X(\alpha t_{2}) \leq h_X(\tau)$. From (3.1), it follows that for all $t_1\leq t_2 \in (\tau, +\infty)$, $h_X(t_2) \geq h_X(t_1) \geq h_X(\tau),$ and, consequently, $X$ is $IFR$. The proof of part (ⅰ) is thus obtained. □

Remark 3.2. The classes of lifetime distributions proposed in Definition 3.1(i) reflect the irregular variation of the hazard rate function over time. For instance, if $X$ possess the $IRFR$ property, then the fluctuations of $h_X$ increase with time, while if $X$ possess the $DRFR$ property, then the hazard rate function is becoming regularly more stable with time. The lifetime distribution classes in Definition 3.1(ii) are closely related to the concept of aging intensity (AI) function. Let $X$ be a non-negative rv with sf $\bar{F}_X$ and hr function $h_X$, then $L_X(t) = \frac{th_X(t)}{-\ln(\bar{F}_X(t))}$ is called the AI function of $X$. In this case, $X\in IFR/A$ ($X\in DFR/A$) is equivalent to saying that $X$ has an increasing (a decreasing) AI function (see, e.g., Nanda et al. ^[25]).

The classes of life distributions given in Definition 3.1 are connected as below.

Proposition 3.3. If $X\in IRFR$ ($X\in DRFR$), then, $X\in IFR/A$ ($X\in DFR/A$).

Proof. Suppose $X$ has $AI$ function $L_X$. From Remark 3.2, it is sufficient to show that $L_X$ is an increasing [a decreasing] function. We have

where the last expression is due to the change of variable $\alpha = \frac{x}{t}$. Now, assume that $X\in IRFR$ [$X\in DRFR$]. Then, according to Definition 3.1(ⅰ), $\frac{h_X(\alpha t)}{h_X(t)}$ is decreasing [increasing] in $t > 0,$ for all $\alpha \in (0, 1)$. Thus, $\int_0^{1}\frac{h_X(\alpha t)}{h_X(t)}d\alpha$ is also decreasing [increasing] in $t > 0$. The required result is obtained. □

Subsequently, we present a counterexample that demonstrates that the implication in Proposition 3.3 cannot be reversed.

Counterexample 3.2. Suppose that $X$ is a non-negative rv with the following sf

where $\lambda > 0$, form which the hazard rate function is derived as

The AI function of $X$ is, therefore, obtained as

which is decreasing in $t\geq 0$, which means that $X\in DFR/A$. However, one can see, after some calculation, that

which is not decreasing in $t\geq 0$, for every $\alpha\in (0, 1)$. As a result, $X\not\in DRFR$.

The following proposition presents a necessary and sufficient conditions under which $X\in IRFR$ ($X\in DRFR$).

Proposition 3.4. Let $h_X$ be a differentiable function.

Then, $X\in IRFR$ ($X\in DRFR$) if, and only if, $\frac{th'_X(t)}{h_X(t)}$ is increasing (decreasing) in $t\geq 0$.

Proof. We give the proof of the non-parenthetical part, as the parenthetical part is similarly proved. Note that $X\in IRFR$ if, and only if, $\frac{\partial}{\partial t}\ln\left(\frac{h_X(t)}{h_X(\alpha t)}\right) \geq 0,$ for all $t\geq 0$ and for all $\alpha \in (0, 1)$, or equivalently if, $t \frac{\partial}{\partial t}\ln\left(\frac{h_X(t)}{h_X(\alpha t)}\right) \geq 0,$ $\forall\; t\geq 0$ and $\forall\; \alpha \in (0, 1)$. It is seen that

which is non-negative if, and only if, $\frac{th'_X(t)}{h_X(t)}\geq \frac{\alpha th'_X(\alpha t)}{h_X(\alpha t)},$ $\forall\; t\geq 0$ and $\forall\; \alpha \in (0, 1)$. This is also equivalent to saying that $\frac{th'_X(t)}{h_X(t)}$ is increasing in $t\geq 0$. The proof is completed. □

In the context of Proposition 3.4, it is notable that the monotonicity of $\frac{th'_X(t)}{h_X(t)}$ in $t\geq 0$ is important to make relative aging order among series systems (see, e.g., Theorem 7 in Li and Li ^[20] and also Theorems 4.8–4.10 in Ding and Zhang ^[11]). Li et al. ^[21] used the monotonicity of $\frac{th'_X(t)}{h_X(t)}$ in Theorems 5.1 and 5.2 of their work to establish some results on stochastic ordering of special order statistics in the scale model. Therefore, it seems that two lifetime distribution classes of $IRFR$ and $DRFR$ have a key role in establishing relative ordering properties of series and parallel systems in the reliability context. The shape of the hazard rate function is not identified when $X$ possesses either $IRFR$ property or $DRFR$ property. In spite of that, in Proposition 3.4, a function was found whose monotonicity characterizes the the $IRFR$ property and the $DRFR$ property of life distributions. However, the log-convexity and the log-concavity of a monotone hr function provide a relative aging behavior in the sense of the $IRFR$ and $DRFR$ properties. The following proposition clarifies the issue.

Proposition 3.5. Let $h_X$ be a differentiable function. $\;$

(i) If $h_X(t)$ is increasing and log-convex, then $X\in IRFR$.

(ii) If $h_X(t)$ is decreasing and log-concave, then $X\in DRFR$.

Proof. Denote $\gamma(t): = \frac{th'_X(t)}{h_X(t)}$. To prove (ⅰ), note that if $h_X(t)$ is increasing and log-convex, then $\frac{d}{dt}(\ln(h_X(t))) = \frac{h'_X(t)}{h_X(t)}$ is non-negative and increasing in $t\geq 0$. Thus, $\gamma(t) = t \frac{d}{dt}(\ln(h_X(t)))$, which is the multiplication of two non-negative increasing functions is also an increasing function in $t\geq 0$. From Proportion 3.4, it is deduced that $X\in IRFR$. In order to prove (ⅱ), set $\gamma^{\star}(t): = t.\frac{-h'_X(t)}{h_X(t)}$. Then, the proof is obtained if we show that $\gamma^{\star}(t)$ is increasing in $t\geq 0$. As $h_X(t)$ is decreasing and log-concave, then $\frac{d}{dt}(\ln(h_X(t)))$ is negative and decreasing in $t\geq 0$, and consequently, $-\frac{d}{dt}(\ln(h_X(t))) = \frac{-h'_X(t)}{h_X(t)}$ is non-negative and increasing in $t\geq 0$. Hence, $\gamma^{\star}(t) = t.\left(-\frac{d}{dt}(\ln(h_X(t)))\right)$ is also increasing in $t\geq 0$. The proof is thus obtained. □

From Proposition 3.5, it follows that if $\frac{\partial^{k}}{\partial t^{k}} \ln(h_X(t))\geq (\leq) \; 0,$ for $k = 1, 2$, then $X\in IRFR$ ($X\in DRFR$). It is to be mentioned here that the log-convexity of the hr function has been utilized by Burkschat ^[10] to obtain some dependence properties in multivariate settings.

It is known that $X\in IFR (X\in DFR)$ implies that $X\in IFRA (X\in DFRA)$. However, the converse is not true in general (see, e.g., Lai and Xie ^[19]). The following proposition provides a sufficient condition under which $X\in IFRA (X\in DFRA)$ yields $X\in IFR (X\in DFR)$.

Proposition 3.6. (i) Let $X\in IFRA$ and also $X\in IFR/A$. Then, $X\in IFR$.

(ii) Let $X\in DFRA$ and also $X\in DFR/A$. Then, $X\in DFR$.

Proof. Denote by $L_X$, the $AI$ function of $X$. Then, it is seen that

which is the product of two non-negative increasing functions provided that the conditions in (ⅰ) are satisfied. From (3.2), $h_X(t)$ is the product of two non-negative decreasing functions under the conditions given in (ⅱ). Hence, the proof is obviously validated. □

To highlight the importance of the presented classes of life distributions in Definition 3.1, some standard parametric families of distributions such as Weibull and gamma are considered in the sequel to see whether these distributions induce the $IRFR$ ($DRFR$) property and, consequently, the $IFR/A$ ($DFR/A$) property.

Example 3.1. Suppose that $X$ has Weibull distribution with shape parameter $c > 0$ and scale parameter $\lambda > 0$, having sf $\bar{F}_X(t) = \exp(-(\lambda t)^{c})$. It is seen that $\gamma(t) = \frac{th'_X(t)}{h_X(t)} = c-1,$ $\forall\; t\geq 0,$ which is constant. Therefore, $X$ simultaneously possesses the $IRFR$ and $DRFR$ properties. By using Proposition 3.3, $X$ also possesses the $IFR/A$ and $DFR/A$ properties. In view of Remark 3.2, the reader may see also Theorem 2.1 in Nanda et al. ^[25], which states that $X$ possesses both the $IFR/A$ and $DFR/A$ properties if, and only if, $X$ has Weibull distribution. This is an indication that, analogous to the exponential distribution that reports no aging, the Weibull distribution also shows that there is no relative aging phenomenon. More accurately, for the purpose of model selection, a life unit which does not experience any shocks and work routinely may have a random lifetime $X$ that follows Weibull distribution.

In some situations, a distribution is defined in terms of its density, but the distribution function and survival function cannot be given in closed form. In addition to the normal distribution, an example includes the gamma distribution. When neither the survival function nor the hazard rate can be given in closed form, a direct study of hazard rate behavior and also the relative aging property of the underlying distribution may not be particularly plain.

In the next example, we bring the gamma distribution as having DRFR and IRFR properties.

Example 3.2. Let $X$ have gamma distribution with shape parameter $b > 0$ and scale parameter $\lambda > 0$, having pdf $f_X(t) = \frac{1}{{\Gamma(b)}}\lambda^{b}t^{b-1}\exp(-\lambda t)$. Depending on the amount of the parameter $b$, for every $\lambda > 0,$ $\gamma(t) = \frac{th'_X(t)}{h_X(t)}$ is either increasing or decreasing in $t\geq 0,$ as we shall show in this example. Then, by using Proposition 3.4, either the $IRFR$ property or the $DRFR$ property holds. We have

It can be easily seen that

Therefore,

where after the second equality, the change of variable $y = x-t$ was made. We show that if $b\leq 1,$ then $\gamma(t)$ is increasing in $t\geq 0$. It will also be shown that if $b\geq 1,$ then $\gamma(t)$ decreases in $t\geq 0$. For $t\geq 0$, define a non-negative rv $Y(t)$ with pdf

It can be easily verified that for $b\leq 1$ (resp. $b\geq 1$) $(y+t)^{b-1} e^{-\lambda y}$ is $TP_2$ (resp. $RR_2$) in $(y, t) \in \mathbb{R}_{+}^{2}$. Thus, in the spirit of (3.4), we conclude that $Y(t_1) \leq_{lr} Y(t_2)$ (resp. $Y(t_1) \geq_{lr} Y(t_2)$), for all $t_1 \leq t_2 \in \mathbb{R}_{+}$. As the $\leq_{lr}$ order is stronger than the $\leq_{st}$ order, it follows that $Y(t_1) \leq_{st} Y(t_2)$ (resp. $Y(t_1) \geq_{st} Y(t_2)$), $\forall\; t_1 \leq t_2 \in \mathbb{R}_{+}.$ In view of (3.3), we have $\gamma(t) = E[\lambda Y(t)-1]$. Since $\phi(y) = \lambda y -1$ is increasing in $y\geq 0$, thus from definition, $E[\lambda Y(t_1)-1]\leq E[\lambda Y(t_2)-1],$ (resp. $E[\lambda Y(t_1)-1]\geq E[\lambda Y(t_2)-1]$), $\forall\; t_1 \leq t_2 \in \mathbb{R}_{+}$. Hence, if $b\leq 1$ (resp. $b\geq 1$), then $\gamma(t)$ is increasing (resp. decreasing) in $t\geq 0$, which reveals that the gamma distribution with the shape parameter $b$ and the scale parameter $\lambda$ has the $IRFR$ property and, as a result of Proposition 3.3, it also has the $IFR/A$ property when $b\leq 1$. In the case, where $b\geq 1$ it can be shown by a similar discussion that the gamma distribution has the $DRFR$ property and, further, the $DFR/A$ property.

4.   Preservation of $DRFR$ class of life distributions

The lifetime of a $(n-k+1)$-out-of-$n$ system with $n$ components with random lifetimes $X_1, \cdots, X_n$ is the $k$th-order statistic of $X_1, \cdots, X_n$. Denoting by $X_{1:n}, \cdots, X_{n:n}$ the ordered values of $X_1, \cdots, X_n$, the lifetime of a $(n-k+1)$-out-of-$n$ system is represented by $X_{k:n}$. In this paper, we will consider systems with homogenous independent components. Thus, it is assumed that $X_1, \cdots, X_n$ are $n$ non-negative rvs following a common absolutely continuous cdf $F_X$, the associated pdf $f_X$ and corresponding sf $\bar{F}_X$. Then, $X_{k:n}$ has pdf

and the sf of $X_{k:n}$ is obtained as

Definition 4.1. (Oliveira and Torrado ^[28]). Suppose that $X$ is a non-negative rv with pdf $f_X$ and cdf $F_X$ that is absolutely continuous. The reversed hazard rate function of $X$ is given by $\widetilde{h}_X = \frac{f_X(t)}{F_X(t)}$. Then, it is said that $X$ has a decreasing proportional reversed failure rate (written as $X\in DPRFR$) whenever $t\widetilde{h}_X(t)$ is decreasing in $t > 0$.

The preservation properties of aging concepts related to $(n-k+1)$-out-of-$n$ and coherent systems have been discussed in the literature, including works by Alimohammadi et al. ^[1], Alimohammadi and Navarro ^[2], Eryilmaz ^[8], Sahoo and Hazra ^[31], Tavangar ^[38], and Torrado ^[39], along with their references. Now, we show the following technical lemma, which is essential to get the main result of this section.

Lemma 4.1. If $X\in DFR/A$, then $X\in DPRFR$.

Proof. First, we show that $\varphi(u): = \frac{-u \ln(u)}{1-u}$ is increasing in $u\in (0, 1)$. We can see that

where $\phi(y) = 1+\ln(y)$, $Y_{u}$ is a non-negative rv with pdf $f_{Y_{u}}(y) = \frac{I[u < y < 1]}{\int_{0}^{1} I[u < y < 1] dy}$ and $I[A]$ represents the indicator function of the set $A$. Since $f_{Y_{u}}(y)$ is $TP_2$ in $(u, y)\in (0, 1)^{2},$ thus $Y_{u_1} \leq_{lr} Y_{u_2}$, for every $u_1\leq u_2 \in (0, 1)$, and therefore, $Y_{u_1} \leq_{st} Y_{u_2},$ for all $u_1\leq u_2 \in (0, 1)$. As $\phi(y) = 1+\ln(y)$ is an increasing function in $y \in (0, 1)$, from definition we obtain $E[\phi(Y_{u_1})] \leq E[\phi(Y_{u_2})], \; \forall\; u_1\leq u_2 \in (0, 1)$. This reveals that $\varphi$ is an increasing function. Now, let us write

Note that $\varphi(\bar{F}_X(t))$ is decreasing in $t > 0$ and also, by assumption, $L_X(t)$ is decreasing in $t > 0$. Hence, $t\widetilde{h}_X(t)$ is decreasing in $t > 0$, or equivalently, $X\in DPRFR$, which completes the proof of the lemma. □

The result of Lemma 4.1 may be of an independent interest. It is known that $X\in DFR$ yields $X\in DRHR$. However, from Lemma 4.1 it is obvious that $X\in DFR/A$ also yields $X\in DRHR$. This is because when $t\widetilde{h}_X(t)$ is decreasing in $t > 0$, $\widetilde{h}_X(t)$ is also decreasing in $t > 0$.

Next, we present a preservation property of the $DRFR$ class under $(n-k+1)$-out-of-$n$ structure, which reveals that if the lifetime of the components of a system with this structure possesses the $DRFR$ property, then the lifetime of the system also possesses the $DRFR$ property.

Theorem 1. Let $X$ be a non-negative rv with sf $\bar{F}_X$ and hazard rate function $h_X$. Let $X_1, \ldots, X_n$ be $n$ independent non-negative rvs, which are identically distributed ($n$ independent copies of $X$). If $X \in DRFR$, then $X_{k:n} \in DRFR, \; \forall\; k = 1, \ldots, n.$

Proof. By dividing (4.1) to (4.2), the hazard rate of $X_{k:n}$ is obtained as

□

By appealing to (4.3), one has:

where $\Psi(u) = \frac{u^{n-k+1}(1-u)^{k-1}}{\int_{0}^{u} y^{n-k}(1-y)^{k-1} dy},$ for $u\in (0, 1)$. It suffices to prove that $\frac{h_{X_{k:n}}(t)}{h_{X_{k:n}}(\alpha t)}$ is decreasing in $t\geq 0$, for every $\alpha \in (0, 1)$. In view of (4.4), one has

As the assumption $\frac{h_{X}(t)}{h_{X}(\alpha t)}$ is decreasing in $t\geq 0$, for every $\alpha \in (0, 1)$, we only need to prove that $\frac{\Psi(\bar{F}_X(t))}{\Psi(\bar{F}_X(\alpha t))}$ is decreasing in $t\geq 0$, for all $\alpha \in (0, 1)$. We show that if $X\in DFR/A$, then $\frac{\Psi(\bar{F}_X(t))}{\Psi(\bar{F}_X(\alpha t))}$ is decreasing in $t\geq 0$, for all $\alpha \in (0, 1)$. Since $X\in DRFR$ yields $X\in DFR/A$, thus the proof is obtained. By a similar method as in the proof of Proposition (3.4), by considering $\Psi(\bar{F}_X(t))$ in place of $h_X(t)$, it can be verified that $\frac{\Psi(\bar{F}_X(t))}{\Psi(\bar{F}_X(\alpha t))}$ is decreasing in $t\geq 0$, for all $\alpha \in (0, 1)$ if, and only if,

Thus, the proof is obtained if we show that

We have

From the assumption, $X\in DRFR$, which by Proposition 3.3, it implies that $X\in DFR/A$. By Lemma 4.1, $t\widetilde{h}_X(t)$ is decreasing in $t\geq 0$. The proof is then obtained by showing that

Set $\phi(u) = n-(n+1)u$ and denote by $U^{t}$, a non-negative rv that has pdf

Then,

It is easy to verify that $(1-u\bar{F}_X(t))^{k-1}$ is $TP_2$ in $(u, t) \in (0, 1) \times \mathbb{R}_{+}$. This concludes that $f_{U^t}(u)$ is $TP_2$ in $(u, t) \in (0, 1) \times \mathbb{R}_{+},$ or equivalently, $U^{t_1} \leq_{lr} U^{t_2}, \; \forall\; t_1 \leq t_2 \in \mathbb{R}_{+}$, which further implies that $U^{t_1} \leq_{st} U^{t_2}, \; \forall\; t_1 \leq t_2 \in \mathbb{R}_{+}.$ As $\phi(u)$ is a decreasing function, it is deduced that $E[\phi(U^{t_1})]\geq E[\phi(U^{t_2})],$ for all $t_1 \leq t_2 \in \mathbb{R}_{+}.$ The proof of the theorem is completed.

Next, we present an example to examine the correctness of the result of Theorem 1.

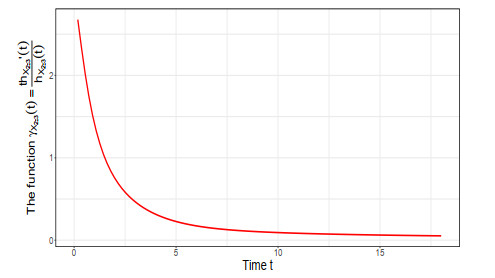
Example 4.1. Suppose that $X_1, X_2$ and $X_3$ are non-negative rvs, which represent the random lifetimes of three independent and identical components such that $X_i \sim G(2, \lambda), i = 1, 2, 3$. From Example 3.2, $X_1 \in DRFR.$ The sf and the hr function of $X_1$ is easily obtained as $\bar{F}_{X_1}(t) = (1+\lambda t)e^{-\lambda t}$ and $h_{X_1}(t) = \frac{\lambda^2 t}{1+\lambda t}$. Consider a 2-out-of-3 system composed of components with i.i.d. lifetimes $X_1, X_2,$ and $X_3$ having common gamma distribution with an specified shape parameter $b = 2$ and an unknown scale parameter $\lambda$. In this case, $k = 2$ and $n = 3$. The formula given in (4.3) reveals the hr function of $X_{2:3}$ as follows

from which one can develop that

The plot depicted in Figure 1 show that $\gamma_{X_{2:3}}(t)$ is a decreasing function which, in view of Proposition 3.4, confirms the result of Theorem 1 that $X_{2:3}\in DRFR$. Similarly, consider a parallel system with three components with i.i.d. lifetimes $X_1, X_2,$ and $X_3$, and so $k = n = 3$. From the hr's formula in (4.3), the hr function of $X_{3:3}$ is obtained as follows:

which further reveals that

In Figure 2, we also plot the graph of the function $\gamma_{X_{3:3}}(t)$. As is shown, this function is also decreasing in $t$ as was expected from Theorem 1. Hence, by Proposition 3.4, we deduce that $X_{3:3}\in DRFR.$

5.   Preservation of $DFR/A$ class of life distributions

In this section, we establish that a system with the $(n-k+1)$-out-of-$n$ structure enjoys the preservation property of the $DFR/A$ class. This property indicates that if the components of such kind of systems have lifetime distributions with $DFR/A$ property, then the lifetime of the system also has the $DFR/A$ property.

Theorem 2. Let $X$ be a non-negative rv with sf $\bar{F}_X$ and AI function $L_X$. Let $X_1, \cdots, X_n$ be $n$ independent and identically distributed ($n$ independent copies of $X$). If $X\in DFR/A$, then $X_{k:n}\in DFR/A,$ for any $k = 1, \ldots, n$.

Proof. From assumption, since $X\in DFR/A$, thus $L_X(t)$ is decreasing in $t\geq 0$. We need to show that if $L_X(t)$ is decreasing in $t\geq 0,$ then $L_{X_{k:n}}(t)$ is also decreasing in $t\geq 0$. Let $\Psi(x) = \frac{x^{n-k+1}(1-x)^{k-1}}{\int_{0}^{x} y^{n-k}(1-y)^{k-1} dy},$ for $x\in (0, 1)$ as defined in the proof of Theorem 1. Then, in view of (4.2), one can write

Using (4.4) and (5.1), we obtain

where $\Psi^{\star}(u): = \frac{-\ln(u)\Psi(u)}{\int_{u}^{1} \frac{\Psi(x)}{x}\; dx}.$ So, by using the relationship among the AI function of $X$ and the AI function of $X_{k:n}$ as revealed in (5.3), the proof is obtained if we prove that $\Psi^{\star}(\bar{F}_X(t))$ is decreasing in $t\geq 0$. Equivalently, it can be shown that $\Psi^{\star}(u)$ is increasing in $u\in (0, 1)$. This is also equivalent to showing that $\Psi^{\star}(e^{-t})$ is decreasing in $t\geq 0$. We have

where the second equality is due to a change of variable as $y = -\ln(u)$, the third equality follows as a result of a change of variable as $\alpha = \frac{y}{t}$, and $T$ is a non-negative rv with exponential distribution with mean one. As $L_T(t) = 1,$ for all $t\geq 0$, therefore, $T \in DFR/A$. As clarified and proved in the proof of Theorem 1, for an arbitrary continuous life distribution $F_T$ where $T\in DFR/A$, it is deduced that $\frac{\Psi(\bar{F}_T(t))}{\Psi(\bar{F}_T(\alpha t))}$ is decreasing in $t\geq 0$, for all $\alpha \in (0, 1)$, which is equivalent to saying that $\frac{\Psi(\bar{F}_T(\alpha t))}{\Psi(\bar{F}_T(t))}$ is increasing in $t\geq 0,$ for all $\alpha \in (0, 1)$. By applying this into (5.3), it follows that $\Psi^{\star}(e^{-t})$ is decreasing in $t\geq 0$. The proof of theorem is thus completed. □

The following example presents a situation where Theorem 2 is applicable. To be more specific, we consider the distribution function given in Counterexample 3.2.

Example 5.1. Suppose that $X$ is a non-negative rv with sf $\bar{F}_X$ and hr function $h_X,$ as given in Counterexample 3.2. Then, we consider a 2-out-of-3 system with i.i.d. component lifetimes (3 independent copies of $X$). The sf and the hr function of $X_{2:3}$ can be obtained from (4.2) and (4.3), respectively. We have

We plot the graph of the function $L_{X_{2:3}}(t) = \frac{th_{X_{2:3}}(t)}{-\ln(\bar{F}_{X_{2:3}}(t))}$ in Figure 3. As it is depicted, this function decreases with time, which confirms the result of Theorem 2, i.e., $X_{2:3}\in DFR/A$. If we consider a parallel system with i.i.d. component lifetimes as three independent copies of $X$, then the sf and the hr function of $X_{3:3}$ are acquired by (4.2) and (4.3), respectively, as follows:

In Figure 4, we also plot the graph of $L_{X_{3:3}}(t)$, where it is shown that this function is decreasing in $t$, which again validates the result obtained in Theorem 2. Hence, it was verified that $X_{3:3}\in DFR/A$.

It is worth mentioning here that, since the DFR/A class is equivalent to the decreasing aging intensity (DAI) class, the result of Theorem 2 confirms that the claim raised by Nanda et al. ^[25] in their counterexample 2.7 is not correct.

6.   Conclusions

The rate (or speed) of aging is generally related to time and can either increase or decrease with time; however, it can also be stable and not fluctuate. Barlow and Proschan ^[4] introduced this concept by considering members of a class of life distributions, such as the IFR class, and then defining some partial stochastic orderings to compare these members in terms of the degree of their IFR property. Nevertheless, the concept of the speed of aging is not limited to the members of specific life distribution classes. For example, the lifetime of an electrical device may exhibit a decreasing hazard rate during an initial time interval, e.g., $[0, \tau_0)$, with a decreasing rate of aging, and then its hazard rate increases at an increasing rate as time passes $[\tau_0, \infty)$. In this paper, we have focused on several monotonic aging classes from which the concept of aging rate is derived. Some interrelationships between these aging classes and some connections between these classes and other known non-parametric classes of life distributions proposed in the literature are validated. This paper concludes that, in addition to some well-known aging classes such as IFR and IFRA, some lesser-known classes of life distributions that incorporate the concept of aging rate are also preserved under the structure of $(n-k+1)$-out-of-$n$ systems. This may provide new insights for reliability engineers and system designers.

In future studies, preservation properties of the aforementioned classes of lifetime distributions will be considered under a range of reliability operations such as monotone transformations, shock models, mixing, and convolution. The aging properties of coherent systems or at least $(n-k+1)$-out-of-$n$ systems with possibly dependent component lifetimes will also be investigated.

Author contributions

Mohamed Kayid: Conceptualization, methodology, writing-original draft; Mansour Shrahili: writing-review and editing, software, validation. All authors contributed equally to the manuscript. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors would like to thank the anonymous reviewers for their helpful comments and feedback, which greatly strengthened the overall manuscript. The authors acknowledge financial support from the Researchers Supporting Project number (RSP2024R464), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

There is no conflict of interest.