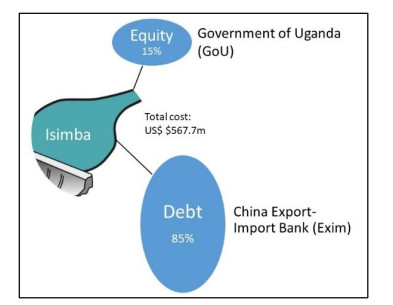
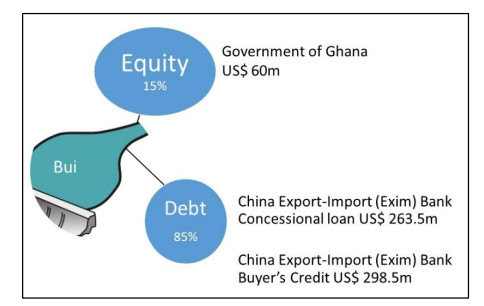
The structure and key actors in large hydropower project financing has changed considerably over the past 50 years, particularly in low and lower-middle income countries (LICs and L-MICs). Exclusively public projects, typically financed by the host country government with support from multilateral development banks (MDBs), have become less common, while public-private-partnerships (PPPs) and new forms of bilateral finance arrangements have become more prevalent. However, fully privately financed projects with no public or MDB finance remain unusual in large hydropower projects. This paper traces the evolution and complexity of hydropower financing in LICs and L-MICs from the early 1970s to the present day, showing how the types and roles of various actors have changed over time and how new types of financing packages have surfaced to meet the growing need for large energy infrastructure projects. Examples from various LICs and L-MICS are used to describe the features of three of the most commonly used models of hydropower project financing: fully public finance, PPPs, and new bilateral finance. Comparative assessment of the key characteristics of different financing models and their strengths and limitations is provided to enable LICs and L-MICs to make informed choices over the allocation of their scarce financing resources in their struggle to balance urgent development needs with long-term sustainability objectives and economic impacts.
1.
Introduction
Let V be an ℓ-dimensional vector space over a field K of characteristic 0. An arrangement of hyperplanes A is a finite collection of codimension one affine subspaces in V. An arrangement A is called central if every hyperplane H∈A goes through the origin.
Let V∗ be the dual space of V, and S=S(V∗) be the symmetric algebra over V∗. A K-linear map θ:S→S is called a derivation if for f,g∈S,
Let DerK(S) be the S-module of derivations. When A is central, for each H∈A, choose αH∈V∗ with ker(αH)=H. Define an S-submodule of DerK(S), called the module of A-derivations by
The arrangement A is called free if D(A) is a free S-module. Then, D(A) has a basis comprising of ℓ homogeneous elements. For an affine arrangement A in V, cA denotes the cone over A [7], which is a central arrangement in an (ℓ+1)-dimensional vector space by adding the new coordinate z.
Let E=Rℓ be an ℓ-dimensional Euclidean space with a coordinate system x1,…,xℓ, and let Φ be a crystallographic irreducible root system in the dual space E∗. Let Φ+ be a positive system of Φ. For α∈Φ+ and k∈Z, define an affine hyperplane Hα,k by
The Shi arrangement Shi(ℓ) was introduced by Shi in the study of the Kazhdan-Lusztig representation theory of the affine Weyl groups in [9] by
when the root system is of type Aℓ−1.
For m∈Z≥0, the extended Shi arrangement Shik of the type Φ is an affine arrangement defined by
There are a lot of researches on the freeness of the cones over the extended Shi arrangements [1,3,4]. The first breakthrough was the proof of the freeness of multi-Coxeter arrangements with constant multiplicities by Terao in [13]. Combining it with algebro-geometric method, Yoshinaga proved the freeness of the extended Shi arrangements in [15]. Nevertheless, there has been limited progress in constructing their bases, and a universal method for determining these bases remains elusive. For types Aℓ−1, Bℓ, Cℓ, and Dℓ, explicit bases for the cones over the Shi arrangements were constructed in [6,10,11]. Notably, a basis for the extended Shi arrangements of type A2 was established in [2]. Recently, Suyama and Yoshinaga constructed explicit bases for the extended Shi arrangements of type Aℓ−1 using discrete integrals in [12]. Feigin et al. presented integral expressions for specific bases of certain multiarrangements in [5]. In these studies, Suyama and Terao first constructed a basis for the derivation module of the cone over the Shi arrangement, as detailed in [11], with Bernoulli polynomials playing a central role in their approach. The following definitions are pertinent to this result.
For (k1,k2)∈(Z≥0)2, the homogenization polynomial of degree k1+k2+1 is defined by
where Bk(x) denotes the k-th Bernoulli polynomial and Bk(0)=Bk denotes the k-th Bernoulli number. Using this polynomial, the basis for D(cShi(ℓ)) was constructed as follows.
Theorem 1.1. [11, Theorem 3.5] The arrangement cShi(ℓ) is free with the exponents (0,1,ℓℓ−1). The homogeneous derivations
form a basis for D(cShi(ℓ)), where 1≤j≤ℓ−1 and ∂i(1≤i≤ℓ), ∂z denote ∂∂xi, ∂∂z respectively. Ik[u,v] represents the elementary symmetric function in the variables {xu,xu+1,…,xv} of degree k for 1≤u≤v≤ℓ.
The above conclusion was reached by using Saito's criterion, which is a crucial theorem for determining the basis of a free arrangement.
Theorem 1.2. [8, Saito's criterion] Let A be a central arrangement, and Q(A) be the defining polynomial of A. Given θ1,…,θℓ∈D(A), the following two conditions are equivalent:
(1)detM(θ1,…,θℓ)≐Q(A),
(2)θ1,…,θℓ form a basis for D(A) over S,
where M(θ1,…,θℓ)=(θj(xi))ℓ×ℓ denotes the coefficient matrix, and A≐B means that A=cB, c∈K∖{0}.
This theorem provides a useful tool for determining when a set of derivations forms a basis for the module of derivations associated with a central arrangement.
Let αℓ=(1,…,1)T and βℓ=(x1,…,xℓ)T be the ℓ×1 column vectors, and define ψ(ℓ)i,j:=ψ(ℓ)j(xi) for 1≤i≤ℓ, 1≤j≤ℓ−1. Suyuma and Terao in [11] proved the equality
which yields
A graph G=(V,E) is defined as an ordered pair, where the set V={1,2,…,ℓ} represents the vertex set, and E is a collection of two-element subsets of V. If {i,j}∈E for some i,j∈V, then {i,j} is referred to as an edge. Writing {i,j}∈G implies {i,j}∈E. Let U⊆V, and define E(U)={{i,j}∣i,j∈U,{i,j}∈E}. We say U induces a subgraph GU=(U,E(U)). Specifically, we use the symbol KU for the induced subgraph of the complete graph Kℓ. For i<j, the interval notation [i,j] represents {i,i+1,…,j}.
For a graph G on the vertex set {1,2,…,ℓ}, the arrangement Shi(G) was defined in [14] by
Then, Shi(G) is an arrangement between the Linial arrangement
and the Shi arrangement Shi(ℓ). Write A(G):=cShi(G). It was classified to be free according to the following theorem.
Theorem 1.3. [14, Theorem 3] The arrangement A(G) is free if and only if G consists of all edges of three complete induced subgraphs G[1,s],G[t,ℓ],G[2,ℓ−1], where 1≤s≤ℓ, t≤s+1. The free arrangement A(G) has exponents (0,1,(ℓ−1)ℓ+t−s−2,ℓs−t+1) for s<ℓ and t>1, and (0,1,ℓℓ−1) for s=ℓ or t=1.
For s,t∈Z+, we may define the arrangement
By Theorem 1.3, for 1≤s≤ℓ and t≤s+1, the arrangement A[s,t] is free with exponents (0,1,(ℓ−1)ℓ+t−s−2,ℓs−t+1) for s<ℓ and t>1, and (0,1,ℓℓ−1) for s=ℓ or t=1.
For 0≤q≤ℓ−2, we write A[q]:=A[ℓ−1,ℓ−q], then A[q] is free with exponents (0,1,(ℓ−1)ℓ−q−1,ℓq).
2.
Main results
In this section, based on the conclusions of Suyama and Terao, we provide an explicit construction of the basis for D(A[q]), 0≤q≤ℓ−2. First, we shall establish a basis for D(A[0]), which is the ingredient of the basis for D(A[q]).
Theorem 2.1. For 1≤j≤ℓ−2, define homogeneous derivations
where
Then, the derivations η1,η2,φ(0)1,…,φ(0)ℓ−1 form a basis for D(A[0]).
Proof. Write φ(0)i,j:=φ(0)j(xi),1≤i≤ℓ,1≤j≤ℓ−1, and from the definitions of φ(0)j and ψ(ℓ)j, we can get
for 1≤i≤ℓ−1, 1≤j≤ℓ−2. Consequently, for 1≤m<n≤ℓ−1, it follows that φ(0)j(xm−xn) is divisible by xm−xn, and φ(0)j(xm−xn−z) is divisible by xm−xn−z. For 1≤m≤ℓ−1, let the congruence notation (m,k)≡ in the subsequent calculation denote modulo the ideal (xm−xℓ−kz). We derive
which implies that φ(0)j(xm−xℓ−z) is divisible by xm−xℓ−z. Thus, φ(0)j∈D(A[0]) for 1≤j≤ℓ−2. Therefore, we have η1,η2,φ(0)1,…,φ(0)ℓ−1∈D(A[0]). Additionally, we obtain
According to the equalities (1.1) and (2.1), we have
Hence, we obtain
By applying Theorem 1.2, we conclude that the derivations η1,η2,φ(0)1,…,φ(0)ℓ−1 form a basis for D(A[0]). □
Definition 2.1. For 1≤q≤ℓ−2, 1≤j≤ℓ−1, define the homogeneous derivations
To prove the derivations η1,η2,φ(q)1,…,φ(q)ℓ−1 form a basis for D(A[q]), first we prove all such derivations belong to the module D(A[q]).
Theorem 2.2. For 1≤m≤ℓ−1, 1≤j≤ℓ−2, we have
Proof. We have the following congruence relation of polynomials modulo the ideal (xm−xℓ).
We complete the proof. □
Remark 2.1 In equality (2.2), we observe that ℓ−1∏s=j+2(xs−xm)=0 for j+2≤m≤ℓ−1. This implies that φ(0)j(xm−xℓ) is divisible by xm−xℓ for 1≤j≤ℓ−3 and j+2≤m≤ℓ−1.
According to Remark 2.1, for 1≤j≤ℓ−q−2, we have φ(0)j(xm−xℓ) is divisible by xm−xℓ for ℓ−q≤m≤ℓ−1, which implies that φ(q)j=φ(0)j∈D(A[q]). Therefore, to prove the derivations belong to the module D(A[q]), it suffices to prove φ(q)j∈D(A[q]) for ℓ−q−1≤j≤ℓ−1.
For the sake of convenience in the proof, let us introduce the notations for f,g,h∈Z+,
If g>h, we agree that A[g,h]f=B[g,h]f=1.
Lemma 2.1. For any u,v,w∈Z+ that satisfy 4≤ℓ−j+1≤u≤ℓ−2, 3≤v≤ℓ−2, and 3≤w≤ℓ−2, we have the following three equalities:
Proof. We will only prove equality (2.5) by induction on w. The proofs of equalities (2.3) and (2.4) are similar. For w=3,
and the equality holds. Assume that for w=k≤ℓ−3, the equality holds. Then, we replace xℓ−k−1 with xℓ−k−2, and multiply both sides of the equality by (xℓ−k−1−xℓ−k−2−z) to get
We have completed the induction. □
Lemma 2.2. The derivation φ(q)j belongs to the module D(A[q]) for 2≤q≤ℓ−2 and ℓ−q−1≤j≤ℓ−3.
Proof. For 2≤q≤ℓ−2 and j=ℓ−q−1, it is evident from Remark 2.1 that
For 3≤q≤ℓ−2 and ℓ−q≤j≤ℓ−3, we will establish this by induction on q. From Theorem 2.2, for ℓ−q≤m≤ℓ−1, we have
(1) For q=3, we get
If m=ℓ−3,ℓ−2,ℓ−1, then we have φ(3)ℓ−3(xm−xℓ)(m,0)≡0, which indicates that φ(3)ℓ−3(xm−xℓ) is divisible by xm−xℓ for m=ℓ−3,ℓ−2,ℓ−1. Therefore, φ(3)j∈D(A[3]).
(2) For q=k≤ℓ−3, assume that φ(k)j∈D(A[k]), which implies that φ(k)j(xm−xℓ) is divisible by xm−xℓ for ℓ−k≤m≤ℓ−1.
For q=k+1, we observe that
According to the induction hypothesis and Remark 2.1, it is sufficient to prove that φ(k+1)j(xℓ−k−1−xℓ) is divisible by xℓ−k−1−xℓ. By using the equality (2.3), we obtain
Therefore, φ(k+1)j(xℓ−k−1−xℓ) is divisible by xℓ−k−1−xℓ, and it follows that φ(k+1)j∈D(A[k+1]). Consequently, we can conclude that for any 3≤q≤ℓ−2 and ℓ−q≤j≤ℓ−3, φ(q)j∈D(A[q]). □
Lemma 2.3. The derivation φ(q)ℓ−2 belongs to the module D(A[q]) for 1≤q≤ℓ−2.
Proof. From Theorem 2.2, we can get the following equality for ℓ−q≤m≤ℓ−1,
(1) For q=1,2, this conclusion is straightforward to verify.
(2) For q=k≤ℓ−3, assume that φ(k)ℓ−2∈D(A[k]), which implies that φ(k)ℓ−2(xm−xℓ) is divisible by xm−xℓ for ℓ−k≤m≤ℓ−1.
For q=k+1, we have
By using the equality (2.4), we have
Therefore, φ(k+1)ℓ−2(xℓ−k−1−xℓ) is divisible by xℓ−k−1−xℓ. According to the induction hypothesis and Remark 2.1, we have φ(k+1)ℓ−2∈D(A[k+1]). Hence, we may conclude that for any 1≤q≤ℓ−2, φ(q)ℓ−2∈D(A[q]).
□
Lemma 2.4. The derivation φ(q)ℓ−1 belongs to the module D(A[q]) for 1≤q≤ℓ−2.
Proof. First, from Theorem 2.2, for ℓ−q≤m≤ℓ−1, we can get
(1) For q=1,2, it is obvious that φ(q)ℓ−1∈D(A[q]).
(2) For q=k≤ℓ−3, assume that φ(k)ℓ−1∈D(A[k]), which implies that φ(k)ℓ−1(xm−xℓ) is divisible by xm−xℓ for ℓ−k≤m≤ℓ−1.
For q=k+1, we can see
By using the equality (2.5), we have
Therefore, φ(k+1)ℓ−1(xℓ−k−1−xℓ) is divisible by xℓ−k−1−xℓ. According to the induction hypothesis and Remark 2.1, we have φ(k+1)ℓ−1∈D(A[k+1]). Hence, we may conclude that for any 1≤q≤ℓ−2, φ(q)ℓ−1∈D(A[q]). □
From the above proof, we finally conclude that φ(q)1,…,φ(q)ℓ−1 belong to the module D(A[q]).
Theorem 2.3. For 1≤q≤ℓ−2, the derivations η1,η2,φ(q)1,…,φ(q)ℓ−1 form a basis for D(A[q]).
Proof. According to Lemmas 2.2–2.4, it suffices to prove that
Let
and
be the (q+1)×1 column vectors, and define a matrix
Write ˜M(q+1)×(q+1):=(M(q+1)×(q−1),γ1,γ2), then
Thus, we obtain the following equality
Hence,
We complete the proof. □
Author contributions
Meihui Jiang: writing-original draft; Ruimei Gao: writing-review and editing, methodology and supervision. All authors have read and approved the final version of the manuscript for publication.
Use of Generative-AI tools declaration
The authors declare they have used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The work was partially supported by Science and Technology Development Plan Project of Jilin Province, China (No. 20230101186JC) and NSF of China (No. 11501051).
Conflict of interest
The authors declare no conflict of interest in this paper.













 DownLoad:
DownLoad: