Optical environmental sensing in wireless smart meter network

Minglong Zhang; Iek Cheong Lam; Arun Kumar; Kin Kee Chow; Peter Han Joo Chong; Minglong Zhang; Iek Cheong Lam; Arun Kumar; Kin Kee Chow; Peter Han Joo Chong

doi:10.3934/ElectrEng.2018.3.103

AIMS Electronics and Electrical Engineering

2018, Volume 2, Issue 3: 103-116. doi: 10.3934/ElectrEng.2018.3.103

Previous Article Next Article

Research article Special Issues

Optical environmental sensing in wireless smart meter network

1.
Department of Electrical and Electronic Engineering, Auckland University of Technology, New Zealand
2.
School of Engineering, Manchester Metropolitan University, United Kingdom
3.
School of Electrical and Computer Engineering, National University of Singapore, Singapore

Received: 11 July 2018 Accepted: 04 October 2018 Published: 12 October 2018

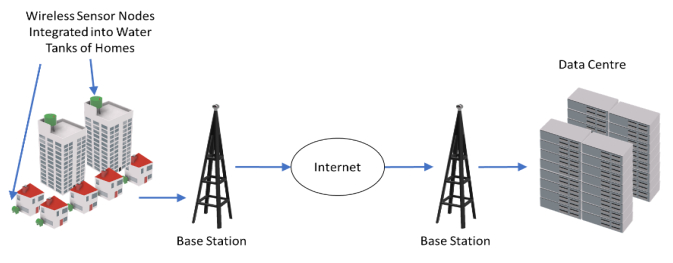
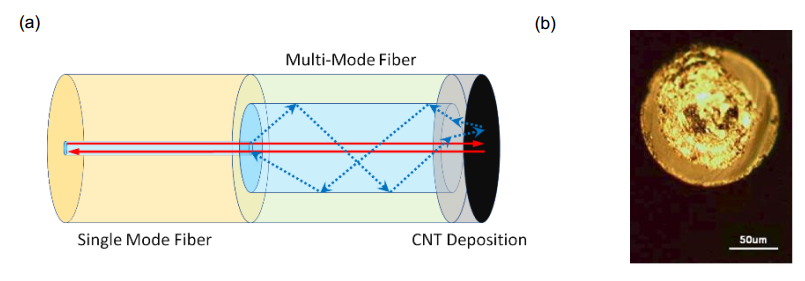
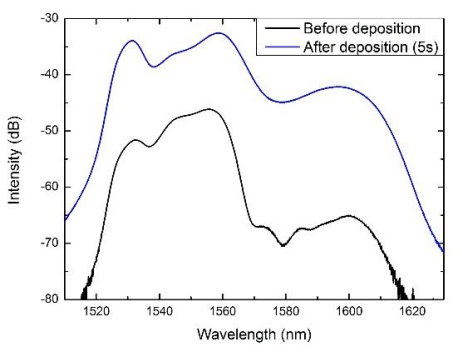
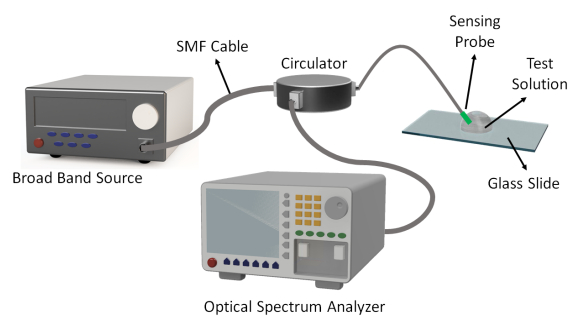
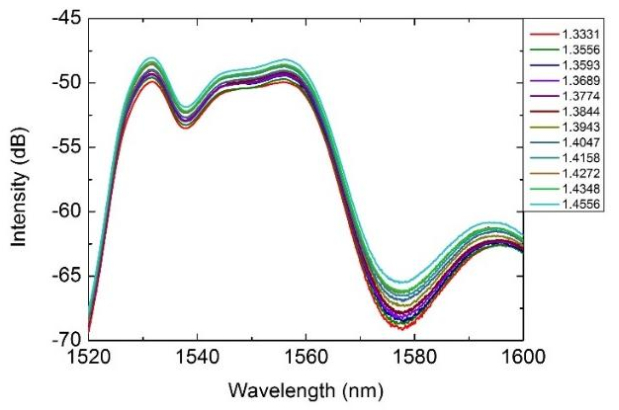
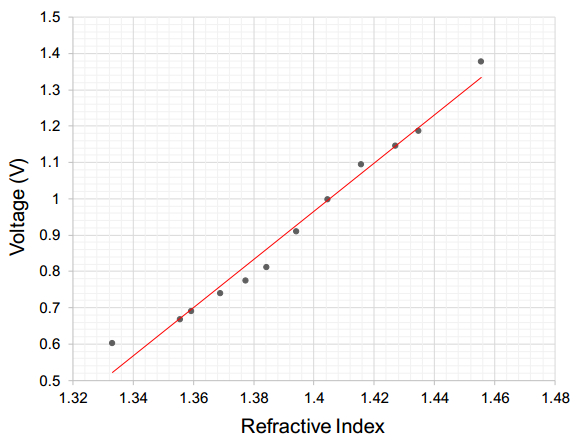
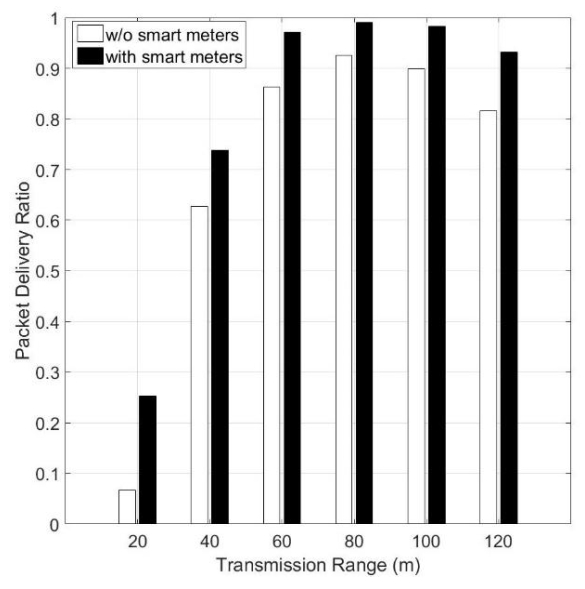
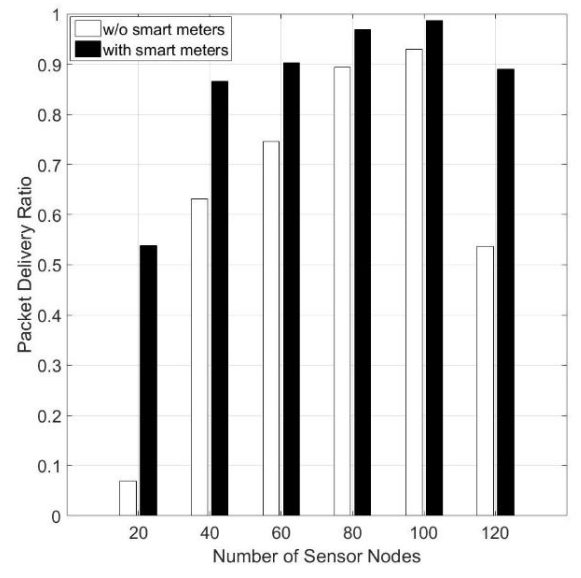
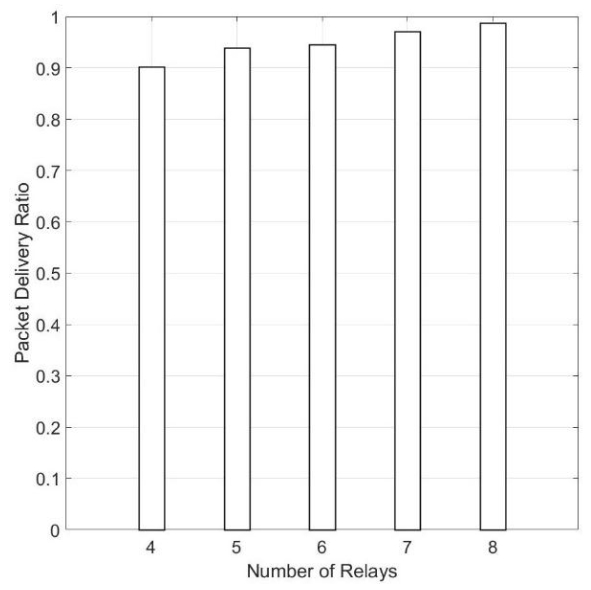
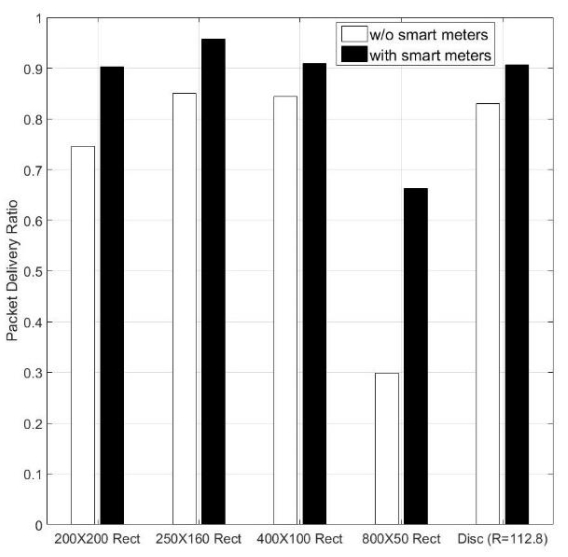
In recent years, the traditional power grid is undergoing a profound revolution due to the advent and development of smart grid. Many hard and challenging issues of the traditional grid such as high maintenance costs, poor scalability, low efficiency, and stability can be effectively handled and solve in the wireless smart grid (WSG) by utilizing the modern wireless sensor technology. In a WSG, data are collected by sensors at first and then transmitted to the base station through the wireless network. The control centre is responsible for taking actions based on this received data. Traditional sensors are failing to provide accurate and reliable data in WSG, and optical fiber based sensor are emerging as an obvious choice due to the advancement of optical fiber sensing technology, accuracy, and reliability. This paper presents a WSG platform integrated with optic fiber-based sensors for real-time monitoring. To demonstrate the validity of the concept, fresh water sensing of refractive index (RI) was first experimented with an optical fiber sensor. The sensing mechanism functions with the reflectance at the fiber’s interface where reflected spectra’s intensity is registered corresponding to the change of RI in the ambient environment. The achieved sensitivity of the fabricated fiber sensor is 29.3 dB/RIU within the 1.33–1.46 RI range. An interface between the measured optical spectra and the WSG is proposed and demonstrated, and the data acquired is transmitted through a network of wireless smart meters.

Keywords:

Citation: Minglong Zhang, Iek Cheong Lam, Arun Kumar, Kin Kee Chow, Peter Han Joo Chong. Optical environmental sensing in wireless smart meter network[J]. AIMS Electronics and Electrical Engineering, 2018, 2(3): 103-116. doi: 10.3934/ElectrEng.2018.3.103

Related Papers:

[1]	Xinpeng Xu, Xuedong Tian, Fang Yang . A retrieval and ranking method of mathematical documents based on CA-YOLOv5 and HFS. Mathematical Biosciences and Engineering, 2022, 19(5): 4976-4990. doi: 10.3934/mbe.2022233
[2]	Xue Wang, Fang Yang, Hongyuan Liu, Qingxuan Shi . Error correction of semantic mathematical expressions based on bayesian algorithm. Mathematical Biosciences and Engineering, 2022, 19(6): 5428-5445. doi: 10.3934/mbe.2022255
[3]	Songlin Liu, Shouming Zhang, Zijian Diao, Zhenbin Fang, Zeyu Jiao, Zhenyu Zhong . Pedestrian re-identification based on attention mechanism and Multi-scale feature fusion. Mathematical Biosciences and Engineering, 2023, 20(9): 16913-16938. doi: 10.3934/mbe.2023754
[4]	Yuting Zhu, Wenyu Zhang, Junjie Hou, Hainan Wang, Tingting Wang, Haining Wang . The large-scale group consensus multi-attribute decision-making method based on probabilistic dual hesitant fuzzy sets. Mathematical Biosciences and Engineering, 2024, 21(3): 3944-3966. doi: 10.3934/mbe.2024175
[5]	Nian Zhang, Yifan Zhou, Qiang Pan, Guiwu Wei . Multi-attribute decision-making method with triangular fuzzy numbers based on regret theory and the catastrophe progression method. Mathematical Biosciences and Engineering, 2022, 19(12): 12013-12030. doi: 10.3934/mbe.2022559
[6]	Muhammad Akram, G. Muhiuddin, Gustavo Santos-García . An enhanced VIKOR method for multi-criteria group decision-making with complex Fermatean fuzzy sets. Mathematical Biosciences and Engineering, 2022, 19(7): 7201-7231. doi: 10.3934/mbe.2022340
[7]	Jin Wang, Liping Wang, Ruiqing Wang . MFFLR-DDoS: An encrypted LR-DDoS attack detection method based on multi-granularity feature fusions in SDN. Mathematical Biosciences and Engineering, 2024, 21(3): 4187-4209. doi: 10.3934/mbe.2024185
[8]	Nian Zhang, Xue Yuan, Jin Liu, Guiwu Wei . Stochastic multiple attribute decision making with Pythagorean hesitant fuzzy set based on regret theory. Mathematical Biosciences and Engineering, 2023, 20(7): 12562-12578. doi: 10.3934/mbe.2023559
[9]	Fankang Bu, Jun He, Haorun Li, Qiang Fu . Interval-valued intuitionistic fuzzy MADM method based on TOPSIS and grey correlation analysis. Mathematical Biosciences and Engineering, 2020, 17(5): 5584-5603. doi: 10.3934/mbe.2020300
[10]	Yefu Zheng, Jun Xu, Hongzhang Chen . TOPSIS-based entropy measure for intuitionistic trapezoidal fuzzy sets and application to multi-attribute decision making. Mathematical Biosciences and Engineering, 2020, 17(5): 5604-5617. doi: 10.3934/mbe.2020301

Abstract

1. Introduction

Most existing search engines support text retrieval, but still have problems retrieving mathematical expressions, especially expressions without natural language annotations. While traditional search engines are losing their roles in this respect, recent research on mathematical expression retrieval has achieved relatively rich results ^[1,2,3,4,5].

Focusing on mathematical expressions in LaTeX format, Zhong et al. ^[6] proposed a mathematical formula retrieval algorithm based on Operator Tree. By matching multiple disjoint common subtrees with the same structure, the maximum number of sub-formulas is matched, which improves the efficiency of formula matching. Although the maximum number of matching sub-forms can improve retrieval accuracy, most sub-forms are more complicated. Therefore, the response time of real-time retrieval is approximately 20 s, which cannot meet the needs of real-time mathematical formula retrieval. To achieve faster sub-formulas retrieval, the team also proposed a strategy based on an inverted index and dynamic pruning ^[7], which improves the time efficiency of retrieval while ensuring that the retrieval results are still valid.

Focusing on mathematical expressions in MathML format, Schubotz et al. ^[8] proposed the VMEXT system, which can realize a visual tree of expressions in MathML format. It can also realize human-computer interaction, which is convenient for users to quickly find and improve the expression tree. In addition, similar or identical elements of two expressions can be visualized to calculate the similarity of expressions.

Focusing on mathematical expression images, Davila et al. ^[9] proposed a mathematical formula matching system. The system is mainly aimed at matching handwritten formulas on the teaching whiteboard with the formulas in course notes. First, the entire image was preprocessed, including formula search and structure correction. Then, the largest match in each image was identified by the symbolic consistent spatial alignment and similar relative sizes. Finally, each mathematical formula was divided into multiple symbol pairs. Symbol pairs are two symbols in a formula that are the nearest geometric neighbor of each other, which indicates the logical relations between them. The angle of a symbol pair is the angle between the line connecting the centers of the symbols and a horizontal line, which is helpful for judging the relationship between the two symbols. The images were sorted by the angle of the symbol pair.

With the development of deep learning, text embedding methods are widely used in natural language processing. Gao et al. ^[10] tried to apply the same method to formula embedding. They applied neural networks to mathematical information retrieval and proposed the "symbol2vec" model. This model was used to learn the vector representation of mathematical symbols and perform similarity calculations. Similarly, the NTFEM model ^[11] used an N-ary tree to convert the mathematical formula into a linear sequence. The word embedding model is used to embed the formula, and a weighted average embedding vector is obtained by using a weighting function. In mathematical formula retrieval, the BERT (bidirectional encoder representations from transformer)-based embedding model ^[12] is proposed to introduce more semantic information when the formula is embedded. The model uses the LaTeX format as the input and the BERT model is used to encode the formula. The index is built according to the embedded formula vector, formula id and post id from which the formula originates, and finally, the cosine similarity is used to obtain the final ranking of the formula.

In terms of fusion retrieval and ranking of mathematical expressions and scientific documents, Pathak et al. ^[13,14,15] committed to fusing expressions and related texts for retrieval. First, they proposed the MathIR system composed of three modules: "TS", "MS" and "TMS". This made scientific documents retrieval a similarity calculation of expression and text fusion rather than a simple expression search. Next, the "context-formula" pair was extracted, and the context of the formula was merged for retrieval. Finally, the modules of the system were optimized, and the formula retrieval was effectively integrated with the retrieval module for the text. Similarly, Schubotz et al. ^[16] regarded formulas and natural text as a single information source. The description of mathematical formula symbols was extracted from the surrounding text of the formula. These mathematical symbol descriptions were used to represent the definition of mathematical symbols. The namespace was formed as an internal data structure for mathematical information retrieval. This method can eliminate the ambiguity of mathematical symbols and better meet the retrieval needs of users. While retrieving mathematical expressions, Wang et al. ^[17] integrated other attributes to rank scientific documents, such as document category, types of journals to which scientific documents belong, and document citations. The sorting results were optimized by fusing these attributes of scientific documents. To better integrate mathematical expressions and text in scientific document retrieval, a weight parameter was proposed ^[18]. Based on formula similarity and text similarity, the proportion of text and mathematical expressions is manually adjusted.

In conclusion, current scientific document retrieval and ranking methods could be roughly divided into two types, the first type recalls by mathematical expression similarity and sorts by text similarity or recalls by text similarity and sorts by expression similarity. Regardless of what kind of similarity is used for the final sorting, it will weaken the similarity of another part. The second type manually adjusts the weight to fuse expression similarity and text similarity, but this method is difficult for users with less experience to control the specific values of the parameters. To solve the above problem, this study proposes a multi-attribute retrieval and ranking model of scientific documents that combines mathematical expressions and related texts. This model is an improvement of the second type, and can eliminate the need to manually adjust the weights of expressions and texts.

The similarity of five attributes is calculated: mathematical expression symbols (MESY), mathematical expression sub-forms (MESF), mathematical expression context (MECT), scientific document keywords (SDKY) and the frequency of mathematical expressions in scientific documents (FOME). A gradient boosting decision tree (GBDT) and logistic regression (LR) are used for feature reorganization and calculation to obtain the final search results, which improves the rationality of the retrieval.

2. Overview

Figure 1 shows a flow chart of the scientific documents retrieval and ranking system (solid lines denote online query flows and dotted lines denote offline index flows). The whole process consists of four parts: query preprocessing, scientific document preprocessing, multi-attribute similarity measure and scientific document retrieval and ranking.

Figure 1. Flow chart of the scientific documents retrieval and ranking system.

DownLoad: Full-Size Img PowerPoint

The query preprocess module is used to process the input query. The query is a combination of mathematical expressions and text, which need to be split. The scientific document preprocessing module is used to extract mathematical expressions and related text, preliminarily decompose mathematical expression symbols and calculate the weights of related text. Then, the module interacts with the database module to store and index the information corresponding to the scientific documents to facilitate subsequent similarity calculations. The multi-attribute similarity measure module calculates the similarity of the five attributes of scientific documents. According to the different characteristics of each attribute, different similarity calculation algorithms are set up. The module interacts with the database module to store the calculated similarity. The scientific document retrieval and ranking module combines the similarity of the multiple attributes of scientific documents to fuse and calculate the attributes. Finally, the similarity between the scientific documents and the input query is obtained, and the scientific documents are ranked according to the similarity.

3. Multi-attribute similarity calculation of scientific documents

3.1. Similarity calculation of mathematical expression symbols (MESY)

For the retrieval of mathematical expressions, there will be problems when inputting query expressions, such as inaccurate input and incorrect input of mathematical symbols. It is necessary to retrieve each mathematical symbol one by one to improve the fault-tolerant performance of the system.

Definition 1 $M{E_{\text{Q}}}$ is the query expression, $M{E_{{\text{D}}t}}(t = 1, 2, ..., {T_{{\text{ME}}}})$ is the mathematical expression dataset from the scientific documents, and ${T_{{\text{ME}}}}$ is the number of mathematical expressions in the dataset.

First, FDS ^[19] is used to normalize the mathematical expressions in various formats into a unified form by decomposing them into multiple mathematical symbols with the corresponding five attribute values called level, flag, count, ratio, and operator.

The "level" attribute represents the level of a mathematical symbol, based on its position relative to the horizontal baseline. For example, in the mathematical expression $\frac{{{b^2}}}{a}$ , the level values of $\frac{\square }{\square }$ , a, b and 2 are 0, 1, 1 and 2, respectively. "Flag" represents the spatial flag bit of a symbol. Table 1 shows the value of the flag taking x as an example. "Count" refers to the sequential position of a symbol in the mathematical expression. "Ratio" refers to the frequency of the operator in the mathematical expression. "Operator" refers to whether a mathematical symbol is an operator. If a symbol is an operator, it is marked as 1; otherwise, it is marked as 0.

Table 1. Examples of flag value.

Meaning of flag	Right	Above	Superscript	Subscript	Below	Contains	Left-superscript	Left-subscript
Example	$2x$	$\frac{x}{2}$	${2^x}$	${2_x}$	$\frac{2}{x}$	$\sqrt x$	${}^x2$	${}_x2$
Value of the flag of x	0	1	2	3	4	5	6	7

| Show Table

DownLoad: CSV

In this way, the mathematical expression is converted into a list, which is convenient for subsequent retrieval of expression symbols. shows the membership functions of the five attributes ^[20]. According to the distribution of values in each attribute by symbols in the data set, the balance factors in the function is determined by using curve fitting. The values of each balance factor are as follows. $\alpha = 0.1$ , $\mu = 0.2$ , $\nu = 0.9$ , $\sigma = 0.2$ .

Table 2. Description of the five attribute membership functions.

Attribute	Membership function	Function description
level	${{M} _{lev}}({T_D}, {T_Q}) = {e^{ - \alpha \left\| {leve{l_D} - leve{l_Q}} \right\|}}$	$leve{l_D}$ and $leve{l_Q}$ respectively represent the level of two terms. $\alpha$ is the balance factor
flag	${{M} _{fla}}({T_D}, {T_Q}) = \left\{ {\left({{f_o}, fla{g_{\left({D, Q} \right)}}} \right)} \right\}$	$fla{g_{\left({D, Q} \right)}}$ refers to the spatial position relationship of the same term, if $fla{g_D}$ = $fla{g_Q}$ , then ${{M} _{fla}}({T_D}, {T_Q}) = 1$ , otherwise it is 0.
count	${{M} _{cou}}({T_{\text{D}}}, {T_{\text{Q}}}) = \frac{1}{{1 + \mu {{\left\| {coun{t_D} - coun{t_{Q} }} \right\|}^\upsilon }}}$	$\mu、\upsilon$ are balance factors
ratio	${{M} _{{\text{rat}}}}({T_{\text{D}}}, {T_{\text{Q}}}) = {e^{ - {{(\frac{{ra{t_{\text{D}}} - ra{t_{\text{Q}}}}}{\sigma })}^2}}}$	$\sigma$ is the balance factor
operator	${{M} _{ope}}({T_D}, {T_Q}) = \left\{ {({s_o}, operato{r_D})} \right\}$	$operato{r_D}$ refers to whether the current term is an operator, If it is an operator, the value of ${{M} _{ope}}({T_D}, {T_Q})$ is 1, otherwise the value is 0.5

| Show Table

DownLoad: CSV

After the membership calculation is completed, each symbol corresponds to a five-tuple membership degree vector, denoted by $lis{t_{sym}}$ . The structure of $lis{t_{sym}}$ is shown in Eq (1).

$lis{t}_{sym} = \left({M}_{{\rm{lev}}\_ex\_term}, {M}_{{\rm{fla}}\_ex\_term}, {M}_{{\rm{cou}}\_ex\_term}, {M}_{{\rm{rat}}\_ex\_term}, {M}_{{\rm{ope}}\_ex\_term}\right)$

(1)

where the term refers to the current mathematical symbol and ex refers to the expression id corresponding to the current mathematical symbol.

Take $M{E_{\text{Q}}}$ = " $x + \sqrt x$ " and $M{E_{{\text{D}}t}}$ = " ${x^2} + y$ " as examples. The three mathematical symbols that are the same in the two expressions are " $x$ ", " $+$ " and " $x$ ". Table 3 shows the attribute values and membership degrees after the decomposition of the three symbols.

Table 3. Membership values of the five attributes in "

$x + \sqrt x$ " and "

${x^2} + y$ ".

Term	level	${M_{{\text{lev}}}}$	flag	${M_{fla}}$	count	${M_{{\text{cou}}}}$	ratio	${M_{rat}}$	operator	${M_{{\text{ope}}}}$
$x$	(0, 0)	1	(0, 0)	1	(1, 1)	1	(0.25, 0.25)	1	(0, 0)	0.5
$+$	(0, 0)	1	(0, 0)	1	(2, 3)	0.8333	(0.25, 0.25)	1	(1, 1)	1
$x$	(1, 0)	0.9048	(5, 0)	0	(4, 1)	0.6503	(0.5, 0.25)	0.2096	(0, 0)	0.5

| Show Table

DownLoad: CSV

Next, hesitant fuzzy sets ^[21,22,23] are used to calculate the membership degree of each mathematical symbol. Hesitant fuzzy sets have advantages in dealing with multi-attribute decision-making problems. The formula for calculating the similarity of expressions using hesitant fuzzy sets is shown in Eq (2).

Finally, the normalization calculation of the mathematical symbols is performed to obtain the similarity of the expressions. The specific algorithm is shown in Algorithm 1.

Algorithm 1 Similarity calculation algorithm of mathematical expressions based on mathematical symbols

INPUT:

$M{E_{\rm{Q}}}$ ,

$M{E_{{\text{D}}t}}(t = 1, 2, ..., {T_{{\text{ME}}}})$
OUTPUT:

$Si{m_{{\text{Symbol}}}}$
1

$ter{m_{\rm{Q}} } = {\text{FDS}}(M{E_{\rm{Q}}})$
2

$ter{m_{\rm{D}} } = {\text{FDS}}\left({M{E_{{\text{D}}t}}} \right)$
3 Update

$lis{t_{\rm{D}}}^\prime$ //

$tre{m_{\rm{sym\_vec}}}$ calculation of the five attributes of the same term in

$ter{m_{\rm{D}} }$ and

$ter{m_{\text{Q}}}$ ,

$tre{m_{\rm{sym\_vec}}}$ is updated in the

$lis{t_{\rm{D}}}^\prime$ together with the id and term in the

$ter{m_{\rm{D}} }$ .
4

${\text{for }}id {\text{ in (1, }}{T_{\rm{ME}}}{\text{):}}$
5

${\text{for }}ter{m_1}{\text{ in }}ter{m_{\text{Q}}}:$
6

$var = lis{t_{\rm{D\_id}}}.{\text{exists(}}ter{m_1}{\text{)}}$
7

${\text{if }}var = {\rm{TRUE}}$ :
8

$lis{t_{{\text{D}}\_id}}.{\text{add}}[MAX{(\frac{{ter{m_{\rm{sym\_vec}}}^2}}{5})^{\frac{1}{2}}}]$ //If the same term exists in the

$lis{t_{\text{D}}}$ , take the one with the greatest similarity
9

$lis{t_{\rm{D}}}^\prime.{\rm{delete}} [MAX{(\frac{{ter{m_{\rm{sym\_vec}}}^2}}{5})^{\frac{1}{2}}}]$ //Delete the corresponding item in the

$lis{t_{\rm{D}}}^\prime$
10 else:
11

$lis{t_{{\text{D}}\_id}}.add(0, 0, 0, 0, 0)$ //If it does not exist, add (0, 0, 0, 0, 0).
12

$Si{m_{{\text{Symbol}}}} = {\rm{SIM}}(lis{t_{\rm{D}}}, lis{t_{\rm{Q}}})$
13 END

| Show Table

DownLoad: CSV

Definition 2 $lis{t_{\text{D}}}$ refers to a normalized list of mathematical symbols. $lis{t_{\text{D}}}$ includes id, term, and five attribute membership values $tre{m_{\rm{sym\_vec}}}$ . $list{}_Q$ refers to the $lis{t_{\text{D}}}$ formed by calculating the membership degree with $M{E_{\rm{Q}}}$ itself, and the five-attribute membership degree of mathematical symbols in $list_{\rm{Q}}$ is (1, 1, 1, 1, 1).

Definition 3 The formula ^[20] for calculating $Si{m_{{\text{Symbol}}}}$ in Algorithm 1 is shown in Eq (2).

$SIM(lis{t_{\rm{D}}}, lis{t_{\rm{Q}}}) = 1 - {\left\{ {\frac{1}{5}\sum {\left[ {\frac{1}{{{N_{{\text{RE}}}}}}\sum\limits_{j = 1}^{{N_{RE}}} {{{\left| {{M_{D} } - {{M_{\rm{Q}}}}} \right|}^\lambda }} } \right]} } \right\}^{1/\lambda }}$

(2)

where ${M_{\rm{D}}}$ and ${{M_{\rm{Q}}}}$ are the five-tuple vector values with the same term in $lis{t_{\rm{D}}}$ and $lis{t_{\rm{Q}}}$ respectively; ${N_{\rm{RE}}}$ is the number of mathematical symbols of $M{E_{\rm{Q}}}$ after FDS decomposition; $\lambda > 0$ . When $\lambda$ = 1, the formula degenerates to the standard Hamming distance. When $\lambda$ = 2, the formula degenerates to the standard euclidean distance. In this study, $\lambda$ = 2.

Take the two mathematical expressions in as an example, we suppose that $x + \sqrt x$ is query and ${x^2} + y$ is the mathematical expression with id = 1 in the data set. Algorithm 1 is used to calculate the similarity of these two expressions. The result of the first update of $lis{t_{\rm{D}}}^\prime$ is {[1, $x$ , (1, 1, 1, 1, 0.5)], [1, +, (1, 1, 0.8333, 1, 1)], [1, $x$ , (0.9048, 0, 0.6503, 0.2096, 0.5)]}. Next, the $lis{t_{\text{D}}}$ is updated in the order of terms in the query, and the result is {[1, $x$ , (1, 1, 1, 1, 0.5)], [1, +, (1, 1, 0.8333, 1, 1)], [1, $\sqrt {}$ , (0, 0, 0, 0, 0)], [1, $x$ , (0.9048, 0, 0.6503, 0.2096, 0.5)]}. Finally, formula (2) is used for similarity calculation and ${N_{{\text{RE}}}} = 4$ , ${M_{\rm{D}}}$ = [(1, 1, 1, 1, 0.5), (1, 1, 0.8333, 1, 1), (0, 0, 0, 0, 0), (0.9048, 0, 0.6503, 0.2096, 0.5)], ${M_{\text{Q}}}$ = [(1, 1, 1, 1, 1), (1, 1, 1, 1, 1), (1, 1, 1, 1, 1), (1, 1, 1, 1, 1)].The final calculated SIM = 0.1425.

3.2. Mathematical expression sub-form similarity calculation (MESF)

The mathematical expression sub-form similarity calculation refers to the retrieval of $M{E_{\rm{Q}}}$ as a whole object. $M{E_{\rm{Q}}}$ is equivalent to a part of $M{E_{{\text{D}}t}}(t = 1, 2, ..., {T_{{\text{ME}}}})$ . The degree of membership of $M{E_{Q} }$ to the three attribute values of $M{E_{{\text{D}}t}}$ is calculated. The three attributes are length, level and flag. "Length" refers to the ratio of the length of the sub-formula to the length of the expression. The meaning of level and flag are the same as 2.1. Table 4 shows the membership functions corresponding to the three attributes ^[16].

Table 4. Three attribute descriptions and membership functions of

$M{E_{\text{Q}}}$ as a sub-form.

Attribute	Attribute description	Membership function
length	The length of ${\text{M}}{{\text{E}}_{{\text{D}}t}}$	${\text{D}}{{\text{M}}_{{\text{len}}}}({\text{M}}{{\text{E}}_{\text{Q}}}{\text{, M}}{{\text{E}}_{{\text{D}}t}}) = \frac{{lengt{h_{\rm{Q}} }}}{{lengt{h_{{\rm{D}} t}}}}$
level	The level of ${\text{M}}{{\text{E}}_Q}$ relative to ${\text{M}}{{\text{E}}_{{\text{D}}t}}$	${\text{D}}{{\text{M}}_{lev}}({{ME} _Q}, M{E_{Dt}}) = {e^{ - \alpha \cdot leve{l_Q}}}$
flag	The flag of ${\text{M}}{{\text{E}}_Q}$ relative to ${\text{M}}{{\text{E}}_{{\text{D}}t}}$	${\text{D}}{{\text{M}}_{fla}}({\text{M}}{{\text{E}}_{\text{Q}}}{\text{, M}}{{\text{E}}_{{\text{D}}t}}) = \left\{ {\left({{f_o}, fla{g_Q}} \right)} \right\}$

| Show Table

DownLoad: CSV

A mathematical expression may contain multiple identical sub-expressions. After the membership of each attribute is calculated, the hesitant fuzzy set is used to calculate the similarity. It is the final similarity of the sub-form of $M{E_{\rm{Q}}}$ as $M{E_{{\text{D}}t}}(t = 1, 2, ..., {T_{{\text{ME}}}})$ . The specific algorithm is shown in Algorithm 2.

Algorithm 2 Similarity calculation algorithm based on mathematical expression as sub-form

INPUT:

$M{E_{Q} }$ ,

$M{E_{{\text{D}}t}}(t = 1, 2, ..., {T_{{\text{ME}}}})$
OUTPUT:

$Si{m_{{\text{Sub}}}}$
1

$M{E}_{\mathrm{MA}t}=M{E}_{\text{Dt}}.\mathrm{Replace}(M{E}_{Q}, "\#")$ // Use # to replace the same string as

${\text{M}}{{\text{E}}_Q}$
2 Num=

$M{E_{MAt}}$ .Count("#")
3

${T_{MAt}} = {\text{FDS}}(M{E_{MAt}})$
4

${\text{for }}ter{m_{ma}}{\text{ }}in{\text{ }}{T_{MAt}}:$
5

$\mathrm{if}\text{ }ter{m}_{ma}=="\#":$
6

$lis{t_{MAt}}.add\left({D{M_{len}}, D{M_{lev}}, D{M_{fla}}} \right)$
7

$si{m_{ma}} = 1 - {\left\{ {\frac{1}{3}\sum {\left[{\frac{1}{{Num}}\sum\limits_{j = 1}^{Num} {{{\left| {lis{t_{Q}} - list{}_{MAt}} \right|}^\lambda }} } \right]} } \right\}^{\frac{1}{\lambda }}}$
8

$lis{t_{MA}}(id, {E_{sim}}).add({T_{MAt}}.id, si{m_{ma}})$ //add the mathematical expression id and similarity to

$lis{t_{MA}}$ in turn
9

$Si{m_{{\text{sub}}}} = lis{t_{MA}}.{sort} ()$ // sort () using the Built-in function in python
10 RETURN

$Si{m_{{\text{Sub}}}}$
11 END

| Show Table

DownLoad: CSV

Definition 4 $D{M_{len}}, D{M_{lev}}, D{M_{fla}}$ represent the membership value of the three attributes length, level, and flag, respectively.

3.3. Contextual text similarity calculation of mathematical expressions (MECT)

BERT (bidirectional encoder representations from transformer) ^[22,23,24] is a pre-training language model that uses unsupervised data for pre-training and fine-tuning on the task corpus, and has excellent performance on tasks for understanding natural language. There are two tasks in the model pre-training phase: masked language mode and next sentence prediction. The joint training of these two tasks makes the word vector obtained by training more accurate and comprehensive. It can solve the polysemy problem that cannot be solved in word2vec.

This study uses mathematical expression contextual text to fine-tune BERT to achieve the similarity calculation of the contextual text. The specific algorithm is shown in Algorithm 3.

Algorithm 3 Contextual text similarity calculation algorithm

INPUT:

$S{E_{Q} }$ ,

$S{E_{{\text{D}}t}}(t = 1, 2, ..., {T_{{\text{SE}}}})$ //

$S{E_{\text{Q}}}$ is the query text.

${T_{{\text{SE}}}}$ is the number of keywords in sentence
OUTPUT:

$Si{m_{{\text{CT}}}}$
1

${V_{E} }{\text{ = Encode(}}S{E_{\text{Q}}}{\text{)}}$ // Sentence embedding to

$S{E_{\text{Q}}}$
2

$WO{R_{\text{Q}}} = {\text{jieba(}}S{E_{\text{Q}}}{\text{)}}$ // The jieba tool (an open word segmentation tool) in python is used to segment

$S{E_{\text{Q}}}$
3

${\text{for }}WO{R_r}{\text{ in }}WO{R_{\text{Q}}}:$
4

$number = {\text{location}}(WO{R_r})$ // Target each keyword
5

${V_w} = {\rm{summed\_layers}} [number]$ // Find word vectors in

${V_E}$
6

$simil = simil + {\rm{MAX}}({\rm{cosine\_similarity}}({V_{w} }, S{E_{{\text{D}}t}}))$
7

$Si{m_{CT}} = simil/{\rm{len}} (WO{R_{\text{Q}}})$
8 RETURN

$Si{m_{\rm{CT}}}$
9 END

| Show Table

DownLoad: CSV

3.4. Similarity calculation of other attributes of scientific documents

3.4.1. Similarity calculation of scientific document keywords (SDKY)

The Jaccard coefficient is used to calculate the similarity of two sets $({G_A}, {G_B})$ . It is expressed as the ratio of the intersection and union of the two sets, and can effectively calculate the degree of overlap between the two sets to obtain the similarity of the sets. Its definition is shown in Eq (3).

${\rm{Jaccard}} ({G_A}, {G_B}) = \frac{{\left| {{G_A} \cap {G_B}} \right|}}{{\left| {{G_A} \cup {G_B}} \right|}} = \frac{{\left| {{G_A} \cap {G_B}} \right|}}{{\left| {{G_A}} \right| + \left| {{G_B}} \right| - \left| {{G_A} \cap {G_B}} \right|}}$

(3)

Each scientific document often contains a specific topic. The keywords of the documents are extracted, and similarity matching with the query words can improve the accuracy of the search results. The contents of the scientific document are divided into words. By calculating the weight of the words, the 5 words with the highest weights are selected as the keywords of the scientific document. The weight calculation method is shown in Eq (4).

${W_{i, wor}} = \frac{{{p_{i, wor}}}}{{\sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {{p_{n, k}}} } }} \cdot \lg \frac{N}{{1 + {m_{wor}}}}$

(4)

where ${W_{i, wor}}$ refers to the weight of the keyword wor in scientific document i, ${p_{i, wor}}$ refers to the total number of times wor appears in i. N refers to the total number of scientific documents. k refers to the number of keywords in the current scientific document. ${m_{wor}}$ refers to the number of documents containing wor.

Since the difference in text length will affect the calculated keyword similarity, this study improves the Jaccard coefficient and adds the length difference part. The calculation of similarity is shown in Eq (5).

$Si{m_{\rm{Wor}}} = {\rm{Jaccard}} (S{E_{\text{Q}}}{, }W{E_{{\text{DT}}}}) = \frac{{\left| {S{E_{\text{Q}}} \cap W{E_{{\text{DT}}}}} \right|}}{{\left| {S{E_{\text{Q}}}} \right| + \left| {W{E_{{\text{DT}}}}} \right| - \left| {S{E_{\text{Q}}} \cap W{E_{{\text{DT}}}}} \right| + \phi \left| {{\rm{len}}(S{E_{\rm{Q}}}) - {\rm{len}}(W{E_{\rm{DT}}})} \right|}}$

(5)

where $W{E_{{\text{DT}}}}$ refers to the keyword collection of scientific documents, and $\phi$ is the balance factor.

3.4.2. The frequency of mathematical expressions in scientific documents (FOME)

When retrieving scientific documents, the same mathematical expression appears differently in different scientific documents, and the importance and retrieval order of scientific documents are also different.

The frequency of mathematical expressions in scientific documents is the product of the frequency of mathematical expressions in the document (EF) and the inverse document frequency (EIDF), which is similar to TFIDF. The difference is that when the text frequency is calculated, the query text must be exactly the same as the text in the document before the text can be considered to appear once. In the process of searching for mathematical expressions, partially identical expressions can also be considered to appear once. For example, when ${\text{M}}{{\text{E}}_Q}$ is $U = IR$ , the appearance of $U = IR$ or $I = \frac{U}{R}$ in a scientific document can be counted as one occurrence of the mathematical expression.

The frequency of occurrence of mathematical expression $M{E_{\rm{Q}}}$ refers to $Si{m_{\rm{Symbol}}}$ and $Si{m_{\rm{Sub}}}$ to calculate.

The frequency of expressions is related to the total number of mathematical expressions in the scientific document. The more expressions contained in the scientific document, the smaller the value of EF. The calculation method of EF is shown in Eq (6).

$EF = \frac{1}{{1 + {e^{ - \frac{{{ROUND} (Si{m_{\rm{Symbol}}}) + {ROUND} (Si{m_{\rm{Sub}}}) - {NUM} (Si{m_{\rm{Symbol}}}.\exp \cap Si{m_{\rm{Sub}}}.\exp )}}{{Do{c_{num}}}}}}}}$

(6)

where $Do{c_{num}}$ refers to the total number of mathematical expressions in the scientific document. ${\text{ROUND()}}$ refers to the rounding function with 0.5 as the demarcation point, and a value greater than 0.5 is recorded as 1; otherwise. it is 0. $Si{m_{{\text{symbol}}}}.\exp$ refers to the expression corresponding to $Si{m_{{\text{symbol}}}}$ . NUM () calculates the number of the same expressions recalled by $Si{m_{{\text{symbol}}}}$ and $Si{m_{{\text{sub}}}}$ .

The calculation of EIDF requires the number of occurrences of ${\text{M}}{{\text{E}}_Q}$ in the dataset. If ${\text{M}}{{\text{E}}_Q}$ appears multiple times in different scientific documents, its importance will decrease accordingly. The calculation method of the EIDF is shown in Eq (7).

$EIDF = \log \left( {\frac{{\text{N}}}{{{\text{INCLUDE}}(exp) + 1}}} \right)$

(7)

where N refers to the total number of scientific documents in the data set, ${INCLUDE} (exp)$ refers to the number of scientific documents containing exp. The specific calculation of ${INCLUDE} (exp)$ is shown in Eq (8).

${INCLUDE} (\exp ) = \left\{ {\begin{array}{*{20}{c}} {1{\text{ ROUND(Si}}{{\text{m}}_{symbol}}{\text{)}} \vee {\text{ROUND(Si}}{{\text{m}}_{sub}}{\text{) = }}1} \\ {0{\text{ ROUND(Si}}{{\text{m}}_{symbol}}{\text{)}} \wedge {\text{ROUND(Si}}{{\text{m}}_{sub}}{\text{) = 0}}} \end{array}} \right.$

(8)

Finally, the calculation method of the frequency of mathematical expressions in scientific documents is shown in Eq (9).

$Si{m_{fre}} = EF \cdot EIDF$

(9)

4. Multi-attribute integration of scientific documents

The LR (logistic regression) model is based on linear regression plus sigmoid function (non-linear) mapping. It is shown as (10).

${h_\theta }\left( x \right) = \frac{1}{{1 + {e^{ - {\theta ^T}x}}}}$

(10)

where ${\theta ^T}x$ is the input of the sigmoid, and $\theta$ and x are both matrices. $\theta$ is the linear regression parameter. T refers to the transpose of matrix. x refers to the feature of the input.

The LR model has a simple structure and fast running speed, but the learning ability and expression ability of the LR model are very limited. A large amount of feature engineering is required for feature dispersion and feature combination to increase the learning ability of the model. Therefore, an approach is needed for automatically discovering effective features and feature combinations and shortening the LR feature experiment cycle. The GBDT model can automatically discover features and carry out effective feature combinations.

GBDT (gradient boosting decision tree) ^{[25,26,27,28]} is a boosted tree model based on the CART regression tree model. In the process of generating each tree, the residual of the previous tree is calculated. The next tree is fitted on the basis of the residuals so that the residuals obtained on the next tree decrease. It is shown in Eq (11).

${f_{CTM}}(x) = \sum\limits_{m = 1}^{CTM} {{T} (x;{\psi _m})}$

(11)

where ${T} (x; {\psi _m})$ refers to the CART regression tree, ${\psi _m}$ refers to the parameters of CART, CTM refers to the number of CART.

The GBDT model construction algorithm is shown in Algorithm 4.

Algorithm 4 GBDT

INPUT

$T = \left\{ {\left({{x_1}, {y_1}} \right), \left({{x_2}, {y_2}} \right), ..., \left({{x_N}, {y_N}} \right)} \right\}$ // Training dataset
OUTPUT

${f_{CTM}}(x)$
1

${f_0}(x) = 0$ // Initialization
2

$L(y, f(x)) = {(y - f(x))^2}$   // Define loss function
3    for m in (1, CTM):
4

${r_{mi}} = {\left[{\frac{{\partial L\left({{y_i}, f\left({{x_i}} \right)} \right)}}{{\partial f({x_i})}}} \right]_{f(x) = {f_{m - 1}}(x)}}$ // The gradient of the i-th sample on the m-th tree
5

${R_{mj}}, j = 1, 2, ..., J$ // The leaf node area of the m-th tree
6

${c_{mj}} = \arg {\min _c}\sum\nolimits_{{x_i} \in {R_{mj}}} {L\left({{y_i}, {f_{m - 1}}({x_i}) + c} \right)}$ // Best fit value for leaf area j
7

${f_m}\left(x \right) = {f_{m - 1}}\left(x \right) + \sum\nolimits_{j = 1}^J {{c_{mj}}I}$
8 RETURN

${f_{CTM}}\left(x \right) = \sum\nolimits_{m = 1}^{CTM} {\sum\nolimits_{j = 1}^J {{c_{mj}}I} }$
9 END

| Show Table

DownLoad: CSV

In this study, a GBDT + LR model is used. The five attributes MESY, MESF, MECT, SDKY and FOME are selected. GBDT can automatically combine and discretize features. After the decision tree is established, the path from the root node to each leaf node is a combination of different features. Each leaf node represents a unique combination of features. After the combination is completed, it is transferred to the LR model for secondary training.

As shown in , $Tre{e_1}$ and $Tre{e_2}$ are two GBDT trees. $si{m_{\text{Symbol}}}$ , $si{m_{\text{Sub}}}$ , $si{m_{{\text{CT}}}}$ , $si{m_{\rm{math\_fre}}}$ and $si{m_{{\text{Wor}}}}$ are represented by S1, S2, S3, S4 and S5 in the figure respectively.

Figure 2. GBDT model diagram.

DownLoad: Full-Size Img PowerPoint

The sample ${x^T}$ is judged by two tree nodes and belongs to different leaf nodes of the two trees. The leaf nodes of the two trees are coded. The leaf nodes to which sample ${x^T}$ belongs are marked as 1, and the others are marked as 0. The leaf node codes of the two trees are connected in series to form a seven-dimensional sample (1, 0, 0, 1, 0, 0, 0).

Each ${x^T}$ will go through multiple GBDT trees to recombine features. For GBDT trees, the path from the root node of the tree to the leaf nodes is a combination of different features. Therefore, the leaf node can uniquely represent this path. The leaf node is input into the LR model as a discrete feature for training.

In the final prediction, the input sample will pass through each tree of GBDT to obtain a discrete feature (a set of feature combinations) corresponding to a certain leaf node. Then, the feature is passed into LR in one-hot form for linear weighted prediction. The final similarity SIM calculation result is obtained. Figure 3 shows the specific flow chart. For the LR model, the L2 penalty term is used, and the value of the inverse of regularization strength is 0.05. For the GBDT model, the metric is "binary_logloss", num_leaves is 32, num_trees' is 60 and the learning_rate is 0.005.

Figure 3. GBDT + LR system flow chart.

DownLoad: Full-Size Img PowerPoint

5. Experimental results and analysis

5.1. Experimental data and environment

The dataset used in the experiment is "MathTagArticles" in NTCIR-12_MathIR_Wikipedia_Corpus, which includes 31742 scientific documents. The "MathTagArticles" includes 16 archive files (they are coded as wpmath0000001-wpmath0000016), and each archive file contains about 2000 scientific documents. In this study, the hold-out method is used: "wpmath0000001-wpmath0000008" are used for training, "wpmath0000008-wpmath0000012" are used for verification, "wpmath0000013-wpmath0000016" are used for testing. Table 5 shows the experimental environment.

Table 5. Experimental environment.

Experimental environment	Configuration
Processor	Intel(R) Xeon(R) Silver 4215 CPU @ 2.50GHz
RAM	32GB
Operating system	Linux
Graphics card	GeForce RTX 2080
Video memory	8G
Python version	3.6
TensorFlow version	1.14.0

| Show Table

DownLoad: CSV

5.2. Evaluation protocol

5.2.1. Relevance ratings

The evaluators are five mathematics graduate students who are familiar with mathematical expressions and scientific documents. For each set of queries, the top 10 results are selected for evaluation. The evaluation indicators are relevant, partially relevant and not relevant. Among them, relevant ones are marked as 2, partially relevant ones are marked as 1, and not relevant ones are marked as 0. The results of the same query will be marked separately by five evaluators. Different evaluators should not mark the same retrieval result too differently. For example, for the same search result, when some commenters are marked as 2, other commenters can mark 1 or 2, but cannot mark 0. So, another labeling rule is set: for the same result, the difference between the scores of different evaluators should be less than or equal to 1. If it is greater than 1, the marks are invalid.

Finally, the results of the five evaluators are summarized. The reviewer's score is converted to a comprehensive score in Table 6. Based on the principle of obedience to the majority, a total score greater than 7 is considered relevant, a total score greater than 2 is considered partially relevant, otherwise it is not relevant. In the subsequent evaluation of results, if the evaluation metrics only require relevant and not relevant, the partial relevant will default to relevant.

Table 6. Relevance assessment.

Assessment	Individual	Combined
Relevant	2	8−10
Partially Relevant	1	3−7
Not Relevant	0	0−2

| Show Table

DownLoad: CSV

5.2.2. Test case

This study conducts a large number of experiments on different types of mathematical expressions and related texts. Twenty representative query expressions and texts are selected by evaluators for statistical experiments. Queries are based on the actual situation of the mathematics set, integrating the different structures of mathematical expressions and the different fields involved in scientific and technological documents. Table 7 provides the query expressions and text.

Table 7. 20 queries in system experiment.

NO.	Expression	Text	NO.	Expression	Text
1	$\sqrt {{b^2} - 4ac}$	discriminant	11	$\frac{1}{2}m{v^2}$	theorem of kinetic energy
2	${\sin ^2}\alpha + {\cos ^2}\alpha$	trigonometric function	12	$f\left(x \right) = \sum\limits_{n = 0}^\infty {\frac{{{f^{(n)}}\left({{x_0}} \right)}}{{n!}}} {\left({x - {x_0}} \right)^n}$	Taylor function
3	$\frac{a}{b}$	proportion	13	${\left({x - a} \right)^2} + {\left({y - b} \right)^2} = {r^2}$	round
4	$\sin \theta$	sine function	14	$U = IR$	Ohm law
5	${{\text{y}}^2} = 2\rho x$	parabola	15	${a^2} + {b^2} = {c^2}$	Pythagorean theorem
6	$S = 4\pi {R^2}$	surface area	16	$\frac{{P\left({{B_i}} \right)P(A\|{B_i})}}{{\sum\nolimits_{j = 1}^n {P\left({{B_j}} \right)P(A\|{B_j})} }}$	Bayes
7	${2^q}$		17	$2\sum\limits_{i = 1}^4 {\frac{1}{{r_i^2}}}$	Descartes theorem
8	$E = m{c^2}$	mass energy	18	$f(b) - f(a) = {\rm{ }}f'(\varepsilon)(b - a)$	Lagrange
9	$f(x + 2\Pi) = f(x)$		19	$\mathop {\lim }\limits_{n \to \infty } {(1 + \frac{1}{n})^n}$	limit theorem
10	${a_n} = {a_1} + \left({n - 1} \right)d$	arithmetic sequence	20	$\frac{1}{{\sigma \sqrt {2\Pi } }}{e^{ - \frac{{{{(x - \mu)}^2}}}{{2{\sigma ^2}}}}}$	normal distribution

| Show Table

DownLoad: CSV

5.3. System experiment

Precision represents the accuracy rate and refers to the proportion of related documents in all the query documents in the returned results of the query. The calculation formula is shown in Eq (12).

${\text{precision}} = \frac{{S{R_{\rm{tp}}}}}{{S{R_{\rm{tp}}} + S{R_{{\rm{fp}} }}}}$

(12)

where $S{R_{\rm{tp}}}$ refers to the number of Query-related documents in the query result. $S{R_{\rm{tp}}}$ refers to the number of documents irrelevant to the Query in the query result.

Reciprocal rank (RR) is the reciprocal of the ranking of the first related document in the retrieved results. MRR is the average of the reciprocal rankings of multiple queries, and the calculation method is shown in Eq (13).

${\rm{MRR}} = \frac{1}{k}\sum\limits_{i = 1}^k {\frac{1}{{{\text{rank}}(i)}}}$

(13)

where ${\text{rank}} (i)$ refers to the ranking of the first related document for the i-th query.

Table 8 shows the values of P@3, P@5, P@10, and MRR for the 20 queries in Table 6, and Figure 4 shows the values of P@3, P@5 and P@10 for the 20 queries in Table 7.

Table 8. Average of precision and average of MRR.

Evaluation indicator	P@3	P@5	P@10	MRR
Average	0.81	0.76	0.58	0.87

| Show Table

DownLoad: CSV

Figure 4. Precision value of different queries.

DownLoad: Full-Size Img PowerPoint

Figure 4 shows that the P@3 of some queries can reach 100%. However, the precision of some queries is low, which is related to the fact that there are fewer scientific documents matching it in the dataset.

5.4. Ablation experiment

Average precision considers the position factor on the basis of precision. It is more sensitive to the position of sorting. The calculation method is shown in Eq (14).

${\text{AP}} = \frac{1}{r}\sum\limits_i^r {\frac{i}{{{\text{pos}} (i)}}}$

(14)

where r refers to the total number of related documents, ${\text{pos}}(i)$ refers to the position of the i-th related document in the retrieved results.

NDCG is the normalized loss cumulative gain. The calculation method of DCG (discounted cumulative gain) is shown in Eq (15).

${\text{DCG}}@k = \sum\limits_{i = 1}^k {\frac{{re{l_i}}}{{{{\log }_2}(i + 1)}}}$

(15)

where $re{l_i}$ refers to the relevance of the i-th document. There are three levels of relevance: good, fair and bad. They are assigned scores of 3, 2 and 1.

In an ideal state, according to the order of relevance from largest to smallest, the case where DCG takes the maximum value is IDCG.

${\text{IDCG}}@k = \sum\limits_{i = 1}^{REL} {\frac{{re{l_i}}}{{{{\log }_2}(i + 1)}}}$

(16)

where REL refers to the sorting situation of the documents in the ideal state, and k refers to the collection of the first k documents.

NDCG uses IDCG to normalize the evaluation indicators.

${\text{nDCG}}@k = \frac{{{\text{DCG}}@k}}{{{\text{IDCG}}@k}}$

(17)

The similarities of the five attributes of scientific documents are calculated separately, they are MESY, MESF, MECT, SDKY and FOME. In order to verify the role of each attribute in the experiment, an ablation experiment was carried out in this study. One of the five attributes is removed in turn, and the remaining four attributes are input into GBDT and LR for training, then five models are obtained. Experiments with these five models are compared with the original model, and the results obtained are shown in the Figure 5. In Figure 5, model A represents MESF + MECT + SDKY + FOME, model B represents MESY + MECT + SDKY + FOME, model C represents MESY + MESF + SDKY + FOME, model D represents MESY + MESF + MECT + FOME, model E represents MESY + MESF + MECT + SDKY, and the model F represents MESY + MESF + MECT + SDKY + FOME.

Figure 5. Results of ablation experiments.

DownLoad: Full-Size Img PowerPoint

As shown in Figure 5, the MESY attribute affects the precision of the model. There are fewer relevant results retrieved, and the less relevant results are ranked relatively higher, so the MAP and nDCG of model A will be slightly higher. MESF also affects the precision of the model, but has little effect on the ranking. The two attributes of MECT and FOME have little effect on precision, but they will affect the ranking of results. The SDKY attribute will get more relevant results and affects the ordering of the model to some extent.

5.5. Comparative experiment

Figures 6 and 7 show the comparison results of the algorithm in this study with Tangent-CFT ^[4] and MIaS ^[3], MIaS system is an open-source system. The Tangent-CFT model was reproduced experimentally. Table 9 gives the average comparisons of MAP and NDCG. Tangent-CFT ^[4] is a mathematical expression embedding model realized by word2Vec, that can achieve precise matching of mathematical expression structure. To locate a scientific document according to a mathematical expression, the retrieval of "mathematical expression-scientific document"(scientific document pairs corresponding to mathematical expressions) is realized. MIaS ^[3] is an open search engine for mathematical expressions. It can also retrieve corresponding scientific and technological documents based on the similarity of mathematical expressions. The system builds an XML tree through the structure of mathematical expressions to retrieve query expressions and expressions with query expressions as sub-expressions.

Figure 6. MAP comparison of different algorithms.

DownLoad: Full-Size Img PowerPoint

Figure 7. nDCG comparison of different algorithms.

DownLoad: Full-Size Img PowerPoint

Table 9. Comparison of the average MAP and NDCG of different algorithms.

Algorithms	Ours	Tangent-CFT	MIaS
MAP	0.8192	0.7805	0.7570
nDCG	0.8605	0.8300	0.8100

| Show Table

DownLoad: CSV

6. Conclusion

This study proposes a multi-attribute retrieval and ranking model based on GBDT + LR to solve the problem of poor integration of mathematical expressions and relevant texts in scientific document retrieval. This method combines the five attributes MESY, MESF, MECT, SDKY and FOME. GBDT is used to reorganize the features, and LR trains the reorganized features. Finally, the similarity of the final scientific documents is obtained and sorted.

Future research is expected to complete the semantic retrieval of expression symbols based on the context of expressions. Meanwhile, in terms of semantics, it is better to effectively integrate expressions and text. When sorting the final scientific documents, the attributes of the scientific documents themselves should be considered, such as, publication year and citation frequency. This can improve the rationality and effectiveness of the final scientific document sorting.

Acknowledgments

This work is supported by the Natural Science Foundation of Hebei Province of China (Grant No. F2019201329).

Conflict of interest

The authors declare no conflict of interest.

References

[1]	Mahmood A, Javaid N and Razzaq S (2015) A review of wireless communications for smart grid. Renew Sust Energ Rev 41: 248–260. doi: 10.1016/j.rser.2014.08.036
[2]	Yick J, Mukherjee B, Ghosal D (2008) Wireless sensor network survey. Comput Netw 52: 2292–2330. doi: 10.1016/j.comnet.2008.04.002
[3]	Pakzad SN, Fenves GL, Kim S, et al. (2008) Design and Implementation of Scalable Wireless Sensor Network for Structural Monitoring. J Infrastruct Syst 14: 89–101. doi: 10.1061/(ASCE)1076-0342(2008)14:1(89)
[4]	Li X, Cheng X, Yan K, et al. (2010) A Monitoring System for Vegetable Greenhouses based on a Wireless Sensor Network. Sensors 10: 8963–8980. doi: 10.3390/s101008963
[5]	Yeo TL, Sun T, Grattan KTV (2008) Fiber-optic sensor technologies for humidity and moisture measurement. Sensor Actuat A-Phys 144: 280–295. doi: 10.1016/j.sna.2008.01.017
[6]	Culshaw B (2004) Optical Fiber Sensor Technologies: Opportunities and Perhaps Pitfalls. J Lightwave Technol 22: 39–50. doi: 10.1109/JLT.2003.822139
[7]	O'Connell E, Healy M, OKeeffe S, et al. (2013) A Mote Interface for Fiber Optic Spectral Sensing With Real-Time Monitoring of the Marine Environment. IEEE Sens J 13: 2619–2625.
[8]	Lloyd SW, Newman JA, Wilding DR, et al. (2007) Compact optical fiber sensor smart node. Rev Sci Instrum 78: 35108. doi: 10.1063/1.2715994
[9]	Kuang KSC, Quek ST, Maalej M (2008) Remote flood monitoring system based on plastic optical fibers and wireless motes. Sensor Actuat A-Phys 147: 449–455.
[10]	Pang C, Yu M, Zhang XM, et al. (2012) Multifunctional optical MEMS sensor platform with heterogeneous fiber optic Fabry–Pérot sensors for wireless sensor networks. Sensor Actuat A-Phys 188: 471–480. doi: 10.1016/j.sna.2012.03.016
[11]	Tan YC, Ji WB, Mamidala V, et al. (2014) Carbon-nanotube-deposited long period fiber grating for continuous refractive index sensor applications. Sensor Actuat B-Chem 196: 260–264.
[12]	Tan YC, Tou ZQ, Mamidala V, et al. (2014) Continuous refractive index sensing based on carbon-nanotube-deposited photonic crystal fibers. Sensor Actuat B-Chem 202: 1097–1102.
[13]	Tan YC, Tou ZQ, Chow KK, et al. (2015) Graphene-deposited photonic crystal fibers for continuous refractive index sensing applications. Opt Express 23: 31286–31294. doi: 10.1364/OE.23.031286
[14]	Nicholson JW, Windeler RS, DiGiovanni DJ (2007) Optically driven deposition of single-walled carbon-nanotube saturable absorbers on optical fiber end-faces. Opt Express 15: 9176–9183. doi: 10.1364/OE.15.009176
[15]	Kashiwagi K, Yamashita S, Set SY (2009) In-situ monitoring of optical deposition of carbon nanotubes onto fiber end. Opt Express 17: 5711–5715.
[16]	Yamashita S (2012) A Tutorial on Nonlinear Photonic Applications of Carbon Nanotube and Graphene. J Lightwave Technol 30: 427–447. doi: 10.1109/JLT.2011.2172574
[17]	Lee H, Shaker G, Naishadham K, et al. (2011) Carbon-nanotube loaded antenna-based ammonia gas sensor. IEEE T Microw Theory 59: 2665–2673.
[18]	Kruss S, Hilmer AJ, Zhang JQ, et al. (2013) Carbon nanotubes as optical biomedical sensors. Adv Drug Deliver Rev 65: 1933–1950. doi: 10.1016/j.addr.2013.07.015
[19]	The Network Simulator tool: ns-3. Available from: https://www.nsnam.org/.

This article has been cited by:

1.	Xinyu Jiang, Bingjie Tian, Xuedong Tian, Retrieval and Ranking of Combining Ontology and Content Attributes for Scientific Document, 2022, 24, 1099-4300, 810, 10.3390/e24060810
2.	Shasha Zhang, Yuyu Yuan, Zhonghua Yao, Jincui Yang, Xinyan Wang, Jianwei Tian, Coronary Artery Disease Detection Model Based on Class Balancing Methods and LightGBM Algorithm, 2022, 11, 2079-9292, 1495, 10.3390/electronics11091495
3.	Wei Wanhua, Lv Renzhi, 2022, Prediction of the Number of Online Doctors’ Followers based on Machine Learning, 978-1-6654-9991-0, 503, 10.1109/ICAICA54878.2022.9844424
4.	Teng Long, XiaoLiang Che, Wenbin Guo, Yubin Lan, Ziran Xie, Wentao Liu, Jinsheng Lv, Yongbing Long, Tianyi Liu, Jing Zhao, Visible-near-infrared hyperspectral imaging combined with ensemble learning for the nutrient content of Pinus elliottii × P. caribaea canopy needles detection, 2023, 6, 2624-893X, 10.3389/ffgc.2023.1203626

Reader Comments

Your name:*

Email:*
© 2018 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)