Hamiltonian lattice dynamics is a very active and relevant field of research. In this Special Issue, by means of some recent results by leading experts in the field, we tried to illustrate how broad and rich it can be, and how it can be seen as excellent playground for Mathematics in Engineering.
1.
Introduction
The human body is a symbiotic community of numerous eukaryotic and prokaryotic cells, including archaebacteria, protists, helminthes, and viruses [1]. At the same time, man is, to a greater extent, a community of prokaryotic than eukaryotic cells. The number of eukaryotic cell species in human tissues and organs is not many more than 200; total content of these cells in the range of 5–10 trillion. The content of bacterial species, which inhabit the human body, reaches 10 thousand, and strains—up to 50 thousand; the total number of bacteria is within hundreds of trillions, and along with viruses—exceeds quadrillion [2]. The gastrointestinal tract (GIT) is the largest biotope in the human body, the total number of microorganisms that inhabit the large intestine is about 1014–1015 CFU/mL [3,4].
The human metagenome consists of the genes of Homo sapiens himself and the genes of colonizing its body microorganisms that are called microbiome [5,6,7,8]. The number of genes in the total metagenome of the intestinal microbiota is more than 100 times higher than in the human genome [9,10,11].
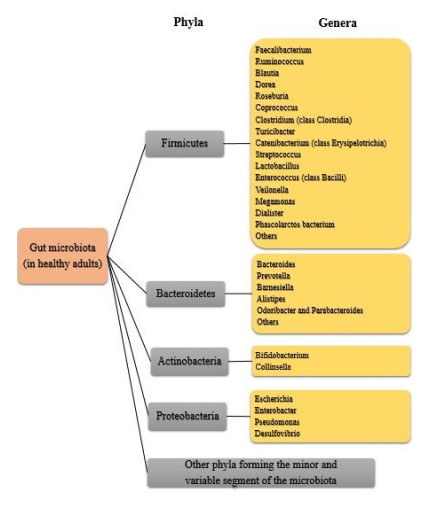
Studies of the last decade, carried out using a metagenomic approach, have shown the digestive tract in healthy adults to include up to 1000 species of microorganisms, 90% of which belonging to the bacterial phyla Firmicutes and Bacteroidetes (Figure 1). Other taxonomic groups of bacteria presented within the intestinal microbiota in healthy adult include phyla Actinobacteria, Proteobacteria and some other phyla forming the minor and variable segment of the microbiota [12,13,14,15,16].
In the course of molecular and genetic research MetaHIT Projects (Human Intestinal Tract Metagenomics) launched in 2008 and funded by the European Commission and American Human Microbiome Project [17,18], scientists concluded that there are at least 160 bacterial species in one person’s intestine [19,20,21,22,23]. It has also been suggested that they constitute the ‘minimal gut genome’. Based on the taxonomic diversity of microbiota, scientists in 2011 discovered 3 enterotype microflora. In general, the first enterotype was characterized by the prevalence of the genus Bacteroides in human intestinal microbiota, the second by Prevotella, the third by Ruminococcus, and a number of others. The theory of the existence of enterotypes is still a subject of intense debate and discussion, but their practical benefit may be to develop a personalized approach in the treatment and prevention of various pathologies [24,25,26].
Microbiota of GIT plays the main role in ensuring normal human activity [27], affects the growth and development of pathogenic and opportunistic microorganisms [28,29,30,31,32], participates in maintaining normal ‘tension’ of human immunity [33,34,35]; regulates metabolic processes [36,37]; treated as an abandoned endocrine organ [38]; is associated with brain activity (e.g. stress response) et al. [39,40,41]. Microbiota can produce a wide range of neuroactive molecules—serotonin, melatonin, gammaaminobutyric acid, catecholamine, histamine and acetylcholine [42,43]. In addition, intestinal bacteria give 90% of the energy required for the functioning of digestive tract cells [5,44,45,46,47,48,49,50,51].
Modern metagenomic methods of research allow monitoring of all (cultivated and uncultivated) species diversity, quantitative ratio of different species and strains of microorganisms in normal and at different dysbiosis of microbiota. The resulting microbiota imbalance, that is, any change in the composition of resident commensal bacteria in the intestine, compared to that found in healthy people, can be a risk factor for many metabolic diseases [5,47,49,50,51,52,53,54]. A separate issue for researchers is the search for common patterns and dynamics of intestinal microflora, variability of individual changes [55]. Potentially, some therapies and drugs can be prescribed to almost all patients, and others should be developed for a certain group of people or even optimized for each individual person. This approach, called personalized medicine, is actively developing and consists in individualization of methods of therapy, including dysbiotic conditions.
According to recent data, the variability of the human microbiome is only 10% related to the genetic characteristics of the individual; the differences in the microbiome between individuals are predominantly related to the effects of various endogenous and exogenous factors on it [56]. Among the exogenous factors that can trigger dysbiosis, one of the most significant is the human diet [47,48,50]. Diet plays an important role in forming the composition and activity of a complex microbial population in the intestine, providing it with macroelements such as carbohydrates, proteins and fats [57,58], affects intestinal permeability, mucosal immune function, intestinal mobility and sensitivity, and intestinal nervous system activity [59,60,61,62]. Functional food reduce the risk of developing nutritional-related diseases, prevent or compensate for nutrient deficiencies in the human body, preserve and improve health due to the presence of physiologically functional food ingredients in their composition. Functional food products restoring human nutritive status belong to non-specific methods of correction of microbial ecology of digestive tract and its immunobiological stability [63,64]. In our review, we would like to consider the impact of probiotic microorganisms, their metabolites and natural plant components on enhancing the functional properties of whey-based beverages normalizing gut microbiota and human health. The selection of whey as a base for functional beverages is based on its beneficial nutritional and biological value. Whey is a coproduct in the production of cheese or casein in the dairy industry. Up to 50% of milk solids remain in it, up to 250 different compounds (nitrous, micro- and macro-compounds, milk fat, mineral salts, lactose, vitamins, enzymes (lactoperoxidase, hydrolases, transferases, lyases, proteases and lipases) and organic acids). Whey proteins are very valuable components; they contain all essential amino acids, have a good digestibility and protein efficiency index above 3.0. Milk whey really quenches thirst, in the form of a beverages it can replace most of the lost organic and inorganic salts in extracellular fluid, is quickly adsorbed due to the absence of a fat emulsion. Whey is used to treat various diseases such as arthritis, impaired liver function and dyspepsia. Milk whey is an excellent nutrient medium for probiotic bacteria. In addition, in many countries it is a coproduct of the dairy industry, and cheap technological solutions are required for its disposal, especially for small industries.
2.
Antimicrobic, antifungal and antiviral properties of whey
Milk whey contains several unique components, such as immunoglobulins (Igs), lactoferrin (Lf), glycomacropeptide (GMP) and sphingolipids, which have some important antimicrobial and antiviral properties, described in some detail by researchers Charu Gupta and Dhan Prakash in their review of the therapeutic potential of milk whey [66]. All these compounds are able to survive after passing through the stomach and small intestine and have their biological effect on the large intestine [65]. Table 1 summarizes the antimicrobial, antifungal and antiviral actions of essential whey proteins.
Thus, immunoglobulins-G (IgGs), Lp and Lf concentrated from whey participate in host immunity, provide antimicrobial action in the intestinal tract. IgGs binds to bacterial toxins (produced by Clostridium divicile et al.), thereby reducing diarrhea, dehydration, and muscle aches. Milk whey proteins as part of complex therapy help in the fight against rotoviral diarrhea, which is a common infection in children [67].
Lactglobulin is a potential agent for preventing the transmission of genital herpes virus infection and the spread of human immunodeficiency virus type 1 (HIV-1) [68]. The uniqueness of whey proteins is also due to their high content of glutathione (GSH), cysteine and methionine. Glutathione protects cells from free radical damage, infections, toxins, contamination and exposure to UV radiation, is a central element of the body’s immune and antioxidant defense systems.
The antibacterial properties of lactoferrin present in whey are due to its ability to bind iron, thus rendering it inaccessible to pathogens and thus inhibit their metabolism and growth [69]. At the same time, lactobacilli can use iron bound to lactoferrin. Lactoferrin and lactoferricin show inhibitory activity against a wide range of microorganisms, including Gram-positive bacteria, yeast, fungi and protozoa parasites [70]. They also inhibit the growth of food pathogens such as E. coli and Listeria monocytogenes [71]. In addition, lactoferrin has important antiviral activity, it directly interacts with the selected viral pathogen, inhibits virus replication and its ability to attach to epithelial cells of the large intestine. Lf shows antiviral properties to HIV, human cytomegalovirus (HCMV), herpes viruses, human papilloma virus (HPV), alpha virus and hepatitis C, B and G viruses [72]. Glycomacropeptide GMP inhibits the binding of cholera toxin to receptors in the intestinal tract.
Phospholipids such as sphingolipids are metabolized in the gastrointestinal tract and produce sphingosine and lysosphingomyelin. These compounds are potent bactericidal agents in vitro. Sphingomyelin has anticancer properties because it is able to inhibit colon cancer.
Another important protein component of whey and a natural protective barrier against infectious microorganisms and viruses is lactoperoxidase (Lp). Lp catalyzes the peroxidation of thiocyanate into the hypothiocinate ion, which is a strong oxidant and destroys bacterial cell membranes [72]. Shin et al in their study proved that oral administration of lactoperoxidase isolated from whey in attenuated pneumonia in mice infected with influenza virus inhibited infiltration of inflamed cells in the lungs [73].
In the global market, for the correction of intestinal microbiota, both native whey (Lactoserum) and various preparations based on whey components are available to consumers. Product labeled Protectamin® (Fresenius Kabi, Bad Hamburg, Germany) or Immunocal, contain whey proteins and are used to protect against Human Immunodeficiency Virus (HIV) and other viruses [74]. Antimicrobial properties of lactoperoxidase have found application in Lactoperoxidase System preservative for dairy and meat industry.
Thus, milk whey or diet with supplements based on individual components of milk whey positively and effectively influence the balance of intestinal microbiota, contribute to immune improvement of human body and restoration of healthy state of gastrointestinal tract due to antimicrobial, antifungal and antiviral properties.
Unfortunately, direct whey use is still not widespread. Increasing demand of modern consumers for innovative products from natural ingredients, having high nutritional qualities and benefits for health, contributes to the development of the market of milk whey beverages.
According to Katarzyna Sryplonek and Malgorzata Jasienska and other researchers, whey-based beverages can be divided into several main groups, including: non-fermented and fermented beverages, milk-type beverages, probiotic beverages, refreshing soft drinks, alcoholic beverages, dietary beverages, protein-rich sports beverages, direct-use beverages and powder beverages [75,76,77]. In our view, this division is rather conditional, as whey-based beverages fermented by probiotic microorganisms can be assigned to the three above-mentioned groups at once. Since our review focuses on functional whey-based beverages with antibacterial, antiviral and antifungal properties, we will consider only some of the above-mentioned whey beverages in more detail.
3.
Functional properties of fermented whey
In the event of dysbiotic disorders, metagenomic studies of intestinal microbiota can help to develop scientifically sound approaches to the restoration of microbiocenosis using microbial therapy—the introduction of individual species of microorganisms or their consortium depending on the type of pathology. In order to preserve and restore microbial ecology, medical practice uses a variety of probiotics, symbiotics, prebiotics, synbiotics, combiotics, genetic engineering probiotics, fecal content transplantation [5,46,63,64].
The global market for such micro-environmental products was estimated at $22.6 billion in 2010; $28.8 billion in 2015; with the prospect of increasing to $45 billion by 2018 [78]. We will not dwell in our review on curative commercial probiotic drugs, but consider the possibility of using fermented functional whey-based beverages to prevent and therapy dysbiosis.
Fermented milk whey can act as a means of delivering probiotic cells in the human body. Also, fermentation allows to increase in milk whey its therapeutic potential, functional properties, nutritional and tasting attractiveness, shelf life, microbial stability, detoxification and safety for the consumer. Fermented whey favorable for those who are contraindicated with lactose load, it has more consumer attractiveness than native, because it has a more pleasant taste and aroma, it is nutritious, cool, less acidic and low in calories, has a light, non-viscous structure, can be easily carbonated, like soft drinks [79,80,81].
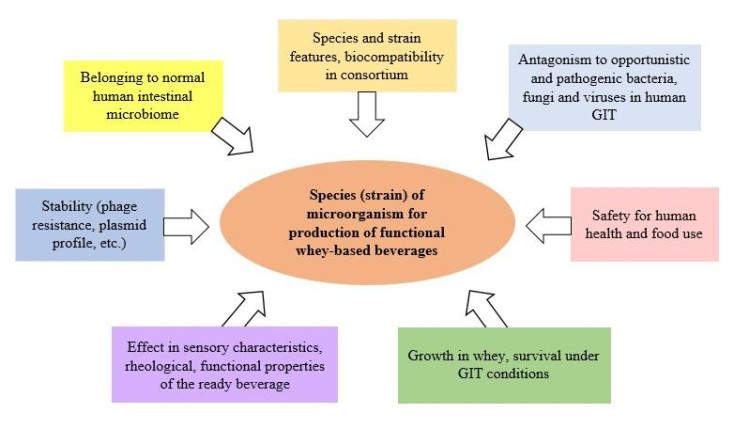
Typically, members of normal human microflora—probiotic bacteria belonging to the genera Lactobacillus, Lactococcus, Streptococcus, Bifidobacterium, Pediococcus, Propionibacterium, Leuconostoc, Acetobacterium, lactose branching yeast Kluyveromyces marxianus/Candida kefyr, Kluyveromyces lactis var. lactis, Debaryomyces hansenii and Dekkera anomala; lactose-free yeast Saccharomyces cerevisiae, Torulaspora delbrueckii, Pichia fermentans, Kazakhstania unispora, Saccharomyces turicensis, Debaryomyces occidentalis and their associations are used for fermentation of milk whey and production of functional beverages [82,83,84,85,86,87,88,89,90,91,92]. Criteria of selection of species and strains of microorganisms—starters, for fermentation of milk whey and production of functional beverages are shown in Figure 2.
It should be emphasized that in 2001–2002, the World Health Organization, the U.S. Food and Drug Administration (FDA), Food and Agriculture Organization (FAO), other major societies and expert groups conclude that overall probiotics can be considered absolutely safe, have GRAS status (Generally Recognized As Safe) and without limitation used in the food and pharmaceutical industry [93,94].
It is necessary to bear in mind the known feature of modern diseases, namely the multipurpose of their development. In this situation, it becomes apparent that rationally combined probiotic microorganisms having a wide range of physiological effects should be selected as starter for functional beverages [95]. G. Zoppi et al., proved that multi-strains (multi-species) probiotics are most promising because they show higher efficacy in the prevention of antibiotic-associated dysbacteriosis in children than traditional mono-strain preparations [96]. Other clinical studies show that the administration of multi-species probiotic VSL #3 to patients with ulcerative colitis and ileitis reduces the need for antibacterial agents and prevents the development of bacterial complications, which is not available to mono-strain probiotics [97]. The use of combined starters based on multi-strain symbiotic cultures increases their survival and functionality in the gastrointestinal tract after consumption of fermented beverages. This effect can be explained by cooperative interaction with exchange of bacterial metabolism products: amino acids, free peptides, formiate and СО2.
Bifidobacteria and lactobacilli benefit human health through antagonism to pathogenic bacteria and the ability to modulate the local and systemic immune response; participate in stabilization and preservation of intestinal barrier, in absorption of calcium, magnesium and iron; are capable of converting various nutritional components into biologically active molecules [98,99,100,101]. By normalizing intestinal microbiocenosis, probiotic bacteria influence not only the regulation of intestinal activity, but also other organs and systems, thus maintaining the general homeostasis of the host body. As a source of antioxidants, lactobacilli and bifidobacteria increase the body’s antioxidant status. In individual strains of bifidobacteria and lactobacilli, the ability to produce gamma-aminobutyricacid (GABA), to exert psychotropic action and to show activity reducing symptoms of depression and anxiety was revealed [102,103,104]. To reduce stress, improve the psychoemotional state of a person and increase his working capacity can be introduced into the body with food of neurotransmitters such as serotonin, dopamine and noradrenaline or their precursors—tryptophan, tyrosine and phenylalanine. One of the sources of introduction into the body of neurotransmitters can be fermented drinks based on milk whey obtained using lactic acid bacteria—producers of neurotransmitters.
At the same time, the potentially possible positive effects of the presence of probiotics in the human body largely depend on the ability and activity of specific strains of bacteria.
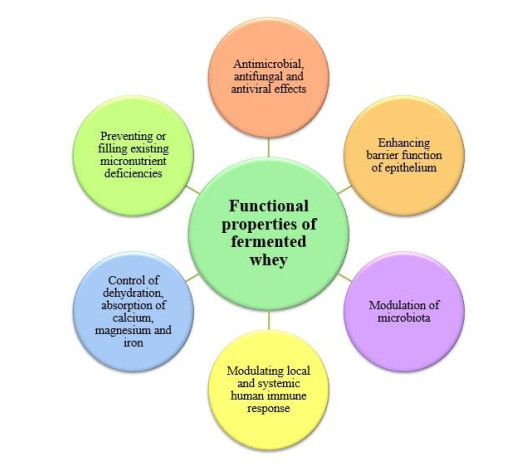
During fermentation with probiotic bacteria, milk whey gains a more significant therapeutic effect in the correction of dysbiosis, improving its functional properties as described in Figure 3.
Due to metabolic activity of probiotic microorganisms during fermentation of protein and carbohydrate components, milk whey is enriched with organic acids (acetic, citric, dairy, etc.), aromatic compounds (diacetyl, etc.), H2O2, bacteriocins, bacteriocin-like peptides, biosurfactants and other metabolites having direct and/or mediated antimicrobial, antifungal or antiviral action [83,105].
Organic acids have antimicrobial properties (particularly against E. coli, Salmonella, Campylobacter, Listeria monocytogenes, etc.) and antifungal properties (against Candida, Fusarium, Penicillium, Aspergillus, etc.) [106,107,108,109]. It should be noted that organic acids are ‘weak acids’, more than 90% of their molecules in the lumen of the intestine are in anionic dissociated form. These natural metabolites are important for regulating adsorption and metabolism in the large intestine. In some physiological and pathological conditions, they initially penetrate rapidly through the membrane of opportunistic and pathogenic bacteria, which colonize the intestinal mucosa, change intracellular pH, reduce energy potential, accumulate toxic anions; lead to ultra-structural defects of the bacterial cell, which eventually suppresses its life functions [110,111]. There is evidence that the inhibitory effect of organic acids is directly dependent on pH, and there is evidence that at low values, stronger antimicrobial activity is observed in lactic and propionic acid, at pH > 4.5 in acetic acid [112,113]. In order to have a fungicidal effect, for example with respect to C. albicans, organic acids must be in a high concentration [114,115].
Inhibitory action against major opportunistic microorganisms of probiotic metabolites such as hydrogen peroxide, diacetyl and bacteriocins is known. Hydrogen peroxide, which accumulates in medium during growth of catalase-negative microorganisms, has inhibitory effect on growth of catalase-positive bacteria due to strong oxidative effect on molecular structures of their proteins. It is noted that high molecular weight bacteriocins suppress closely related species of bacteria that live in the same biotope, and microcins (low molecular weight metabolites) have a wider spectrum of antimicrobial activity and therefore a more significant bacteriostatic effect [110,111,116,117,118,119]. The involvement of nitric oxide (NO) in the development of physiological and pathological conditions is currently being actively studied. In many experimental studies it has been shown that NO refers to key signaling molecules of the gastrointestinal tract, it is synthesized not only by cells of the human body, but also by some bacteria-commensals (E. coli, Lactobacillus) [120,121]. The cytotoxic effect of NO is enhanced by association with acidic medium (bifidobacteria lower pH to 5.0, lactobacilli to 4.0). It is under these conditions that nitrites are formed—highly toxic endogenous metabolites, which disrupt the normal functioning of many opportunistic and pathogenic microorganisms, and the ability of a number of representatives of normal microflora to be resistant to these compounds has been proved [122]. A feature of these nitrites is also that they potentiate the simultaneous antibacterial effect of hydrogen peroxide and lactic acid, which are formed by saccharolytic bacteria [121].
Antibiotics produced by lactic acid bacteria (Reuterin), bacteriocins or bacteriocin-like substances (Nisin, Leukocin, Sakacin, Pediocin PAl/AcH, Enterocins AS-48, A and B, Lactacin B, Lactocin 27, Plantaricin A, Platacin B and Helveticin J., etc.)—antimicrobial agents that are active against bacteria and fungi. They can affect microorganisms by inhibiting cell wall synthesis, increasing the cell permeability of target cell membranes, or inhibiting the activities of RNase or DNase. They have been found to be non-toxic to animals and humans, do not change the nutritional properties of food products, are effective at low concentration, do not lose activity when cooled, and can also be used for bio-preservation of food products [123,124,125,126,127,128,129,130].
Probiotics can be attributed to anti-endotoxin agents. It has been experimentally proved that bifidobacteria have endotoxin binding ability, reduce endotoxin-dependent induction and release of interleukin (IL) 8 [131]. It is believed that bacterial lipopolysaccharides and peptidoglycans of various strains of normophlora have immunoregulatory effects. In parallel, it has been established that the key importance of anti-endotoxin immunity is not the absolute protection of the body from endotoxin, but the limitation of its concentration and biological activity to the level necessary for the realization of physiological functioning of the immune system [132].
It is known that the introduction of live probiotic bacteria, including lactic acid bacteria, into the human body through the consumption of fermented products and beverages, including milk whey, has a positive effect on human health [133]. Living microorganisms compete in the gut with pathogens for nutrients or adhesion sites. Saturation of adhesion sites and co-agammaegation allow Lactobacillus spp. prevent Candida spp. adhesion to epithelial cell wall. [115]. Thus, the presence of Lactobacillus cells can alter the host’s immune response in the case of Candida colonization to attract granulocytes and stimulate immune defense. In addition, the presence of Lactobacillus and direct interaction leads to down regulation of several C. albicans genes associated with adhesion, invasion, and opposition to host protection [134].
Lactic acid bacteria cells (Lactobacilus bulgaricus and Streptococcus thermophilus) can induce cytokine production (IFN-g, IL-6 and TNF-α) by immunocompetent cells in healthy people, which contributes to more effective protection of the body from infections [135].
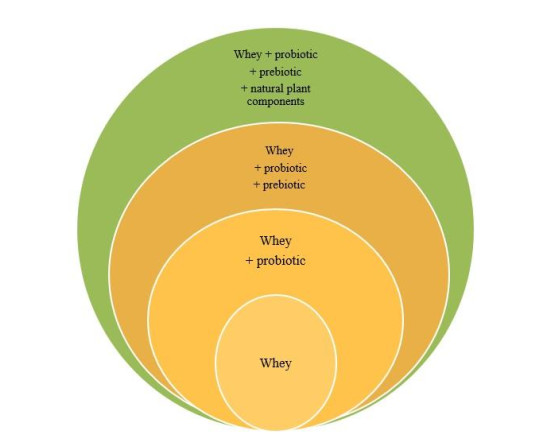
The functional properties of whey can be enhanced not only by fermentation, but also by the addition of various bioactive ingredients, as shown in Figure 4.
Prebiotics (oligosaccharides, oligofructans, dietary fibres, sorbents, etc.) are used to increase the functional effectiveness and stability of probiotics during fermentation of milk whey, when it is ingested or stored. Prebiotics increase the survival and activity of probiotic microorganisms in the gastrointestinal tract (protecting against antibiotics, hydrochloric acid, gastric juice, bile acids, digestive enzymes), as well as selectively modulate the main microbiota, providing health benefits. The process of reactivation of starter bacteria immobilized on sorbent (plant fibres) is also accelerated by ‘group’ behavior (‘quorum sense’) of cells closely located on sorbent (plant fibres), and biodegradable sorbent also serves as a source of nutrition both for introduced bacteria and for representatives of resident microflora [136,137,138,139,140,141,142,143,144]. The industrial use of prebiotics from plant sources such as Arrowroot (Maranta arundinacea) and Raftilose ® (commercially available inulin) carbohydrates is known to enhance the vitality of Lactobacillus sp. in bioyogurt during storage in a refrigerator [139]. These prebiotic substances increase the survival of probiotics in the gastrointestinal tract and colonization to the intestinal epithelium. In addition, prebiotics have such stability that they can be incorporated into the food matrix as a carrier for delivering the desired substances and living cells of probiotics [145,146,147].
Whey-based functional beverages may contain a variety of natural plant components: fruit or fruit juices (e.g. pomegranate, acai, acerola, noni and mangosteen), berries (e.g. cranberries, blueberries, strawberries, sea buckthorn, silk, etc.) and whey extracts or CO2-extracts of berries, vegetable juices or puree (Girasol, beet, carrots, pumpkin, etc.) or botanical extracts (e.g. Aloe vera, ginger, ginkgo and melissa) [84,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168], which increase the nutritional and functional value of the beverage, improve its organoleptic and texture, as well as have antimicrobial, antiviral and antifungal properties. It is known that in the presence of fruit-berry and fruit-vegetable juices, the viability of probiotic strains of lactic acid bacteria decreases after 2 weeks of storage. Their survival rate is increased by introducing grape seed extract, green tea extract or vitamin C extract or other vegetable components [169,170,171,172] into the beverage composition. Antimicrobial activity of plant extracts is based on phenolic compounds (simple phenols, phenolic acids, quinones, flavones, flavonoids, flavonols, tannins and coumarins), terpenoids and essential oils, alkaloids, lectins, polypeptides, etc. [173].
Lucera et al. showed the possibility of using essential oils of sage, juniper, lemon for apple juice preservation [174]. The antimicrobial effect of these essential oils was observed in the acid range of pH and could result from a combination of different active complexes. The combination of different preservation systems allows taking advantage of each while at the same time significantly reducing the amount of antimicrobial agent.
4.
Functional beverages and metabiotics
Functional beverages are special drinks intended for systematic consumption in the composition of food rations by all age groups of a healthy population, having scientifically sound and confirmed properties, reducing the risk of developing nutritional diseases, preventing deficiency or filling nutrient deficiency in the human body, preserving and improving health due to the presence of physiologically functional food ingredients in their composition. Four main groups are distinguished in functional beverages category: sports, energy, nutraceuticals and healthy. The ratio of the beverages to one or another grouping is determined by the largest component proportion in the beverages composition that provides its functional properties. It is possible to assign beverage to the functional group when meeting the requirements for the content of one or more functional ingredients in them in amount of 10 to 50% of the recommended daily norm.
Despite many technological solutions developed in different countries for preparing probiotic functional beverages containing whey, their industrial production has not become widespread. Yakult and Sofyl (manufactured by Yakult), Chamyto (Nestlé), Activia, Actimel, Danito (Danone) and a few other brands are available on the market.
Perhaps in part, this is due to recent disputes over the effectiveness and usefulness of probiotics. In 2012, the European Food Safety Authority (EFSA), on labels of products containing live probiotic microorganisms, does not recommend the use of designations of any positive medical effects from their use; according to EFSA experts, traditional probiotics lack real objective evidence of their effects on health and well-being, as well as due to the increase in the number of observations of side effects in such probiotics when they are used [175]. A similar ban in 2014 was adopted by Food & Drug Administration USA [176]. In recent years, in order to maintain and restore the microbial ecology of humans, a variety of low molecular weight compounds of microbial origin have been rapidly introduced, which have been called metabiotics (or metabolite probiotics, postbiotics, biological drugs, pharmacabiotics) in the scientific literature [5,63,177,178,179,180,181]. Metabiotics are structural components of probiotic microorganisms, and/or their metabolites, and/or signaling molecules with known chemical structure, which are able to optimize physiological functions, metabolic, epigenetic, informational, regulatory, transport, immune, neurogormonal, and/or behavioral responses associated with the activity of the host body’s symbiotic (indigenic) microbiota. Metabiotics, compared to probiotics based on living organisms, have a longer retention period, clear application targets, they are better dosed, their safety is better controlled, they are better absorbed, metabolized, distributed across the body, tissues and organs, faster and more eliminated from the body. New types of locally active antimicrobial compounds, (such as phagobiotics, bacteriocins, other antimicrobial peptides, new antibiotic variants, etc.) are examples of metabiotics that affect intestinal microbiotic correction. They will further improve the specificity, efficacy and safety of microecological techniques for the prevention and treatment of various diseases, including those associated with human symbiotic microbiota imbalance. These metabiotics will be able to act both as independent drugs and as enriching additives in functional foods and beverages, including milk whey. An example of functional beverage with metabiotics is Calpis sour milk (Calpis Co. Ltd, Tokyo, Japan), containing two peptides: valine-proline-proline (VPP) and isoleucine-proline-proline (IPP), inhibiting ACE and responsible for antihypertensive activity. These peptides are obtained from caseins during fermentation of milk with Lactobacillus helveticus and Saccharomyces cerevisiae.
At present, however, the mass production and use of metabiotics for various purposes is also limited in many countries due to a number of objective reasons. Among the most important of these, according to Shenderov B., are the variety of biological and pharmacological effects and targets of many known low molecular weight molecules of microbial origin, lack of economically reasonable methods of industrial isolation and evaluation of physical and chemical structure of potential metabiotics, and reacting the biologically and pharmacologically active microbial compounds included in them with other food and endogenous molecules; insufficient use of OMIC-technologies and gnotobiological models to assess the safety and effectiveness of this new class of biologically active additives and pharmacological agents of microbial origin, shortage of biotechnological enterprises and skilled personnel, lack of sufficient number of museums of microorganisms and microbiocenoses of human origin [182].
5.
Conclusion
Monitoring of species diversity, quantitative ratio of different species and strains of intestinal microbiota in normal and in different pathological conditions allows investigating in detail the mechanisms of such disorders and creating methods of control over them. Understanding the patterns of human interaction and the intestinal microflora that inhabits it helps to significantly advance the development of new approaches to microbial therapy and the prevention of dysbiotic disorders, and many other dysbiosis-induced metabolic diseases. Among non-specific methods of intestinal microbiota correction functional food products are found. Whey in untreated form and fermented with probiotic microorganisms is a very effective functional beverages with an antibacterial, antifungal, and antiviral effect; able to regulate not only the activities of the intestine, but also other organs and systems, contributing to the maintenance of general homeostasis of the host organism. Introduction into whey of probiotics, prebiotics, various bioactive natural plant ingredients or metabiotics with certain properties and chemical structure contributes to improvement functional properties of whey beverages, as well as their stability. The functional beverages thus produced can serve as a target agent optimizing host-specific physiological functions, including those associated with symbiotic microbiota activity.
Acknowledgments
This research was funded by the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan (Grant No. AP05132352, BR05236330).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: