1. Introduction

Microglia are long-living tissue-resident macrophages of the central nervous system (CNS) that derive from erythromyeloid progenitors of the yolk sac ^[1,2,3,4]. Explosive progress in microglia research during the past two decades has unraveled their important physiological roles in CNS development and maintenance of homeostasis. They provide essential support through their sensing and phagocytic activities, and release of trophic factors ^[5]. Lineage tracing studies conducted in mouse and human showed that the self-renewal rates of microglia vary across brain compartments ^[6,7,8,9]. However, mammalian microglial cells are generally long-lived, which may lead to the accumulation of negative alterations over time, eventually leading to undesired influences on cognitive functions. While the term glia refers to “glue” in Greek, in vivo 2-photon imaging of ramified microglial cells with actively surveying processes ^[10,11] revealed that they are not rigid structures that simply hold the complex components of the CNS together. In this short review, we focus on the roles of microglia in learning and memory. Moreover, we apply our understanding of microglial function into a disease context by examining how microglia may be implicated in learning deficits and memory loss under conditions of microglial dysfunction, environmental risk factors, as well as aging.

2. Physiological roles of microglia critical to learning and memory

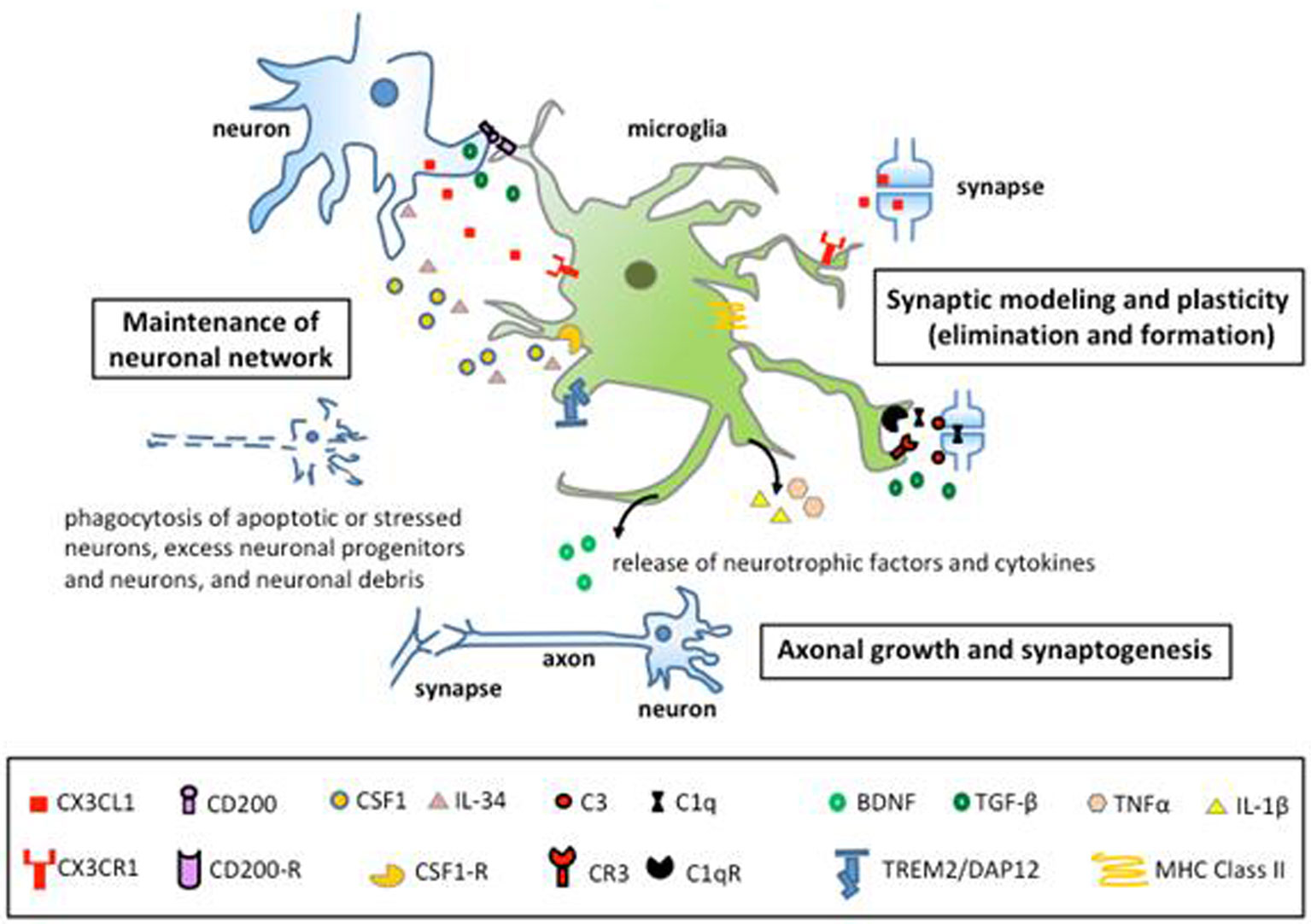
With an impressive array of ion channels, receptors and transmembrane transporters ^[12], microglia are well endowed to sense and rapidly react to heterogeneous conditions in the steady state CNS across the lifespan. Their physiological role as regulators of brain development and homeostasis through detection and clearance of cellular debris, synaptic modeling, and secretion of cytokines, chemokines and growth factors, are dependent on their local environment and ongoing neuronal activity ^{[13,14,15,16]}. We focus on three aspects of microglial function that exert major influence on the neural network for learning and memory (Figure 1).

2.1. Microglial regulation of neuronal density

During CNS development, microglia coordinate neurogenesis and neuronal turnover through the release of trophic factors and scavenging activities. Microglia were shown to support neuronal survival, neurogenesis and oligodendrogenesis in vivo during pre- and postnatal development ^{[17,18,19,20]}. The recruitment of microglia into specific CNS compartments requires neurogenesis-dependent CXCL12/CXCR4 signaling ^[17] and fractalkine CX3CL1/CX3CR1 signaling ^{[20,21,22,23]}. From embryonic (E) day 14 to E17, microglia maintain the pool of basal progenitors in the forebrain throughout neurogenesis ^[17]. In the early postnatal cerebral cortex, microglia lining the subcortical white matter tracts secrete insulin-like growth factor 1 to maintain the layer V neurons ^[20]. Reactive microglia in the early postnatal subventricular zone (SVZ) release pro-inflammatory cytokines, such as IL (interleukin)-1β, IL-6, TNFα (tumour necrosis factor α), and IFNγ (interferon γ), which support neurogenesis and oligodendrogenesis ^[19]. Microglial phagocytosis was shown to regulate the number of neural precursors in proliferative regions of the developing telencephalon in perinatal rats and macaques ^[24]. Indeed, phagocytic microglia were found to proliferate and accumulate in areas containing high densities of apoptotic neurons during developmental cell death ^[25,26,27]. Microglia may also phagocytose live but stressed neurons when presented with the appropriate signal ^[28]. Increased rates of cell death in neurogenic regions such as the SVZ led to the release of macrophage migration inhibitory factor, which triggered microglial proliferation ^[17]. Upon massive neuronal death induced by neonatal alcohol exposure, cortical microglia adopted a pro-inflammatory state with an acute increase in TNFα, IL1β and CD68, and decrease of purinergic receptor P2RY12, to encourage the clearance of neuronal debris ^[29]. Taken together, these studies demonstrate that microglia are essential to the formation of healthy neurons at the appropriate density during embryonic development up to early postnatal stages.

Figure 1. Microglia in the steady state developing and adult brains are essential to learning and memory. Axonal growth, synaptogenesis, synaptic modeling, plasticity, and maintenance of the neuronal network are modulated by microglia either through direct interaction with neurons or via the release of soluble factors. These different roles may be sex-dependent in certain contexts. This schematic representation summarizes the physiological microglial functions relevant to cognitive processes and the major cell surface receptors, adaptor protein and cytokines mentioned in this review.

DownLoad: Full-Size ImgPowerPoint

In the healthy brain, neurogenesis persists throughout adulthood in neurogenic regions containing neural stem cells, and is implicated in cognitive processes such as learning and memory ^[30]. In humans and rodents, the neurogenic areas include the SVZ and the hippocampal subgranular zone (SGZ) ^[31]. Microglia were shown to maintain homeostasis in the adult SGZ by phagocytosing newborn cells targeted for elimination by apoptosis ^[32]. Depletion of murine SVZ microglia expressing low levels of P2RY12 in vivo impeded the survival and migration of newly generated neuroblasts to the olfactory bulb ^[33], suggesting the importance of this particular microglial population in maintaining the adult olfactory circuitry. Some reports suggested the involvement of doublecortin (DCX)-positive cells (e.g., neuronal precursor cells and immature neurons) in spatial memory retrieval and pattern separation ^[34,35]. Since microglia reportedly impair the proliferation of DCX-positive cells in the SGZ of the dentate gyrus by releasing IL-1β in rodent models of deficient CX3CL1/CX3CR1 signaling ^[36,37], their production of pro-inflammatory mediators and phagocytic activity may have important functional consequences on hippocampal cognitive processing. Using the Morris water maze paradigm for assessing hippocampal learning and memory in mice, a subsequent study claimed that microglial CX3CR1 could also promote adult neurogenesis by inhibiting Sirt1/p65 signaling in a CX3CL1-independent manner ^[38]. These studies support a continual regulation of neuronal density by microglia throughout the lifetime of the animal.

2.2. Microglial modulation of synaptic plasticity

Learning and memory are mediated by activity-dependent modulations of the synaptic transmission at chemical synapses in a process referred to as synaptic plasticity. Mechanisms underlying synaptic plasticity include long-lasting increases or decreases in synaptic efficacy, respectively termed long-term potentiation (LTP) and long-term depression (LTD). These processes are achieved by modulating the quantity of neurotransmitter released at the synapse, or by replacing the type of receptor expressed by the postsynaptic compartment ^[39]. LTP and LTD have been particularly well described in the hippocampus, a brain region involved in memory formation ^[40]. Accumulating evidence suggest that they are not autonomously regulated by neurons, but also involve several signaling pathways related to microglia.

A potentially important signaling pathway implicated in learning and memory involves DAP12 (TYRO protein tyrosine kinase binding protein). This protein is a transmembrane protein that serves as an adaptor to several myeloid receptors and is exclusively expressed by microglia in the brain. Mutations in Dap12 resulted in enhanced hippocampal LTP, increased AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid) contribution, decreased level of tropomyosin receptor kinase B [which binds brain-derived neurotrophic factor (BDNF) at high affinity] at the synapse, and increased levels of the pro-inflammatory cytokines IL-1β and IL-6 ^[41,42]. Conversely, deficiency in the microglia-expressed CD200 receptor for the CD200 ligand produced by neurons resulted in impaired LTP and increased production of IL-1β, IL-6 and TNFα ^[43]. LTP impairment was proposed to be mediated by TNFα ^[43], which was found to control homeostatic synaptic scaling ^[44] and to regulate synaptic transmission when expressed at physiological level ^[45]. These studies implicate cytokines, which within the brain are mainly produced by reactive microglia, in the modulation of synaptic plasticity ^[46,47]. For example, IL-1β was shown to be released by microglia in the hippocampus in vivo during normal learning ^[48]. Deficiency in the cytokine transforming growth factor β (TGFβ) resulted in impaired LTP and impaired object recognition memory ^[49]. Furthermore, Tgfβ knockout (KO) mice displayed a drastic decrease in microglial cell number ^[50], which could have mediated the effects of Tgfβ deficiency on synaptic plasticity. In the Cx3cr1 KO mouse model, a transient reduction in microglial cell number in the hippocampus at early postnatal stages was correlated to enhanced LTD, immature synaptic properties ^[22], and reduced adult functional brain connectivity ^[23]. This suggested the importance of the CX3CL1/CX3CR1 pathway for synaptic function. Lack of CX3CR1 also dysregulated the increase in AMPA receptors at glutamatergic synapses of the barrel cortex during CNS development ^[21]. Such impairments in synaptic plasticity were proposed to be mediated by microglial release of cytokines in a study where Cx3cr1 KO mice elicited impaired LTP, learning deficits, and increased IL-1β and TNFα expression ^[37]. Both LTP and learning defects were reversed by hippocampal infusion of IL-1β receptor antagonist, implicating IL-1β in mediating these effects ^[37]. Taken together, these studies support an essential role for microglia in synaptic maturation and plasticity.

2.3. Microglial modulation of structural plasticity

Synaptic wiring of neurons is achieved during the early postnatal stages of brain development, and is mainly dictated by genetic programming ^[51]. However, the connectivity pattern is not entirely pre-determined and involves a stochastic process of activity-driven elimination of inappropriate synapses and de novo formation, which is referred to as structural plasticity ^[52]. This is particularly obvious from analyzing dendritic spine turnover in the first postnatal weeks. Nearly half of the spines were observed to be eliminated in the cortex between P16 and P18 ^[53], suggesting a critical period of strong selective pressure in which synapses are formed and eliminated. Structural plasticity is not only restricted to the developmental period, as it persists in adulthood where it is believed to underlie long-term memory formation ^[52,54].

In the past decade, multiple studies have demonstrated the importance of microglia in structural plasticity, as they appeared to be involved in both synapse elimination, or so-called pruning, and synapse formation. The first suggestion for microglial involvement in synapse elimination came from an early study showing that microglia could physically separate, or strip, pre- and postsynaptic compartments upon axotomy of the facial nerve ^[55]. Synaptic stripping by microglia was also observed in the cortex after the induction of immune-mediated lesions ^[56]. Live-imaging experiments showed that ischemia increased the duration of microglial contact on presynaptic boutons and consequently accelerated the disappearance of the boutons ^[57]. While these findings were derived from pathological contexts, it was subsequently observed that dendritic spines were more likely to disappear when contacted by microglia in the normal cortex under physiological conditions ^[58]. This led to the hypothesis that microglia might eliminate synapses by phagocytosing the synaptic compartment, which was first proposed in a study demonstrating the colocalization of synaptic markers with microglia in the developing hippocampus ^[22]. A decrease in microglial cells concomitant with an increase in spine density in Cx3cr1 KO mice suggested that microglial phagocytosis of dendritic spines was dependent on fractalkine signaling ^[22]. These findings were supported by the observations that microglial depletion led to an increase in the density of functional hippocampal synapses in vitro ^[59] and impairment in spatial learning in vivo ^[60]. However, the identity of the preferentially phagocytosed synaptic compartment remains unclear. While both pre- and postsynaptic markers were reported to colocalize with microglia in the hippocampus ^[22], a later study found that only the presynaptic inputs were targeted by microglia in the retinogeniculate system ^[16]. In addition, the complement pathway was proposed to be necessary for the developmental pruning of retinal ganglion cell inputs to the thalamus. Mice deficient for the microglial complement receptor CR3 failed to segregate eye-specific projection territories in the thalamus, and showed increased density of presynaptic markers exclusively ^[16]. Signaling through microglial CX3CR1 was reportedly not required for activity-dependent plasticity in the mouse visual system ^[61]. Findings derived from studies of different developmental periods and brain regions, and performed on different animal models, may contribute to these discrepancies, thereby highlighting the necessity for direct evidence of microglia-mediated synaptic pruning by in vivo methods and high resolution imaging techniques.

The first indication of an alternate role of microglia in mediating synapse formation came from a study that correlated microglial maturation and distribution with the development of mouse hippocampal circuits ^[62], followed by observations suggesting that microglia might control axonal growth ^[63] and synaptogenesis ^[64]. Supporting this hypothesis, microglia-derived BDNF was shown to be necessary for activity- and learning-induced formation of functional synapses in a microglia-specific inducible Bdnf KO mouse model ^[65]. However, it should be noted that the absence of detectable Bdnf mRNA in steady state microglia was reported ^[66]. Furthermore, live imaging experiments demonstrated that Ca²⁺-dependent formation of filopodia, the precursors of dendritic spines, was induced after microglial contact on the dendritic shaft of cortical neurons and indicated by microglia-induced Ca²⁺ transients in the dendrites ^[67]. Treatment with minocycline, a tetracycline antibiotic with anti-inflammatory properties, reduced the rate of filopodia formation, leading the authors to claim that microglial activation favored filopodia formation ^[67]. Concomitantly, the induction of inflammation in the hippocampus increased the number of thin spines ^[68]. In accordance with this argument, deficiency in fractalkine signaling, which was shown to result in microglial activation ^[69], could induce microglia-mediated synapse formation and explain the increased hippocampal spine density observed in Cx3cr1 KO mice ^[22]. Here, we call for caution when interpreting synaptic phenotype noting the duality of microglial function in structural plasticity, as an elevated number of spines due to microglial dysfunction could result from reduced synaptic pruning mentioned earlier, or increased spine formation. Taken together, these data are in line with previous studies showing axotomy-induced microglial activation, followed by increased synaptogenesis ^[70]. Since microglia were found to produce the synaptogenic factor thrombospondin upon axotomy ^[71,72,73], activated microglia might participate in the reafferentation process by favoring the formation of new synapses. Nevertheless, it should be emphasized that in the physiological CNS, regulation of synaptic and structural plasticity that supports normal cognitive functions more likely involve ramified steady state microglia ^[74].

The synaptogenic effect of microglia was proposed to mediate sexual dimorphism of some brain regions. Variations in rat microglial density between male and female parietal cortex, amygdala, hippocampus, and preoptic area ^[75,76], and sex differences in murine microglial response to neuropathic pain ^[77] have been reported. In the preoptic area, a region typically associated with male-specific behaviors, male rats have a higher spine density and more reactive microglial phenotype compared to females ^[76]. Interestingly, treatment of females with the brain-masculinizing hormone estrogen ^[78] increased microglial activation and spine density in the preoptic area, and induced male-like behaviors. Sexual differentiation including estrogen-induced masculinization of dendritic spine density could be blocked by minocycline treatment ^[76]. These findings were similar to a previous study in which estrogen induced new hippocampal spine formation and growth ^[79]. Sex differences in microglial phenotype were reported in the rodent hippocampus ^[75,80]. However it remains to be investigated whether any sex difference exists in microglia and synapse maturation at the time of hippocampal circuit formation that could explain the sex differences in spatial learning observed in the adult mice ^[81,82]. Overall, it is conceivable that sex-specific induction of synapse formation by reactive microglia could have a profound effect on learning and memory.

3. Impacts of dysfunctional microglia on learning and memory

Throughout the lifetime of an individual, multiple innate and external factors are likely to influence microglial physiology and phenotype, resulting in an altered functionality of the CNS tissue-resident macrophages and inadvertently impacting cognitive capacities. We examine the key risk factors such as gene mutations, potential environmental insults, and normal aging that may lead to the formation of dysregulated microglia.

3.1. Genetic risk factors

Human diseases associated with behavioral and cognitive alterations resulting from mutations in genes expressed by microglia are termed “microgliopathies” ^[83]. Earlier, we mentioned that DAP12-deficiency in a mouse model resulted in deficient synaptic plasticity such as enhanced hippocampal LTP and impaired synaptic transmission. In humans, recessive genetic mutations in DAP12 or TREM2 (Triggering Receptor Expressed On Myeloid Cells 2) ^[84,85,86] are responsible for the microgliopathy Nasu-Hakola disease (NHD), a rare inherited neuropsychiatric condition characterized by early dementia, formation of bone cysts and premature death ^[87,88]. DAP12 transduces signals from several lymphoid and myeloid receptors including TREM2, however the molecular mechanisms linking both proteins to NHD are unclear. A role for the TREM2-DAP12 pathway in clearing apoptotic neurons was demonstrated in vitro ^[89] and in vivo ^[90] during murine developmental cell death. In prenatal mice, absence of DAP12 impaired the outgrowth of dopaminergic axons and altered the positioning of neocortical interneurons ^[63]. Another microgliopathy is the hereditary diffuse leukoencephaly with spheroids (HDLS), a rare autosomal dominant disease defined by progressive motor, behavioral, and cognitive deficits leading to severe dementia ^[91]. HDLS is caused by mutations in the tyrosine kinase domain of the colony-stimulating factor 1 receptor (CSF1R) ^[83]. Signaling through the CSF1R ^[92,93], in particular via the alternative CSF1R ligand IL-34, was found to be necessary for the development, survival and proliferation of microglia throughout the lifespan ^[94,95]. The mechanisms linking CSF1R dysfunction to HDLS are unknown. However, DAP12 was shown to regulate the ability of CSF1R to control the survival and proliferation of macrophages in vitro ^[96]. HDLS patients present degenerative alterations reminiscent of NHD ^{[83,91,97,98]}. It is plausible that NHD and HDLS may implicate the same defective signaling pathway involving DAP12, TREM2 and CSF1R.

3.2. Environmental risk factors

There are many external or environmental causes in life beginning from prenatal stages to adulthood that may alter the steady state functions and responses of microglia. Pathological activation of microglia potentially leads to non-physiological release of cytokines that cause learning and memory deficits via modulation of synaptic plasticity. The microglial developmental program is susceptible to environmental perturbations such as prenatal infections and microbiome alteration ^[99]. Maternal infection with bacterial lipopolysaccharides (LPS) was shown to sensitize or “prime” fetal microglia to later challenge, as mice injected with a subsequent dose of LPS in adulthood presented greater learning impairment when prenatally primed ^[100]. Early postnatal priming induced similar effects, as young pups infected with Escherichia coli showed memory deficits in adulthood upon exposure to a second LPS-stimulus, right before or after learning ^[101,102]. These effects were likely mediated by microglial IL-1β, as treatment with minocycline or caspase-1, an inhibitor of IL-1β synthesis, prevented the learning deficits ^[48,102]. However a conflicting report found that young mice that had been primed at neonatal stages did not display any learning impairment upon LPS exposure, and priming did not further increase LPS-induced IL-1β production ^[103]. The discrepancy could lie in the difference in ages of the animals tested and in the brain regions analyzed for IL-1β expression. Early exposure to infection or trauma also has the potential to activate microglia with long lasting consequences on the behavior ^[104].

Similar to microglial priming due to bacterial infection at an early age, mice that received high-fat diet at weaning age showed learning deficits and increased cytokine production in the hippocampus upon exposure to LPS ^[105]. Long-term hippocampal-dependent learning and memory deficits were also observed in adolescent rats treated with sugar-enriched diet ^[106] and in adult rats that were overfed during the neonatal period ^[107]. In the adult mice, high-fat diet induced the activation of hippocampal microglia, reduction in spine density, impairment of synaptic plasticity, reduced LTP, and reduction in hippocampus-dependent spatial memory test performance, all alterations of which were reversible by resuming a low fat diet ^[108].

Local treatment of the hippocampus with LPS led to microglial activation and increased IL-1β and TNFα production as well as learning and memory deficits, suggesting that local brain inflammation may impact learning and memory ^[109]. However, microglia-dependent synaptic deficits are not only induced by local inflammatory stimuli, as peripheral inflammation can also affect microglia and in turn interfere with synaptic function. Colonic inflammation led to microglial activation, overproduction of TNFα, increased excitability, and impairment of both LTP and LTD, all effects of which could be reversed by administration of minocycline ^[110,111]. Peripheral organ inflammation has been linked to behavioral alterations, fatigue and cognitive dysfunction, which collectively termed “sickness behaviors”, were associated with microglial activation indicated by elevated TNFα and nitric oxide levels in mouse brain ^[112]. Furthermore, microglia-mediated memory impairment was associated with the West Nile virus infection via the loss of hippocampal synapses, reportedly through dysregulated CR3-dependent microglial phagocytosis during viral infection and recovery ^[113].

Stress-induced learning deficits could also be mediated by microglial activation. While moderate stress can reinforce memory, chronic and strong acute forms of stress were shown to induce learning deficits associated with IL-1β ^{[114,115,116]}, IL-18 ^[117] and TNFα ^[118] production. Since these stress-induced pro-inflammatory cytokines are released by microglia ^[119,120], it led to the hypothesis that cognitive deficits due to microglial activation ^[121,122] could be induced by stress ^[123,124]. Other studies suggested that microglia could be activated or primed by glucocorticoids recognized by receptors expressed by microglial cells ^[125]. The glucocorticoids were reportedly produced during stressful events and induced learning deficits at high concentration ^[126].

Other external stressors that result in microglial activation leading to learning and memory impairments include depression, a neuropsychiatric disorder with core symptoms that resemble sickness behavior ^[127]; alcohol and drug abuse, that act on microglia via their toll-like receptor (TLR) 4 ^[128]; and sleep deprivation ^[129]. Exposure of rodents to low and high doses of environmental agents such as lead ^[130] and aluminum ^[131] for varying durations was also correlated to microglial activation, increased release of pro-inflammatory cytokines, oxidative stress, neuroinflammation, neurodegeneration and LTP deficits.

3.3. Physiological aging as a risk factor

In contrast to healthy ramified microglia, aged microglia tend to be dystrophic, more reactive or activated, prone to priming, and less competent in responding to pathological stimuli ^[5]. Dystrophic or senescent microglia with reduced cell density, morphological changes such as enlarged soma, reduced ramifications and shorter processes with diminished motility, accumulation of cellular debris, and altered expression of activation markers, were described to be prevalent in aged human and rodent brains ^{[132,133,134,135,136]}. Aged microglia exhibit increased oxidative stress via overproduction of reactive oxygen species and decreased antioxidant glutathione activity ^[133,137]. Highly ramified and hyperactive dark microglia with characteristics of oxidative stress and that more frequently encircled synaptic elements than normal ramified microglia were reportedly more commonly detected during aging ^[138].

Despite the absence of overt pathology, aged microglia display a more reactive phenotype such as upregulation of pro-inflammatory genes, antigen-presenting markers (e.g., complement components, TLR signaling, inflammasomes, increased major histocompatibility complex class II-immunoreactivity ^[139]). In rodent brain, age-dependent and microglia-associated pro-inflammatory cytokines TNFα, IL-1β and IL-6 mRNA or proteins were measured at higher levels ^{[137,140,141]}. Concomitantly, anti-inflammatory cytokines including IL-10 and TGFβ1, and microglial activation inhibitory factors such as CD200 and fractalkine receptors were down-regulated ^[139]. Despite the apparent overall increase in inflammatory profile, the reaction of aged microglia to pathological changes was reportedly delayed or impaired. Analysis of morphology and dynamic behavior of microglial response to injury in vivo in the aged neocortex in mice revealed the reduction of microglial reactivity, process motility and speed of cellular migration ^[132].

Human and rodent studies revealed that a significant population of yolk sac-derived microglia persists for a long period that may include the entire lifespan of the organism ^[8,9,142]. Thus, age-associated priming related to the accumulation of protein aggregates such as amyloid-β (Aβ) in microglia over time may induce an exaggerated inflammatory response to a subsequent stimulus in the aged CNS ^{[143,144,145]}. Changes to the microglial network and density, activation phenotype, as well as secretion of pro-inflammatory cytokines in the murine neurogenic niche of the SVZ associated with aging, was proposed to lead to the decline in neurogenesis ^[146]. Microglia were implicated in synaptic remodeling via the complement pathway during aging in a study where mice deficient for C3 were protected from synaptic loss and neuronal death in the aged hippocampus ^[147]. Taken together, normal microglial aging likely leads to various irregularities in their physiological functions, such as augmenting synaptic losses and altering brain plasticity, and presents a strong risk for the development of neurodegenerative diseases.

3.4. Multiple risk factors for Alzheimer's disease via the microglial route

Alzheimer's disease (AD) is an age-associated progressive neurodegenerative disease that represents the most common type of dementia for which no effective cure exists ^[148]. The extracellular deposition of Aβ protein, which aggregate to form compact plaques, and the intraneuronal aggregation of hyperphosphorylated microtubule-associated protein Tau (MAPT) in the form of neurofibrillary tangles, represent the two main pathological hallmarks of AD ^[149,150]. A heavy inflammatory response has been associated with AD pathology due to marked glial reactivity (microgliosis and astrogliosis) that resulted in a loss of synapses and neurons, subsequent decline in cognitive functions, and striking signs of memory deficits ^[151,152]. The association between microglia and plaques was first observed by Alois Alzheimer in post-mortem human brains ^[153]. The advent of technical approaches such as two-photon imaging in live animals revealed that brain resident microglia rapidly migrate to Aβ-plaques with which they establish intimate contacts ^{[154,155,156]}. Moreover, in APPPS1 or APP23 mouse models for AD, the number of reactive microglia increases proportionately to the plaque size via local proliferation ^{[142,154,157]}.

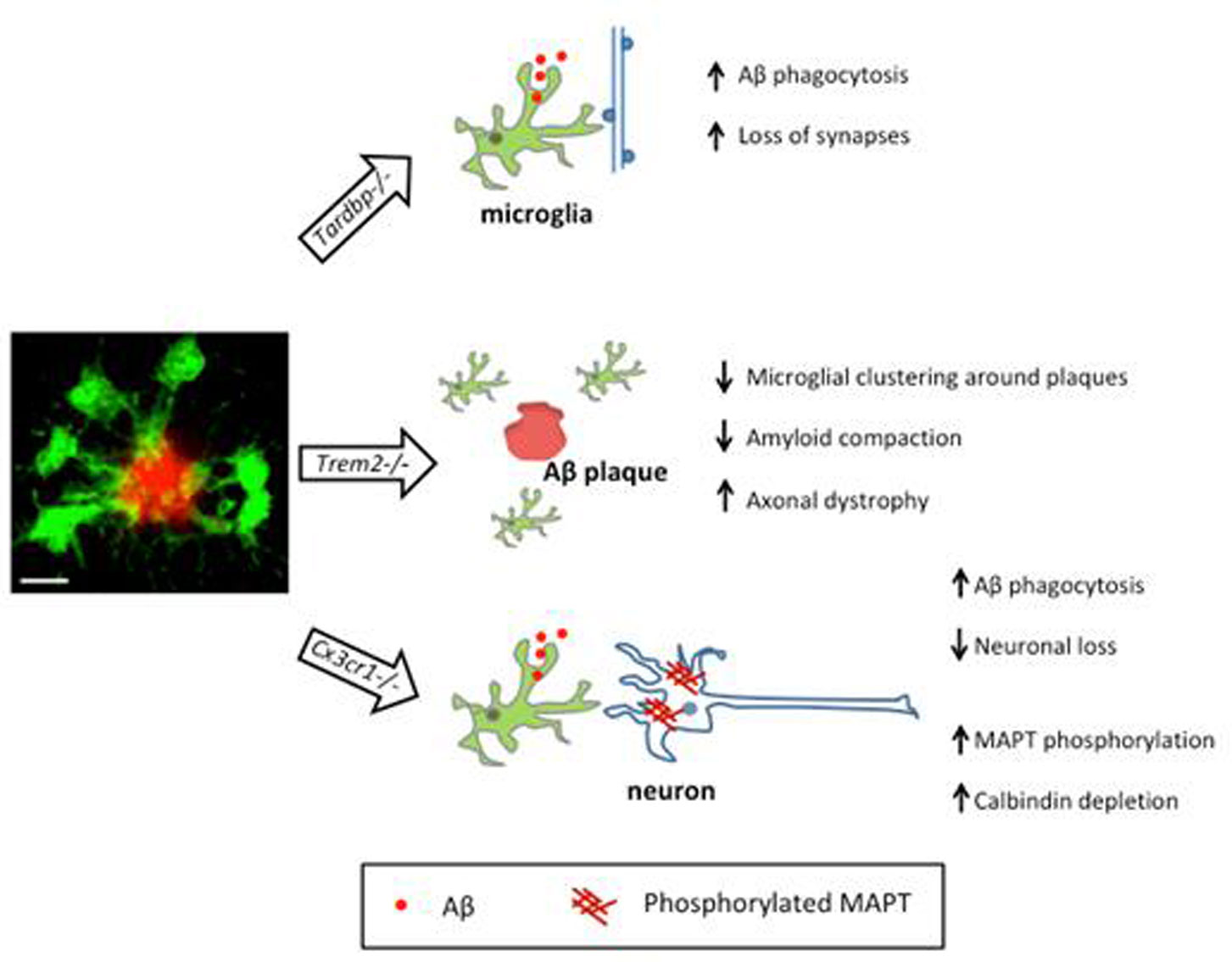
The capacity for microglia to phagocytose Aβ efficiently is compromised in aging and AD, as demonstrated by less microglial clearance of Aβ fibrils in older mice ^[158] and downregulation of microglial genes encoding Aβ receptors and Aβ-degrading enzymes ^[159]. In the APP AD mouse model, microglia-specific knockout of Tardbp, which encodes the DNA-RNA binding protein TDP-43, displayed reduced Aβ load and spine density ^[160]. Furthermore, microglial colocalization with synapsin-PSD95 puncta and expression of scavenger receptor CD68 were increased, implicating microglial TDP-43 in phagocytosis of both Aβ and dendritic spines ^[160] (Figure 2).

Early in AD progression, microglia-mediated synaptic pruning was reportedly impaired, affecting synaptic viability directly. This impairment in synaptic plasticity was linked to higher Aβ load and implicated the complement cascade based on the detection of increased C1q protein colocalization with PSD95 puncta and decreased microglial expression of CD68 in the hippocampus of J20 and APP/PS1 AD mouse models ^[161]. Genetic or pharmacological depletion of C1q in the AD models could arrest the loss of PSD95 puncta and rescue LTP in acute hippocampal slices ^[161]. Furthermore, deficiency in C3 in the APP/PS1 background resulted in the recovery of ramified surveillant microglia morphology, increased Vglut2-GluR1 puncta and expression of synaptic markers in the aged hippocampus, reduced CNS levels of pro-inflammatory TNFα, IFNγ and IL-12, and increased anti-inflammatory IL-10 expression ^[162].

Genome-wide association studies have linked numerous microglia-related polymorphisms to AD ^{[163,164,165,166,167,168]}, in particular placing the spotlight on TREM2. TREM2 expression is upregulated in plaque- or disease-associated microglia ^{[169,170,171,172]}, dark microglia ^[138], and TREM2-APOE pathway-dependent microglia ^[173]. In brains of AD patients harboring the R47H variant of TREM2 and in AD-like mice with TREM2 deficiency, reduced plaque-associated microglia with a consequent reduction in Aβ compaction and a subsequent increase in axonal dystrophy were observed ^[174,175]. This phenomenon potentially compromises the formation of a neuroprotective barrier by microglia. Another TREM2 missense mutation, T66M, which has been linked to frontotemporal dementia (discussed below), was also demonstrated in a loss-of-function knock-in mouse model to lead to impaired microglial functions including delayed immune response and reduced phagocytic activity ^[176]. Preliminary evidence suggests that TREM2 deficiency ameliorates or exacerbates amyloid pathology dependent on disease progression in the APPPS1-21 mouse model of AD ^[177]. However, it remains unclear whether microglial activation is beneficial or detrimental to AD progression and when the ineffective microglial clearance of amyloid burden begins. We briefly discuss several studies with contradictory findings and inconsistencies that possibly arose from differences in AD mouse models and disease stages investigated. In 8 months old 5XFAD mice that express 5 human familial AD gene mutations, the knockout of TREM2 resulted in an increased hippocampal Aβ accumulation consistent with a protective role of TREM2 ^[178]. However in 4 months old APPPS1 mice, the absence of TREM2 reduced inflammation and mitigated amyloid and Tau pathologies ^[179]. In another study, haploinsufficiency of TREM2 in 3 months old APPPS1-21 mice had no effect on Aβ deposition despite a marked decrease in the number and size of plaque-associated microglia ^[180]. A similar analysis done in 4 months old 5XFAD mice showed that Aβ accumulation was quantitatively similar in the presence or absence of TREM2, but the plaques appeared more diffuse without TREM2 ^[174]. TREM2 was proposed to act through mammalian target of rapamycin (mTOR) signaling in a study where TREM2-deficient microglia in AD patients and mouse model had abundant autophagic vesicles and thus impaired microglia metabolic functions and altered ATP levels ^[181]. In addition, it was demonstrated that loss of TREM2 led to reduced microglial chemotaxis and delayed responses to neuronal damage ^[182]. Dietary supplementation of cyclocreatine in Trem2-deficient 5XFAD mice tempered autophagy and restored microglial clustering around plaques, ultimately leading to decreased neuritic dystrophy ^[181]. Genetic deletion of Trem2 in the PS19 mouse model of Tau pathology led to an attenuated atrophy of the entorhinal and piriform cortices, increased detection of PSD95 in the hippocampus, normalization of microglial density and morphology, and downregulation of pro-inflammatory markers (IL-1α, IL-1β, TNFα and C1q) in the piriform cortex ^[183]. Altogether, these data suggest that TREM2 might also mitigate microglial response to Tau pathology (Figure 2).

Targeting fractalkine signaling in various AD mouse models by knockout of Cx3cr1 appeared to mitigate some pathological aspects of the disease. These were exemplified in the rescue of neuronal loss in 3XTg-AD ^[184], reduction of amyloid deposition with alteration of APP level in APPPS1 (rapid onset) and R1.40 (gradual onset) AD mouse models, and elevated uptake of Aβ ^[185,186]. Contrary to the potential beneficial effect on Aβ plaque deposition, Cx3cr1 knockout in hAPP or hTau mouse models increased microglia activation, enhanced MAPT phosphorylation and aggregation, as well as exacerbated calbindin depletion in the hippocampus and memory impairment ^{[187,188,189]} (Figure 2). In sum, microglia represent an attractive therapeutic target for mitigating the cognitive and memory deficits associated with dementia or AD.

Figure 2. Impact of microglia-specific gene mutations on the pathogenesis of Alzheimer's disease (AD). The confocal image (left) depicts a typical observation of microglial cells (labeled by CX3CR1-GFP; green) associating closely with amyloid-β (Aβ) plaques (stained with thiazine red; red) in AD mouse models. The depletion of Tardbp or TDP-43 in microglia in the APP background reduced amyloid load through the elevation of phagocytosis, but at the same time increased synaptic loss. In the R47H variant of Trem2-knockout mice, microglia failed to cluster around Aβ plaques, leading to a reduction in amyloid compaction and a subsequent increase in axonal dystrophy. The AD mouse models that lacked CX3CR1 exhibited higher Aβ-phagocytic ability and rescue of neuronal loss, or an increased phosphorylation of neuronal MAPT (microtubule-associated protein Tau) and exacerbated depletion of calbindin, within model-dependent conditions. Scale bar, 10 µm.

DownLoad: Full-Size ImgPowerPoint

3.5. Other CNS diseases associated with dysfunctional microglia

Of note, several other diseases that include symptoms involving cognitive deficits have been associated with impaired microglial functions and are briefly discussed here. Epilepsy is a disorder in which neurons are hyperactive and thus generate recurrent seizures, resulting in excitotoxicity and neuronal damages. Microglial activation has been reported in epileptic tissue, and is thought to mediate the clearance of damaged neurons to protect the intact neighboring cells ^[190]. However, protracted periods of microglial activation and inflammatory response may lead to excessive elimination of neuronal cells and neurodegeneration. Mesial temporal lobe epilepsy reportedly disrupts normal microglial phagocytosis of apoptotic newborn neuronal progenitors, subsequently propagating a damaging pro-inflammatory milieu ^[191]. Seizure-induced release of tissue plasminogen activator by microglia was proposed to mediate axonal sprouting, which favors recurrent long-term seizures ^[192,193]. Inhibition of microglial activation using minocycline in the context of epilepsy was found to be neuroprotective both in mice ^[194,195] and in humans ^[196].

Frontotemporal dementia (FTD) is characterized by neuronal loss in the frontal and temporal lobes, impairments in social behavior, comprehension skills and working memory, manifestation of compulsive behavior, and has been linked to microglia-related genetic risk factors. These factors include mutations in Progranulin ^[197,198], chromosome 9 open reading frame 72 (C9orf72) ^[199,200] and Trem2 ^[201], although the latter seems to be restricted to a few familial cases ^{[202,203,204]}. On the other hand, aggregation and subsequent loss-of-function of TDP-43 have been commonly observed in FTD patients ^[205,206]. Microglial depletion of Tardbp, which encodes TDP-43, was recently shown to induce cell death ^[207] and synaptic loss ^[160].

Trem2 was also identified as a risk factor for Parkinson's disease (PD) ^[208,209], which is characterized by the loss of dopaminergic neurons in the substantia nigra, chronic increased levels of CNS inflammatory responses ^{[210,211,212]}, and impairment of movement, cognition, learning, memory and attention. However, the association of PD with Trem2 was not confirmed in other studies and remains controversial ^[213]. While the number of reactive, antigen-presenting microglial cells with altered morphologies have been reported in postmortem PD brains and animal models for PD, the link between defective microglia and PD progression has not clearly been established at present ^[214]. On the whole, these studies demonstrate the delicate interplay between healthy microglia and neuronal function, even though the precise roles of microglial impairment in the etiology of these CNS diseases remain to be investigated.

4. Caveats, perspectives and conclusion

The precise functions and impacts of microglia in regulating learning and memory during health and disease in different brain compartments, sex and life stages have to be carefully teased apart. Of note, microglial activation could have an indirect effect on synaptic plasticity, as shown in an in vitro study where ATP released by LPS-induced activated microglia recruited astrocytes that in turn mediated the increased frequency in spontaneous excitatory post-synaptic currents ^[215]. Neurotoxic reactive astrocytes that discourage neuronal survival, outgrowth and synaptogenesis could also be induced by microglial IL-1α, TNFα and C1q ^[216]. To date, numerous studies on microglial regulation of neurogenesis, synaptic and structural plasticity have relied on heterozygous or homozygous Cx3cr1 knockout mice, as we have discussed earlier, in addition to the Cx3cr1^creER lines ^[65,217,218] that have been particularly helpful towards microglia-specific gene knockout strategies. Nevertheless, caveats exist for these animal models as oligodendrocyte progenitor cells were shown to also express Cx3cr1 in postnatal stages ^[219]. Furthermore, Cx3cr1-positive bone marrow-derived monocytes reportedly mediated microglia-independent synaptic remodeling via TNFα in a mouse model for poly (I:C)-induced sickness behavior ^[220]. Using Cx3cr1^creER lines, long-lived yolk sac-derived non-parenchymal brain macrophages ^[221] may be partially targeted in parallel and lead to confounding observations. While a true microglia-specific marker that labels all microglia from embryonic stage up to old age is still unavailable, markers such as transcription factor Sal-like 1 ^[222,223] and transmembrane protein TMEM119 ^[66] were described to be selectively expressed by microglia within the family of mononuclear phagocytes across various contexts of health and disease. Moving forward, the interference of microglial function in learning and memory could be investigated by targeting these genes.

Genetic (using the conditional Cx3cr1^creER mouse lines ^[65,217,218]) or pharmacological ^[60,92,224] depletion of microglia has been used to understand microglial function in the regulation of synaptic plasticity during postnatal CNS development as well as in AD mouse models. Transient microglial depletion during early postnatal and juvenile stages had a prolonged impact on cognition and social behavior ^[65,224] in contrast to the reversible alterations induced by treatment using the selective CSF1R inhibitor PLX3397 at adult stages ^[60,92]. Microglial depletion in preclinical animal studies related to AD did not support the hypothesis of microglial modulation of amyloid deposition. Ablation of microglia after ganciclovir application over a period of 2-4 weeks in a conditional myeloid-specific mouse model using CD11b-HSV-TK (herpes simplex virus thymidine kinase) in an APP background resulted in no change in amyloid deposits and neuronal damage ^[225]. Elimination of microglia or prevention of microglial proliferation in aged or pre-pathological 5XFAD or APPPS1 mouse models by administration of CSF1R inhibitors PLX5622 or PLX3397 ^[226,227] and GW2580 ^[228], respectively, also showed no effect on amyloid deposition. However, AD progression was delayed by prevention of neuronal loss, recovery of dendritic spine density, and reduction in CNS inflammation, as revealed by improved performances in memory and behavioral tests ^[227,228]. Microglial depletion by PLX3397 or intracerebroventricular infusion of clodronate liposomes in a mouse model carrying a viral-driven neuron-specific mutant human Tau transgene in contrast revealed a suppression of Tau pathology ^[229]. Together, these findings hint that chronically reactive microglia could mediate neuronal degeneration and alter synaptic remodeling resulting in cognitive decline. However, a 13% increase in plaque size in the cortex of aged APPPS1 mice over one week of Cx3cr1^creER-dependent microglial ablation followed by stabilization of plaque area after microglial repopulation ^[230], supports the hypothetical neuroprotective role of microglia in limiting plaque expansion by forming a barrier around existing plaques ^[231].

In conclusion, steady state microglia have a critical lifelong role in maintaining CNS homeostasis through the modulation of neuronal density, synaptic remodeling and structural plasticity, thereby affecting learning and memory. Apart from rare microglia-related gene mutations that lead to microgliopathies with symptoms of dementia, physiological aging and environmental risk factors are significant inducers of reactive, pro-inflammatory and/or neurodegenerative microglial phenotypes. The potential for microglial dysregulation over time that results in learning and memory deficits in the absence of overt pathology could in part be due to the relatively slow turnover of these tissue-resident macrophages. It remains to be addressed whether microglial reactivity and microgliosis contribute neuroprotective or neurodegenerative aspects in the etiology and progression of neurodegenerative diseases such as AD. Finally, reducing the exposure of microglia to external stressors is currently the best option for delaying or ameliorating memory loss.

Acknowledgements

The authors are grateful to Zachary Z. Freyberg and Senthilkumar Deivasigamani for their insightful comments on our manuscript. TLT was supported by the German Research Foundation (DFG, TA1029/1-1) and the Ministry of Science, Research and the Arts of Baden-Wuerttemberg (Research Seed Capital).

Conflict of interest

All authors declare no conflicts of interest in this paper.