Phage “delay” towards enhancing bacterial escape from biofilms: a more comprehensive way of viewing resistance to bacteriophages

Stephen T. Abedon; Stephen T. Abedon

doi:10.3934/microbiol.2017.2.186

AIMS Microbiology

2017, Volume 3, Issue 2: 186-226. doi: 10.3934/microbiol.2017.2.186

Previous Article Next Article

Opinion paper

Phage “delay” towards enhancing bacterial escape from biofilms: a more comprehensive way of viewing resistance to bacteriophages

Stephen T. Abedon ^,

Department of Microbiology, the Ohio State University, 1680 University Dr., Mansfield, OH 44906, USA

Received: 15 January 2017 Accepted: 17 March 2017 Published: 31 March 2017

In exploring bacterial resistance to bacteriophages, emphasis typically is placed on those mechanisms which completely prevent phage replication. Such resistance can be detected as extensive reductions in phage ability to form plaques, that is, reduced efficiency of plating. Mechanisms include restriction-modification systems, CRISPR/Cas systems, and abortive infection systems. Alternatively, phages may be reduced in their “vigor” when infecting certain bacterial hosts, that is, with phages displaying smaller burst sizes or extended latent periods rather than being outright inactivated. It is well known, as well, that most phages poorly infect bacteria that are less metabolically active. Extracellular polymers such as biofilm matrix material also may at least slow phage penetration to bacterial surfaces. Here I suggest that such “less-robust” mechanisms of resistance to bacteriophages could serve bacteria by slowing phage propagation within bacterial biofilms, that is, delaying phage impact on multiple bacteria rather than necessarily outright preventing such impact. Related bacteria, ones that are relatively near to infected bacteria, e.g., roughly 10+ µm away, consequently may be able to escape from biofilms with greater likelihood via standard dissemination-initiating mechanisms including erosion from biofilm surfaces or seeding dispersal/central hollowing. That is, given localized areas of phage infection, so long as phage spread can be reduced in rate from initial points of contact with susceptible bacteria, then bacterial survival may be enhanced due to bacteria metaphorically “running away” to more phage-free locations. Delay mechanisms—to the extent that they are less specific in terms of what phages are targeted—collectively could represent broader bacterial strategies of phage resistance versus outright phage killing, the latter especially as require specific, evolved molecular recognition of phage presence. The potential for phage delay should be taken into account when developing protocols of phage-mediated biocontrol of biofilm bacteria, e.g., as during phage therapy of chronic bacterial infections.

Keywords:

Citation: Stephen T. Abedon. Phage “delay” towards enhancing bacterial escape from biofilms: a more comprehensive way of viewing resistance to bacteriophages[J]. AIMS Microbiology, 2017, 3(2): 186-226. doi: 10.3934/microbiol.2017.2.186

Related Papers:

[1]	Noman Zahid, Ali Hassan Sodhro, Usman Rauf Kamboh, Ahmed Alkhayyat, Lei Wang . AI-driven adaptive reliable and sustainable approach for internet of things enabled healthcare system. Mathematical Biosciences and Engineering, 2022, 19(4): 3953-3971. doi: 10.3934/mbe.2022182
[2]	Hao Yuan, Qiang Chen, Hongbing Li, Die Zeng, Tianwen Wu, Yuning Wang, Wei Zhang . Improved beluga whale optimization algorithm based cluster routing in wireless sensor networks. Mathematical Biosciences and Engineering, 2024, 21(3): 4587-4625. doi: 10.3934/mbe.2024202
[3]	Tingting Yang, Yi He . Design of intelligent robots for tourism management service based on green computing. Mathematical Biosciences and Engineering, 2023, 20(3): 4798-4815. doi: 10.3934/mbe.2023222
[4]	Angel Martin-del Rey . A novel model for malware propagation on wireless sensor networks. Mathematical Biosciences and Engineering, 2024, 21(3): 3967-3998. doi: 10.3934/mbe.2024176
[5]	Naila Naz, Muazzam A Khan, Suliman A. Alsuhibany, Muhammad Diyan, Zhiyuan Tan, Muhammad Almas Khan, Jawad Ahmad . Ensemble learning-based IDS for sensors telemetry data in IoT networks. Mathematical Biosciences and Engineering, 2022, 19(10): 10550-10580. doi: 10.3934/mbe.2022493
[6]	Haitao Huang, Min Tian, Jie Zhou, Xiang Liu . Reliable task allocation for soil moisture wireless sensor networks using differential evolution adaptive elite butterfly optimization algorithm. Mathematical Biosciences and Engineering, 2023, 20(8): 14675-14698. doi: 10.3934/mbe.2023656
[7]	B. Kiruthika, Shyamala Bharathi P . Intelligent dynamic trust secure attacker detection routing for WSN-IoT networks. Mathematical Biosciences and Engineering, 2023, 20(2): 4243-4257. doi: 10.3934/mbe.2023198
[8]	Peng-Yeng Yin, Chih-Chun Tsai, Rong-Fuh Day, Ching-Ying Tung, Bir Bhanu . Ensemble learning of model hyperparameters and spatiotemporal data for calibration of low-cost PM_2.5 sensors. Mathematical Biosciences and Engineering, 2019, 16(6): 6858-6873. doi: 10.3934/mbe.2019343
[9]	Faten S. Alamri, Khalid Haseeb, Tanzila Saba, Jaime Lloret, Jose M. Jimenez . Multimedia IoT-surveillance optimization model using mobile-edge authentic computing. Mathematical Biosciences and Engineering, 2023, 20(11): 19174-19190. doi: 10.3934/mbe.2023847
[10]	Huanhai Yang, Shue Liu . A prediction model of aquaculture water quality based on multiscale decomposition. Mathematical Biosciences and Engineering, 2021, 18(6): 7561-7579. doi: 10.3934/mbe.2021374

Abstract

1. Introduction

Shigellosis is an acute gastroenteritis infection that leads to approximately 165 million infections and 1.1 million deaths per annum [1]. Most of the deaths are related to children in the age group of less than 5 years old [2]. Shigellosis is caused by facultatively anaerobic, non-motile Gram-negative, rod-shaped bacteria belonging to the genus Shigella. Shigella infection involves invasion and replication within the colonic epithelium, resulting in severe inflammation and epithelial destruction [3]. There are four groups of Shigella in the genus, which includes Shigella dysenteriae, S. boydii, S. flexneri and S. sonnei. Each group is further classified into serotypes and sub-serotypes based on their lipopolysaccharide O-antigen repeats [3]. Epidemiological studies showed that S. dysenteriae was a dominant cause of large epidemics in the past and is now rarely found while S. boydii is infrequently isolated [4]. On the other hand, S. flexneri and S. sonnei are the major causes for Shigellosis. However, the two Shigella strains show distinct geographic distribution patterns, which relies on the socioeconomic conditions of the area. Specifically, S. sonnei is more tightly linked to countries with higher human development index such as Europe and North America while S. flexneri dominates in the low-income regions such as Africa and some of the Asian countries [3]. With the improvement of socioeconomic conditions, transition of dominant strains from S. flexneri to S. sonnei was also observed [5].

S. flexneri and S. sonnei were earlier susceptible to a spectrum of antibiotics. New drug resistant phenotype normally develops within a decade of their release [3]. However, due to antibiotics abuse, drug or multi-drug resistant (MDR) strains emerge more frequently than ever [6]. In addition, international travellers and unprotected sex between men increase the dissemination of Shigella across countries and lead to potential increase of antibiotic resistance [3]. Historically, Shigella was treated with antibiotic drugs such as sulphonamides, tetracycline, and chloramphenicol successively [7]. Antibiotics such as ampicillin, co-trimoxazole, nalidixic acid, and fluoroquinolones were then introduced for combating the bug due to resistance to former drugs [7]. When fluoroquinolones resistant Shigella strains emerged, stronger drugs like ceftriaxone, pivmecillinam, and azithromycin were used for treating the infection [7]. Thus, MDR Shigella strains present a heavy burden and emerging threats to the society. Common strategies of bacterial antibiotic resistance include but not limited to reduced drug penetration, antibiotics efflux, target modification by mutation and antibiotics hydrolysis [7]. Currently, many shigellosis outbreaks are linked to resistant Shigella strains [7]. Rapid increase and widening of spectrum in antibiotics resistance makes Shigella hard to be adequately controlled by existing prevention and treatment measures [8]. Thus, endeavours have been tried to accelerate the development of Shigella vaccines. Vaccine antigens, Shigella subunit vaccines, live oral Shigella vaccines, and also killed whole-cell oral Shigella vaccines are currently under development [3].

Shigella spp. were evolved from non-pathogenic E. coli ancestors by acquisition of chromosomal pathogenicity islands and a large virulence plasmid while genes related with anti-virulence such as cadA and ompT, bacterial mobility like flagella and fimbriae, and catabolism were lost [9]. Pathogenicity of Shigella virulence mainly involves Type III secretion system (T3SS), adherence, invasion, intracellular mobility and spread, immune system manipulation and evasion, and toxin, etc [10]. Accepted paradigm indicated that increased antibiotic resistance is associated with fitness costs, resulting in reductions in in vivo virulence [11]. However, experimental validation of this accepted paradigm is modest. Recent studies suggested that there may be a complex interplay between bacterial virulence and resistance [12]. It has been observed that enhanced virulence and advent of antibiotic resistance often arise almost simultaneously [12]. In addition, a global sensory-transduction system BfmRS in Acinetobacter baumannii controls both enhanced virulence and resistance [13]. Accordingly, loss of aminoglycoside resistance regulator, AmgRS, was found to enhance aminoglycoside action against bacteria while reducing bacterial virulence [14]. Moreover, an experimental study found that increase in antibiotic resistance might be exacerbated by fitness advantages that enhance virulence in drug-resistant microbes, which was consistently verified in three pathogenic bacteria Pseudomonas aeruginosa, Acinetobacter baumannii and Vibrio cholerae [15]. Although recent progresses suggested that resistance and virulence might be coupled, genetic linkages between the two factors are still insufficient and largely ignored, which hinders further experimental verification of the relationship.

In this study, we collected 15 S. flexneri strains from 7 municipal Centers for Disease Control and Prevention (CDC) in Jiangsu province. Profiles of resistance to 9 antibiotics, that is, Amoxicillin/Clavulanic acid (AMC), Ceftiophene (CFT), Cefotaxime (CTX), Gentamicin (GEN), Nalidixic acid (NAL), Norfloxacin (NOR), Tetracycline (TBT), and compound Sulfamethoxazole (SMZ), were experimentally verified. All strains were sequenced via next-generation high-throughput sequencing platform, which were then analysed for core-/pan-genomes and phylogenomic relationships. Distribution patterns of virulence factors under 4 categories belonging to 31 functional groups were studied. Differential distribution patterns of virulence factors were observed in sequenced strains by comparing antibiotic sensitive and resistant strains. In addition, abundance of specific groups of virulence factors and extent of resistance were also correlated, which may provide genetic support for the positive relationship between virulence and resistance.

2. Methods and materials

2.1. Bacterial isolates, growth conditions and DNA extraction

Shigella is currently categorized as class B infectious disease in China. Pathogenic bacteria detected in local hospitals should be reported to the provincial CDC by municipal CDC. Through collaboration with provincial CDC, 15 Shigella flexneri strains from different patients with either diarrhea or dysentery in different hospitals of 7 municipal cities were isolated by using routine biochemical techniques. Resistance profile to 9 antibiotics (AMC, CFT, CTX, GEN, NAL, NOR, TBT and SMZ) as previously described for each strain was provided by CDC based on their routine screening procedures. Isolates of Shigella flexneri were plated on trypticase soya agar (TSA). Picked-up single colony was then inoculated in 5ml trypticase soya broth (TSB) and incubated overnight at 37 °C with shaking rate of 200 rpm. DNA isolation was performed using Easy-DNA™ Kit for genomic DNA isolation (Invitrogen Life Technologies, Carlsbad, CA, USA)

2.2. Genome sequencing, assembly, and annotation

Genomes of the 15 Shigella flexneri isolates were sequenced at Beijing Genome Institute (BGI) in Shenzhen, China by using next-generation sequencing platforms. Genomic DNA (1.5 µg) was fragmented in a microTube using M220 Focused Ultrasonicator (Covaris Inc., Woburn, MA, USA), which were then validated by average molecule length using the Agilent 2100 bioanalyzer instrument (Agilent DNA 1000 Reagents) and quantified by real-time quantitative PCR (qPCR). The qualified libraries were amplified within the flow cell on the cBot instrument for cluster generation (Hiseq 4000 PE Cluster Kit Illumina). The clustered flow cell was loaded onto the Hiseq 4000 Sequencer for paired-end sequencing (Hiseq 4000 SBS Kit, Illumina) with recommended read lengths 100bp or 150bp. Obtained sequences were assessed via FastQC, assembled via SPAdes [16], recorded and reordered via MAUVE [17] based on reference genome S. flexneri 2a str. 301 by following Edwards and Holt's beginner's guide to comparative bacterial genome analysis using next-generation sequence data (Version 2) [18]. For the annotation process, assembled DNA sequences of the new draft genomes from the 15 isolates were run through an automatic annotation pipeline via Prokka (rapid prokaryotic genome annotation), followed by manual curation in some cases [19]. Ten files were generated in the specified output directory, such as FASTA file of translated coding genes (protein), FASTA file of all genomic features (nucleotide), and Genbank file containing sequences and annotations, etc.

2.3. Orthologous gene prediction and genome sequence comparison

Core-/pan-genome analysis was performed by using standalone software Roary [20]. Core genes (99% ≤ strains ≤ 100%), soft core genes (95% ≤ strains < 99%), shell genes (15% ≤ strains < 95%) and cloud genes (0% ≤ strains < 15%) were calculated. Core and unique genes in the genomes were illustrated in Venn diagram. S. flexneri genomes were visualized in circular form genome by comparing to the reference genome S. flexneri 2a str. 301 via standalone software BRIG [21]. Bacterial analysis pipeline from Center for Genomic Epidemiology (https://cge.cbs.dtu.dk/services/cge/index.php) was used to compare the genomes. Only pre-assembled contig files were submitted to the online server. Theoretical distributions of antibiotic resistance genes and virulence genes were identified, together with plasmid sequences. Multilocus sequence type (MLST) was also performed based on seven housekeeping genes adk, fumC, gyrB, icd, mdh, purA, and recA.

2.4. Phylogenomic analysis and tree visualization

A Newick tree for 15 Shigella flexneri strains, together with another 12 Shigella sonnei strains (unpublished data), was generated based on 3052 core genes in each genome by the phylogenomic analysis with default 1000-time bootstrapping tests via FastTree incorporated in software Roary [22]. The tree was then visualized through online webserver interactive Tree of Life (iTOL) [23]. Genome size, number of MDR, and antibiotic resistance profiles for each strain were then added to the tree by using multi-bar and binary templates in iTOL server.

2.5. Identification and comparison of putative virulence factors in the Shigella genomes

31 groups of bacterial virulence factors that belong to four categories were downloaded from the Virulence Factor Database (VFDB) [24]. These virulence factors were then used to screen Shigella translated CDSs via phmmer command (E-value < 0.00001) in HMMER package [25]. For each group of virulence factors, multiple homologous sequences were found in corresponding proteomes. These homologous sequences were then processed to get rid of redundant sequences. MDR (resistance to more than 1 antibiotics) and sensitive S. flexneri strains (resistance to 0 antibiotics) were compared in terms of the abundance of specific groups of virulence factors via in-house Python scripts.

2.6. Correlational analysis between virulence and antibiotics resistance

The total number of non-redundant putative virulence factors in each group for each proteome was calculated. Distinct distribution patterns of virulence factors were observed. Correlation between virulence and resistance were further studied by principal component analysis (PCA), which clustered sensitive and resistant strains separately based on the differences of virulence factors.

3. Results

3.1. Collection of clinically isolated Shigella strains

15 Shigella flexneri strains with different antibiotic resistance profiles were isolated from 7 cities in Jiangsu province of China. Another 12 strains belonging to S. sonnei were also collected and used here only as a comparison for phylogenomic study. Four serotypes of S. flexneri were experimentally verified, which includes F1a (4 strains), F1b (1 strain), F2a (8 strains), and F2b (2 strains). Sequence type ST245 was identified in these Shigella isolates according to MLST based on seven housekeeping genes. As for antibiotic resistant profiles of the 27 strains, MDR strains ranges from 5 to 9 drug resistance while no or single resistance strains were considered as sensitive. A phylogenomic tree was constructed via core genomes of studies strains, which was incorporated with genome sizes and resistance profiles (Figure 1). Distinct features were observed between the two bacterial strains. A clear genome reduction was identified in sensitive strains when compared with MDR strains (P-value < 0.05). In addition, all S. sonnei strains are sensitive to Norfloxacin (NOR) and more labile toward Amoxicillin/Clavulanic acid (AMC) when compared with S. flexneri.

Figure 1. Phylogenomic tree generated via core genes of 27 Shigella strains, which divided S. sonnei and S. flexneri into two branches. Genome size (black bar) and degree of antibiotic resistance (red bar) were incorporated, accordingly. Bootstrapping values (1000 times) were visualized through red square symbols of varying size on the branches. The presence (filled squares) and absence (empty squares) of nine antibiotics that were tested in this study, which included Amoxicillin/Clavulanic acid (AMC), Ceftiophene (CFT), Cefotaxime (CTX), Gentamicin (GEN), Nalidixic acid (NAL), Norfloxacin (NOR), Tetracycline (TBT), and compound Sulfamethoxazole (SMZ), were presented. No square means intermittent level of resistance. AMC and NOR shows the most apparent resistance difference between S. flexneri and S. sonnei. ^# Most sensitive strains with MDR value of 0 and 1 (vertical line 1). *Most resistant strains with MDR value of 8 and 9 (vertical line 8).

DownLoad: Full-Size Img PowerPoint

3.2. Genome assembly, annotation, and comparison

General features of the 15 S. flexneri genomes are presented in Table 1, which were obtained by integrating genome assembly and annotation results. Genome size ranges from 4.21 Mbps to 4.63 Mbps. The number of predicted protein-encoding open reading frames (ORFs) in the 15 isolates varied from 4160 (S15054) to 4608 (S13028). The total GC content ranges from 50.38% to 50.78% and is relatively consistent among isolates. All strains have a single tmRNA coding gene. The number of ribosome RNA (rRNA) and transfer RNA (tRNA) coding genes among strains varies slightly with no significant difference.

Table 1. Comparison of 15 S. flexneri strains based on key genome assembly and annotation parameters.

ID	Serotype	BPs^#	N50	Contigs	CG%^#	CDS^#	tmRNA^#	tRNA^#	rRNA^#
S13016	F2a	4253276	24106	379	50.75	4173	1	80	6
S13028	F2b	4633307	28586	418	50.38	4608	1	79	5
S13048	F1a	4354182	30242	320	50.7	4305	1	81	6
S13068	F2b	4480462	30192	356	50.5	4434	1	81	6
S13073	F1a	4608113	29656	382	50.5	4577	1	79	5
S13091	F2a	4586630	28583	403	50.47	4538	1	81	5
S13109	F2a	4387425	22591	472	50.66	4309	1	78	6
S13126	F2a	4616160	19223	600	50.52	4532	1	81	4
S14007	F2a	4542085	29286	391	50.45	4487	1	77	5
S14013	F2a	4601323	29308	398	50.47	4554	1	80	5
S14046	F1a	4557758	29656	394	50.46	4520	1	81	5
S14131	F2a	4475708	29656	360	50.42	4417	1	79	6
S15008	F1a	4608066	30073	381	50.48	4581	1	80	5
S15054	F1b	4212908	31762	292	50.78	4160	1	79	6
S15097	F2a	4542196	30475	371	50.4	4507	1	79	5

^#BPs: Base pairs; CDS: coding sequences; GC%: Percentage of GC pairs. tmRNA: transfer-messenger RNA gene. tRNA: transfer RNA gene. rRNA: ribosomal RNA gene.

| Show Table

DownLoad: CSV

By using progressive Mauve from the Mauve software, we compared the ordered genome assembly of S. flexneri with S. flexneri 2a str. 301 as a reference genome. It seems that the chromosomal alignments of these strains are approximately identical. Additional genomic features of the 15 S. flexneri strains against reference genome S. flexneri 2a str. 301, such as sequence similarity and distribution of GC content were also analyzed and presented in Figure 2, which indicated that S. flexneri genomes are comparatively well reserved among strains.

Figure 2. Genome comparison of 15 isolated S. flexneri strains against reference genome S. flexneri 2a str. 301 generated by BRIG 0.95. The inner cycle (black) represents the complete genome of the reference strain and the shade of each colors denote the similarities between each strain with reference strain. GC content and GC skew (+/-) were illustrated in-between.

DownLoad: Full-Size Img PowerPoint

3.3. Core- and pan-genome of 15 Shigella flexneri isolates

Core and pan-genome analyses for 15 S. flexneri isolates were determined by Roary through comparison of the translated CDS set, followed by clustering of orthologous proteins and the representatives of each orthologous cluster and strain-specific CDS in the total pan-genome. The total pan-genome for the 15 compared S. flexneri strains encompasses 5626 CDS. Of these, 3742 (66.51% of total CDS) are core conserved genes across all 15 Shigella genomes. A total of 1884 protein CDS (33.49% of the pan-genome total) constitute the accessory fraction, which are unique to each genome. The lowest numbers of specific genes were encoded by S. flexneri strains S13016 and S15054, with 476 and 464, respectively. The highest numbers of specific genes belong to S. flexneri strains S13028 and S13073, with 908 and 883, respectively (Figure 3). Interestingly, the former two strains are completely sensitive to the nine antibiotics while the latter two strains are resistant to all the tested antibiotics. This is consistent with theoretical prediction of antibiotic resistance genes (ARGs) via Bacterial Analysis Pipeline from Center for Genomic Epidemiology, in which S13016 has no resistance genes and S15054 was found to harbour a single resistance gene sul2 only. In contrast, other MDR strains have abundant ARGs. In addition, MDR S. flexneri strains are commonly equipped with virulence factors such as capU, gad, ipaD, lpfA, pic, sepA, sigA, and virF. In contrast, sensitive strains only have partial set of these genes, that is, gad, lpfA, pic, and sigA. Theoretical analysis found that S13016 has no known plasmid while S15054 harbors plasmid replicons of Col(MG828) and ColRNAI with no known typing. On the other hand, MDR strains have replicon typing IncN, IncI, and IncF except for S13048. For details, please refer to Table S1.

Figure 3. Venn diagram of core- and pan-genome of 15 S. flexneri strains. 3742 core genes were shared by all strains while varied number of genes were present in each strain as unique genes. The two sensitive strains (S13106 and S15054) have the lowest number of unique genes (476 and 464) while the two most resistant strains (S13028 and S13073) have the highest number of unique genes (908 and 993).

DownLoad: Full-Size Img PowerPoint

3.4. Distribution of virulence factors among S. flexneri strains

In silico identification of the putative virulence genes were performed on the translated CDSs of all isolated S. flexneri strains. All the putative virulence factors were classified into 4 major categories, that is, adhesion and invasion, secretion system and effectors, toxin, and iron acquisition, which were further divided into 31 functional groups. Distribution patterns of the virulence factors and their abundance in each strain were presented in Table 2. Nine groups of virulence factors are completely missing in all S. flexneri strains, which are β-PFTs (pore-forming toxin), superantigens and superantigen like protein, surface acting enzymes, glucosyltransferase, guanylate adenylate cyclase, deamidase, rRNA N-glycosidase, metalloprotease, intracellular PFTs. Five groups of virulence factors, that is, sortase assembled pili, fibrinogen-binding protein, collagen-binding protein, T7SS, and ADP Ribosyltransferase, are highly conserved and equally distributed in these strains. For the rest of the 17 functional groups, most of them were skewedly distributed in highly resistant strains (MDR = 9) when compared with sensitive strains, especially for Chaperone usher and T3SS. In order to better understand the relationship between resistance and virulence, principal component analysis was performed. Although many factors interfere, an apparent cluster could be observed for sensitive and resistant strains in terms of abundance of functional groups of virulence factors (Figure 4).

Figure 4. Principal component analysis (PCA) of the relationship between antibiotic resistance and virulence factors in 15 sequenced Shigella flexneri strains. S13016 and S15054 are antibiotics-sensitive strains while the rest strains are multi-drug resistant. The two sensitive strains have comparatively less virulence factors in a majority of functional groups while resistant strains have comparatively higher number of certain groups of virulence factors. Thus, resistance and virulence could have a mutual improvement relationship, although exceptions do exist.

DownLoad: Full-Size Img PowerPoint

Table 2. Distribution patterns of 4 categories of virulence factors that belong to 31 groups among 15 Shigella flexneri strains in terms of antibiotic resistance. Sensitive strains have no resistance or only resist to one antibiotics. The four categories of VFs are Adhesion & Invasion, Secretion system & Effectors, Toxin, Iron acquisition. MDR strains have more than one resistance. PTS: Pore-forming toxins. It is noteworthy that the number of virulence factors represents the number of hits identified in bacterial proteomes via blastp.

	Shigella flexneri Strains	S13016	S15054	S13048	S14007	S14131	S13068	S14013	S14046	S15008	S15097	S13109	S13028	S13073	S13091	S13126
	MDR	0	0	6	6	6	7	7	7	7	7	8	9	9	9	9
Adhesion & Invasion	Chaperone usher	129	131	135	137	135	134	136	137	138	137	135	138	138	137	135
	Extracellular nucleation precipitation	14	13	14	14	14	14	14	14	14	14	14	14	14	14	13
	Type 4 pili	122	130	125	129	127	135	142	130	140	135	124	138	140	139	129
	Flagella	192	192	191	197	198	197	198	197	197	196	192	198	197	197	197
	Autotransporter	17	13	17	19	19	19	19	19	19	19	18	19	19	19	19
	Fibronectin-binding protein	51	45	51	53	53	49	53	53	53	50	53	53	53	53	53
	Other adherence invasion related VFs	62	59	60	61	61	57	62	61	61	58	63	61	61	61	60
Secretion system & Effectors	T2SS	8	8	8	9	9	13	12	9	13	13	8	14	13	13	9
	T3SS	159	157	161	214	211	213	214	217	218	210	168	218	217	215	212
	T4SS	32	33	31	33	32	40	41	35	42	41	32	53	41	41	34
	T5SS	18	14	18	20	20	20	20	20	20	20	19	20	20	20	20
	T6SS	152	152	153	154	154	152	154	153	154	154	152	154	154	154	155
Toxin	α-PFTs	2	2	2	2	2	2	2	2	2	2	1	2	2	2	1
Toxin	Dnase1 genotoxin	29	27	29	28	29	28	29	28	28	28	29	29	28	29	29
	MDR	0	0	6	6	6	7	7	7	7	7	8	9	9	9	9
Iron acquisition	Siderophore mediated iron uptake	272	259	275	277	277	273	279	277	277	274	275	278	279	279	280
	Heme-mediated iron uptake	109	105	108	108	108	106	108	108	108	108	108	108	108	108	108
	Transferrin and lactoferrin mediated iron uptake	3	2	3	3	3	3	3	3	3	3	2	3	3	3	3

^#Nine groups of virulence factors are not present in all S. flexneri strains, which are β-PFTs, Superantigens and superantigen like protein, Surface acting enzymes, Glucosyltransferase, Guanylate adenylate cyclase, Deamidase, rRNA N-glycosidase, Metalloprotease, and Intracellular PFTs. *Five groups of virulence factors have equal number of virulence factors in all strains, which are Sortase assembled pili (n = 1), Fibrinogen-binding protein (n = 3), Collagen-binding protein (n = 8), T7SS (n = 1) and ADP Ribosyltransferase (n = 1).

| Show Table

DownLoad: CSV

3.5. Genes exclusively associated with antibiotic resistant and sensitive strains

The gene presence and absence matrix for all S. flexneri strains were produced by Roary. A complete list of total genes for all strains were listed against 15 S. flexneri strains with 0 as absence and 1 as presence (Table S2). Function for translated protein is also annotated except for hypothetical proteins. By using filter function in Excel table, genes that are exclusively associated with resistant strains (12 genes) or sensitive strains (9 genes) were selected and presented in Table 3.

Table 3. Genes exclusively associated with antibiotic resistant and sensitive strains, respectively. Corresponding functions were obtained from UniProt database. Each gene was assigned into functional groups of virulence factors if there is any match.

S. flexneri	Gene	Functions	VF Groups
Resistant strains	aidB_2	Putative acyl-CoA dehydrogenase	DNase I genotoxin
	bisC	Biotin sulfoxide reductase	-
	dhfrI	Trimethoprim resistance protein	-
	flgE	Flagellar hook protein	Flagella
	tnsA	Transposon Tn7 transposition protein	-
	tnsB
	tnsC
	tnsE
	wecD_2	dTDP-fucosamine acetyltransferase	-
	xerC_4	Tyrosine recombinase	Chaperone usher pathway
	xerD_3	Tyrosine recombinase	Chaperone usher pathway
	ydiN_1	Amino acid/amine transport protein	-
Sensitive Strains	alkA	DNA-3-methyladenine glycosylase	-
	bcsC_1	Cellulose synthase subunit	-
	dgcE_1	Putative diguanylate cyclase	Type IV pill
	dgcE_2
	dgcE_3
	dnaK_2	Putative chaperone	Adherence and invasion
	dnaK_3	Putative chaperone	Adherence and invasion
	pgrR_3	HTH-type transcriptional regulator	Siderophore mediated iron uptake
	ycaM	Inner membrane transporter	-

^#Genes with unknown functions are not included.

| Show Table

DownLoad: CSV

4. Discussion

15 newly isolated and completely sequenced S. flexneri strains were thoroughly analysed in terms of distributions of virulence factors. Although classical thoughts support that virulence and resistance are negatively related, more evidence suggested that virulence and resistance could be enhanced simultaneously [11],[12],[15]. Initial phylogenomic analysis separated sensitive and resistant strains into different clusters (Figure 1), which reflected the intrinsic differences of evolutionary pathways between the two groups. Genome sizes of sensitive and resistant groups also show apparent difference, that is, smaller genomes (4167 CDSs on average) associated with sensitive strains and larger genome (4490 CDSs on average) linked to resistant strains. Similarly, another study focusing on sensitive and resistant E. coli isolates also found that more antibiotic sensitive Sudanese strain have smaller genome size while the genome of the resistant Chinese strain is larger [26]. Physically, it is rather difficult for bacteria to develop genetic systems with small genomes. In fact, it has been observed that multidrug resistance phenotype is a function of genome size based on comparative analysis of 22 bacterial species, which is also known as the ‘size matters’ hypothesis [27].

Core-/pan-genome analysis identified that S. flexneri strains have different number of unique genes except for the 3742 shared core genes, which reflects the heterogeneity within the same strains. In addition, the two sensitive strains, S13106 and S15054, have the lowest number of unique genes (476 and 464) while bacteria with the highest number of unique genes (908 and 993) are two most resistant strains, S13028 and S13073 (Figure 3). Specific genes in these strains could reflect bacterial characteristics and dynamics, leading to a better understanding of epidemiological features of S. flexneri [28]. Insights into these genes are out of the scope of this study and will be explored for future studies.

As for the distribution patterns of functional groups of virulence factors in S. flexneri strains, specific patterns were observed, which may provide evidence to support the positive correlation between increased virulence and enhanced antibiotic resistance. It was clear and consistent that nine groups of virulence factors are not present, and another five groups of virulence factors are equally distributed in all S. flexneri strains. Among the 17 virulence factors that are differentially distributed in the studied strains, chaperon usher, type 4 pili, flagella, T3SS, T6SS, siderophore mediated iron uptake, and heme-mediated iron uptake are abundantly present in the genomes of all strains. As for these seven groups of virulence factors, T3SS shows most distinct differences between sensitive strains (158 VFs) and resistant strains (207 VFs) on average. As previously reported, T3SS is a group of specialized protein export systems utilized by bacteria to effectively exploit eukaryotic hosts and contributes to bacterial adherence, invasion, and manipulation of the host's intracellular trafficking and immune systems [10]. Thus, in the multi-resistant Shigella strains, high number of virulence factors in T3SS groups could be very likely to occur at the same time. In fact, virulence mechanisms functioning to overcome host defence systems and antibiotic resistance are necessary for bacteria to survive antimicrobial treatments. Their collaborative work facilitates the MDR S. flexneri strains to adapt to and survive in competitive and demanding environments [29]. In addition, principal component analysis incorporating antibiotic resistance profile and 17 functional groups of virulence factors also showed that sensitive strain S. flexneri strain S15054 is isolated from other strains and most closely related to another sensitive strain S13016. All other resistant strains were all closely clustered together. Thus, from statistical point of view, it was also shown that virulence and antibiotic resistance are closely and positively correlated [12]. However, it should be notified that the spread of the two low resistant isolates in Figure 4 is a bit large. More S. flexneri strains should be included in future to further validate the claim.

Unique genes associated with sensitive and resistant strains were also identified based on the gene presence and absence table generated by core-/pan-genome analysis. It was found that all multi-drug resistant S. flexneri strains uniquely harbors four Tn7 transposon genes (tnsA, tnsB, tnsC, tnsE) and a trimethoprim resistance protein, which reflects that these strains are probably and comparatively more plastic and versatile at genome level and are more capable of acquiring resistance [30]. On the other hand, sensitive strains uniquely have type IV pill related genes (dgcE_1, dgcE_2, dgcE_3), genes involved in adherence and invasion (dnaK_2, dnaK_3), and the HTH-type transcriptional regulator gene pgrR_3 that is responsible for iron uptake. All these features emphasize that sensitive strains are more likely have specialized tools to exploit cells for reproduction. Studies confirmed that bacterial strains acquiring antibiotic resistance have a lower growth rate and are less transmissible than their susceptible counterparts [31].

Except for the interplay between virulence and resistance, several studies also proposed that antibiotic resistance is linked with bacterial intracellular and environmental persistence. In specificity, antibiotic-resistant strains such as Escherichia coli have been reported to survive longer in macrophages [32]. Further study confirmed that resistance to antibiotics and to immune system are interconnected [33]. Moreover, Vogwill et al. showed that survival of antibiotic and environmental stressors is positively correlated while specific mechanisms are unrelated in Pseudomonas strains [34]. Thus, survival and resistance could have potential interactions in bacteria. However, it was also reported that antibiotic-resistant fecal enterococci did not survive longer than antibiotic sensitive strains [35]. The possession of the antibiotic resistance plasmids in E. coli did not promote bacterial survival under starvation conditions, neither [36]. Considering the controversial conclusions, it would also be interesting to investigate this relationship via theoretical analysis, which could provide more insights into this issue and support for experimental studies in future.

5. Conclusions

15 newly sequenced S. flexneri genomes isolated from clinical samples were assembled, annotated and compared by following several standardized genome analysis pipelines [16],[19],[20]. We then identified strain-specific differences in the gain and loss of putative virulence factors in this preliminary study. In addition, abundance of certain functional groups of virulence factors is positively correlated with the extent of antibiotic resistance based on the comparison of the highly resistant and susceptible strains. Several groups of virulence factors were highlighted due to their tight relationships with strong resistant phenotypes, such as chaperone usher and T3SS, etc. Although virulence and resistance develop on different timescales and share no much common mechanisms, they may share some common characteristics [29]. Thus, antibiotic resistance and virulence are likely to have synergistic effects toward efficiently exploiting host cells in order to reproduce and transmit extensively. However, association between virulence and resistance is an increasing problem and the answer to this question is becoming more beneficial for pathogenic bacteria [29]. This study provides a starting point to address the question of how virulence and antibiotic resistance may interplay in Shigella flexneri by looking into the subtle classification of virulence factors into 31 functional groups. Although the result would be much more convincing if we can incorporate other Shigella flexneri genomes from the public database (1121 sub-strains in PATRIC database version 3.5.39) into the study, antibiotic resistance and susceptibility phenotype data for these strains are largely missing, which greatly hinders the understanding of the interactions between the two factors. Thus, in further studies, more antibiotic resistance phenotypes should be deposited into database, together with virulence phenotypes and genomic data. In addition, fitness costs should also be incorporated to tackle the intriguing relationship among virulence, stress resistance, and antibiotic resistance from the bioinformatics point of view.

References

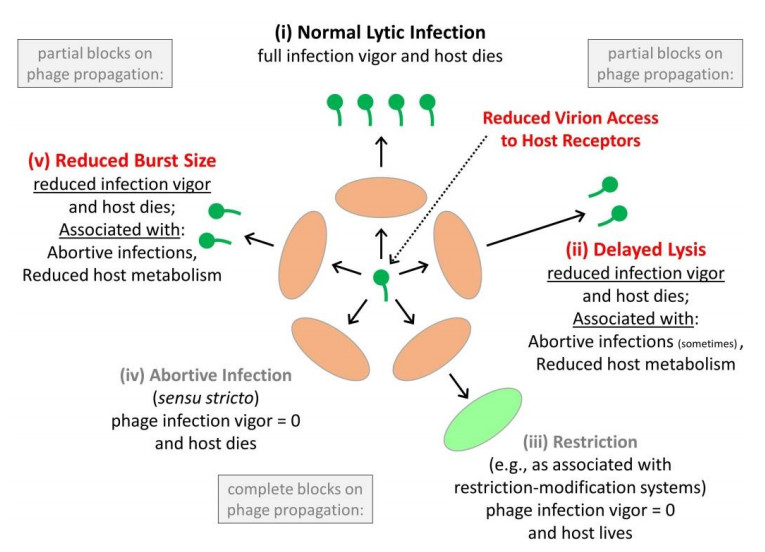
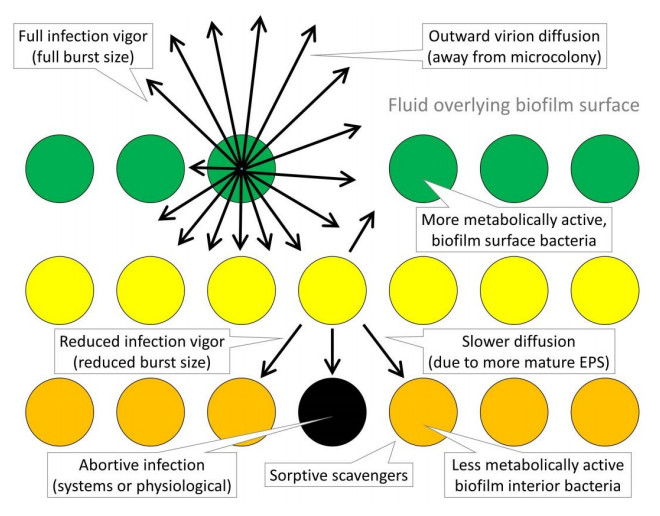
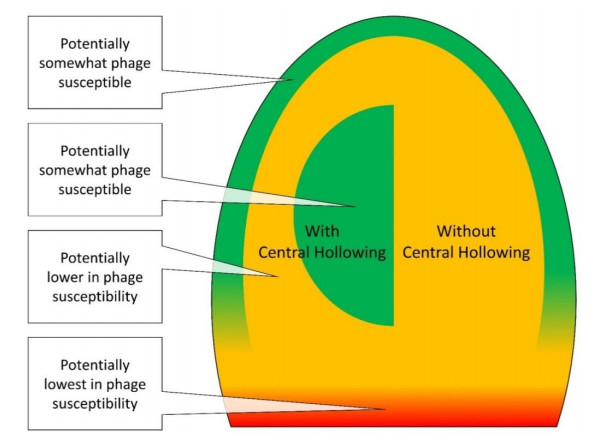
[1]	Whitman WB, Coleman DC, Wiebe WJ (1998) Prokaryotes: The unseen majority. Proc Natl Acad Sci USA 95: 6578–6583.
[2]	Flemming HC, Wingender J (2010) The biofilm matrix. Nat Rev Microbiol 8: 623–633.
[3]	Hall MR, McGillicuddy E, Kaplan LJ (2014) Biofilm: basic principles, pathophysiology, and implications for clinicians. Surg Infect (Larchmt ) 15: 1–7.
[4]	Hyman P, Abedon ST (2012) Smaller fleas: viruses of microorganisms. Scientifica 2012: 734023.
[5]	Wommack KE, Colwell RR (2000) Virioplankton: viruses in aquatic ecosystems. Microbiol Mol Biol Rev 64: 69–114.
[6]	Weinbauer MG (2004) Ecology of prokaryotic viruses. FEMS Microbiol Rev 28: 127–181.
[7]	Abedon ST (2015) Ecology of anti-biofilm agents I. antibiotics versus bacteriophages. Pharmaceuticals 8: 525–558.
[8]	Abedon ST (2015) Ecology of anti-biofilm agents II. bacteriophage exploitation and biocontrol of biofilm bacteria. Pharmaceuticals 8: 559–589.
[9]	Briandet R, Lacroix-Gueu P, Renault M, et al. (2008) Fluorescence correlation spectroscopy to study diffusion and reaction of bacteriophages inside biofilms. Appl Environ Microbiol 74: 2135–2143.
[10]	Fukuyo M, Sasaki A, Kobayashi I (2012) Success of a suicidal defense strategy against infection in a structured habitat. Sci Rep 2: 238.
[11]	Hyman P, Abedon ST (2010) Bacteriophage host range and bacterial resistance. Adv Appl Microbiol 70: 217–248.
[12]	Labrie SJ, Samson JE, Moineau S (2010) Bacteriophage resistance mechanisms. Nat Rev Microbiol 8: 317–327.
[13]	Dy RL, Richter C, Salmond GP, et al. (2014) Remarkable mechanisms in microbes to resist phage infections. Annu Rev Virol 1: 307–331.
[14]	Seed KD (2015) Battling phages: How bacteria defend against viral attack. PLoS Path 11: e1004847.
[15]	Parma DH, Snyder M, Sobolevski S, et al. (1992) The rex system of bacteriophage l: tolerance and altruistic cell death. Genes Dev 6: 497–510.
[16]	Shub DS (1994) Bacterial viruses. Bacterial altruism? Curr Biol 4: 555–556.
[17]	Dy RL, Przybilski R, Semeijn K, et al. (2014) A widespread bacteriophage abortive infection system functions through a Type IV toxin-antitoxin mechanism. Nucl Acids Res 42: 4590–4605.
[18]	Iranzo J, Lobkovsky AE, Wolf YI, et al. (2015) Immunity, suicide or both? Ecological determinants for the combined evolution of anti-pathogen defense systems. BMC Evol Biol 15: 43.
[19]	Dennehy JJ, Abedon ST, Turner PE (2007) Host density impacts relative fitness of bacteriophage f6 genotypes in structured habitats. Evolution 61: 2516–2527.
[20]	Abedon ST, Yin J (2008) Impact of spatial structure on phage population growth, In: Abedon, S.T. Editor, Bacteriophage Ecology, Cambridge, UK: Cambridge University Press, 94–113.
[21]	Abedon ST (2011) Bacteriophages and biofilms: ecology, phage therapy, plaques, Hauppauge, New York: Nova Science Publishers.
[22]	Abedon ST (2016) Bacteriophage exploitation of bacterial biofilms: phage preference for less mature targets? FEMS Microbiol Lett 363: fnv246.
[23]	Abedon ST (2012) Spatial vulnerability: bacterial arrangements, microcolonies, and biofilms as responses to low rather than high phage densities. Viruses 4: 663–687.
[24]	Abedon ST (2012) Thinking about microcolonies as phage targets. Bacteriophage 2: 200–204.
[25]	Abedon ST (2008) Phage population growth: constraints, games, adaptation, In: Abedon, S.T. Editor, Bacteriophage Ecology, Cambridge, UK: Cambridge University Press, 64–93.
[26]	Abedon ST (2009) Impact of phage properties on bacterial survival, In: Adams, H.T. Editor, Contemporary Trends in Bacteriophage Research, Hauppauge, New York: Nova Science Publishers, 217–235.
[27]	Payne RJH, Jansen VAA (2001) Understanding bacteriophage therapy as a density-dependent kinetic process. J Theor Biol 208: 37–48.
[28]	Abedon ST, Thomas-Abedon C (2010) Phage therapy pharmacology. Curr Pharm Biotechnol 11: 28–47.
[29]	Hamilton WD (1964) The genetical evolution of social behaviour. I. J Theor Biol 7: 1–16.
[30]	West SA, Gardner A (2010) Altruism, spite, and greenbeards. Science 327: 1341–1344.
[31]	Iranzo J, Lobkovsky AE, Wolf YI, et al. (2014) Virus-host arms race at the joint origin of multicellularity and programmed cell death. Cell Cycle 13: 3083–3088.
[32]	West SA, Griffin AS, Gardner A, et al. (2006) Social evolution theory for microorganisms. Nat Rev Microbiol 4: 597–607.
[33]	Ewald PW (1994) Evolution of Infectious Disease, New York: Oxford University Press.
[34]	Michod RE, Nedelcu AM, Roze D (2003) Cooperation and conflict in the evolution of individuality. IV. Conflict mediation and evolvability in Volvox carteri. Bio Systems 69: 95–114.
[35]	van Gestel J, Vlamakis H, Kolter R (2015) Division of labor in biofilms: the ecology of cell differentiation. Microbiol Spectr 3: MB-0002-2014.
[36]	Andrews JH (1998) Bacteria as modular organisms. Ann Rev Microbiol 52: 105–126.
[37]	Kaplan JB (2010) Biofilm dispersal: mechanisms, clinical implications, and potential therapeutic uses. J Dent Res 89: 205–218.
[38]	McDougald D, Rice SA, Barraud N, et al. (2012) Should we stay or should we go: mechanisms and ecological consequences for biofilm dispersal. Nat Rev Microbiol 10: 39–50.
[39]	Davies DG (2011) Biofilm disperson, In: Flemming, H.C., Wingender, J., Szewzyk, U. Editors, Biofilm Highlights, Berlin: Springer, 1–28.
[40]	Barraud N, Kjelleberg S, Rice SA (2015) Dispersal from microbial biofilms. Microbiol Spectr 3: MB-0015-2014.
[41]	Petrova OE, Sauer K (2016) Escaping the biofilm in more than one way: desorption, detachment or dispersion. Curr Opin Microbiol 30: 67–78.
[42]	Kim SK, Lee JH (2016) Biofilm dispersion in Pseudomonas aeruginosa. J Microbiol 54: 71–85.
[43]	Ronce O (2007) How does it feel to be like a rolling stone? Ten questions about dispersal evolution. Ann Rev Ecol Evol Syst 38: 231–253.
[44]	Korber DR, Lawrence JR, Lappin-Scott HM, et al. (1995) Growth of microorganisms on surfaces, In: Costerton, J.W., Lappin-Scott, H. Editors, Microbial biofilms, Cambridge, UK: Cambridge University Press, 15–45.
[45]	Bjarnsholt T (2013) The role of bacterial biofilms in chronic infections. Apmis 121: 1–51.
[46]	Battin TJ, Besemer K, Bengtsson MM, et al. (2016) The ecology and biogeochemistry of stream biofilms. Nat Rev Microbiol 14: 251–263.
[47]	Costerton JW, Lappin-Scott H (1995) Introduction to microbial biofilms, In: Costerton, J.W., Lappin-Scott, H. Editors, Microbial biofilms, Cambridge, UK: Cambridge University Press, 1–11.
[48]	Costerton JW, Marrie TJ, Cheng KJ (1985) Phenomena of bacterial adhesion, In: Savage, D.C., Fletcher, M. Editors, Bacterial Adhesion: Mechanisms and Physiological Significance, New York: Plenum Press, 3–43.
[49]	Somerville DA, Noble WC (1973) Microcolony size of microbes on human skin. J Med Microbiol 6: 323–328.
[50]	Mitarai N, Brown S, Sneppen K (2016) Population dynamics of phage and bacteria in spatially structured habitats using phage l and Escherichia coli. J Bacteriol 198: 1783–1793.
[51]	Kreft JU (2004) Biofilms promote altruism. Microbiology 150: 2751–2760.
[52]	Nadell CD, Bassler BL (2011) A fitness trade-off between local competition and dispersal in Vibrio cholerae biofilms. Proc Natl Acad Sci USA 108: 14181–14185.
[53]	Bryers JD (1988) Modeling biofilm accumulation, In: Brazin, M.J., Prosser, J.I. Editors, Physiological Models in Microbiology, Eds., FL: CRC Press, 109–144.
[54]	Garny K, Horn H, Neu TR (2008) Interaction between biofilm development, structure and detachment in rotating annular reactors. Bioprocess Biosyst Eng 31: 619–629.
[55]	Brading MG, Jass J, Lappin-Scott HM (1995) Dynamics of bacterial biofilm formation, In: Costerton, J.W., Lappin-Scott, H. Editors, Microbial biofilms, Cambridge, UK: Cambridge University Press, 46–63.
[56]	Vanysacker L, Boerjan B, Declerck P, et al. (2014) Biofouling ecology as a means to better understand membrane biofouling. Appl Microbiol Biotechnol 98: 8047–8072.
[57]	Bester E, Wolfaardt G, Joubert L, et al. (2005) Planktonic-cell yield of a pseudomonad biofilm. Appl Environ Microbiol 71: 7792–7798.
[58]	Knowles B, Silveira CB, Bailey BA, et al. (2016) Lytic to temperate switching of viral communities. Nature 531: 466–470.
[59]	Gonzalez S, Fernandez L, Campelo AB, et al. (2017) The behavior of Staphylococcus aureus dual-species biofilms treated with bacteriophage phiIPLA-RODI depends on the accompanying microorganism. Appl Environ Microbiol 83: AEM-02821-16.
[60]	Sutherland IW, Hughes KA, Skillman LC, et al. (2004) The interaction of phage and biofilms. FEMS Microbiol Lett 232: 1–6.
[61]	Nale JY, Chutia M, Carr P, et al. (2016) "Get in early"; biofilm and wax moth (Galleria mellonella) models reveal new insights into the therapeutic potential of Clostridium difficile bacteriophages. Front Microbiol 7: 1383.
[62]	Doolittle MM, Cooney JJ, Caldwell DE (1996) Tracing the interaction of bacteriophage with bacterial biofilms using fluorescent and chromogenic probes. J Indust Microbiol 16: 331–341.
[63]	Abedon ST (1992) Lysis of lysis inhibited bacteriophage T4-infected cells. J Bacteriol 174: 8073–8080.
[64]	Abedon ST (1989) Selection for bacteriophage latent period length by bacterial density: A theoretical examination. Microb Ecol 18: 79–88.
[65]	Wang IN, Dykhuizen DE, Slobodkin LB (1996) The evolution of phage lysis timing. Evol Ecol 10: 545–558.
[66]	Hadas H, Einav M, Fishov I, et al. (1997) Bacteriophage T4 development depends on the physiology of its host Escherichia coli. Microbiology 143: 179–185.
[67]	Abedon ST (2012) Bacterial "immunity" against bacteriophages. Bacteriophage 2: 50–54.
[68]	Koonin EV, Zhang F (2017) Coupling immunity and programmed cell suicide in prokaryotes: Life-or-death choices. BioEssays 39: 1–9.
[69]	Hoyland-Kroghsbo NM, Paczkowski J, Mukherjee S, et al. (2017) Quorum sensing controls the Pseudomonas aeruginosa CRISPR-Cas adaptive immune system. Proc Natl Acad Sci USA 114: 131–135.
[70]	Goldfarb T, Sberro H, Weinstock E, et al. (2015) BREX is a novel phage resistance system widespread in microbial genomes. EMBO J 34: 169–183.
[71]	Abedon ST (2015) Bacteriophage secondary infection. Virol Sin 30: 3–10.
[72]	McLean RJ, Corbin BD, Balzer GJ, et al. (2001) Phenotype characterization of genetically defined microorganisms and growth of bacteriophage in biofilms. Meth Enzymol 336: 163–174.
[73]	Azeredo J, Sutherland IW (2008) The use of phages for the removal of infectious biofilms. Curr Pharm Biotechnol 9: 261–266.
[74]	Sillankorva S, Azeredo J (2014) The use of bacteriophages and bacteriophage-derived enzymes for clinically relevant biofilm control, In: Borysowski, J., Miedzybrodzki, R., Górski, A. Editors, Phage Therapy: Current Research and Applications, Norfolk, UK: Caister Academic Press, 305–325.
[75]	Kutter E, Kellenberger E, Carlson K, et al. (1994) Effects of bacterial growth conditions and physiology on T4 infection, In: Karam, J.D., Kutter, E., Carlson, K., Guttman, B. Editors, The Molecular Biology of Bacteriophage T4, Washington, DC: ASM Press, 406–418.
[76]	Miller RV, Day M (2008) Contribution of lysogeny, pseudolysogeny, and starvation to phage ecology, In: Abedon, S.T. Editor, Bacteriophage Ecology, Cambridge, UK: Cambridge University Press, 114–143.
[77]	Pearl S, Gabay C, Kishony R, et al. (2008) Nongenetic individuality in the host-phage interaction. PLoS Biol 6: e120.
[78]	Abedon ST (2009) Disambiguating bacteriophage pseudolysogeny: an historical analysis of lysogeny, pseudolysogeny, and the phage carrier state, In: Adams, H.T. Editor, Contemporary Trends in Bacteriophage Research, Hauppauge, New York: Nova Science Publishers, 285–307.
[79]	Los M, Wegrzyn G (2012) Pseudolysogeny. Adv Virus Res 82: 339–349.
[80]	Golec P, Karczewska-Golec J, Los M, et al. (2014) Bacteriophage T4 can produce progeny virions in extremely slowly growing Escherichia coli host: comparison of a mathematical model with the experimental data. FEMS Microbiol Lett 351: 156–161.
[81]	Harper DR, Parracho HMR, Walker J, et al. (2014) Bacteriophages and biofilms. Antibiotics 3: 270–284.
[82]	Bryan D, el-Shibiny A, Hobbs Z, et al. (2016) Bacteriophage T4 infection of stationary phase E. coli: life after log from a phage perspective. Front Microbiol 7: 1391.
[83]	Yin J (1991) A quantifiable phenotype of viral propagation. Biochem Biophys Res Com 174: 1009–1014.
[84]	Filippini M, Buesing N, Bettarel Y, et al. (2006) Infection paradox: high abundance but low impact of freshwater benthic viruses. Appl Environ Microbiol 72: 4893–4898.
[85]	Wilkinson JF (1958) The extracellualr polysaccharides of bacteria. Bacteriol Rev 22: 46–73.
[86]	van Benthum WAJ, van Loosdrecht MCM, Tijhuis L, et al. (1995) Solids retention time in heterotrophic and nitrifying biofilms in a biofilm airlift suspension reactor. Water Sci Technol 32: 35–43.
[87]	Reichert P, Wanner O (1997) Movement of solids in biofilms-significance of liquid phase transport. Water Sci Technol 36: 321–328.
[88]	Davey ME, O'Toole GA (2000) Microbial biofilms: from ecology to molecular genetics. Microbiol Mol Biol Rev 64: 847–867.
[89]	Hanlon GW, Denyer SP, Olliff CJ, et al. (2001) Reduction in exopolysaccharide viscosity as an aid to bacteriophage penetration through Pseudomonas aeruginosa biofilms. Appl Environ Microbiol 67: 2746–2753.
[90]	Resch A, Fehrenbacher B, Eisele K, et al. (2005) Phage release from biofilm and planktonic Staphylococcus aureus cells. FEMS Microbiol Lett 252: 89–96.
[91]	Forde A, Fitzgerald GF (2003) Molecular organization of exopolysaccharide (EPS) encoding genes on the lactococcal bacteriophage adsorption blocking plasmid, pCI658. Plasmid 49: 130–142.
[92]	Flood JA, Ashbolt NJ (2000) Virus-sized particles can be entrapped and concentrated one hundred fold within wetland biofilms. Adv Environ Res 3: 403–411.
[93]	Storey MV, Ashbolt NJ (2001) Persistence of two model enteric viruses (B40-8 and MS-2 bacteriophages) in water distribution pipe biofilms. Water Sci Technol 43: 133–138.
[94]	Lacroix-Gueu P, Briandet R, Lévêque-Fort S, et al. (2005) In situ measurements of viral particles diffusion inside mucoid biofilms. C R Biol 328: 1065–1072.
[95]	Brüssow H (2013) Bacteriophage-host interaction: from splendid isolation into a messy reality. Curr Opin Microbiol 16: 500–506.
[96]	Fan X, Li W, Zheng F, et al. (2013) Bacteriophage inspired antibiotics discovery against infection involved biofilm. Crit Rev Eukaryot Gene Expr 23: 317–326.
[97]	Parasion S, Kwiatek M, Gryko R, et al. (2014) Bacteriophages as an alternative strategy for fighting biofilm development. Pol J Microbiol 63: 137–145.
[98]	Chan BK, Abedon ST (2015) Bacteriophages and their enzymes in biofilm control. Curr Pharm Des 21: 85–99.
[99]	Gutierrez D, Rodriguez-Rubio L, Martinez B, et al. (2016) Bacteriophages as weapons against bacterial biofilms in the food industry. Front Microbiol 7: 825.
[100]	Khalifa L, Shlezinger M, Beyth S, et al. (2016) Phage therapy against Enterococcus faecalis in dental root canals. J Oral Microbiol 8: 32157.
[101]	Motlagh AM, Bhattacharjee AS, Goel R (2016) Biofilm control with natural and genetically-modified phages. World J Microbiol Biotechnol 32: 67.
[102]	Abedon ST (2014) Phage therapy: eco-physiological pharmacology. Scientifica 2014: 581639.
[103]	Arber W, Linn S (1969) DNA modification and restriction. Annu Rev Biochem 38: 467–500.
[104]	Korona R, Levin BR (1993) Phage-mediated selection and the evolution and maintenance of restriction-modification. Evolution 47: 556–575.
[105]	Chao L, Levin BR, Stewart FM (1977) A complex community in a simple habitat: an experimental study with bacteria and phage. Ecology 58: 369–378.
[106]	Bohannan BJM, Travisano M, Lenski RE (1999) Epistatic interactions can lower the cost of resistance to multiple consumers. Evolution 53: 292–295.
[107]	Hill C (1993) Bacteriophage and bacteriophage resistance in lactic acid bacteria. FEMS Microbiol Rev 12: 87–108.
[108]	Nissen SB, Magidson T, Gross K, et al. (2016) Publication bias and the canonization of false facts. eLife 5: e21451.
[109]	Costerton JW, Cheng JJ, Geesey GG, et al. (1987) Bacterial biofilms in nature and disease. Ann Rev Microbiol 41: 435–464.
[110]	Oh YJ, Jo W, Yang Y, et al. (2007) Influence of culture conditions on Escherichia coli O157:H7 biofilm formation by atomic force microscopy. Ultramicroscopy 107: 869–874.
[111]	Cheng KJ, Costerton JW (1980) The formation of microcolonies by rumen bacteria. Can J Microbiol 26: 1104–1113.
[112]	Lacqua A, Wanner O, Colangelo T, et al. (2006) Emergence of biofilm-forming subpopulations upon exposure of Escherichia coli to environmental bacteriophages. Appl Environ Microbiol 72: 956–959.
[113]	Shen Y, Mitchell MS, Donovan DM, et al. (2012) Phage-based enzybiotics, In: Hyman, P., Abedon, S.T. Editors, Bacteriophages in Health and Disease, Wallingford, UK: CABI Press, 217–239.
[114]	Yan J, Mao J, Xie J (2014) Bacteriophage polysaccharide depolymerases and biomedical applications. BioDrugs 28: 265–274.
[115]	Gutiérrez D, Briers Y, Rodríguez-Rubio L, et al. (2015) Role of the pre-neck appendage protein (Dpo7) from phage vB_SepiS-phiIPLA7 as an anti-biofilm agent in staphylococcal species. Front Microbiol 6: 1315.
[116]	Pires DP, Oliveira H, Melo LD, et al. (2016) Bacteriophage-encoded depolymerases: their diversity and biotechnological applications. Appl Microbiol Biotechnol 100: 2141–2151.
[117]	Westra ER, van HS, Oyesiku-Blakemore S, et al. (2015) Parasite exposure drives selective evolution of constitutive versus inducible defense. Curr Biol 25: 1043–1049.
[118]	Berngruber TW, Lion S, Gandon S (2013) Evolution of suicide as a defence strategy against pathogens in a spatially structured environment. Ecol Lett 16: 446–453.
[119]	Refardt D, Kummerli R (2013) Defying bacteriophages: contrasting altruistic with individual-based resistance mechanisms in Escherichia coli. Commun Integr Biol 6: e25159.
[120]	Heilmann S, Sneppen K, Krishna S (2012) Coexistence of phage and bacteria on the boundary of self-organized refuges. Proc Natl Acad Sci USA 109: 12828–12833.
[121]	Abedon ST, Kuhl SJ, Blasdel BG, et al. (2011) Phage treatment of human infections. Bacteriophage 1: 66–85.
[122]	Borysowski J, Miedzybrodzki R, Górski A (2014) Phage Therapy: Current Research and Applications, Norfolk, UK: Caister Academic Press.
[123]	Scali C, Kunimoto B (2013) An update on chronic wounds and the role of biofilms. J Cutan Med Surg 17: 371–376.
[124]	Cooper RA, Bjarnsholt T, Alhede M (2014) Biofilms in wounds: a review of present knowledge. J Wound Care 23: 570–580.
[125]	Macia MD, Rojo-Molinero E, Oliver A (2014) Antimicrobial susceptibility testing in biofilm-growing bacteria. Clin Microbiol Infect 20: 981–990.
[126]	Abedon ST (2015) Phage therapy of pulmonary infections. Bacteriophage 5: e1020260.
[127]	Fish R, Kutter E, Wheat G, et al. (2016) Bacteriophage treatment of intransigent diabetic toe ulcers: a case series. J Wound Care 25: S27–S33.
[128]	Abedon ST (2017) Bacteriophage clinical use as antibactertial "drugs": utility precident. Microbiol Spectr.
[129]	Stewart PS, Franklin MJ (2008) Physiological heterogeneity in biofilms. Nat Rev Microbiol 6: 199–210.
[130]	Davis KM, Mohammadi S, Isberg RR (2015) Community behavior and spatial regulation within a bacterial microcolony in deep tissue sites serves to protect against host attack. Cell Host Microbe 17: 21–31.
[131]	Harmsen M, Yang L, Pamp SJ, et al. (2010) An update on Pseudomonas aeruginosa biofilm formation, tolerance, and dispersal. FEMS Immunol Med Microbiol 59: 253–268.
[132]	Purevdorj-Gage B, Costerton WJ, Stoodley P (2005) Phenotypic differentiation and seeding dispersal in non-mucoid and mucoid Pseudomonas aeruginosa biofilms. Microbiology 151: 1569–1576.
[133]	Hamilton WA (1987) Biofilms: microbial interactions and metabolic activities, In: Fletcher, M., Gray, T.R.G., Jones, J.G. Editors, Ecology of Microbial Communities, Cambridge: Cambridge University Press, 361–385.
[134]	Abedon ST, Herschler TD, Stopar D (2001) Bacteriophage latent-period evolution as a response to resource availability. Appl Environ Microbiol 67: 4233–4241.
[135]	Levin BR, Bull JJ (2004) Population and evolutionary dynamics of phage therapy. Nat Rev Microbiol 2: 166–173.
[136]	Gill JJ (2008) Modeling of bacteriophage therapy, In: Abedon, S.T. Editor, Bacteriophage Ecology, Cambridge, UK: Cambridge University Press, 439–464.
[137]	Stent GS (1963) Molecular Biology of Bacterial Viruses, San Francisco, CA: WH Freeman and Co.
[138]	Gallet R, Shao Y, Wang IN (2009) High adsorption rate is detrimental to bacteriophage fitness in a biofilm-like environment. BMC Evol Biol 9: 241.
[139]	Yin J, McCaskill JS (1992) Replication of viruses in a growing plaque: a reaction-diffusion model. Biophys J 61: 1540–1549.
[140]	Abedon ST, Culler RR (2007) Bacteriophage evolution given spatial constraint. J Theor Biol 248: 111–119.
[141]	Hewson I, Fuhrman JA (2003) Viriobenthos production and virioplankton sorptive scavenging. Microb Ecol 46: 337–347.
[142]	Hoyland-Kroghsbo NM, Maerkedahl RB, Svenningsen SL (2013) A quorum-sensing-induced bacteriophage defense mechanism. MBio 4: e00362.
[143]	Boots M, Mealor M (2007) Local interactions select for lower pathogen infectivity. Science 315: 1284–1286.
[144]	Abedon ST (2016) Commentary: phage therapy of staphylococcal chronic osteomyelitis in experimental animal model. Front Microbiol 7: 1251.
[145]	Kutter E, De Vos D, Gvasalia G, et al. (2010) Phage therapy in clinical practice: treatment of human infections. Curr Pharm Biotechnol 11: 69–86.
[146]	Hyman P, Abedon ST (2009) Practical methods for determining phage growth parameters. Meth Mol Biol 501: 175–202.
[147]	Mirzaei MK, Nilsson AS (2015) Isolation of phages for phage therapy: a comparison of spot tests and efficiency of plating analyses for determination of host range and efficacy. PLoS One 10: e0118557.
[148]	Abedon ST (2014) Bacteriophages as drugs: the pharmacology of phage therapy, In: Borysowski, J., Miedzybrodzki, R., Górski, A. Editors, Phage Therapy: Current Research and Applications, Norfolk, UK: Caister Academic Press, 69–100.

This article has been cited by:

1.	Lingjun Zhan, Jie Wang, Liang Wang, Chuan Qin, The correlation of drug resistance and virulence in Mycobacterium tuberculosis, 2020, 2, 25900536, 18, 10.1016/j.bsheal.2020.02.004
2.	Abolfazl Hajialibeigi, Jafar Amani, Seyed Latif Mousavi Gargari, Identification and evaluation of novel vaccine candidates against Shigella flexneri through reverse vaccinology approach, 2021, 105, 0175-7598, 1159, 10.1007/s00253-020-11054-4
3.	Mónica F. Torrez Lamberti, Lucrecia C. Terán, Fabián E. Lopez, María de las Mercedes Pescaretti, Mónica A. Delgado, Genomic and proteomic characterization of two strains of Shigella flexneri 2 isolated from infants’ stool samples in Argentina, 2022, 23, 1471-2164, 10.1186/s12864-022-08711-5
4.	Wei Liu, Jia-Wei Tang, Jing-Yi Mou, Jing-Wen Lyu, Yu-Wei Di, Ya-Long Liao, Yan-Fei Luo, Zheng-Kang Li, Xiang Wu, Liang Wang, Rapid discrimination of Shigella spp. and Escherichia coli via label-free surface enhanced Raman spectroscopy coupled with machine learning algorithms, 2023, 14, 1664-302X, 10.3389/fmicb.2023.1101357
5.	Poonam Daswani, Vigneshwaran Muthuraman, Ragini Macaden, Mary Dias, Tannaz Birdi, Effect of Psidium guajava (guava) L. Leaf Decoction on Antibiotic-resistant Clinical Diarrhoeagenic Isolates of Shigella spp., 2020, 8, 2345-3362, 122, 10.34172/ijep.2020.26
6.	Mohammad Shahnaij, Mohammed Badrul Amin, M. Mozammel Hoque, Abdus Salam Mondol, Kazi Jewel Rana, Ishrat J. Azmi, Kaisar A. Talukder, Conrad W. Mullineaux, Characterization of Shigella flexneri Serotype 6 Strains Isolated from Bangladesh and Identification of a New Phylogenetic Cluster, 2023, 0021-9193, 10.1128/jb.00406-22
7.	Marija Miljkovic, Sonia Lozano, Isabel Castellote, Cristina de Cózar, Ana I. Villegas-Moreno, Pablo Gamallo, Dolores Jimenez-Alfaro Martinez, Elena Fernández-Álvaro, Lluis Ballell, George A. Garcia, Paul M. Dunman, Novel inhibitors that target bacterial virulence identified via HTS against intra-macrophage survival of Shigella flexneri , 2023, 8, 2379-5042, 10.1128/msphere.00154-23
8.	Li-Yan Zhang, Benshun Tian, Yuan-Hong Huang, Bin Gu, Pei Ju, Yanfei Luo, Jiawei Tang, Liang Wang, Classification and prediction of Klebsiella pneumoniae strains with different MLST allelic profiles via SERS spectral analysis, 2023, 11, 2167-8359, e16161, 10.7717/peerj.16161
9.	Elizabeth A. Rucks, Type III Secretion in Chlamydia, 2023, 87, 1092-2172, 10.1128/mmbr.00034-23
10.	Khalifa Binkhamis, Sarah Alangari, Fatema Juma, Sahar Althawadi, Ahmed A. Al-Qahtani, Marie Fe F. Bohol, Fatimah S. Alshahrani, Fawzia Alotaibi, Shigella flexneri Outbreak at a Rehabilitation Center: First Report from Saudi Arabia, 2025, 13, 2227-9032, 971, 10.3390/healthcare13090971

Reader Comments

Your name:*

Email:*
© 2017 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)