1. Introduction
Leveraging continuous advancements in electronics, communication and computers, the health industry is being quickly reshaped, allowing for more and more promising smart/mobile health solutions [1,2,3,4,5,6,7,8]. However, along with dramatically increased assistive devices, connection needs and big data, the security and privacy issue is also rising. It is highly necessary to pay enough attention to concerns such as how to provide confidential biomedicine applications, and how to effectively protect the sensitive data of patients. Biometric human identification is attracting tremendous attentions focusing on the security and privacy issue. As an emerging technology, biometric is more robust than traditional methods, such as token (identity card) and knowledge-based (username/password) ones which may be stolen or lost. Biometric is usually unique to individuals and highly difficult to be duplicated [9]. There are several categories of biometric modalities, such as the behavioral and physiological ones. The examples for the former one include gait, signature, face, etc. We take special interest in the latter one in this paper. The physiological signals can be easily collected by wearable computers which are part of the body sensor network. Then the signals acquired can be processed either by personal digital devices or cloud computing servers, for user identification purpose toward confidential smart digital health.
Among different physiological signals, the heart electrocardiogram (ECG) [10] and the brain electroencephalogram (EEG) [11] are two key modalities. The former one reflects the electrical behavior of the heart which is modulated by both sympathetic and parasympathetic nerves. To measure the ECG signal, ECG electrodes are used to detect the tiny electrical changes on the human body. These changes are generated by heart muscle's electrophysiological movements during depolarization and repolarization phases of one heartbeat. Therefore, it is hard to be duplicated and safer than traditional identification methods. In daily applications, the ECG signal can be easily collected by wearable computers and then sent to cellphone devices or other personal digital platforms. The ECG signal can be collected at any time since the live human body continuously generates heart electrical signals which are propagated to all the body parts.
EEG signal is another famous modality that can be used in many applications, such as seizure detection, sleep quality monitoring and emotion tracking. Here, we focus on its application in biometric human identification. EEG signal is also unique to individuals, and is somehow, more difficult to be duplicated considering the underlying signal generation mechanism is much more complicated. The EEG signal is usually collected by EEG electrodes placed on the head fixed by a specific EEG cap. There are also some easy-wearing EEG caps which only collect data from several locations with the scarification of accuracy. EEG signal is usually highly weak and of a log signal-to-noise ratio, therefore, many EEG electrodes are still used in practical application scenarios to obtain more redundant information for performance enhancement purpose. Of course, this may lower the wearability. But considering EEG signal is highly difficult to be duplicated, it is still attracting more and more attentions in human identification applications.
However, a thorough comparison between ECG and EEG-based biometric human identification lacks enough attention. This study is necessary, because ECG and EEG have different advantages and disadvantages in many aspects mentioned above, including sensor placement methods, signal quality, wearability of the signal acquisition device, difficulty of duplication, and so on. A detailed comparative analysis of these two modalities can effectively advance the practical application of an appropriated signal in pervasive assisted personal devices, for confidential biomedicine purpose.
Another aspect lacking enough study is the signal processing and machine learning algorithms used to perform the feature extraction and user classification tasks. Many different machine learning classifiers have been used to learn the features extracted and identify users on the fresh unseen data. However, which algorithm is more effective is not thoroughly compared and analyzed. Considering machine learners are usually built based on diverse mechanisms, the comparison is thus highly necessary. For example, the neural network is inspired by the brain structures and introduces a large number of neurons which are expected to generate neuron spikes reflecting the data patterns. The random forest, instead, is based on a totally different assumption, which includes forests of simple decision trees and applies an ensemble strategy to get an averaged classification result.
Focusing on above aspects lacking of study, in this paper, we investigate different advanced machine learning approaches on two physiological modalities, i.e., heart ECG and brain EEG, to gain insights on how to select an effective machine leaner and an appropriate signal for human identification purpose. The machine learning methods taken in consideration include Neural Network, K-nearest Neighbor, Bagging, Random Forest and AdaBoost [12]. Moreover, we also extract multi-domain features for the ECG signal, and the gamma-band spectral power ratio feature for the EEG signal. These features are fed to different machine learners to build the model on the training data, or to test the model on the unseen testing data. The identification rate is reported for different modalities and different machine learners. The discussion on the effectiveness of the features and classifiers is also given to point out future research directions.
The following article is organized as follows: section 2 gives the detailed methods in terms of datasets, feature extraction and classifiers; section 3 includes experimental results and discussion, and also comparison with state-of-the-art works; section 4 concludes the study.
2. Materials and Methods
2.1. Datasets
To evaluate two physiological modalities, we have used two widely-applied public datasets, the Fantasia ECG dataset [13,14] and the UCI (University of California, Irvine) EEG dataset [15].
The Fantasia ECG dataset was acquired for aging trend study purpose and thus owns diverse ECG morphologies. This dataset has been used in many studies focusing different problems. Here, we choose 20 recordings from 20 subjects for human identification purpose.
The UCI EEG dataset was collected using the 64-electrode configuration. Each subject was exposed to the picture stimulation, and thus their EEG signals reflected this external visual input. EEG data corresponding to 20 nonalcoholic subjects are also used to evaluate the proposed algorithm.
2.2. Pre-Processing
There are two pre-processing steps, including filtering and signal segmentation. For ECG signal, a Butterworth band-pass filter (2 to 50 Hz) is applied to remove the low frequency baseline wander and the high frequency power line interference. Then ECG heartbeats are segmented based on the middle point between two heartbeat R peaks. Considering this study focuses on the effectiveness of the ECG heartbeat in terms of user identification, we directly use the ground truth heartbeat R peak locations to perform the heartbeat segmentation. This is because of the fact that ECG signal is usually acquired continuously, and we need to firstly segment the ECG heartbeats and then extract features from these heartbeats. But heartbeat detection algorithm may induce some faking heartbeats when the ECG signal is impacted by motion artifacts and other noise. In this study, the heartbeats selected do not include faking heartbeats, which is important for a fair comparison purpose with the ECG signal.
For EEG signal, a band-pass filter (30 to 50 Hz) is applied to the raw signal to get the gamma band signal, which corresponds to the visual stimulation-related signal fluctuation. In the UCI EEG dataset, each stimulation is stored in a single file, so there is no need to segment the data stream. It means we treat each data file as an instance, similar as a heartbeat.
Based on the ECG heartbeats or the EEG stimulation-related responses, we now can extract features to represent the signal characteristics that can be fed to the machine learners.
2.3. ECG Feature Extraction
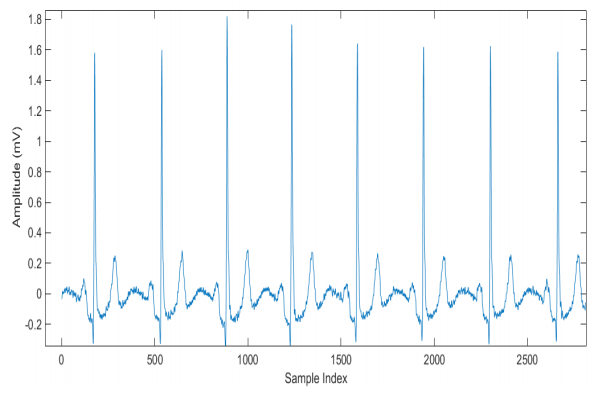
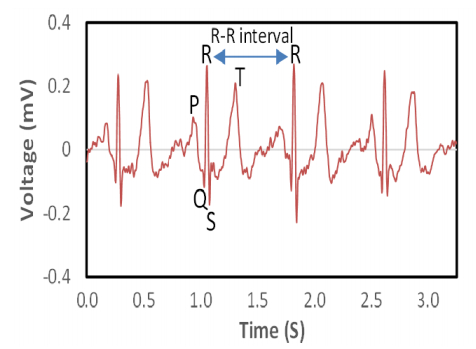
For ECG feature extraction, we have considered eleven features from multi-domains. An example of ECG signal with characteristic points is given in Figure 1 and the extracted features are listed in Table 1. Some of these features have been used in other areas, such as EMG signal processing and body activity recognition [16,17]. But we extract them here for biometric human identification purpose.
Table 1. Summary of extracted ECG features.
| No. |
Name |
| 1 |
Skewness |
| 2 |
Kurtosis |
| 3 |
Auto-regression coefficient 1 |
| 4 |
Auto-regression coefficient 2 |
| 5 |
Auto-regression coefficient 3 |
| 6 |
Auto-regression coefficient 4 |
| 7 |
Median frequency |
| 8 |
Mean frequency |
| 9 |
Root mean square |
| 10 |
Modified median frequency |
| 11 |
Modified mean frequency |
(1) Skewness [16]
Skewness is used to measure the symmetry of the distribution of the samples around the R peak region. The definition is SKNS[X]=μ3σ3=E[(X−μ)3](E[(X−μ)2])3/2, where μ3 is the third central moment and σ is the standard deviation, of signal X.
(2) Kurtosis [16]
Kurtosis is used to measure the distribution of samples around the R peak region. The definition is Kurt[X]=μ4σ4=E[(X−μ)4](E[(X−μ)2])2, where μ4 is the fourth central moment and σ is the standard deviation, of signal X.
(3) Auto-regression coefficient 1
Coefficient 1 of the normalized four order auto-regression. (Coefficient 0 is not used since it is a constant)
(4) Auto-regression coefficient 2
Coefficient 1 of the normalized four order auto-regression.
(5) Auto-regression coefficient 3
Coefficient 1 of the normalized four order auto-regression.
(6) Auto-regression coefficient 4
Coefficient 1 of the normalized four order auto-regression.
(7) Median frequency
The median frequency of the power spectrum of the R peak region.
(8) Mean frequency
The mean frequency of the power spectrum of the R peak region.
(9) Root mean square
Root mean square value calculated based on the R peak region.
(10) Modified median frequency [17]
The modified median frequency is the frequency which equally divides the amplitude of the spectrum of the R peak region.
(11) Modified mean frequency [17]
The modified mean frequency is the frequency which averages amplitude of the spectrum of the R peak region.
2.4. EEG Feature Extraction
For EEG feature extraction, it is difficult to apply similar methods used in ECG feature extraction, because the EEG signal is highly noise (which will be shown in the result section) and it is hard to distinguish meaning morphologies. Therefore, we have introduced the gamma-band spectral power ratio feature [18], defined in (1-5):
Sc,t=Sc,t∗Sc,t,∀c∈[1,64],∀t∈[1,256](1)
SSSc=T∑t=1Sc,t,∀c,T=256 (2)
FSc,t=Fc,t∗Fc,t,∀c,∀t (3)
FSSc=T∑t=1FSc,t,∀c (4)
GRc=FSSc/SSSc,∀c (5)
where,
Sc,t: the voltage value of the t−th sample in the c−th channel, from the unfiltered raw EEG data,
Fc,t: the voltage value of the t−th sample in the c−th channel, from the band-pass filtered EEG data,
SSc,t: the energy of the t−th sample in the c−th channel, from the unfiltered raw EEG data,
FSc,t: the energy of the t−th sample in the c−th channel, from the filtered EEG data,
SSSc: the energy of the t−th channel, from the unfiltered raw EEG data,
FSSc: the energy of the t−th channel, from the filtered EEG data,
GRc: gamma band energy ratio over the raw data, for the c−th channel.
Therefore, we can get GRc which is channel-wise gamma band energy ratio over the raw data. This feature vector (64 values) is expected to give the signal strength in the gamma band which is correlated with the visual stimulation [18].
To extract the features, MATLAB is used, which performs the data segmentation, filtering, feature calculation and.csv file generation which will be used by the RStudio [19] to perform the classification later.
2.5. Machine Learning Model Training and Testing
After extracting features for each instance, we now can train the machine learning classifiers to learn the model parameters based on the training data. Considering we have extracted 11 features for the ECG signal and 64 features (64 channels) for the EEG signal, we thus choose more ECG instances for algorithm evaluation for fairness purpose. 300 heartbeats are chosen for each subject and in total, there are 6000 instances for 20 subjects.
For EEG signal, there are in total 1137 instances for 20 subjects and each subject has around 60 measurements (each measurement includes 64 time series corresponding to 64 EEG signal channels).
We have introduced the 10-fold cross validation method to test the generalization ability of the trained models [20], and the averaged performance (accuracy) is reported. We have extracted the features directly from the database, therefore there is no null or redundant data. Null or redundant data may exist when using some databases which are already extracted features. Five different classifiers are evaluated in this study, including Neural Network, K-nearest Neighbor, Bagging, Random Forest and AdaBoost, and the identification rate over two datasets is given.
2.5.1. Neural Network
The neural network [12] is inspired by the brain structures where layer-wise neurons are organized in a way that can represent high-level abstraction. To accelerate the training process, we have used a four-layer neural network, with one input layer, two hidden layers and one output layer. For ECG, the number of nodes for four layers are 11 (11 features), 50, 50 and 20 (20 subjects), respectively. And for EEG, they are 64,100, 50 and 20, respectively, where more nodes for the second layer is used to more effectively learn patterns from 64 features.
2.5.2. K-nearest Neighbor
The K-nearest neighbor (KNN) classifier [12] is a non-parametric method, which analyzes the distribution of the instances to build the model. KNN does not make any assumption on the data distribution which is its advantage since practical data does not obey typical distribution assumptions. So KNN usually generates nonlinear boundaries for different groups. K is selected as 20 here since we have 20 subjects in each dataset.
2.5.3. Bagging
The bagging classifier (Bootstrap Aggregating) [12] can effectively decrease the variance of the prediction, because it can generate more data based on the original dataset to train the classifier. It is actually a special case of model averaging. Here we build the bagging classifier based on the decision trees and get the smoothed results.
2.5.4. Random Forest
The random forest [12] is based on a totally different assumption, which includes forests of simple decision trees and applies an ensemble strategy to get an averaged classification result. Random forest has been used in many areas and demonstrated effective classification ability. Here we choose 100 trees to build the random forest.
2.5.5. Adaboost
The Adaboost classfier (Adaptive Boosting) [12] is designed to be able to get a weighted sum results from weak learners. It is adaptive since it can adjust the selection of training samples based on historical training performance (previous iterations). It means that it can learn to select samples more useful to improve the prediction performance of the model.
3. Results and Discussion
In this section, we give detailed experimental results of pre-processing, feature extraction and classification.
3.1. Pre-Processing
The ECG data after band-pass filtering is shown in Figure 2. Clear ECG morphology can be observed, leveraging a relatively high signal-to-noise ratio. Therefore it should be able to effectively extract multi-domain features from ECG heartbeats with a good signal quality.
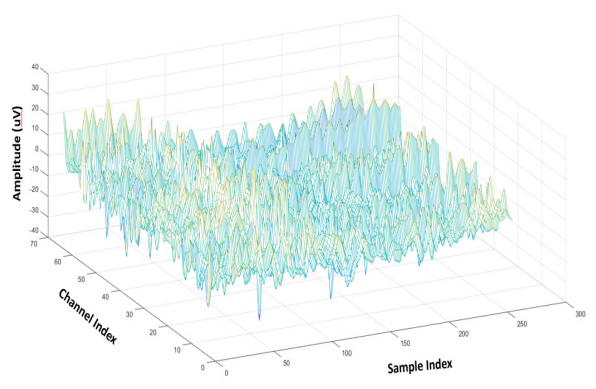
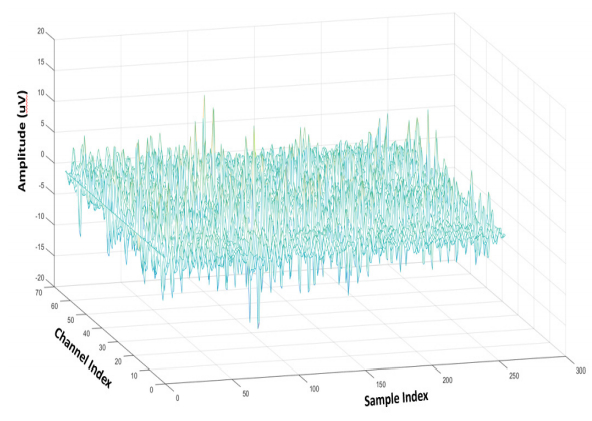
The EEG signal is much noisier than the ECG signal. To clearly demonstrate the signal quality, both raw and band-pass filtered signals are given, as shown in Figure 3 and 4, respectively. In Figure 3, the EEG data for one instance (64 × 256 points) is plotted where it is hard to find out potential patterns. After filtering, Figure 4 still does not show observable signal behaviors. This is to say, even with 64 channels, it is still highly challenging to analyze the behavior from the ECG signal. This is the major reason we choose the gamma band spectral power ratio as the feature.
3.2. Feature Extraction
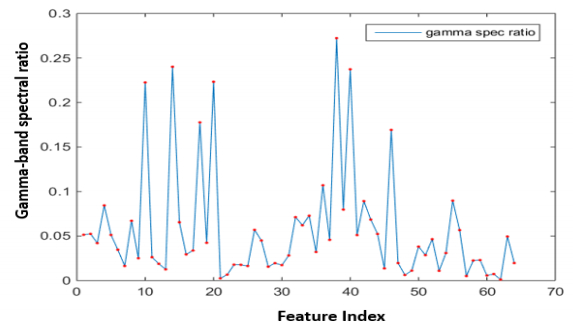
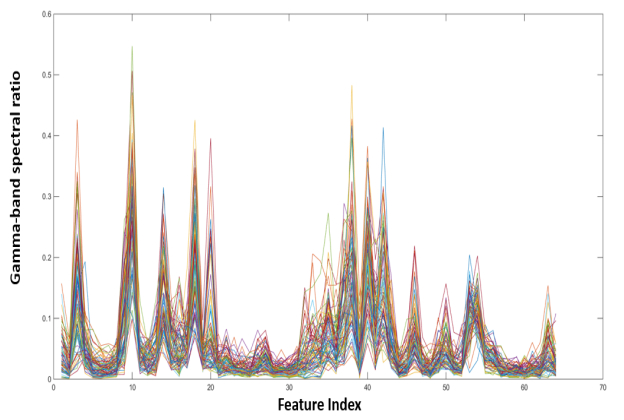
We have visualized the extracted features only for the EEG signal because we are interested in whether the gamma band spectral feature can reflect some meaningful behaviors of the EEG signal. An example is given in Figure 5, where 64 features are plotted for one EEG instance and there are several spikes corresponding to some specific EEG channels.
If we further plot all instances for one subject, as shown in Figure 6, we can find relatively consistent trend for these instances, with similar feature spikes. That means the gamma band spectral feature does reflect underlying brain behaviors related to visual stimulation. But at the same time, it is also worth noting that these instances are also very noisy and have a large variance. This indicates that EEG features may not be as effective as ECG features, which will be further introduced later.
Another thing worth noting is that the spikes in Figure 6 correspond to several EEG channels, which are connected to EEG electrodes placed on some specific locations of the head. This also gives some hints to remove some non-significant electrodes to enhance the wearability and power efficiency of the algorithm. But in this study, we keep all these features considering that EEG is highly noisy and we want to leverage as much information as possible to fully explore the potential of the EEG-based human identification method.
3.3. Performance
The performance of five advanced classifiers is summarized in Table 2. For ECG dataset, the random forest shows the best accuracy, followed by the Adaboost and neural network. For EEG dataset, all accuracy is no more than 90% because the signals are not as strong as the ECG signals and of much noise. The random forest still shows a best accuracy, 86%, followed by the neural network and the KNN.
Table 2. Summarization of five machine learners over two datasets.
| Data |
Classifier |
10-fold cross validation accuracy (%) |
Averaged |
| ECG |
NN |
94.2 |
90.8 |
90.2 |
93.8 |
91.3 |
94.0 |
91.2 |
92.7 |
92.3 |
92.3 |
92.3 |
| KNN |
86.3 |
85.5 |
84.3 |
87.0 |
86.0 |
86.5 |
87.3 |
85.3 |
85.5 |
86.0 |
86.0 |
| Bagging |
93.0 |
91.0 |
90.2 |
91.7 |
89.3 |
93.0 |
93.3 |
92.7 |
92.7 |
91.7 |
91.9 |
| RF |
97.7 |
98.0 |
97.5 |
97.8 |
97.2 |
98.3 |
99.2 |
97.7 |
98.5 |
97.8 |
98.0 |
| Adaboost |
97.0 |
96.8 |
96.7 |
97.5 |
95.7 |
98.0 |
97.3 |
97.5 |
96.3 |
96.3 |
96.9 |
| EEG |
NN |
85.1 |
77.2 |
86.8 |
86.8 |
88.6 |
80.7 |
83.3 |
89.5 |
84.2 |
88.3 |
85.1 |
| KNN |
77.2 |
68.4 |
81.6 |
75.4 |
78.9 |
75.4 |
73.7 |
81.6 |
83.3 |
84.7 |
78.0 |
| Bagging |
72.8 |
63.2 |
64.9 |
67.5 |
65.8 |
69.3 |
70.2 |
66.7 |
63.2 |
64.0 |
66.7 |
| RF |
86.8 |
78.9 |
89.5 |
81.6 |
91.2 |
83.3 |
87.7 |
87.7 |
87.7 |
85.6 |
86.0 |
| Adaboost |
78.1 |
71.1 |
71.9 |
69.3 |
68.4 |
71.9 |
79.8 |
79.8 |
75.4 |
73.0 |
73.9 |
| NN: neural network; KNN: K-nearest neighbor; RF: random forest. |
Therefore, we can get two important insights here. Firstly, ECG signal is much more appropriate for human identification, leveraging a high signal-to-noise ratio, and EEG signal even with 64 channels cannot provide an identification rate higher than 90%. Secondly, the random forest classifier is the most powerful one compared with other four methods, leveraging the ensemble ability of many decision trees. The neural network can also provide relatively good performance because the brain-inspired neuron connections can learn the underlying patterns from data effectively. Overall, the ECG-based biometric identification method using the random forest machine learner is the best combination according to our study.
3.4. Comparison
To further illustrate the effectiveness of the proposed ECG & RF-based method leveraging the extracted multi-domain features, we also compare our method with four state-of-the-art works as shown in Table 3. EEG-based method is not listed in Table 3 considering that its accuracy is much lower than ECG-based method and we only suggest ECG-based method for practical application scenarios. Our method owns a much higher identification rate than other works, demonstrating that the extracted multi-domain features and the random forest machine learner is very powerful in human subject identification. The other works did not compare different modalities and different machine learning classifiers, however, we compared EEG and ECG modalities and showed that ECG is superior to EEG leveraging a better signal quality, and we also compared different classifiers and demonstrate that the random forest more effective than other method.
Table 3. Performance comparison with state-of-the-art works.
| Methods |
Signal |
Datasets |
ID Rate |
| Proposed |
ECG |
20 subjects |
98.0% |
| Yao et al. [10] |
ECG |
20 subjects |
91.5% |
| Tan et al. [21] |
ECG |
10 subjects |
91.7% |
| Lourenco et al. [22] |
ECG |
16 subjects |
94.3% |
| Ting et al. [23] |
ECG |
13 subjects |
87.5% |
| ID: identification. |
3.5. Limitations and Future Work
In future, there are several directions to further enhance the study. Firstly, extracting more features and selecting critical ones may further enhance the accuracy and power efficiency; secondly, more datasets can also be introduced to evaluate the identification rate when more human subjects need to be distinguished; thirdly, the ensemble of different classifiers may also contribute to the performance enhancement, since different classifiers usually leverage different assumptions and their combination may help to cover more mechanisms behind the data.
Besides, EEG signal also shows different characteristics during different sleep stages [24,25,26,27,28], which may result in different user identification rates and can be further studied.
Currently available ECG and EEG datasets were not acquired at the same time. Although we tried to balance the selection of these two datasets to make the comparison fairer, we believe if we can collect ECG and EEG from same subjects at the same time, we can make the comparison more robust. Meanwhile, it is also necessary to consider more datasets in future work. Moreover, we will further evaluation more classifier configurations to explore their impact. Currently, we empirically selected the parameters for these classifiers.
4. Conclusion
In this paper, we have proposed the ECG & RF-based biometric human identification approach toward practical confidential biomedicine applications. Firstly, we have considered both ECG and EEG modalities and investigated their appropriateness in terms of human identification, by evaluating their signal quality, feature effectiveness and identification rate. Experimental results show that ECG is more robust than EEG levering a high signal-to-noise ratio and effectively extracted features. Secondly, we thoroughly compared five advanced machine learners and determined that the random forest classifier is much more powerful than other methods benefitting from its ensemble learning strategy. Specifically, for ECG & RF-based approach, a user identification rate as high as 98.0% is achieved, which is much higher than state-of-the-art works. This study is expected to show that properly selected biometric empowered by an effective machine learner owns a great potential, to enable confidential biomedicine applications in the era of smart digital health.
Acknowledgments
This research is supported partly by the Recruitment Program of Global Experts (the Thousand Talents Plan) and partly by National Natural Science Foundation of China (NSFC) research, No. 61574044,61376040 and 61574046.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: