Figure 1.
Schematic diagram of full earth pressure theory.
Citation: Ryan T. Borne, Arash Aghel, Amit C. Patel, Robert K. Rogers. Innominate Steal Syndrome: A Two Patient Case Report and Review[J]. AIMS Medical Science, 2015, 2(4): 360-370. doi: 10.3934/medsci.2015.4.360
| [1] | Jizhi Huang, Guoyuan Xu, Yu Wang, Xiaowei Ouyang . Equivalent deformation modulus of sandy pebble soil—Mathematical derivation and numerical simulation. Mathematical Biosciences and Engineering, 2019, 16(4): 2756-2774. doi: 10.3934/mbe.2019137 |
| [2] | Mette S. Olufsen, Ali Nadim . On deriving lumped models for blood flow and pressure in the systemic arteries. Mathematical Biosciences and Engineering, 2004, 1(1): 61-80. doi: 10.3934/mbe.2004.1.61 |
| [3] | Zhenqi He, Lu Yao . Improved successive approximation control for formation flying at libration points of solar-earth system. Mathematical Biosciences and Engineering, 2021, 18(4): 4084-4100. doi: 10.3934/mbe.2021205 |
| [4] | Aftab Ahmed, Javed I. Siddique . The effect of magnetic field on flow induced-deformation in absorbing porous tissues. Mathematical Biosciences and Engineering, 2019, 16(2): 603-618. doi: 10.3934/mbe.2019029 |
| [5] | Xu Bie, Yuanyuan Tang, Ming Zhao, Yingxi Liu, Shen Yu, Dong Sun, Jing Liu, Ying Wang, Jianing Zhang, Xiuzhen Sun . Pilot study of pressure-flow properties in a numerical model of the middle ear. Mathematical Biosciences and Engineering, 2020, 17(3): 2418-2431. doi: 10.3934/mbe.2020131 |
| [6] | Panagiotes A. Voltairas, Antonios Charalambopoulos, Dimitrios I. Fotiadis, Lambros K. Michalis . A quasi-lumped model for the peripheral distortion of the arterial pulse. Mathematical Biosciences and Engineering, 2012, 9(1): 175-198. doi: 10.3934/mbe.2012.9.175 |
| [7] | Scott R. Pope, Laura M. Ellwein, Cheryl L. Zapata, Vera Novak, C. T. Kelley, Mette S. Olufsen . Estimation and identification of parameters in a lumped cerebrovascular model. Mathematical Biosciences and Engineering, 2009, 6(1): 93-115. doi: 10.3934/mbe.2009.6.93 |
| [8] | Favour Adenugba, Sanjay Misra, Rytis Maskeliūnas, Robertas Damaševičius, Egidijus Kazanavičius . Smart irrigation system for environmental sustainability in Africa: An Internet of Everything (IoE) approach. Mathematical Biosciences and Engineering, 2019, 16(5): 5490-5503. doi: 10.3934/mbe.2019273 |
| [9] | Benchawan Wiwatanapataphee, Yong Hong Wu, Thanongchai Siriapisith, Buraskorn Nuntadilok . Effect of branchings on blood flow in the system of human coronary arteries. Mathematical Biosciences and Engineering, 2012, 9(1): 199-214. doi: 10.3934/mbe.2012.9.199 |
| [10] | Derek H. Justice, H. Joel Trussell, Mette S. Olufsen . Analysis of Blood Flow Velocity and Pressure Signals using the Multipulse Method. Mathematical Biosciences and Engineering, 2006, 3(2): 419-440. doi: 10.3934/mbe.2006.3.419 |
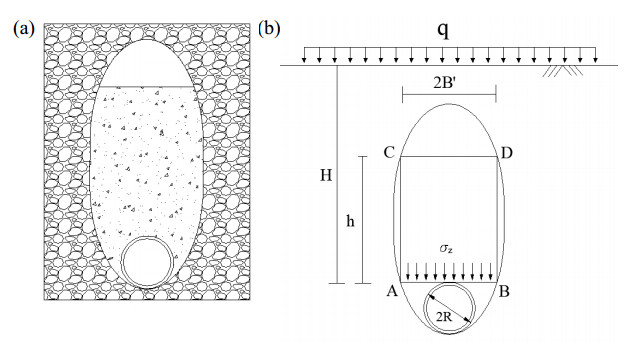
Sandy cobble soils are mainly composed of cobbles, gravels, sand and some clayey soil, the structure of sandy cobble soil is discrete and easy to be disturbed. Different from other soils and rocks, the mechanical properties of cobble soil are rather complex, shield construction in this kind of stratum may cause land subsidence and collapse easily [1,2]. For all land settlement accidents in cobble soil layer, the most typical one is lagged settlement. If the thrust of TBM (Tunnel Boring Machine) is insufficient, it is easy to cause over excavation and form a soil cavity, with the cavity moving to the ground, lagged settlement will happen.
The lagged settlement (or delayed settlement) in sandy cobble soil is related to its mechanical properties. Under natural conditions, sandy cobble soil has a slight of initial cohesion, and cobbles usually interlock together forming a skeleton structure. But once disturbed, it will lose the initial cohesion and change into a loose structure [3]. During shield construction, when over excavation happens the land subsidence will not happen immediately, instead, a cavity will form in disturbed zone, the undisturbed soil above the cavity will be stable for a long time due to the arching effect. However, under the vibration of ground vehicles, the self-stability will fail and the cavity will eventually move to ground surface resulting in land subsidence or collapse. This process usually lasts for months, sometimes even years and that is why we call it lagged settlement. At present, there are many investigations on the process and mechanism of lagged settlement in sandy cobble soils [4,5,6,7], but the research of stress distribution in disturbed zone and evolution of earth pressure on shield tunnel is still insufficient.
In terms of earth pressure theories, the simplest is the full earth pressure theory, i.e. the pressure on tunnel is the weight of overlying soil column. In fact, due to the soil arching effect, earth pressure on tunnel is usually smaller than the weight of the overlying soil. The earliest experimental study on tunnel earth pressure was conducted by Terzaghi [8]. Terzaghi [8,9] designed a trap-door experiment on sand which confirmed the existence of soil arching effect. He thinks that the soil arching effect was caused by the uneven displacement of soil and derived the calculation formula. Terzaghi's theory has been widely used in the calculation of earth pressure on the mined tunnel [8]. However, shield tunnel is quite different from traditional mining method. In addition, Terzaghi formula is not suitable for sandy cobble soil due to the special properties of this stratum. M. M. Protodyakonov proposed another earth pressure theory which is often named as Po's arch theory [10]. Protodyakonov assumes that there is a intact arch area above the tunnel which separates the disturbed zone from surrounding stratum, the pressure on tunnel is the weight of soil within the arch area. Actually, the morphology of disturbed zone in sandy cobble soil is quite different from that in Protodyakonov's theory. Besides, the application condition of Protodyakonov's theory is rather strict, its basic assumptions are quite different from the actual state of sandy cobble soil. Jun Wu [11], Quanmei Gong [12] et al. believe that the disturbed zone is a limited ellipsoid, in sand layers, with the outflow of soil particles from trap-door, the loosened area will gradually expand to the limit ellipsoid whereas the soil outside the ellipsoid are in static state [13]. Ellipsoid theory of particle flows has been successfully applied on sandy stratum, but it still needs effort to apply on sandy cobble stratum since the self-stability of cobble soil is much better. Besides, in different phases of lagged settlement, the stress distribution in disturbed zone and earth pressure on tunnel are different and they need to be analyzed respectively.
This paper aims to investigate the stress distribution characteristics in loosened sandy cobble stratum, which is related to the stability of soil stratum and mechanical control of shield excavation. In this paper, the process and mechanism of lagged settlement or collapse in sandy cobble stratum were analyzed. Based on ellipsoid theory of particle flows, the coefficient of lateral earth pressure in loosened zone is derived. For the earth pressure on tunnel, the evolution of lagged settlement in different phases including soil disturbance, formation of cavity, cavity moving upward and land subsidence are analyzed, and theoretical formulas of loosened earth pressure are derived respectively. Results are helpful for understanding the stress distribution in disturbed cobble soil, providing theoretical guidance for control of shield thrust and calculation of tunnel support.
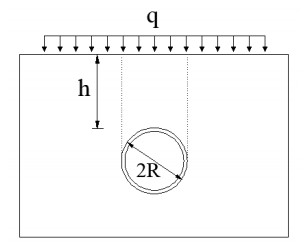
Full earth pressure theory is the simplest theory for earth pressure calculation. As shown in Figure 1, if the tunnel is shallow or the soil is soft, it can be approximately considered that the earth pressure on the tunnel is the weight of soil within the width of the tunnel. Considering the effect of external load, theoretical formula for calculating earth pressure can be expressed as:
| ${\sigma _z}{\rm{ = }}\gamma \cdot h + q$ | (1) |
where $\gamma $ is unit weight of soil.
Full earth pressure theory is effective when tunnel is shallow and the soil is soft. However, it has not taken into consideration of the shear action of soil and the arching effect.
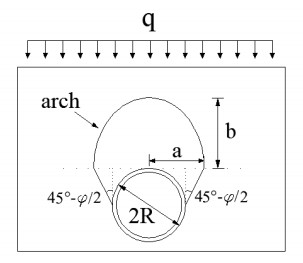
M. M. Protodyakonov (Михаил Михайлович Протодьяконов) [14] assumed that after excavation, a naturally balanced arch will form above the tunnel, and two sliding surfaces will form at both sides of the tunnel. Due to the arching effect, soil outside the arch does not exert pressure on the tunnel, and earth pressure on the tunnel is the weight of the soil within the arch. Regarding the morphology of the soil arch, Protodyakonov deduced that the morphology of the arch curve is a parabola.
As shown in Figure 2, the parameters of the arch can be expressed as follows
| $a = R + R\tan (45^\circ - \frac{\phi }{2})$ | (2) |
| $b = \frac{a}{f}$ | (3) |
where $f$ is coefficient of rock solidity.
The earth pressure on the tunnel is
| ${\sigma _z} = \gamma b = \frac{{\gamma a}}{f}$ | (4) |
The Protodyakonov arch theory takes into consideration of soil arching effect, but its application scope is relatively small, because different rocks usually have different properties. In addition, it is difficult to form a complete arch in many soils and the morphology of arches in different soils are also difficult to determine.
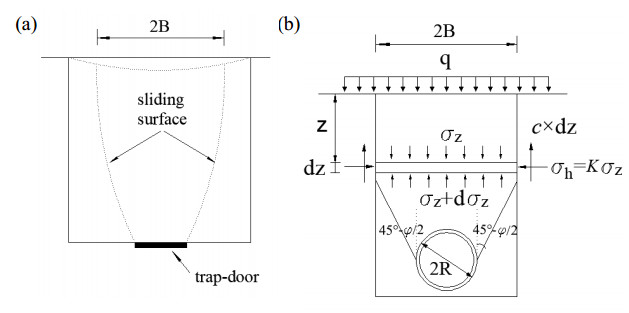
Terzaghi [9,15] designed and conducted a trap-door experiment as shown in Figure 3a. According to the experiment result, the sliding boundary is a curved surface and the width of sliding zone will decrease with the increase of depth. By simplifying the calculation model, he derived the analytical formula of vertical stress on trap-door.
Figure 3b is a simplified calculation model for earth pressure on tunnel. Assuming that within a certain width, the soil column tends to move downward due to the tunnel deformation. According to the balance of vertical stresses, the equilibrium equation of the soil unit can be expressed as
| ${\rm{2}}B{\sigma _{\rm{z}}} + 2B\gamma dz = 2B\left( {{\sigma _z} + d{\sigma _z}} \right) + 2cdz + 2K{\sigma _z}dz \cdot \tan \varphi $ | (5) |
where $\gamma $ is unit weight of soil, are cohesion and internal friction angle of soil respectively, K is the lateral pressure coefficient of soil, 2B is the width of sliding soil, and
| ${\rm{2}}B{\rm{ = }}2R{\rm{ + 2}}R\left[ {\tan (45^\circ - \frac{\varphi }{2})} \right]$ | (6) |
According to the boundary condition of $z = 0, {\sigma _z} = q$, the earth pressure at depth z can be expressed as
| ${\sigma _{\rm{z}}} = \frac{{B\gamma - c}}{{K\tan \varphi }}\left( {1 - {e^{ - \frac{{K\tan \varphi \cdot z}}{B}}}} \right) + q{e^{ - \frac{{K\tan \varphi \cdot z}}{B}}}$ | (7) |
It is not difficult to find that, in this theory, the sliding surface of soil column is related to the active earth pressure. As an extension of full earth pressure theory, Terzaghi considered the effect of soil cohesion and friction. We can conclude from the basic assumption that, the application condition of this theory is the soil column has a tendency to move downward, or the boundary condition of the sliding zone is at the critical equilibrium state.
Terzaghi formula is also a simplified method since the sliding boundary was simplified by a broken line and the upper part is simplified to vertical surface. In addition, the arching effect in soil is not considered in Terzaghi formula. This theory is more accurate for the earth pressure on pipeline buried in trench.
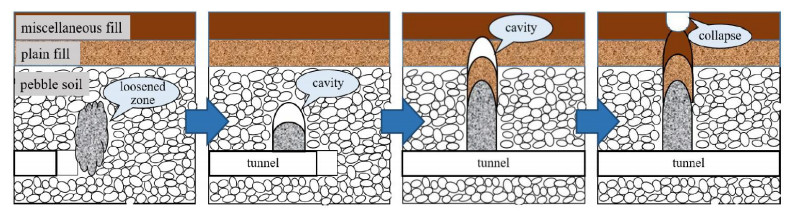
The mechanism of lagged settlement in sandy cobble strata has been proposed by several researchers. According to Yingchao Jiang [16,17] and Yongxue Bai [1,18], there are four phases throughout the evolution of lagged settlement, including instability of excavation face, over excavation and formation of cavity, cavity moving upward, land collapse. Cavities are usually on right top of the tunnel because of disturbance, gravity and over excavation. For cobble soil outside the disturbed zone, the structure is relatively stable and the arching effect can maintain the cavity for a long time if no extra disturbance exists. As time going on, many factors will break the balance of arch, such as the change of groundwater level, creep of soil and disturbance from traffic load. Under the action of gravity and disturbance, the soil on top of the cavity keeps falling off and the cavity will gradually move upward, finally the cavity develops to the surface leading to a sudden collapse.
Figure 4 illustrates the evolution process of lagged settlement. Firstly, under the disturbance of TBM, a loosened zone appears in front of the tunnel face. Then, under the action of gravity and excavation, loosened cobble soil pours into the cutter head leading to over excavation and formation of a cavity in cobble stratum. Thirdly, under the action of external disturbance, the cavity gradually moves upward and eventually leads to a land collapse. Figure 5a is internal view of the cavity, black lines show the outline of the cavity. Figure 5b is a typical pavement collapse in sandy cobble strata induced by shield construction. Both theoretical research and engineering practice show that, in cobble soil strata, the loosened zone and cavity caused by shield tunneling are mostly elliptically shaped.
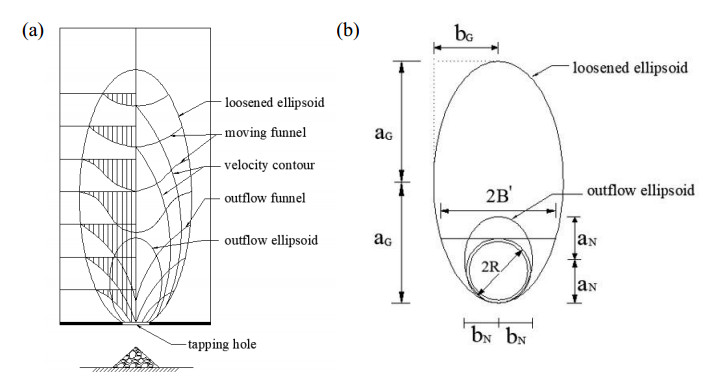
Ellipsoid theory of particle flows was proposed by Malakhov (Γ. Mарахоф) in 1952 [12,19], and the theory was applied in mining and metallurgy at first. Janelid et.al. [20,21] divided the ellipsoid into two parts according to the moving state of inside particles, i.e., the loosened ellipsoid and the outflow ellipsoid, and he proposed the concept of loosening coefficient to describe the relaitonship between them.
As shwon in Figure 6a, Ellipsoid theory of particle flows assumes that there is a bunker filled with mineral particles and there is a tapping hole at the bottom, when the tapping hole opens, the particles will flow out through it. In a steady state of outflow, the particles will flow out from a zone named outflow ellipsoid. Correspondingly, there is a loosened ellipsoid (or limit ellipsoid) in a certain range outside the outflow ellipsoid. Based on the boundaries of outflow ellipsoid and loosened ellipsoid, the particles in the bunker can be divided into three patrts, within the outflow ellipsoid is the outflow zone, between outflow ellipsoid and limit ellipsoid is the loosened zone, patricles outside the limit ellipsoid is the static zone.
Figure 6b is a diagram of ellipsoid theory adapted for shield construction in sandy cobble soil. Different from ore drawing theory, the position of tapping hole is the cutter head of TBM (or the section of the tunnel). In Figure 6b, we can get some dimension parameters about loosened ellipsoid and outflow ellipsoid. Assuming that the long axis and short axis of outflow ellipsoid are ${a_N}$ and ${b_N}$ respectively. Similarly, ${a_G}$ and ${b_G}$ for limit ellipsoid.
The eccentricity of the outflow ellipsoid can be expressed as formula 8, and in practice, the value of $\varepsilon $ is 0.90–0.98 [23].
| $\varepsilon {\rm{ = }}{\left( {{\rm{1}} - b_N^2/a_N^2} \right)^{1/2}}$ | (8) |
Assuming that the volume of outflow ellipsoid and loosened ellipsoid are ${E_N}$ and ${E_G}$ respectively. According to [24], the loosening coefficient in limit ellipsoid will be
| $\beta = \frac{{{E_G}}}{{{E_G}{\rm{ - }}{E_N}}}$ | (9) |
where $\beta $ is a constant within 1.066–1.100 [11,12].
In Figure 6b, the outflow of particles is concentrated in the face of TBM, so the area of outflow ellipsoid can be assumed to be the area of tunnel section. Namely
| $\pi {a_N}{b_N} = \pi {R^2}$ | (10) |
By calculation of equation 8 and 10, we can get
| ${a_N} = R{\left( {1 - {\varepsilon ^2}} \right)^{ - \frac{1}{4}}}$ | (11) |
| ${b_N} = R{\left( {1 - {\varepsilon ^2}} \right)^{\frac{1}{4}}}$ | (12) |
Similarly, by calculating simultaneous equation 8 to 12, the long axis and short axis of loosened ellipsoid are
| ${a_G} = R{\left( {\frac{\beta }{{\beta {\rm{ - 1}}}}} \right)^{\frac{1}{2}}}{\left( {1 - {\varepsilon ^2}} \right)^{ - \frac{1}{4}}}$ | (13) |
| ${b_G} = R{\left( {\frac{\beta }{{\beta {\rm{ - 1}}}}} \right)^{\frac{1}{2}}}{\left( {1 - {\varepsilon ^2}} \right)^{\frac{1}{4}}}$ | (14) |
Many investigation results show that, ellipsoid theory of particle flows is applicable for earth pressure analysis in sand stratum, because both soil arching effect and the characteristics of disturbed zone have been taken into account [11,12,19]. Here, by analyzing the characteristics of sandy cobble soil in section 3.1, it is not difficult to find that, the mechanism and process of lagged settlement in sandy cobble strata are consistent with the ellipsoid theory, and the morphology of the loosened zone is in good agreement with limit ellipsoid.
Based on ellipsoid theory of particle flows, this paper will analyze the coefficient of lateral earth pressure in critical equilibrium state, and also derive the loosened earth pressure on tunnel in several states including the limit equilibrium state, the formation of cavity by over excavation, the upward moving of cavity.
In this section, we will mainly discuss the pressure on boundary of the loosened ellipsoid, because cobble soil on the boundary is in the state of critical slip, i.e. the 'critical stress state' in soil mechanics. For cobble soil inside the ellipsoid, the stress states are more complicated since they keep moving at different speeds, and that is beyond the scope of our research. On the other hand, for soil outside the loosened ellipsoid, they are not disturbed and keep in a static state, the stress state can be analyzed through general method which is also not discussed in this paper.
The coefficient of lateral earth pressure is related to the stress state at different positions [8,25]. As will be discussed later, the critical state at different positions are caused by different factors, it is necessary to divide the ellipsoid into two parts, the arch zone and the excavation zone, here we simplify it as the upper and lower half ellipsoid.
The arch zone discussed here is the condition when the loosened zone extends to the critical state, i.e., the loosened zone has extended to the limit ellipsoid and the cavity has not formed yet. In fact, at beginning the disturbed zone is very small, with the gradual expansion, the disturbed zone will finally expand to the limit ellipsoid and reach the critical state [26]. In critical state, the arching effect will be very obvious on top of upper ellipsoid due to the skeleton structure of cobble soil. In this condition, the boundary curve of limit ellipsoid can be considered as the arch axis. For the distribution of stress, it can be assumed that the major principal stress is distributed along the arch axis, which has been proposed in many studies [8,27,28,29].
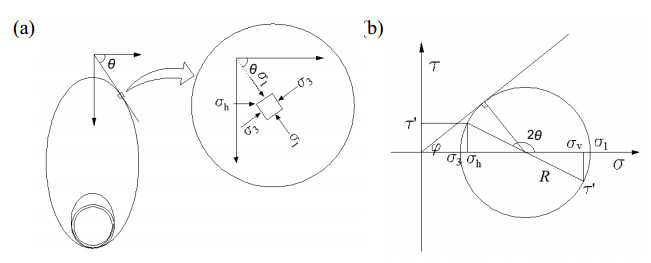
In order to analyze the lateral earth pressure on boundary element, we pick a point on the upper half of the ellipsoid. As shown in Figure 7a, ${\sigma _{\rm{1}}}$ and ${\sigma _{\rm{3}}}$ are major and minor principal stress respectively. ${\sigma _h}$ and ${\sigma _v}$ are the horizontal stress and vertical stress at that point. $\tau '$ is the shear stress on the vertical surface. Assuming that the angle between ${\sigma _{\rm{1}}}$ and ${\sigma _h}$ is $\theta $ and the internal friction angle of sandy cobble soil is $\varphi $. Then the stress state of boundary element at this point can be described by a Mohr circle in Figure 7b.
The following results can be obtained from the Mohr circle:
| $R = \frac{{{\sigma _1} - {\sigma _3}}}{2}$ | (15) |
| ${\sigma _h} = \frac{{{\sigma _1} + {\sigma _3}}}{2} - R\cos (180 - 2\theta )$ | (16) |
| ${\sigma _v} = \frac{{{\sigma _1} + {\sigma _3}}}{2} + R\cos (180 - 2\theta )$ | (17) |
Substituting equation 15 back to 16 and 17 then results
| ${\sigma _h} = {\sigma _1}{\cos ^2}\theta + {\sigma _3}{\sin ^2}\theta $ | (18) |
| ${\sigma _v} = {\sigma _1}{\sin ^2}\theta + {\sigma _3}{\cos ^2}\theta $ | (19) |
Equation 18 divided by equation 19, then result
| $\frac{{{\sigma _h}}}{{{\sigma _v}}} = \frac{{{\sigma _1}{{\cos }^2}\theta + {\sigma _3}{{\sin }^2}\theta }}{{{\sigma _1}{{\sin }^2}\theta + {\sigma _3}{{\cos }^2}\theta }}$ | (20) |
Divide numerator and denominator by ${\sigma _1}{\cos ^2}\theta $ simultaneously, then
| $\frac{{{\sigma _h}}}{{{\sigma _v}}} = \frac{{1 + \frac{{{\sigma _3}}}{{{\sigma _1}}}{{\tan }^2}\theta }}{{{{\tan }^2}\theta + \frac{{{\sigma _3}}}{{{\sigma _1}}}}}$ | (21) |
As we can see from Figure 7b
| $\sin \varphi = \frac{{({\sigma _1} - {\sigma _3})/2}}{{({\sigma _1} + {\sigma _3})/2}}$ | (22) |
By transformation, it is
| $\frac{{{\sigma _3}}}{{{\sigma _1}}} = \frac{{1 - \sin \varphi }}{{1 + \sin \varphi }} = {\tan ^2}(45 - \varphi /2) = {K_a}$ | (23) |
Substituting equation 23 back to 21 then result
| $K = \frac{{{\sigma _h}}}{{{\sigma _v}}} = \frac{{1 + {K_a}{{\tan }^2}\theta }}{{{{\tan }^2}\theta + {K_a}}}$ | (24) |
It can be seen from formula 24 that, the coefficient of lateral earth pressure on ellipsoid boundary is a function of $\theta $, which is related to the position of the arch. Particularly, at the short axis of the ellipse ($\theta = 90^\circ $), $K$ will be ${K_a}$ (which can be deduced from equitation 23). This means when $\theta = 90^\circ $, cobble soil is in an active earth pressure state, this is consistent with the theory of soil mechanics. For another particular position, the vault ($\theta = 0^\circ $), that will be $K = \frac{1}{{{K_a}}} = {K_p}$, which means soil at this point is in a passive earth pressure state.
For different cobble soils, the range and morphology of loosened ellipsoid are slightly different, which is related to the properties of soils such as particle size distribution, water content, cohesion and internal friction angle. Besides, the extent of soil arching effect also plays an important role. Before extending to limit ellipsoid, the soil arch is called 'incomplete arch'. For incomplete arch, the vault is difficult to determine and the major principal stress does not necessarily distribute along the arch axis, as a result, the formula 24 will be not very accurate.
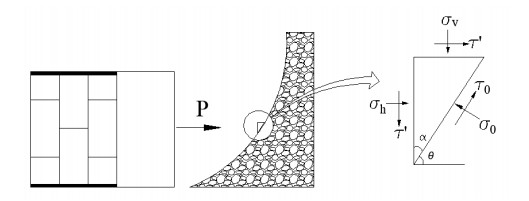
Different from the arch zone in section 4.1, the formation of sliding surface in excavation zone is not due to gravity. Although it is also related to the mechanical disturbance, the main reason is the thrust of shield machine. To simplify the derivation process, we assume that the excavation zone is the lower half ellipsoid. For excavation zone, there is no arching effect on the sliding surface, so the principal stress is no longer distributed along the curve of sliding surface. In this condition, the shear stress on boundary element reaches the critical state under the action of shield excavation, which leads to a shear failure on the sliding surface, as shown in Figure 8. Based on the theory of loosened ellipsoid, we assume that the morphology of sliding surface is also ellipsoid.
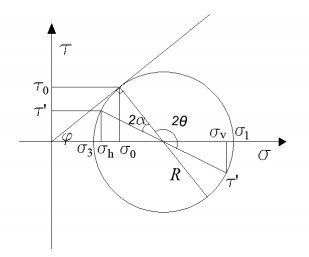
Under the action of thrust and excavation from TBM, the stress state of boundary element on loosened ellipsoid can be illustrated in Figure 8 and the Mohr circle can be represented as Figure 9. Assuming that the angle between horizontal plane and the tangent to boundary element is $\theta $, the angle between vertical plane and the tangent will be $\alpha {\rm{ = 90}}^\circ {\rm{ - }}\theta $, on the Mohr circle they are ${\rm{2}}\theta $ and ${\rm{2}}\alpha $ respectively.
It can be obtained from the Mohr circle that:
| ${\rm{2}}\alpha {\rm{ = 180}}^\circ - {\rm{2}}\theta $ | (25) |
| ${\sigma _h} = \frac{R}{{\sin \varphi }} - R\cos (90^\circ - \varphi - 2\alpha ) = \frac{R}{{\sin \varphi }} - R\sin (\varphi + 2\theta )$ | (26) |
| ${\sigma _v} = \frac{R}{{\sin \varphi }} + R\cos (90^\circ - \varphi - 2\alpha ) = \frac{R}{{\sin \varphi }} + R\sin (\varphi + 2\theta )$ | (27) |
Eq 26 divided by Eq 27, then result
| $K{\rm{ = }}\frac{{{\sigma _h}}}{{{\sigma _v}}} = \frac{{\frac{R}{{\sin \varphi }} - R\sin (\varphi {\rm{ + }}2\theta )}}{{\frac{R}{{\sin \varphi }} + R\sin (\varphi + 2\theta )}}$ | (28) |
By transformation, it is
| $K{\rm{ = }}\frac{{{\rm{1}} - \sin (2\theta - \varphi )\sin \varphi }}{{{\rm{1}} + \sin (2\theta - \varphi )\sin \varphi }}$ | (29) |
Formula 29 is the coefficient of lateral earth pressure in excavation zone, as we can see it is a function of $\theta $ and $\varphi $ and it has nothing to do with the depth of the turnel. It can be explained that the disturbed zone is limitted in the range of loosened ellipsoid, soils outside this zone remain static in a equilibrium state and exert no influence. Similar result was reported by Quanmei Gong in reference [12]. Particularly, if $\theta {\rm{ = 90}}^\circ $ then $K{\rm{ = }}\frac{{{\rm{1}} - {{\sin }^2}\varphi }}{{{\rm{1 + }}{{\sin }^2}\varphi }}$, it is a value less than 1, because at the short axes, the vertical stress (which originates from the unloading of excavation below) is a dominant factor which leads to the critical state. As a result, the vertical stress will be greater than horizontal stress. On the contrary, if $\theta {\rm{ = 0}}^\circ $ then $K{\rm{ = }}\frac{{{\rm{1 + }}{{\sin }^2}\varphi }}{{{\rm{1}} - {{\sin }^2}\varphi }}$, here $K > 1$ because at the bottom of the ellipsoid, the critical state of cobble soil is caused by the thrust action of TBM and the horizontal stress will be greater than that on vertical.
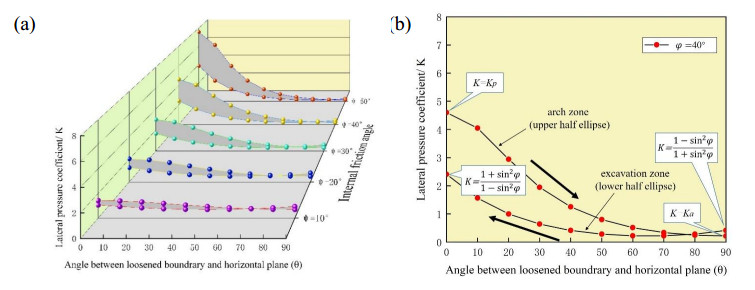
Figure 10a illustrates the variation of lateral earth pressure coefficients on the loosened ellipsoid when $\varphi {\rm{ = 10}}^\circ {\rm{\sim50}}^\circ $, where $\varphi $ is the internal friction angle of sandy cobble soil. Figure 10b highlights the variation of lateral earth pressure coefficients when $\varphi {\rm{ = 40}}^\circ $. It can be found that the coefficient of arch zone is larger than that of excavation zone, which can be explained by the full exertion of arching effect. Besides, when $\theta $ is close to $90^\circ $ the coefficients of lateral earth pressure in two different zones gradually coincide, in fact this position is the intersection of arch zone and excavation zone. When $\theta {\rm{ = 90}}^\circ $, the coefficients calculated by two methods are slightly different, because the assumptions of stress states in two conditions are different, but in fact the calculation results are very close.
Through the analysis in chapter 3, it can be seen that the disturbed zone originates from the excavation face and then gradually extends to the limit ellipsoid, with the cavity gradually moves to ground surface the land collapse occurs. During this process only soil inside the loosened ellipsoid exerts pressure on tunnel, whereas the soils outside the loosened zone remain in a static state due to the soil arching effect. As a result, the pressure on tunnel will mainly come from the soil in the loosened area, and will be in constant change with the expansion of the loosened zone and movement of the cavity. In this chapter, the loosened earth pressure in sandy cobble soil under three typical states will be derived respectively. Here the Terzaghi formula is adapted and the Protodyakonov's theory of soil arch is also taken into account.
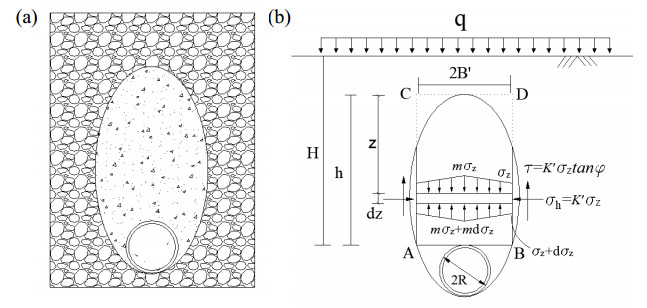
Limit state is the condition when loosened zone expands to limit ellipsoid and the cavity has not formed yet. As shown in Figure 11a, if the tunnel is a deep-buried tunnel, the limit ellipsoid will be beneath the ground. In this condition, the external load has no influence on the tunnel because of the arching effect. In figure 11b, the area of $ABCD$ is selected as the soil column, where $AB$ is tangent to the top of the tunnel and $CD$ is tangent to the top of the limit ellipse. It should be pointed out that for safety consideration, the width of soil column in arch zone is assumed equal to the bottom. i.e. $CD = AB$. On the other hand, in most conditions the soil arch manifests as incomplete arch, and the boundary of arch zone is not very distinct. For this assumption, the stress distribution in arch zone will be reflected on the calculation element as will be discussed later.
In Figure 11b, the width of soil column, i.e. the length of $AB$ can be expressed as
| $2B' = 4\sqrt {(1 - {\varepsilon ^2})({a_G} - R)R} $ | (30) |
For the stress distribution on the calculation element, since the earth pressure mainly comes from the weight of soil in the loosened ellipsoid, the stress on right top of tunnel will be greater than that on both sides. Assuming that the earth pressure on the middle line is $m$ times of that on both sides ($m > 1$). For element in Figure 11b the equilibrium equation of vertical stress is
| $B'\left( {{\sigma _z} + m{\sigma _z}} \right) + 2B'\gamma 'dz = B'\left( {{\sigma _z} + d{\sigma _z} + m{\sigma _z} + md{\sigma _z}} \right) + 2K'{\sigma _z}\tan \varphi dz$ | (31) |
where $\gamma '$ is the unit weight of loose soil, $K'$ is lateral pressure coefficient on the vertical surface.
It can be obtained after conversion that
| $\frac{{B'\left( {1 + m} \right)d{\sigma _z}}}{{2B'\gamma ' - 2K'\tan \varphi {\sigma _z}}} = dz$ | (32) |
Integrate the two sides of Eq 32, then
| $ - \frac{{B'\left( {1 + m} \right)}}{{2K'\tan \varphi }}\ln \left( {2B'\gamma ' - 2K'\tan \varphi {\sigma _z}} \right) = z + {C_1}$ | (33) |
Taking boundary conditions $z = 0, {\sigma _z} = 0$ into Eq 33, then
| ${C_1} = - \frac{{B'\left( {1 + m} \right)\ln \left( {2B'\gamma '} \right)}}{{2K'\tan \varphi }}$ | (34) |
Assuming $Q = - \frac{{B'\left({1 + m} \right)}}{{2K'\tan \varphi }}$, then Eq 34 will be
| ${C_1} = Q\ln \left( {2B'\gamma '} \right)$ | (35) |
And Eq 33 will be
| $Q\ln \left( {2B'\gamma ' - 2K'\tan \varphi {\sigma _z}} \right) = z + {C_1}$ | (36) |
It can be obtained after conversion
| ${\sigma _z} = \frac{{B'\gamma '}}{{K'\tan \varphi }} - \frac{1}{{2K'\tan \varphi }}{e^{\frac{{z + {C_1}}}{Q}}}$ | (37) |
Combining Eqs 35 and 37, result is
| ${\sigma _z} = \frac{{B'\gamma '}}{{K'\tan \varphi }} - \frac{1}{{2K'\tan \varphi }}{e^{\frac{z}{Q} + \ln \left( {2B'\gamma '} \right)}} = \frac{{B'\gamma '}}{{K'\tan \varphi }} - \frac{{B'\gamma '}}{{K'\tan \varphi }}{e^{\frac{z}{Q}}}$ | (38) |
Substituting $Q = - \frac{{B'\left({1 + m} \right)}}{{2K'\tan \varphi }}$ back into Eq 38 then result
| ${\sigma _z} = \frac{{B'\gamma '}}{{K'\tan \varphi }}\left( {1 - {e^{ - \frac{{2K'\tan \varphi \cdot z}}{{B'\left( {1 + m} \right)}}}}} \right)$ | (39) |
Formula 39 is the loosened earth pressure at different depth in the limit ellipsoid. Assuming that $z = h$, the earth pressure on top of the tunnel can be obtained from formula 39.
It should be noted that the lateral pressure coefficient $K'$ here is different from that in section 4. The $K$ in section 4 refers to the points on the boundary of the loosened ellipsoid, while $K'$ here refers to the lateral pressure coefficient on the vertical surface, i.e. the $AC$ and $BD$ sides. For the value of $K'$, Maston [30] suggested that the value can be taken as ${K_a}$. This is reasonable since the soil at the vertical surface is in active earth pressure state.
In this section we only discuss the condition when disturbed zone extends to limit ellipsoid, the previous periods (initial disturbance and expansion) are not discussed here, because they last for only a short time during excavation. Moreover, the constant changing state also makes it difficult to investigate.
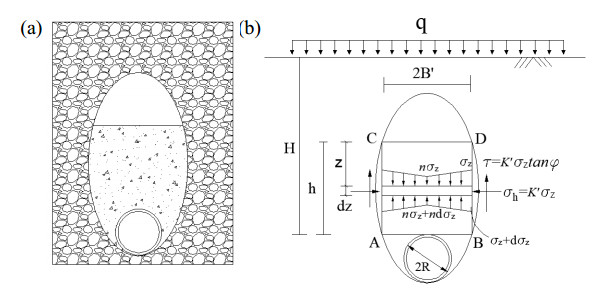
Similar to section 5.1, if the tunnel is deep enough, land collapse will also not occur immediately in the state of over excavation. On the contrary, a cavity will form at the top of loosened ellipsoid (internal view is shown in Figure 5a). In this condition, the loosened zone is similar to a silo filed with loose particles (see Figure 12a) and the earth pressure on tunnel is only related to the gravity of loosened soil in it. As shown in Figure 12b, the effective soil column is the area of $ABCD$. Similar to section 5.1, the width of soil column ($2B'$) can also be expressed as formula 30, and the section of $AB$ is taken as the calculation surface of earth pressure on tunnel.
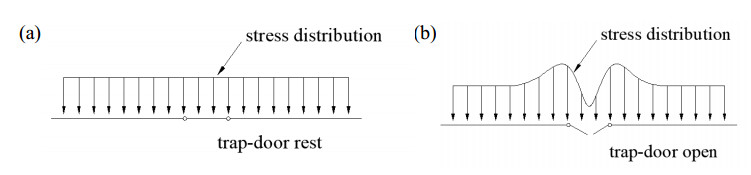
It should be noted that for calculation element, the distribution of vertical stress is contrary to limit state condition in section 5.1. As shown in Figure 12b, the stress on top of tunnel is smaller compared with two edges. This phenomenon can be explained by the trap-door experiment conducted by Terzaghi. As shown in Figure 13, when the trap-door opens the vertical stress on top of trap-door will decrease, and the major principal stress will move to both sides [12,31]. In this condition, the actual stress distribution is like Figure 13b.
In this case, it can be assumed that the stress on the midline is $n$ times that on both sides ($n < 1$ and $\frac{{\rm{1}}}{n}{\rm{ = 3}}{\rm{.256\sim3}}{\rm{.745}}$ according to [11]). For the element in Figure 12b, the equilibrium equation of vertical stress can be expressed as
| $B'\left( {{\sigma _z} + n{\sigma _z}} \right) + 2B'\gamma 'dz = B'\left( {{\sigma _z} + d{\sigma _z} + n{\sigma _z} + nd{\sigma _z}} \right) + 2K'{\sigma _z}\tan \varphi dz$ | (40) |
It can be obtained after conversion:
| $\frac{{B'\left( {1 + n} \right)d{\sigma _z}}}{{2B'\gamma ' - 2K'\tan \varphi {\sigma _z}}} = dz$ | (41) |
Similar to the calculation process in section 5.1, the earth pressure at different depth is
| ${\sigma _z} = \frac{{B'\gamma '}}{{K'\tan \varphi }}\left( {1 - {e^{ - \frac{{2K'\tan \varphi \cdot z}}{{B'\left( {1 + {\rm{n}}} \right)}}}}} \right)$ | (42) |
Formula 42 is the loosened earth pressure in over excavation state. Assuming that $z = h$, the earth pressure on top of the tunnel can be obtained. As for the coefficient of lateral earth pressure ($K'$), since the soil in the ellipsoid is loose and also in the active earth pressure state, the lateral pressure coefficient of $K'$ is also ${K_a}$.
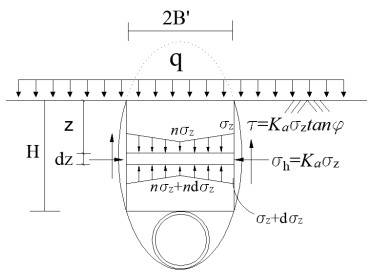
Here we will consider another condition. As shown in Figure 14, if the tunnel is shallow, the loosened ellipsoid will be partly above the ground and that is impossible. Obviously, in this condition the disturbed range is ground surface to top of the tunnel. In this condition, even though the arch zone no longer exists, the morphology of disturbed zone is still consistent with ellipsoid theory of particle flows. Besides, the earth pressure on tunnel will be affected by external loads.
The schematic diagram is shown in Figure 14. The equilibrium equation of the element can be expressed as
| $B'\left( {{\sigma _z} + n{\sigma _z}} \right) + 2B'\gamma 'dz = B'\left( {{\sigma _z} + d{\sigma _z} + n{\sigma _z} + nd{\sigma _z}} \right) + 2K'{\sigma _z}\tan \varphi dz$ | (43) |
Similar to the derivation process in section 5.1, the earth pressure at different depth is
| ${\sigma _z} = \frac{{B'\gamma '}}{{K'\tan \varphi }}\left( {1 - {e^{ - \frac{{2K'\tan \varphi \cdot z}}{{B'\left( {1 + {\rm{n}}} \right)}}}}} \right)$ | (44) |
Considering the influence of external load, the boundary condition of equation 44 will be $z = 0, {\sigma _z} = q$. Taking this boundary condition into equation 44, then result
| ${\sigma _z} = \frac{{B'\gamma '}}{{K'\tan \varphi }}\left( {1 - {e^{ - \frac{{2K'\tan \varphi \cdot z}}{{B'\left( {1 + n} \right)}}}}} \right) + q{e^{ - \frac{{2K'\tan \varphi \cdot z}}{{B'\left( {1 + n} \right)}}}}$ | (45) |
Similarly, the coefficient of lateral earth pressure ($K'$) is also ${K_a}$. Besides, the coefficient of stress distribution is also $n$, because it is a special condition of Figure 12, and the external load can be regarded as equivalent soil weight with a certain thickness.
Before land collapse occurs, the cavity will gradually move upward under the action of external disturbance. Actually, before the cavity extends to ground, the loosened ellipsoid is still separated from external environment and the external load has no effect on the earth pressure, as shown in Figure 15.
Generally speaking, in this condition the tunnel has already been supported and cobble soil no longer flows out. As a result, the stress on the calculation surface will be uniformly distributed over time via stress redistribution. In this condition, if the tunnel has no obvious deformation, we can refer to Protodyakonov's theory in section 2.2, and the earth pressure on the tunnel is
| ${\sigma _z} = \gamma 'h$ | (46) |
In particular, if the tunnel deforms the earth pressure can be derived with formula 40-42.
Lagged settlement or collapse is a typical accident induced by shield excavation in sandy cobble soil, there are several phases throughout the evolution including disturbance in front of excavation face, over excavation, formation of cavity, cavity moves upward and ground collapse. The mechanism and process of lagged settlement in sandy cobble soil matches ellipsoid theory of particle flows well, based on this theory, the distribution of lateral earth pressure coefficient and earth pressure on tunnel are derived.
For coefficients of lateral earth pressure, the limit ellipsoid is divided into the arch zone and the excavation zone, and the formulas are derived respectively. Results show that the coefficient of lateral earth pressure is a function of the tangent angle of the boundary element, and the coefficient in arch zone is larger than that in excavation zone because of the soil arching effect.
For the loosened earth pressure on tunnel, three typical states are derived based on Terzaghi formula and Protodyakonov's theory. The first two cases are the limit ellipsoid state and over excavation state. For these two conditions, if the tunnel is deep-buried tunnel, loosened ellipsoid will be separated from surrounding soils due to the arching effect, and the pressure on tunnel depends on the weight of soil inside the ellipsoid. On the contrary, for shallow tunnel the pressure will be affected by external load. The third case is the cavity moving upward. For this case, if the tunnel does not deform, the earth pressure can be calculated by Protodyakonov's theory, otherwise the adapted Terzaghi formula will be more accurate.
Considering the insufficiencies in this paper, the following aspects still need more research. First of all, the ellipsoid theory of particle flows is an approximation in morphology, the actual state is related to the properties of cobble soils and degree of disturbance. Secondly, only typical states are covered in this paper, more details about stress distribution and deformation of cobble soil still need more research. Finally, for incomplete arch the major principal stress does not necessarily distribute along the arch axis, and the accuracy of the formula needs to be verified.
This work has been supported by Guangzhou Municipal Science and Technology Bureau (201904010290), the authors gratefully acknowledge this funding support. Besides, the authors would like to express their sincere thanks to anonymous referees for their valuable comments and suggestions.
All authors declare no conflict of interest in this paper.
| [1] | Hass WK, Fields WS, North RR, et al. (1968) Joint study of extracranial arterial occlusion. II. Arteriography, techniques, sites, and complications. JAMA 203: 961-968. |
| [2] | Brunholzl C, von Reutern GM (1989) Hemodynamic effects of innominate artery occlusive disease. Evaluation by Doppler ultrasound. Ultrasound Med Biol 15: 201-204. |
| [3] | Rooke T (2007) Vascular Medicine and Endovascular Intervention. 1st ed: Wiley-Blackwell. |
| [4] |
Fisher C (1961) A new vascular syndrome: the subclavian steal. England J Med 265: 912-913. doi: 10.1056/NEJM196111022651812
|
| [5] |
Blakemore WS, Hardesty WH, Bevilacqua JE, et al. (1965) Reversal of blood flow in the right vertebral artery accompanying occlusion of the innominate artery. Ann Surg 161: 353-356. doi: 10.1097/00000658-196503000-00005
|
| [6] | Cronewett, Johnston. Rutherford's Vascular Surgery. 7th ed: Saunders Elsevier. |
| [7] |
Palchik E, Bakken AM, Wolford HY, et al. (2008) Evolving strategies in treatment of isolated symptomatic innominate artery disease. Vascu Endov Surgery 42: 440-445. doi: 10.1177/1538574408315994
|
| [8] | Brountzos EN, Malagari K, Kelekis DA (2006) Endovascular treatment of occlusive lesions of the subclavian and innominate arteries. Cardio Inter Radio 29: 503-510. |
| [9] | Patel SN, White CJ, Collins TJ, et al. (2008) Catheter-based treatment of the subclavian and innominate arteries. J Soc Cardiac Angiogra Inter 71: 963-968. |
| [10] |
Aiello F, Morrissey NJ (2011) Open and endovascular management of subclavian and innominate arterial pathology. Sem Vascu Surg 24: 31-35. doi: 10.1053/j.semvascsurg.2011.04.001
|
| [11] |
Brott TG, Halperin JL, Abbara S, et al. (2011) ASA/ACCF/AHA/AANN/AANS/ACR/ASNR/CNS/SAIP/SCAI/SIR/SNIS/SVM/SVS guideline on the management of patients with extracranial carotid and vertebral artery disease: executive summary. J Cereb Circu 42: e420-463. doi: 10.1161/STR.0b013e3182112d08
|
| [12] |
Grosveld WJ, Lawson JA, Eikelboom BC, et al. (1988) Clinical and hemodynamic significance of innominate artery lesions evaluated by ultrasonography and digital angiography. J Cereb Circu 19: 958-962. doi: 10.1161/01.STR.19.8.958
|
| [13] | Laloux P, Richelle F, Meurice H, et al. (1995) Cerebral blood flow and perfusion reserve capacity in hemodynamic carotid transient ischemic attacks due to innominate artery stenosis. J Nuc Med 36: 1268-1271. |
| [14] |
Grant EG, El-Saden SM, Madrazo BL, et al. (2006) Innominate artery occlusive disease: sonographic findings. Am J Roentgenol 186: 394-400. doi: 10.2214/AJR.04.1000
|
| [15] |
von Reutern GM, Pourcelot L (1978) Cardiac cycle-dependent alternating flow in vertebral arteries with subclavian artery stenoses. J Cereb Circu 9: 229-236. doi: 10.1161/01.STR.9.3.229
|
| [16] |
Berguer R, Morasch MD, Kline RA (1998) Transthoracic repair of innominate and common carotid artery disease: immediate and long-term outcome for 100 consecutive surgical reconstructions. J Vascu Surg 27: 34-41. doi: 10.1016/S0741-5214(98)70289-7
|
| [17] |
Kieffer E, Sabatier J, Koskas F, et al. (1995) Atherosclerotic innominate artery occlusive disease: early and long-term results of surgical reconstruction. J Vascu Surg 21: 326-336. doi: 10.1016/S0741-5214(95)70273-3
|
| [18] |
Rhodes JM, Cherry KJ, Clark RC, et al. (2000) Aortic-origin reconstruction of the great vessels: risk factors of early and late complications. J Vascu Surg 31: 260-269. doi: 10.1016/S0741-5214(00)90157-5
|
| [19] | Paukovits TM, Lukacs L, Berczi V, et al. (2010) Percutaneous endovascular treatment of innominate artery lesions: a single-centre experience on 77 lesions. Eur J vascu endovascu surg 40: 35-43. |
| [20] |
Brountzos EN, Petersen B, Binkert C, et al. (2004) Primary stenting of subclavian and innominate artery occlusive disease: a single center's experience. Cardiovas Inter Radio 27: 616-623. doi: 10.1007/s00270-004-0218-y
|
| [21] |
Huttl K, Nemes B, Simonffy A, et al. (2002) Angioplasty of the innominate artery in 89 patients: experience over 19 years. Cardiovas Inter Radio 25: 109-114. doi: 10.1007/s00270-001-0074-y
|
| [22] |
Peterson BG, Resnick SA, Morasch MD, et al. (2006) Aortic arch vessel stenting: a single-center experience using cerebral protection. Arch Surg 141: 560-563. doi: 10.1001/archsurg.141.6.560
|
| [23] | van Hattum ES, de Vries JP, Lalezari F, et al. (2007) Angioplasty with or without stent placement in the brachiocephalic artery: feasible and durable? A retrospective cohort study. J Vascu Inter Radio 18: 1088-1093. |
| [24] | Ryer EJ, Oderich GS (2010) Two-wire (0.014 & 0.018-inch) technique to facilitate innominate artery stenting under embolic protection. J Inter Soc Endovas Special 17: 652-656. |
| 1. | Tong Liu, Yuan Xie, Zhihua Feng, Yanbin Luo, Ke Wang, Wei Xu, Better understanding the failure modes of tunnels excavated in the boulder-cobble mixed strata by distinct element method, 2020, 116, 13506307, 104712, 10.1016/j.engfailanal.2020.104712 | |
| 2. | Juan Alonso, Marina Moya, Laura Asensio, Gema de la Morena, Jorge Pedro Galve, Vicente Navarro, A catenary model for the analysis of arching effect in soils and its application to predicting sinkhole collapse, 2021, 0016-8505, 1, 10.1680/jgeot.20.P.235 | |
| 3. | Qian Zhang, Jie Hu, Jing Wang, Peng He, Lili Hou, Peng Lin, Shuguang Song, Study on the mechanical behavior of a foundation pit retaining structure adjacent to the pile foundation of a subway station, 2021, 80, 1866-6280, 10.1007/s12665-021-09996-7 | |
| 4. | Shaohui He, Chenghui Li, Dahai Wang, Xiabing Liu, Surface Settlement Induced by Slurry Shield Tunnelling in Sandy Cobble Strata—A Case Study, 2021, 51, 0971-9555, 1349, 10.1007/s40098-021-00543-6 | |
| 5. | Tao Li, Zhongyu Zhang, Muchi Luo, Bo Liu, Yanlong Wang, Lingfeng Li, Analytical Solution of Loosening Pressure Model for Shallow Tunnel Based on Pile-Beam-Arch Method, 2022, 26, 1226-7988, 3648, 10.1007/s12205-022-2190-y | |
| 6. | Fan Wang, Xiuli Du, Pengfei Li, Shiwei Hou, A meso-scale numerical modelling method for the stability analysis of tunnels in sandy cobble stratum, 2023, 38, 22143912, 100921, 10.1016/j.trgeo.2022.100921 | |
| 7. | V.H Shapova, O.V Solodyankin, O.Ye Hryhoriev, O.I Dubovyk, Determining the parameters of a natural arch while forming support load of a horizontal roadways, 2021, 20712227, 17, 10.33271/nvngu/2021-2/017 | |
| 8. | Xiaobin Li, Ying Zhao, Haifang Xue, Lei Zhang, Xiaoqin Gong, Stability analysis of tunnel in sandy cobble strata under different pre-reinforcement techniques, 2023, 11, 2296-6463, 10.3389/feart.2023.1212726 | |
| 9. | Yinjun Tan, Qianshen Wang, Study on the Applicability of Load Calculation Method for Large-Diameter Shield Tunnel in Argillaceous Sandstone Stratum under High Water Pressure, 2023, 27, 1226-7988, 5401, 10.1007/s12205-023-1997-5 | |
| 10. | Meimei Wang, Jianwei Zheng, Shanshan Xue, Mechanics and Stability of Force Chain Arch in Excavated Granular Material, 2024, 14, 2076-3417, 2485, 10.3390/app14062485 |
Figures(3) / Tables(2)
Ryan T. Borne, Arash Aghel, Amit C. Patel, Robert K. Rogers. Innominate Steal Syndrome: A Two Patient Case Report and Review[J]. AIMS Medical Science, 2015, 2(4): 360-370. doi: 10.3934/medsci.2015.4.360
DownLoad:
