1. Introduction
Many differential equations have been proposed (see [8,11,13], [17]-[19], [21]-[22], [24,27] and references therein) to model the dynamic changes of substrate concentration and product one in enzyme-catalyzed reactions. Among those models, a typical form ([7]) is the following skeletal system
|
$
\left\{
˙x=v−V1(x,y)−V3(x),˙y=q(V1(x,y)−V2(y)),
\right.
\label{sp0}
$
|
(1)
|
where $x$ and $y$ denote the concentrations of the substrate and the product respectively, $v$ and $q$ are both positive constants, $V_1(x, y)$ and $V_2(y)$ denote the enzyme reaction rate and the output rate of the product respectively and satisfy that
|
$
V_{1}(0, y)=0, ~~
\partial V_{1}/\partial x>0, ~~
\partial V_{1}/\partial y>0, ~~
V_2(y)\geq0, ~~
\forall x, y>0,
$
|
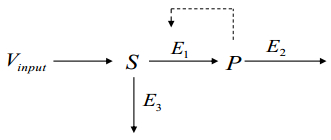
and $V_3(x)$ denotes the branched-enzyme reaction rate. Figure 1 shows the scheme of the enzyme-catalyzed reaction which comprises a branched network from the substrate. In Figure 1, $S$ and $P$ represent the substrate and product, respectively, and $E_1, E_2$ and $E_3$ are the three enzymes.
The case that $V_3(x)\equiv0$ in system (1), which represents an unbranched reaction, has been discussed extensively in [1,6,7,9,20]. Recently, more efforts were made to the case that $V_3(x)\not\equiv0$. One of the efforts ([12,23]) is made for $V_1(x, y)=x^my^n, V_2(y)=y$ and $V_3(x)=lx$ and $v=1$, with which system (1) reduces to
|
$
\left\{
˙x=1−xmyn−lx,˙y=q(xmyn−y),
\right.
$
|
called the multi-molecular reaction model sometimes, where $m, n\geq1$ are integers and $l\geq0$ is real. All local bifurcations of this system such as saddle-node bifurcation, Hopf bifurcation and Bogdanov-Takens bifurcation were discussed in [12] and [23]. Reference [15] is concerned with the case that $V_1(x, y)=\gamma x^my^n$, $V_3(x)=\beta x$, $q=1$ and $V_2(y)$ is a saturated reaction rate, i.e., $V_2(y)=v_2y/(\mu_2+y)$, with which (1) reduces to
|
$
\left\{
˙x=v−γxmyn−βx,˙y=γxmyn−v2yμ2+y,
\right.
$
|
where $v, \gamma>0, {\mu}_{2}, v_2$ and $\beta\geq0$. Results on existence and nonexistence of periodic solutions on Hopf bifurcation were obtained in [15] with $n=1$ and $\beta=0$. When $V_2(y)$ and $V_3(x)$ are both saturated reaction rates, system (1) was considered in [16] as
|
$
\left\{
˙x=v−V1(x,y)−v3xu3+x,˙y=q(V1(x,y)−v2yu2+y)
\right.
$
|
with $V_1(x, y)=v_1x(1+x)(1+y)^2/[L+(1+x)^2(1+y)^2]$, where $L$ is the allosteric constant of $E_1$. Varying the parameter $v_2$ but fixing the other parameters, Liu ([16]) investigated numerically how the enzyme saturation affects the emergence of dynamical behaviors such as the change from a stable oscillatory state to a divergent state. Later, Davidson and Liu ([3]) discussed the saddle-node bifurcation, Hopf bifurcation and the global bifurcation corresponding to the appearance of homoclinic orbit. When $V_2(y)$ and $V_3(x)$ are both saturated reaction rates, system (1) was also considered in [4] as
|
$
\label{sp1} \left\{
˙x=v−v1xy−v3xu3+x,˙y=q(v1xy−v2yu2+y)
\right.
$
|
(2)
|
with $V_1(x, y)=v_{1}xy$. With a change of variables $x=u_{3} \tilde{x}, \ y=u_{2}\tilde{y}$ and the time rescaling $t\to v_{1}^{-1}\mu_{2}^{-1}t$, system (2) can be written as
|
$
\left\{
˙x=a−xy−bx1+x,˙y=κy(x−c1+y),
\right.
\label{xy0}
$
|
(3)
|
where we still use $x$, $y$ to present $\tilde{x}$, $\tilde{y}$ and take notations $a:=v_{1}^{-1}u_{3}^{-1}u_{2}^{-1}v$, $b:=v_{1}^{-1}u_{3}^{-1}u_{2}^{-1}v_{3}$, $c:=v_{1}^{-1}u_{3}^{-1}u_{2}^{-1}v_{2}$ and $\kappa:=u_{2}^{-1}q u_{3}$ for positive constants. Actually, system (3) is orbitally equivalent to the following quartic polynomial differential system
|
$
\left\{
˙x=(1+y){(1+x)(a−xy)−bx},˙y=κ(1+x)y{(1+y)x−c},
\right.
\label{xy1}
$
|
(4)
|
in the first quadrant ${\mathcal Q}_+:=\{(x, y):x\ge0, y\ge0\}$ by a time scaling $d\tau=(x+1)(y+1)dt$. In [4] Davidson, Xu and Liu discussed the case that $k=1$ and $a<c$, where the system has at most two equilibria, giving the existence of limit cycles (by the Poincaré-Bendixson Theorem seen in [10] or [26]) and the non-existence of periodic orbits (by the Dulac Criterion seen in [10] or [26]), proving the uniqueness of limit cycles (by reducing to the form of Liénard system) with some restrictions, and illustrating with the software AUTO saddle-node bifurcation, transcritical bifurcation and Hopf bifurcation for fixed $\kappa=1, b=1.5$ and $c=5$. Recently, the general case that $\kappa, a, b, c>0$ was discussed in [27], where all codimension-one bifurcations such as saddle-node, transcritical and pitchfork bifurcations were investigated and the weak focus was proved to be of at most order $2$.
In this paper we continue the work of [27] to give conditions for the existence of a cusp and compute the parameter curves for the Bogdanov-Takens bifurcation, which induces the appearance of homoclinic orbits and periodic orbits, indicating the tendency to steady-states or a rise of periodic oscillations for the concentrations of the substrate and product.
2. Condition for cusp
It is proved in [27] that system (4) has at most 3 equilibria, i.e., $E_0: (a/(b-a), 0)$, $E_1:(p_1, c/p_1-1)$ and $E_2:(p_2, c/p_2-1)$, where
|
$
p1:=−12{(a−b−c+1)−[(a−b−c+1)2−4(a−c)]1/2},p2:=−12{(a−b−c+1)+[(a−b−c+1)2−4(a−c)]1/2}.
\label{p12}
$
|
(5)
|
Moreover, if $a=a_*:=c+(b^{1/2}-1)^2$, then $E_1$ and $E_2$ coincide into one, i.e., the equilibrium $E_*: (b^{1/2}-1, c(b^{1/2}+1)/(b-1)-1)$. There are found in [27] totally 6 bifurcation surfaces
|
$
TE0:={(a,b,c,κ)∈R4+|a=bc/(1+c),b≠(c+1)2}:=4⋃i=1T(i)E0,PE0:={(a,b,c,κ)∈R4+|a=bc/(1+c),b=(c+1)2},HE1:={(a,b,c,κ)∈R4+|κ=κ1,bc/(1+c)<a<c,0<b≤1}∪{(a,b,c,κ)∈R4+|κ=κ1,bc/(1+c)<a<c+(b1/2−1)2,1<b<(c+1)2},SNE∗:={(a,b,c,κ)∈R4+|a=a∗, 1<b<(c+1)2,κ≠κ∗}:=4⋃i=1SN(i)E∗,B1:={(a,b,c,κ)∈R4+|a=c},B2:={(a,b,c,κ)∈R4+|a=b},
$
|
which divide $\mathbb{R}_+^4:=\{(a, b, c, \kappa): a>0, b>0, c>0, \kappa>0\}$ into 8 subregions
|
$
R1:={(a,b,c,κ)∈R4+|c<a<a∗,1<b<c,c>1, or b<a<a∗,c<b<(c+1)2/4,c>1},R2:={(a,b,c,κ)∈R4+|b<a<c,0<b<c}R3:={(a,b,c,κ)∈R4+|bc/(1+c)<a<b,0<b<c or bc/(1+c)<a<c,c<b<c+1},R4:={(a,b,c,κ)∈R4+|0<a<bc/(1+c),0<b<c+1 or 0<a<c,b>c+1},R5:={(a,b,c,κ)∈R4+|c<a<bc/(1+c),b>c+1},R6:={(a,b,c,κ)∈R4|c<a<b,c<b<(c+1),c>3 or bc/(1+c)<a<b,c+1<b<(c+1)2/4,c>3 or bc/(1+c)<a<a∗,(c+1)2/4<b<(c+1)2,c>3 or c<a<b,c<b<(c+1)2/4,1<c≤3 or c<a<a∗,(c+1)2/4<b<c+1,1<c≤3 or bc/(1+c)<a<c+(b1/2−1)2,(c+1)<b<(c+1)2,c≤3 or c<a<a∗,1<b<c+1,c≤1},R7:={(a,b,c,κ)∈R4+|c+(b1/2−1)2<a<b,(c+1)2/4<b<(c+1)2,c>1 or bc/(1+c)<a<b,b>(c+1)2 or c<a<b,c<b<1,c≤1 or c+(b1/2−1)2<a<b,1<b<(c+1)2,c≤1},R0:=R4+∖{PE0∪SNE∗∪TE0∪(2⋃i=1Bi)∪B∪(7⋃i=1Ri)},
$
|
where
|
$
T(1)E0:={(a,b,c,κ)∈R4+|a=bc/(1+c),0<b<c+1},T(2)E0:={(a,b,c,κ)∈R4+|a=bc/(1+c),c+1<b<(c+1)2},T(3)E0:={(a,b,c,κ)∈R4+|a=bc/(1+c),b>(c+1)2},T(4)E0:={(a,b,c,κ)∈R4+|a=bc/(1+c),b=c+1},SN(1)E∗:={(a,b,c,κ)∈R4+|a=a∗, 1<b<(c+1)2/4,c>1,κ≠κ∗},SN(2)E∗:={(a,b,c,κ)∈R4+|a=a∗, b=(c+1)2/4,c>1,κ≠κ∗},SN(3)E∗:={(a,b,c,κ)∈R4+|a=a∗, (c+1)2/4<b<(c+1)2,c>1,κ≠κ∗},SN(4)E∗:={(a,b,c,κ)∈R4+|a=a∗, 1<b<(c+1)2,c≤1,κ≠κ∗},κ1:=p−21{(p1+1)(c−p1)}−1c{p1(c−p1)+a},κ∗:=(c−b1/2+1)−1(b1/2−1)−2c2.
\label{pa0k0}
$
|
(6)
|
The following lemma is a summary of Theorems 1, 2 and 3 of [27].
Lemma 2.1. (ⅰ) System (4) has a saddle-node $E_0$ if $(a, b, c, \kappa)\in {\mathcal T}_{E_0}\cup{\mathcal P}_{E_0}$. Moreover, as $(a, b, c, \kappa)$ crosses either ${\mathcal T}_{E_0}^{(1)}$ from ${\mathcal R}_3$ to ${\mathcal R}_4$, ${\mathcal T}_{E_0}^{(2)}$ from ${\mathcal R}_6$ to ${\mathcal R}_5$, or ${\mathcal T}_{E_0}^{(4)}$ from ${\mathcal R}_6$ to ${\mathcal R}_4$, a saddle $E_0$ and a stable (resp. unstable) node $E_1$ merge into a stable node $E_0$ on the boundary of the first quadrant ${\mathcal Q}_+$ for $\kappa<\kappa_1$(resp. $\kappa>\kappa_1$) through a transcritical bifurcation; as $(a, b, c, \kappa)$ crosses ${\mathcal T}_{E_0}^{(3)}$ from ${\mathcal R}_5$ to ${\mathcal R}_7$, a stable node $E_0$ and a saddle $E_2$ merge into a saddle $E_0$ on the boundary of ${\mathcal Q}_+$ through a transcritical bifurcation; as $(a, b, c, \kappa)$ crosses ${\mathcal P}_{E_0}$ from ${\mathcal R}_7$ to ${\mathcal R}_5$, a saddle $E_0$ changes into a stable node $E_0$, a saddle $E_2$ through a pitchfork bifurcation at $E_0$ on the boundary of ${\mathcal Q}_+$.
(ⅱ) System (4) has a weak focus $E_1$ of at most order 2 for $(a, b, c, \kappa)\in {\mathcal H}_{E_1}$, which is of order $\ell$ exactly and produces at most $\ell$ limit cycles through Hopf bifurcations as $(a, b, c, \kappa)\in {\mathcal H}_{E_1}^{(\ell)}$, $\ell=1, 2$, where ${\mathcal H}_{E_1}^{(1)}:={\mathcal H}_{E_1}\backslash{\mathcal H}_{E_1}^{(2)}$ and
|
$
H(2)E1:={(a,b,c,κ)∈HE1:2p1(p1+1)a3+{(p21+p1+1)c2+p1(2p21+p1−2)c−3p31(p1+1)}a2−(c−p1){(p31+3p21+p1+1)c2+2p21(p21+3p1+3)c+3p41(p1+1)}a+p21{(p1+2)c+p21}{c−p1(p1+1)}(c−p1)2=0}.
$
|
(ⅲ) System (4) has a saddle-node $E_*$ if $(a, b, c, \kappa)\in {\mathcal SN}_{E_*}$. Moreover, as $(a, b, c, \kappa)$ crosses either ${\mathcal SN}_{E_*}^{(1)}$ from ${\mathcal R}_0$ to ${\mathcal R}_1$, ${\mathcal SN}_{E_*}^{(2)}$ from ${\mathcal R}_0$ to ${\mathcal R}_6$, or ${\mathcal SN}_{E_*}^{(3)}\cup{\mathcal SN}_{E_*}^{(4)}$ from ${\mathcal R}_7$ to ${\mathcal R}_6$, a stable (resp. unstable) node $E_1$ and a saddle $E_2$ arise through a saddle-node bifurcation for $\kappa<\kappa_1$(resp. $\kappa>\kappa_1$).
The above Lemma 2.1 does not consider parameters in the set
|
$
\mathcal{B} := \{(a, b, c, \kappa)\in \mathbb{R}_+^4| a=a_*, ~1<b<(c+1)^2, \kappa=\kappa_*\},
\label{BT}
$
|
(7)
|
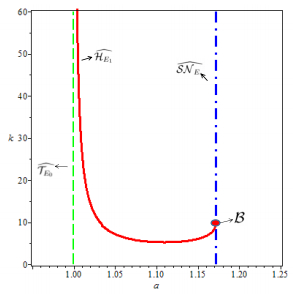
where $a_*$ is given below (5) and $\kappa_*$ is given in (6). $\mathcal{B}$ is actually the intersection of the saddle-node bifurcation surface ${\mathcal SN}_{E_*}$ and the Hopf bifurcation surface ${\mathcal H}_{E_1}$, which are described by the curves $\widehat{{\mathcal SN}_{E_*}}$ and $\widehat{{\mathcal H}_{E_1}}$ respectively on the section $\{(a, b, c, \kappa)\in \mathbb{R}_+^4 | b=2, ~c=1\}$ in Figure 2. The intersection of $\widehat{{\mathcal SN}_{E_*}}$ and $\widehat{{\mathcal H}_{E_1}}$ indicates ${\mathcal B}$.
This paper is devoted to bifurcations in $\mathcal{B}$. For $(a, b, c, \kappa)\in \mathcal{B}$, equilibrium $E_*$ is degenerate with two zero eigenvalues. In the following lemma we prove that $E_*$ is a cusp.
Lemma 2.2. If $(a, b, c, \kappa)\in \mathcal{B}\backslash\mathcal{C}$, where
|
$
\mathcal{C}:=\big\{(a, b, c, \kappa)\in \mathcal{B} | c=\varsigma(b):=\frac{1}{4b^{1/2}}(b^{1/2}-1)\{b^{1/2}+2+(17b-12b^{1/2}+4)^{1/2}\}\big\},
$
|
then equilibrium $E_*$ is a cusp in system (4).
Proof. For simplicity in statements, we use the notation
|
$
p:=b^{1/2}-1.
\label{p}
$
|
(8)
|
For $(a, b, c, \kappa)\in{\mathcal B}$, system (4) can be transformed into the form
|
$
\left\{
˙x=y+c(p2+cp+c)p3x2+1p+1xy−pc2(p+1)y2−c(p2+c)p4x3−p2+2pc+2cp2c(p+1)x2y−2p+1c2(p+1)2xy2−c2p4x4−2p2(p+1)x3y−1c2(p+1)2x2y2,˙y=−c3(p+1)p3x2−c2(p+1)p2(c−p)xy−1c−py2−(p+1)(p2+c)p5(c−p)x3−c(p2+2pc+2c)p3(c−p)x2y−2p+1p(p+1)(c−p)xy2−c4(p+1)p5(c−p)x4−2c2p3(c−p)x3y−1p(p+1)(c−p)x2y2,
\right.
\label{bt0}
$
|
(9)
|
by translating $E_*$ to the origin $O$ and Jordanizing the linear part of system (4). For convenience, introducing new variables $(x, y)\mapsto (u, v)$, where $u=x$ and $v$ denotes the right-hand side of the first equation in (9), we change (9) into the Kukles form
|
$
\left\{
˙u=v,˙v=−c3(p+1)p3u2+c{(2p+2)c2−(p2+3p)c−2p3}p3(c−p)uv+c−2p−1(p+1)(c−p)v2+c3(p2+c)p4(c−p)u3−c{(p+1)(p+3)c2+p(p2−3p−3)c−p3(3p+2)}p4(p+1)(c−p)u2v−(5p2+8p+4)c+2p2(p+1)cp2(p+1)2uv2−1c2(p+1)v3−c2(c2+2p2c−p3)p5(c−p)u4+1p5(p+1)2(c−p){(p+4)(p+1)2c3+p(7p3+7p2−3p−4)c2−p3(8p2+15p+8)c−2p5(p+1)}u3v+(3p3+6p2+6p+2)c2+p(2p+1)(2p2+2p−1)c−p3(p+1)(7p+4)cp3(p+1)3(c−p)u2v2−(3p+4)c2−3p(p+2)c−2p3c3p(p+1)2(c−p)uv3−2c−3pc4(p+1)2(c−p)v4+O(|u,v|5).
\right.
\label{bt1}
$
|
(10)
|
Since the linear part is nilpotent, by Theorem 8.4 in [14] system (10) is conjugated to the Bogdanov-Takens normal form, i.e., the right-hand side of the second equation is a sum of terms of the form $au^k+bu^{k-1}v$. Hence, one can use the transformation $u\rightarrow u$, $v\rightarrow v-\frac{c-2p-1}{(p+1)(c-p)} uv$ together with the time-rescaling $dt=(1-\frac{c-2p-1}{(p+1)(c-p)}u)d\tau$ to change system (10) into the following
|
$
\left\{
˙u=v,˙v=−c3(p+1)p3u2+c{(2p+2)c2−(p2+3p)c−2p3}p3(c−p)uv+O(|u,v|3),
\right.
\label{bt2}
$
|
(11)
|
where the term of $v^2$ is eliminated and terms of degree 2 are normalized. The term of $u^2$ exists since $-{c^3(p+1)}/{p^3}\neq 0$. For the existence of the term of $uv$, we need to discuss on the quadratic equation
|
$
c^2-\frac{p^2+3p}{2(p+1)}c-\frac{p^3}{p+1}=0,
\label{eq2}
$
|
(12)
|
which comes from the numerator of the coefficient of $uv$. Since the constant term is negative for $p>0$, the quadratic equation (12) has exactly one positive root
|
$
c=\frac{1}{4}(p+1)^{-1}p\{p+3+(17p^2+22p+9)^{1/2}\},
$
|
which defines the function $\varsigma(b)$ as shown in Lemma 2.2 with the replacement (8). It implies by Theorem 8.4 of [14] that for $c\neq\varsigma(b)$, i.e., $(a, b, c, \kappa)\in {\mathcal S}\backslash{\mathcal C}$, $O$ is a cusp of system (11). The proof of this lemma is completed.
3. Bogdanov-Takens bifurcation
In this section we discuss in the case that $(a, b, c, \kappa)\in {\mathcal B}\backslash{\mathcal C}$, in which system (4) is of codimension 2. We choose $a, \kappa$ as the bifurcation parameters and unfold the Bogdanov-Takens normal forms of codimensions $2$ when $(a, \kappa)$ is perturbed near the point $(a_*, \kappa_*)$, where $a_*$ is given below (5) and $\kappa_*$ is given in (6).
Theorem 3.1. If $(a, b, c, \kappa)\in \mathcal{B}\backslash{\mathcal C}$, where ${\mathcal B}$ is defined in (7) and ${\mathcal C}$ is defined as in Lemma 2.2, then there are a neighborhood $U$ of the point $(a_*, \kappa_{*})$ in the $(a, \kappa)$-parameter space and four curves
|
$
SN+:={(a,κ)∈U|a=a∗, κ>κ∗,0<c<ς(b)}∪{(a,κ)∈U|a=a∗, κ<κ∗,c>ς(b)},SN−:={(a,κ)∈U|a=a∗, κ<κ∗,0<c<ς(b)}∪{(a,κ)∈U|a=a∗, κ>κ∗,c>ς(b)},H:={(a,κ)∈U|a=a∗−((2b1/2+1)c2−((b1/2−1)2+3(b1/2−1))c −2(b1/2−1)3)−2b1/2(b1/2−1)6(c−b1/2+1)4(κ−κ∗)2+O(|κ−κ∗|3), κ>κ∗,0<c<ς(b)}∪{(a,κ)∈U|a=a∗−((2b1/2+1)c2−((b1/2−1)2+3(b1/2−1))c −2(b1/2−1)3)−2b1/2(b1/2−1)6(c−b1/2+1)4(κ−κ∗)2+O(|κ−κ∗|3), κ<κ∗,c>ς(b)},L:={(a,κ)∈U|a=a∗−49/25((2b1/2+1)c2−((b1/2−1)2+3(b1/2−1))c −2(b1/2−1)3)−2b1/2(b1/2−1)6(c−b1/2+1)4(κ−κ∗)2+O(|κ−κ∗|3), κ>κ∗,0<c<ς(b)}∪{(a,κ)∈U|a=a∗−49/25((2b1/2+1)c2−((b1/2−1)2+3(b1/2−1))c −2(b1/2−1)3)−2b1/2(b1/2−1)6(c−b1/2+1)4(κ−κ∗)2+O(|κ−κ∗|3), κ<κ∗,c>ς(b)},
$
|
such that system (4) produces a saddle-node bifurcation near $E_{*}$ as $(a, c)$ acrosses $\mathcal{SN}^{+}\cup
\mathcal{SN}^{-}$, a Hopf bifurcation near $E_{*}$ as $(a, \kappa)$ acrosses $\mathcal{H}$, and a homoclinic bifurcation near $E_{*}$ as $(a, \kappa)$ acrosses $\mathcal{L}$, where $\kappa_*$ and $\varsigma(b)$ are given in (6) and Lemma 2.2 respectively.
The above bifurcation curve ${\mathcal H}$ is exactly the same as ${\mathcal H}_{E_1}$ given in Lemma 2.1, and the union $\mathcal{SN}^{+}\bigcup \mathcal{SN}^{+}$ is exactly the bifurcation curves $\mathcal{SN}_{E_*}$ given in Lemma 2.1.
Proof. Let $p=b^{1/2}-1$ and
|
$
\varepsilon_{1}:=a-a_*, \varepsilon_{2}:=\kappa-\kappa_*,
\label{eee}
$
|
(13)
|
and consider $|\varepsilon_{1}|$ and $|\varepsilon_{2}|$ both to be sufficiently small. Expanding system (4) at $E_{*}$, we get
|
$
\label{btb0} \left\{
˙x=c(p+1)pε1+(−c2(p+1)p2+cpε1)x+(−c(p+1)+(p+1)ε1)y−c(c−p)p2x2+(−c(2+3p)p+ε1)xy−p(p+1)y2+O(‖(x,y)‖3),˙y=(c3(p+1)p4+c(p+1)(c−p)p2ε2)x+(c2(p+1)p2+(p+1)(c−p)ε2)y+(c3p4+c(c−p)p2ε2)x2+(c3(2+3p)−c2p(2p+1)(c−p)p3+c(3p+2)−p(2p+1)pε2)xy+(c2(p+1)(c−p)p+p(p+1)ε2)y2+O(‖(x,y)‖3).
\right.
$
|
(14)
|
Introducing new variables $(x, y)\mapsto (\xi_1, \eta_1)$, where $\xi_1=x$ and $\eta_1$ denotes the right-hand side of the first equation in (14), we change (14) into the Kukles form, whose second order truncation is the following
|
$
\left\{
˙ξ1=η1,˙η1=E00(ε1,ε2)+E10(ε1,ε2)ξ1+E20(ε1,ε2)ξ21+F(ξ1,ε1,ε2)η1+E02(ε1,ε2)η21,
\right.
$
|
(15)
|
where $
F(\xi_{1}, \varepsilon_{1}, \varepsilon_{2}):=E_{01}(\varepsilon_{1}, \varepsilon_{2})
+E_{11}(\varepsilon_{1}, \varepsilon_{2})\xi_{1}
$ and $E_{ij}$ s ($i, j=0, 1, 2$) are given in Appendix. Notice that $(a, b, c, \kappa)\in {\mathcal B}\backslash{\mathcal C}$ implies that $c\neq\varsigma(b)$. From (12) we see that the quadratic equation has exactly one positive root $c=\varsigma(b)$. Thus, for $c\neq\varsigma(b)$ we can check that
|
$
F(0, 0, 0)=0, ~~~
\frac{\partial F}{\partial\xi_{1}}(0, 0, 0)=E_{11}(0, 0)=(2p+2)(c^2-\frac{p^2+3p}{2(p+1)}c-\frac{p^3}{p+1})\ne 0.
$
|
By the Implicit Function Theorem, there exists a function $\xi_{1}=\xi_{1}(\varepsilon_{1}, \varepsilon_{2})$ defined in a small neighborhood of $(\varepsilon_{1}, \varepsilon_{2})=(0, 0)$ such that $\xi_{1}(0, 0)=0$ and $F(\xi_{1}(\varepsilon_{1}, \varepsilon_{2}), \varepsilon_{1}, \varepsilon_{2})=0$. Thus, from the definition of $F$ we obtain $\xi_{1}(\varepsilon_{1}, \varepsilon_{2})=
-{E_{01}(\varepsilon_{1}, \varepsilon_{2})}/{E_{11}(\varepsilon_{1}, \varepsilon_{2})}$ near $(0, 0)$. Then, we use a parameter-dependent shift
|
$
\xi_{2}=\xi_{1}-\xi_{1}(\varepsilon_{1}, \varepsilon_{2}),
\eta_{2}=\eta_{1}
$
|
to vanish the term proportional to $\eta_2$ in the equation for $\eta_2$ from system (15), which leads to the following system
|
$
\label{btphi} \left\{
˙ξ2=η2,˙η2=ψ1(ε1,ε2)+ψ2(ε1,ε2)ξ2+E20(ε1,ε2)ξ22+E11(ε1,ε2)ξ2η2+E02(ε1,ε2)η22,
\right.
$
|
(16)
|
where
|
$
ψ1(ε1,ε2):=E00(ε1,ε2)+E10(ε1,ε2)ξ1(ε1,ε2)+E20(ε1,ε2)ξ21(ε1,ε2),ψ2(ε1,ε2):=E10(ε1,ε2)+2ξ1(ε1,ε2)E20(ε1,ε2).
$
|
In order to eliminate the $\eta_2^2$ term, one can use the transformation
|
$
\xi_3= \xi_2, ~~~
\eta_3= \eta_2-E_{02}(\varepsilon_{1}, \varepsilon_{2})\xi_2\eta_2
$
|
together with the time-rescaling $dt=(1-E_{02}(\varepsilon_{1}, \varepsilon_{2})\xi_2)d\tau$ to change system (16) into the following
|
$
\label{btphi2} \left\{
˙ξ3=η3,˙η3=ζ1(ε1,ε2)+ζ2(ε1,ε2)ξ3+˜E20(ε1,ε2)ξ23+E11(ε1,ε2)ξ3η3,
\right.
$
|
(17)
|
where
|
$
ζ1(ε1,ε2):=ψ1(ε1,ε2), ζ2(ε1,ε2):=ψ2(ε1,ε2)−ψ1(ε1,ε2)E02(ε1,ε2),˜E20(ε1,ε2):=E20(ε1,ε2)−E10(ε1,ε2)E02(ε1,ε2).
$
|
Further, in order to reduce coefficient of $\xi_3^2$ to $1$, we apply the transformation
|
$
u=\frac{\tilde{E}_{20}(\varepsilon_{1}, \varepsilon_{2})}{E_{11}^2(\varepsilon_{1}, \varepsilon_{2})}\xi_{3},
v={\rm sign}\Big(\frac{E_{11}(\varepsilon_{1}, \varepsilon_{2})}{\tilde{E}_{20}(\varepsilon_{1}, \varepsilon_{2})}\Big)
\frac{\tilde{E}_{20}^2(\varepsilon_{1}, \varepsilon_{2})}{E_{11}^3(\varepsilon_{1}, \varepsilon_{2})},
$
|
where $
\tilde{E}_{20}(0, 0)=-\frac{c^3(p+1)}{p^3}<0,
$ and the time-scaling $dt=|\frac{E_{11}(\varepsilon_{1}, \varepsilon_{2})}{\tilde{E}_{20}(\varepsilon_{1}, \varepsilon_{2})}|d\tau$ to system (17) and obtain
|
$
\label{btf} \left\{
˙u=v,˙v=ϕ1(ε1,ε2)+ϕ2(ε1,ε2)u+u2+ϑuv,
\right.
$
|
(18)
|
where $\vartheta={\rm sign}\Big(\frac{E_{11}(0, 0)}{\tilde{E}_{20}(0, 0)}\Big)$,
|
$
ϕ1(ε1,ε2):=E411(ε1,ε2)˜E320(ε1,ε2)ζ1(ε1,ε2)={(2p+2)c2−(p2+3p)c−2p3}4ε1ϕ11(ε1,ε2)p4(c−p)4ϕ212(ε1,ε2), ϕ2(ε1,ε2):=E211(ε1,ε2)˜E220(ε1,ε2)ζ2(ε1,ε2)=√2{(2p+2)c2−(p2+3p)c−2p3}ϕ21(ε1,ε2)c3/2(c−p)2(p+1)1/2pϕ3/212(ε1,ε2),
$
|
and polynomials $\phi_{ij}$ s are given in the Appendix.
Let
|
$
\label{muphi}
\mu_{1}=\phi_{1}(\varepsilon_{1}, \varepsilon_{2}),
\mu_{2}=\phi_{2}(\varepsilon_{1}, \varepsilon_{2}),
$
|
(19)
|
where $\phi_{1}$ and $\phi_{2}$ are defined just below (18). Clearly, $\phi_{1}(0, 0)=\phi_{2}(0, 0)=0$. Compute the Jacobian determinant of (19) at the point $(0, 0)$
|
$
\left|
∂ϕ1(ε1,ε2)∂ε1∂ϕ1(ε1,ε2)∂ε2∂ϕ2(ε1,ε2)∂ε1∂ϕ2(ε1,ε2)∂ε2
\right|_{(\varepsilon_{1}, \varepsilon_{2})=(0, 0)}
=
-\frac{\{(2p+2)c^2-(p^2+3p)c-2p^3\}^5}{p^6c^4(c-p)^4(p+1)}\neq0,
\label{Jacob}
$
|
(20)
|
implying that (19) is a locally invertible transformation of parameters. This transformation makes a local equivalence between system (18) and the versal unfolding system
|
$
\label{btw} \left\{
˙˜u=˜v,˙˜v=μ1+μ2˜u+˜u2+ϑ˜u˜v,
\right.
$
|
(21)
|
where $\vartheta$ is given in (18). As indicated in Section 7.3 of [10], system (21) has the following bifurcation curves
|
$
\label{btbifur}
SN+:={(μ1,μ2)∈V0 | μ1=0, μ2>0},SN−:={(μ1,μ2)∈V0 | μ1=0, μ2<0},H:={(μ1,μ2)∈V0 | μ1=−μ22, μ2>0},L:={(μ1,μ2)∈V0 | μ1=−4925μ22+o(|μ2|2), μ2>0},
$
|
(22)
|
where $V_{0}$ is a small neighborhood of $(0, 0)$ in $\mathbb{R}^{2}$.
In what follows, we present above bifurcation curves in parameters $\varepsilon_1$ and $\varepsilon_2$ in explicit forms. For this purpose, we need the relation between $(\varepsilon_1, \varepsilon_2)$ and $(\mu_1, \mu_2)$. Note that $\phi_1$ and $\phi_2$ defined just below (18) are $C^{k}$ near the origin (0, 0)($k$ is an arbitrary integer). By condition (20), the well-known Implicit Function Theorem implies that there are two $C^k$ functions
|
$
\varepsilon_1=\omega_1(\mu_1, \mu_2), ~~~~\varepsilon_2=\omega_2(\mu_1, \mu_2)
\label{eps12}
$
|
(23)
|
in a small neighborhood of $(0, 0, 0, 0)$ such that $\omega_1(0, 0)=\omega_2(0, 0)=0$ and
|
$
\mu_1=\phi_1(\omega_1(\mu_1, \mu_2), \omega_2(\mu_1, \mu_2)), ~~~ \mu_2=\phi_2(\omega_1(\mu_1, \mu_2), \omega_2(\mu_1, \mu_2)).
\label{compare-coeff}
$
|
(24)
|
Substitute the second order formal Taylor expansions of $\omega_1$ and $\omega_2$ in (24) while expand $\phi_1$ and $\phi_2$ in (24) to the second order
|
$
ϕ1(ε1,ε2)={(2p+2)c2−(p2+3p)c−2p3}4ε1/{p6c2(c−p)4(p+1)}−{(2p+2)c2−(p2+3p)c−2p3}4(24p2c4+42c4p+21c4−8p3c3−54c3p2−44c3p−36c2p4−12p3c2+27p2c2+8p5c+32cp4+16p6)ε21/{2c4p8(c−p)6(p+1)2}−{(2p+2)c2−(p2+3p)c−2p3}4ε1ε2/{(c4p4(c−p)3(p+1)}+o(|ε1,ε2|2),
$
|
(25)
|
|
$
ϕ2(ε1,ε2)={(2p+2)c2−(p2+3p)c−2p3}ε1/{2c2(p3−2cp+p2+c2p+c2−2cp2)p4}−{(2p+2)c2−(p2+3p)c−2p3}ε2/c2−{(2p+2)c2−(p2+3p)c−2p3}(−243p3c3+832p3c4+513p2c4+455p4c3−594p5c2−1347p3c5−1209p2c5+165p4c4+1138p5c3−324p6c2−424p7c−200p5c4+382p6c3+512p7c2−520cp8−396c5p−48p9+108c6−48p10+384c6p3+414c6p−104cp9+264c2p8+594c6p2−672c5p4+96c6p4−136c5p5−44c4p6−76c3p7)ε21/{4c3(p+1)2(c−p)4p6}−{(2p+2)c2−(p2+3p)c−2p3}(8p2c4+23c4p+12c4+30p3c3+8c3p2−22c3p−58c2p4−85p3c2+6p2c2−8p5c+46cp4+24p6)ε1ε2/{4c4p2(p+1)(c−p)2}+(c−p)p2{(2p+2)c2−(p2+3p)c−2p3}ε22/c4+o(|ε1,ε2|2).
$
|
(26)
|
Then, comparing the coefficients of terms of the same degree in (24), we obtain the second order approximations
|
$
ε1=c2p6(c−p)4(p+1)μ1/{(2p+2)c2−(p2+3p)c−2p3}4+c2p10(c−p)6(p+1)(32p2c4+56c4p+27c4−16p3c3−79c3p2−59c3p−48c2p4−19p3c2+36p2c2+12p5c+50cp4+24p6)μ21/{2{(2p+2)c2−(p2+3p)c−2p3}8}+c2p8(c−p)5(p+1)μ1μ2/{(2p+2)c2−(p2+3p)c−2p3}5+o(|μ1,μ2|2),
$
|
(27)
|
|
$
ε2=c2p2(c−p)2(−8p5−12cp4−18cp3+8c3p2−11p2c2−9c2p+14c3p+6c3)μ1/{2{(2p+2)c2−(p2+3p)c−2p3}4}−c2μ2/{(2p+2)c2−(p2+3p)c−2p3}+c2p6(c−p)4(1314c7p2+630pc7−270p3c4+2068p3c5+612p2c5+677p4c4−1134p5c3+4387p5c4−1056p6c3−1804p7c2−3741c6p3+756c5p4+1160c3p8−2268c6p4+1176c7p3−1272c5p6−352c6p5+384c7p4−320p11+108c7−704cp10+224c2p9−2046c5p5+4258c4p6+832p7c4−1464p8c2−2289c6p2+1544p7c3−450c6p−1344cp9)μ21/{8{(2p+2)c2−(p2+3p)c−2p3}8}+c2p4(c−p)2(40p2c4+61c4p+24c4−78p3c3−158c3p2−68c3p−14c2p4+43p3c2+48p2c2+32p5c+62cp4+24p6)μ1μ2/{4{(2p+2)c2−(p2+3p)c−2p3}5}+c2p2(c−p)μ22/{(2p+2)c2−(p2+3p)c−2p3}2+o(|μ1,μ2|2).
$
|
(28)
|
Then we are ready to express those bifurcation curves in parameters $\varepsilon_1$ and $\varepsilon_2$.
For curves ${\mathcal SN}^\pm$, we need to consider $\mu_1=0$. From the first equality of (19) we see that $\mu_1=0$ if and only if $\varepsilon_1=0$ because in the expression of $\phi_1(\varepsilon_1, \varepsilon_2)$ we have $
{\phi_{11}(0, 0)}/{\phi_{12}^2(0, 0)}={1}/{p^2c^2(p+1)}\neq0.
$ Thus, for $\mu_1=0$ we obtain from (28) that
|
$
\varepsilon_2=-\frac{c^2}{(2p+2)\Psi(c)}\mu_2+O(|\mu_2|^2),
\label{Psi(c)}
$
|
(29)
|
where $\Psi(c)$ is the same quadratic polynomial as given in (12). It follows that the inequality $\mu_2>0$ (or $<0$) together with the sign of $\Psi(c)$ determines the sign of $\varepsilon_2$. From the analysis of the quadratic equation (12) we see that $\Psi(c)<0$ (or $>0$) if $0<c<\varsigma(b)$ (or $c>\varsigma(b)$), where $\varsigma(b)$ is defined in Lemma 2.2. Hence from (22) we obtain that
|
$
SN+:={(ε1,ε2) | ε1=0,ε2>0,0<c<ς(b)}∪{(ε1,ε2) | ε1=0,ε2<0,c>ς(b)},SN−:={(ε1,ε2) | ε1=0,ε2<0,0<c<ς(b)}∪{(ε1,ε2) | ε1=0,ε2>0,c>ς(b)}.
$
|
For curve $\mathcal{H}$, we need to consider $\mu_{1}=-\mu_{2}^{2}$, which is equivalent to $\Upsilon(\varepsilon_1, \varepsilon_2):=
\phi_{1}(\varepsilon_{1}, \varepsilon_{2})+\phi_{2}^{2}(\varepsilon_{1}, \varepsilon_{2})=0$ by (19). Clearly, $\Upsilon(0, 0)=0$ and
|
$
\frac{\partial\Upsilon}{\partial \varepsilon_1}\Big|_{(\varepsilon_{1}, \varepsilon_{2})=(0, 0)}
=
\{
(2p+2)\Psi(c)
\}^4
/
\{p^6c^2(c-p)^4(p+1)\}\ne 0.
$
|
By the Implicit Function Theorem, there exists a unique $C^k$ function $\varepsilon_1=\epsilon_1(\varepsilon_2)$ such that $\epsilon_1(0)=0$ and $\Upsilon(\epsilon_1(\varepsilon_2), \varepsilon_2)=0$. Similarly to (27) and (28), expanding $\Upsilon$ at $(\varepsilon_1, \varepsilon_2)=(0, 0)$ and substituting with a formal expansion of $\epsilon_1(\varepsilon_2)$ of order 2, we obtain by comparison of coefficients that
|
$
\varepsilon_1=\epsilon_1(\varepsilon_2)
=
-\frac{p^6(c-p)^4}{4(p+1)\Psi^2(c)}\varepsilon_2^2+o(|\varepsilon_2|^2).
\label{Hp}
$
|
(30)
|
Further, replacing $\mu_1$ with $\mu_{1}=-\mu_{2}^{2}$ in (28), we get
|
$
\varepsilon_2=-\frac{c^2}{(2p+2)\Psi(c)}\mu_2+o(|\mu_2|).
$
|
Similarly to (29), from (22) we obtain that
|
$
H:={(ε1,ε2) | ε1=−p6(c−p)44(p+1)Ψ2(c)ε22+o(|ε2|2), ε2>0,0<c<ς(b)}∪{(ε1,ε2) | ε1=−p6(c−p)44(p+1)Ψ2(c)ε22+o(|ε2|2), ε2<0,c>ς(b)}.
$
|
For curve $\mathcal{L}$, we need to consider $\mu_{1}=-\frac{49}{25}\mu_{2}^{2}
+o(|\mu_{2}|^{2})$, i.e., $\phi_{1}(\varepsilon_{1}, \varepsilon_{2})
=-\frac{49}{25}\phi_{2}^{2}(\varepsilon_{1}, \varepsilon_{2})
+o(|\phi_{2}|^{2})$. Similarly to $\mathcal{H}$, we apply the Implicit Function Theorem to obtain
|
$
\varepsilon_{1}=-\frac{49p^6(c-p)^4}{100(p+1)\Psi^2(c)}\varepsilon_{2}^2+o(|\varepsilon_{2}|^{2}).
$
|
Similarly to (29), from (22) we obtain that
|
$
L:={(ε1,ε2) | ε1=−49p6(c−p)4100(p+1)Ψ2(c)ε22+o(|ε2|2), ε2>0,0<c<ς(b)}∪{(ε1,ε2) | ε1=−49p6(c−p)4100(p+1)Ψ2(c)ε22+o(|ε2|2), ε2<0,c>ς(b)}.
$
|
Finally, with the replacement (13) we can rewrite the above bifurcation curves ${\mathcal SN}^\pm, {\mathcal H}$ and ${\mathcal L}$ expressed in parameters $(\varepsilon_{1}, \varepsilon_{2})$ in expressions in the original parameters $(a, b, c, \kappa)$ as shown in Theorem 3.1.
4. Conclusions
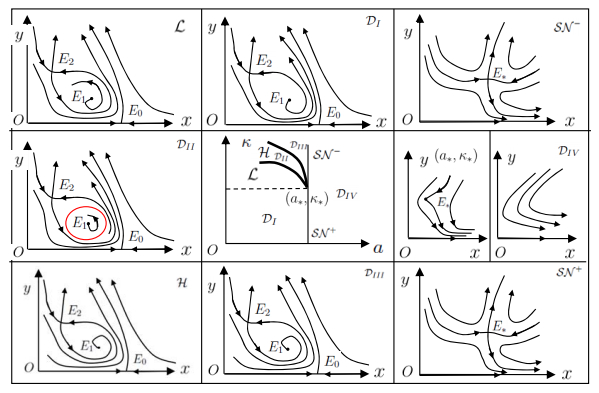
In this paper we analyzed the dynamics of system (4) near the equilibrium $E_*$ when parameters lie near ${\mathcal B}\backslash{\mathcal C}$. We proved that $E_*$ is a cusp when parameters lie on ${\mathcal B}\backslash{\mathcal C}$. We investigated the Bogdanov-Takens bifurcation near the cusp and compute in Theorem 3.1 the four bifurcation curves $\mathcal{SN}^{+}$, $\mathcal{SN}^{-}$, $\mathcal{H}$ and $\mathcal{L}$ in the practical parameters. Those bifurcation curves can be observed in Figure 3 in the case that $c>1$ and $b=(c+1)^2/4$ (which implies $p=(c-1)/2$). They display the merge of equilibria and the rise of homoclinic orbits and periodic orbits.
More concretely, in this case,
|
$
a_*=\frac{(c+1)^2}{4}, ~\kappa_*=\frac{8c^2}{(c+1)(c-1)^2}.
$
|
Moreover, the four bifurcation curves divide the neighborhood $U$ of $(a_*, \kappa_*)$ into the following regions:
|
$
DI:={(a,κ)∈U| a<(c+1)24, κ≤8c2(c+1)(c−1)2}⋃{(a,κ)∈U| a<(c+1)24−49(c−1)6(c+1)33200(2c2+c+1)2{κ−8c2(c+1)(c−1)2}2+O(|κ−8c2(c+1)(c−1)2|3), κ>8c2(c+1)(c−1)2},DII:={(a,κ)∈U| (c+1)24−49(c−1)6(c+1)33200(2c2+c+1)2{κ−8c2(c+1)(c−1)2}2+O(|κ−8c2(c+1)(c−1)2|3)<a<(c+1)24−(c−1)6(c+1)3128(2c2+c+1)2{κ−8c2(c+1)(c−1)2}2+O(|κ−8c2(c+1)(c−1)2|3), κ>8c2(c+1)(c−1)2},DIII:={(a,κ)∈U| (c+1)24−(c−1)6(c+1)3128(2c2+c+1)2{κ−8c2(c+1)(c−1)2}2+O(|κ−8c2(c+1)(c−1)2|3)<a<(c+1)24, κ>8c2(c+1)(c−1)2},DIV:={(a,κ)∈U| a>(c+1)24}.
$
|
Theorem 3.1 gives dynamical behaviors of system (4) near $E_*$ in the first quadrant in Table 4. The coordinates of equilibria $E_0:(x_0, 0)$, $E_1:(p_1, q_1)$ and $E_2:(p_2, q_2)$ are given by $x_0:=a/(b-1)$ and
|
$
p_1:=-\frac{1}{2}\big\{(a-b-c+1)-\{(a-b-c+1)^2-4(a-c)\}^{1/2}\big\},
\\
p_2:=-\frac{1}{2}\big\{(a-b-c+1)+\{(a-b-c+1)^2-4(a-c)\}^{1/2}\big\}
$
|
as in [27]. $E_0$ exists in the first quadrant when $(a, \kappa)\in\mathcal{D}_{I}\cup\mathcal{L}\cup\mathcal{D}_{II}\cup\mathcal{H}\cup\mathcal{D}_{III}$ but disappears when $(a, \kappa)\in\mathcal{D}_{IV}$ (appearing in other quadrants) or $(a, \kappa)\in\mathcal{SN}^+\cup\{(a_*, \kappa_*)\}\cup\mathcal{SN}^-$ (not existing).
Table 4. Dynamics of system (4) in various cases of parameter $(a, \kappa)$.
| Parameters $(a, \kappa)$ |
Equilibria |
Limit cycles and homoclinic orbits |
Region in bifurcation diagram |
| $E_0$ |
$E_1$ |
$E_2$ |
$E_*$ |
| $ \mathcal{D}_{I}$ |
saddle |
unstable focus |
saddle |
|
|
$\mathcal{D}_{I}$ |
| $ \mathcal{L}$ |
saddle |
unstable focus |
saddle |
|
one homoclinic rrbit |
$\mathcal{L}$ |
| $\mathcal{D}_{II}$ |
saddle |
unstable focus |
saddle |
|
one limit cycle |
$\mathcal{D}_{II}$ |
| $\mathcal{H}$ |
saddle |
stable focus |
saddle |
|
|
$\mathcal{H}$ |
| $\mathcal{D}_{III}$ |
saddle |
stable focus |
saddle |
|
|
$\mathcal{D}_{III}$ |
| $ \mathcal{SN}^+$ |
|
|
|
saddle-node |
|
$\mathcal{SN}^+$ |
| $ \mathcal{D}_{IV}$ |
|
|
|
|
|
$\mathcal{D}_{IV}$ |
| $(a_*, \kappa_*)$ |
|
|
|
cusp |
|
$(a_*, \kappa_*)$ |
| $ \mathcal{SN}^-$ |
|
|
|
saddle-node |
|
$\mathcal{SN}^-$ |
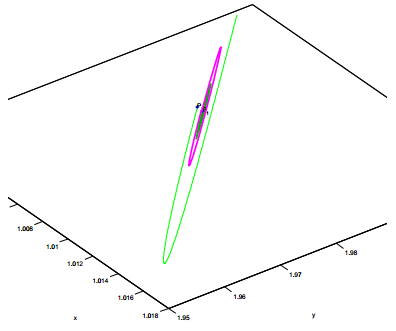
The appearance of limit cycle displays a rise of oscillatory phenomenon in system (4). Choosing parameters $a=3.99999, b=4, c=3$ and $\kappa=4.495$ in $\mathcal{D}_{II}$, we used the command ODE45 in the software Matlab Version R2014a to simulate the orbit initiated from $(x_0, y_0)=(1.00432, 1.98662845)$ numerically, which plots an attractive limit cycle in Figure 4 and shows a dynamic balance and permanence of the substrate and the product in the enzyme-catalyzed reaction. The homoclinic loop actually gives a boundary for the break of the dynamic balance and permanence.
In this paper we only considered parameters in ${\mathcal B}\backslash {\mathcal C}$. When parameters lie in ${\mathcal C}$, higher degeneracy may happen at $E_*$. Although efforts have been made for higher degeneracies, for example, versal unfolding was discussed in [5] for a normal form of cusp system of codimension 3, it is still difficult to compute bifurcation curves in original parameters in the case of codimension 3. Such a computation with original parameters is indispensible for practical systems and for system (4) it will be our next work.
Appendix. Some coefficients
The functions in system (15) are
|
$
E00:={(2p+2)c2−(p2+3p)c−2p3}4ε1/{c2(p+1)p6(c−p)4},E10:=−{(2p+2)c2−(p2+3p)c−2p3}2ε1{(−6c3p−4c3p2−4p3c2+3p2c2+4cp4+4c4p+3c4)−(p2c2−3c3p−3c2p+cp2+2cp3−2p4)ε1−(p3c2−2cp4+p5+4c2p4−5p5c−p3c3+2p6)ε2}/{(p+1)p4c3(c−p)4},E20:={(−2c6(p+1)2(c−p)2)+(9c3p2+4c2p4−13c4p+4p5c2+6p3c3+9c5p−15p2c4−2p4c3+4p2c5−4p3c4+6c5)ε1−(2p7c−6p7c2−6p6c2−2p5c4+6p6c3+2cp8−2p4c4+6p5c3)ε2+(6p5c2−2p4c3−6p6c−6p7c+6p6c2−2p5c3+2p7+2p8)ε1ε2+(6p3c3−4p2c4−2c2p4−10p3c2−9c4p−2cp4+17c3p2−2p5c+13c3p−9p2c2−6c4)ε21}/{2c3p2(c−p)2(p+1)},E01:=−{(2p+2)c2−(p2+3p)c−2p3}{2c3ε1+(cp4−2p3c2+c3p2)ε2+(2p4−6cp3+4p2c2)ε1ε2+(12c2−6cp)ε21}/{p2(c−p)2c3},E11:={(3c3p2−8p2c4−p4c3+2c5+2c2p4+4c5p+2p2c5−5c4p+2p5c2+2p3c3−3p3c4)+(3c2p4+3c3p+p2c2+2p5c+3p2c4+3p3c2+2c4p+2cp4−4p3c3+c3p2)ε1+(5p6c2−2p7c−3p6c+7p5c2+2c2p4−p5c−5p4c3−p3c3+p3c4+p4c4−4p5c3)ε2−(5p6c−4p5c2+p4c3−5c2p4−p3c2+7p5c+p3c3+2cp4−2p7−p5−3p6)ε1ε2+(13cp2−8cp4+9c3p2−38p2c2+5cp3+10p4+10p5+19c3p+10c3−13p3c2−25c2p)ε21}/{c2(p+1)(−p+c)},E02:={(c−2p−1)+(5c3−2c2p)ε1−(3p3c2−2c3p2−cp4)ε2+(p4−cp3)ε1ε2−(2cp−c2)ε21}/{(p+1)2(c−p)2}.
$
|
The functions below system (18) are
|
$
ϕ11:=24c6p5+4c8p2−16c7p4+4c8p3−16c5p6+4p7c4+24c6p4−16c7p3−16c5p5+4c4p6+(9p4c4−16p6c3+40c3p7+68p5c4−26p3c5+3c8−6c8p+42c6p3+36c6p4−94c5p4+6c7p2−4c4p6−16c2p8−56c5p5−8c8p2+8c7p3+28c6p2−14c7p)ε1+(4c7p4+40c5p7−4c2p9−4c2p10+20c3p8+20c3p9−20c6p5+40c5p6−20c6p6−40c4p8+4c7p5−40p7c4)ε2−(40p2c5+12p4c3+32c7p2+8p5c3+12c7+92p3c5+8p6c2−32p3c4−12p6c3−28p7c2+4c5p4−88c6p2−56p4c4+36c7p+48p5c4−60c6p3+16cp8−32c6p)ε21+(12cp9−24p7c4−8c7p4−6c7p3−88c5p5−32c2p8+20cp10−24c5p4+6c6p3+2c3p7−24p6c3+36c6p5+72c4p6+96c3p8−76c2p9+36p5c4+40c6p4−44c5p6+6p7c2)ε1ε2+(8p7c−9p2c4−16p5c2+6p3c3−c2p4+11p4c4+6p3c5+10p4c3−16p5c3−18p2c5+12p3c4−9c6p2+4p6c−4p8)ε31+(−34c4p6+2c3p7+4p9−28cp9−16cp8+6p4c4+8p10−2p7c+32c2p8+32p7c2−32p6c3−14p5c3+10p6c2−6c6p4+26c5p5+12p5c4)ε21ε2+(4c3p7−c6p6+44c3p9−41c2p10−c4p6+4cp9+2c5p6−4p11+28c3p8−32c2p9+8c5p7−26c4p8+20p11c−12p7c4−p10−4p12+18cp10−6c2p8)ε1ε22,ϕ12:=(2p5c3−4p3c4+2p4c3+2p3c5+2p2c5−4p4c4)+(9c3p2+4c2p4−13c4p+4p5c2+6p3c3+9c5p−15p2c4−2p4c3+4p2c5−4p3c4+6c5)ε1+(−2p7c+6p7c2+6p6c2+2p5c4−6p6c3−2cp8+2p4c4−6p5c3)ε2+(6p3c3−4p2c4−2c2p4−10p3c2−9c4p−2cp4+17c3p2−2p5c+13c3p−9p2c2−6c4)ε21+(6p5c2−2p4c3−6p6c−6p7c+6p6c2−2p5c3+2p7+2p8)ε1ε2,ϕ21:=(6c10+12c8p5+69c8p4−77c9p3+20c7p6+9c6p4−33c7p3+18c5p6−34c6p5+45c8p2−26c7p4+102c8p3−27c9p−80c9p2+27c7p5+6c5p7+8c4p8−12c5p8−55c6p6−12c6p7+8c4p9+22c10p2−24c9p4+8c10p3+20c10p)ε1+(4p10c4+20p9c6−10p10c5−4p5c9+2p11c4−2c9p4−2p6c9+10p7c8+20p6c8+10c8p5−20p9c5+2c4p9−40p7c7−20c7p8−10c5p8−20c7p6+40c6p8+20c6p7)ε2+(−12c9+12c3p9−47c8p4+10c9p3−86c6p4−19c7p3+102c5p6−220c6p5+60c8p2+159c7p4−40c8p3+61c5p5+2c4p6−16p7c4−18c9p+3c9p2+92c7p5+12c3p8+26c5p7−14c4p8+53c8p+35c6p3−76c7p2−79c6p6)ε21+(2p5c9−34c8p5+2c3p9+19c8p4−10c9p3+151c7p6−17c5p6+39c6p5−45c7p4+26c8p3−2c3p10+3p7c4−6c9p2+23c7p5+77c5p7−26c4p8+145c5p8−85c6p6−227c6p7−31c4p9−2c9p4−103c6p8+83p7c7+51p9c5−2p10c4−4p11c3−27p6c8)ε1ε2+(−4p7c8−2p6c8−30p10c4−60p11c4+40p9c5−2p8c8+12p11c3+24c7p8+12c7p9−60p9c6+12p13c3−30p10c6+40p11c5−30p12c4−4p13c2−2p14c2−2p12c2+24p12c3−30c6p8+80p10c5+12p7c7)ε22+(−30c8+69p3c5−16p4c4−212p5c4+58p6c3+331c5p4−232c6p4+79c7p3+117c5p6−65c6p5−21c8p2−3c7p4+5c8p3+379c5p5−187c4p6+4p7c4−94c3p8+44c2p8+44c2p9+91c7p−53c8p−263c6p3+163c7p2−106c6p2−38c3p7)ε31+(36c2p10−10c8p5−199c3p9−41c8p4+9c7p6+18c2p11−166c6p4+84c7p3+165c5p6−297c6p5−18c8p2+193c7p4−48c8p3−110c3p10+164c5p5−76c4p6+47p7c4+123c7p5−78c3p8+18c2p9−208c5p7+351c4p8−219c5p8−62c6p6+79c6p7+233c4p9+12c3p7)ε21ε2+(−2p14c+c2p10−4c3p9−8c7p6+21c2p11−2p12c−72c3p10−4p13c−4c5p7+6c4p8−102c5p8+c6p6+45c6p7+118c4p9+58p9c6−114p10c5+121p11c4+102c6p8−22p7c7−212p9c5+233p10c4−138p11c3+40p12c2−70p12c3+20p13c2−14c7p8+p7c8+p6c8)ε1ε22(−176p3c4+41p4c3+769p3c5+293p2c5−388p4c4+27p5c3+28p6c2−178p5c4−58p6c3+4p7c2+20cp8+20cp9+603c5p4−192c6p4+75c7p3+127c5p5+34c4p6+72c7−234c6p−24c2p8+210c7p−616c6p3+213c7p2−658c6p2−44c3p7)ε41+(−286p5c4+154p6c3−32p7c2+136c2p10−56cp10−198c3p9−24cp9+262c5p4−32cp11−330c6p4+70c7p3+438c5p6−284c6p5+68c7p4+636c5p5−580c4p6−210p7c4+22c7p5−154c3p8+30c2p8+198c2p9+64c5p7+84c4p8−122c6p3+24c7p2−76c6p6+198c3p7)ε31ε2+(4p12+102c2p10−cp10−158c3p9−c7p6+198c2p11−64p12c−33cp11−c5p6−313c3p10−32p13c+4p7c4+8p13−6c3p8+4c2p9−57c5p7+132c4p8−126c5p8+10c6p6+26c6p7+272c4p9+4p14+16c6p8−p7c7−70p9c5+144p10c4−161p11c3+100p12c2)ε21ε22.
$
|









 DownLoad:
DownLoad: