
- Home
-
Journals
- Communications in Analysis and MechanicsAIMS MathematicsMathematics in EngineeringElectronic Research ArchiveNetworks and Heterogeneous MediaSTEM EducationAIMS Agriculture and FoodAIMS Allergy and ImmunologyAIMS BioengineeringAIMS BiophysicsAIMS Electronics and Electrical EngineeringAIMS EnergyAIMS Environmental ScienceAIMS GeosciencesAIMS Materials ScienceAIMS Medical ScienceAIMS MicrobiologyAIMS Molecular ScienceAIMS NeuroscienceAIMS Public HealthApplied Computing and IntelligenceBig Data and Information AnalyticsClean Technologies and RecyclingData Science in Finance and EconomicsGreen FinanceJournal of Dentistry and Multidisciplinary SciencesMathematical Biosciences and EngineeringMathematical Modelling and ControlMetascience in AerospaceNational Accounting ReviewQuantitative Finance and EconomicsUrban Resilience and SustainabilityAIMS Animal Science
- Home
- Journal Home
-
Journals
- Communications in Analysis and MechanicsAIMS MathematicsMathematics in EngineeringElectronic Research ArchiveNetworks and Heterogeneous MediaSTEM EducationAIMS Agriculture and FoodAIMS Allergy and ImmunologyAIMS BioengineeringAIMS BiophysicsAIMS Electronics and Electrical EngineeringAIMS EnergyAIMS Environmental ScienceAIMS GeosciencesAIMS Materials ScienceAIMS Medical ScienceAIMS MicrobiologyAIMS Molecular ScienceAIMS NeuroscienceAIMS Public HealthApplied Computing and IntelligenceBig Data and Information AnalyticsClean Technologies and RecyclingData Science in Finance and EconomicsGreen FinanceJournal of Dentistry and Multidisciplinary SciencesMathematical Biosciences and EngineeringMathematical Modelling and ControlMetascience in AerospaceNational Accounting ReviewQuantitative Finance and EconomicsUrban Resilience and SustainabilityAIMS Animal Science
-
About

-
Contribute

-
Articles

Copyright © AIMS Press






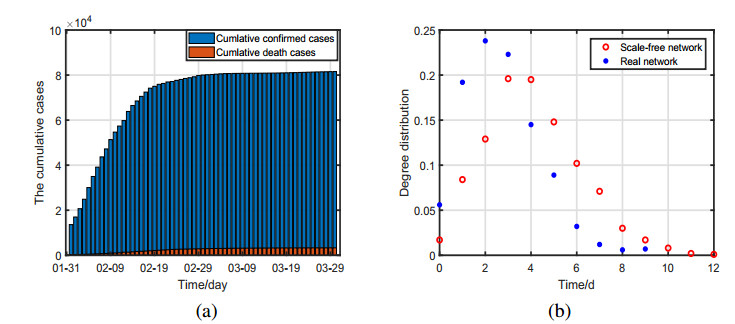

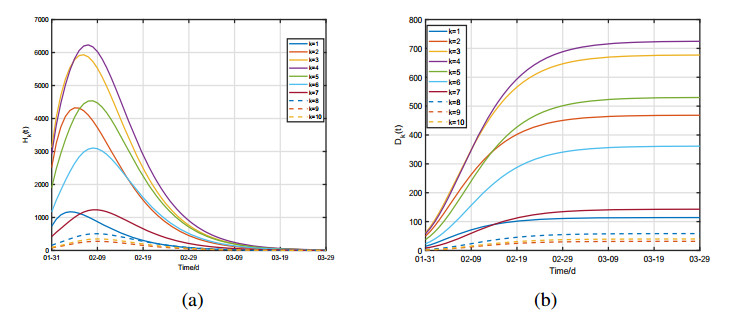
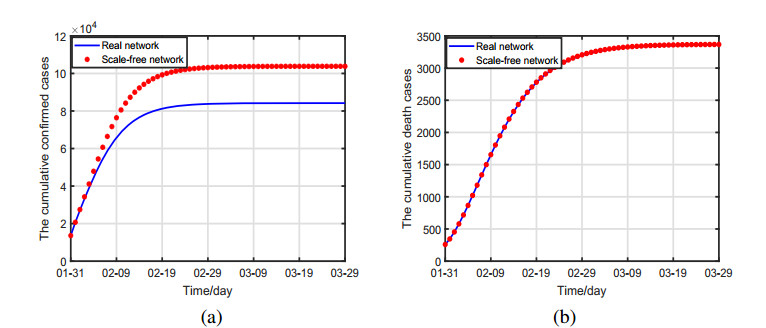


 DownLoad:
DownLoad: