1. Introduction
The future smart grid is being designed to mitigate or avoid consequences derived from power quality events (e.g., voltage sags), improve reliability indices (e.g., by reducing the number of interruptions and their duration), and increase the system efficiency (e.g., by reducing losses). The increasing penetration of renewable generation and a fast implementation of the electric vehicle are two trends that can stress the current grid by causing voltage variations larger than those the system can withstand. A solution for many of these problems is the Solid State Transformer (SST).
Transformers are widely used to perform functions such as voltage transformation and isolation. Although the conventional transformer has been, and still is, the traditional link between end-users and the distribution network, the high-frequency SST design could cope with many of the challenges of the future smart grid since it can enhance power quality performance and expand the capabilities of the conventional transformer: voltage sag compensation, instantaneous voltage regulation, harmonic compensation, power factor correction, auto-balancing, short-circuit protection, variable-frequency output, bidirectional power flows. Since the size of a conventional copper-and-iron based transformer is inversely proportional to the operating frequency, an increase of this frequency would provide a higher utilization of the magnetic core and a reduction in transformer size. In addition, the SST can be used as a link between standard ac power-frequency systems and systems operating with either dc or ac at any power frequency.
The first patent on a device that could be seen a predecessor of the current SST designs was presented in 1992 [1]. Since then several patents have been presented; see, for instance [2,3,4,5].
The SST design can be seen as a universal interface that can provide not only power quality improvements but efficient management of distributed resources. By incorporating the SST, utilities can integrate various power requirements, monitoring, and communications into a universal customer interface such as the SST, which can also provide some operational benefits (e.g., reduced environmental concerns by introducing a design that does not use liquid dielectrics, efficient management of distribution resources by incorporating online monitoring and other automation functionalities). The goal of this paper is to provide a bibliographical review of the work carried out to date on the SST. The main contribution of this work is a list of references ordered by publication year. However, since there are many aspects of the SST that make this device so attractive as a component of the future power systems, several short sections have been included to discuss some important features of the SST. Each section is aimed at summarizing the current status with a selection of relevant works. Readers interested in an introduction to the SST can consult references [6,7,8].
Although the list of references covers SST designs of various voltage levels and different applications, it might be assumed by default that the primary SST application is to function as a medium voltage/low voltage (MV/LV) distribution transformer. Since standardized voltages used for MV distribution grids are usually equal or higher than 10 kV, multilevel topologies must be considered for the MV side of the SST if conventional Si-based semiconductors are used. In general, it can be assumed that if the highest SST voltage is equal or above the lowest standardized voltage (i.e., 3.3 kV), a SST design must be based on a multilevel converter configuration at the MV side.
Different topologies of multilevel converters have been proposed for SST applications. Irrespective of the selected topology, the operation of a multilevel converter has to face important challenges (e.g., capacitor voltage balancing and complex control strategies). Once the converter topology has been selected, the selection of a proper control strategy for each SST stage becomes crucial for a correct performance of the device. In addition, the SST capabilities (e.g., bidirectional power flow, harmonic compensation, current balance) and performance (e.g., reliability, efficiency) are closely connected with the selected configuration and control strategies; Section 2 provides a summary of the work related to multilevel converter designs for SST implementation and the corresponding control strategies. A fundamental component of the SST is the high-frequency transformer (HFT); Section 3 summarizes the current state of HFT designs for SST implementation.
It is widely accepted that the efficiency of current SST designs is lower than that of their conventional iron-and-copper counterpart; Section 4 discusses this aspect and reviews the main works related to analyze SST efficiency.
The performance and benefits of the SST as a part of large distribution system can be predicted by implementing and testing reliable and accurate computer models; Section 5 summarizes the work carried out on modelling and simulation of the SST, including the experience collected with real-time simulation platforms.
The SST can be seen as a replacement of the conventional transformer. However, the foreseen applications of the SST cover an area wider than that of the conventional transformer. Section 6 summarizes the work dedicated to date for fixing the potential applications of the SST.
Other important aspects, such as the semiconductor technologies that could be adequate for this device are not covered here. Readers are referred to the literature; see for instance [6,7,8,9,10,11,12].
Although other designations have been used to name this device (i.e., Intelligent Universal Transformer, Electronic Power Transformer), this paper exclusively uses the acronym SST to name it.
2. SST topologies and control strategies
2.1. Introduction
If it is assumed that the SST can be used to link DC and AC systems running at medium and low voltage levels, a very high number of combinations may result; for instance, the SST can be used to link MV and MV, MV and LV, or LV and LV DC and/or AC systems. Remember that in case of AC systems, they can be single-or multi-phase. In fact, a myriad of configurations have been proposed and even analyzed under the concept SST (or any other designation used to date for this device). To facilitate the study, those configurations will be classified taking into account the number of stages and the configuration of converters to be installed at both MV and LV sides.
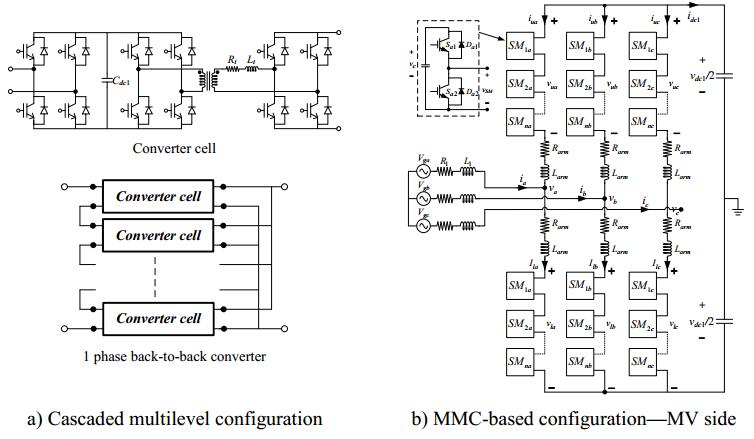
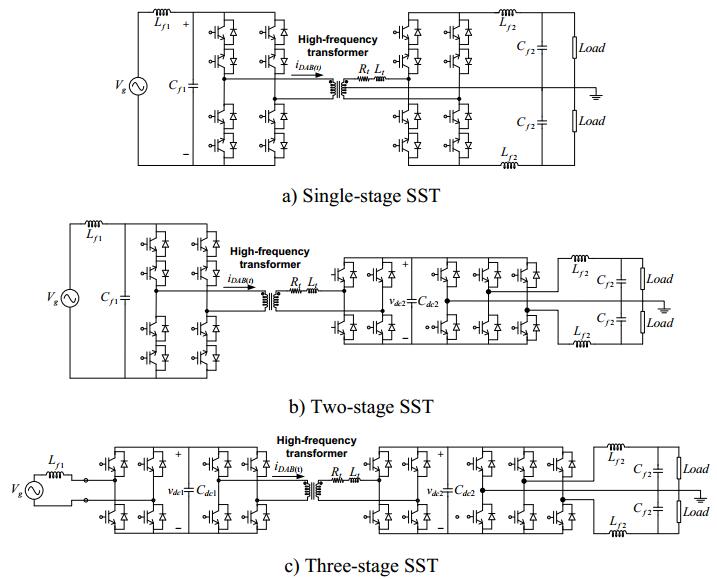
Figure 1 shows three examples of single-phase SST configurations that can be used to illustrate the concept of stage when applied to this device. One can observe that a common component to all of these configurations is the HFT. For a discussion about SST configurations taking into account the number of stages, see [13]. SST MV-side converters must be multilevel. Although many configurations have been proposed, multilevel converters can be broadly classified into two main groups, depending on whether the configuration is based on a cascaded connection of converters or not; Figure 2 shows two examples.
On the other hand, note that Figure 2b displays only the MV input stage. As for LV converters, those for three-phase systems can be classified into two groups depending on whether they have three or four wires (i.e., they include the neutral). The control strategies to be used in a SST will depend of the overall configuration, the topology selected for each SST stage, and the desired functionalities. The rest of this section provides a short summary of the work carried out to date on these topics. For a discussion of SST configurations and control strategies, see reference [14]. Table 1 provides a short list of the SST prototypes presented to date.
Table 1. SST Prototypes.
| Ratings |
Configuration |
Control |
Capabilities |
Laboratory tests |
Refs. |
| 10 kVA, 7.2 kV/240V |
Three stage, cascaded H-bridge |
PWM |
Unidirectional power flow, power-factor correction |
Steady state, load unbalanced |
[51,52] |
| 20 kVA, 2.4kV/120-240 VAC or 48V DC |
Single phase, three stage, NPC multilevel, multiport-output DC/AC inverter |
PWM |
Unidirectional power flow |
Steady state, load change, load unbalance, voltage sag, nonlinear load, |
[53,54,55] |
| 50 kVA, 2.4 kV/240V/ 120V |
Three stage, Three level NPC in MV side |
PWM |
Voltage sag compensation, fault isolation |
voltage sag, load variation, load unbalance |
[56] |
| 5 kVA, 220 V/380 V |
Two stage, direct AC/AC high-frequency link, dual bridge matrix converter topology |
PWM |
bidirectional power flow, low harmonic distortion |
Load unbalance, unbalanced input voltage |
[57] |
| 100 kVA, 13.8 kV/120V or 240 V |
Three phase, three stage, cascaded blocks |
PWM |
Unidirectional power flow |
Steady state, load unbalance, voltage sag, non-linear load, load variation, capacitor switching transient, |
[58] |
| 1.5 kW, 230 V/39V |
Three stage, cascaded H-bridge |
PWM |
Bidirectional power flow, harmonic voltage compensation, reactive power compensation |
Voltage sag, nonlinear load |
[59] |
| 2 kW, 110V/20V |
Single-stage, AC/AC, two level |
PWM |
Bidirectional power flow, maximum power-point tracking |
Steady state |
[60] |
| 20 kVA, 7.2 kV/240 V |
Three stage, cascaded H-bridge |
PWM |
Bidirectional power flow |
Steady-state |
[61,62,63,64,65,66,67,68,69,70,71] |
| 54 kW, 1.5 kVAC/60VDC |
Two stage, cascaded H-bridge |
PWM |
Bidirectional power flow |
Steady state, load variation, power flow reversal |
[72,73] |
| 1 kW, 208V/120V |
Three-stage, two level |
PWM |
Bidirectional power flow |
Start-up transient |
[74] |
| 100 kW, 10kVAC/750VDC |
Two stage, AC/DC/DC, MMC |
PWM |
Bidirectional power flow |
Steady state |
[75] |
| 2 kVA, 1.9 kV/127 V |
Three stage, multilevel converter |
PWM, ZVS |
Bidirectional power flow, voltage sag compensation |
Steady state, voltage sag, power flow reversal |
[76,77] |
| 10 kW, 3.6 kV/120 V |
Three stage, two level |
PWM |
Bidirectional power flow, harmonic voltage compensation |
Steady state, nonlinear load, load variation |
[78,79,80,81,82] |
| 1 kW, 353.55/220 |
Two stage AC/AC, MMC |
PWM |
Unidirectional power flow |
Steady state |
[83] |
| 600 kVA, 3.3 kV DC/3.3 kV DC |
Three stage, cascaded H-bridge in MV side |
PWM |
Bidirectional power flow |
Steady state |
[84] |
| 5 kW, 3300V AC/ 380VDC |
Two stage, cascaded H-bridge |
Phase shift modulation |
Bidirectional power flow |
Steady state |
[85] |
| 2 kVA, 380V/120V |
Three stage, cascaded |
PWM |
Bidirectional power flow |
Steady state, power flow reversal, startup transient |
[86] |
| 5.8 kVA, 5KVDC/ 800VDC |
Three stage, NPC with SiC |
PWM |
Bidirectional power flow |
Steady state |
[87] |
| 2 kW, 300 V/60 V |
Three stage, two level |
PWM |
Bidirectional power flow |
Steady state, load variation |
[88] |
| 50 kVA, 480V/480V |
Single stage, Dyna-C AC/AC topology |
PWM |
Bidirectional power flow |
Steady state |
[89,90] |
| 150 kVA, port1:750VDC port2:375VDC port3:750VDC |
Triple active-bridge with energy storage |
Phase shift modulation |
Bidirectional power flow |
Steady state |
[91,92] |
| 2 kW, 400V/208V |
Single stage, AC/AC, matrix based |
Predictive Control |
Bidirectional power flow |
Steady state, load variation, unbalanced voltage and current |
[93,94] |
| 3-kVA, 2.4kV/127V |
Three stage, two level |
PWM |
Unidirectional |
Steady state, nonlinear load |
[95] |
| 10 kVA, 208 V |
Single stage AC/AC, two level |
ZVS |
Bidirectional power flow |
Steady state |
[96] |
| 2 kW, 600VDC/200VDC |
Three phase modular multilevel dc/dc converter |
PWM, ZVS, dual-phase-shift method |
Bidirectional power flow |
Steady state |
[97] |
| 10 kVA, 3.8 kVDC/ 200VDC |
Three stage, single phase single converter cell based SST for wind energy conversion system |
PWM |
Bidirectional power flow |
Steady state, load variation |
[98] |
Other SST prototypes, not listed in the table, were presented in [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50].
2.2. Converter topologies for SST application
The possible configuration of a SST has been analysed in many works. References [13,99,100,101,102,103,104,105,106,107,108,109] are some of the works in which the SST configurations were analysed and/or compared. With respect to the number of stages, the main conclusions from the present literature can be summarized as follows: single-and two-stage topologies provide limited functionalities as compared to three-stage topologies, which can provide all the desired SST functionalities while simplifying the control design. A list of selected references in which some of the most popular SST configurations were analyzed is presented below.
Three possible topologies for the higher voltage side of a SST were identified in [101]: the diode clamped multilevel converter, the flying capacitor multilevel converter, and the series stacked converter. Reference [110] analyzed different topologies that can provide a reliable energy management with the SST. References [111,112] proposed a two-level three-stage bidirectional SST.
For the MV side converter configuration, references [113,114,115] proposed a neutral point clamped (NPC) topology; references [10,116] presented a cascaded H-bridge multilevel inverter configuration, while references [106,107,109,117] suggested a modular multilevel converter (MMC) configuration.
References [89,90] proposed a bidirectional SST configuration, named as dynamic-current (or Dyna-C), with a minimal device count: the topology has two current-source inverter stages with a high-frequency galvanic isolation, and 12 switches for four-quadrant three-phase ac/ac power conversion. The input and output stages can work with arbitrary power factors and frequencies. Dyna-C can be configured as isolated power converters for single-or multi-terminal dc, and single-or multiphase ac systems. Its modular nature allows Dyna-C to be connected in series and/or parallel for high-voltage high-power applications.
References [118,119] presented a 270 kVA SST based on 10 kV SiC MOSFET: five levels were needed in order to support a 24 kV input voltage; each device has a 10 kV blocking capability. Three flying capacitors enable the operation of zero voltage switching (ZVS) with phase shift control. Reference [120] introduced a new SST topology that included a reduced number of SiC MOSFETs and smaller switching losses.
The configuration of the SST has been the subject of many other works; see [107,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,
152,153,154,155,156,157,158].
2.3. Control strategies
A three-stage SST includes up to four different converters (see Figure 1c). Dozens of strategies have been proposed for controlling the various converters of a SST; they primarily depend on each converter configuration and the SST functionalities (e.g., bidirectionality). A summary of control strategies used with lab prototypes is provided in this subsection. For a discussion on strategies to be used with a three-stage SST, see [14].
Reference [159] presented a linear-quadratic-regulator with integral action to improve dynamic performance; the integral action is added to cancel the steady-state errors.
A source-based commutation method for a HFT controlled through a matrix converter was proposed in [160,161,162].
Reference [163] presented a simple predictive control technique for multilevel configurations either on the line-side (high voltage) or on the load-side (low voltage); the control is performed in two steps: (ⅰ) generation of the reference value of the primary current; (ⅱ) evaluation of the optimized delay-angle between primary and secondary voltages using a predictive algorithm.
An energy-based control design method for a three-stage cascaded multilevel SST was proposed in [164]; by selecting the total energy in the two dc link capacitors as the control objective, this approach resulted in a control design.
An advanced control methodology based on fuzzy logic controllers was proposed in [165,166,167].
References [65,168] analyzed up to four different control strategies for a 20 kVA SST with a seven-level cascaded rectifier stage, three output parallel dual active bridges (DAB), DC/DC stage and an inverter stage. References [169,170] studied soft-switching techniques for MV isolated bidirectional DC/DC NPC-based converters.
A control strategy for a cascaded H-bridge based converter was proposed [171]: the input-stage part was responsible for the power quality improvement and high-voltage DC link voltage balance; the DAB stage was responsible for maintaining the low-voltage DC link voltage; the output-stage part was responsible for the output terminal voltage regulation and parallel module current sharing control. Power synchronization and interleaving modulation were adopted in the output-stage part.
Reference [68] presented a cascaded H-bridge converter-based SST to interface a 7.2 kV AC grid and a 400 V DC distribution; a single-phase dq vector control was used. A new voltage balance control method was proposed to resolve the voltage unbalance of the dc links in H-bridges; see also [85,172].
A hierarchical power management strategy, including primary, secondary, and tertiary control, for a DC microgrid was proposed in [70,173].
Reference [174] investigated the concept of convertible static transmission controller (CSTC) using modular converter. Algebraic models of the CSTC were derived in two different configurations (series–shunt and shunt–shunt).
References [175,176,177] analyzed the black start operation of a single phase SST with the master-slave control mode and using dual loop structures.
Reference [178] proposed a current sensorless controller for balancing the power in the DC-DC stage of a cascaded multilevel converter-based SST; the equalization of the active power component of duty cycles in the cascaded multilevel rectifier stage can be a good indicator of power balance. Additionally, the power balance of the DC-DC stage can guarantee the voltage balance in the rectifier stage if the differences among the power devices are negligible. Reference [179] proposed a trapezoid current modulated discontinuous conduction mode AC-DC DAB converter for a two-stage SST; the soft switching converter exhibited a high efficiency, and could be operated in open loop control without current sensors.
Reference [116] presented a power and voltage balance control scheme of a cascaded H-bridge modular inverter for microgrid applications operating under unbalanced conditions; the control method was designed to address the presence of power and voltage unbalance.
A control architecture with two communication networks aimed at improving the communication modularity among power modules of a SST was presented in [180]. The communication structure was based on a two full-duplex RS-485 networks (one for each SST side) from which the central unit communicates and controls the local units using of a custom protocol.
Reference [181] proposed a sliding mode control scheme for the rectifier stage with constant power load. This approach can stabilize the dc-link voltage and guarantee the input current sinusoidal in the presence of significant variations in the load power.
References [93,94,182,183] presented a predictive control for a matrix converter-based SST; the goal was to reduce the complexity of the traditional modulation strategy and improve its performance.
Other works related to control strategies of SST were presented in [128,150,152,158,184,185,186,187,188,189,190,191,192,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,
212,213,214,215,216,217,218].
3. High-frequency transformer
The high-frequency transformer (HFT) is a fundamental component of the SST, and a requirement to achieve a reduction of size with respect to conventional transformers. To fulfill high-voltage, high-power, and high-frequency operation requirements, several issues and challenges need to be addressed [9]: (ⅰ) the selection of the magnetic material is critical to achieve high power density and low losses; (ⅱ) the winding configuration can significantly affect the efficiency at high frequency; (ⅲ) thermal behavior is a challenge to consider in order to avoid breakdown for a high-voltage and high-power designs; (ⅳ) a high-voltage operation makes the insulation requirement another challenge, especially when oil is eliminated and a compact design is required.
It is important to keep in mind that a higher frequency causes extra losses in the magnetic core (as a result of eddy currents) and in windings (due to skin and proximity effects); that is, a volume reduction at higher frequencies is at the expense of increased (core and winding) losses. A thermal management strategy is also important to more accurately evaluate the power losses.
Consequently, multiple degrees of freedom exist when optimizing the design of a HFT; they can be categorized in electric, geometric, and material parameters. For instance, two electric parameters to be accounted for are the number of turns (it determines the ratio of flux density and current density, so it has to be set such that the sum of core and winding losses is minimized) and the operating frequency (when increased it reduces the core losses but increases the proximity losses in the winding and the switching losses of the semiconductors). Two very important specifications of a HFT are the power rating and the operating frequency since, when combined with the magnetic core and conductor materials, they strongly influence the efficiency and power-density.
Reference [219] proposed a transformer for 12 and 24-pulse rectifier systems; a size reduction of 1/3 with respect to a conventional 60 Hz design could be achieved by operating the transformer core at 990 Hz and utilizing conventional grain oriented steel.
Reference [61] proposed optimum size and weight reduction of a 7 kVA dry-type HFT, whose high-voltage side insulation should withstand 15 kV. The design required a relatively high leakage inductance (lack of leakage inductance may lead to additional inductors which results in higher size, weight, and cost), so meeting the leakage inductance requirement became an important issue. Since the leakage inductance depends on the winding arrangement and the number of turns, to adjust the leakage flux, a two-winding arrangement (the windings on both sides are totally separated and one winding is totally covered up with the other winding) and several core materials were considered. Metglas amorphous alloy cores turned out to be the best choice.
Reference [220] presented an accurate equivalent circuit of a MV coaxial winding by comparing results from a finite element method (FEM) and lab measurements. The design provides uniformly and symmetrically distributed electromagnetic flux with good electric and magnetic shielding. An overall efficiency of 99.5% remaining below 100 ℃ under oil-free and natural convection was achieved for a 30 kVA transfer.
Reference [221] presented the optimization of a HFT with different targets (i.e., weight, volume, and cost) under certain constraints like a given cooling performance, insulation requirements, and selected semiconductors. By means of a detailed transformer model it was possible to find the optimum frequency with respect to size, weight or efficiency for different designs, and systematically investigate improvements arising from different core materials, wire structures, geometries and cooling designs.
A design and optimization method for HFTs was proposed in [9]. The authors carried out a comparison of different magnetic materials; the main conclusion was that a nanocrystalline core is the option that better satisfies both power density and efficiency requirements.
Reference [222] presented the optimization of a water-cooled HFT prototype for maximum power density and efficiency; the electric and thermal specifications, as well as certain dimensions that define clearance space and cooling system, were specified.
Reference [223] presented an optimization methodology applied to a 50 kW, 5 kHz HFT, and aimed at finding the highest power density while the efficiency, isolation, thermal and leakage inductance requirements are meet taking into account thermal management.
Reference [224] proposed a toroidal design for a Metglas core using a procedure aimed at optimizing the number of turns and minimizing (core plus winding) losses.
Reference [225] detailed an optimization procedure for a 166 kW/20 kHz prototype. The authors could achieve 99.4% efficiency at a power density of 44 kW/dm3. As a consequence of the relatively high-power rating, the cooling system became a major challenge. The work also provided analytic solutions for high-frequency losses, which were separated into skin and proximity losses.
Reference [226] presented the optimal design of 20/0.4 kV HFT; the goal was to maximize efficiency and power density, and minimize weight. The maximum allowable temperature rise was considered as an inequality constraint while desired values of leakage and magnetizing inductances were considered as equality constraints. Results did show that an efficiency and power density above 99.70% and 13 kW/dm3 can be achieved using a nanocrystalline-based core.
For more details on the design of HFTs for SST applications, see references [202,227,228,229,230,231,232,233,234,235,236].
4. Solid state transformer efficiency
It is widely accepted that the efficiency of the current SST designs is lower than that of their conventional iron-and-copper counterpart; see, for instance, [6,8,237]. To accurately evaluate SST efficiency, the losses of all SST components must be taken into account; these losses include conduction and switching losses in power electronics converters, filter and HFT losses. The losses can be estimated through experimental test setups or by detailed modelling in simulation tools such as Matlab/Simulink or EMTP-like tools. The lower SST efficiency is basically due to the high losses of power electronic converters and the need of filters at both SST sides.
There are some great challenges regarding to the design of efficient converter topologies. Standardized voltages equal or above 10 kV are considered for MV side applications by most utilities. Since the maximum operating voltage of Si semiconductors is about 3.6 kV, multilevel topologies are necessary for the MV side of actual SST configurations. An alternative is to use SiC semiconductors. Although, this technology is not mature enough at the time this work is prepared, it appears as one of the best options for highly efficient and compact SST designs.
Basically, the improvement of SST efficiency can be accomplished by means of the following approaches: (ⅰ) advanced converter configurations combined with optimized control strategies for all SST stages; (ⅱ) optimized design of the HFT; (ⅲ) use of wide band gap semiconductors (i.e., SiC), since they can provide lower losses even when working at higher switching frequencies. This latter improvement is due, among other things, to the significant reduction of the number of semiconductors that can be accomplished with this technology.
Although not many works have been dedicated to the estimation and reduction of SST losses, some experience is already available.
An interesting conclusion of a study presented in [238] was that soft switching control might be a good option for enhancing SST efficiency.
Reference [239] analyzed the efficiency of five different topologies of SST with considering commercially available Si semiconductors. Reference [240] studied the efficiency of three modular SSTs under daily loading profile. A computer model for representing semiconductor losses was proposed in [241].
Reference [242] analyzed the behavior of a SST model implemented in OpenDSS for power flow calculations; the SST efficiency was estimated as a function of load level and power factor.
The efficiency of the SST was also analyzed in [100,137,140,232,243,244,245,246,247,248,249,250,251,252,253,254,255,256,257,258,259].
5. Computer modeling and simulation
The SST is a versatile device that can provide new power quality solutions to the future smart grid. Given the complexity of the actual designs and the difficulties that arise when its performance as component of an actual power system has to be analyzed, computer-based simulation appears as a reasonable alternative.
A significant experience is already available in SST modeling. Several types of SST models have been developed and tested; they depend of the application to be analyzed and can be categorized into three main types: switching (detailed) models, average models, and steady-state models. Other approaches (i.e., state-variable model) have been considered. Table 2 provides a selection of SST models implemented to date; the table provides the main characteristics of the implemented models, the simulation tool and the modeling approach.
Table 2. SST simulation tools.
| Simulation tool |
Modeling approach |
Configuration |
References |
| Matlab/Simulink |
Switching model |
Single phase, three-stage, multilevel |
[59,262] |
| Matlab/Simulink |
Switching model |
Single phase, three stage, multilevel, bidirectional |
[68] |
| Matlab/Simulink |
Average model |
Three phase, three stage, multilevel, bidirectional |
[84] |
| Matlab/Simulink |
Switching model |
Three phase, single stage, multilevel, bidirectional |
[97] |
| Matlab/Simulink |
Switching model |
Single phase, three stage, multilevel, bidirectional |
[106,107,109,281] |
| Matlab/Simulink |
Average model |
Three phase, three stage, two level, bidirectional |
[111,112,279,280] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[117,241] |
| Matlab/Simulink |
Average model |
Three phase, three stage, two level, bidirectional |
[159] |
| Matlab/Simulink |
Switching model |
Three-phase, single-stage, two level, bidirectional |
[160,162,263,264,265,266,267] |
| Matlab/Simulink |
Average model |
Single phase, three stage, multilevel, bidirectional |
[164,270] |
| Matlab/Simulink |
Average model |
Single phase, three stage, multilevel, bidirectional |
[168] |
| Matlab/Simulink |
Average model |
Single phase, three stage, multilevel, bidirectional |
[173] |
| Matlab/Simulink |
Switching model |
Three phase, single stage, two level, bidirectional |
[260] |
| Matlab/Simulink |
Average model |
Three phase, three stage, two level, bidirectional |
[261] |
| Matlab/Simulink |
Average model |
Three phase, three stage, multilevel, bidirectional |
[268] |
| Matlab/Simulink |
Average model |
Single phase, three stage, multilevel, bidirectional |
[269] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[271] |
| Matlab/Simulink |
Average model |
Three phase, three stage, two level, bidirectional |
[272] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, two level, bidirectional |
[273,274] |
| Matlab/Simulink |
Switching model |
Single phase, three stage, multilevel, bidirectional |
[275,276,277] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, two level |
[278] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[282] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, two level, bidirectional |
[283] |
| Matlab/Simulink |
Average model |
Single phase, three stage, two level, bidirectional |
[284] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, two level, bidirectional |
[285] |
| Matlab/Simulink |
Average model |
Three phase, two stage, multilevel, bidirectional |
[286] |
| Matlab/Simulink |
Average model |
Single phase, two and three stage, two level, bidirectional |
[287] |
| Matlab/Simulink |
Switching model |
Single phase, two stage, two level, bidirectional |
[288] |
| Matlab/Simulink |
Switching model |
Three-phase, three-stage, multilevel, bidirectional |
[289] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[290] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, two level, bidirectional |
[291] |
| Matlab/Simulink |
Average model |
Single phase, three stage, two level, bidirectional |
[292] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, two level, bidirectional |
[293] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[294] |
| Matlab/Simulink |
Switching model |
Single phase, two stage, multilevel, bidirectional |
[295] |
| Matlab/Simulink |
Switching model |
Single phase, three stages, multilevel, bidirectional |
[296] |
| Matlab/Simulink |
Average model |
Single phase, two stage, two level, bidirectional |
[297] |
| Matlab/Simulink |
Switching model |
Three phase, three stage, two level, bidirectional |
[298] |
| Matlab/PLECS |
Average model |
Single phase, two stage, multilevel, bidirectional |
[62] |
| Matlab/PLECS |
Switching model |
Single phase, three stage, two level, bidirectional |
[177] |
| Matlab/PLECS |
Switching model |
Single phase, single stage, multilevel, bidirectional |
[299] |
| Matlab/ PLECS |
Average model |
Single phase, three stage, two level, bidirectional |
[300,301] |
| Matlab/PLECS |
Switching/Average models |
Single phase, three stage, two level, bidirectional |
[302] |
| Matlab/PLECS |
Switching model |
Three phase, three stage, multilevel |
[303] |
| Matlab/PLECS |
Switching model |
Single phase, two stage, two level, bidirectional |
[304] |
| Matlab/PLECS/RTDS |
Average model |
Single-phase, three-stage, two level, bidirectional |
[305] |
| PLECS |
Switching model |
Three phase, single stage, two level, bidirectional |
[306] |
| PLECS |
Average model |
Single phase, three stage, two level, bidirectional |
[307] |
| PLECS |
Average model |
Single phase, three stage, multilevel, bidirectional |
[308] |
| PLECS/Shttps://www.aimspress.com/aimspress-data/aimse/2018/2/PICE |
Phasor-based model |
Three phase, three stage, multilevel, bidirectional |
[309] |
| PShttps://www.aimspress.com/aimspress-data/aimse/2018/2/PICE |
Switching model |
Single phase, three stage, two level, bidirectional |
[80] |
| Shttps://www.aimspress.com/aimspress-data/aimse/2018/2/PICE |
Switching model |
Single phase, two stage, two level |
[310,311] |
| Shttps://www.aimspress.com/aimspress-data/aimse/2018/2/PICE/SABER |
Switching model |
Single phase, single stage, multilevel |
[118] |
| SABER |
Switching model |
Single phase, single stage, two level, bidirectional |
[312] |
| PSCAD/EMTDC |
Switching model |
Single phase, three stage, multilevel, bidirectional |
[76] |
| PSCAD/EMTDC |
Average model |
Single phase, three stage, multilevel, bidirectional |
[176] |
| PSCAD/EMTDC |
Switching model |
Single phase, single stage, two level, bidirectional |
[313,314] |
| PSCAD/EMTDC |
Switching model |
Three phase, three stage, multilevel |
[315] |
| PSCAD/EMTDC |
Switching model |
Three phase, three stage, two level, bidirectional |
[316] |
| PSCAD/EMTDC |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[317] |
| PSCAD/EMTDC |
Average model |
Three phase, three stage, two level, bidirectional |
[318] |
| PSCAD/EMTDC |
Average model |
Three phase, three stage, two level, bidirectional |
[319] |
| PSCAD/EMTDC |
Switching model |
Single phase, three stage, multilevel, bidirectional |
[320,321] |
| PSCAD/EMTDC |
Switching model |
Three phase, three stage, two level, bidirectional |
[322] |
| PSCAD/EMTDC |
Switching model |
Three phase, three stage, two level, bidirectional |
[323] |
| PSCAD/EMTDC |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[324] |
| PSCAD/EMTDC |
Average model |
Single phase, three stage, two level, bidirectional |
[325] |
| PSCAD/EMTDC |
Switching model |
Three phase, three stage, two level, bidirectional |
[326] |
| PSCAD/EMTDC |
Average model |
Three phase, three stage, multilevel, bidirectional |
[327] |
| PSCAD/EMTDC |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[328] |
| PSCAD/EMTDC |
Switching model |
Single stage, DC/DC, multilevel, bidirectional |
[329] |
| EMTP/ATP |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[115] |
| EMTP/ATP |
Switching model |
Three phase, three stage, two level, bidirectional |
[330] |
| EMTP/ATP |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[331] |
| PSIM |
Switching model |
Single-phase, two-stage, multilevel, bidirectional |
[85] |
| PSIM |
Switching model |
Single stage, DC/DC, multilevel, bidirectional |
[170,333] |
| PSIM |
Switching model |
Single-phase, two-stage, multilevel, bidirectional |
[179] |
| PSIM |
Switching model |
Single stage, DC/DC, two level, bidirectional |
[332] |
| PSIM |
Switching model |
Three phase, three stage, multilevel, bidirectional |
[334,335] |
| PSIM |
Average model |
Single phase, single stage, two level, bidirectional |
[336] |
| Digsilent |
Average model |
Three phase, three stage, two level, bidirectional |
[337] |
| Simplorer |
Switching model |
Three phase, three stage, multilevel |
[338] |
| RTDS |
Average model |
Single phase, three stage, multilevel, bidirectional |
[339] |
| RTDS |
Average model |
Single phase, three stage, two level, bidirectional |
[340] |
| OPAL-RT |
Switching model |
Single phase, three stage, two level, bidirectional |
[341] |
| Multisim/Labview |
Switching model |
Single phase, single stage, two level, bidirectional |
[342,343] |
| OPENDSS |
Steady-state model |
Three phases, three stage, two level, bidirectional |
[242] |
Not much experience on SST models is currently available for steady-state power flow calculations. Reference [242] presented a SST model for OpenDSS implementation. The model can be used to explore and assess the impact of the SST on distribution system performance (i.e., in steady-state power flow calculations) considering either a short-or long-term evaluation.
On the other hand, a significant experience is already available with switching (detailed) models. The use of these models generally requires the use of very short time-step sizes (i.e., equal or shorter than 1 μs), which implies long simulation times and limits the size of the system that can be practically analyzed. The most popular tool for this type of models is MATLAB/Simulink, although some important experience is also available with EMTP-like tools.
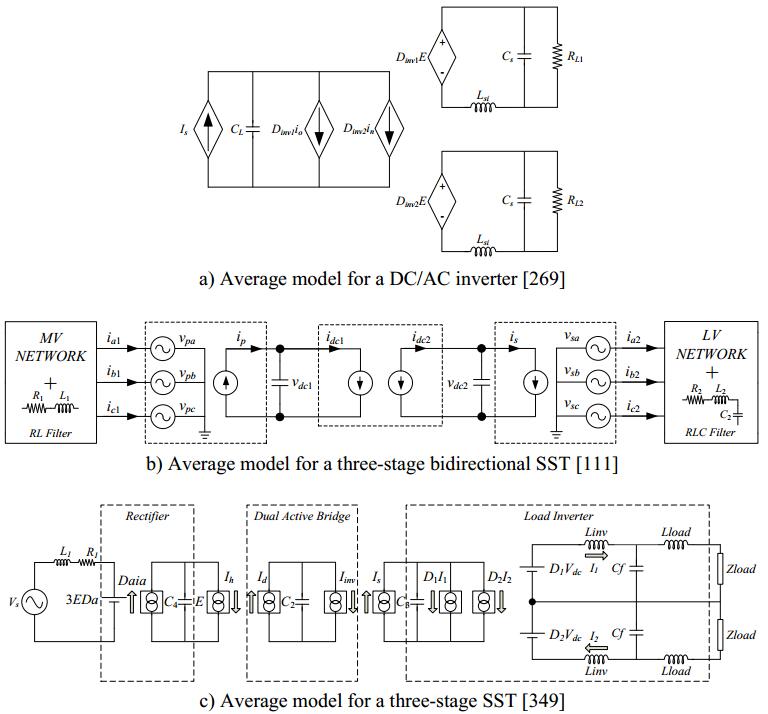
Real-time simulation platforms are widely used for transient simulation of power systems, testing of protection devices, or rapid control prototyping. The need of a very short time-step for switching models of SSTs can be a drawback with many of these simulation platforms. To mitigate or circumvent this limitation the so-called dynamic average models (DAM) can be developed: a DAM approximates the behavior of a converter by applying the moving average operator at the switching frequency to the detailed switching model; the switching effects are removed from the model, but the dynamic behavior is preserved. DAMs, named average models hereinafter, can reproduce with a high accuracy the transient behavior of the original detailed switching model but using a larger time step size, facilitating the implementation of transient models in real-time simulation platforms. Figure 3 shows three different average models proposed in the literature.
Simulation results with an average model of the three-stage SST for the Future Renewable Electric Energy Delivery and Management (FREEDM) green hub system were presented in [270,344].
Reference [269] presented a SST average model that was validated by comparing results from those with the detailed switching model; see also [345,346].
Reference [347] proposed a SST average model aimed at analyzing the transient performance of a distribution network.
References [111] and [348] presented an average model of a bidirectional SST for feasibility studies and real-time implementation; several cases were studied to evaluate the behavior of the model under different operating conditions, check its feasibility for power quality improvements, and explore the implementation in a real-time simulation platform; see also [112,279].
Reference [349] presented a SST average model for studying renewable energy integration. A three-phase test system model including substation and loads was implemented in PSCAD.
Reference [261] proposed a model for transient stability studies; the dynamic model neglects high-frequency transients. To verify the accuracy of the proposed model, a comparison between results from such simplified dynamic model and a detailed model implemented in Matlab/Simulink were carried out; see also [350]. Reference [309] proposed a modular dynamic-phasor SST model for stability analysis; the model provided a significant reduction of simulation time. Reference [337] detailed the implementation of a SST model in Digsilent Power Factory; the model was based on the dynamic average technique and is compatible with LV-side three-phase, four-wire configuration.
The SST performance was analyzed in [351] by means of a 70th-order state-space model. The system model included renewable generation and storage systems and their corresponding interface circuits to DC and AC buses. The model was used to evaluate the performance of a distribution system under grid connected and islanded conditions.
Reference [331] presented a model of a MV/LV bidirectional SST. A multilevel converter configuration of the MV side is obtained by cascading a single-phase cell made of the series connection of an H bridge and a dual active bridge (DC/DC converter); the aim was to configure a realistic SST design suitable for MV levels. The SST model, including the corresponding controllers, was built and encapsulated as a custom-made model in the ATP version of the EMTP for application in distribution system studies [115,352].
Reference [117] presented a model of a bidirectional MV/LV SST for distribution system studies. A modular multilevel converter configuration is used in the MV side of the STT. The LV side uses a three-phase four-wire configuration that can be connected to both load and generation. The model developed was implemented in MATLAB/Simulink, and its behavior was tested by carrying out several case studies under different operating conditions.
Detailed dynamic analysis of buck-type SST under general load condition was presented in [353]; the study showed that under general inductive load condition, the open-loop system is marginally stable and serious output voltage oscillation can be provoked by any random disturbance upon input voltage, control signal or output current.
A SST model and its mapping to IEC 61850 was presented in [354].
A significant experience is also available on SST modeling for implementation in real-time simulation platforms. Reference [302] proposed an average model suitable for simulation with RTDS; the model was tested and validated by comparing its performance to that of detailed full switching model and a cycle-by-cycle average model built in Matlab and PLECS [305].
Reference [63] introduced the development of a platform intended as a distributed controller for grid intelligence system at FREEDM Systems Center. This platform can serve as a real-time local converter controller and a communication node for distributed deployment of energy management schemes. One device it controls is the SST, a key element to interface renewable energy sources to distribution systems in FREEDM Center. Both the hardware design and software structure for SST control were presented. The communication part used the Distributed Network Protocol 3.0.
Reference [340] proposed a new protection technique for SST; it was verified by hardware in the loop (HIL) testing.
Reference [95] proposed a platform based on the Xilinx Zynq®-7000 family to test SST performance; SST functions include: link to information and communication technologies, voltage transformation, integration of distributed renewable energy resources. The platform embedded a double-core ARM® Cortex™-A9 processor and Field Programmable Gates Array technology; all within a programmable system on a chip.
The implementation and simulation of the SST in either off-and on-line simulation platforms has been the subject of many works not listed in Table 2; see [126,178,355,356,357,358,359,360,361,362,363,364,365,366,367,368,369,370,371,372,373,374,375,376,377,378,379,380,381,382,383,384,
385,386,387,388,389,390,391,392,393,394,395,396,397,398,399,400,401,402,403,404,405,406,407,408,409,410,411,412,413,414,415].
6. Applications of the solid state transformer
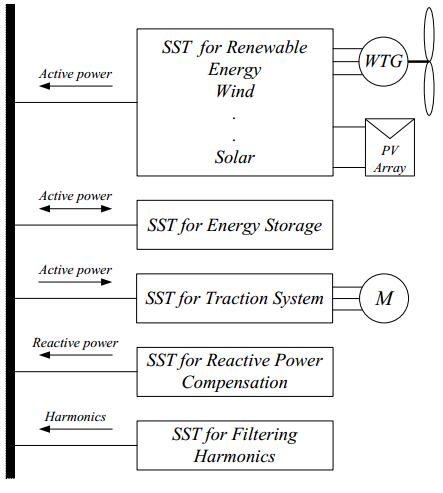
Future distribution grids will be characterized by a growing need for integration of renewable energy sources, energy storage devices and other smart grid technologies. The SST can perform as a universal interface for integrating distributed energy resources or as part of microgrids of any architecture. The potential applications of the SST have been analyzed in some references; see, for instance, [6,100,416,417,418,419]. In general, it is assumed that instead of using SST as a simple replacement of a conventional transformer, the SST will provide additional functionalities that could significantly improve power quality. Figure 4 schematizes some potential applications of the SST in a future distribution system. The SST might work as an interface of a DC-based fast charger (not shown in the figure), a traction system, a distributed energy source with or without energy storage capability [300], in microgrid architectures [420], or providing reactive power compensation and active harmonic filtering to any type of loads. A review of the SST applications proposed in the literature is provided in this section. The applications have been classified into three groups: the SST as a component of the distribution system, application in traction systems, and other applications (heating, lighting, smart house).
SST in the future grid: Reference [64] presented the next generation power distribution system architecture: the FREEDM system, which enables the plug-and-play of distributed renewable energy resources and storage devices. The FREEDM system is a highly attractive candidate for the future power distribution system; for more details, see references [67,71,292,421,422,423].
Reference [86] proposed the application of the SST in hybrid microgrids: converters use SiC-based semiconductors commercially available; high-frequency magnetic components are made of iron-based nanocrystalline soft magnetic material; the high-voltage grid interface adopts multilevel cascade structure; the isolated bidirectional DC/DC converter employs dual-phase-shift control to decrease circulating current and increase efficiency; the isolation unit is responsible to control voltage and power balancing to avoid control coupling. Experimental results were presented in [424].
References [425,426] studied the application of the SST as an energy router in future smart grids.
A three-port converter based on the Cuk topology was presented in [427]: the converter interfaces one unidirectional input power port (envisioned to be a DC power source such as PV or fuel cell) and two bidirectional output ports, representing respectively a grid-tied inverter DC bus and a storage system.
Reference [286] presented the SST as interface of hybrid DC and AC microgrid systems. Reference [75] proposed a three-phase MMC-based SST that can be link a DC systems and LV renewable energy systems. Reference [428] presented a SST topology based on a quad-active-bridge converter that can provide isolation for load, generation and storage; see also [288].
Reference [429] proposed the application to grid connected PV systems; see also [430]. Reference [313] proposed the SST as interface of a system that combined a PV array and a battery storage: since the power can flow from the network to the PV-battery side and vice versa, the battery can be charged from either the network or the PV array. Reference [431] presented the SST as interface in a PV-assisted charging station with an autonomous energy management strategy. For application of the SST as interface of PV systems, see also [297,430], and [432,433,434,435,436,437,438].
References [69,439] studied a SST-interfaced wind energy conversion system with integrated active power transfer, reactive power compensation and voltage conversion functions; the proposed configuration can effectively suppress the voltage fluctuation caused by the transient nature of wind energy without additional reactive power compensation. For the application of the SST in wind energy conversion systems, see also [98,298,322,440,441].
Reference [442] described the design and performance of a bidirectional isolated DC/DC converter using a 20 kHz HFT for a 53.2 V, 2 kWh lithium-ion battery energy storage system.
Reference [443] analyzed a flywheel energy storage system for wind farms fed from a DC system via a SST. The application of the SST in wind energy systems was also studied in [204,438,444,445]. For more details on the application of SSTs in microgrids, see references [66,116,173,326,341,446,447,448,449].
The application of the SST in distribution system has also been analyzed in [206,215,253,256,259,337,382,404,405,450,451,452,453,454,455,456,457,458,459,460,461,462,463,464,465,466].
SST application in traction: The constraints of weight and size on the traction transformer are becoming stronger with the new generation of trains, in which reliability and efficiency become very important. The SST is considered a viable solution for the replacement of bulky low-frequency transformers in railway systems operating at 16⅔ Hz. Reference [467] presented an overview of SST technology for traction applications. The multilevel converter proposed in [468] exhibited reduced weight and size, and an improved global life cycle cost; the proposed multilevel topology consisted of sixteen bidirectional direct current converters (cycloconverters), fed from a 15 kV/16.7 Hz catenary through a choke inductor and connected to sixteen medium frequency transformers (400 Hz) supplied by sixteen four-quadrant converters connected in parallel to a 1.8 kV DC link. For more information on the application of the SST in traction, see references [469,470,471,472].
Other applications: A single-stage bidirectional SST for induction heating applications was proposed in [60,473]: the SST can simultaneously track the maximum power point and improve the output power factor by using an adjustable switching frequency controller. Reference [474] presented a single-stage bidirectional SST for lighting: the system supplies multi-lamp units that are controlled simultaneously by the SST using a PWM scheme; the SST contains a single-input multi-output HFT that provides galvanic isolation in each unit; the design exhibits good efficiency, low weight and small volume, and allows operation without any bulky storage elements; the control strategy may achieve fluorescent lamps operation free from voltage flicker and disturbances, improving illumination, protecting lamps, and increasing lifetime of lamps.
Reference [314] proposed the combination of a bidirectional SST and a dynamic voltage restorer to correct voltage distortions on a sensitive load.
Reference [475] presented the application of a dynamic power limiter at the PCC of a microgrid; the limiter was a high-frequency isolated power-converter system comprised of a HFT and three-phase to single-phase matrix converters.
Reference [476] presented the SST potential in integrating sources and appliances at the domestic level. Reference [477] proposed a smart house fed from a microgrid-supplied SST.
7. Conclusion
The solid state transformer (SST) offers several benefits for future smart grids: DC and high-frequency AC power supply, enhanced power quality performance, fast voltage control, reactive power compensation, reactive power control at both primary and secondary sides. The SST can also provide operational benefits, such as an efficient management of distribution resources by incorporating on-line monitoring. In a few words, the SST can be seen as a universal interface that can provide power quality improvements, efficient management of distributed resources, and a link between systems operating at different power frequencies.
This paper has presented a bibliographical survey on the work carried out to date on design, testing, modelling, and potential applications of the SST. The number of references included in this paper confirms the interest in the SST and the foreseen benefits that this device can offer.
The paper has been organized taking into account the aspects mentioned above; the various sections has been dedicated to summary the work made on SST configurations and control strategies, design of the HFT to be used in the isolation stage, efficiency, modelling and validation, and SST applications.
The two tables included in the paper provide a selected list of prototypes and computer models implemented in different simulations tools, including real-time simulation platforms. The high number of both lab prototypes and computer models already built prove that the SST technology is becoming mature. Actually, some SST designs are already working; for instance, in traction systems.
The most challenging issue is the low SST efficiency: the high number of semiconductors needed for any multilevel configuration, the amount of semiconductor losses and the need of filters at both SST sides are three important factors that have impact on efficiency. Not much field experience is currently available with actual designs and real costs (including operation and maintenance costs).
Reliability is another aspect for which some work is required: the high number of semiconductors that are needed to build a multilevel configuration increase the probability of failure and losses. Redundant designs that could increase reliability would also increase losses and costs, and in turn reduce efficiency. For more details on this subject see [53,54].
Although the field experience does not yet suffice to decide about the most convenient SST configuration, it seems that those configurations based on a three-stage offer the best operational benefits in most power system applications.
Some studies show that with the present technology the volume, weight and manufacturing cost of a SST could exceed those of a traditional iron-and-copper transformer [478]. The usage of SiC-based technologies could provide a solution to all these drawbacks and permit smaller, lighter, more efficient, and cheaper designs.
Conflict of interest
The authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: