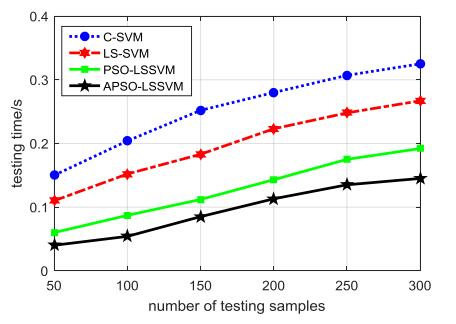
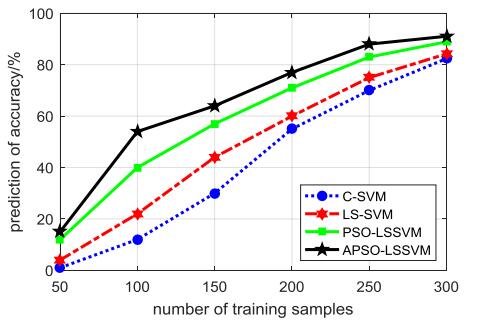
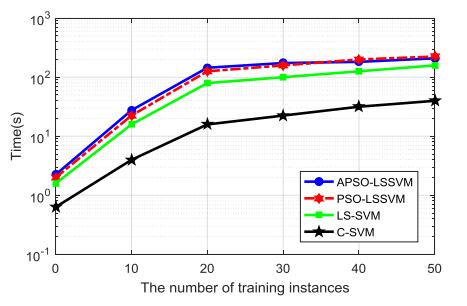
The problem of coal spontaneous combustion prediction is very complex, and there are many factors that affect the prediction results. In order to solve the issues of high dimension and redundancy among features and limited samples in the prediction of coal spontaneous combustion, this paper proposes a prediction algorithm of coal spontaneous combustion based on least squares support vector machine and adaptive particle swarm optimization (APSO-LSSVM). The adaptive PSO algorithm is used to solve the problems such as high computational complexity and slow calculation speed of the LS-SVM model for large-scale samples, so that it can always obtain the optimal solution, and its training speed and accuracy are improved. This method adjusts the inertia weight based on the convergence degree of group and the adaptive value of an individual for accelerating the training speed of swarm. After that, the improved PSO is used to iteratively solve the matrix equations in LS-SVM. APSO-LSSVM avoids the matrix inversion, saves the internal memory and obtains the optimum solution. The experiment results show that this method simplifies the training sample, accelerates the training speed, and also offers superior classification accuracy, fast convergence speed and good generalization ability.
1.
Introduction
Appropriate mathematical models of infectious diseases are helpful to reveal the mechanism of disease transmission and to predict the final scale of the epidemic [1]. The social contact network of a population plays a significant role in controlling the propagation of infectious diseases [2,3]. However, directly analyze the propagation of disease on stochastic contact networks is very difficult, one often relies on deterministic mean-field models that are aimed at approximating some average quantities derived from the stochastic models [4,5,6,7].
Based on the probability generating function for the degree distribution on a contact network, Volz introduced an edge-based SIR epidemic model, which has the great advantage of having a system with only three differential equations [8]. This method describes the SIR disease spread process with heterogeneous connectivity by the contact network structure. Its core is to track the change of the probability that the neighboring nodes around the susceptible nodes are infected. Furthermore, Miller derived a single differential equation with only a single higher order term that governs the dynamics of the disease [9]. Recently, using the EBCM approach for the spread of susceptible-infected-recovered (SIR) diseases in contact networks, Miller et al. [10] derived some simple ordinary differential equation models capturing social heterogeneity and heterogeneous contact rates while explicitly considering the impact of partnership duration. However, the theoretical analysis of such models is usually difficult, and their validity is usually demonstrated through numerical simulations. For an edge-based epidemic model with large initial value, Miller [11] obtained the threshold of disease transmission and the final infection size. Using the same method, in a recent paper[12], we established a sexually transmitted disease model on a bidirectional contact network with large initial value and analyzed in detail the global dynamics of the model. We refer the reader to references [13,15,14,16] and references therein for related works in this direction.
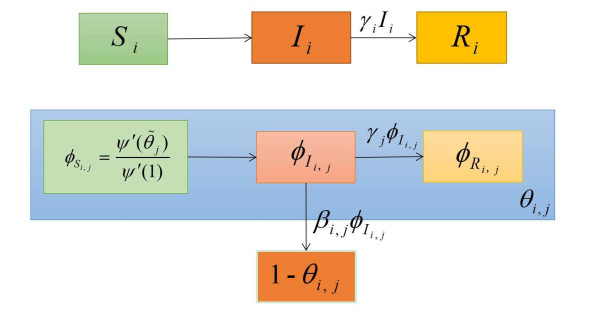
Vaccination in disease control strategies generally reduces the susceptibility of a node of network, but could either increase or decrease the infectiousness of a node by reducing the severity of symptoms. Modelling a disease with heterogeneous infectiousness and susceptibility in stochastic contact network can be seen in [17,18]. Using the EBCM technique, in a recent paper [19], Miller and Volz proposed an SIR model considering the heterogeneous susceptibility and infectiousness of individuals. Assume i is a parameter measuring a node's ability to become infected and cause infection, but that is does not influence the contact structure of the population. Without loss of generality, we assume that the population is divided into M types. The model proposed in [19] takes the following form:
with initial value θi,j(0)=1 and I(0)=R(0)=0, where ˜θj=∑Ml=1θj,lQ(l). The variables and parameters in model (1) are summarized in Table 1. For this model, the authors provided a numerical example to confirm its validity [19]. Here, we investigate the dynamics of the model (1) through mathematical analysis.
The organization of this paper is as follows. In the next section, we recall the derivation process of model (1), then we present our main results, including the derivation of the final size of an epidemic. In section 3, we provide the detailed proof of our main theorem. Finally, in section 4, we provide two simple scenarios for the special cases when M=1 and M=2 to make our results easier to understand.
2.
Derivation of model (1) and its global stability results
In this section, we recall the derivation process of model (1), then we present our main results.
2.1. Recalling the derivation process of model (1)
Assume the network structure is unchanged, that is the degree distribution P(k) of the network is fixed. The nodes of the network are classified into M types according to their ability to become infected and cause infection. Now randomly choose a test node u from the network, and assume that the probability it is of type i is Q(i), then ∑Mi=1Q(i)=1. It is easy to deduce the probability that the test node u is susceptible, infected or recovered. In fact,
where Si, Ii and Ri are respectively the probabilities that a type-i node is susceptible, infected and recovered at time t, and therefore
Let θi,j denote the probability that an edge from a type-j partner v to the test node u of type-i has not transmitted infection from v to u, and let ϕS:i,j be the probability v is still susceptible, ϕI:i,j the probability v is infected but the edge has not transmitted, and ϕR:i,j the probability that v has recovered without transmitting. Then θi,j=ϕS:i,j+ϕI:i,j+ϕR:i,j, and therefore,
Define ˜θi as the probability that a random edge to a type-i node u has not transmitted infection to u, then ˜θi=∑Mj=1θi,jQ(j), and therefore,
and
where ψ(x)=∑kP(k)xk is the probability generating function of degree distribution P(k). The transmission rate βi,j from a type-j node to a type-i node and the recovery rate γi of a type-i node are type dependent, and they are assumed to be positive. From the probability fluxes between Si, Ii and Ri compartments (upper) and those between ϕS:i,j, ϕI:i,j and ϕR:i.j (lower) as shown in Figure 1, we have that
We can derive from the last two equations in Eq (6) with initial value
that ϕRi,j=γjβi,j(1−θi,j). Combining Eqs (3) and (5) and the second equation of ϕR:i,j in Eq (6), we then derive system (7) from the last equation of θi,j in Eq (6) (see [19] for more details). Thus, the whole dynamics of the disease transmission are summarized by model (1).
2.2. Main results
Notice that the dynamics of model (1) is determined by the dynamics of the following subsystem:
where i,j=1,2,…,M. Define
Then Ω is a positive invariant set of system (7). We only need to consider the dynamics of system (7) constrained in Ω. Notice that system (7) always contains the disease free equilibrium E0=(1,1,…,1,1,…,1).
Let DθF(θ)=(DθFi,j)(θ) be the jacobian matrix of system (7), where
and denote
where DθF(E0) is the jacobian matrix DθF(θ) at E0. Our main result can be summarized in the following theorem.
Theorem 2.1. System (7) has at most two equilibria in the region Ω. Moreover,
(a) When ρ0<0, then the system has only the disease free equilibrium
which is globally asymptotically stable in Ω.
(b) When ρ0>0, then the disease free equilibrium E0 becomes unstable, and another outbreak equilibrium
appears which is globally asymptotically stable in the region Ω∖{E0}.
Remark 1. Based on Theorem Theorem 2.1, we know from model (1) that if ρ0>0, then after the epidemic is over, the fraction of individuals who have never been infected is
where ˜θ(∗)i=∑Mj=1θ(∗)i,jQ(j). Thus, the final size of an epidemic in the population is
3.
Proof of Theorem Theorem 2.1
We first introduce the following lemma which is used in the proof of our main theorem.
Lemma 3.1 ([20]). For system ddtx=F(x), let F(x) be a C1 cooperative vector field in Rn, whose flow ϕ preserves Rn+ for t≥0 and is irreducible in Rn+. Assume that the origin is an equilibrium and that all trajectories in Rn+ are bounded. Suppose the matrix-valued map DF: Rn→Rn×n is strictly antimonotone, in the sense that if x>y, then DF(x)<DF(y). Then either all trajectories in Rn+ tend to the origin, or else there is a unique equilibrium p∈Int Rn+ and all trajectories in Rn+∖{0} tend to p.
Proof. The jacobian matrix DθF(θ) of system (7) is
where i, j, l, m=1,2…,M, and when i=l,
when i≠l,
The off-diagonal elements of DθF(θ) are non-negative, and it is easy to check that DθF(θ) is strongly connected* when βi,j>0. Thus, system (7) is a irreducible cooperative system in Ω [20]. Consequently, when ρ0<0, the equilibrium E0 is locally asymptotically stable, and when ρ0>0, the equilibrium E0 is unstable.
*The definition of strongly connected and irreducible cooperative systems, refer to [20].
To prove the global results of system (7) in Ω applying Lemma 3.1, we make the coordinate transformation ϑi,j=1−θi,j, under which system (7) becomes
where i,j=1,2,⋯,M, and ˜ϑj=∑Ml=1(1−ϑj,l)Q(l)=1−∑Ml=1ϑj,lQ(l). Notice that Ω is still the positive invariant set of system (10), and the disease free equilibrium E0 is now transformed into the zero equilibrium E0 of system (10), where
Denote F(ϑ)=(F1,1,F1,2,⋯,F1,M,F2,1,⋯,FM,M)(ϑ). Noticing that F(ϑ)=−F(1M2−ϑ), we can deduce that
where DϑF(E0) is the jacobian matrix DϑF(ϑ) of system (10) at E0. Moreover, from Lemma 3.1 we know that E0 is locally asymptotically stable when ρ(DθF(E0))≤0, and unstable when ρ(Dθ(E0))>0.
We first consider the global stability results of system (10). Notice the following:
(a) System (10) is still an irreducible cooperative system in the bounded region Ω as
(b) DϑF(ϑ) is strictly antimonotone in Ω. Since ψ(˜θi) and ψ″(˜θi) are both monotone increasing functions with respect to θi,j in the bounded region Ω, and therefore both ψ(˜ϑi) and ψ″(˜ϑi) are monotone decreasing functions of ϑi,j in Ω due to the relationship ˜ϑi=1−∑Mj=1ϑi,jQ(j). By comparison, we can check that when ϑ1<ϑ2, we have DϑF(ϑ1)>DϑF(ϑ2).
According to Lemma 3.1, either all trajectories in Ω tend to the zero equilibrium E0 of system (10), or else there is a unique equilibrium
and all trajectories in Ω∖E0 tend to E∗. These, together with the local stability results of E0, indicates that when ρ0<0, E0 is globally asymptotically stable in Ω, and when ρ0>0, it becomes unstable and the equilibrium E∗ is globally asymptotically stable in Ω∖E0.
Now let E∗=1M2−E∗, then E∗∈Int Ω is the unique outbreak equilibrium of system (7). Based on the arguments above, we deduce that when ρ0<0, E0 is globally asymptotically stable in Ω, and when ρ0>0, it becomes unstable and the outbreak equilibrium E∗ is globally asymptotically stable in Ω∖E0. The proof of Theorem Theorem 2.1 is thus completed.
Remark 2. Theorem 2.1 provides a theoretical basis for the prevention and control of heterogeneous infectious and heterogeneous infectious diseases. For example, vaccination generally reduces the susceptibility of a node in community, then the population can be divided into those who have or have not received vaccination. The results of our analysis can be used to analyze the effectiveness of vaccination strategies.
4.
Two simple scenarios
Scenario 4.1. In the special case when M=1, i.e., there is only one type of node in contact network, system (7) is reduced to the model established in Miller [9]:
Here E0=(1) and ρ0=−(β1,1+γ1)+β1,1ψ″(1)ψ′(1). Moreover, ρ0=0 can be equivalently written as β1,1(β1,1+γ1)ψ″(1)ψ′(1)=1. Define
Then R0 is the basic reproduction number of the disease. Notice that R0≤1 if and only if ρ0≤0. We have the following result.
Corollary 1. System (11) has at most two equilibria in the region
Moreover,
(a) When R0≤1, then the system has only the disease free equilibrium E0 which is globally asymptotically stable in Ω.
(b) When R0>1, then the disease free equilibrium E0 is unstable, and the outbreak equilibrium E∗=(θ(∗)1,1)∈IntΩ appears and it is globally asymptotically stable in the region Ω∖{E0}={θ1,1:0≤θ1,1<1}.
Proof. We only need to prove that when R0=1 (i.e., ρ0=0), E0=(1)1×1 is globally asymptotically stable. In fact, denote
We compute that
for θ1,1∈[0,1) due to ρ0=0. Thus, F1,1(θ1,1) is strictly monotonically decreasing on the interval [0,1] with F1,1(1)=0 and therefore E0=(1) is the unique equilibrium of system (11). It then follows from dθ1,1dt>0 that for any solution with initial value θ1,1(0)∈[0,1), E0 is globally asymptotically stable in Ω=[0,1]. The proof is thus completed.
Scenario 4.2. In the special case when M=2, i.e., there have two difference type of node in contact network, system (7) takes the form:
Here E0=(1,1,1,1). The jacobian matrix DθF(θ) of system (13) at E0 is
where △i,i(1)=(βi,i+γi)−βi,iψ″(1)ψ′(1)Q(i), i=1,2. Define ρ0 as in Eq (8). We have the following result.
Corollary 2. System (7) has at most two equilibria in the region
Moreover,
(a) When ρ0<0, then the system has only the disease free equilibrium E0 which is globally asymptotically stable in Ω.
(b) When ρ0>0, then the disease free equilibrium E0 is unstable, and the outbreak equilibrium
appears and it is globally asymptotically stable in the region Ω∖{E0}.
Remark 3. From Scenario 1 we know that for the special case when M=1, the disease free equilibrium E0=(1) is globally asymptotically stable (GAS) when ρ0=0 (i.e., R0=1), but we can not prove that a similar result holds for the special case when M=2. We guess the disease free equilibrium E0 of model (1) is also GAS for all M≠1. We leave it as an open problem.
5.
Discussions and conclusions
Considering the fact that the individuals may have different susceptibility and infectiousness to the disease spreading in the population, in a recent paper [19], Miller and Volz proposed an SIR disease network model (i.e., model (1)) with heterogeneous infectiousness and susceptibility. The authors have provided a numerical example to demonstrate its validity but its mathematical analysis remain unsolved. In this paper, with the aid of the nature of irreducible cooperative system in the theory of monotonic dynamical system, we prove that the dynamics of the model are completely determined by a critical value ρ0: When ρ0>0, the disease persists in a globally stable outbreak equilibrium; while when ρ0<0, the disease dies out in the population and the disease free equilibrium is globally stable.
Notice that it is assumed that in model (1) the random network considered is statically fixed and does not take into account the influence of new nodes, deleted nodes and other factors on the network. This is an approximation of the reality. More proper and reasonable model should consider these facts and be based on dynamic random networks. Moreover, how to characterize the epidemic process of heterogeneous infectious networks through numerical simulation is also a challenging problem. We leave all these for our future consideration.
Acknowledgments
Research is supported by the National Natural Science Foundation of China (No. 11671260).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: