1. Introduction
Lipids and proteins contribute to the formation of the aromas and flavours of coffee beverages [1,2]. Lipids are responsible for flavour retention, and they influence the stability of foam in the beverage [1,3]. Lipids are also known to have a taste and aroma trapping volatile compounds within the foam layer [4]. Proteins are important precursors of aromas and flavours of the beverage due to reactions with sugars during roasting. Lipids and proteins are influenced by growing conditions, and negative correlations with accumulation in coffee beans have been observed between them [5,6,7]. Lipids are found in amounts ranging from 10 to 15% in coffee, of which 75% are triglycerides and 20% are esters of fatty acids diterpenics. Cafestol, kahweol, and 16-O-methyl cafestol in free form (16-OMC) are the primary diterpenes found in coffee oil [8]. Diterpenes have been the subject of many studies, especially those characterizing relationships to human health. Desirable [9,10,11,12,13] and adverse effects [14] have been reported.
Agronomic factors (genetic origin, types and levels of fertilization), environmental conditions (altitude, temperature, hydric demand), harvesting and post harvesting conditions, and processing methods (roasting and storage) can influence the composition of coffees [15,16,17,18] as well as diterpenes content.
Differences in kahweol, cafestol and 16-OMC levels were observed among several species of coffee [8,19] and have become an important tool to discriminate coffee species. More recently, studies conducted by Kitzberger et al. [20] and Kitzberger et al. [21] showed differences in diterpene content in pure Arabica coffees and Arabica coffees and arabica coffees with Coffea canephora introgressions grown in standard soil and climate conditions.
A genetic population from the centre of origin (Ethiopian C. arabica collection) and modern cultivars showed cafestol values ranging from 182.62 g to 1308.62 mg 100g−1 and kahweol values ranging from 182.69 to 1265.41 mg 100g−1. These variations in cafestol and kahweol levels can be attributed to the genetic diversity of Ethiopian accessions [22].
The amino acids and proteins found in green coffee beans are known to be precursors of many important aroma compounds found in roasted coffee. Green coffee storage proteins, the 11S storage protein in particular, account for 45% of the total protein content of green coffee beans and represent an important reservoir for free amino acids and peptides [23,24,25,26].
During the roasting process, pyrolytic reactions take place and lead to the formation of particular volatile and semi-volatile aroma compounds responsible for the sensory qualities of roasted coffee [27]. These complex reactions may be attributed to both Maillard and Strecker reactions and the degradation of proteins, polysaccharides, trigonelline, and chlorogenic acids [28]. Furthermore, this process seems to be preceded by intensive interactions between nitrogenous compounds and phenolic compounds (mainly CQAs) during the roasting process [24]. In this sense, the crude protein content (CPC) of green coffee beans may constitute important information when deciding the best roasting conditions and blend composition [26]. The protein content of coffee beans is relatively high, representing 8.7-12.2% of the coffee bean dry weight, based on crude nitrogen and corrected for non-protein nitrogenous components. After roasting coffee beans at different temperatures, the protein content decreases. Only 13% of the roasted coffee protein is extracted into the brewed coffee. This can be explained by the denaturation of protein, reduced water solubility, and chemical reactions during roasting [29].
The phenological cycle of coffee plants presents a succession of the vegetative and reproductive stage spread over two years. After the development of the vegetative branches in the previous year, flowering occurs during the next spring, and then the second phenological year begins. During this period, the pollinated flowers form pinheads that expand gradually until approximately 120 days after pollination. At the end of the process, the grains reach their normal size and fruit maturation begins. The availability of water and the temperature during this period must be adequate for the complete development of beans and to facilitate the accumulation of the main precursors of aromas and flavours of the beverage [30].
The phenological cycle frequently results in biannual yields. Vegetative branches and a proper foliar biomass results in a large number of flowers and fruits but lowers the development of new branches with a consequently lower production for the next year. Despite this important biannual behaviour, several studies on the characterization of coffee compounds are performed for only one year of harvest or do not have control of the exact edapho-climatic conditions of coffee cultivation.
To study the stability of some compounds of interest during this cycle biannual phenological discloses compounds, which can be used as molecular markers specific for the different crosses, employed in coffee. These molecular markers are linked to quality coffee beverage as well as the functionality of this beverage such as proteins and lipids for quality and functionality for the diterpenes.
In the past few years, the Agronomic Institute of Paraná (IAPAR) has developed new cultivars with better characteristic for plant architecture, plant vigour, different ripening periods, resistance to pests and diseases, and adaptation to different conditions of temperature and soil fertility. These modern C. arabica crosses, with introgressions of C. canephora, could likely be influenced the content of chemical compounds in coffee beans [31].
Therefore, due the importance of the genetic and edapho-climatic factors on chemical compounds and production, as well as the phenological biannual behaviour of coffee plants, the aim of this study was to evaluate the profile of cafestol, kahweol, lipids and proteins from coffee cultivars with different genetic background grown in the same edapho-climatic conditions during three consecutive years.
2. Material and methods
2.1. Raw material and experimental conditions
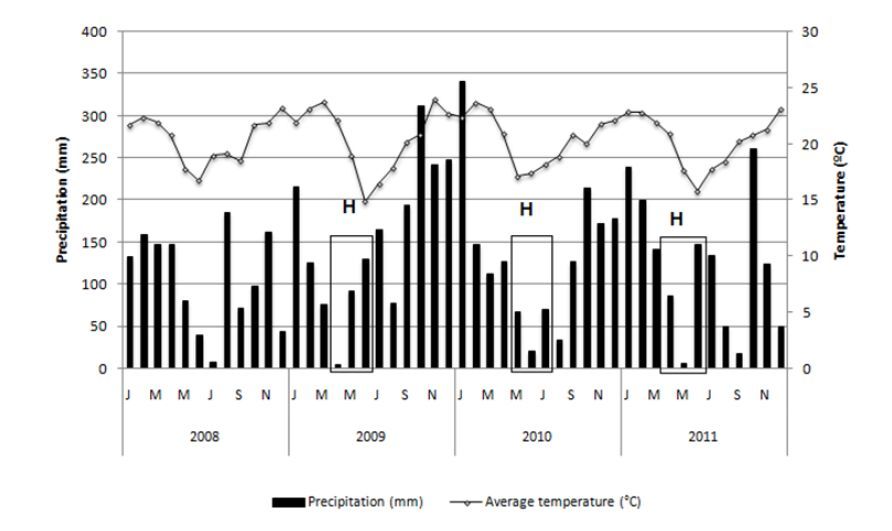
Arabica coffee beans were collected from plants growing in Mandaguari PR, Brazil at the Agriculture Technologic Park of Coop COCARI, located at latitude 23°32'52" (South), with an altitude of 650 m and an average annual temperature of 22-23 °C. Conditions suitable for coffee culture usually predominate in these locations [32]. The mean values of temperature and precipitation during the period of the experiments are described in Table 1 and Figure 1. The mean values are for the periods of the phenological cycle of coffee from flowering to harvest, i.e., from September to August.
Table 1. The average values of temperature and precipitation for the experimental period
| Harvests
|
Average Temperature ( °C)
|
Precipitation (mm)
|
| Set2008/set2009
|
20.38
|
|
1463.6
|
|
| Out2009/set2010
|
20.82
|
|
1858.4
|
|
| Out2010/set2011
|
20.18
|
|
1595.8
|
|
In the harvest years (2009, 2010 and 2011), there were adequate conditions of pluviometric precipitation and a gradual increase of temperature in the period of the first phase of the coffee phenological cycle (spring of the year before the harvest). Although different levels of precipitation during the phenological cycle of each year were observed, the conditions at the period of development for the beans (October to March) were favourable for the complete formation of the fruits (Figure 1 and Table 1). Lower pluviometric precipitation occurred when the fruits were already in the final phase of the cycle (May to June) and were dried, ripened fruit. This pluviometric precipitation in this last phase of the phenological cycle in the years of the experiment was suitable for fast drying of the fruit (Figure 1 and Table 1).
Thirteen cultivars from the IAPAR coffee-breeding programme were studied. The genetic backgrounds of the cultivars are described in Table 2.
Table 2. Genetic backgrounds of the cultivars studied
| Genotype
|
Breeding
|
| Iapar 59, IPR 97, IPR 98, IPR 99 and IPR 104
|
Timor Hybrid × Villa Sarchi (Sarchimor)
|
| IPR 100, IPR 101, IPR 105
|
Catuaí Sh2Sh3
|
| IPR 102
|
Catuaí and Icatu derived
|
| IPR 103
|
Red Catuaí IAC 99 and Yellow IAC 66 × Icatu
|
| IPR 106
|
Icatu genetic background
|
| IPR 107
|
IAPAR 59 (Sarchimor) × Mundo Novo
|
| IPR 108
|
IAPAR 59 (Sarchimor) × IcatuCatuaí
|
| Reference: [31]. |
Fruits were harvested from May to July in each year (2009, 2010 and 2011) according to the periods when the fruits cultivars were mostly ripe (70-80% total fruits). Cherry fruits were manually selected, washed and sun-dried on a “patio”. The coffee beans were processed (husk and parchment removal) and standardized in grade 16-sized sieves (6.5 mm); all defective beans were removed [33].
The coffee beans were frozen using liquid nitrogen to prevent oxidation of compounds in the matrix and ground (0.5 mm particles) in a disk mill (PERTEN 3600, Kungens Kurva, Sweden) [34]. The milled samples were stored in plastic bags and kept in a freezer (−18 °C) until analysis.
The moisture content (oven set at 105 °C to constant weight) was also determined to express the results in terms of dry weight.
The diterpenes cafestol and kahweol were analysed by direct extraction using saponification and clean up in methyl tert-butyl ether and water [34]. The extracts were identified and quantified by HPLC at 220 and 290 nm as cafestol and kahweol, respectively. A reversed-phase Spherisorb ODS 1 column (250 mm × 4.6 mm id 5 mm) (Waters, Milford, USA) and a acetonitrile:water (55:45) mobile phase were used to separate the compounds. Quantification was carried out by external standardization, generating calibration curves with cafestol and kahweol concentrations between 50 and 1000 mg 100g−1 (six different concentrations in triplicate).
To determine the protein and lipid content of ground green coffee beans, the methods described in the Association of Official Analytical Chemists [35] were employed. The protein content was determined by the Kjeldahl method, after digestion of the organic matter with sulfuric acid, the protein concentration was obtained by multiplying the value of the nitrogen by a factor of 6.25. The lipids were solvent extracted (petroleum ether) over 16 h with heating (45-50 °C) [35,36].
ANOVA, considering the genotype and harvests as the sources of variation, Tukey’s test (p > 0.05) and component principal analysis a multivariate analysis was employed for analysis of the data using the statistical software XLStat version 2008.4.02 [37].
3. Results and Discussion
The cafestol, kahweol, lipid and protein content in cultivars with different genetic backgrounds showed great variability [12,20,21]. The compositions of the coffee produced from 13 cultivars in three consecutive harvests are shown in Table 3.
Table 3. Mean values, minimum and maximum, standard deviation and coefficient of variance (CV) of cafestol, kahweol, lipids, proteins, kahweol/cafestol relationship and the sum of the diterpenes in 13 harvested cultivars over three years at a single location
| Variable
|
Minimum
|
Maximum
|
Means
|
Standard deviation
|
CV%
|
| Cafestol (mg 100g−1)
|
221.20
|
607.08
|
380.75
|
93.58
|
24.58
|
| Kahweol (mg 100g−1)
|
500.60
|
1082.74
|
843.19
|
143.33
|
17.00
|
| Kah/caf
|
0.82
|
3.88
|
2.36
|
0.70
|
29.68
|
| Sum of the diterpenes (mg 100g−1)
|
894.01
|
1610.07
|
1223.95
|
152.87
|
12.49
|
| Lipids (g 100g−1)
|
11.23
|
16.29
|
13.86
|
1.24
|
8.98
|
| Proteins (g 100g−1)
|
13.56
|
18.06
|
15.76
|
1.30
|
8.24
|
A global analysis shows a broad range of values for cafestol content. Some introgressed cultivars showed higher values than pure arabica cultivars such as Bourbon (476 mg 100g−1) and Catuaí (604 mg 100g−1), as previously reported [21]. Others cultivars had low values, similar to the values found for other species, such as C. liberica and C. canephora (273 and 239 mg 100g−1, respectively) [19].
The kahweol values for the IPR cultivars were also variable and higher than those observed in pure arabica cultivar. Previous studies showed kahweol values of 313 and 371 mg 100g−1 for Bourbon and Catuaí, respectively [21].
On the other hand, protein and lipid values showed low variability (Table 3), and the values were similar to those found for the other cultivars in different locations. A range of 14.5 to 17 g 100g−1 and 10.8 to 15.2 g 100g−1 for proteins and lipids, respectively, as found by several authors [38,39,40].
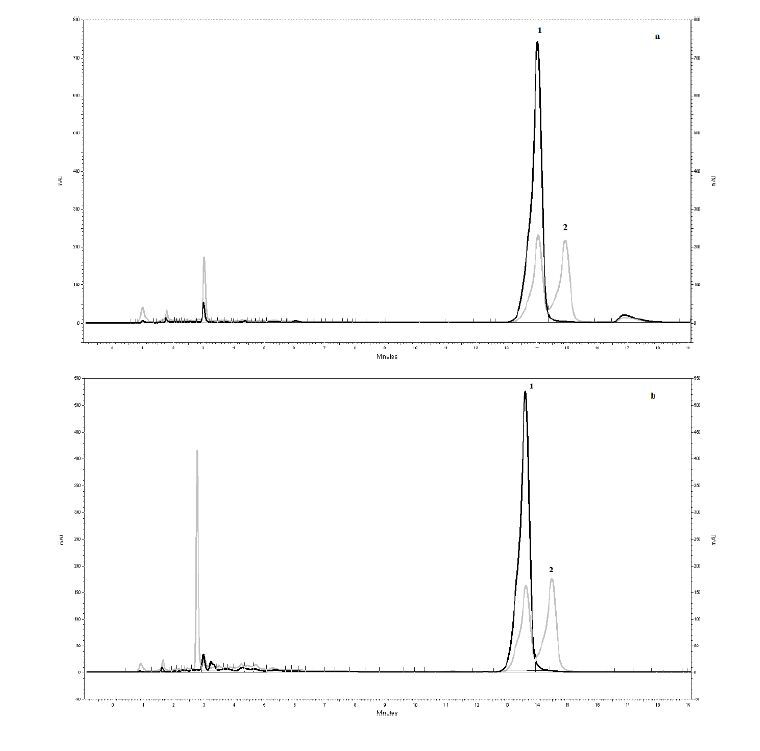
The sum of diterpene levels showed a narrow range of values, although a great degree of variability has been observed for the levels of cafestol and kahweol among cultivars (Table 3), and a typical chromatogram is shown in Figure 2. The proportion of kahweol and cafestol, indicated by the ratio kah/caf, evidences the different profiles of these compounds in these cultivars. This variability provides different combinations of kahweol and cafestol in cultivars. These different combinations of diterpenes allow for the selection of cultivars that have higher kahweol and lower cafestol values, which are believed to be most suitable to human health.
The correlations between the compounds showed a significant and positive relationship between cafestol and lipid (r = 0.28) and a negative correlation between proteins and lipids (−0.46) and between protein and cafestol (−0.39). These observations show the importance of controlling for factors that alter the levels of proteins and lipids, which negatively influence the cafestol content.
The environmental effect and stability of these compounds was evaluated for these three harvested. ANOVA indicates that despite the variability of chemical composition observed among the cultivars (Table 3), only kahweol content and ratio kah/caf showed significant differences among the cultivars. Significant difference in the kah/caf ratio, lipid and protein content was observed for the crop years examined.
The environmental conditions observed during the three years of this study promoted changes in the composition of some cultivars, which showed differences between the years of cultivation. However, no significant interaction between “cultivar × year” was observed, thus the changes in cultivars were not sufficient to show a significant interaction between year and cultivar. Those results are important because shows that the value of these compounds in cultivars was not crop year dependent.
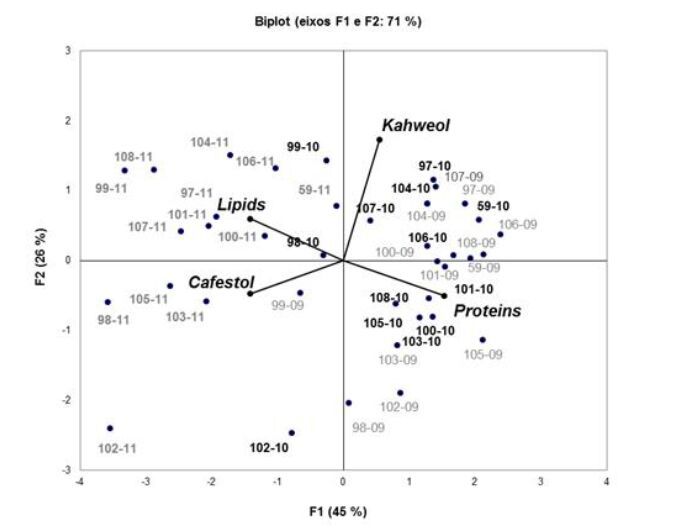
In principal component analysis (PCA), cultivars are evaluated under a multivariate vision, allowing for an understanding of the relationship between variables and the relationship of the cultivars among themselves and with the variables. In our work, the first two components (F1 and F2) accounted for a high percentage of the total variation among the cultivars: 45 and 26% of variability found among the samples, respectively. The two principal components of the cultivars for the crop years were plotted on biplots (Figure 3). The production years were differentiated mainly by F1, whereas the cultivars were more differentiated by F2. The separation between crop years can be seen in the horizontal direction due to the variability of these compounds between cultivars in crops of different years. The coffee cultivars from the harvests of 2009 and 2010 are grouped on the right, primarily due to high protein levels (F1+). On the other hand, the harvested 2011 cultivars fell onto the left side and are separated due to the high lipid content and cafestol (F1−).
It is still possible to note that the cultivars separated by F1 are spread on the biplot by F2, mainly due to the kahweol content. Cultivars IPR 102, IPR 103 and IPR 105 during the three years of crops and cultivars IPR 98 (2009 and 2011) and IPR 101 (2009 and 2010) were located at the bottom of the biplot as a consequence of the low levels of kahweol.
Located at the top of the biplot are the cultivars containing high kahweol content. The cultivars showed different behaviours among the three crops: the cultivars IPR 97, IPR 104, IPR 106, IPR 107 and the Iapar 59 are plotted nearby, in the three years of harvest, suggesting stable composition in these three crops. Other cultivars, for example, IPR 99 (2010 and 2011), IPR 100 (2009 and 2011) and IPR 108 (2009 and 2011), had similar compositions in at least two crops. From a genetic point of view, it is possible to note that most cultivars with C. canephora introgression from the Sarchimor crosses (Timor Hybrid × Villa Sarchi) showed high kahweol content. The exceptions to this rule were the cultivars IPR 100 and IPR 106 with a genetic basis of Catuaí Sh2 Sh3 and Icatu, respectively, which also had relatively high kahweol values, and IPR 98 that despite the Sarchimor background, had low kahweol values. Moreover, cultivars with various genetic backgrounds, IPR 101 and IPR 105 (Catuaí Sh2 Sh3), IPR 102 (Catuaí × Icatu) and IPR 103 (Yellow Catuaí × Red Catuaí × Icatu), presented low values of kahweol.
The different responses to the environment and the composition of these cultivars demonstrated that kahweol content seemed to be more stable for certain cultivars in crops during the three years and presented a wide variability in values among cultivars (Table 4). On the other hand, the cafestol (factor loading = F1 = −0.73), lipid (F1 = −0.73) and protein content (F1 = 0.80) were more influenced by years of growing, and forming the F1 was mainly responsible for the separation of these crops.
Table 4. ANOVA for cafestol, kahweol, kah/caf ration, total diterpenes, lipids and proteins
| Source
|
|
Cafestol
|
Kahweol
|
Kah/caf
|
Total diterpenes
|
Lipids
|
Proteins
|
| Cultivars
|
F
|
5.787
|
971.561
|
1413.267
|
23.400
|
16.796
|
7.07
|
|
p
|
0.315
|
0.025
|
0.021
|
0.160
|
0.189
|
0.287
|
| Year
|
F
|
24.587
|
111.873
|
3365.710
|
29.584
|
265.691
|
214.968
|
|
p
|
0.141
|
0.067
|
0.012
|
0.129
|
0.043
|
0.048
|
| Cultivars × Year
|
F
|
1.180
|
167.060
|
120.514
|
8.303
|
6.957
|
1.435
|
|
p
|
0.634
|
0.061
|
0.072
|
0.268
|
0.292
|
0.588
|
| Significant p values are in bold numbers. |
It was also possible to note that the cultivars containing genes from the Coffea canephora species, especially from Sarchimor, showed the highest overall levels of kahweol. This fact is interesting because several studies reported that kahweol is present in small quantities, or even absent, in C. canephora [12,19].
The collection of IPRs cultivars also showed stability in the content of diterpenes, i.e., low cafestol and high kahweol content in the three harvests evaluated. These coffees are particularly interesting from a health point of view since several studies have noted the benefits of kahweol for health and the hypercholesterolemic action of cafestol [41]. Cultivars with this genetic background would be an alternative for beverage consumption without worrying about the unwanted hypercholesterolemic action regardless of the coffee beverage preparation.
4. Conclusions
The collection of IPRs cultivars showed high variability of diterpene content and low variability for lipid and protein content. The levels of these compounds were stable throughout the three-year study period. There was a positive and significant correlation between lipids and cafestol and negative correlations between lipids and proteins. The genetic crosses obtained by introgression of C. canephora genes presented high kahweol content and low cafestol values in the three harvests. In addition, the relationship between cultivars and harvests, as shown in PCA, indicated that cafestol, protein and lipid content were primarily responsible for the differentiation of cultivars during the three years. In contrast, the kahweol content remained stable during the three years of cultivation for most cultivars and is more associated with the genetic origin than the environmental conditions. Due to this possible stability of kahweol in different harvests, we propose the study of this compound as a molecular marker between different crosses. Finally, our results allow choosing cultivars more suitable for production of beverages with health benefits based on the diterpene profiles.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: