1. Introduction
Water is crucial for sustaining life on the earth. However, the ongoing uses making it contaminated, resulting in the production of a large amount of wastewater. Wastewater encompasses liquid wastes discharged from domestic residences, commercial properties, industry, and/or agricultural activities and can contain a wide range of potential contaminants. In the most common usage, it refers to the municipal wastewater that contains a broad spectrum of contaminants resulting from the mixing of wastewaters from different sources [1]. Based on the different factors (for example, socio-economic, water usage, the degree of infiltration, nature, and magnitude of industrial content etc.) municipal wastewaters cannot be considered as a unique group of effluents [2]. However, the main component of wastewater is water (about 99.9%) and the rest are suspended and dissolved organic solids (carbohydrates, lignin, fats, soaps, synthetic detergents, synthetic organic chemicals from the process industries), inorganic solids including metals and also pathogenic viruses and bacteria [3]. These pollutants could exhibit toxic effects on aquatic life and the public leading to a less suitable environment, poor health, a less flourishing economy, and ultimately, a poor quality of life [4]. Therefore, it is necessary to know details about different physico-chemical properties such as temperature, pH, electrical conductivity, dissolved oxygen (DO), biochemical oxygen demand (BOD), chemical oxygen demand (COD), total solids (TS), total suspended solids (TSS), and total dissolved solids (TDS) which are used for evaluating wastewater quality.
Although waste management strategies adopted in Bangladesh, it has failed to keep pace with the industrial growth and urbanization. Several studies have documented in Bangladesh on physico-chemical properties of wastewater.
Recently, Ali et al. [5] have investigated physico-chemical properties of wastewater from industries in Chittagong whereas; Hasan et al. [3] have investigated sewage wastewater for physico-chemical parameters in Pagla sewage plant, Dhaka. In addition, physico-chemical properties and heavy metals in industrial wastewater from Kushtia industrial area [6], physico-chemical parameters of tannery effluent in Dhaka [7], effluents of leather industries in Hazaribagh area of Dhaka city [8], and effects of physico-chemical properties of textile dyeing effluents on the surface water quality in the Dhaka-Narayanganj-Demra industrial area [9] have been studied in Bangladesh. Furthermore, a review study on textile wastewater in Bangladesh during 2005–2014 has been documented [10].
In Bangladesh, there is a little study on wastewater comprising a large study area. It may be due to the high population density and high industrial activities. The studies investigated only the quality of wastewater and simply compared with the standard values. Nevertheless, the source of physico-chemical parameters has investigated there is a lack of statistical analysis. At the same time, most of the studies in this field have focused on big cities and industrial areas rather than sub-urban and residential areas.
Therefore, the objectives of this research were aimed to determine the physico-chemical characteristics of municipal wastewater effluent from five sewage points of Jhenaidah town (a sub-urban area) and to investigate the correlation among them using Pearson's correlation analysis.
2. Materials and methods
2.1. Study area
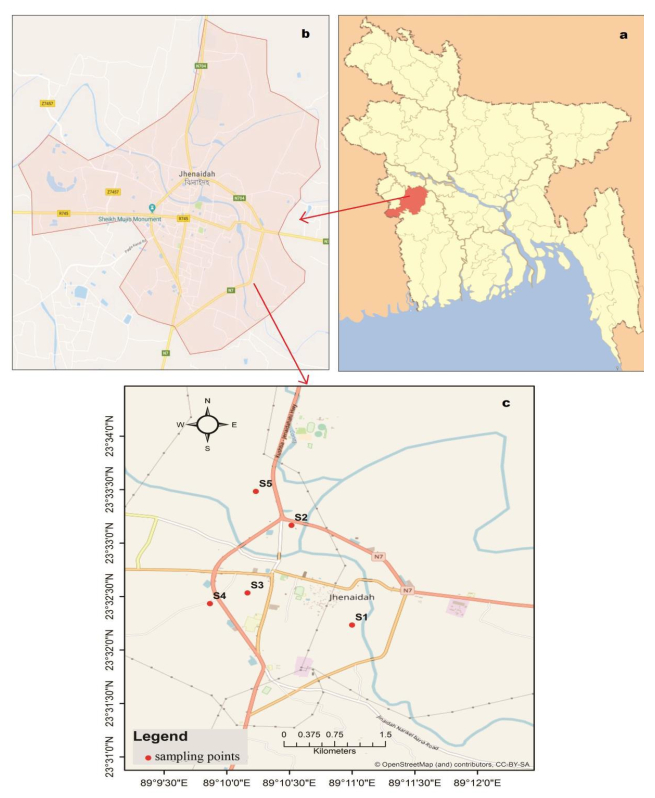
The wastewater samples were collected from the municipality areas of Jhenaidah district, which is situated in the southwestern part of Bangladesh under Khulna division. The district geographically is situated between latitudes of 23˚15'N to 23˚45'N and between longitude of 88˚45'E to 89˚15'N. The district is bordered by Kushtia district to the north, Jessore and 24 Parganah of West Bengal (India) to the south, Magura and partly of Rajbari district to the east, Chuadanga and 24 Parganah of West Bengal (India) to the west. The sampling locations and study areas are indicated in Figure 1.
2.2. Collection of samples
The experimental method involved the collection of raw samples in clean plastic high density polyethylene (HDPE) containers of 3 liters capacity at five different locations inlet chamber, drainage, and sewage line. Samples were collected from the depth of 6 inches below the water surface in a thoroughly cleaned HDPE container of 3 liters capacity of each provided with the cap in February 2016. A total of 70 samples were collected in the morning and evening time for seven consecutive days. The collected samples were homogenized for each location. Prior to collecting samples, the containers were cleaned by 25% (w/v) HNO3 and rinsed several times with distilled water. The preservation procedure includes keeping the samples in the dark, adding a chemical preservative, lowering the temperature to retard reactions or combinations of these.
2.3. Physico-Chemical analysis
The physico-chemical analysis was implemented according to the standard methods of analysis of each parameter. Each of them is described below in details.
pH of the wastewater samples was measured using a digital pH meter (model BT-600, BOECO, Germany) whereas, Electrical Conductivity (EC) was measured using an electrical conductivity meter (CM-230). Standard procedures were maintained to avoid false reading and contamination. pH and EC were measured during collection of samples at each sampling points.
The total solids (mg/L) of the samples were determined as described by Punmia and Jain [11]. In brief, a cleaned dish was taken and ignited to constant weight (W1) on which 25 mL of well-mixed sample was transferred. Then the sample evaporated to dryness at 103 ℃ for 24 hours, in a constant temperature oven. After cooling the dish in a desiccator the weight was determined (W2). Then total solids content was calculated as follows:
|
TotalSolid(TS)=W2−W1V×40
|
(1)
|
Where V is the volume of the sample.
In addition, the total suspended solids (mg/L) were determined according to the method described by Punmia and Jain [11]. In brief, a cleaned crucible with filter paper was ignited to constant weight in an electric oven (W1). Then 25 mL sample was taken and filtered through the crucible. After that, the crucible was dried in an oven at 103 ℃ for 24 hours; cooled in a dedicator and weighed out (W2). The total suspended solids were then calculated using the following formula:
|
TotalSuspendedSolids(TSS)=W2−W1V×40
|
(2)
|
Another physical parameter; the total dissolved solids (mg/L) were determined by evaporating the waste samples to dryness [12]. In this method, 50 mL of sample were transferred to a weighed evaporating dish and evaporated to dryness by heating for 1–2 hours at 180 ℃ to a constant weight. Total dissolved solids were calculated as follows:
|
TotalDissolvedSolids(TDS)=mgofresiduemLofsample×1000
|
(3)
|
COD was measured using to the American Public Health Association (APHA) standard closed reflux titrimetric method [13]. Potassium dichromate (0.01667M K2Cr2O7) and sulphuric acid (98% H2SO4) solution was added to water sample taken in culture tube. Then it was refluxed for two hours at 150 ℃. The digested solution was transferred to conical flask to cool at room temperature and titrated with ferrous ammonium sulphate (FAS) solution (0.025M) using 2 drops ferroin indicator until color changed from blue-green to radish-brown.
|
CODasmgofO2/L=(A−B)×M×8000mLofsample
|
(4)
|
Here, A = mL of FAS used for blank; B = mL of FAS used for sample; M = Molarity of FAS; 8000 = milliequivalent weight of oxygen × 1000 mL/L.
BOD was determined by 5-day testing method according to the APHA standard method [13]. In brief, two 100 mL bottles were obtained with lid and cleaned thoroughly with distilled water. Then, 25 mL sample was taken in each bottle and distilled water was added into each bottle to make the total volume 100 mL. Then the two bottles were closed tight enough with the lid. 10 mL of manganese sulfate (MnSO4) solution and 2 mL of alkali-azide solution were added into the both bottle. Then the bottle was closed and mixed properly by inverting the bottle several times. When the precipitate settled down leaving a clear supernatant above the precipitate, it was agitated again slowly by inverting the bottle as described above. When the settling had completed, 8 mL of concentrated phosphoric acid was added into the suspension. The bottle was closed and mixed by gentle inversion until dissolution was completed. Finally, 100 mL of the aqueous sample was taken into a conical flask and titrated with 0.05 M Na2S2O3 solution until a pale yellow solution is reached. After that, 2 mL of freshly prepared starch solution was added into the conical flask and titration was continued until a blue color appeared. At the same time, one sample was kept at 20 ℃ in an incubator for 5 days containing MnSO4, alkali-azide and phosphoric acid solution. After 5 day, the same method was followed for the 5 day incubated samples. Blank titration was carried out using distilled water instead of wastewater. BOD5d (at 20 ºC) was calculated using the following equation:
|
BOD5dasmgofO2/L=16(V1−V2)
|
(5)
|
Where V1 = mL of Na2S2O3 used for the sample before incubation (at day 1); V2 = mL of Na2S2O3 used for the sample after 5 day incubation (at 5 day).
Calcium hardness was determined through adding 1 mL of 1N NaOH solution and 0.1 mg of murexide P indicator into 50 ml of the water sample and finally titrated with standard 0.02N EDTA solution until the red color of the solution turned to purple. Calcium hardness was calculated from the equation:
|
HardnessasCaCO3=BurettereadingSampletakeninmL×1000
|
(6)
|
2.4. Data analysis
Descriptive statistics and Pearson correlation coefficient (p-value of < 0.05 was considered to indicate statistical significance were performed using the open source statistical software R (Version 3.4.3).
3. Results and discussion
3.1. Physico-chemical parameters
The physico-chemical parameters of the wastewater in the Jhenaidah municipality area have been summarized in Table 1.
Table 1. Descriptive statistics of physio-chemical parameters of wastewater from Jhenaidah municipality area.
| Parameters |
Units |
Minimum |
Maximum |
Mean |
Standard Deviation |
Standard Value [14] |
| pH |
- |
6.72 |
7.60 |
7.17 |
0.32 |
6–9 |
| EC |
S/cm |
0.0015 |
0.0085 |
0.0036 |
0.0028 |
0.0012 |
| Hardness as CaCO3 |
mg/L |
422 |
745 |
585.20 |
126.08 |
N/A |
| TS |
mg/L |
218.00 |
327.20 |
256.16 |
42.15 |
N/A |
| TSS |
mg/L |
184 |
258 |
212 |
27.68 |
150–500 |
| TDS |
mg/L |
72 |
173 |
110.40 |
39.09 |
2100 |
| DO |
mg/L |
0.40 |
2.83 |
1.05 |
1.01 |
4.5–8 |
| BOD5d (at 20 ℃) |
mg/L |
16 |
71 |
48.60 |
21.87 |
50 (inland surface)–250 (irrigated land) |
| COD |
mg/L |
69 |
269 |
175.4 |
74.59 |
200 (inland surface)–400 (irrigated land) |
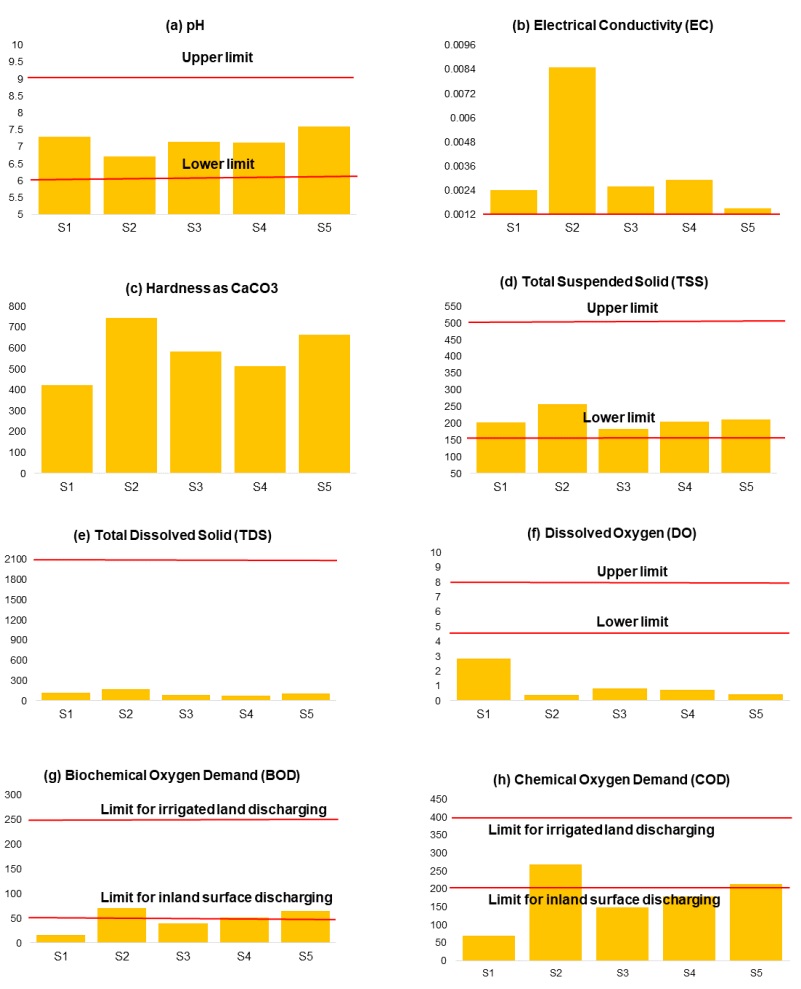
pH is a measure of the acidity or alkalinity of water and is one of the stable measurements to evaluate wastewater quality. It is a simple parameter but is extremely important, since most of the chemical reactions in the aquatic environment are controlled by any change in its value. In addition, aquatic organisms are sensitive to pH changes and biological treatment requires pH control or monitoring. Moreover, the toxicity of heavy metals also is enhanced at particular pH. Thus, pH is having primary importance in deciding the quality of wastewater effluent. Waters with a pH value of about 10 are exceptional and may reflect contamination by a strong base such as NaOH and Ca(OH)2. The pH of wastewater in this study varies between 6.72 and 7.60 with an average value of 7.17. These values are within the standard limit (6.0–9.0) of pH in wastewater in Bangladesh [14].
All the samples surpassed the lower limit but below the upper limit of pH (Figure 2a). A study of municipal wastewater in Sylhet [15] showed almost the same results of pH (Table 2), whereas, wastewater from industrial areas in Bangladesh is different from this study. Industrial wastewater shows pH as low as 3.9 to as high as 14 in different industrial areas [10]. This can be attributed that the wastewater from industries is more polluted than municipal wastewater in terms of pH.
Table 2. Comparison of physico-chemical parameters with other studies in Bangladesh.
| Study Area |
pH |
EC (s/cm) |
Hardness as CaCO3 (mg/L) |
TS (mg/L) |
TSS (mg/L) |
TDS (mg/L) |
DO (mg/L) |
BOD (mg/L) |
COD (mg/L) |
Reference |
| Jhenaidah (n = 70) |
7.17 (6.72–7.60) |
0.0036 (0.0015–0.0085) |
585.20 (422–745) |
256.16 (218–327.20) |
212 (184–258) |
110.40 (72–173) |
1.05 (0.40–2.83) |
48.60 (16–71) |
175.40 (69–269) |
This Study |
| Sylhet City (n = 6) |
6.24–6.89 |
- |
- |
450 (300–600) |
150 (100–200) |
300 (200–400) |
40 (0–80) |
138 (108–168) |
- |
[15] |
| Narayanganj (n = 9) |
9.88 |
0.014 (0.001–0.06) |
- |
- |
1123.11 (736–1960) |
9123.78 (791–46700) |
2.36 (0.42–4.6) |
573.89 (415–770) |
1223.33 (860–1560) |
[9] |
| Hazaribag, Dhaka (n = 10) |
7.19 |
0.006 |
- |
- |
1613 |
3455 |
1.74 |
548.50 |
1441 |
[8] |
| Hazaribag, Dhaka (n = 12) |
6.56 |
0.005 |
- |
- |
2048.42 |
3516.50 |
1.58 |
754.50 |
2776.83 |
[7] |
| Different areas of Bangladesh |
3.9–14 |
0.00025–0.064 |
- |
- |
24.9–39.50 |
90.7–5980 |
0–7 |
10–786 |
41–2430 |
[10] |
| Kushtia (n = 8) |
4.19 –8.49 |
0.00084–0.003 |
485–848 |
- |
- |
- |
- |
57–88 |
150–108 |
[6] |
| Chittagong (n = 10) |
8.23 (6.80–10.21) |
0.004 (0.0005–0.025) |
78.02 (9.20 –192) |
- |
186.50 (16–480) |
2577.90 (233–12570) |
1.72 (0.1–3.6) |
155.59 (12.40–276.90) |
507.54 (145.47 –1854.60) |
[5] |
The hardness of wastewater is the amount of dissolved calcium and magnesium in it. In this study, hardness due to calcium was estimated. It ranged between 422 and 745 mg/L with an average value of 585.2 mg/L. Currently, there is no standard value for the hardness of wastewater in Bangladesh. Recently, Islam et al. [6] have found hardness 485–848 mg/L from the industrial wastewater in Kushtia that is similar to this study. On the contrary, hardness as CaCO3 in industrial wastewater from Chittagong ranges between 9.20–192 mg/L [5], which is lower than this study.
The parameter of EC is an indication of the concentration of TDS and major ions in a given water body, whereas the parameters TS, TSS, and TDS refer mainly to inorganic substances dissolved in water [5]. Electrical Conductivity (S/cm) is the capacity of water to carry an electrical current and varies both with the number and with types of ions in the solutions, which in turn is related to the concentration of ionized substances in the water. The mean value of EC in this study was found 0.0036 S/cm, which is three times higher than the standard value (0.0012 S/cm) (Table 1). All the samples exceeded the standard limit of EC (Figure 2b). This value is similar to the most of the findings in Bangladesh; on the contrary, wastewater from Narayanganj industrial areas shows 0.014 S/cm. This value of electrical conductivity is much higher than the acceptable limit and may be due to the heavy industrial activities in this area. TS ranges from 218.00–327.20 mg/L (256.16 mg/L by average), which is almost half of Alam et al. [15]. Currently, there is no standard value for TS in Bangladesh. The mean values of TSS and TDS in the study area are 212 mg/L and 110.40 mg/L respectively.
TSS exceeded the lower standard value 150 mg/L, whereas, it was with in the upper standard limit (500 mg/L) (Figure 2d) [14]. In addition, TSS value in this study is higher than municipality wastewater from Sylhet [15] and industrial wastewater from Chittagong [5]. Although, other studies of industrial wastewater from Hazaribagh and Narayanganj show the higher value of TSS (Table 2). In this study, TSS in wastewater samples higher than 200 mg/L, which is considered strong wastewater and therefore should not be discharged into environment [16]. Relatively higher value of TSS in this study area is due to small-scale industrial activities. The values of TDS in the wastewater were between 72–173 mg/L. It is less than the standard value of 2100 mg/L [14] and all the samples have relatively lower values than the standard one (Figure 2e). Therefore, it is considered desirable before discharging into the surface water bodies.
Dissolved oxygen (DO) is an essential element in the biological treatment process for aerobic bacteria. Therefore, higher values of DO are desirable in wastewater to decompose organic contents into it. There is an inverse relationship between DO and BOD5d (at 20 ºC), i.e., when DO is minimum BOD5d (at 20 ºC) rates are higher [5]. The DO in wastewater in this study was found at 1.05 mg/L, which is lower the standard value 4.5–8.0 mg/L (Table 1). All the samples contain a very low amount of DO. Although it is desired to have a sufficient amount of DO in order to oxidize the organic content properly. Industrial wastewater from different areas of Bangladesh shows similar value to this study except for municipality wastewater from Sylhet city contains as high as 80 mg/L (Table 2). BOD5d (at 20 ºC) in wastewater from Jhenaidah municipality area ranges between 16 and 71 with an average value of 48.60 mg/L. It is less than the standard value of 50 mg/L (inland surface) and 250 mg/L (irrigated land). Two samples (S2 and S5) have values higher than the standard limit for discharging into the inland surface water system (Figure 2g). Nevertheless, all the samples are appropriate for discharging into irrigated land in terms of BOD5d (at 20 ºC). This finding is similar to industrial wastewater from Kushtia [6], but lower than the other studies in Bangladesh (Table 2).
COD is an indirect measurement of organic content in wastewater [17]. In this study, COD ranged between 69 and 269 mg/L with an average value of 175.4 mg/L. This mean value is lower than the prescribed limit 200 mg/L (inland water) and 400 mg/L (irrigated land) [14]. Although two samples (S2 and S5) have surpassed the lower limit (Figure 2h). High level of BOD5d (at 20 ºC) and COD is due to the presence of chemicals that may be organic or inorganic caused by the inflow of domestic, livestock and industrial waste that contains elevated levels of organic pollutants [16].
3.2. Correlation between different physico-chemical parameters
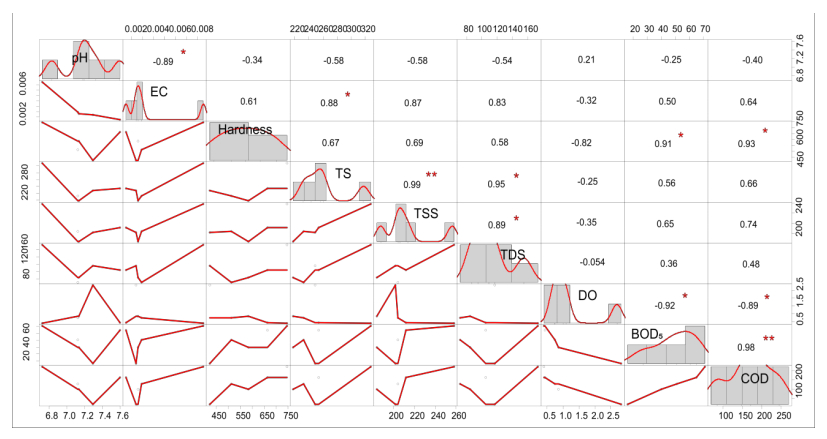
Pearson's correlation analysis was performed in order to analyze correlations between different physico-chemical parameters analyzed in this study. Results of correlation analysis and their corresponding trend lines are presented in Figure 3.
It represents the intercorrelations among the measured physico-chemical parameters. From Figure 3, it is apparent that TS with TSS (r = 0.99) and BOD5d (at 20 ºC) with COD (r = 0.98) show a strong positive correlation. In contrast, pH with EC (r = -0.89) and DO with BOD5d (at 20 ºC) and COD (r = -0.92, -0.89 respectively) indicate a strong but negative correlation. Other parameters such as pH, EC, TS, TSS, TDS, Hardness as CaCO3, BOD5d (at 20 ºC), and COD show a moderate correlation with each other. The negative correlation among DO, BOD5d at 20ºC and COD establish the inverse relationship between them. In contrast, a positive correlation between TS and TSS indicate that TS is largely dependent on TSS rather than TDS.
4. Conclusions
This study was set out to measure and assess the physico-chemical characteristics of municipal wastewater effluents from five sewage points of Jhenaidah town along with to investigate the correlation among them using Pearson's correlation analysis. This experiment confirmed that some wastewater parameters like pH, TDS, BOD5d (at 20 ºC), and COD meet the standard acceptable limit in Bangladesh. On the other hand, DO showed very lower values than the standard limit. TSS surpassed the acceptable limit, whereas hardness and TS showed a moderate value, which was not comparable due to the lack of standard values. Pearson's correlation analysis affirmed the inverse relation between DO and BOD5d (at 20 ºC). In addition, it confirmed the large dependency of TS on TSS rather than TDS. Therefore, the results of this study indicated a moderate quality of wastewater in Jhenaidah municipality area. The effluent could be posed a health and environmental risk to the communities rely on the receiving water, in particular to the flora and fauna, and finally the human being. So, this study recommended the further development and the necessary steps to take before discharging this wastewater into the receiving ponds, lakes, canals, rivers, and agricultural fields.
Acknowledgements
Authors are thankful to the authority of Islamic University, Kushtia 7003, Bangladesh, for providing the laboratory facilities. Furthermore, we are also thankful for the kind help from the members of the Department of Applied Chemistry and Chemical Engineering, Islamic University, Kushtia 7003, Bangladesh, during the field based wastewater sampling.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: