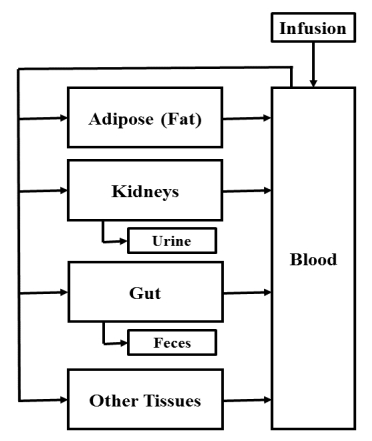
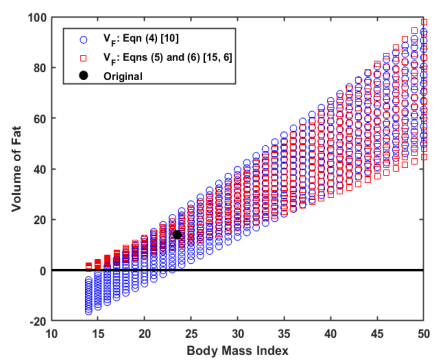
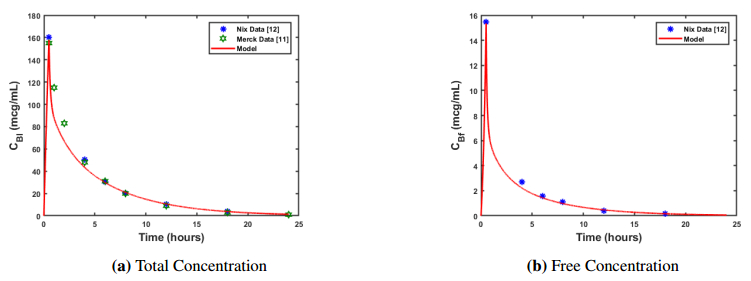
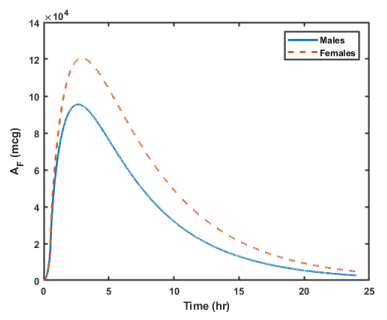
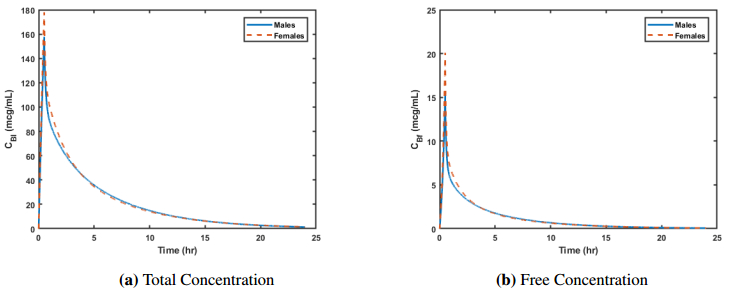
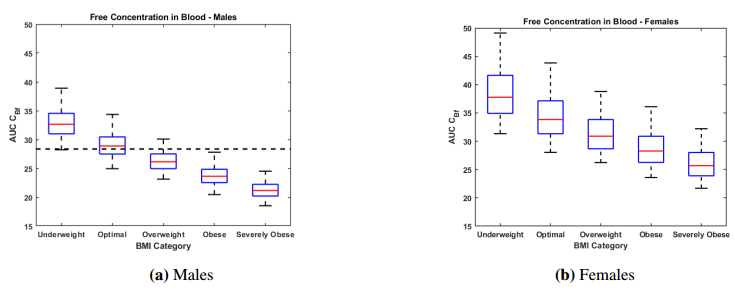
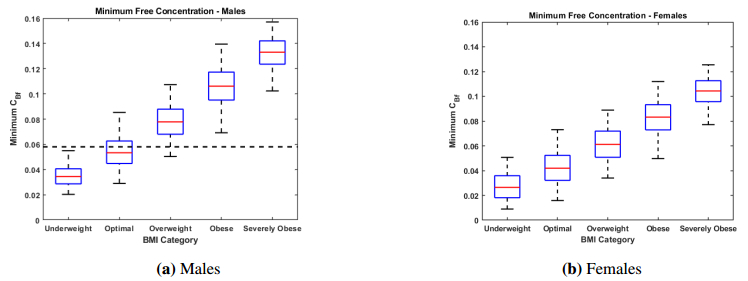
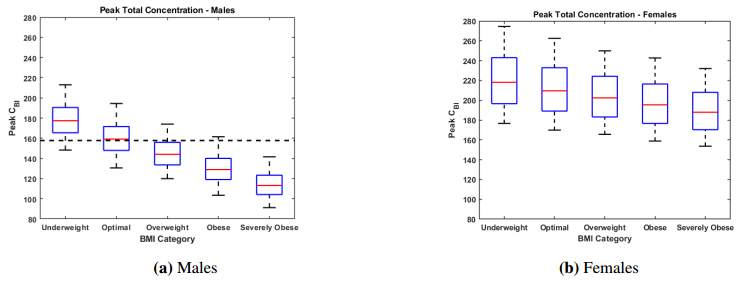
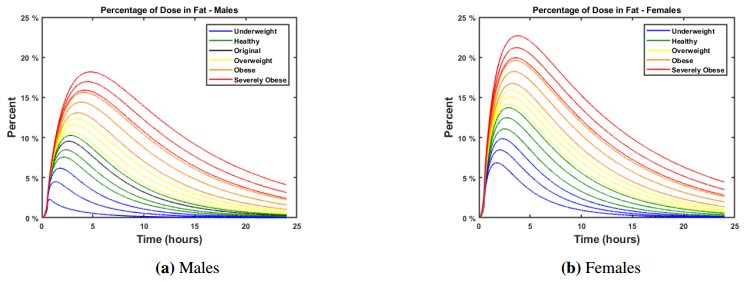
Ertapenem is an antibiotic commonly used to treat a broad spectrum of infections and is part of a broader class of antibiotics called carbapenems. Unlike other carbapenems, ertapenem has a longer half-life and thus only has to be administered once a day. Previously, a physiologically-based pharmacokinetic (PBPK) model was developed to investigate the uptake, distribution, and elimination of ertapenem following a single one gram dose in normal height, normal weight males. Due to the absorption properties of ertapenem, the amount of fat in the body can influence how the drug binds, how quickly the drug passes through the body, and thus how effective the drug might be. Thus, we have revised the model so that it is applicable to males and females of differing body mass index (BMI). Simulations were performed to consider the distribution of the antibiotic in males and females with varying body mass indexes. These results could help to determine if there is a need for altered dosing regimens in the future.
Abbreviations
HF: Heart failure; ceRNA: competing endogenous RNA; lncRNAs: long noncoding RNAs; miRNAs: microRNAs; CAD: coronary artery disease; ncRNAs: Noncoding RNAs; DAVID: Database for Annotation, Visualization, and Integrated Discovery; PPI: Protein-protein Interaction; STRING: Search Tool for the Retrieval of Interacting Genes; DELs: differentially expressed lncRNAs; DEMs: differentially expressed mRNAs; DEMis: differentially expressed miRNAs; BP: biological process; CC: cell component; MF: molecular function; WEE1: WEE1 G2 checkpoint kinase; MCM7: mini-chromosome maintenance complex component 7; E2F2: E2F transcription factor 2
1.
Introduction
Heart failure, a syndrome characterized by cardiac dysfunction-caused signs as well as symptoms, are recognized as an important cause of global morbidity and mortality [1]. An estimated 64.3 million people are living with heart failure worldwide, HF prevalence is generally estimated at 1-2% in Western countries while HF incidence reaches 5-10 per 1000 persons annually [2,3]. HF could be caused by multiple situations, such as high blood pressure, coronary artery disease (CAD), valvular and congenital heart disease as well as cardiomyopathies [4,5,6]. Various existing researches have shed new lights on the pathobiology and molecular mechanism of HF. Nevertheless, it is still unclarified of the exact molecular etiology, which deserves further exploration to reveal new therapeutic targets.
Noncoding RNAs (ncRNAs) have been reported to be critically involved in various diseases [7]. Long noncoding RNAs are the largest class of ncRNAs and are defined as transcribed RNA molecules > 200 nucleotides in length and without significant protein-coding potential [8]. Accumulative researches have recently revealed the functions of lncRNAs in multiple biological activities [9], with aberrant expression of lncRNAs in HF [10,11].
Growing attention has been paid to the vital roles of miRNAs in cardiovascular disorders, including HF [12]. Additionally, lncRNA is capable of modulating mRNA expression via the interaction with miRNA, giving rise to ceRNA hypothesis [13]. Nevertheless, the correlation between HF ceRNA remains barely clarified.
This research might offer a new regulatory mechanism between noncoding and coding RNAs in HF, and also widen the understanding concerning the development and progression of HF.
2.
Materials and methods
1.2. LncRNA, miRNA and mRNA microarray data
GEO publicly provides genomic data to support MIAME-compliant data submissions [14]. Human lncRNA, miRNA and mRNA expression were freely accessible from NCBI-GEO (GSE124401 and GSE136547). To be specific, the threshold of up-regulated or down-regulated lncRNA/mRNA was |log2 (fold-change) | > 1 with adjust P < 0.05; the significant difference in miRNA data was |log2 (fold-change) | > 0.5 with adjust P < 0.05.
2.2. LncRNA-miRNA-mRNA network establishment
The ceRNA network establishment was based on miRcode (http://www.mircode.org/) [15], miRDB (http://mirdb.org/) [16], miRTarBase (http://mirtarbase.mbc.nctu.edu.tw/php/index.php) [17] as well as TargetScan (http://www.targetscan.org/mamm_31/) [18] databases.
The detailed process was listed as follows: (1) the prediction of lncRNAs-targeted differential miRNAs by the highly conserved miRNA family of miRcode databases; (2) the prediction of mRNAs targeted by candidate miRNAs via TargetScan, miRTarBase as well as miRDB databases, wherein all predictive values should satisfy a matching number of 3; (3) the final construction of ceRNA network was accomplished by combining differential lncRNAs, miRNAs and miRNA-targeted mRNAs; (4)Cytoscape version 3.5.1(https://cytoscape.org/) was adopted for constructing and visualizing the lncRNA-miRNA-mRNA network, followed by calculation of all node degrees of the ceRNA network.
2.3. Functional enrichment analysis
Database for Annotation, Visualization, and Integrated Discovery (DAVID 6.8, https://david.ncifcrf.gov/) was utilized for analyzing functional enrichment. Moreover, we also explored the biological processes in Gene Ontology (GO) as well as Kyoto Encyclopedia of Genes and Genomes pathway (KEGG) (p < 0.05).
2.4. Protein-protein Interaction (PPI) network and hub gene analysis
For assessing the associations among DEGs within the ceRNA network, this study adopted the Search Tool for the Retrieval of Interacting Genes (STRING, https://string-db.org/) to comprehensively examine protein-gene interactions and construct a PPI network based on the ceRNA network. Afterwards, our constructed PPI network was visualized using Required Confidence (combined score) > 0.4 [19]. Thereafter, gene topology within this PPI network was analyzed by Cytoscape, and scale-free PPI network was utilized to detect pivotal proteins.
2.5. Critical lncRNA-miRNA-mRNA subnetwork re-construction
Cytoscape software was employed to extract all lncRNAs along with their relevant mRNAs as well as miRNAs in the global triple network for novel subnetwork construction, followed by calculation of the number of relevant lncRNA-miRNA-mRNA triplets. We further revealed target lncRNAs via the comparison of lncRNA node degree as well as relevant lncRNA-miRNA and miRNA-mRNA.
3.
Results
3.1. Screening for differentially expressed lncRNAs and mRNAs in patients with HF
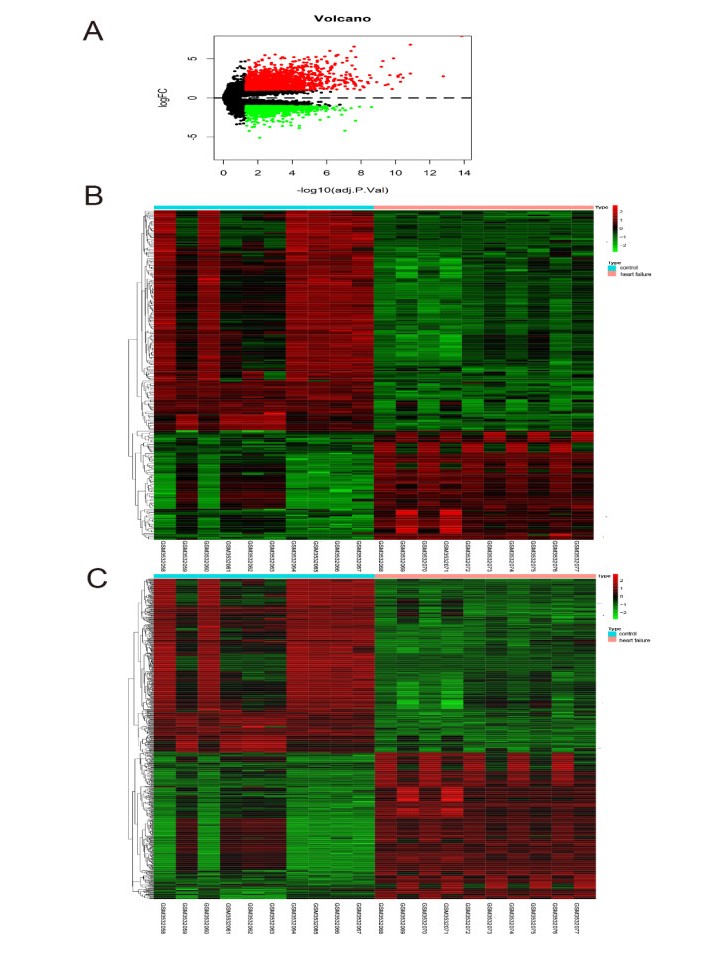
GSE124401 and GSE136547 was used for extracting human lncRNA/mRNA expression profile. The -pre-processing of raw data revealed 2587 differentially expressed genes (DEGs) (Figure 1A), including 694 differentially expressed lncRNAs (DELs), among which 472 DELs were up-regulated and 222 DELs were down-regulated (Figure 1B). Moreover, there were 2115 differentially expressed mRNAs (DEMs), including 1254 up-regulated DEMs and 861 down-regulated DEMs (Figure 1C). Besides, there were 67 differentially expressed miRNAs (DEMis), including 32 up-regulated DEMis and 35down-regulated ones (Figure 2A, 2B).
3.2. LncRNA-miRNA-mRNA ceRNA network
The ceRNA network analysis was further performed. In total, TargetScan, miRDB as well as miRTarBase databases successfully predicted 96 pairs of miRNA-mRNA interactions, and miRcode database successfully predicted 156 pairs of IncRNA-miRNA interactions. Cytoscape was further adopted for visualizing ceRNA network establishment. Finally, we successfully established the lncRNA-miRNA-mRNA network consisting of 82 lncRNA nodes, 58 mRNA nodes as well as 5 miRNA nodes (Figure 3). The gene expression is shown in Tables 1-3.
3.3. GO and KEGG analysis of DEGs
We analyze 58 mRNA in the ceRNA network. GO analysis revealed the significant enrichment of DEGs in transcription regulation (including positive and negative regulation of transcription), positive regulation of apoptotic process as well as miRNAs generation involved in gene silencing by miRNA in terms of biological process (BP) changes (Figure 4A); nucleoplasm, nucleus and cytoplasm in terms of cell component (CC) changes (Figure 4B); DNA binding, protein binding as well as transcription factor activity in terms of molecular function (MF) changes (Figure 4C). KEGG pathway analysis identified the enrichment of DEGs in cell cycle, circadian rhythm and DNA replication (Table 4).
3.4. Establishment of PPI network
Next mRNAs from ceRNA network were up-loaded to STRING database for further identification of key mRNAs in the HF-associated ceRNA network. we established a PPI network, we hide disconnected nodes in the network. The PPI network revealed 30 nodes and 27 edges (Figure 5A). Afterwards., degree of linkage between DEMs was adopted to select key mRNAs from PPI network, which gave rise to key mRNAs, including WEE1 G2 checkpoint kinase (WEE1), minichromosome maintenance complex component 7 (MCM7), E2F transcription factor 2 (E2F2) (Figure 5B). The scores of these genes were far higher than others. Notably, E2F2, WEE1 and MCM7, which were extensively studied, were also involved in the subnetwork, which was indicative of the regulatory role of s the subnetwork on biological activities via diverse pathways.
3.5. Topological analysis of HF-correlated ceRNA network
For further identification of hub RNAs as well as their relevant networks, Cytoscape plugin cytoHubba was utilized for calculation of all node degrees in the ceRNA network. To be specific, AC010336, KCNQ1OT1 and XIST were three of the top-ranked nodes, which all had 5 target miRNA, indicating their significance in regulating transcription, all consisting of 1 lncRNA node, 5 miRNA nodes as well as 58 mRNA nodes (Figure 6A), Five miRNAs serve as the center of ceRNA, a subnetwork of lncRNA-miR-17-5p-mRNA, lncRNA-miR-20b-5p-mRNA, lncRNA-miR-107-mRNA, lncRNA-miR-125a-5p-mRNA and lncRNA-miR-140-5p-mRNA was extracted from the ceRNA network (Figure 6B-F), The information on the ceRNA network for lncRNA-miRNA-mRNA ceRNA are shown in Table 5.
4.
Discussion
HF is caused by myocardial defects from either functional or structural aspects, further leading to impaired ventricular filling or blood ejection, which is a common clinical syndrome. Moreover, HF is recognized as a universal disorder with a high rate of morbidity, hospitalization as well as mortality worldwide [20,21].
Recently, more attention has been paid to ncRNAs owing to the rapidly developed high-throughput genomic platforms, which have been uncovered to be critically involved in modulating diverse biological activities, including metabolism, differentiation as well as development. Despite rapid progress, its representative molecular signatures are still incompletely clear, especially their roles in HF progression. LncRNAs are capable of binding to complementary binding sites of miRNAs and modulating gene expression by sponging 3'-UTR of downstream target genes [13]. By guiding transcript stability, nuclear export, subcellular localization and translation efficiency, RNA 3′-end cleavage and polyadenylation play an important role in pathogenesis, diagnosis and therapy of human disorders [22,23]. A substantial amount of genes with a potential role in HF seem to be in fact regulated at the RNA 3'end, as summarized in the article written by Jamie Nourse and Stefano Spada [23]. The regulation of RNA 3'end also influences binding of miRNAs and lnRNAs. Therefore, a comprehensive understanding of the RNA regulatory network sheds novel light on gene regulatory mechanisms.
Therefore, interaction data from GEO were extracted for creating a global triple network on the basis of the ceRNA theory, indicating the same miRNA shared by lncRNAs and mRNAs in one triplet. To be specific, 82 lncRNA nodes, 5 miRNA nodes, 58 mRNA nodes as well as 244 edges were contained in the lncRNA-miRNA-mRNA network. GO and KEGG analysis was conducted for better annotation of the biological functions of downstream mRNAs. Remarkably enriched KEGG pathways were cell cycle pathways, which have been reported to be involved in mechanism of regulating HF, causing apoptosis and proliferation of HF [24,25,26]. Through the analysis of GO, we observed that a large number of genes were located in nucleoplasm, nucleus and cytoplasm, suggesting that these genes participate in regulation of transcription by DNA binding.
We further calculated the hub nodes for identification of possible key gene candidates as diagnostic biomarkers as well as therapeutic targets of HF. Of note, hub nodes that share high degree of connectivity to other ones might be utilized as topological markers of the ceRNA network for further assessment of important genes. Three lncRNAs (AC010336, KCNQ1OT1 and XIST) had significantly higher degrees than other lncRNA nodes and were therefore identified as key hub nodes. Due to the similar miRNA targets, the above three lncRNAs showed common trends in terms of significant GO terms.
LncRNA Kcnq1ot1, localized in KCNQ1 locus at 11p15.5 [27], has been previously demonstrated have correlation with multiple diseases, especially heart disease [28,29,30]. In a new study, significant up-regulation of Kcnq1ot1 was found in DCM. Bioinformatics as well as luciferase assays shown that Kcnq1ot1 could function as a ceRNA for modulating caspase-1 expression by sponging miR-214-3p in high glucose-treated cardiac fibroblasts [31]. Moreover, KCNQ1OT1 not only is capable of mediating pyroptosis in diabetic cardiomyopathy, but also aggravates cardiomyocyte apoptosis by targeting FUS in HF [32]. In acute myocardial infarction model, lncRNA Kcnq1ot1 renders cardiomyocytes apoptosis by up-regulating Tead1 [33].
lncRNA XIST also plays essential roles in different types of diseases [34,35,36], which can modulate cardiac hypertrophy through targeting miR-101 [37]. LncRNA XIST knockdown could repress myocardial cell apoptosis in AMI model rats by downregulating miR-449 level [38]. In addition, XIST suppression was capable of relieving myocardial I/R injury by regulating miR-133a/SOCS2 axis as well as suppressing autophagy in a study investigating the functions of lncRNA XIST in myocardial I/R injury both in vitro and in vivo [39].
Previous studies have shown that Kcnq1ot1 and XIST regulate cardiomyocyte apoptosis in cardiac research. This is consistent to our KEGG analysis, which shows that the main pathway of ceRNA network is in cell cycle regulation. HF is dominated by cardiac remodeling, causing progressive enlargement of heart chambers and deterioration of contractile function [40]. Myocardial cell apoptosis is recognized as an important process in HF progression [41]. Apoptosis is a delicately regulated biological activity modulating the balance between pro-death and pro-survival signals, which is essential for cell fate. The majority of apoptosis signaling pathways in extra-cardiac cell types also play critical roles in inducing heart apoptosis. Human failing hearts in NYHA classes III-IV generally show apoptotic rates ranging from 0.12% to 0.70% [42,43,44,45]. Moreover, although apoptosis might not be the initial focus in several studies, apoptosis generally accompanies heart disease progression [46].
By contrast, relieving HF progression is generally accompanied with suppressed apoptosis [47]. Unlike necrosis, apoptosis is a highly and orderly modulated event. Thus, restricting cardiac muscle loss via apoptotic suppression is of therapeutic implication in HF. From KEGG and GO enrichment, KCNQ1OT1 and XIST may become therapeutic alternatives associated with apoptosis in HF.
These ncRNAs, found in tissue, participate in several pathophysiological processes associated with HF, including hypertrophy and cardiac fibrosis. Micro RNAs are single-stranded ncRNAs with 22 to 24nt in length with endogenous expression [48]. Bioinformatic analysis identifies target‐specific miRNAs and regulatory hubs miRNAs to many novel pathophysiological processes, such as hemostatic system [49]. Besides, miRNAs have been shown to be of diagnostic and prognostic value in HF [50,51,52].
Hsa-miR-17-5p, hsa-miR-20b-5p, hsa-miR-107, hsa-miR-125a-5p as well as hsa-miR-140-5p are center of ceRNA. Besides, miRNA can modulate various cellular process. For example, knockdown of miR-17-5p suppresses proliferation and autophagy, but enhances apoptosis in thyroid tumor by targeting PTEN. MiR-20b-5p is capable of relieving hypoxia-induced apoptosis in cardiomyocytes through HIF-1α/NF-κB pathway [53]. miR-107 is capable of regulating apoptosis, synthesis of extracellular matrix as well as proliferation of chondrocytes by targeting PTEN [54]. Recently, a new class of RNA therapeutic has attracted considerable attention, that of miRNA targeting. RNA-based therapeutics have attracted considerable attention in the past decade because of their potential to treat numerous diseases, including cardiovascular disorders [55]. There are many researches showing the discovery of miRNA-based therapeutic targets in the hemostatic system [56] In the future, RNA-based therapies also have strong appeal in the treatment of cardiovascular diseases.
Conclusion
Collectively, this study uncovered the expression profiles of DEMs, DELs and DEMis, followed by prediction of their functions as well as potential pathways in HF. Nevertheless, intervention assays of RNAs were not performed in this research, which is a limitation and requires further validations of possible roles of these RNAs on HF.
Availability of data and materials
The datasets generated and/or analysed during the current study are available in the GEO database, https://www.ncbi.nlm.nih.gov/geo/
Authors' contributions
Qin Zhang: Conceptualization, Methodology, Writing Reviewing, Xudan Ma: Editing, Software, Weina Pang: Data curation, Writing- Original draft preparation. Qijun Zhang: Visualization, Investigation. Kefeng Huang and Haihong Zhu: Supervision.
Acknowledgements
This study was supported by the Natural Science Foundation of Zhejiang Province (Effect of lncRNA MHRT on dedifferentiation like state of cardiomyocytes in patients with atrial fibrillation and its mechanism) (LY20H020001).
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: