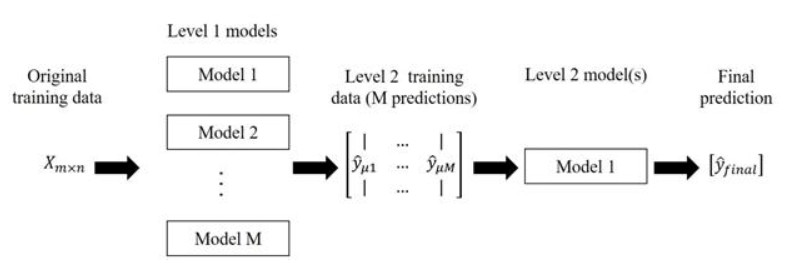
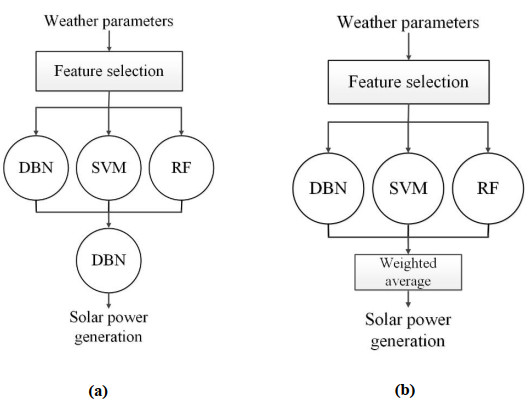
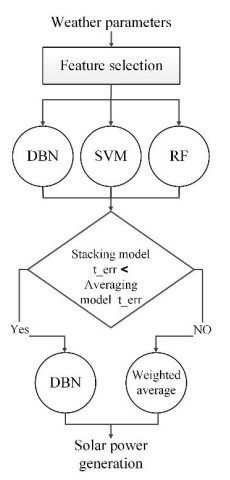
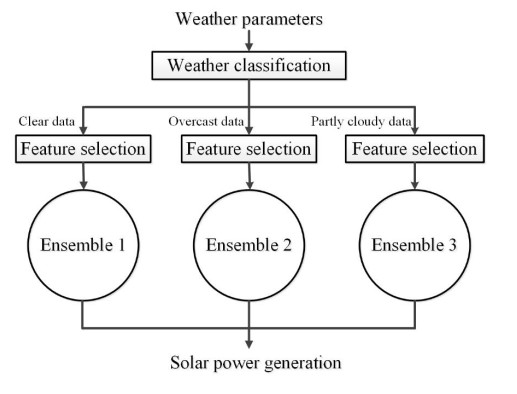
|
[1]
|
[M. Adimy and F. Crauste, Modeling and asymptotic stability of a growth factor-dependent stem cell dynamics model with distributed delay, Discrete & Continuous Dynamical Systems-Series B, 8 (2017), 19-38.
|
|
[2]
|
[E. Alzahrani, H. Akca and X. Li, New synchronization schemes for delayed chaotic neural networks with impulses, Neural Computing and Applications, 28 (2017), 2823-2837.
|
|
[3]
|
[ F. Amato, G. De Tommasi and A. Pironti, Necessary and sufficient conditions for finite-time stability of impulsive dynamical linear systems, Automatica, 49 (2013), 2546-2550.
|
|
[4]
|
[ G. Ballinger and X. Liu, On boundedness of solutions of impulsive systems, Nonlinear Studies, 4 (1997), 121-131.
|
|
[5]
|
[ G. Ballinger and X. Liu, On boundedness of solutions for impulsive systems in terms of two measures, Nonlinear World, 4 (1997), 417-434.
|
|
[6]
|
[ T. Caraballo, M. Hammami and L. Mchiri, Practical exponential stability of impulsive stochastic functional differential equations, Systems & Control Letters, 109 (2017), 43-48.
|
|
[7]
|
[ W. Chen, X. Lu and W. Zheng, Impulsive stabilization and impulsive synchronization of discrete-time delayed neural networks, IEEE Transactions on Neural Networks and Learning Systems, 26 (2015), 734-748.
|
|
[8]
|
[ W. Chen, D. Wei and X. Lu, Exponential stability of a class of nonlinear singularly perturbed systems with delayed impulses, Journal of the Franklin Institute, 350 (2013), 2678-2709.
|
|
[9]
|
[ W. Chen and W. Zheng, Input-to-state stability and integral input-to-state stability of nonlinear impulsive systems with delays, Automatica, 45 (2009), 1481-1488.
|
|
[10]
|
[ W. Chen and W. Zheng, The effect of delayed impulses on stability of impulsive time-delay systems, IFAC Proceedings Volumes, 44 (2011), 6307-6312.
|
|
[11]
|
[ W. Chen and W. Zheng, Exponential stability of nonlinear time-delay systems with delayed impulse effects, Automatica, 47 (2011), 1075-1083.
|
|
[12]
|
[ P. Cheng and F. Deng, Global exponential stability of impulsive stochastic functional differential systems, Statistics and Probability Letters, 80 (2010), 1854-1862.
|
|
[13]
|
[ S. Dashkovskiy and A. Mironchenko, Input-to-State stability of nonlinear impulsive systems, SIAM J. Control Optim, 51 (2012), 1962-1987.
|
|
[14]
|
[ M. Dellnitz, M. Hessel and A. Ziessler, On the computation of attractors for delay differential equations, Journal of Computational Dynamics, 3 (2016), 93-112.
|
|
[15]
|
[ S. Gao, D. Xie and L. Chen, Pulse vaccination strategy in a delayed sir epidemic model with vertical transmission, Discrete & Continuous Dynamical Systems-B, 7 (2007), 77-86.
|
|
[16]
|
[ K. Gopalsamy, Stability and Oscillations in Delay Differential Equations of Population Dynamics, Dordrecht, The Netherlands: Kluwer, 1992.
|
|
[17]
|
[ J. Grizzle, G. Abba and F. Plestan, Asymptotically stable walking for biped robots: Analysis via systems with impulse effects, IEEE Transaction on Automatic Control, 46 (2001), 51-64.
|
|
[18]
|
[ K. Gu, J. Chen and V. Kharitonov, Stability of Time-delay Systems, Springer Science & Business Media, 2003.
|
|
[19]
|
[ K. Gu, V. Kharitonov and J. Chen, Stability of Time-Delay Systems, Birkhauser, Boston, MA, USA, 2003.
|
|
[20]
|
[ Y. Guo, G. Xu and Y. Guo, Stabilization of the wave equation with interior input delay and mixed Neumann-Dirichlet boundary, Discrete & Continuous Dynamical Systems-B, 21 (2016), 2491-2507.
|
|
[21]
|
[ J. Hale and S. M. Verduyn Lunel, Introduction to Functional Differential Equations, Springer-Verlag, New York, NY, USA, 1993.
|
|
[22]
|
[ W. He, F. Qian and J. Cao, Pinning-controlled synchronization of delayed neural networks with distributed-delay coupling via impulsive control, Neural Networks, 85 (2017), 1-9.
|
|
[23]
|
[ J. Hespanha and A. Morse, Stability of switched systems with average dwell-time, Proceedings of the 38th IEEE Conference on Decision and Control, (1999), 2655-2660.
|
|
[24]
|
[ L. Hetel, J. Daafouz and C. Iung, Equivalence between the lyapunov-Krasovskii functionals approach for discrete delay systems and that of the stability conditions for switched systems, Nonlinear Analysis: Hybrid Systems, 2 (2008), 697-705.
|
|
[25]
|
[ J. Hu, G. Sui, S. Du and X. Li, Finite-time stability of uncertain nonlinear systems with time-varying delay, Mathematical Problems in Engineering, 2017 (2017), Article ID 2538904, 9 pages.
|
|
[26]
|
[ A. Huseynov, Positive solutions of a nonlinear impulsive equation with periodic boundary conditions, Applied Mathematics and Computation, 217 (2010), 247-259.
|
|
[27]
|
[ H. Jin and M. Zacksenhouse, Oscillatory neural networks for robotic yo-yo control, IEEE Transactions on Neural Networks and Learning Systems, 14 (2003), 317-325.
|
|
[28]
|
[ A. Kartsatos, Advanced Ordinary Differential Equations, Mariner Publishing Co., Inc., Tampa, Fla., 1980.
|
|
[29]
|
[ A. Khadra, X. Liu and X. Shen, Analyzing the robustness of impulsive synchronization coupled by linear delayed impulses, IEEE Transactions on Automatic Control, 54 (2009), 923-928.
|
|
[30]
|
[ A. Khadra, X. Liu and X. Shen, Impulsively synchronizing chaotic systems with delay and applications to secure communication, Automatica, 41 (2005), 1491-1502.
|
|
[31]
|
[ Y. Kuang, Delay Differential Equations with Applications in Population Dynamics, volume 191 in the series of Mathematics in Science and Engineering, Academic Press, 1993.
|
|
[32]
|
[ L. Lee, Y. Liu, J. Liang and X. Cai, Finite time stability of nonlinear impulsive systems and its applications in sampled-data systems, ISA Transactions, 57 (2015), 172-178.
|
|
[33]
|
[ R. Leine and T. Heimsch, Global uniform symptotic attractive stability of the non-autonomous bouncing ball system, Physica D: Nonlinear Phenomena, 241 (2012), 2029-2041.
|
|
[34]
|
[ B. Li, Y. Chen and X. Lu, et al. A delayed HIV-1 model with virus waning term, Mathematical Biosciences and Engineering, 13 (2016), 135-157.
|
|
[35]
|
[ C. Li, X. Liao, X. Yang and T. Huang, Impulsive stabilization and synchronization of a class of chaotic delay systems, Chaos, 15 (2005), 043103, 9pp.
|
|
[36]
|
[ X. Li, New results on global exponential stabilization of impulsive functional differential equations with infinite delays or finite delays, Nonlinear Analysis: Real World Applications, 11 (2010), 4194-4201.
|
|
[37]
|
[ X. Li, Existence and global exponential stability of periodic solution for impulsive CohenGrossberg-type BAM neural networks with continuously distributed delays, Applied Mathematics and Computation, 215 (2009), 292-307.
|
|
[38]
|
[ X. Li, M. Bohner and C. Wang, Impulsive differential equations: Periodic solutions and applications, Automatica, 52 (2015), 173-178.
|
|
[39]
|
[ X. Li and J. Cao, An impulsive delay inequality involving unbounded time-varying delay and applications, IEEE Transactions on Automatic Control, 62 (2017), 3618-3625.
|
|
[40]
|
[ X. Li and Y. Ding, Razumikhin-type theorems for time-delay systems with Persistent impulses, Systems and Control Letters, 107 (2017), 22-27.
|
|
[41]
|
[ X. Li and X. Fu, Effect of leakage time-varying delay on stability of nonlinear differential Systems, Journal of the Franklin Institute, 350 (2013), 1335-1344.
|
|
[42]
|
[ X. Li and X. Fu, Lag synchronization of chaotic delayed neural networks via impulsive control, IMA Journal of Mathematical Control and Information, 29 (2012), 133-145.
|
|
[43]
|
[ X. Li and X. Fu, On the global exponential stability of impulsive functional differential equations with infinite delays or finite delays, Communications in Nonlinear Science and Numerical Simulation, 19 (2014), 442-447.
|
|
[44]
|
[ X. Li, P. Li and Q. Wang, Input/output-to-state stability of impulsive switched systems, Systems & Control Letters, 116 (2018), 1-7.
|
|
[45]
|
[ X. Li and R. Rakkiyappan, Delay-dependent global asymptotic stability criteria for stochastic genetic regulatory networks with Markovian jumping parameters, Applied Mathematical Modelling, 36 (2012), 1718-1730.
|
|
[46]
|
[ X. Li and R. Rakkiyappan, Stability results for Takagi-Sugeno fuzzy uncertain BAM neural networks with time delays in the leakage term, Neural Computing and Applications, 22 (2013), 203-219.
|
|
[47]
|
[ X. Li, R. Rakkiyappan and N. Sakthivel, Non-fragile synchronization control for Markovian jumping complex dynamical networks with probabilistic time-varying coupling delay, Asian Journal of Control, 17 (2015), 1678-1695.
|
|
[48]
|
[ X. Li, J. Shen and R. Rakkiyappan, Persistent impulsive effects on stability of functional differential equations with finite or infinite delay, Applied Mathematics and Computation, 329 (2018), 14-22.
|
|
[49]
|
[ X. Li and S. Song, Impulsive control for existence, uniqueness, and global stability of periodic solutions of recurrent neural networks with discrete and continuously distributed delays, IEEE Transactions on Neural Networks and Learning Systems, 24 (2013), 868-877.
|
|
[50]
|
[ X. Li and S. Song, Stabilization of delay systems: delay-dependent impulsive control, IEEE Transactions on Automatic Control, 62 (2017), 406-411.
|
|
[51]
|
[ X. Li and J. Wu, Stability of nonlinear differential systems with state-dependent delayed impulses, Automatica, 64 (2016), 63-69.
|
|
[52]
|
[ X. Li and J. Wu, Sufficient stability conditions of nonlinear differential systems under impulsive control with state-dependent delay, IEEE Transactions on Automatic Control, 63 (2018), 306-311.
|
|
[53]
|
[ X. Li, X. Zhang and S. Song, Effect of delayed impulses on input-to-state stability of nonlinear systems, Automatica, 76 (2017), 378-382.
|
|
[54]
|
[ X. Li, Q. Zhu and Donal O'Regan, pth Moment exponential stability of impulsive stochastic functional differential equations and application to control problems of NNs, Journal of the Franklin Institute, 351 (2014), 4435-4456.
|
|
[55]
|
[ Y. Li, H. Li, X. Ding and G. Zhao, Leader-follower consensus of multi-agent systems with time delays over finite fields, IEEE Transactions on Cybernetics, pp (2018), 1-6.
|
|
[56]
|
[ X. Liao, L. Wang and P. Yu, Stability of Dynamical Systems, Elsevier Press, Oxford, 2007.
|
|
[57]
|
[ D. Lin, X. Li and D. Regan, Stability analysis of generalized impulsive functional differential equations, Mathematical and Computer Modelling, 55 (2012), 1682-1690.
|
|
[58]
|
[ B. Liu, X. Liu, K. Teo and Q. Wang, Razumikhin-type theorems on exponential stability of impulsive delay systems, IMA Journal of Applied Mathematics, 71 (2006), 47-61.
|
|
[59]
|
[ C. Liu, X. Li and Donal O' Regan, Asymptotically practical stability of impulsive functional differential systems in terms of two measurements, Dynamic Systems and Applications, 22 (2013), 621-640.
|
|
[60]
|
[ J. Liu, X. Liu and W. Xie, Input-to-state stability of impulsive and switching hybrid systems with time-delay, Automatica, 47 (2011), 899-908.
|
|
[61]
|
[ L. Liu, T. Caraballo and X. Fu, Exponential stability of an incompressible non-Newtonian fluid with delay, Discrete & Continuous Dynamical Systems-B.
|
|
[62]
|
[ X. Liu, Stability results for impulsive differential systems with applications to population growth models, Dynamics and Stability of Systems, 9 (1994), 163-174.
|
|
[63]
|
[ X. Liu and G. Ballinger, Uniform asymptotic stability of impulsive delay differential equations, Computers and Mathematics with Applications, 41 (2001), 903-915.
|
|
[64]
|
[ X. Liu, X. Shen, Y. Zhang and Q. Wang, Stability criteria for impulsive systems with time delay and unstable system matrices, IEEE Transactions on Circuits ond Systems-Ⅰ: Regular Papers, 54 (2007), 2288-2298.
|
|
[65]
|
[ X. Liu and Q. Wang, On stability in terms of two measures for impulsive systems of functional differential equations, Journal of Mathematical Analysis and Applications, 326 (2007), 252-265.
|
|
[66]
|
[ X. Liu and Q. Wang, The method of Lyapunov functionals and exponential stability of impulsive systems with time delay, Nonlinear Analysis, 66 (2007), 1465-1484.
|
|
[67]
|
[ X. Liu, S. Zhong and X. Ding, Robust exponential stability of impulsive switched systems with switching delays: A Razumikhin approach, Communications in Nonlinear Science and Numerical Simulation, 17 (2012), 1805-1812.
|
|
[68]
|
[ J. Lu, D. Ho and J. Cao, A unified synchronization criterion for impulsive dynamical networks, Automatica, 46 (2010), 1215-1221.
|
|
[69]
|
[ Z. Luo and J. Shen, Stability results for impulsive functional differential equations with infinite delays, J. Comput. Appl. Math, 131 (2001), 55-64.
|
|
[70]
|
[ Z. Luo and J. Shen, Stability of impulsive functional differential equations via the Lyapunov functional, Appl. Math. Lett, 22 (2009), 163-169.
|
|
[71]
|
[ X. Lv and X. Li, Finite time stability and controller design for nonlinear impulsive sampleddata systems with applications, ISA Transactions, 70 (2017), 30-36.
|
|
[72]
|
[ H. Miao, Z. Teng and C. Kang, Stability and Hopf bifurcation of an HIV infection model with saturation incidence and two delays, Discrete & Continuous Dynamical Systems-B, 22 (2017), 2365-2387.
|
|
[73]
|
[ P. Naghshtabrizi, J. Hespanha and A. Teel, Exponential stability of impulsive systems with application to uncertain sampled-data systems, Systems & Control Letters, 57 (2008), 378-385.
|
|
[74]
|
[ S. Nersesov and W. Haddad, Finite-time stabilization of nonlinear impulsive dynamical systems, Nonlinear Analysis: Hybrid Systems, 2 (2008), 832-845.
|
|
[75]
|
[ E. Nikolopoulou, L. R. Johnson, D. Harris, J. D. Nagy, E. C. Stites and Y. Kuang, Tumour-immune dynamics with an immune checkpoint inhibitor, Letters in Biomathematics, 5 (2018), S137-S159.
|
|
[76]
|
[ T. Nishikawa, Y. Lai and F. Hoppensteadt, Capacity of oscillatory associative-memory networks with error-free retrieval, Phys. Rev. Lett., 92 (2004), 108101.
|
|
[77]
|
[ L. Pan and J. Cao, Exponential stability of impulsive stochastic functional differential equations, Journal of Mathematical Analysis and Applications, 382 (2011), 672-685.
|
|
[78]
|
[ L. Pan and J. Cao, Robust stability for uncertain stochastic neural network with delay and impulses, Neurocomputing, 94 (2012), 102-110.
|
|
[79]
|
[ G. Peralta and K. Kunisch, Interface stabilization of a parabolic-hyperbolic pde system with delay in the interaction, Discrete & Continuous Dynamical Systems-A, 38 (2018), 3055-3083.
|
|
[80]
|
[ R. Rakkiyappan, R. Sivasamy and X. Li, Synchronization of identical and nonidentical memristor-based chaotic systems via active backstepping control technique, Circuits, Systems, and Signal Processing, 34 (2015), 763-778.
|
|
[81]
|
[ R. Rakkiyappan, G. Velmurugan, X. Li and D. Regan, Global dissipativity of memristor-based complex-valued neural networks with time-varying delays, Neural Computing and Applications, 27 (2016), 629-649.
|
|
[82]
|
[ A. Ruiz, D. Owens and S. Townley, Existence, learning, and replication of periodic motion in recurrent neural networks, IEEE Transactions on Neural Networks and Learning Systems, 9 (1998), 651-661.
|
|
[83]
|
[ E. Rutter and Y. Kuang, Global dynamics of a model of joint hormone treatment with dendritic cell vaccine for prostate cancer, DCDS-B, 22 (2017), 1001-1021.
|
|
[84]
|
[ J. Shen, J. Li and Q. Wang, Boundedness and periodicity in impulsive ordinary and functional differential equations, Nonlinear Analysis, 65 (2006), 1986-2002.
|
|
[85]
|
[ J. Shen, Z. Luo and X. Liu, Impulsive stabilization of functional differential equations via liapunov functionals, Journal of Mathematical Analysis and Applications, 240 (1999), 1-15.
|
|
[86]
|
[ W. Shen and Z. Shen, Transition fronts in nonlocal Fisher-KPP equations in time heterogeneous media, Communications on Pure & Applied Analysis, 15 (2016), 1193-1213.
|
|
[87]
|
[ X. Song and J. H. Park, Linear optimal estimation for discrete-time measurement-delay systems with multi-channel multiplicative noise, IEEE Transactions on Circuis and Systems Ⅱ-Express Brief, 64 (2017), 156-160.
|
|
[88]
|
[ X. Song, J. H. Park and X. Yan, Linear estimation for measurement-delay systems with periodic coefficients and multiplicative noise, IEEE Transactions on Automatic Control, 62 (2017), 4124-4130.
|
|
[89]
|
[ I. Stamova, Stability Analysis of Impulsive Functional Differential Equations, Walter de Gruyter, Berlin, 2009.
|
|
[90]
|
[ I. Stamova, Vector Lyapunov functions for practical stability of nonlinear impulsive functional differential equations, Journal of Mathematical Analysis and Applications, 325 (2007), 612-623.
|
|
[91]
|
[ I. Stamova, T. Stamov and X. Li, Global exponential stability of a class of impulsive cellular neural networks with supremums, Internat. J. Adapt. Control Signal Process, 28 (2014), 1227-1239.
|
|
[92]
|
[ I. Stamova, T. Stamov and N. Simeonova, Impulsive effects on the global exponential stability of neural network models with supremums, European Journal of Control, 20 (2014), 199-206.
|
|
[93]
|
[ X. Tan, J. Cao and X. Li, Consensus of Leader-Following Multiagent Systems: A Distributed Event-Triggered Impulsive Control Strategy, IEEE Transactions on Cybernetics, 99 (2018), 1-10.
|
|
[94]
|
[ X. Tan, J. Cao and X. Li, Leader-following mean square consensus of stochastic multi-agent systems with input delay via event-triggered control, IET Control Theory & Applications, 12(2018), 299-309.
|
|
[95]
|
[ J. Tseng, Global asymptotic dynamics of a class of nonlinearly coupled neural networks with delays, Discrete & Continuous Dynamical Systems-A, 33 (2013), 4693-4729.
|
|
[96]
|
[ B. Vadivoo, R. Ramachandran, J. Cao, H. Zhang and X. Li, Controllability analysis of nonlinear neutral-type fractional-order differential systems with state delay and impulsive effects, International Journal of Control, Automation and Systems, 16 (2018), 659-669.
|
|
[97]
|
[ D. Wang, Emergent synchrony in locally coupled neural oscillators, IEEE Transactions on Neural Networks and Learning Systems, 6 (1995), 941-948.
|
|
[98]
|
[ H. Wang, S. Duan, T. Huang and J. Tan, Synchronization of memristive delayed neural networks via hybrid impulsive control, Neurocomputing, 267 (2017), 615-623.
|
|
[99]
|
[ H. Wang, S. Duan, C. Li, L. Wang and T. Huang, Stability of impulsive delayed linear differential systems with delayed impulses, Journal of the Franklin Institute, 352 (2015), 3044-3068.
|
|
[100]
|
[ H. Wang, J. Li and Y. Kuang, Enhanced modeling of the glucose-insulin system and its applications in insulin therapies, J. Biological Dynamics, 3 (2009), 22-38.
|
|
[101]
|
[ L. Wang, M. Yu and P. Niu, Periodic solution and almost periodic solution of impulsive Lasota-Wazewska model with multiple time-varying delays, Computers and Mathematics with Applications, 64 (2012), 2383-2394.
|
|
[102]
|
[ Q. Wang and X. Liu, Exponential stability for impulsive delay differential equations by Razumikhin method, Journal of Mathematical Analysis and Applications, 309 (2005), 462-473.
|
|
[103]
|
[ Q. Wang and X. Liu, Impulsive stabilization of delay differential systems via the LyapunovRazumikhin method, Applied Mathematics Letters, 20 (2007), 839-845.
|
|
[104]
|
[ Q. Wang and X. Liu, Stability criteria of a class of nonlinear impulsive switching systems with time-varying delays, Journal of the Franklin Institute, 349 (2012), 1030-1047.
|
|
[105]
|
[ Q. Wang and X. Liu, The method of Lyapunov functionals and exponential stability of impulsive systems with time delay, Nonlinear Analysis, 66 (2007), 1465-1484.
|
|
[106]
|
[ Y. Wang, X. Shi, Z. Zuo, M. Chen and Y. Shao, On finite-time stability for nonlinear impulsive switched systems, Nonlinear Analysis: Real World Applications, 14 (2013), 807-814.
|
|
[107]
|
[ N. Wouw, P. Naghshtabrizi, M. Cloosterman and J. Hespanha, Tracking control for sampleddata systems with uncertain timevarying sampling intervals and delays, International Journal of Robust and Nonlinear Control, 20 (2010), 387-411.
|
|
[108]
|
[ Q. Wu, J. Zhou and L. Xiang, Global exponential stability of impulsive differential equations with any time delays, Applied Mathematics Letters, 23 (2010), 143-147.
|
|
[109]
|
[ T. Yang, Impulsive Control Theory, Berlin, Germany: Springer, 2001.
|
|
[110]
|
[ X. Yang, J. Cao and J. Lu, Stochastic synchronization of complex networks with nonidentical nodes via hybrid adaptive and impulsive control, IEEE Transactions On Circuits And Systems-Ⅰ: Regular Papers, 59 (2012), 371-384.
|
|
[111]
|
[ X. Yang, X. Li and J. Cao, Robust finite-time stability of singular nonlinear systems with interval time-varying delay, Journal of Franklin Institute, 355 (2018), 1241-1258.
|
|
[112]
|
[ X. Yang and J. Lu, Finite-time synchronization of coupled networks with Markovian topology and impulsive effects, IEEE Transaction on Automatic Control, 61 (2016), 2256-2261.
|
|
[113]
|
[ X. Zeng, C. Li, T. Huang and X. He, Stability analysis of complex-valued impulsive systems with time delay, Applied Mathematics and Computation, 256 (2015), 75-82.
|
|
[114]
|
[ W. Zhang, Y. Tang, J. Fang and X. Wu, Stability of delayed neural networks with timevarying impulses, Neural Networks, 36 (2012), 59-63.
|
|
[115]
|
[ W. Zhang, Y. Tang, Q. Miao and W. Du, Exponential synchronization of coupled switched neural networks with mode-dependent impulsive effects, IEEE Transactions on Neural Networks and Learning Systems, 24 (2013), 1316-1326.
|
|
[116]
|
[ X. Zhang and X. Li, Input-to-state stability of non-linear systems with distributed delayed impulses, IET Control Theory & Applications, 11 (2017), 81-89.
|
|
[117]
|
[ X. Zhang, X. Li, J. Cao and F. Miaadi, Design of delay-dependent controllers for finite-time stabilization of delayed neural networks with uncertainty, Journal of Franklin Institute, 355 (2018), 5394-5413.
|
|
[118]
|
[ X. Zhang, X. Lv and X. Li, Sampled-data based lag synchronization of chaotic delayed neural networks with impulsive control, Nonlinear Dynamics, 90 (2017), 2199-2207.
|
|
[119]
|
[ Y. Zhang and J. Sun, Stability of impulsive functional differential equations, Nonlinear Analysis: Theory, Methods and Applications, 68 (2008), 3665-3678.
|
|
[120]
|
[ Y. Zhang and J. Sun, Stability of impulsive infinite delay differential equations, Applied Mathematics Letters, 19 (2006), 1100-1106.
|
|
[121]
|
[ Y. Zheng, H. Li, X. Ding and Y. Liu, Stabilization and set stabilization of delayed Boolean control networks based on trajectory stabilization, Journal of the Franklin Institute, 354 (2017), 7812-7827.
|
|
[122]
|
[ Q. Zhu and X. Li, Exponential and almost sure exponential stability of stochastic fuzzy delayed Cohen-Grossberg neural networks, Fuzzy Sets and Systems, 203 (2012), 74-94.
|
|
[123]
|
[ Q. Zhu, F. Xi and X. Li, Robust exponential stability of stochastically nonlinear jump systems with mixed time delays, Journal of Optimization Theory and Applications, 154 (2012), 154-174.
|
|
[124]
|
[ M. Zou, A. Liu and Z. Zhang, Oscillation theorems for impulsive parabolic differential system of neutral type, Discrete & Continuous Dynamical Systems-B, 22 (2017), 2351-2363.
|









 DownLoad:
DownLoad: