1. Introduction
In ecological systems, spatially heterogeneous distributions of many species have been observed, for example, patchiness of plankton in aquatic systems [36]. Although such heterogeneity of species may be attributed to unevenly distributed landscapes, it may also occur in an almost homogeneous environment [36,19]. One interesting question is that what are the mechanisms behind the spatial heterogeneity of species in a homogeneous environment? Generally, movement or dispersal of a species and its interactions with other species may lead to pattern formation, and predator-prey type is such an interaction.
Pattern formation of predator-prey systems has been studied extensively (see [23,3,33,31,21,45,39,34] for example). In general, if both prey and predators move randomly in habitats, prey-dependent only functional responses, including the Holling type Ⅰ, Ⅱ, Ⅲ functional responses, can't generate spatially heterogeneous distributions. In such systems, the density-dependent death rate of predators or the Allee effect in prey's growth plays a critical role in determining spatial patterns [23,24,29,25,38,27,20]. On the other hand, competition between predators alone may allow pattern formation in predator-prey systems, which includes ratio-dependent functional response, the Beddington-DeAngelis functional response, and their generalizations [3,33,31]. Pattern formation of predator-prey models with time delay in the functional response due to handing time of the predator is also studied [47,44,9].
In addition to pure random movement of prey and predators, directed movement of predators has attracted much attention in recent years and has inspired numerous research about the so called prey-taxis problems (see [1,8,18,37,41,43,35] for example). A common feature of the models in the aforementioned papers lies in that the movement of predators is affected by the density gradient of prey, in addition to random movement. In analogy to the well-known chemotaxis, predators are attracted by prey-taxis and tend to move to habitats with higher prey density. Such biased movement allows predators to forage prey more effectively. In [1,37], the global existence of weak solution and classical solution were proved respectively. As an extension of [1,37], the authors in [43] proved the global existence of classical solution with more general local reaction terms and established the uniform persistence of the solutions as well. Global stability result of a predator-prey model with prey-taxis is obtained in recent work [17], where a broad range of growth and predation functions are considered. In [18], pattern formation was studied under various functional responses between prey and predators. The authors concluded that pattern formation may occur if the prey-taxis was small and certain functional responses or growth functions were chosen [18].
Besides the fact that predators forage prey, prey may avoid predators actively as well. Almost all species perceive predation risk to some extent and avoid predation by showing various anti-predator behaviors [10,11]. More importantly, such anti-predator behaviors carry a cost on the reproduction success of prey [46]. Zanette et al. [46] experimentally verified that anti-predator behaviors alone caused a 40% reduction in the reproduction rate of song-sparrows when all direct predations were eliminated (see [40] for a thorough discussion about the cost of fear). Recent work of Ryan and Cantrell [30] modelled avoidance behaviors of prey in an intraguild predation community with heterogeneous distribution of resources. Biktashev et al. [8] also considered avoided prey but in a homogeneous environment and identified several patterns numerically. However, the cost of anti-predator behaviors of prey is ignored in the models of Ryan and Cantrell and Biktashev et al. [30,8].
In this paper, we extend the model based on Wang et al.. by explicitly incorporating spatial effects, where spatial structures are ignored in [40]. We study how the anti-predator behaviors and the corresponding cost would affect the spatial distribution of prey and predators. In Section 2, the model formulation including the so-called predator-taxis is proposed. In Section 3, the global existence of classical solution is established. In Section 4, pattern formation is analyzed both theoretically and numerically for different functional responses. We end the paper in Section 5 by giving conclusions and discussions.
2. Model formulation
Let u(x,t) and v(x,t) represent the densities of prey and predators at position x and time t respectively. As discussed in the introduction, we assume that predators move randomly to forage prey but prey can perceive predation risk and act accordingly to avoid predators actively [10,11]. As a consequence, the dispersal of prey is a directed movement towards lower density of predators in addition to random movement. Ideally, the avoidance behavior of prey leads to a repulsion of prey to lower gradient of predator density. Therefore, the flux of prey is
and the flux of predators is
where γ(u,v)≥0 represents the repulsion effect of the predator-taxis. Hence, a general reaction-diffusion-advection model with avoidance behaviors of prey is
|
ut=∇⋅(du∇u+γ(u,v)u∇v)+f(u,v),vt=dvΔv+g(u,v),
|
(1)
|
where f(u,v) and g(u,v) represent local interactions of predators and prey, du,dv are random diffusion rates of prey and predators respectively, γ(u,v) is the sensitivity of prey to predation risk (i.e. predator-taxis). Here, we assume that
Taking into account the volume filling effect [14,28,13] for γ(u,v), we adopt α(v)=α as a constant and
|
β(u)={1−uM,if0≤u≤M,0,ifM<u,
|
(3)
|
where M measures the maximum number of prey that a unit volume can accommodate. If the number of prey goes beyond the volume M, prey can no longer squeeze into nearby space and therefore the tendency of directed movement goes to 0. For local reaction terms, we consider
|
f(u,v)=f0(k0α,v)r0u−du−au2−up(u,v)v,g(u,v)=v[−m(v)+cup(u,v)],
|
(4)
|
where
satisfies the same hypotheses as f(k,v) in [40] with k0 as a nonnegative constant. In fact, this function models the cost of anti-predator responses in the reproduction rate of prey. The successful reproduction rate of prey decreases if the defense level or equivalently predator-taxis sensitivity α increases. Similarly, higher predator density also decreases the local reproduction rate of prey because it would be easier for the prey to perceive predation risk and adopt corresponding avoidance behaviors in the presence of more predators. Here k0 is a constant which reflects the magnitude that anti-predator behaviors exert on the local reproduction of prey. In (4), d is the natural death rate of prey, a represents the death due to intra-species competition, p(u,v) denotes the functional response between predators and prey, and m(v) is the death rate of predators. We consider either density-independent death rate or density-dependent death rate of predators, i.e.
|
m(v)=m1orm(v)=m1+m2v.
|
(6)
|
As indicated in [23,24,20], the density dependence of predator mortality plays a critical role in pattern formation under certain situations.
We assume that individuals live in an isolated bounded domain Ω∈Rn with homogeneous environment and ∂Ω is smooth. Hence, no-flux boundary condition is imposed
|
Ju⋅n=du∂u∂μ+γ(u,v)u∂v∂μ=0,Jv⋅n=dv∂v∂μ=0,
|
(7)
|
where μ is the unit outward normal vector at ∂Ω. In fact, no-flux boundary condition (7) is equivalent to Neumann boundary condition
Therefore, by (1), (2), (4) and (8), we obtain a spatial model with the avoidance behaviors of prey and the cost of anti-predator behaviors, given by the following system
|
∂u∂t=duΔu+α∇⋅(β(u)u∇v)+r0u1+k0αv−du−au2−up(u,v)v,∂v∂t=dvΔv+v[−m(v)+cup(u,v)],∂u∂μ=0,∂v∂μ=0,∀x∈∂Ω,u(x,0)=u0(x)≥0,v(x,0)=v0(x)≥0,
|
(9)
|
where u0(x),v0(x) are continuous functions.
3. Global existence of classical solution
First, we establish the global existence of classical solutions of (9). It is clear that the carrying capacity of prey in (9) is K=(r0−d)/a. By [28], we assume that
which is reasonable because K measures the maximum capacity of the environment but M merely represents the maximum number that one unit volume can be filled by prey. Notice that β(u) is not differentiable at u=M. In order to obtain classical solutions, similar to [42], we make a smooth extension of β(u) by
|
ˉβ(u)={>1,u<0,β(u),0≤u≤M,<0,M<u.
|
(11)
|
By proving the global existence of classical solutions of system
|
∂u∂t=duΔu+α∇⋅(ˉβ(u)u∇v)+r0u1+k0αv−du−au2−up(u,v)v,∂v∂t=dvΔv+v[−m(v)+cup(u,v)],∂u∂μ=0,∂v∂μ=0,∀x∈∂Ω,u(x,0)=u0(x)≥0,v(x,0)=v0(x)≥0,
|
(12)
|
we obtain the global existence of classical solutions of (9) because β(u)=ˉβ(u) if 0≤u≤M and we will show that u∈[0,M] later. Let ρ∈(n,+∞), then W1,ρ(ˉΩ,R2) is continuously embedded in C(Ω,R2). We consider solutions of (12) in
|
X:={ω∈W1,ρ(Ω,R2)⏐∂ω∂μ=0on∂Ω}.
|
Then we have the following lemma.
Lemma 3.1. The following statements hold:
(ⅰ) System (12) has a unique solution (u(x,t),v(x,t))∈X defined on Ω×(0,T) satisfying (u,v)∈C((0,T),X)∩C2,1((0,T)×ˉΩ,R2), where T depends on initial data (u0,v0)∈X.
(ⅱ) Define X1={(u,v)∈R2|0≤u≤M,v≥0} at G⊂R2 such that X1⊂G. If for every G⊂R2 containing X1, (u,v) is bounded away from the boundary of G in L∞(Ω) norm for t∈(0,T), then T=∞, meaning that the solution (u,v) exists globally.
Proof. Let ω=(u,v)T. Then system (12) can be written as
|
{ωt=∇⋅(a(ω)∇ω)+F(ω)inΩ×(0,+∞),Bω=0on∂Ω×(0,+∞),ω(⋅,0)=(u0,v0)TinΩ,
|
(13)
|
where
|
a(ω)=(duαˉβ(u)u0dv),
|
(14)
|
and
|
F(ω)=(r0u1+k0αv−du−au2−up(u,v)v,v[−m(v)+cup(u,v)])T,Bω=∂ω∂n.
|
(15)
|
Because eigenvalues of a(ω) are all positive, then (13) is normally elliptic [4,6]. Hence local existence in (ⅰ) follows from Theorem 7.3 in [4]. Because (13) is an upper-triangular system, global existence of solution in (ⅱ) follows from Theorem 5.2 in [5].
From (ⅱ) of Lemma 3.1, to prove the global existence of solutions, it remains to show that (u,v) are bounded away from the boundary of G in L∞ norm.
Theorem 3.2. Assume that 0≤u0≤M, then the solution (u,v) satisfies u(x,t)≥0,v(x,t)≥0, and it exists globally in time.
Proof. Define the operator
|
Lu=ut−duΔu−α∇(ˉβ(u)u∇v)−r0u1+k0αv+du+au2+p(u,v)uv.
|
(16)
|
Because 0≤u0, u=0 is a lower solution of the equation. Plug in u=M into (16) to obtain
|
LM=−r0M1+k0αv+dM+aM2+p(M,v)Mv=M(d+aM+p(M,v)v−r01+k0αv).
|
(17)
|
If v≥0, then we obtain
Because of the restriction (10), choosing sufficiently large M gives
In addition, we have
By (19) and (20), we know that u=M is an upper solution of the u equation. Therefore, by comparison principle of parabolic equations [32], we have
Now we prove the L∞ norm of v is bounded. Here we show only the proof for the case of m(v)=m1 because the proof of the case where m(v)=m1+m2v is similar and is thus omitted. Choose v(0)=v0≥0. Then it is obvious that v=0 is a lower solution of the v equation, which gives v≥0. It remains to show that ‖v‖L∞(Ω) is bounded. Integrating the first equation of (12), we obtain
|
∫Ωutdx=∫Ω∇⋅(du∇u+αˉβ(u)u∇v)dx+∫Ω(r0u1+k0αv−du−au2−p(u,v)uv)dx=∫∂Ω(du∇u+αˉβ(u)u∇v)⋅ndS+∫Ω(r0u1+k0αv−du−au2−p(u,v)uv)dx=∫Ω(r0u1+k0αv−du−au2−p(u,v)uv)dx.
|
(22)
|
Similarly, integrating the second equation of (12) gives
|
∫Ωvtdx=∫Ωv[−m1+cp(u,v)u]dx.
|
(23)
|
Multiplying (22) by c and adding the resulting equation to (23) gives
|
ddt∫Ω(cu+v)dx=∫Ω(r0cu1+k0αv−cdu−cau2−m1v)dx=c∫Ω(r01+k0αv+m1−d−au)udx−m1∫Ω(cu+v)dx≤c∫Ω(r0+m1)udx−m1∫Ω(cu+v)dx≤c|Ω|(r0+m1)M−m1∫Ω(cu+v)dx.
|
(24)
|
By (24), we obtain
|
ddt‖cu+v‖L1≤c|Ω|(r0+m1)M−m1‖cu+v‖L1
|
(25)
|
From (25), we obtain that
which shows that \Vert c\, u+v \Vert_{L^1} is bounded. From (12), the growth of v is dependent only on u, (i.e. predators are specialist predators), which falls into "food pyramid" condition in [2]. Hence by Theorem 3.1. in [2], the boundedness of \Vert v \Vert_{L^1} implies that of \Vert v \Vert_{L^{\infty}} and this completes the proof.
4. Pattern formation
Now we analyze the pattern formation of (9) with general reaction terms defined in (4). Assume that (u_s, v_s) is a spatially homogeneous steady state of (9). Let
|
u(x, t) = u_s+\epsilon\, \tilde{u}(x, t), \;\;v(x, t) = v_s+\epsilon\, \tilde{v}(x, t),
|
(26)
|
where \epsilon \ll 1. By substituting (26) into (9) with general reaction terms, equating first-order terms with respect to \epsilon and neglecting higher-order terms, we obtain the linearized system at (u_s, v_s):
|
\frac{\partial u}{\partial t} = d_u\, \Delta u+\alpha\, \beta(u_s)\, u_s\, \Delta v+f_u(u_s, v_s)\, u+f_v(u_s, v_s)\, v, \\
\frac{\partial v}{\partial t} = d_v\, \Delta v+g_u(u_s, v_s)\, u+g_v(u_s, v_s)\, v,
|
(27)
|
where u(x, t), v(x, t) are still used instead of \tilde{u}(x, t), \tilde{v}(x, t) for notational convenience. The linearized system (27) can be written as the matrix form:
|
\frac{\partial \omega}{\partial t} = D\, \Delta \omega+A\, \omega,
|
(28)
|
where
|
\omega = \left(\begin{array}{c}
u\\
v\\
\end{array}\right), \;\;\;
D = \left( \begin {array}{cc}
d_u&\alpha\, \beta(u_s)\, u_s\\
0&d_v\\
\end {array} \right), \;\;\;
A = \left( \begin {array}{cc}
f_u&f_v\\
g_u&g_v\\
\end {array} \right).
|
By (28), the characteristic polynomial of the linearized system at (u_s, v_s) is
|
\vert \lambda\, \mathrm{I}+k^2\, D-A \vert = 0,
|
(29)
|
where k \geq 0 is the wave number [26]. Expanding the left side of (29), we obtain that
|
\lambda^2+a\left(k^2\right)\, \lambda+b\left(k^2\right) = 0,
|
(30)
|
where
|
a\left(k^2\right) = \left(d_u+d_v\right)k^2-\left(f_u+g_v\right), \\
b\left(k^2\right) = d_u\, d_v\, k^4+\left(g_u\, \alpha\, \beta(u_s)\, u_s-f_u\, d_v-g_v\, d_u\right)k^2+f_u\, g_v-f_v\, g_u.
|
(31)
|
Here in (30), \lambda = \lambda \left(k\right) are eigenvalues which determine the stability of the steady state (u_s, v_s). For k = 0, the two roots of (30) satisfy
|
\lambda_1^0+\lambda_2^0 = f_u+g_v, \;\;\;\lambda_1^0\, \lambda_2^0 = f_u\, g_v-f_v\, g_u.
|
(32)
|
Assume that
|
f_u+g_v<0, \;f_u\, g_v-f_v\, g_u>0,
|
(33)
|
meaning that the steady state (u_s, v_s) is linearly stable when there is no spatial effect. Now for k>0, the two roots of (30) satisfy
|
\left\{ \begin{array}{l}
\lambda _1^k + \lambda _2^k =\left( {{f_u} + {g_v}} \right) - \left( {{d_u} + {d_v}} \right){\mkern 1mu} {k^2}, \\
\lambda _1^k{\mkern 1mu} \lambda _2^k ={d_u}{\mkern 1mu} {d_v}{\mkern 1mu} {k^4} + \left( {{g_u}{\mkern 1mu} \alpha {\mkern 1mu} \beta ({u_s}){\mkern 1mu} {u_s} - {f_u}{\mkern 1mu} {d_v} - {g_v}{\mkern 1mu} {d_u}} \right){k^2} + {f_u}{\mkern 1mu} {g_v} - {f_v}{\mkern 1mu} {g_u}.
\end{array} \right.
|
(34)
|
Because of d_u>0, d_v>0 and assumption (33), we obtain that \lambda_1^k+\lambda_2^k<0 for all k = 1, 2 \cdots from (34). Therefore, if \lambda_1^k\, \lambda_2^k>0 for all k>0, then (u_s, v_s) remains stable. If \lambda_1^k\, \lambda_2^k<0 for some k>0, then (u_s, v_s) becomes unstable, and such diffusion driven instability is often referred to as the Turing instability, which will lead to occurrence of spatially heterogeneous steady state, implying formation of spatial patterns. Summarizing the above analysis, we have the following Theorem.
Theorem 4.1. Assume (33) holds, spatial homogeneous steady state (u_s, v_s) of (9) may lose stability only if
|
g_u\, \alpha\, \beta(u_s)\, u_s-f_u\, d_v-g_v\, d_u<0,
|
(35)
|
|
\left(g_u\, \alpha\, \beta(u_s)\, u_s-f_u\, d_v-g_v\, d_u\right)^2-4\, d_u\, d_v\, \left(f_u\, g_v-f_v\, g_u\right)>0
|
(36)
|
hold.
Remark 1. Under the assumption (33), f_u\, g_v-f_v\, g_u>0, and hence, by Theorem 4.1, pattern formation of (9) can not occur if
|
g_u\, \alpha\, \beta(u_s)\, u_s>f_u\, d_v+g_v\, d_u.
|
(37)
|
4.1. Linear functional response
Following above general analysis of pattern formation of spatial homogeneous equilibrium, we now proceed to further detailed analysis when a particular functional response is chosen. First, we analyze possible pattern formation of (9) with the linear functional response, where p(u, v) = p in (9). Either for the density-independent death rate or for the density-dependent death rate of predators in (6), system (9) admits several spatial homogeneous steady states. For (9), in addition to a trivial equilibrium E_0(0, 0), a semi-trivial equilibrium E_1((r_0-d)/a, 0) exists if r_0>d is satisfied. There exists a unique positive equilibrium E(\bar{u}, \bar{v}) for either predator death function in (6) if
|
r_0>d+\frac{a\, m_1}{c\, p}
|
(38)
|
holds. However, formulas for E(\bar{u}, \bar{v}) are different for each function, where
|
\left\{ \begin{array}{l}
\bar u =\frac{{{m_1}}}{{c{\mkern 1mu} p}}, \;\bar v =\frac{{\left( {\alpha {\mkern 1mu} c{\mkern 1mu} d{\mkern 1mu} {k_0}{\mkern 1mu} p + a{\mkern 1mu} \alpha {\mkern 1mu} {k_0}{\mkern 1mu} {m_1} + c{\mkern 1mu} {p^2}} \right) - \sqrt {{\Delta _1}} }}{{ - 2{\mkern 1mu} {k_0}{\mkern 1mu} \alpha {\mkern 1mu} {p^2}{\mkern 1mu} c}}, \\
{\Delta _1} =4{\mkern 1mu} \alpha {\mkern 1mu} c{\mkern 1mu} {k_0}{\mkern 1mu} {p^2}{\mkern 1mu} ( - c{\mkern 1mu} d{\mkern 1mu} p + c{\mkern 1mu} p{\mkern 1mu} {r_0} - a{\mkern 1mu} {m_1}) + {( - \alpha {\mkern 1mu} c{\mkern 1mu} d{\mkern 1mu} {k_0}{\mkern 1mu} p - a{\mkern 1mu} \alpha {\mkern 1mu} {k_0}{\mkern 1mu} {m_1} - c{\mkern 1mu} {p^2})^2}
\end{array} \right.
|
(39)
|
if m(v) = m_1 while
|
\left\{ \begin{array}{l}
\bar{v} = \frac{\left(c\, p^2+a\, m_2+k_0\, \alpha\, (d\, c\, p+a\, m_1)\right)-\sqrt{\Delta_2}}{-2\, k_0\, \alpha\, (c\, p^2+a\, m_2)},
\;\bar{u} = \frac{m_1+m_2\, \bar{v}}{c\, p}, \\
\Delta_2 = 4\, k_0\, \alpha\, (c\, p^2+a\, m_2)\, (-c\, d\, p+c\, p\, r_0-a\, m_1)\\
+(-\alpha\, c\, d\, k_0\, p-a\, \alpha\, k_0\, m_1-c\, p^2-a\, m_2)^2
\end{array} \right.
|
(40)
|
if m(v) = m_1+m_2\, v. Direct calculations show that pattern formation can not occur around any constant steady state if the functional response is linear, which leads to the following proposition.
Proposition 1. Either for m(v)=m_1 or for m(v)=m_1+m_2\, v, pattern formation can not occur around any of the constant steady states E_0, E_1, and E(\bar{u}, \bar{v}).
Proof. Because the proofs for all steady states are similar, we show only the proof of non-existence of pattern formation around E(\bar{u}, \bar{v}) when m(v) = m_1 here. Calculations give
|
{f_u} =- a{\mkern 1mu} \bar u < 0, \;{f_v} =\bar u{\mkern 1mu} \left( { - \frac{{{r_0}{\mkern 1mu} {k_0}{\mkern 1mu} \alpha }}{{{{(1 + {k_0}{\mkern 1mu} \alpha {\mkern 1mu} \bar v)}^2}}} - p} \right) < 0, \;{g_u} =c{\mkern 1mu} p{\mkern 1mu} \bar v, \;{g_v} =0.
|
(41)
|
This immediately verifies (33), implying that E(\bar{u}, \, \bar{v}) is locally stable if it exists when there is no spatial effect. Further substitution of (41) also shows that (37) holds, and then there is no pattern formation around E(\bar{u}, \bar{v}), by Remark 1.
In fact, under additional conditions, we can prove that the unique positive equilibrium E(\bar{u}, \bar{v}) is globally stable if m(v) = m_1+m_2\, v.
Theorem 4.2. Under existence condition (38) for E(\bar{u}, \bar{v}), with density-dependent death rate m(v) = m_1+m_2\, v for the predator, E(\bar{u}, \bar{v}) is globally asymptotically stable if
|
\left\{ \begin{array}{l}
c\, p\, M>m_1, \;4\, d_u\, d_v\, \bar{v}>c\, \alpha^2\, \bar{u}\, {v^{*}}^2, \\
\min \left\{a, \frac{m_2}{c}\right\}>\frac{r_0\, k_0\, \alpha}{2\, (1+k_0\, \alpha\, \bar{v})}
\end{array} \right.
|
(42)
|
hold, where v^{*} = (c\, p\, M-m_1)/m_2 and \bar{u}, \bar{v} are given in (40).
Proof. As indicated in the proof of Lemma 3.1, the L^{\infty} norm of v(x, t) is bounded for either m(v) = m_1 or m(v) = m_1+m_2\, v. In fact, if the death rate of predators is the density-dependent one, then a constant upper solution for the v equation exists. Define
|
\mathcal{F}v = v_t-d_v\, \Delta v-v\, \left(-m_1-m_2\, v+c\, p\, u\right).
|
(43)
|
Then by substituting v = v^{*} into (43), we obtain
|
\mathcal{F} v^{*} = -v^{*}\, \left(-m_1-m_2\, v^{*}+c\, p\, u\right) \geq 0
|
(44)
|
because 0 \leq u \leq M. By the parabolic comparison principle [32], we obtain that v = v^{*} is an upper solution of v(x, t) if v_0(x, t) \leq v^{*}. Therefore, X: = \{(u, v)\in R^2 \vert 0 \leq u \leq M, \; 0 \leq v \leq v^{*}\} is positive invariant for (9). Choose a Lyapunov functional as
|
V(u, v) = \int_{\Omega}\left( \int_{\bar{u}}^{u} \frac{u-\bar{u}}{u} du +\frac{1}{c} \int_{\bar{v}}^v \frac{v-\bar{v}}{v} dv \right)\, dx.
|
(45)
|
If (u, v) is the solution to system (9), then we obtain
|
\begin{align}\label{lyapfun0} \frac{dV(u, v)}{dt}& = \int_{\Omega} \left(\frac{u-\bar{u}}{u} u_t+\frac{1}{c} \frac{v-\bar{v}}{v}v_t\right)dx \nonumber\\ & = \int_{\Omega} \frac{u-\bar{u}}{u} \Big(d_u\, \Delta u+\alpha \nabla \cdot(\beta(u)\, u\nabla v)+\frac{r_0\, u}{1+k_0\, \alpha\, v}-d\, u-a\, u^2 \nonumber\\ &-p\, u\, v\Big) dx\\ &+\frac{1}{c} \int_{\Omega}\frac{v-\bar{v}}{v} \left[d_v\, \Delta_v+v(-m_1-m_2\, v+c\, p\, u)\right] dx.
\nonumber \end{align}
|
(46)
|
Rearranging (46) by separating the reaction and dispersal terms gives
|
\frac{dV(u, v)}{dt} = V_1(u, v)+V_2(u, v),
|
(47)
|
where
|
\begin{align}\label{V1V2} V_1(u, v)& = \int_{\Omega} \frac{u-\bar{u}}{u} \lbrack d_u\, \Delta u+\alpha \nabla \cdot(\beta(u)\, u\nabla v) \rbrack+ \frac{v-\bar{v}}{c\, v} d_v\, \Delta v \, dx, \nonumber\\ V_2(u, v)& = \int_{\Omega} (u-\bar{u})\left(\frac{r_0}{1+k_0\, \alpha\, v}-d-a\, u-p\, v\right) \\ &+\frac{v-\bar{v}}{c} (-m_1-m_2\, v+c\, p\, u) \, dx. \nonumber \end{align}
|
(48)
|
By using Neumann boundary condition (8) and divergence theorem, we obtain that
|
\begin{align}\label{V1} V_1(u, v)& = -d_u \int_{\Omega} \nabla \left(\frac{u-\bar{u}}{u}\right)\cdot \nabla u \, dx -\frac{d_v}{c}\int_{\Omega}\nabla v \cdot \, \nabla \left(\frac{v-\bar{v}}{v}\right)\, dx \nonumber\\ &-\alpha\int_{\Omega} \beta(u)\, u\, \nabla v\, \cdot \nabla \left(\frac{u-\bar{u}}{u}\right)\, dx \nonumber\\ &\leq -d_u\, \bar{u} \int_{\Omega} \frac{\vert \nabla u \vert^2}{u^2} \, dx-\frac{d_v\, \bar{v}}{c} \int_{\Omega} \frac{\vert \nabla v \vert^2}{v^2} \, dx +\alpha\, \bar{u} \int_{\Omega} \frac{\beta(u)}{u} \vert\nabla u\vert\, \vert\nabla v\vert\, dx
\end{align}
|
(49)
|
|
= -\int_{\Omega} X^{\mathsf{T}}\, A\, X
|
(50)
|
where
|
X = \left(\begin{array}{c}
\vert\nabla u\vert\\
\vert\nabla v\vert\\
\end{array}\right), \;\;\;
A = \left( \begin {array}{cc}
\displaystyle{ \frac{d_u\, \bar{u}}{u^2}}&\displaystyle -{\frac{\alpha\, \bar{u}\, \beta(u)}{2\, u}}\\
\displaystyle -{\frac{\alpha\, \bar{u}\, \beta(u)}{2\, u}}&\displaystyle{\frac{d_v\, \bar{v}}{c\, v^2}}\\
\end {array} \right).\;\;\;
|
It is clear that V_1(u, v)<0 if A is a positive definite matrix, which is equivalent to show that the trace and determinant of A are positive. The trace of A, which is tr {A} = (d_u\, \bar{u})/(u^2)+(d_v\, \bar{v})/(2\, v^2) is clearly positive. The determinant of A is
|
\det{A} = \frac{d_u\, d_v\, \bar{u}\, \bar{v}}{c\, u^2\, v^2}-\frac{\alpha^2\, \bar{u}^2\, \beta^2(u)}{4\, u^2}.
|
(51)
|
From (51), we obtain that \det{A}>0 is equivalent to
|
4\, d_u\, d_v\, \bar{v}>c\, \alpha^2\, \bar{u}\, v^2\, \beta^2(u).
|
(52)
|
Because 0 \leq u \leq M, 0 \leq v \leq v^{*}, a sufficient condition for (52) to hold is
|
f_1: = 4\, d_u\, d_v\, \bar{v}>c\, \alpha^2\, \bar{u}\, {v^{*}}^2.
|
(53)
|
Therefore, we obtain that
|
V_1(u, v) = -\int_{\Omega} X^{\mathsf{T}}\, A\, X \leq 0
|
(54)
|
if (53) is satisfied.
Now we estimate V_2(u, v) as
|
\begin{align}\label{V2} V_2(u, v)& = \int_{\Omega} (u-\bar{u})\Bigg( \frac{r_0}{1+k_0\, \alpha\, v}-a\, u-p\, v-\left(\frac{r_0}{1+k_0\, \alpha\, \bar{v}}-a\, \bar{u}-p\, \bar{v}\right)\Bigg)\nonumber\\ &+\frac{v-\bar{v}}{c}\left(m_2\, \bar{v}-c\, p\, \bar{u}-m_2\, v+c\, p\, u\right)\, dx \nonumber \\ & = -a\, \int_{\Omega}(u-\bar{u})^2\, dx-\frac{m_2}{c}\int_{\Omega}(v-\bar{v})^2\, dx \nonumber \\ &-\int_{\Omega}\frac{r_0\, k_0\, \alpha}{1+k_0\, \alpha\, \bar{v}}\, \frac{(u-\bar{u})(v-\bar{v})}{1+k_0\, \alpha\, v}\, dx\\ &\leq -a\, \int_{\Omega}(u-\bar{u})^2\, dx-\frac{m_2}{c}\int_{\Omega}(v-\bar{v})^2\, dx \nonumber\\ &+\int_{\Omega}\frac{r_0\, k_0\, \alpha}{1+k_0\, \alpha\, \bar{v}}\, \frac{1}{1+k_0\, \alpha\, v}\, \vert(u-\bar{u})\vert \vert(v-\bar{v})\vert \, dx \nonumber \end{align}
|
(55)
|
|
\begin{align} &\leq -a\, \int_{\Omega}(u-\bar{u})^2\, dx-\frac{m_2}{c}\int_{\Omega}(v-\bar{v})^2\, dx \nonumber \\ &+\frac{r_0\, k_0\, \alpha}{2\, (1+k_0\, \alpha\, \bar{v})}\, \int_{\Omega} \left((u-\bar{u})^2+(v-\bar{v})^2\right)\, dx \nonumber \\ & = -\left(a-\frac{r_0\, k_0\, \alpha}{2\, (1+k_0\, \alpha\, \bar{v})}\right)\int_{\Omega}(u-\bar{u})^2\, dx \nonumber \\ &-\left(\frac{m_2}{c}-\frac{r_0\, k_0\, \alpha}{2\, (1+k_0\, \alpha\, \bar{v})}\right) \int_{\Omega} (v-\bar{v})^2\, dx \nonumber \\ &\leq 0 \end{align}
|
(56)
|
if
|
f_2: = \min \left\{a, \frac{m_2}{c}\right\}>\frac{r_0\, k_0\, \alpha}{2\, (1+k_0\, \alpha\, \bar{v})}
|
(57)
|
holds. From (55), under (57), the only possibility such that \dot{V}(u, v) = 0 is (u, v) = (\bar{u}, \bar{v}). Hence, by the LaSalle invariance principle [22], we obtain the global stability of E(\bar{u}, \bar{v}) if (42) holds.
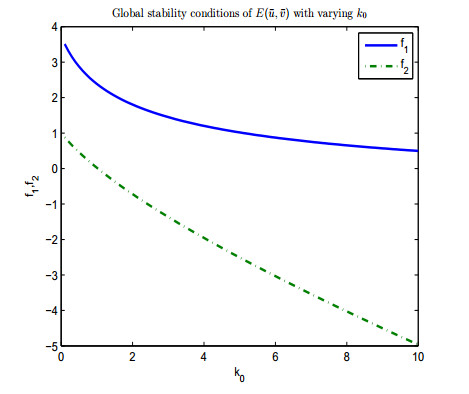
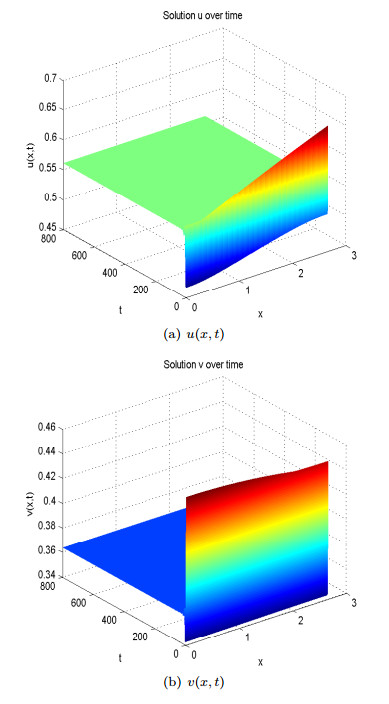
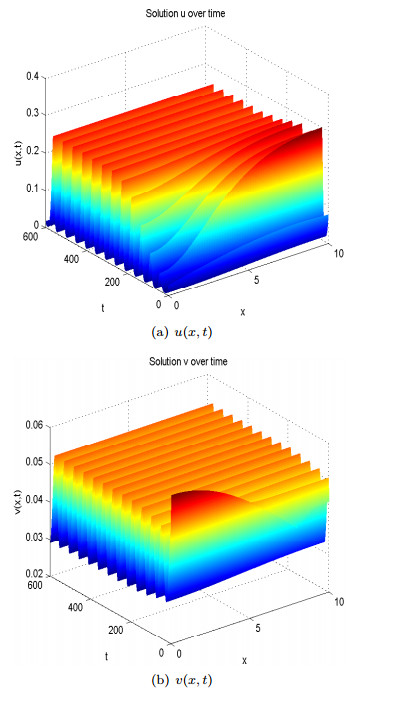
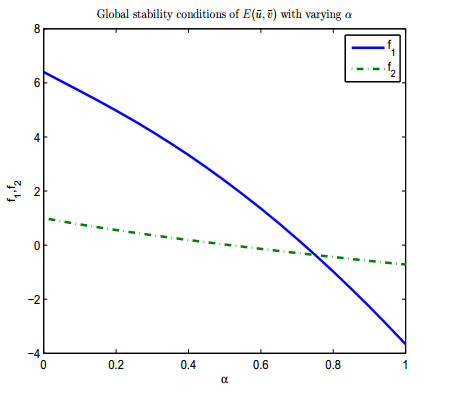
By checking conditions in (42), we can not obtain an explicit formula for the predator-taxis sensitivity \alpha due to the complex expressions of \alpha in E(\bar{u}, \bar{v}). Hence, we employ numerical simulations to explore the role that \alpha plays in global stability of E(\bar{u}, \bar{v}) by testing the parameter dependence of \alpha in (53) and (57). As shown in Figure 1, we see that E(\bar{u}, \bar{v}) is globally asymptotically stable if \alpha is small. Similarly, by examining the impact of k_0 on the global stability of E(\bar{u}, \bar{v}), we observe that E(\bar{u}, \bar{v}) is globally asymptotically stable if k_0 is small, as indicated in Figure 2. In biological interpretation, Figures 1 and 2 show that prey and predators will tend to a steady state if prey are less sensitive to perceive predation risk or the cost of anti-predator defense on the local reproduction rate of prey is small, regardless of spatial effect, provided that the linear functional response is adopted.
4.2. The Holling-type Ⅱ functional response
Now we analyze possible pattern formation of system (9) with the Holling type Ⅱ functional response [15,16] i.e.,
|
p(u, v) = \frac{p}{1+q\, u}.
|
(58)
|
For general death function of predators defined in (6), a trivial equilibrium E_0(0, 0) always exists and a semi-trivial equilibrium E_1((r_0-d)/a, 0) exists if r_0>d holds. If the death function of predators is density-independent, i.e. m(v) = m_1, a unique positive equilibrium E(\bar{u}, \bar{v}) exists if
|
c\, p>m_1\, q \,\,\,\,\,\,\mbox{and}\,\,\,\,\,\, r_0-d>\frac{a\, m_1}{c\, p-m_1\, q}
|
(59)
|
hold, where
|
\begin{align}\label{holling2posiuv} \bar{u}& = \frac{m_1}{c\, p-m_1\, q}, \;\bar{v} = \frac{-a_2-\sqrt{a_2^2-4\, a_1\, a_3}}{2\, a_1}, \nonumber \\ a_1& = -k_0\, \alpha\, (c\, p-m_1\, q)^2, \nonumber \\ a_2& = -\alpha\, c^2\, d\, k_0\, p +\alpha\, c\, d\, k_0\, m_1\, q-a\, \alpha\, c\, k_0\, m_1-c^2\, p^2+2\, c\, m_1\, p\, q-m_1^2\, q^2, \\ a_3& = -c\, (c\, d\, p-c\, p\, r_0-d\, m_1\, q+m_1\, q\, r_0+a\, m_1). \nonumber \end{align}
|
(60)
|
Calculations indicate that pattern formation can not occur around any of these steady states E_0, E_1, and E(\bar{u}, \bar{v}) if m(v) = m_1, which is shown in the following proposition.
Proposition2. Choose the functional response in (58) for (9). If the death function of predators is density-independent, then pattern formation can not occur around all the steady states E_0, E_1, and E(\bar{u}, \bar{v}) of system (9).
Proof. Here we only show the proof for the unique positive equilibrium E(\bar{u}, \bar{v}) because the proofs for E_0, \, E_1 are similar and are thus omitted. Direct calculations lead to
|
f_u = \bar{u}\left(\frac{p\, q\, \bar{v}}{(1+q\, \bar{u})^2}-a\right), \;
f_v = -\frac{r_0\, k_0\, \alpha\, \bar{u}}{(1+k_0\, \alpha\, \bar{v})^2}-\frac{p\, \bar{u}}{1+q\, \bar{u}}, \\
g_u = \frac{c\, p\, \bar{v}}{(1+q\, \bar{u})^2}, \;g_v = -m_1+\frac{c\, p\, \bar{u}}{1+q\, \bar{u}}.
|
(61)
|
By substituting \bar{u}, \bar{v} in (60) into (61), we obtain that f_v<0, \, g_u>0, \, g_v = 0. Then (33) can be simplified to f_u<0, and hence, (37) holds and therefore, pattern formation is impossible to occur around E(\bar{u}, \bar{v}).
Now we proceed to analyze the case where the death function of predators is the density-dependent one in (6). Similar analyses to that in Proposition 2 show that there is no pattern formation around E_0 and E_1. For the positive equilibrium E(\bar{u}, \bar{v}) when m(v) = m_1+m_2\, v, explicit formula of E(\bar{u}, \bar{v}) can not be obtained due to the complexity. However, under the extra conditions in (59), the existence of at least one positive equilibrium E(\bar{u}, \bar{v}) of (9) is guaranteed, as stated in the following lemma.
Lemma 4.3. If m(v) = m_1+m_2\, v, then there exists at least one positive equilibrium E(\bar{u}, \bar{v}) for (9) if (59) holds.
Proof. From (9), the positive equilibrium E(\bar{u}, \bar{v}) satisfies
|
\bar{u} = \frac{m_1+m_2\, \bar{v}}{(c\, p-m_1\, q)-m_2\, q\, \bar{v}}.
|
(62)
|
By (62), the positivity of \bar{u} requires that \bar{v}<\bar{v}_{\max}, where \bar{v}_{\max} is defined by
|
\bar{v}_{\max} = \frac{(c\, p-m_1\, q)}{m_2\, q}.
|
(63)
|
In addition, \bar{v} is determined by
|
L(\bar{v}): = a_1\, \bar{v}^4+a_2\, \bar{v}^3+a_3\, \bar{v}^2+a_4\, \bar{v}+a_5 = 0,
|
(64)
|
where
|
\begin{align} a_1& = -\alpha\, k_0\, m_2^2\, q^2, \;a_2 = m_2\, q\, (2\, \alpha\, c\, k_0\, p-2\, \alpha\, k_0\, m_1\, q-m_2\, q), \nonumber \\ a_3& = -(c^2\, p^2+((-d\, m_2-2\, m_1\, p)\, q+a\, m_2)\, c+q^2\, m_1^2)\, k_0\, \alpha+2\, q\, m_2\, (c\, p-m_1\, q), \nonumber\\ a_4& = (-\alpha\, d\, k_0\, p-p^2)\, c^2+(((\alpha\, d\, k_0+2\, p)\, m_1+m_2\, (d-r_0))\, q\\ &-a\, (\alpha\, k_0\, m_1+m_2))\, c -q^2\, m_1^2, \nonumber \\ a_5& = -c\, ((-d\, q+q\, r_0+a)\, m_1+c\, p\, (d-r_0)). \nonumber \end{align}
|
(65)
|
By substituting \bar{v} = 0 into (64), we obtain
|
L(\bar{v} = 0) = a_5>0 \Leftrightarrow (c\, p-m_1\, q)(r_0-d)>a\, m_1,
|
(66)
|
which is equivalent to (59). Moreover, substituting \bar{v} = \bar{v}_{\max} into (64) gives
|
L(\bar{v} = \bar{v}_{\max}) = -\frac{a\, c^2\, p\, (\alpha\, c\, k_0\, p-\alpha\, k_0\, m_1\, q+m_2\, q)}{m_2\, q^2}<0
|
(67)
|
if (59) holds. Therefore, by the intermediate value theorem, there exists at least one \bar{v} \in [0, \, \bar{v}_{\max}] such that L(\bar{v}) = 0. Hence, the existence of at least one positive equilibrium E(\bar{u}, \bar{v}) is guaranteed if (59) holds.
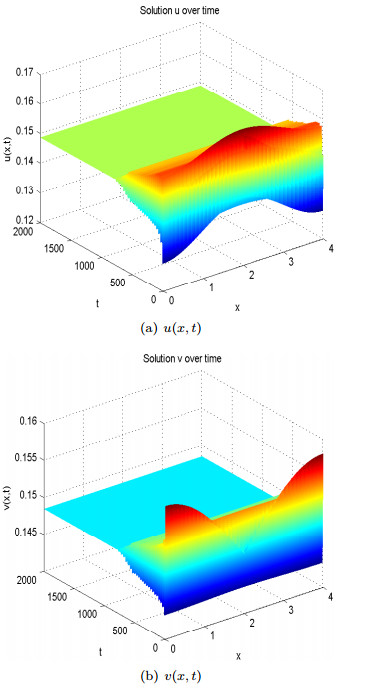
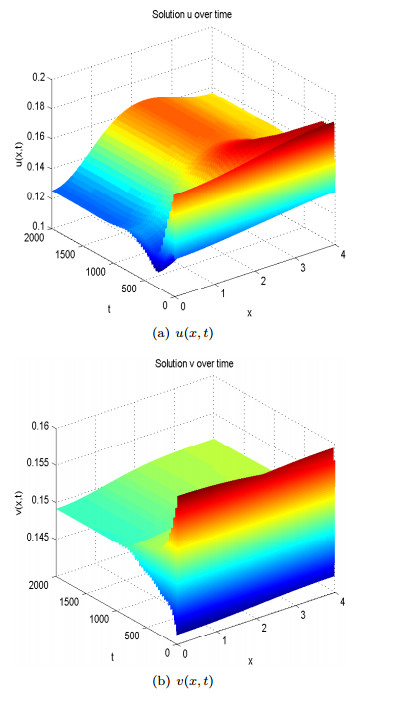
When E(\bar{u}, \bar{v}) exists under m(v) = m_1+m_2\, v, we employ numerical simulations to examine how \alpha would change the stability of E(\bar{u}, \bar{v}) when spatial effects exist and generate possible spatial heterogenous patterns. Figure 3 indicates that if \alpha is large, the population of both prey and predators tend to a spatial homogeneous steady state. However, if \alpha is small, spatial heterogenous pattern appears, as indicated in Figure 4. Biologically, weak prey sensitivity to predation risk is an underlying mechanism for generating spatial patterns in the predator-prey system. Notice that anti-predator behaviors of prey also lead to a cost on the local reproduction of prey. However, the magnitudes of impact that anti-predator behaviors exert on the dispersal of prey and on the local reproduction of prey may be different. Therefore, we also test the role that k_0 plays in predator-prey system. By increasing the value of k_0 to k_0 = 20 while holding other parameters in Figure 4 unchanged, we obtain a figure similar to Figure 3 (omitted). Further check by substituting parameters into (35) and (36) gives a contradiction, which confirms the non-existence of pattern formation. Therefore, we conclude that large cost of anti-predator response of prey in its reproduction has a stabilizing effect by excluding the appearance of pattern formation and ensures the stability of the positive spatial homogeneous steady state.
4.3. Ratio-dependent functional response
In this section, we analyze (9) with the ratio-dependent functional response, i.e.
|
p(u, v) = \frac{b_1}{b_2\, v+u}
|
(68)
|
again with the predator death rate functions given in (6). For either death function of predators, system (9) with (68) admits a spatial homogeneous semi-trivial equilibrium E_1\left((r_0-d)/a, 0\right), which exists if r_0>d. Direct calculations show that pattern formation can not occur around E_1. The proof is similar to the proof in Proposition 2 and is omitted here.
4.3.1. With density independent death rate for the predator
Consider the case with m(v) = m_1 first for simplicity. A unique positive equilibrium E(\bar{u}, \bar{v}) exists when m(v) = m_1 if
|
c\, b_1>m_1\,\,\,\,\, \mbox{and}\,\,\,\,\, r_0-d>\frac{c\, b_1-m_1}{c\, b_2},
|
(69)
|
where
|
\left\{ \begin{array}{l}
\bar{u} = \frac{m_1\, b_2\, \bar{v}}{c\, b_1-m_1}, \;\bar{v} = \frac{-a_2-\sqrt{a_2^2-4\, a_1\, a_3}}{2\, a_1}, \\
a_1 = -k_0\, \alpha\, a\, m_1\, b_2^2\, c, \\
a_2 = -k_0\, \alpha\, (m_1-c\, b_1)^2-c\, b_2\, \left(a\, m_1\, b_2+k_0\, \alpha\, d\, (c\, b_1-m_1)\right), \\
a_3 = -(c\, b_1-m_1)\left((c\, b_1-m_1)+c\, b_2\, (d-r_0)\right).
\end{array} \right.
|
(70)
|
Assume E(\bar{u}, \bar{v}) exists and we analyze necessary conditions for pattern formation around E(\bar{u}, \bar{v}). First consider a special case where prey avoid predation towards lower gradient of predator density but there is no cost on the reproduction success of prey (i.e. k_0 = 0 in (9)). When k_0 = 0, \bar{u}, \bar{v} are simplified to
|
\bar{u} = \frac{c\, b_2\, (r_0-d)-(c\, b_1-m_1)}{b_2\, a\, c}, \;\bar{v} = \frac{(c\, b_1-m_1)\left(c\, b_2\, (r_0-d)-(c\, b_1-m_1)\right)}{a\, m_1\, c\, b_2^2},
|
(71)
|
which do not involve \alpha. In this case, substituting (71) into (35) and (36) gives the following proposition.
Proposition 3. When (69) holds and k_0 = 0, pattern formation around E(\bar{u}, \bar{v}) may occur if
|
\begin{align}
r_0-d>\frac{(c\, b_1-m_1)(c\, b_1+m_1-c\, b_2\, m_1)}{b_1\, b_2\, c^2},
\end{align}
|
(72)
|
|
\alpha<\frac{f_u\, d_v+g_v\, d_u-2\, \sqrt{d_u\, d_v\, \left(f_u\, g_v-f_v\, g_u\right)}}{g_u\, \beta(\bar{u})\, \bar{u}}
|
(73)
|
hold.
Proof. Direct calculations show that at E(\bar{u}, \bar{v}), we have
|
f_u = \bar{u}\left(-a+\frac{b_1\, \bar{v}}{(b_2\, \bar{v}+\bar{u})^2}\right), \;
f_v = \bar{u}\, \left(-\frac{b_1}{b_2\, \bar{v}+\bar{u}}
+\frac{b_1\, b_2\, \bar{v}}{(b_2\, \bar{v}+\bar{u})^2}\right), \\
g_u = \frac{c\, b_1\, b_2\, \bar{v}^2}{(b_2\, \bar{v}+\bar{u})^2}, \;g_v = -\frac{c\, b_1\, b_2\, \bar{u}\, \bar{v}}{(b_2\, \bar{v}+\bar{u})^2}.
|
(74)
|
Substituting (74) into (35) and (36) gives
|
\left\{ \begin{array}{l}
\alpha<\frac{f_u\, d_v+g_v\, d_u}{g_u\, \beta(\bar{u})\bar{u}}, \\
\alpha<\frac{f_u\, d_v+g_v\, d_u-2\, \sqrt{d_u\, d_v\, \left(f_u\, g_v-f_v\, g_u\right)}}{g_u\, \beta(\bar{u})\, \bar{u}},
\end{array} \right.
|
(75)
|
which leads to (73). Moreover, (33) needs to be satisfied to guarantee the local stability of E(\bar{u}, \bar{v}) without spatial effect. From (74), it is clear that \lambda_1^0\, \lambda_2^0>0 is always satisfied if E(\bar{u}, \bar{v}) exists and \lambda_1^0+\lambda_2^0<0 gives (72).
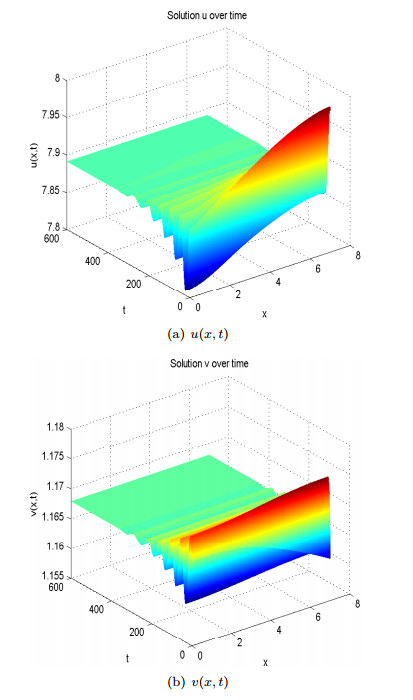
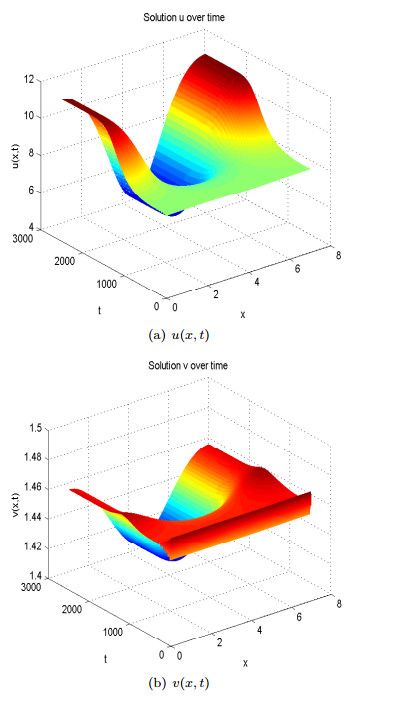
Proposition 3 implies that when there is no cost of anti-predator defense on the reproduction success of prey, small predator-taxis sensitivity \alpha may lead to pattern formation around E(\bar{u}, \bar{v}). Taking \alpha as a bifurcation parameter, then bifurcation from the spatial homogeneous steady state E(\bar{u}, \bar{v}) to a spatial heterogeneous steady state occurs at
|
\alpha_c = \frac{f_u\, d_v+g_v\, d_u-2\, \sqrt{d_u\, d_v\, \left(f_u\, g_v-f_v\, g_u\right)}}{g_u\, \beta(\bar{u})\, \bar{u}}.
|
(76)
|
By choosing parameter values as shown in Figure 5 and substituting them into (76), we obtain the critical value of bifurcation \alpha_c = 9.874. Figure 5 shows that if \alpha>\alpha_c, local stability of \bar{u}, \bar{v} remains even if spatial effects exist. Notice that for model (9), a bounded domain \Omega is considered. Therefore, conditions (72) and (73) only give necessary conditions of pattern formation around E(\bar{u}, \bar{v}). To proceed with more detailed analysis, consider a one-dimensional domain [0, \, L] with no-flux boundary condition, where the wave number k can be expressed explicitly as k = (n\, \pi)/L with n = 0, \, \pm 1, \, \pm 2\, \cdots. From (31), the instability of E(\bar{u}, \bar{v}) may only occur if b(k^2) changes from positive to negative for some k>0 such that
where
|
k_1^2 = \frac{-\left(g_u\, \alpha\, \beta(\bar{u})\bar{u}-f_u\, d_v-g_v\, d_u\right)-\sqrt{\Delta}}{2\, d_u\, d_v}, \\
k_2^2 = \frac{-\left(g_u\, \alpha\, \beta(\bar{u})\bar{u}-f_u\, d_v-g_v\, d_u\right)+\sqrt{\Delta}}{2\, d_u\, d_v}, \\
\Delta = \left(g_u\, \alpha\, \beta(\bar{u})\, \bar{u}-f_u\, d_v-g_v\, d_u\right)^2-4\, d_u\, d_v\, \left(f_u\, g_v-f_v\, g_u\right).\\
|
(78)
|
Equivalently, (77) in terms of modes n becomes
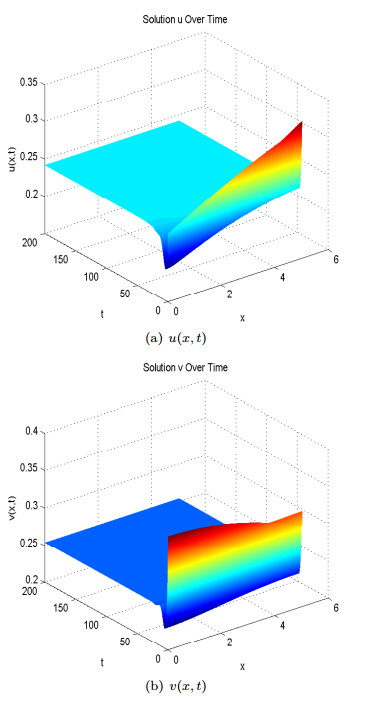
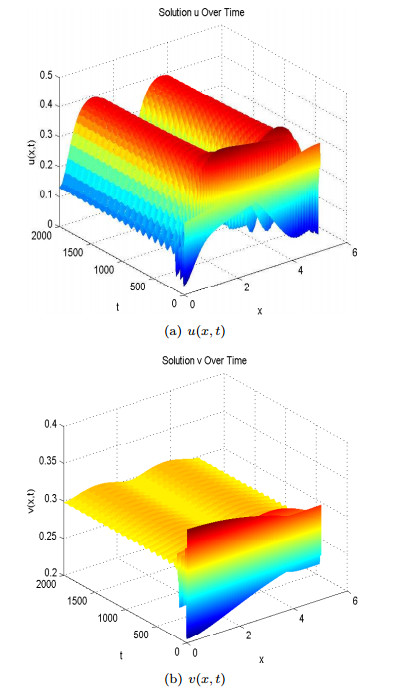
where n_1 = (k_1\, L)/\pi, \;n_2 = (k_2\, L)/\pi. For a bounded domain, the wave number is discrete [26]. Therefore, the critical value of bifurcation \alpha_c = 9.874 we obtained above may not be the actual bifurcation value because an integer n satisfying (79) may not exist. However, by choosing parameters in Figure 6, we obtain that n_1 = 0.6177, n_2 = 8.0317, which admits at least one integer n such that (79) is satisfied. Hence, for this parameter set, conditions (72) and (73) are in fact sufficient and necessary conditions for pattern formation. With parameters in Figure 6, positive equilibrium E(\bar{u}, \bar{v}) loses stability for some spatial modes and heterogeneous spatial patterns emerge.
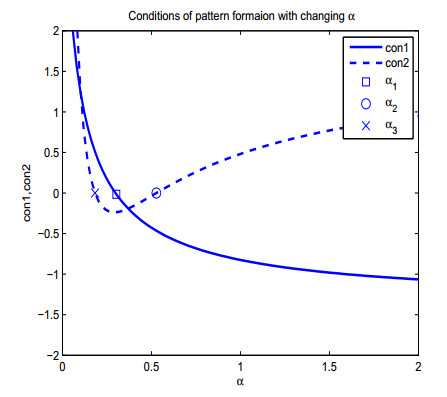
Now we analyze the case where k_0 \neq 0, i.e. there exists cost on the reproduction rate of prey due to anti-predator behaviors of prey. Noticing from (70) that \bar{u} and \bar{v} contain \alpha if k_0 \neq 0. Still regarding \alpha as a bifurcation parameter in the following analysis but with k_0 \neq 0, an explicit formula of \alpha can not be obtained due to the complexity of (70). Therefore, we employ numerical simulations to explore the role that \alpha plays in pattern formation when k_0 \neq 0. By choosing parameters in Figure 7, conditions in (33) are satisfied. Furthermore, the solid line in Figure 7 corresponds to (35) and the dashed line in Figure 7 represents (36). It is clear that \alpha should satisfy
|
\left\{ \begin{array}{l}
\alpha>\alpha_1 = 0.2979, \\
\alpha>\alpha_2 = 0.5277\;\text{or}\;\alpha<\alpha_3 = 0.1833
\end{array} \right.
|
(80)
|
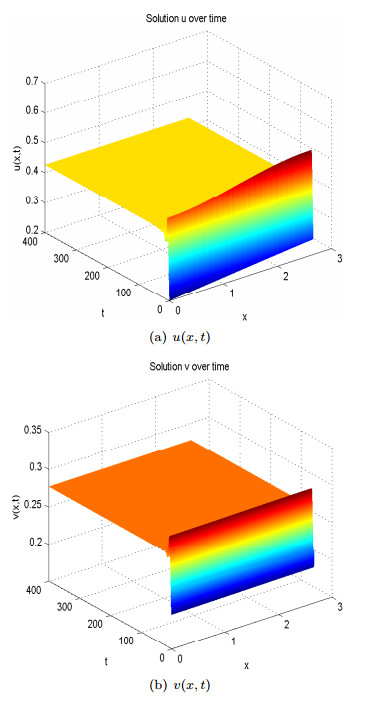
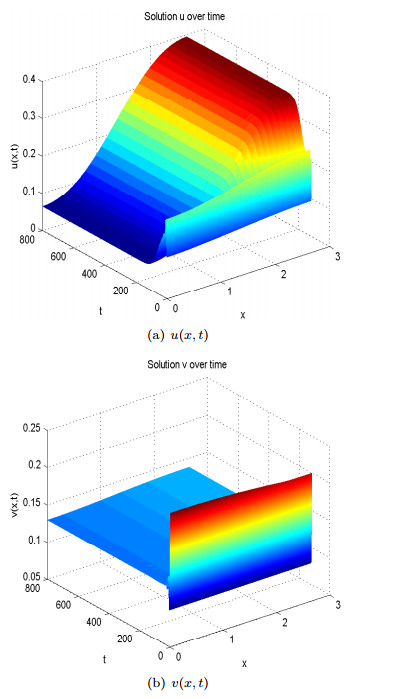
to ensure the pattern formation of E(\bar{u}, \bar{v}). Hence, we obtain that \alpha>\alpha_2 is a necessary condition for diffusion-taxis-driven instability of E(\bar{u}, \bar{v}) by (80). We conjecture that \alpha>\alpha_2 is also a sufficient condition. Indeed, numerical simulations support this conjecture, implying that \alpha = \alpha_2 is the bifurcation value for pattern formation. Figure 8 confirms that if \alpha is relatively small, the density of prey and predators tend to a spatial homogeneous steady state eventually. However, if we increase the value of \alpha until it passes the critical bifurcation value \alpha = \alpha_2, then spatial heterogeneous steady state emerge, as shown in Figure 9.
By comparing the two cases where k_0 = 0 and k_0 \neq 0, we find some interesting distinctions between the two cases. If k_0 = 0, then prey avoid predators by moving towards lower predator density locations but there is no cost of anti-predator behaviors on the local reproduction success of prey. In this circumstance, small predator-taxis leads to instability of spatial homogeneous steady state of predator-prey system, which eventually form spatial heterogeneous patterns. Similar results have been obtained in [18], in which the opposite scenario where prey move randomly but predators chase prey by moving towards higher prey density gradient in addition to random diffusion was studied. In [18], by considering the same ratio dependent functional response between prey and predators, the authors concluded that spatial pattern formation may occur if the prey-taxis was small. However, in contrast to the case where k_0 = 0 or the similar conclusion in [18], if k_0 \neq 0, (i.e. the cost of anti-predator response is incorporated), analyses above show that large predator-taxis may result in spatial pattern formation. Biologically, when the cost of anti-predator behaviors exists, strong anti-predator behaviors of prey have a destabilizing effect by destroying the stability of the uniformly distributed equilibrium, and giving rise to spatial non-homogeneous patterns. On the other hand, weak anti-predator behaviors of prey have a stabilizing effect in predator-prey system by excluding the emergence of spatial pattern formation. Notice that stronger anti-predator behaviors of prey also carry larger cost on the reproduction success of prey. In order to examine the impact that the cost of avoidance behaviors of prey exerts on spatial distribution of prey and predators, we also conduct simulations by varying the value of k_0. Decreasing the value of k_0 while holding other parameters in Figure 9 unchanged gives Figure 10, which shows that solutions tend to a homogeneous steady state. Further computation confirms that small k_0 leads to the violation of conditions (35) and (36), which excludes the possibility of pattern formation. In biological interpretation, small cost of anti-predator behaviors has a stabilizing effect by converting a spatial heterogeneous steady state into a spatial homogeneous one if the functional response between predators and prey is ratio dependent.
We also point out here that in [3], the authors analyzed pattern formation of a predator-prey system where both prey and predators disperse randomly. By using numerical simulations, and considering the same ratio-dependent functional response, the authors concluded that the most possible Turing pattern occurred at places where the growth rate of prey and the death rate of predators were similar [3]. As a special case of (9), we also analyze the model
|
\frac{\partial u}{\partial t} = d_u\, \Delta u+\frac{r_0\, u}{1+k_0\, \alpha\, v}-d\, u-a\, u^2-\frac{b_1\, u\, v}{b_2\, v+u}, \\
\frac{\partial v}{\partial t} = d_v\, \Delta v+v\left(-m_1+\frac{c\, b_1\, u}{b_2\, v+u}\right).\\
|
(81)
|
As shown in (81), different from model (9), prey have no directed movement but disperse randomly in the habitat. However, in local reaction between prey and predators, the cost of anti-predator behaviors still exists and the reproduction success of prey is reduced as a result. For notational convenience, let k_1 = k_0\, \alpha, which represents the level of anti-predator behaviors. Higher level of anti-predator defense of prey (i.e. larger value of k_1) leads to lower reproduction rate of prey. Again similar to the analysis above when k_0 \neq 0, we conduct numerical simulations to analyze the role that k_1 exerts in pattern formation. By plotting (35) and (36) with respect to varying k_1, a figure which is very similar to Figure 7 is obtained, indicating that large k_1 may lead to pattern formation. Further numerical simulations of (u(x, t), v(x, t)) over time and space confirm that spatial heterogeneous patterns are formed if k_1 is large, which are similar to Figures 6(a) and 6(b) respectively and are thus omitted. The above analyses of (81) indicate that small cost of anti-predator behaviors has a stabilizing effect on predator-prey system by excluding the possibility of Turing bifurcation when both prey and predators move randomly. Different from [3], by incorporating the cost of fear into modelling, Turing instability may or may not occur when birth rate of prey r_0 and death rate of predators m_1 are similar, depending on the value of k_1 indeed.
4.3.2. With density dependent death rate for the predator
Now we proceed to the case where the death function of predators is density dependent, where m(v) = m_1+m_2\, v. The existence of positive equilibrium is shown in the following lemma.
Lemma 4.4. If m(v) = m_1+m_2\, v, then at least one positive equilibrium E(\bar{u}, \bar{v}) exists if (69) holds.
Proof. From (9), it is obvious that \bar{u} satisfies
|
\bar{u} = \frac{b_2\, \bar{v}\, (m_2\, \bar{v}+m_1)}{(b_1\, c-m_1)-m_2\, \bar{v}}.
|
(82)
|
Obviously, the existence of \bar{u} requires that
|
\bar{v}<\frac{b_1\, c-m_1}{m_2}: = \bar{v}_{\max},
|
(83)
|
where b_1\, c>m_1 holds by (69). Moreover, \bar{v} is determined by
|
F(\bar{v}): = a_1\, \bar{v}^3+a_2\, \bar{v}^2+a_3\, \bar{v}+a_4 = 0,
|
(84)
|
where
|
\begin{align}\label{coeffr} a_1& = -\alpha\, k_0\, m_2\, (a\, b_2^2\, c+m_2), \nonumber \\ a_2& = -m_2^2+(((b_2\, d+2\, b_1)\, c-2\, m_1)\, k_0\, \alpha-a\, b_2^2\, c) \, m_2-a\, \alpha\, b_2^2\, c\, k_0\, m_1, \nonumber \\ a_3& = -\alpha\, b_1\, k_0\, (b_2\, d+b_1)\, c^2+(k_0\, m_1\, (b_2\, d+2\, b_1)\, \alpha -a\, b_2^2\, m_1\\ &+m_2\, (d-r_0)\, b_2+2\, b_1\, m_2)\, c-\alpha\, k_0\, m_1^2-2\, m_1\, m_2, \nonumber \\ a_4& = -(b_1\, c-m_1)\, (b_2\, c\, d-b_2\, c\, r_0+b_1\, c-m_1). \nonumber \end{align}
|
(85)
|
From (85), a_4>0 is equivalent to
|
(r_0-d)\, b_2\, c>b_1\, c-m_1,
|
(86)
|
which is implied by (69). Furthermore, substituting \bar{v} = \bar{v}_{\max} into (84) gives
|
F(\bar{v}_{\max}) = -\frac{a\, b_1\, b_2^2\, c^2\, (b_1\, c-m_1)\, (\alpha\, b_1\, c\, k_0-\alpha\, k_0\, m_1+m_2)}{m_2^2}<0
|
(87)
|
if b_1\, c>m_1 is satisfied. Therefore, by the intermediate value theorem, there exists at least one positive equilibrium E(\bar{u}, \bar{v}) if (69) holds.
When E(\bar{u}, \bar{v}) exists with m(v) = m_1+m_2\, v, we analyze possible pattern formation and conduct numerical simulations, following the same procedures as in the previous case where m(v) = m_1. Both theoretical and numerical results are similar to the previous case, in which strong anti-predator behaviors (i.e. large \alpha) induces a spatial heterogeneous steady state, while weak anti-predators behaviors stabilize the system by converting solutions to spatial homogeneous ones. Moreover, small cost of anti-predator behaviors on prey reproduction (i.e. small k_0) may also exclude the occurrence of pattern formation. The difference between the two cases where m(v) = m_1 and m(v) = m_1+m_2\, v lies in that for m(v) = m_1+m_2\, v, large k_0 induces spatial homogeneous but time-periodic solutions (Hopf bifurcation), as shown in Figure 11. However, if m(v) = m_1, increasing the value of k_0 can not give time-periodically solutions but remain spatial heterogeneous solutions. By further substituting parameters in Figure 11 into (33), we find that large k_0 leads to f_u+g_v>0, which implies that time-periodic solutions emerge due to Hopf bifurcation.
4.4. Beddington-DeAngelis functional response
In this section, we analyze possible pattern formation when p(u, v) in (9) is chosen as the Beddington-DeAngelis functional response [7,12], i.e.,
|
p(u, v) = \frac{p}{1+q_1\, u+q_2\, v}.
|
(88)
|
For either death function m(v) of predators in (6), a trivial equilibrium E_0(0, 0) always exists and a semi-trivial equilibrium E_1((r_0-d)/a, 0) exists if r_0>d. Mathematical analyses show that pattern formation can not occur around E_0 or E_1. Because the result is similar to the results in previous sections and the analyses follow standard procedures, we omit the proof here. Due to the complexity of the Beddington-DeAngelis functional response (88), pattern formation around positive equilibrium is explored by numerical simulations. As shown in Figure 12 and Figure 13 respectively, for the case where m(v) = m_1, small \alpha may induce pattern formation but large \alpha inhibits the emergence of spatial heterogeneous patterns. The simulation results hold for either k_0 = 0 or k_0 \neq 0. Also, we obtain a figure which is very similar to Figure 12 by increasing the value of k_0 to k_0 = 10 while holding other parameters in Figure 13 unchanged. Biologically, it indicates that large cost of anti-predator behaviors on the reproduction of prey has a stabilizing effect by converting a spatially heterogeneous steady-state to spatially homogeneous one. The same conclusions hold for the case where m(v) = m_1+m_2\, v, for which we conduct simulations and do not observe difference from the previous density-independent case.
5. Conclusions and discussions
In this paper, we propose a spatial predator-prey model with avoidance behaviors in the prey as well as the corresponding cost of anti-predator responses on the reproduction success of prey. The focus is on the formation of spatial patterns. Various functional responses and both density-independent and density-dependent death rates of predators are considered for the model.
Mathematical analyses show that pattern formation cannot occur if the functional response is linear, or it is the Holling type Ⅱ but the death rate of the predators is density-independent. However, pattern formation may occur if the death rate of predators is density-dependent with the Holling type Ⅱ functional response. Moreover, functional responses other than the prey-dependent only ones, including ratio-dependent functional response and the Beddington-DeAngelis functional response, may also allow the emergence of spatial heterogeneous patterns. Under conditions for pattern formation, the common point for the case with the Holling type Ⅱ functional response and the case where the functional response is chosen as the Beddington-DeAngelis type is that small prey sensitivity to predation risk (i.e. small \alpha) induces spatial heterogeneous steady states while large \alpha excludes pattern formation. In addition, large cost of anti-predator behaviors on the reproduction rate of prey (i.e. large k_0) has a stabilizing effect by transferring spatial heterogeneous steady states into homogeneous ones. The case where the functional response is a ratio-dependent one exhibits different mechanisms for pattern formation, compared with other cases. For a special case where the prey avoid predation by moving toward habitats with lower predator density but the cost of such anti-predator behaviors is ignored (i.e. k_0 = 0), we obtain similar conclusions. However, if the cost of anti-predator responses is incorporated, mathematical analyses give an opposite result. To elaborate, large prey sensitivity to predation risk (i.e. large \alpha) may lead to a spatially heterogeneous steady state by destroying the local stability of a positive constant equilibrium while small \alpha excludes the possibility of pattern formation. Moreover, different from other cases where large k_0 stabilizes system, in the case of ratio dependent functional response, small k_0 inhibits the emergence of pattern formation and stabilize a homogeneous equilibrium as well. By these results obtained by both mathematical analyses and numerical simulations, we may conclude that anti-predator behaviors of prey and the cost on prey's reproduction success have important impacts on pattern formation in spatial predator-prey systems. Avoidance behaviors of prey and the cost of fear may have either stabilizing effect or destabilizing effect, when they interplay with different functional responses.
In this paper, we mainly focused on modelling avoidance behaviors and the cost of anti-predator behaviors in the reproduction of prey in a spatial predator-prey system. Therefore, predators are assumed to move randomly in their habitats. In reality some predator species demonstrate prey-taxi when they forage for their preys (see, e.g., [43]). It is interesting to see how the prey-taxis effect on the predators and the predator-taxi effect on the prey (fear effect) will jointly affect the population dynamics in the predator-prey system. A even more interesting question would be how these two types of taxi effects will interplay with the cost of anti-predator behaviors. We leave these as possible future work.
Acknowledgments
The authors would like to thank Dr. Yixiang Wu for his reading and commenting on the manuscript, which helped us to improve the presentation of the paper. The authors also thank two anonymous reviewers for their careful reading and valuable feedback.









 DownLoad:
DownLoad: