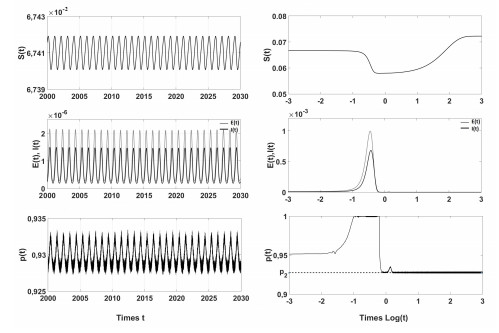
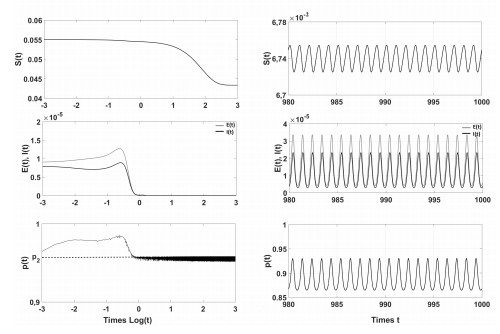
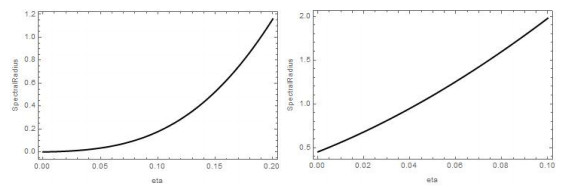
We extend here the game-theoretic investigation made by d'Onofrio et al (2012) on the interplay between private vaccination choices and actions of the public health system (PHS) to favor vaccine propensity in SIR-type diseases. We focus here on three important features. First, we consider a SEIR-type disease. Second, we focus on the role of seasonal fluctuations of the transmission rate. Third, by a simple population-biology approach we derive -with a didactic aim -the game theoretic equation ruling the dynamics of vaccine propensity, without employing 'economy-related' concepts such as the payoff. By means of analytical and analytical-approximate methods, we investigate the global stability of the of disease-free equilibria. We show that in the general case the stability critically depends on the 'shape' of the periodically varying transmission rate. In other words, the knowledge of the average transmission rate (ATR) is not enough to make inferences on the stability of the elimination equilibria, due to the presence of the class of latent subjects. In particular, we obtain that the amplitude of the oscillations favors the possible elimination of the disease by the action of the PHS, through a threshold condition. Indeed, for a given average value of the transmission rate, in absence of oscillations as well as for moderate oscillations, there is no disease elimination. On the contrary, if the amplitude exceeds a threshold value, the elimination of the disease is induced. We heuristically explain this apparently paradoxical phenomenon as a beneficial effect of the phase when the transmission rate is under its average value: the reduction of transmission rate (for example during holidays) under its annual average over-compensates its increase during periods of intense contacts. We also investigate the conditions for the persistence of the disease. Numerical simulations support the theoretical predictions. Finally, we briefly investigate the qualitative behavior of the non-autonomous system for SIR-type disease, by showing that the stability of the elimination equilibria are, in such a case, determined by the ATR.
1.
Introduction
Hepatocellular carcinoma (HCC), featured by poor prognosis, frequent relapse and high mortality, is one of the leading malignancies, which gives rise to serious financial burden worldwide [1]. Even if the carcinoma tissues in liver can be completely resected or ablated, the remnant carcinogenic tissue microenvironment may still cause recurrent de novo HCC tumors, eventually progressing into advanced-stage disease in most patients [2]. Therefore, screening specific and sensitive biomarkers as well as potential targets in HCC is of great significance for better diagnosis, more precise treatment, and more favorable prognosis.
Chemokines have been traditionally defined as small (10–14 kDa) secreted leukocyte chemoattractants, the interactions of which could direct cell migration in immunity, inflammation, development, and cancer [3]. There is a total of 22 chemokines receptors and approximately 45 chemokines expressing in humans, thus forming a pharmacologically complex system [4]. According to the spacing of conserved cysteine residues about 10 residues from the N-terminal end of the peptide chain, chemokines are usually classified into four subfamilies (CC, CXC, CX3C and XC) [5]. The CXC chemokines is further subdivided in the ELR 61 and ELR+ chemokines, which exert a vital effect in the development of cancer, especially in tumor angiogenesis. The members containing the ELR motif bind to CXC chemokine receptor 2 (CXCR2) and exhibit an angiogenic effect while most of the CXC chemokines without ELR motif bind to CXCR3 and display an angiostatic effect [6].
Up to now, sixteen CXC chemokines in mammalian cells have been verified and named based on the order of their discovery (CXCL1, CXCL2, CXCL3, PF4, CXCL5, CXCL6, PPBP, CXCL8, CXCL9, CXCL10, CXCL11, CXCL12, CXCL13, CXCL14, CXCL16 and CXCL17) [6]. Among these CXC chemokines, CXCL1, CXCL2, CXCL3, CXCL5, CXCL6, CXCL8, CXCL9, CXCL10, CXCL12, CXCL13, CACL14 and CXCL17 are considered oncogenes and potential biomrkers in HCC development, as indicated by evidence in human HCC tissues, animal models and HCC cell lines. For example, CXCL5 overexpression could promote HCC cell proliferation, invasion, as well as intratumoral neutrophil infiltration by activating the PI3K-Akt and ERK1/2 signaling pathways [7]. Additionally, in HCC cells, hypoxia inducible factor-u03b1 (HIF-1u03b1) could promote the progression and metastasis of HCC through upregulating CXCL6 at transcriptional level [8]. Nevertheless, the potential mechanism by which CXC chemokines are suppressed and activated and the underlying functions of the CXC chemokines in HCC have yet to be completely illustrated.
Although the abnormal expression levels of CXC chemokines as well as their relationship with clinicopathological characteristics and outcomes have incompletely reported in HCC, to our knowledge, the exploration of CXC chemokines based on bioinformatics analysis in HCC is absent. The development of microarray technology has thoroughly revolutionized the DNA and RNA research in biomedical studies [9]. Previous study unveiled that the expression levels of several members in CXC cytokines differed between normal group and HCC group [10]. Hence, in this study, we further analyzed the expression and mutations of different CXC cytokines in patients with HCC by analyzing abundant online gene expression or variation in copy numbers, aiming to determine the expression patterns, underlying function and potential prognosis values of these CXC cytokines.
2.
Materials and methods
2.1. Ethics statement
The collection and use of human liver tissues were approved by the Human Research Ethics Committee of the Lishui Municipal Central Hospital. All the datasets used in this study were retrieved from the published literature, meaning that all the written informed consent acquired was confirmed.
2.2. ONCOMINE analysis
ONCOMINE is a cancer microarray database and web-based data-mining platform (http://www.oncomine.org), aiming to facilitate discovery from genome-wide expression analyses [11]. In this study, the ONCOMINE was used to analyze the transcription levels of CXC cytokines in different types of cancers. The mRNA expressions of CXC cytokines in clinical cancer specimens were compared with that in normal controls, using a Students’ t-test to generate a p value. The cut-off of p value and fold change were defined as 0.01 and 2, respectively.
2.3. GEPIA dataset
GEPIA (http://gepia.cancer-pku.cn/index.html) is a newly developed interactive web server which was designed by Zefang Tang, Chenwei Li and Boxi Kang of Zhang Lab, Peking University, in order to analyze the RNA sequencing expression data of 8,587 normal samples and 9,736 tumors from the TCGA and the GTEx projects, using a standard processing pipeline [12]. GEPIA possesses customizable functions such as tumor/normal differential expression analysis, profiling on the basis of pathological stages or cancer types, similar gene detection, patient survival analysis, correlation analysis and dimensionality reduction analysis. In this study, we used GEPIA to construct visualized the expression levels of CXC cytokines at transcription and protein levels. Additionally, we used GEPIA to analyzed the correlation between CXC cytokines expression and tumor stage in HCC patients.
2.4. The Kaplan-Meier plotter
Based on GEPIA (http://gepia.cancer-pku.cn/), we acquired the correlations between these genes and their prognostic information. The hazard ratio (HR) with 95% confidence intervals and logrank P value were calculated and displayed on the plot. P < 0.05 was considered statistically different.
2.5. TCGA data and cBioPortal
The Cancer Genome Atlas possessed both pathological data and sequencing of 30 different cancers [13]. The liver hepatocellular carcinoma (TCGA, Provisional) dataset involving data from 442 samples with pathology reports was chosen for comprehensive analyses of CXC cytokines using cBioPortal. The genomic profiles included mutations, putative copy-number alterations (CNA) from GISTIC, mRNA expression z-scores (RNASeq V2 RSEM) and protein expression Z-scores (RPPA). Co-expression and network were calculated on the basis of the cBioPortal's online instruction.
2.6. Western Blotting
Protein extraction, SDS-PAGE, and immunodetection of the carcinoma tissues and adjacent tissues were performed according to previous research [14]. Protein expression levels were normalized to the matched total proteins or GAPDH.
2.7. CXCLs in serum
Inflammatory cytokines in this study included CXCL2, 9, 10 and 14. These cytokines in serum were detected using commercially available ELISA kits from Abcam on the basis of the manufacturer's instructions.
2.8. Gene ontology (GO) and Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway analysis of CXC cytokines
GO serves as a useful approach to annotate genes and gene products and also identifies characteristic biological attributing to high-throughput genome or transcriptome data. And KEGG is a collection of databases which helped to handle genomes, biological pathways, diseases, chemical substances and drugs [15]. We input these CXC cytokines separately into the Database for Annotation, Visualization and Integrated Discovery (https://david.ncifcrf.gov/) (DAVID) which could be used to perform GO and KEGG analysis [15]. P < 0.05 was the choice criterion.
3.
Results
3.1. Transcriptional levels of CXC cytokines in patients with HCC
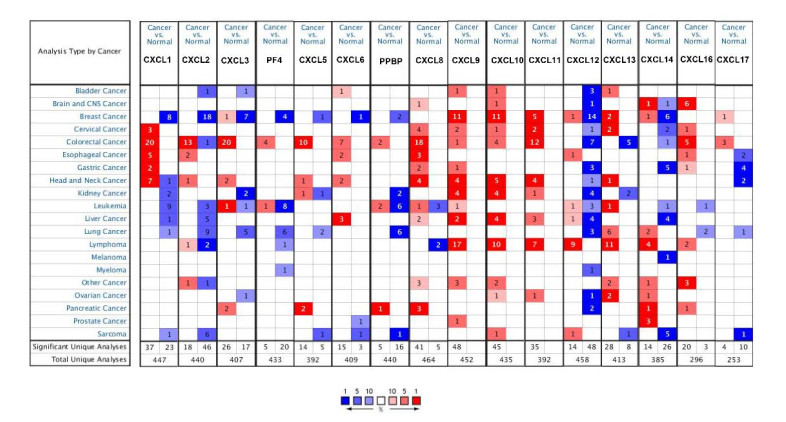
Sixteen CXC cytokines have been discovered and verified in mammalian cells. We employed ONCOMINE databases to compare the transcriptional levels of CXC cytokines in normal samples with those in HCC samples (Figure 1). The mRNA expression levels of CXCL6, CXCL9 and CXCL10 were significantly upregulated in patients with HCC. By contrast, the mRNA expression levels of CXCL1, CXCL2, CXCL12 and CXCL14 were significantly downregulated in patients with HCC. Consistent with these datasets, CXCL6, CXCL9 and CXCL10 were also overexpressed in patients with HCC with a fold change of 3.749, 5.334 and 9.272 in V Mas,dataset [16]. Additionally, another two CXC cytokines involving CXCL8 and CXCL11 were also overexpressed with a fold change of 3.323 and 2.188, respectively (Table 1). Intriguingly, in patients with cirrhosis, the expression level of CXCL6 even had a fold change of 11.046 compared with that in normal groups in V Mas,dataset [16]. As for CXCL10, Wurmbach E,dataset demonstrated that its upregulated expression level had a fold change of 17.69317.
3.2. Relationship between the mRNA levels of CXC cytokines and the clinicopathological parameters of patients with HCC
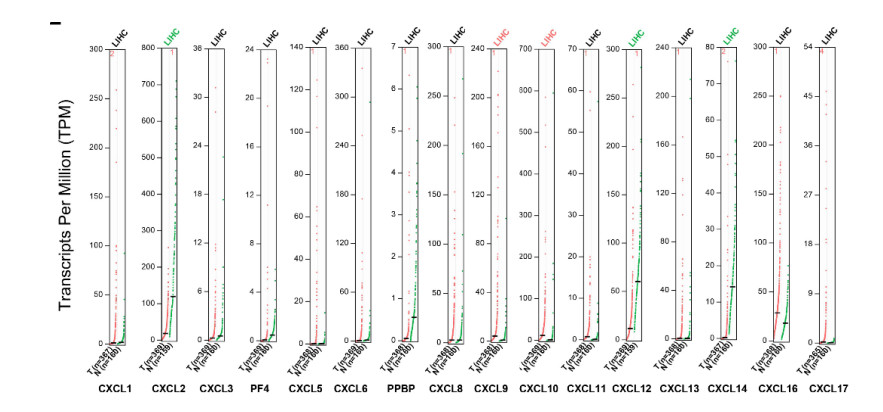
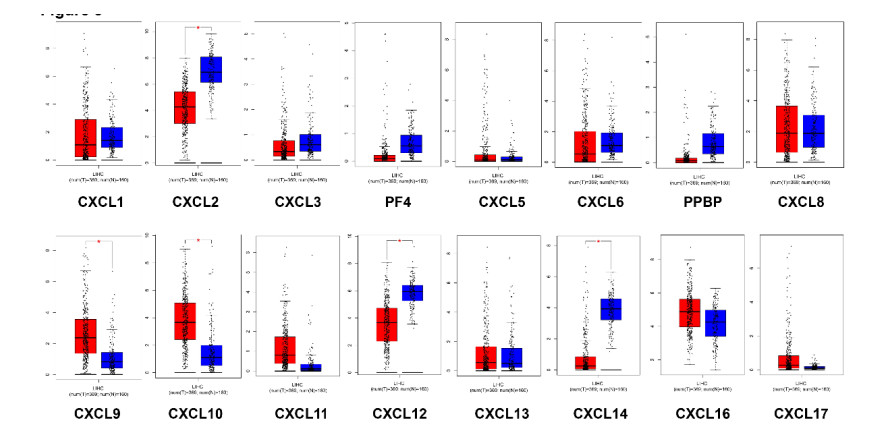
We analyzed the transcripts per million (TPM) (Figure 2) and the mRNA expression levels (Figure 3) of CXC cytokines between HCC and normal liver tissues by using GEPIA online analysis tool. The obtained results showed that TPM and the mRNA levels of CXCL2, CXCL9, CXCL10, CXCL12 and CXCL14 displayed significant difference (P < 0.05). To be more specific, the expression levels of CXCL2 and CXCL14 were significantly lower in HCC tissues while the levels of CXCL9, CXCL10 and CXCL12 were significantly higher in HCC tissues (P < 0.05).
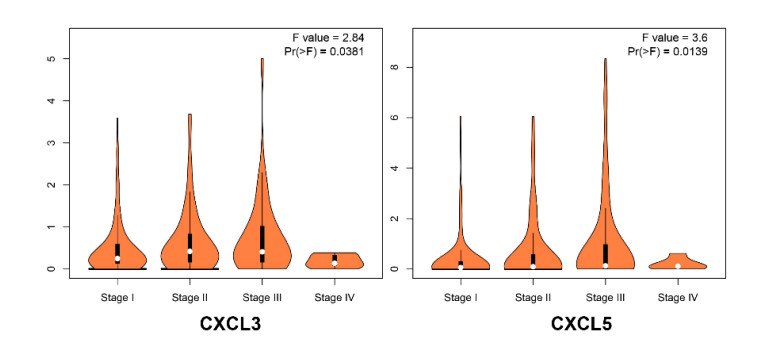
Meanwhile, we also analyzed the expression of CXC cytokines with tumor stage for HCC (Figure 4). Intriguingly, only CXCL3 and CXCL5 significantly varied while other CXC cytokines did not show obvious difference.
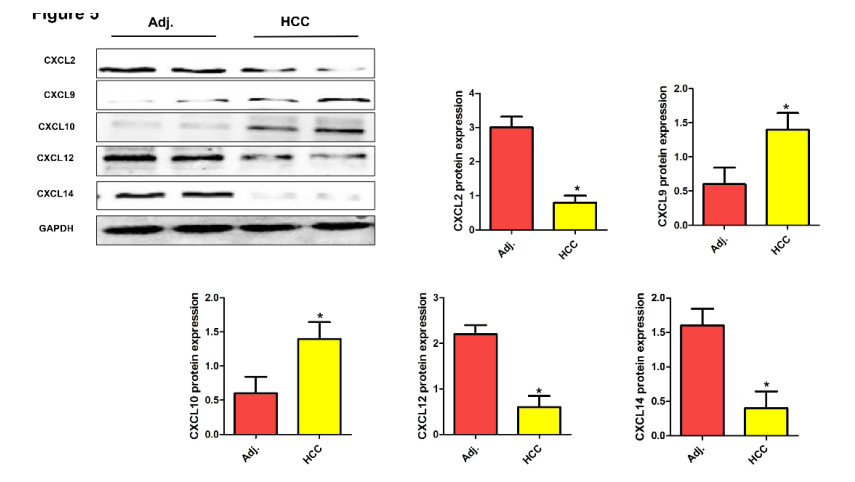
We also performed western blot to re-identify the differentially expressed CXC cytokines in 10 patients with HCC (Figure 5). As expected, the protein levels of CXCL2 and CXCL14 in adjacent tissues were significantly higher compared with HCC tissues while the protein levels of CXCL9, CXCL10 and CXCL12 significantly increased in carcinoma tissues (P < 0.05).
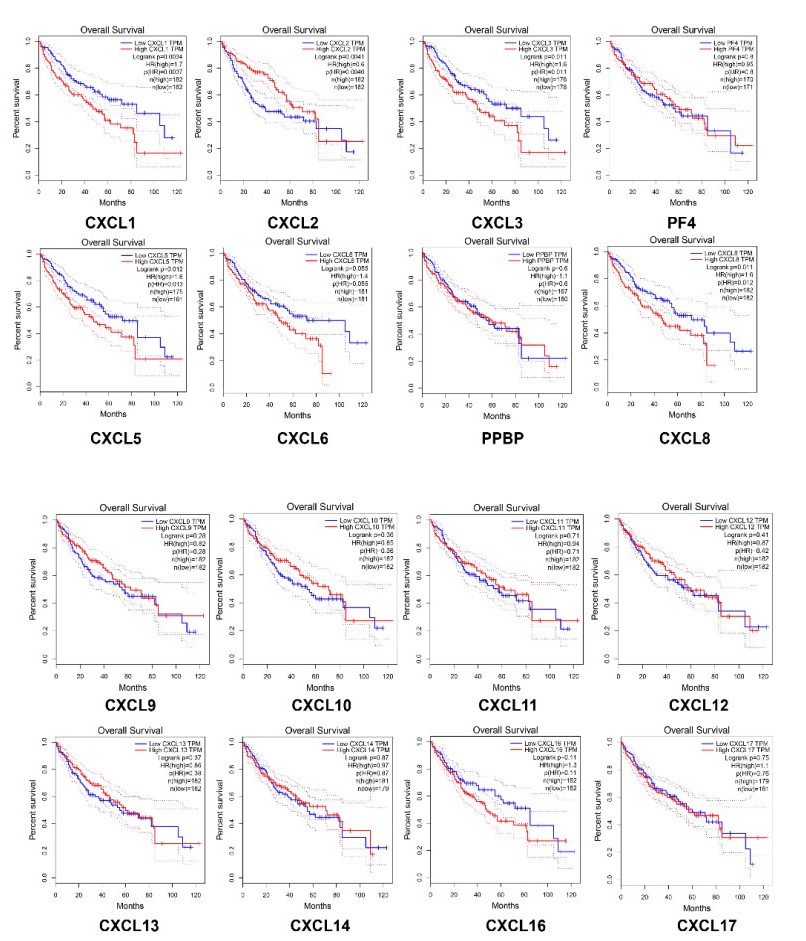
3.3. Association of the expression levels of CXC cytokines and the prognosis of patients with HCC
Subsequently, we investigated the vital efficiency of CXC cytokines in the survival of patients with HCC. The Kaplan-Meier Plotter based on GEPIA analyzed the relationships between the mRNA expression levels of CXC cytokines and the survival of 364 patients with HCC (Figure 6). The Kaplan-Meier curve and log-rank test analyses uncovered that the low expression levels of CXCL1, CXCL3, CXCL5 and CXCL8 as well as the high expression level of CXCL2 were significantly correlated with the overall survival (OS) (P < 0.05). Thus the patients with high mRNA levels of CXCL1, CXCL3, CXCL5 and CXCL8 or low level of CXCL2 were supposed to possess a poor prognosis.
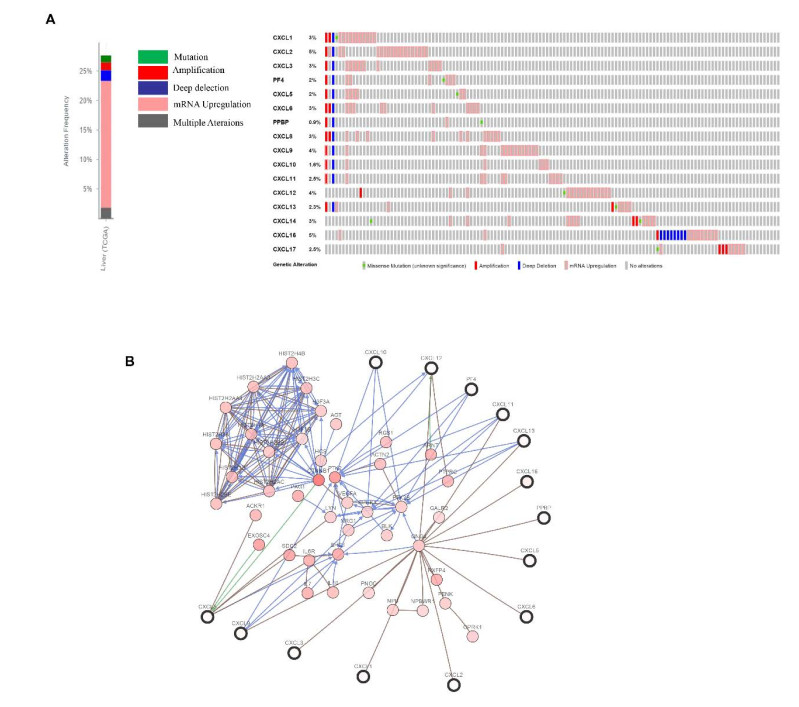
3.4. Possible pathways and functions of the alterations in CXC cytokines and their frequently changed neighbor genes in patients with HCC
We further explored the CXC cytokines alterations, relationships, and networks by employing the cBioPortal tool for HCC (http://www.cbioportal.org/). CXC cytokines were altered in 87 samples out of 461 patients with HCC (27%). Nearly half of these samples have 2 or more alterations (Figure 7A). Then the network for CXC cytokines as well as their 45 most frequently altered neighbor genes were constructed. The results showed that the cytoplasmic protein (PTK2B), G protein subunit (GNG4) and reactive oxygen protein (SHC1) closely associated with CXC cytokines alterations (Figure 7B).
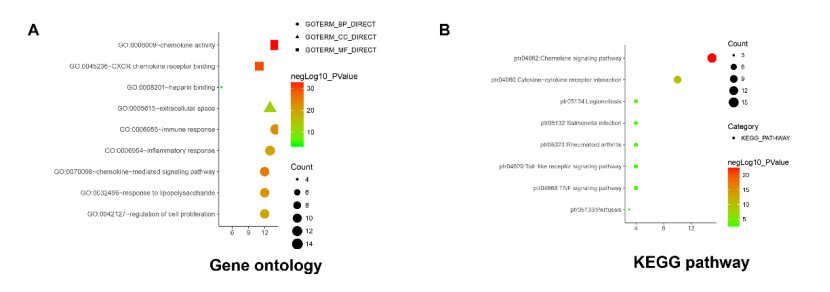
The functions of CXC cytokines and the genes significantly associated with CXC cytokines alterations were predicted by analyzing GO involving biological processes (BP), molecular function (MF) and cell composition (CC) as well as KEGG pathways via DAVID. We found that GO: 0006955 (immune response), GO: 0006954 (inflammatory response), GO: 0070098 (chemokine-mediated signaling pathway), GO: 0032496 (response to lipopolysaccharide), and GO: 0042127 (regulation of cell proliferation) were mainly enriched in BP. The GO: 0008009 (chemokine activity), GO: 0045236 (CXCR chemokine receptor binding) and GO: 0008201 (heparin binding) were focused in CC. The MF of these CXC cytokines was mainly responsible for GO: 0005615 (extracellular space) (Figure 8A). Eight pathways associated with the functions of CXC cytokines alterations in HCC were revealed using KEGG analysis (Figure 8B), namely ptr04062: Chemokine signaling pathway, ptr04060: Cytokine-cytokine receptor interaction, ptr05134: Legionellosis, ptr05132: Salmonella infection, ptr05323: Rheumatoid arthritis, ptr04620: Toll-like receptor signaling pathway, ptr04668: TNF signaling pathway and ptr05133: Pertussis.
4.
Discussion
Cancer is a type of disease due to the abnormal function of cytokine-regulated networks. Previous studies demonstrated that beneficial cytokines could exert potent anti-tumor effects by directly suppressing growth and survival of tumor cells (promotion of senescence and apoptosis, cell cycle arrest, restriction of cell motilit, enhancing the immune response against tumor cells, regulating the behavior of non-immune stromal cells [16,17,18,19,20]. By contrast, some chemokines, cytokines or their combinations could promote recruitment of immunosuppressive cells into the tumor microenvironment [21]. What is more, some pro-inflammatory chemochines or cytokines could promote cancer cell proliferation and inhibit its apoptosis in a number of instances [22]. Hence, it is necessary to clarify the roles and underlying mechanisms of the CXC chemokines in the progression of HCC. In this study, we explored the mRNA as well as the protein expression and prognostic values of different CXC cytokines in HCC for the first time. We found that the mRNA and the protein levels of CXCL9, CXCL10 and CXCL12 significantly increased in HCC tissues while the level of CXCL2 were significantly lower in carcinoma tissues. Meanwhile, another finding in our study is that CXCL3 and CXCL5 significantly differed with tumor stage. Meanwhile, the prognosis analysis showed that the low level of CXCL1, CXCL3, CXCL5 and CXCL8 as well as the high level of CXCL2 may correlate with the overall survival of patients with HCC. The GO and KEGG analysis showed that these genes were mainly enriched in chemokine activity, cytokine-cytokine interaction as well as immune and inflammatory response.
CXCL1 was reported to play a vital role in wound healing, angiogenesis, inflammation, and tumorigenesis. Upregulation of CXCL1 has been proved in various cancers and was correlated with poor prognosis. A clinical study uncovered that abnormal level of CXCL1 significantly promoted HCC cells invasion and proliferation, the CXCL1 could give rise to cell invasion in a NF-κB-dependent manner. Additionally, CXCL1 expression in HCC was significantly correlated with clinical stage as well as distant metastasis. Patients with low CXCL1 expression level had better OS than those with high CXCL1 expression [23]. What is more, CXCL1 can also regulate neutrophil infiltration into HCC tumor tissues, which could attenuate T cell responses by expressing PD-L1 and induce the generation of regulatory T (Treg) cells to accelerate tumor progression by suppressing macrophages in the tumor nest [24,25]. On the other one hand, by releasing MMP9, the accumulated neutrophils in the peri-tumoral regions of HCC patients could promote angiogenesis [26]. In our study, we obtained consistent conclusion that high CXCL1 expression conferred a poor prognosis in patients with HCC.
CXCL2 is produced by epithelial cell, macrophages, endothelial cells, and tumor cells, which also exerts critical roles in mutiple biological progresses including inflammation, angiogenesis, cancer biological behaviors and immune response [27,28]. As for HCC, CXCL2 could enhance liver cancer cell migration, proliferation and invasion while the expression of CXCL2 is regulated by miR-532-5p [29]. In our report, we showed that the TPM and the mRNA level of CXCL2 were downregulated in HCC tissues and significantly associated with the prognosis of patients with HCC, but its level was not correlated with tumor stage.
CXCL3 is subclassified as a Glu-Leu-Arg (ELR+) CXC chemokine, which is upregulated in most agammaessive tumors [30]. CXCL3 is widely expressed in liver tissue and plays essential roles in inflammatory response and liver injury [31]. Zhang L et al showed that CD133 overexpression could contribute to CXCL3 expression in HCC cells while Knockdown of CXCL3 inhibited CD133+ liver cancer stem cell (CSC) self-renewal and tumorigenesis by suppressing Erk1/2 and ETS1 phosphorylation. HCC patients with lower CXCL3 expression exhibited a better prognosis, the high level of which was significantly correlated with and tumor capsule formation and vascular invasion [32]. We uncovered that CXCL3 may potentially affect the clinical stage of HCC. In stage Ⅳ, the level of CXCL3 was significantly lower.
CXCL5, epithelial neutrophil-activating peptide-78, is a small, secreted proteins, which is mainly responsible for angiogenesis. Study showed that CXCL5 could promote HCC cell invasion, proliferation by mediating intratumoral neutrophil infiltration [7]. Also, CXCL5 could indicate poor prognosis in patients with HCC. Additionally, CXCL5 resulted in epithelial-mesenchymal transition (EMT) of HCC cells via activating PI3K/Akt/GSK-3β/Snail axis [33]. In our study, we found that the level of CXCL3 significantly decreased in patients of stage Ⅳ.
CXCL8, known as interleukin-8 (IL-8), is usually secreted by tumor and inflammatory cells. In HCC tissues and cell lines, the level of CXCL8 was significantly increased. Meanwhile, CXCL8 can cause HCC progression and metastasis through activating AKT/mTOR/STAT3 signaling pathway [34]. Here we uncovered that patients with lower level of CXCL8 may have better prognosis.
CXCL9 is implicated with liver damage and the infiltration of inflammatory cells and after Hepatitis B virusinfection. Meantime, CXCL9 was involved in the invasion ability of HCC by increasing the level of phosphatidylinositol-3, 4, 5-trisphosphate RAC Exchanger 2 (PREX2) [35]. Based on bioinformatics analysis, we disclosed that the expression level of CXCL9 were significantly increased in carcinoma tissues.
CXCL10 is reported to regulate leukocyte trafficking, inflammation, angiogenesis, hematopoiesis, adaptive immunity and tumor metastasis mediated by G-protein-coupled (chemokine) receptors [36]. CXCL10 participates in the metastasis of HCC through up-regulating the level of matrix metallopeptidase-2 (MMP-2) [37]. In this study, we found that the level of CXCL10 significantly increased in HCC group, but its level was not associated with clinical stage and prognosis in patients with HCC.
CXCL14, also known as breast and kidney-expressed chemokine (BRAK), is a new-found CXC chemokine with unclear function as well as receptor selectivity [38]. Till now, no research has focused on the role of CXCL14 on the progression of HCC. Our study showed that the expression of CXCL14 was significantly inhibited in HCC tissue. However, the potential mechanism of CXCL9 in HCC should be further explored.
In this study, we systemically analyzed the expression and prognostic value of CXC cytokines in HCC, providing a comprehensive insight of the complexity and heterogeneity of the molecular biological characteristics of HCC. Our bioinformatics analysis firstly disclosed the potential prognosis and therapeutic values of CXC cytokines in HCC. We sincerely hope that our research will make some contributions to available knowledge, optimize treatment strategy, and improve the accuracy of prognosis for patients with HCC.
Acknowledgements
This study was approved by the Human Research Ethics Committee of the Lishui Municipal Central Hospital.
Conflict of Interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad: