1. Introduction
Dengue is a vector-borne disease spread by the female mos-quitoes Aedes aegypti and Aedes albopictus. The mosquitoes Aedes aegypti were originated from Africa but have now been spread in tropical, subtropical and temperate regions of the world. The fast growth in human population, uncontrolled urbanization and inadequate waste management systems have led to abundance of mosquito breeding sites [6]. These are the main causes which bring this global distribution of mosquitoes and consequently spread of the mosquito-borne diseases. Before 1970, dengue was reported from only nine countries, now it has been widespread in the areas of North America, South America, Africa and Southeast Asia [7]. It is important to control dengue disease as more than 50 million people are affected every year [27]. Interestingly, only the female mosquitoes can transmit the virus. The female mosquitoes bite the human as they require blood for reproduction process. On biting the dengue infected person, these female mosquitoes become infected and can transmit the dengue virus to another person [7]. One of the ways to control dengue infection is to control mosquito population. Mosquito population can be chemically controlled by the use of insecticides and / or biological controlled by wolbochia [9,18,26]. The human awareness campaigns can also reduce the spread of infection.
One of the efficient ways to combat the infection is the use of sterile insect technique (SIT). In SIT, sterile male mosquitoes are released near the mosquito breeding sites. Female mosquitoes will not be able to fertilize when mating with these male mosquitoes. In this way, the mosquito population as well as the spread of infection is controlled. The idea of SIT was first conceived by American entomologist, Dr Edward F. Knipling and was successfully implemented to control the spread of screwworm fly in Florida [14]. After that, the SIT technique has been used for many flying insects by various countries [15,16]. To eradicate dengue infection, the government of China and Brazil have also released the sterile male mosquitoes to combat the dengue infection [10,11].
In literature, some mathematical models on control of vector-borne diseases are available [1,2,3,4,9,13,18,19,20,21,23,25]. Few mathematical models have also been formulated to control dengue infection by SIT [3,4,25]. In particular, Esteva and Yang proposed a mathematical model to control the mosquito density by releasing sterile male mosquitoes [3]. Optimal control analysis to control the Aedes aegypti female mosquitoes by SIT strategy has been performed by Thomˊe, Yang and Esteva [25]. A pulsed spatial discrete time model using SIT method has also been proposed by Evans and Bishop [4]. They concluded that increased number of sterile will have no further benefit above a threshold. The effectiveness is highly reduced by density dependent mortality of sterile insects. Hendron and Bonsall have developed the n patch dengue model with two control strategies namely vaccination and vector control by SIT method. The dynamics of two serotypes of dengue viruses with effect of cross immunity and antibody-dependent enhancement have been considered without explicitly incorporating the male/female vector (mosquito) dynamics [8].
In this paper, a host-vector model has been proposed to control the primary dengue transmission using SIT strategy. In SIT, the male mosquitoes (Aedes aegypti) are sterilized in the laboratory and are released into the environment to compete with wild male mosquitoes for mating with female mosquitoes. In section 2, a network model for n patches has been formulated. The model analysis of an isolated patch is carried out in section 3. In section 4, the model analysis for n patch network model has been carried out to explore the behavior of system. Conclusions are given in the last section.
2. Formulation of host-vector model
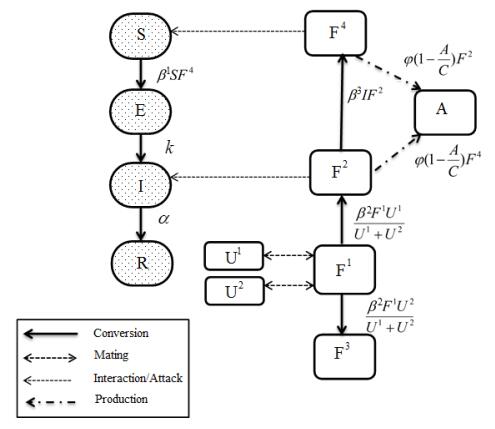
Consider A be the class of mosquitoes in aquatic stage (eggs, larvae or pupae). Let U1 and U2 be the normal male mosquitoes and sterile male mosquitoes population respectively. Let the female mosquitoes are divided in four compartments: F1, F2,F3 and F4. The unmated and uninfected mosquitoes are in F1 compartment. Let F2 be the class of fertilized female mosquitoes and are uninfected. The female mosquitoes (F3) mated with sterile male mosquitoes are unfertilized and will not reproduce. The fertilized female mosquitoes need multiple blood meals to complete the reproduction cycle. The fertilized female mosquitoes who bite infected individuals become infected and transfer to F4 class and play crucial role in the spread of dengue infection. The remaining female fertilized mosquitoes bite susceptible/exposed/recovered human population before laying eggs and remain uninfected. No separate class is considered for them. As such both female mosquitoes F2 and F4 contribute to aquatic stage. Let the susceptible (S), exposed (E), infected (I) and recovered (R) be the host population in the four compartments. Consider the SEIR dynamics in the host population interacting with susceptible female mosquitoes F2 and infected female mosquitoes F4. The model also incorporates the interstate transition between different classes of male and female mosquitoes. No vertical transmission has been assumed for vector dynamics. Let there be a network of n patches. The host-vector dynamics in each patch is shown in the schematic diagram in Figure 1. Let the subscript i represents the respective variable/parameter in the ith patch; i=1, ...n. The human migration is considered between patches while no interpatch migration between mosquitoes is considered. The superscripts S, E, I and R are used to incorporate the differential ability of migration in various compartments (e.g. mSij represents migration in susceptible compartment). The following n patch metapopulation model is formulated according to the schematic diagram, Figure 1.
|
dSidt=ωi−β1iSiF4i−μiSi+n∑j=1,j≠imSijSj−n∑j=1,j≠imSjiSi
|
(1)
|
|
dEidt=β1iSiF4i−(ki+μi)Ei+n∑j=1,j≠imEijEj−n∑j=1,j≠imEjiEi
|
(2)
|
|
dIidt=kiEi−(αi+μi)Ii+n∑j=1,j≠imIijIj−n∑j=1,j≠imIjiIi
|
(3)
|
|
dRidt=αiIi−μiRi+n∑j=1,j≠imRijRj−n∑j=1,j≠imRjiRi
|
(4)
|
|
dAidt=ϕi(1−AiCi)(F2i+F4i)−(γi+di)Ai
|
(5)
|
|
dF1idt=piγiAi−β2iF1iU1iU1i+U2i−β2iF1iU2iU1i+U2i−d1iF1i
|
(6)
|
|
dF2idt=β2iF1iU1iU1i+U2i−β3iIiF2i−d1iF2i
|
(7)
|
|
dF3idt=β2iF1iU2iU1i+U2i−d1iF3i
|
(8)
|
|
dF4idt=β3iIiF2i−d1iF4i
|
(9)
|
|
dU1idt=(1−pi)γiAi−d1iU1i
|
(10)
|
All model parameters are defined in Table 1 and are assumed to be non-negative. The initial conditions associated with the above system are:
|
Si(0)≥0,Ei(0)≥0,Ii(0)≥0,Ri(0)≥0,0≤Ai(0)≤Ci,F1i(0)≥0,F2i(0)≥0,F3i(0)≥0,F4i(0)≥0,U1i(0)≥0,U2i(0)≥0
|
Table 1. Parameters of the Model.
| Parameters |
Description of parameters |
| α |
Human recovery rate |
| β1 |
Transmission rate of infection from female mosquitoes to human |
| β2 |
Mosquitoes mating rate |
| β3 |
Transmission rate of infection from human to female mosquito |
| γ |
Transition rate from aquatic stage to adult mosquito |
| μ |
Natural death rate of human |
| ω |
Birth rate of human |
| ω1 |
Constant recruitment rate of sterile male mosquito |
| ϕ |
Recruitment rate for aquatic mosquito |
| C |
Carrying capacity for aquatic/adult mosquito |
| d |
Natural death rate of mosquito at aquatic state |
| d1 |
Natural death rate of mosquito |
| k |
Rate at which exposed human become infectious |
| mij |
Migration rate from patch j to patch i |
| p |
Proportion of female mosquito |
In the next section, the dynamics of the model (1)-(11) is discussed for an isolated patch (i.e mSij=mEij=mIij=mRij=0).
3. Model analysis for an isolated patch
In absence of interpatch migration, the patches are decoupled and isolated. The dynamics of each isolated patch is given below where the subscript i is suppressed:
|
dAdt=ϕ(1−AC)(F2+F4)−(γ+d)A
|
(16)
|
|
dF1dt=pγA−β2F1U1U1+U2−β2F1U2U1+U2−d1F1
|
(17)
|
|
dF2dt=β2F1U1U1+U2−β3IF2−d1F2
|
(18)
|
|
dF3dt=β2F1U2U1+U2−d1F3
|
(19)
|
Let X(t)=(S(t),E(t),I(t),R(t),A(t),F1(t),F2(t),F3(t),F4(t),U1(t),U2(t))⊺∈R11+. The system (12)-(22) with non-zero initial conditions can be written in the following form:
|
dXdt=Q(X(t),t),X(0)=X0≥0Q(X(t),t)=(Q1(X,t),Q2(X,t),Q3(X,t)....,Q11(X,t))⊺
|
(23)
|
3.1. Positivity and boundedness of the solution
Proposition 1. The positive cone Int(R11+) is invariant for the system (23).
Proof. Observe that the boundaries of non-negative cone R11+ are invariant for the system (23) and Q(X(t),t) is smooth enough. Applying the existence and uniqueness theorem [22] for differential equations, the system (23) will possess the positive solution.
Proposition 2. Solutions of system (12)-(22) are bounded in the domain Ω= {(S,E,I,R,A,F1,F2,F3,F4,U1,U2)∈R11+|S+E+I+R≤ωμ, A(t)≤C,F1+F2+F3+F4+U1+U2≤ω1+γCd1}.
Proof. Let N(t)=S(t)+E(t)+I(t)+R(t) be the total host population at time t. Adding corresponding equations for host dynamics gives
|
dNdt=ω−μN⟹lim supt→∞N(t)≤ωμ.
|
For vector dynamics, it is clear that A(t)≤C∀ t. Let us prove it by contradiction.
Let t0 be the smallest value of t such that A(t0)=C. Assume A(t)≤C for t∈[0,t0) and A(t)>C, for t∈(t0,T) where, T<∞. Accordingly, ˙A(t)>0 for t∈(0,t0) and ˙A(t)<0 for t∈[t0,T) from (16). By mean value theorem ˙A(t)>0 for t∈[t0,T) which is contradiction.
Let M(t)=F1+F2+F3+F4+U1+U2, now adding equations from (17)-(22) gives
|
dMdt=ω1+γA(t)−d1(F1(t)+F2(t)+F3(t)+F4(t)+U1(t)+U2(t))dMdt≤ω1+γC−d1M(t)⟹lim supt→∞M(t)≤ω1+γCd1.
|
Therefore, the system (23) is bounded.
3.2. Equilibrium states
The equilibrium states for the system (12)-(22) are obtained by solving
The trivial disease-free state ˘P1 always exists and it is given as
|
˘S=ωμ,˘U2=ω1d1,˘E=0,˘I=0,˘R=0,˘A=0,˘F1=0,˘F2=0,˘F3=0,˘F4=0,˘U1=0.
|
Note that, this state is without native mosquitoes. Only the susceptible human and sterile male mosquitoes survive.
Let us define the non-dimensional number T, the basic offspring number, as
|
T=β2ϕpγ(β2+d1)d1(γ+d).
|
(24)
|
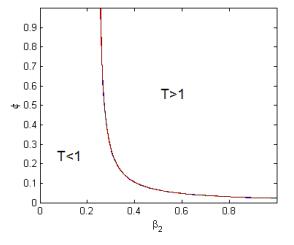
It represents the average number of secondary female mosquitoes produced by single female mosquito, Esteva and Yang [3]. To maintain the mosquito population in environment, T should be greater than 1. The existence of another non-trivial disease-free equilibrium state is established for T>1.
Proposition 3. The system admits two non-trivial disease-free states P+2 and P−2 when
|
T>1and ω1<W(=(T−1)2Cγ(1−p)4T).
|
(25)
|
Proof. Let us denote P±2=(ˉS,ˉE,ˉI,ˉR,ˉA,¯F1,¯F2,¯F3,¯F4,¯U1,¯U2). For the disease-free state of the system (12)-(22), substituting I=0 gives
|
ˉS=ωμ,ˉE=0,ˉR=0,¯F4=0and ¯U2=ω1d1.
|
(26)
|
The other state variables ¯F1,¯F2,¯F3 and ¯U1 at equilibrium level are obtained in terms of ˉA:
|
¯F1=pˉAγ(β2+d1),¯F2=β2pˉAγˉU1(ˉU1+ˉU2)(β2+d1)d1,¯F3=β2pˉAγˉU2d1(β2+d1)(ˉU1+ˉU2),¯U1=ˉAγ(1−p)d1
|
(27)
|
ˉA is the root of following quadratic polynomial:
|
s(ˉA)=B1ˉA2+B2ˉA+B3=0B1=β2pϕγ(β2+d1)(γ+d)d1C,B2=−β2ϕpγ(β2+d1)d1(γ+d)+1,B3=ω1γ(1−p)
|
By writing the quadratic s(ˉA) in terms of T gives
|
s(ˉA)=TCˉA2−(T−1)ˉA+ω1γ(1−p)=0.
|
(28)
|
Since p<1, no positive root of equation (28) is admissible for T≤1. Clearly, the quadratic has real positive roots when the condition (25) is satisfied. The roots are given as
|
ˉA±=(T−1)C2T(1±√1−ω1W); W=(T−1)2Cγ(1−p)4T.
|
(29)
|
Accordingly, there exists two non-trivial disease-free equilibrium states P−2 and P+2 corresponding to ˉA− and ˉA+ respectively under condition (25).
These two roots ˉA− and ˉA+ collapse at ω1=W. This gives a critical value T=T∗ where the quadratic has the unique solution:
|
T∗=(1+2ω1Cγ(1−p))[1+√(1−1(1+2ω1Cγ(1−p))2)]>1
|
(31)
|
Therefore, the unique non-trivial disease-free equilibrium point P∗2 exists at T=T∗.
Let us denote the endemic states by P±3 (ˆS,ˆE,ˆI,ˆR,ˆA,^F1,^F2,^F3,^F4,^U1,^U2). Now, the conditions for the existence of the endemic states P±3 are explored. The equilibrium level of state variables are obtained as ˆS=ω(β1^F4+μ),ˆE=β1ˆSˆF4(k+μ),ˆI=β1kˆSˆF4(k+μ)(α+μ),ˆR=αˆIμ, ^F1=pγˆA(β2+d1), ^F2=((γ+d)ˆACβ1+μϕ(C−ˆA))d1(k+μ)(α+μ)ϕ(C−ˆA)(β1β3kω+β1d1(k+μ)(α+μ)), ^F3=β2pγˆAω1d1(β2+d1)(^U1+^U2), ^F4=β1β3kω^F2−μd1(α+μ)(k+μ)β1d1(α+μ)(k+μ), ^U1=(1−p)γˆAd1,^U2=ω1d1.
Here, ˆA is the root of same quadratic polynomial s(ˆA)=0 as given in (28). Accordingly, the condition (25) is necessary for the existence of both the non-trivial disease-free states P±2 as well as the endemic states P±3. Another condition ^F4>0 is required for existence of P±3 states.
Remark 1. It is to be noted that for the non-trivial disease-free states P±2 and endemic states P±3, the equilibrium densities of following variables are found to be the same:
|
ˉA=ˆA,ˉF1=ˆF1,ˉU1=ˆU1,ˉU2=ˆU2
|
Remark 2. Simplifying the expression for ˆF2 gives
|
^F2=β2γpˆA^U1(^U1+^U2)(β2+d1)(β3ˆI+d1).
|
Comparing it with ¯F2 yields,
Let us define
|
R+0=β1β3kωˉF2+μd1(α+μ)(k+μ) and R−0=β1β3kωˉF2−μd1(α+μ)(k+μ).
|
(33)
|
Further, for positive ^F4+ and ^F4−, the following conditions should be satisfied:
|
β1β3kωˆF2+μd1(α+μ)(k+μ)>1 and β1β3kωˆF2−μd1(α+μ)(k+μ)>1
|
(34)
|
Using (32) gives the conditions for the existence of the endemic states P±3.
Remark 3. It can be seen from (29) that ˉA+>ˉA−. Similarly, it can be easily proved that ˉF2+>ˉF2−. Accordingly, it can be concluded that:
Let us define R0 as
|
R0=max(R+0,R−0)(>1).
|
(36)
|
Accordingly, the following proposition is established for the existence of endemic states P±3:
Proposition 4. When condition (25) is satisfied, the two positive endemic equilibrium states P−3 and P+3 will exist provided the equation (36) is satisfied.
Consider the following choice of parameters [3]:
|
d=0.05,d1=0.0714,p=0.5,γ=0.075
|
The existence of P±2 and P±3 states depend on the T and W. The parameters β2 and ϕ are considered to be critical for their existence. The curve T=1 in Figure 2 divides the β2−ϕ plane into two regions. On the right of this curve (T>1) both the equilibrium states P±2 and P±3 may exist depending on the other conditions. In particular, the states P±2 and P±3 will not exist on the left of the curve T=1 (T<1).
3.3. The basic reproduction number
The basic reproduction number has been computed by next generation approach [12]. It is defined as the average number of secondary infections produced by single infected individual in susceptible population. Using the Remark 3, it is given as
|
R0=β1β3kωˉF2+(α+μ)d1μ(μ+k).
|
(37)
|
3.4. Stability of trivial disease-free state (P1)
For local stability, the Jacobian matrix J[P] of the system (12)-(22) about a state P is given as:
|
[−β1F4−μ0000000−β1S00β1F4−k−μ000000β1S000k−α−μ0000000000α−μ00000000000j5,50j5,70j5,9000000pγ−β2−d10000000−β3F200j7,6−d1−β3I00j7,10j7,1100000j8,60−d10j8,10j8,1100β3F2000β3I0−d1000000(1−p)γ0000−d100000000000−d1]
|
|
j5,5=−γ−d+−ϕC(F2+F4),j7,6=β2U1U1+U2,j7,10=β2F1U2(U1+U2)2,j7,11=−β2F1U1(U1+U2)2,j8,6=β2U2(U1+U2),j8,10=−j7,10,j8,11=−j7,11j5,7=ϕ(1−AC)=j5,9
|
The eleven eigenvalues of the Jacobian matrix about the trivial disease-free state P1 are obtained as
|
−α−μ,−μ(multiplicity 2),−β2−d1,−d1(multiplicity 5),−μ−k,−γ−d1.
|
Since all the eigenvalues have negative real part, the state P1 will always be locally asymptotically stable.
Proposition 5. The locally asymptotically stable trivial disease-free state P1 is also globally stable for
Proof. Consider the positive definite function L(A,F1,F2,F4) for arbitrarily chosen positive constants C1,C2, C3 and C4:
|
L(A,F1,F2,F3,F4)=C1A+C2F1+C3F2+C4F4
|
Computing its time derivative ˙L(A,F1,F2,F4) along the trajectories of system (12)-(22),
|
˙L(A,F1,F2,F4)=C1˙A+C2˙F1+C3˙F2+C4˙F4˙L(A,F1,F2,F4)=C1(ϕ(1−AC)(F2+F4)−(γ+d)A)+C2(pγA−β2F1−d1F1)+C3(β2F1U1(U1+U2)−β3IF2−d1F2)+C4(β3IF2−d1F4)˙L(A,F1,F2,F4)≤−F2(C3d1−C1ϕ)−F4(C4d1−C1ϕ)−A(C1(γ+d)−C2pγ)−F1(C2(β2+d1)−C3β2)
|
For the derivative of the function L(A,F1,F2,F4) to be negative definite
|
d1C3>ϕC1;d1C4>ϕC1;(γ+d)C1>pγC2;(β2+d1)C2>β2C3
|
or
|
C3C1>ϕd1,C4C1>ϕd1,C1C2>pγ(γ+d),C2C3>β2(β2+d1)
|
Now, choosing C3=C4=1 and using above inequalities give
|
β2ϕpγ(β2+d1)d1(γ+d)(=T)<1.
|
Accordingly, the function L(A,F1,F2,F4) is a Lyapunov function for the condition (38). Since {P1} is the largest invariant set that contains the subset in which ˙L=0 for A=0,F1=0,F2=0,F4=0. By applying LaSalle's invariance principle [17], locally asymptotically stable disease-free state P1 is also globally asymptotically stable under (38).
3.5. Local stability of non-trivial disease-free states (P±2)
Proposition 6. For the local stability of non-trivial disease-free states P±2, the following conditions should be satisfied:
|
R0(=β1β3¯F2+kω(α+μ)μd1(μ+k))<1
|
(39)
|
and
|
k(ˉA)(=D4)=TˉA2C−ω1γ(1−p)>0
|
(40)
|
Proof. For the local stability of P±2 states, the 11 eigenvalues of Jacobian matrix of the system (12)-(22) about the states P±2 are given as: −μ (multiplicity 2), -d1 (multiplicity 2) and the remaining eigenvalues are the roots of cubic polynomial (q3(λ)) and fourth degree polynomial (q4(λ)), given as
|
B1=α+2μ+d1+kB2=μ(μ+2d1)+(μ+d1)k+α(μ+d1+k)B3=(α+μ)d1(μ+k)−β1β3ˉF2kˉS
|
The fourth degree polynomial is given as
|
q4(λ)=λ4+D1λ3+D2λ2+D3λ+D4=0.
|
|
D1=β2+d+3d1+ˉF2ϕC+γ>0D2=(ˉF2ϕ+C(d+d1+γ))(β2+3d1)C+β2d1>0D3=d1((γ+d)(β2+2d1)+d1(β2+d1)+(γ+d)(2β2+3d1)d1(ˉU1+ˉU2)(TˉA2C−ω1d1γ(1−p)(2β2+3d1)))D4=TˉA2C−ω1γ(1−p)
|
By Routh-Hurwitz criteria, all the roots of q3(λ) will be negative provided
|
R0(=β1β3¯F2+kω(α+μ)μd1(μ+k))<1.
|
Further, all the roots of fourth degree polynomial q4(λ) will have negative real part iff
Note that D1 and D2 are positive and also D4 is positive provided the condition (40) is satisfied. This condition also ensures the positivity of D3. The condition (42) is simplified and found to be satisfied for D4>0.
All eigenvalues have negative real part provided the conditions (39) and (40) are satisfied simultaneously and this completes the proof.
Corollary 1. The non-trivial disease-free state P−2 remains unstable always while the state P+2 is found to be locally asymptotically stable under the condition (39).
Proof. For the stability of the two non-trivial disease-free states P±2 explicitly namely P−2 and P+2, the sign of k(A−) and k(A+) are critical. The k(ˉA) is defined in (40). For the point A∗ where A+ and A− collapse, we have A−≤A∗≤A+. Using the expression for A∗ as given in (30), k(A∗) is found to be zero. Accordingly, k(A−) will be of negative sign giving instability of P−2 and k(A+) will be of positive sign. Hence, P−2 is always unstable while P+2 will be locally asymptotically stable for (39) to be satisfied.
Remark 4. The condition (40) is always satisfied for P+2. Therefore its stability depends on the condition (39).
Remark 5. When condition (39) is not satisfied, the non-trivial disease-free state P+2 will also become unstable. Consequently, the endemic states P+3 and P−3 will start to exist by (36).
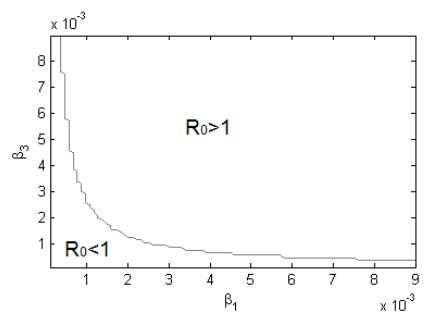
The Figure 3 is two parameter bifurcation diagram with respect to β1 and β3 showing the region of stability of the states P±2 as well as the existence of the P±3 states. Consider the following choice of parameters with varying transmission rates β1 and β3:
|
ω=0.039,β2=0.5,k=0.1667,ϕ=0.5,μ=0.00004,d=0.1096,d1=0.0714,α=0.7,p=0.5,ω1=0.97,γ=0.7,C=500
|
In Figure 3, the curve R0=1 bifurcates the parameter plane β1−β3 into two regions. The non-trivial disease-free state P+2 is locally stable in the region R0<1. The existence of endemic states P+3 and P−3 is possible in the region R0>1.
3.6. Numerical simulations
The local stability of P±3 states could not be achieved analytically due to large and complex expressions. To discuss the local stability of P±3 states, the numerical simulations have been performed for the data given in Table 2.
| Parameters |
Parameters values |
| α |
0.3 |
| β1 |
0.02 |
| β2 |
0.7 |
| β3 |
0.03 |
| γ |
0.075 |
| ω |
0.002 |
| ϕ |
5 |
| μ |
0.0000456 |
| C |
450 |
| d |
0.05 |
| d1 |
0.0714 |
| k |
0.1667 |
| p |
0.5 |
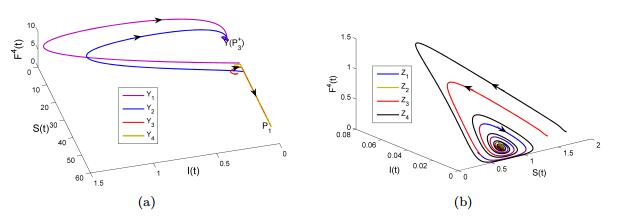
Further, the ratio between the carrying capacity to the net sterile male mosquitoes i.e. (Cω1/d1) is assumed to be 0.8 [3]. It is found that for the data set given in Table 2, the basic offspring number T(=19.06388689)>1 and the threshold R0 =8.179178686(>1). Accordingly, the states P3+(0.76383733, 0.01181548, 0.00656461, 50.31770846,394.752323, 19.19005978, 46.75477253,141.25412, 0.128961,207.32790,624.64985) and P3−(15.250814, 0.008414931, 0.00467529, 35.836020, 79.020, 3.8413960, 2.3417136, 35.314431, 0.00460008, 41.502141, 624.64985) exist by condition (36). For the stability of P−3 state, numerical simulations have been performed for the four initial conditions Y1, Y2, Y3 and Y4 (defined in caption) in the neighborhood of the state P−3.
It is observed that the trajectories starting from the initial conditions Y1 and Y2 converge to the point Y which is the projection of the state P+3 on the hyperplane. Moreover, it is checked that all other state variables also tend to corresponding values of P+3. Thus, the solution trajectories converge to P+3. Similarly, the trajectories starting from the initial conditions Y3 and Y4 converge to the state P1. It shows the unstable behavior of P−3 state. The phase plot in 3D hyperplane S−I−F4 has been drawn in Figure 4a. Further, for the stability of P+3 state, numerical simulations have been carried out for the four initial conditions (defined in caption) in the neighborhood of the state P+3.
It is found that starting with the initial conditions Z1, Z2, Z3 and Z4, the solution converges to the P+3 state. The phase plot in 3D hyperplane S−I−F4 has been drawn in Figure 4b.
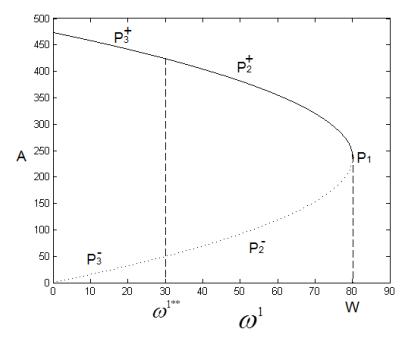
A bifurcation diagram has been drawn for the system (12)-(22) with respect to sterile male mosquitoes rate ω1 in Figure 5. The transmission rates from vector to host(β1) and host to vector (β3) are considered to be 0.002 nd 0.003 and rest of the parameter values are taken from Table 2. It is observed that the non-trivial disease-free states P+2 and P−2 exist from ω1=0 to W=80.0699 and collapse in P∗2 at ω1=W(=80.0699). The expression for W is given in (29). For W>80.0699, only the state P1 exists and stable. Further, it is found that at ω1=ω∗∗1 =30, R0= 1.002868566. The value of ω∗∗1 can be obtained using the condition (37). Therefore, for ω1>30, the non-trivial disease-free state P+2 is found to be stable. However, for ω1<30, the endemic states P+3 and P−3 start to exist while the disease-free state P+2 becomes unstable. Thus, for ω1<W, the control on natural mosquitoes will depend on the initial conditions and beyond this W, the control will work successfully irrespective of any initial condition.
3.7. Discussion
In this paper, a host-vector model has been formulated to analyze the effect of SIT control. It is observed from the analysis that when basic offspring number (T) is less than one then all the natural mosquitoes will be eliminated and only the sterile mosquitoes will survive in the long run. On the other hand if T is greater than T∗ (given in (31)), the two non-trivial disease-free states start to exist in which bigger one is found to be stable for R0<1 while the lower one is unstable always. At T=T∗, the non-trivial disease-free states collapse. However, for R0>1, two endemic states exist. Numerical simulations have been carried out to analyze the stability of endemic states. It is found that one state gets stable while other remains unstable for choice of relevant data from literature. To control the disease, a threshold has been computed for the rate ω1 at which the sterile mosquitoes be introduced. If the initial population size is in neighborhood of disease-free state then SIT control will work effectively and disease will die out for ω∗∗1<ω1<W. However, when ω1<ω∗∗1, the disease will persist, as after this value endemic states start to exist (shown in Figure 5).
To study the effect of human migration in disease transmission, the model (1)-(11) has been analyzed in next section.
4. n patch network model analysis
4.1. Basic reproduction number for n patch model
When no movement of human is considered, R0 is given as
|
R0=max(R0i);i=1,2,3...nwhere,R0i=kiβ1iβ3iωiF20i(μi+αi)(ki+μi)μid1i
|
When the patches are coupled due to movement of human population, the basic reproduction number for the network model (1)-(11) is computed below:
Let us denote the susceptible human population and fertilized female population at disease free state for the ith node be S0i and F20i and define
Further, define n×n diagonal matrices Dq, Dl, Dk and D1d as
Dq= diag(q1,q2,....qn), Dl= diag(l1,l2,....ln), Dk= diag(k1,k2,....kn) and D1d= diag(d11,d12,....d1n)
The matrices QE and QI are also defined as
|
QE=[μ1+k1+∑1=nj=1mEj1−mE12...−mE1n−mE21μ2+k2+∑1=nj=1mEj2...−mE2n.................−mEn1.......μn+kn+∑1=nj=1mEjn]
|
and
|
QI=[μ1+α1+∑1=nj=1mIj1−mI12...−mI1n−mI21μ2+α2+∑1=nj=1mIj2...−mI2n...................−mIn1......μn+αn+∑1=nj=1mIjn]
|
The basic reproduction number is computed by next generation approach [12]. The Jacobian matrices of the system (1)-(11) for the new infections (F) and transfer from one compartment to another (Y) are given below:
and
|
FY−1=[00DqD−1d1000Q−1EQ−1IDkDlDlQ−1E0]
|
The dominant eigenvalue of the next generation matrix FY−1 is the basic reproduction number for n patch model, Rn0(say)
|
Rn0=ρ(Q−1EQ−1IDkDlDqD−1d1).
|
(43)
|
Particularly, for single node (n=1), R0 is obtained as
|
R0=k1β11β31S01F201(μ+α1)(k1+μ)d1.
|
4.2. Numerical examples
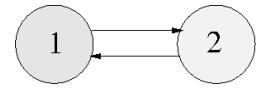
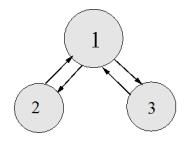
Let us perform the numerical experiments to control the disease in a network using SIT. For n=2 and n=3, the network topologies are given in Figure 6 and Figure 7 respectively. Let us assume that mSij=mEij=mIij=mRij=mij and ω1i and mij are varying in different patches. For simplicity, rest of the data is considered to be the same in all patches given in Table 3.
| Parameters |
Parameters values |
| αi |
0.5 |
| β1i |
0.001 |
| β2i |
0.7 |
| β3i |
0.001 |
| γi |
0.075 |
| ωi |
0.029 |
| ϕi |
5 |
| μi |
0.0000456 |
| Ci |
450 |
| di |
0.05 |
| d1i |
0.0714 |
| ki |
0.1667 |
| pi |
0.5 |
Observe that R0=3.6819(>1) in all the isolated patches for the data set given in Table 3. Accordingly, the disease is endemic in patches. Let us apply SIT in patch-1 so that the disease is controlled in it. The role of network coupling in controlling the disease in the network is explored for different combinations of migration parameters mij in Table 4. Further, if SIT control is reduced in patch-1 i.e. ω11=60 and no control is applied in patch-2 then for different combinations of migration parameters, the cases have been discussed in Table 5. It may be noted from Table 4, case (a) that the disease is controlled in the first patch where SIT is applied. The migration from second patch may bring infection in first patch. If the adequate number of sterile mosquitoes are present in the first patch, this additional infection will be eliminated. Consequently, the network is disease-free and SIT is successful. When ω11 is reduced (Table 5), the number of sterile mosquitoes present in the first patch are not sufficient enough to control the disease. Accordingly, the disease persists in the network (case (e)). However, changing the coupling (migration) suitably may again control the disease in the network (case (f)).
Table 4. When SIT is applied only in the patch-1 i.e.(ω11=70, ω12=0).
| Cases |
Migration in patch-1 |
Migration in patch-2 |
Conclusions |
| (a) |
m12=0 |
m21=0 |
Isolated patches with R0 of patch-1 is 0.2515<1 (37). Disease is controlled in patch-1 only. |
| (b) |
m12=0.005 |
m21=0.0006 |
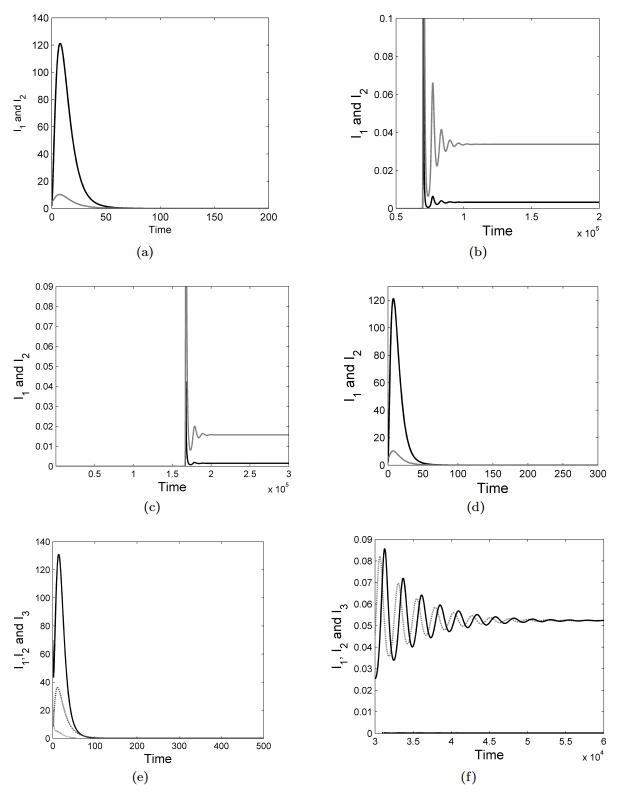
R20 for two patch network model is 0.7678<1 (43). Two patch network model may be disease-free. The time-series confirms that the infection level tends to zero in both the patches Figure 8a. |
| (c) |
m12=0.009 |
m21=0.0025 |
R20 for two-patch network model is 1.4763>1 (43). SIT method will not be able to control disease with this migration combination Figure 8b. |
Table 5. When SIT is applied only in the patch-1 i.e.(ω11=60, ω12=0).
| Cases |
Migration in patch-1 |
Migration in patch-2 |
Conclusions |
| (d) |
m12=0 |
m21=0 |
Isolated patches with R0 of patch-1 is 0.2515<1. Disease is controlled in patch-1 only. |
| (e) |
m12=0.005 |
m21=0.001 |
R20 for two-patch network model is 1.1778>1. SIT method will not be able to control disease with this migration combination. Disease may persist in the network Figure 8c. |
| (f) |
m12=0.009 |
m21=0.001 |
R20 for two-patch network model is 0.7273<1. The network may now be disease free Figure 8d. |
In this case, the following two cases have been considered in Table 6: From the Table 6, it is observed that the basic reproduction number for case (g) is less than one. The disease may be controlled in 3 node network model for this case. By numerically solving the network model (1)-(11) for n=3, it is found that the infection level converges to zero as shown in Figure 8e. Further, for case (h), (Rn0)>1. The time series for infective population (I1, I2 and I3) have been drawn in Figure 8f. It is evident that the infection persists. Thus, disease is controlled in case(g), but there is a failure of SIT in case (h).
Table 6. When SIT is applied only in the patch-1 i.e.(ω11=70, ω12=0 and ω13=0).
| Cases |
Migration in patch-1 |
Migration in patch-2 |
Migration in patch-3 |
Rn0 for network model |
| (g) |
m12=0.0001, m13=0.002 |
m21=0.0001 |
m31=0.0001 |
0.6762(<1) |
| (h) |
m12=0.0002, m13=0.0002 |
m21=0.001 |
m31=0.001 |
2.6813(>1) |
Keeping the results of above numerical experiments, the following conclusions can be drawn:
It is not necessary to apply SIT in the whole network. The disease can be controlled in network by applying SIT in one patch only. This is possible with suitable coupling of patches. Further, this selective way of applying SIT is more economical (cost effective). The success of SIT depends on the coupling strength of the network (migration parameters mij) and the recruitment rate of sterile mosquitoes ω11. Accordingly, they are suggested to be critical parameters.
5. Conclusion
In this paper, n patch network model has been formulated to control disease transmission by using SIT. First, the dynamics of an isolated patch has been analyzed. The basic reproduction number has been computed. For the existence and stability of disease-free and endemic states, the two critical parameters namely basic offspring number (T) and basic reproduction number (R0) have been identified. The bifurcation diagram has been plotted to show the existence and stability regions of disease-free and endemic states for an isolated patch. The critical level of sterile male mosquitoes has been obtained to control the disease. For n patch model, the basic reproduction number has been computed. The numerical simulations have been performed by considering two and three nodes with different combinations of migration and SIT recruitment to study the effects in disease elimination and persistence. It is concluded that the cost effective way to control the disease in suitably coupled network is to apply SIT in one patch only.
Acknowledgments
We would like to thank IFCAM for visiting support for this research collaboration. Authors also would like to thank anonymous reviewers for their valuable comments. Their comments have enhanced the clarity and the quality of results and text.









 DownLoad:
DownLoad: