1. Introduction

The 20th century is the period that human has made most brilliant achievements in the conquest of infectious diseases: raging smallpox for about a thousand years was finally eradicated; the day that people get rid of leprosy and poliomyelitis will be not far off; the occurrence rate of diphtheria, measles, whooping cough and tetanus has been reducing in numerous countries; the advent of many antibiotics has made the "plague", which once caused great calamity to human, no longer harm the world [16]. However, the World Health Report published by World Health Organization (WHO) has shown that infectious disease is still the greatest threat to mankind [39]. For example, the most widespread epidemic of Ebola virus in history began in Guinea in December 2013 and has continued for over two years. As of 17 March 2016, WHO and respective governments have reported over 28,000 suspected cases and about 11,000 deaths [17]. In 2014, dengue fever broke out in Guangdong, China and it was reported that there were more than 30,000 infected cases [18]. There are about 20,000 people died of dengue fever worldwide each year [33]. The latest threat is from Zika [13] and there is no vaccine or medicine for it. The Zika virus has now been detected in more than 50 countries and the epidemic situation it caused is declared by WHO a public health emergency of international concern.

The earliest differential equation model, concerning malaria transmission, was probably introduced by Dr. Ross. He showed from this mathematical model that if the number of malaria-carrying mosquitoes reduced below a critical value, the prevalence of malaria would be controlled. In 1927, Kermack and Mckendrick constructed the famous SIR compartment model to study the transmission dynamics of the Black Death in London from 1665 to 1666 and those of plague in Mumbai in 1906 [20]. They also proposed the SIS compartment model [21], and presented a "threshold value" which would determine the extinction and persistence of diseases based on the analysis of the established model.

Over the past 30 years, the research on epidemic dynamics has made much progress, and a large number of mathematical models are used to describe and analyze various infectious diseases. Most of mathematical models are governed by ordinary differential systems ([11,12,19,26,37]). Considering the spatial diffusion, the reaction-diffusion systems are used to describe spatial transmission of infectious diseases [1,5,22,23]. These models usually assume that the effective contact rate and recovery rate are constants ([1,23]). However, this assumption may hold only for a short time and for the homogeneous environment. To capture the impact of spatial heterogeneity of environment on the dynamics of disease transmission, Allen et al. proposed in [2] an epidemic model as follows,

$\left\{ \begin{array}{lll} S_{t}-d_S\Delta S=-\frac{\beta(x)S I}{S+I}+\gamma(x)I,\; & x\in\Omega,\; t>0, \\ I_{t}-d_I\Delta I=\frac{\beta(x)S I}{S+I}-\gamma(x)I,\; & x\in\Omega,\; t>0, \\ \frac{\partial S}{\partial \eta}=\frac{\partial I}{\partial \eta}=0,\; & x\in\partial\Omega, t>0,\\ \end{array} \right. \label{a11}$

(1)

where $S$ and $I$ represent the density of susceptible and infected individuals, respectively. $\beta(x)$ and $\gamma(x)$ account for spatial dependent rates of disease contact transmission and disease recovery at $x$, respectively.

Infectious disease often starts at a source location and gradually spreads over places where contact transmission occurs. For example, West Nile virus (WNv) is endemic in Africa, the Middle East and other regions. This virus was first detected in New York in 1999 [6], but it reached New Jersey and Connecticut in the second year and till 2002, it has spread across almost the whole America continent. This implies that the disease gradually spreads and the infected environment is changing with time $t$. Hence, for infectious diseases such as WNv, it is natural to understand the changing of the infected environment. Considering the moving front of the infected environment, the following epidemic model with the free boundary was recently studied in [23],

$\left\{ \begin{array}{lll} S_{t}-d_1\Delta S=b-\beta S I-\mu _1S,\; & r>0,\; t>0, \\ I_{t}-d_2\Delta I=\beta S I-\mu _2I-\alpha I,\; & 0<r<h(t),\; t>0, \\ R_{t}-d_3 \Delta R=\alpha I-\mu _3R,\; & 0<r<h(t),\; t>0, \\ S_r(0, t)=I_r(0,t)=R_r(0,t)=0,&t>0,\\ I(r,t)=R(r,t)=0,&r\geq h(t),\, t>0,\\ h'(t)=-\mu I_{r}(h(t),t),\; h(0)=h_0>0, & t>0, \\ S(r,0)=S_{0}(r),\; I(r,0)=I_{0}(r),\; R(r, 0)=R_{0}(r), & r\geq 0, \end{array} \right. \label{a12}$

(2)

where $r=|x|$ and $x \in \mathbb{R}^n$. The governed equation for the moving front $r=h(t)$ is the well-known Stefan condition, which was established in [28] for an invasive species. Stefan condition can be found in research of many applied areas, such as ice melting in contact with water [32], image processing [3], vapor infiltration of pyrolytic carbon in chemistry [31], tumor cure [35] and wound healing [7] in medicine, and spreading of invasive species [8,9,10,15,25,36,38,40]. Recently, it has been used to describe the moving front of diseases [1,14,23,29].

In addition, the spread of disease is different from the "random walk" of particle, which follows the Fick's law. The disease tends to move towards the feasible environment and spread along the human's movement. For instance, in the second year after WNv was detected, the wave front traveled 1100 km to the warmer South and 187 km to the colder North [30]. In 2008, according to reports from the Division of Disease Control, Public Health Department (DPH) of Indonesia, dengue cases (about 217-668 cases) were found in some more prosperous and densely-populated cities such as Makassar and Gowa, but no case was found in other sparsely-populated cities such as Jeneponto and Selayar [34]. To consider the impact of advection on transmission of disease, the authors in [14] proposed the following simplified SIS epidemic model,

$\left\{ \begin{array}{lll} I_{t}-d_I I_{xx}+\alpha I_x=(\beta(x)-\gamma(x))I-\frac{\beta(x)}{N^*}I^2,\; & g(t)<x<h(t),\; t>0, \\ I(g(t),t)=0, g'(t)=-\mu I_x(g(t),t),& t>0,\\ I(h(t),t)=0, h'(t)=-\mu I_x(h(t),t),& t>0, \\ g(0)=-h_0, h(0)=h_0, I(x,0)=I_0(x), & -h_0\leq x\leq h_0, \end{array} \right. \label{a14}$

(3)

in which they presented the sufficient conditions for the disease to spread or vanish, and discussed the impacts of the advection and the expanding capability on the spreading fronts.

Motivated by the above research, we will study the general SIR epidemic model with moving fronts and spatial advection,

$\left\{ \begin{array}{lll} S_{t}-S_{xx}+\alpha S_x=b-\beta(x) S I-\mu _1S,& -\infty<x<\infty,\; t>0, \\ I_{t}-I_{xx}+\alpha I_x=\beta(x) S I-\gamma(x)I-\mu _2I,& g(t)<x<h(t),\; t>0, \\ R_{t}-R_{xx}+\alpha R_x=\gamma(x) I-\mu _3R,& g(t)<x<h(t),\; t>0, \\ I(x,t)=R(x,t)=0,&x\leq g(t)\, \textrm{or}\, x\geq h(t),\, t>0,\\ g'(t)=-\mu I_{x}(g(t),t),\; g(0)=-h_0<0, & t>0, \\ h'(t)=-\mu I_{x}(h(t),t),\; h(0)=h_0>0, & t>0, \\ S(x,0)=S_0(x), I(x,0)=I_0(x), R(x,0)=R_0(x), & -\infty<x<\infty, \end{array} \right. \label{a15}$

(4)

where $x=g(t)$ and $x=h(t)$ are the moving left and right boundaries to be determined, the governing equations $g'(t)=-\mu I_x(g(t),t)$ and $h'(t)=-\mu I_x(h(t),t)$ are the special Stefan conditions. The death rates for the $S$, $I$ and $R$ classes are given by $\mu_1$, $\mu_2$ and $\mu_3$, respectively. The influx of the $S$ class comes from a constant recruitment rate $b$, and $h_0$, $\mu$, $\alpha$ are all positive constants, where $\mu$ and $\alpha$ represent the expanding capability and advection rate, respectively. The functions $\beta(x)$ and $\gamma(x)$ are positive H$\ddot{o}$lder continuous and satisfy

$(H_1)\ \lim\limits_{x\rightarrow\pm\infty}\beta(x)=\beta_{\infty}>0\ \textrm{and}\ \lim\limits_{x\rightarrow\pm\infty}\gamma(x)=\gamma_{\infty}>0.$

Epidemiologically, it means that the far sites are similar.

As in [2], if the disease transmission rate $\beta(x)$ at the site $x$ is greater than the recovery rate $\gamma(x)$, we call the location $x$ a high-risk site, we say it is low-risk if the disease transmission rate $\beta(x)$ is less than the recovery rate $\gamma(x)$. If the spatial average value $\frac{1}{|\Omega|}\int_{\Omega}\beta(x)dx$ of transmission rate is greater than (or less than) the spatial average value $\frac{1}{|\Omega|}\int_{\Omega}\gamma(x)dx$ of the recovery rate, we call the habitat $\Omega$ a high-risk (or low-risk) domain.

Furthermore, we only consider the case of the small advection in a habitat with high-risk far sites for problem (4) and assume that

$(H_2)\ \frac{b}{\mu_1}\beta_{\infty}-\gamma_{\infty}-\mu_2>0\ \textrm{and}\ \alpha<2\sqrt{\frac{b}{\mu_1}\beta_{\infty}-\gamma_{\infty}-\mu_2}\, .$

It is well-known that the basic reproduction number for the system

$\left\{ \begin{array}{l} \dot{S}(t)= b-\beta_{\infty}S I-\mu_1S,\\ \dot{I}(t)=\beta_{\infty}S I-\gamma_{\infty}I-\mu_2I,\\ \dot{R}(t)=\gamma_{\infty}I-\mu_3R. \end{array} \right. \label{150}$

is $R_0=\frac{b\beta_{\infty}}{\mu_1(r_{\infty}+\mu_2)}$, $R_0$ is the number of secondary cases which one case would produce on average over the course of its infectious period, in a completely susceptible population. The first inequality in $(H_2)$ means that $R_0>1$ and the far sites are high-risk. The constant $2\sqrt{\frac{b}{\mu_1}\beta_{\infty}-\gamma_{\infty}-\mu_2}$ in $(H_2)$ is the minimal speed of the traveling waves to the Cauchy problem

$I_t-I_{xx}=I\Bigr(\frac{b}{\mu_1}\beta_{\infty}-\gamma_{\infty}-\mu_2-d I\Bigl)$

with any $d>0$.

The initial functions $S_0$, $I_0$ and $R_0$ are nonnegative and satisfy

$\left\{ \begin{array}{lll} S_0\in C^2(-\infty, \infty)\bigcap L^{\infty}(-\infty, +\infty), ~I_0, R_0\in C^2([-h_0, h_0]);\\ I_0(x)=R_0(x)=0, \ \ x\in(-\infty,-h_0]\bigcup[h_0, \infty), \\ I_0(x)>0, R_0(x)>0, \ \ x\in(-h_0, h_0), \\ \end{array} \right. \label{a16}$

(5)

here (5) indicates that the infected individuals exist in the area $x\in(-h_0, h_0)$ at the beginning, and no infection happens in the area $|x|\geq h_0$. For model (4), one can see that there are no infected or recovered individuals beyond the left boundary $x=g(t)$ and the right $x=h(t)$.

We are interested in the impacts of environmental heterogeneity and small advection on the persistence of the disease, and the paper is organized as follows. Firstly, we present the global existence and uniqueness of the solution to problem (4) by the contraction mapping theorem in section 2. In section 3, we first present the definition and exhibit properties of the basic reproduction number for the corresponding model with Dirichlet boundary conditions, and then give the definition and properties of the spatio-temporal risk index $R_0^F(t)$ for problem (4). Section 4 deals with the sufficient conditions for the disease to vanish and Section 5 is devoted to the sufficient conditions for the disease to spread. The paper closes with some numerical simulations and a brief discussion.

---

2. Preliminaries

The contraction mapping theorem will be first used to prove the local existence and uniqueness of the solution to (4). Then suitable estimates will be exhibited to show that the solution is defined for all $t>0$, and the comparison principle will also be presented.

Theorem 2.1. Given any $\nu\in (0, 1)$ and $(S_0, I_0, R_0)$ satisfying (5), there is a $T>0$ such that problem $(4)$ admits a unique bounded solution

$(S, I, R; g,h)\in C^{1+\nu,\frac{1+\nu}{2}}(D^\infty_{T})\times[C^{ 1+\nu,\frac{1+\nu}{2}}(\overline{D}^{(g,h)}_{T})]^2\times [C^{1+\frac{\nu}{2}}([0,T])]^2,$

and

$\|S\|_{C^{1+\nu,\frac{1+\nu}{2}}({D}^\infty_{T})}+\|I\|_{C^{1+\nu, \frac{1+\nu}{2}}(\overline{D}^{(g,h)}_{T})}+\|R\|_{C^{1+\nu, \frac{1+\nu}{2}}(\overline{D}^{(g,h)}_{T})}\leq C,$

$\|g\|_{C^{1+\frac{\nu}{2}}([0,T])} +\|h\|_{C^{1+\frac{\nu}{2}}([0,T])}\leq C,$

where

$\begin{array}{lll} D_T^{\infty}~~=\{(x,t)\in \mathbb{R}^2: x\in(-\infty, \infty),t\in[0,T]\},\\ D_T^{(g,h)}=\{(x,t)\in\mathbb{R}^2: x\in(g(t), h(t)), t\in(0,T]\}. \end{array} \label{q1}$

(6)

Here $C$ and $T$ only depend on $h_0, \nu, \|S_0\|_{C^{2}((-\infty, \infty))}, \|S_0\|_{L^{\infty}((-\infty, \infty))}, \|I_0\|_{C^{2}([-h_0, h_0])}$ and $\|R_0\|_{C^{2}([-h_0, h_0])}$.

Proof. The idea of this proof is to straighten the free boundaries to circumvent the difficulty caused by the unknown boundaries, and then to construct a mapping. The conclusions of this theorem follow from the contraction mapping theorem together with $L^p$ theory and Sobolev's imbedding theorem [24], we omit it here since it is similar to that of Theorem 2.1 in [23] with obvious modifications, see also [7,8] and references therein.

We derive the following estimates, which will be used to show that the local solution obtained in Theorem 2.1 can be extended to all $t>0$.

Lemma 2.2. Let $T_0\in(0,+\infty)$ and $(S,I,R;g,h)$ be a solution to problem $(4)$ defined for $t\in [0, T_0]$. Then there exist the constants $C_1$ and $C_2$, independent of $T_0$, such that

$\begin{eqnarray*} 0<S(x,t)\leq C_1, & -\infty<x<+\infty, \, 0<t\leq T_0,\\ 0<I(x,t),\ R(x,t)\leq C_2,& g(t)<x<h(t),\, 0<t\leq T_0. \end{eqnarray*}$

Proof. It is easy to see that $S\geq 0, I\geq 0$ and $R\geq 0$ in $(-\infty, +\infty)\times [0, T_0]$ as long as the solution exists. Moreover, using the strong maximum principle to the first equation of (4) in $[g(t), h(t)]\times [0, T_0]$ gives that

$S(x, t)>0, -\infty<x<\infty, 0<t\leq T_0,$

$I(x, t),\ R(x,t)>0, g(t)<x<h(t), 0<t\leq T_0.$

It is easily verified that any constant $C$ is an upper solution of $S$ in $(-\infty, +\infty)\times [0, T_0)$ if $C>\frac{b}{\mu_1}$ and $C\geq S_0(x)$. Hence,

$0<S(x,t)\leq\max\Bigr\{\frac{b}{\mu_1}, \|S_0\|_{L^{\infty}}\Bigl\}:=C_1, \ \ -\infty<x<\infty,\, 0<t< T_0.$

Furthermore, adding the first three equations of (4) leads to

$(S+I+R)_t-(S+I+R)_{xx}+\alpha(S+I+R)_x\\ = b-\mu_1S-\mu_2I-\mu_3R\leq b-\mu_0(S+I+R)$

for $g(t)<x<h(t)$ and $0<t\leq T_0$, where $\mu_0=\min\{\mu_1, \mu_2, \mu_3\}$. Therefore, we have

$S+I+R\leq\max\Bigr\{\frac{b}{\mu_0}, \|S_0+I_0+R_0\|_{L^{\infty}}\Bigl\}:=C_2.$

The next lemma displays the monotonicity of free boundaries for problem (4). The proof is similar as that of Lemma 2.3 in [23] for an SIR epidemic model without advection, or that of Lemma 2.3 in [27] for a mutualistic model with advection, we omit it here.

Lemma 2.3. Let $T_0 \in (0,+\infty)$ and $(S,I,R;g,h)$ be a solution to problem $(4)$ defined for $t\in (0,T_0]$. Thenthere exists a constant $C_3$ independent of $T_0$ such that

$-C_3\leq g'(t)<0 \;\;and\;\; 0<h'(t)\leq C_3 \;\;for\;\; t\in(0,T_0].$

With the above bounds independent of $T_0$, we can extend the solution. The following theorem guarantees the global existence of the solution to problem $(4)$, and the reader can refer to [23] for a similar standard proof.

Theorem 2.4. Problem $(4)$ admits a unique solution $(S,I,R;g,h)$, which exists globally in $[0,\infty)$ with respect to $t$.

In what follows, we exhibit the comparison principle for convenience of later analysis, which are similar to Lemma 3.5 in [9].

Lemma 2.5. (Comparison principle) Assume that $T\in(0, \infty)$, $\overline{g},\underline{g}$, $\overline{h}, \underline{h}\in C^1([0, T])$, $\overline{S}(x,t), \underline{S}(x,t)\in C(D^{\infty}_T)\bigcap C^{2,1}(D^{\infty}_T )$, $\overline{I}(x,t)\in C(D^{(\overline{g},\overline{h})}_T)\bigcap C^{2,1}(D^{(\overline{g},\overline{h})}_T)$, $\underline{I}(x,t)\in C(D^{(\underline{g},\underline{h})}_T)\bigcap C^{2,1}(D^{(\underline{g},\underline{h})}_T)$, here the definitions of $D^{\infty}_T, D^{(\overline{g},\overline{h})}_T$ and $D^{(\underline{g},\underline{h})}_T$ are the same as those in $(6)$. Moreover, assume

$\left\{ \begin{array}{lll} \overline{S}_t-\overline{S}_{xx}+\alpha\overline{S}_x\geq b-\mu_1\overline{S}\underline{I}-\mu_1\overline{S}, & -\infty<x<\infty,\, 0<t\leq T, \\[6pt] \underline{S}_t-\underline{S}_{xx}+\alpha\underline{S}_x\leq b-\mu_1\underline{S}\overline{I}-\mu_1\underline{S}, & -\infty<x<\infty,\, 0<t\leq T, \\[6pt] \overline{I}_t-\overline{I}_{xx}+\alpha\overline{I}_x\geq (\beta(x)\overline{S}-\gamma(x)-\mu_2)\overline{I}, &\overline{g}(t)<x<\overline{h}(t),\, 0<t\leq T, \\[6pt] \underline{I}_t-\underline{I}_{xx}+\alpha\underline{I}_x\leq (\beta(x)\underline{S}-\gamma(x)-\mu_2)\underline{I}, &\underline{g}(t)<x<\underline{h}(t), \, 0<t\leq T, \\[6pt] \overline{I}(x,t)=0,\ \overline{g}'(t)\leq-\mu\overline{I}_x(\overline{g}(t), t), & x\leq\overline{g}(t),\, 0<t\leq T,\\[6pt] \underline{I}(x,t)=0,\ \underline{g}'(t)\geq-\mu\underline{I}_x(\underline{g}(t), t), &x\leq\underline{g}(t),\, 0<t\leq T,\\[6pt] \overline{I}(x,t)=0,\ \overline{h}'(t)\geq-\mu\overline{I}_x(\overline{h}(t), t), &x\geq\overline{h}(t),\, 0<t\leq T,\\[6pt] \underline{I}(x,t)=0,\ \underline{h}'(t)\leq-\mu\underline{I}_x(\underline{h}(t), t), &x\geq\underline{h}(t),\, 0<t\leq T,\\[6pt] \overline{g}(0)\leq-h_0\leq\underline{g}(0)<\underline{h}(0)\leq h_0\leq\overline{h}(0),\\[6pt] \underline{I}(x, 0)\leq I_0(x)\leq\overline{I}(x,0), &-h_0\leq x\leq h_0,\\[5pt] \underline{S}(x, 0)\leq S_0(x)\leq \overline{S}(x,0), &-\infty< x<\infty. \end{array} \right.$

Then the solution $(S,I, R; g,h)$ of problem $(4)$ satisfies

$\begin{array}{lll} \overline{g}(t)\leq g(t)\leq\underline{g}(t),\ \underline{h}(t)\leq h(t)\leq\overline{h}(t),&0<t\leq T,\\[6pt] \underline{S}(x,t)\leq S(x,t)\leq\overline{S}(x,t), &-\infty<x<\infty,\, 0<t\leq T,\\[6pt] \underline{I}(x,t)\leq I(x,t)\leq\overline{I}(x,t),&g(t)\leq x\leq {h}(t),\, 0<t\leq T. \end{array}$

---

3. The risk index

The objective of this section is to discuss the risk index for the free boundary problem (4), we first present the basic reproduction number of the following reaction-diffusion-advection problem with Dirichlet boundary condition,

$\left\{ \begin{array}{lll} I_t-I_{xx}+\alpha I_x=\frac{b}{\mu_1}\beta(x)I-\gamma(x)I-\mu_2I,\; & x\in (p, q),\, t>0, \\ I(x,t)=0,\; & x=p~\mbox{or}~q, t>0, \end{array} \right. \label{a31}$

(7)

where $p<q$. Now the basic reproduction number of (7) is defined by

$R_0^{DA}=R_0^{DA}((p, q),\beta(x),\gamma(x))=\sup\limits_{\phi\in H^1_0((p, q))\, \phi\neq 0}\frac{\int^{q}_{p}\frac{b}{\mu_1}\beta(x)\phi^2dx}{\int^{q}_{p}\bigr(\phi^2_x+(\frac{\alpha^2}{4}+\gamma(x)+\mu_2)\phi^2\bigl)dx} \label{a32}$

(8)

and the following lemma was given in [14].

Lemma 3.1. $sign(1-R_0^{DA})=sign(\lambda_0)$, where $\lambda_0$ is the principal eigenvalue for the reaction-diffusion-advection problem

$\left\{ \begin{array}{lll} -\psi_{xx}+\alpha\psi_x=\frac{b}{\mu_1}\beta(x)\psi-\gamma(x)\psi-\mu_2\psi+\lambda_0\psi,\; & x\in(p, q), \\ \psi(x)=0,\; & x=p~\mbox{or}~ q, \end{array} \right. \label{Hb}$

here $\psi(x)$ is the corresponding eigenfunction and $\psi(x)>0$ in $(p, q)$.

With the above definition of $R_0^{DA}$, we have some properties for it.

Theorem 3.2. The following assertions hold.

$(i)$ If $\Omega_1\subseteq\Omega_2\subseteq\mathbb{R}^1$, then $R_0^{DA}(\Omega_1)\leq R_0^{DA}(\Omega_2)$, and the strict inequality holds if $\Omega_2\setminus\Omega_1$ is a nonempty open set. Moreover, $\lim\limits_{(q-p)\rightarrow+\infty}R_0^{DA}((p, q))\geq\frac{\beta_{\infty}}{\frac{\alpha^2}{4}+\gamma_{\infty}+\mu_2}$ provided by $(H_1)$ holds;

$(ii)$ If $\beta(x)\equiv\beta_{\infty}$ and $\gamma(x)\equiv\gamma_{\infty}$, then

$R_0^{DA}=\frac{\frac{b}{\mu_1}\beta_{\infty}}{(\frac{\pi}{q-p})^2+\frac{\alpha^2}{4}+\gamma_{\infty}+\mu_2}.$

Proof. The proof of the monotonicity in assertion (ⅰ) is similar as that of Corollary 2.3 in [5], and the limit in assertion (ⅱ) can be calculated directly.

We now turn to the limit in (ⅰ). Since $\lim\limits_{x\rightarrow\infty}\beta(x)=\beta_{\infty}, \lim\limits_{x\rightarrow\infty}\gamma(x)=\gamma_{\infty}$, we deduce that for any $\varepsilon>0$, there exists $L>0$ such that for $|x|\geq L,$

$\beta_{\infty}-\varepsilon\leq\beta(x)\leq\beta_{\infty}+\varepsilon, \gamma_{\infty}-\varepsilon\leq\gamma(x)\leq\gamma_{\infty}+\varepsilon.$

If $q\geq 2L$, according to (8) and the monotonicity in assertion (ⅰ), we can get

$\begin{array}{lll} R_0^{DA}\bigr((p,q),\beta(x),\gamma(x)\bigl) &\geq & R_0^{DA}((L,2L), \beta(x), \gamma(x))\\ &\geq & R_0^{DA}((L,2L), \beta_{\infty}-\varepsilon, \gamma_{\infty}+\varepsilon)\\ &=& \sup\limits_{\phi\in H_0^1(L,2L)\, \phi\neq0} \frac{\int^{2L}_L\frac{b}{\mu_1}(\beta_{\infty}-\varepsilon)\phi^2dx}{\int^{2L}_L\bigr(\phi^2_x+(\frac{\alpha^2}{4}+\gamma_{\infty}+\varepsilon+\mu_2)\phi^2\bigl)dx}. \end{array} \label{a33}$

(9)

At the same time, $\lambda=(\frac{\pi}{L})^2$ is the principal eigenvalue for the following problem

$\left\{ \begin{array}{lll} -\phi_{xx}=\lambda\phi, x\in(L, 2L),\\ \phi(L)=\phi(2L)=0 \end{array} \right. \label{a34}$

with the corresponding eigenfunction $\phi=\sin(\frac{\pi(x-L)}{L})$. Plugging such $\phi$ into (9), one easily obtains

$R_0^{DA}\bigr((p,q),\beta(x),\gamma(x)\bigl)\geq\frac{\frac{b}{\mu_1}(\beta_{\infty}-\varepsilon)}{(\frac{\pi}{L})^2+(\frac{\alpha^2}{4}+\gamma_{\infty}+\varepsilon+\mu_2)}. \label{a3500}$

(10)

Similarly, if $p\leq -2L$, we can also obtain (10) by replacing $(L, 2L)$ by $(-2L, -L)$. Hence, if $(q-p)\geq 4L$, the inequality (10) holds. Letting $L\rightarrow\infty$ gives

$\lim\limits_{(q-p)\rightarrow +\infty}R_0^{DA}\geq\frac{\frac{b}{\mu_1}(\beta_{\infty}-\varepsilon)}{\frac{\alpha^2}{4}+\gamma_{\infty}+\varepsilon+\mu_2}.$

Because of the arbitrariness of $\varepsilon$, it follows that

$\lim\limits_{(q-p)\rightarrow +\infty}R_0^{DA}\geq\frac{\frac{b}{\mu_1}\beta_{\infty}}{\frac{\alpha^2}{4}+\gamma_{\infty}+\mu_2}.$

For the free boundary problem (4), the infected interval $(g(t), h(t))$ is changing with $t$, so the basic reproduction number is not a constant and should be a function of $t$. Now we define it as the risk index $R_0^F(t)$, whose expression is given by

$\begin{array}{lll} R_0^F(t):&= & R_0^{DA}\bigr((g(t), h(t)), \beta(x), \gamma(x)\bigl)\\ &= & \sup\limits_{\phi\in H_0^1((g(t),h(t)))\, \phi\neq0}\frac{\int_{g(t)}^{h(t)}\frac{b}{\mu_1}\beta(x)\phi^2dx}{\int_{g(t)}^{h(t)}\bigr(\phi^2_x+(\frac{\alpha^2}{4}+\gamma(x)+\mu_2)\phi^2\bigl)dx}. \end{array} \label{a350}$

(11)

Owing to the monotonicity of $g(t)$ and $h(t)$ in Lemma 2.3, we have the limits $g_{\infty}\in[-\infty, -h_0]$ and $h_{\infty}\in[h_0, +\infty]$ such that $\lim\limits_{t\rightarrow -\infty}g(t)=g_{\infty}$ and $\lim\limits_{t\rightarrow\infty}h(t)=h_{\infty}$. Moreover, $(g(t), h(t))$ is expanding and then $R_0^F(t)$ is increasing, we then denote

$\begin{array}{lll} R_0^F(\infty):=\lim\limits_{t\rightarrow\infty}R_0^F(t)=R_0^{DA}\bigr((g_{\infty},h_{\infty}),\beta(x), \gamma(x)\bigl). \end{array} \label{a35}$

(12)

Using the above notations, Lemma 2.3 and Theorem 3.2 lead to the following result.

Theorem 3.3. $R_0^F(t)$ is a strictly monotone increasing function of $t$, that is $R_0^F(t_1) <R_0^F(t_2)$ if $t_1<t_2$. Additionally, under the assumption of $(H_1)$, if $h_{\infty}-g_{\infty}=\infty$, then $R_0^F(\infty)\geq\frac{\frac{b}{\mu_1}\beta_{\infty}}{\frac{\alpha^2}{4}+\gamma_{\infty}+\mu_2}.$

Remark 1. Epidemiologically, the monotonicity in Theorem 3.3 implies that the risk of the disease increases with time. By Theorem 3.3, we further obtain that $R_0^F(\infty)> 1$ if $(H_2)$ holds and $h_{\infty}-g_{\infty}=\infty$.

---

4. The vanishing of disease

Usually, if the infected domain no longer expands and the infected individuals eventually disappear, we say the epidemic has been controlled. Mathematically, we say the disease vanishes and have the following definition.

Definition 4.1. The disease is vanishing if $h_{\infty}-g_{\infty}<\infty$ and $\lim\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}$ $=0$, while the disease is spreading if $h_{\infty}-g_{\infty}=\infty$ and $\limsup\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}$ $>0$.

Thus, our natural question is: What conditions can make the disease vanish?

Theorem 4.2. Assume that $(H_2)$ holds. If $R_0^F(\infty)< 1$, then $h_{\infty}-g_{\infty}<\infty$ and

$\lim\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}=0.$

Moreover, we have $\lim\limits_{t\rightarrow\infty}\|R(\cdot,t)\|_{C([g(t),h(t)])}=0$ and $\lim\limits_{t\rightarrow\infty}S(x,t)=\frac{b}{\mu_1}$ uniformly for $x\in(-\infty,\infty)$.

Proof. On the contrary we assume that $h_{\infty}-g_{\infty}\rightarrow +\infty$ as $t\rightarrow\infty$. Together with assumption $(H_2)$ and Remark 1, we can get $R_0^F(\infty)\geq\frac{\frac{b}{\mu_1}\beta_{\infty}}{\frac{\alpha^2}{4}+\gamma_{\infty}+\mu_2}>1$. This contradicts to $R_0^F(\infty)<1$.

Now it follows from Lemma 2.5 that $S(x,t)\leq\overline{S}(t)$ for $(x,t)\in(-\infty,\infty)\times[0,\infty)$, where

$\overline{S}(t)=\frac{b}{\mu_1}+\Bigr(\|S_0\|_{L^{\infty}}-\frac{b}{\mu_1}\Bigl)e^{-\mu_1t},$

which satisfies

$\left\{ \begin{array}{lll} \frac{\mathrm{d}\overline{S}}{\mathrm{dt}}=b-\mu_1\overline{S}, ~~~ t\in[0,\infty), \\ \overline{S}(0)=\|S_0\|_{L^{\infty}}. \end{array} \right. \label{Hb1}$

Since $\lim\limits_{t\rightarrow\infty}\overline{S}(t)=\frac{b}{\mu_1}$, we deduce that

$\begin{array}{lll} \limsup\limits_{t\rightarrow\infty}S(x,t)\leq\lim\limits_{t\rightarrow\infty}\overline{S}(t)=\frac{b}{\mu_1} \mbox{uniformly for}~x\in(-\infty,\infty). \end{array} \label{a48}$

(13)

Next we claim that $\lim\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}=0$. Noting

$R_0^F(\infty)=R_0^{DA}((g_{\infty},h_{\infty}), \beta(x), \gamma(x))<1$

and $h_{\infty}-g_{\infty}< +\infty$, it follows from the continuity that $R_0^{DA}((g_{\infty},h_{\infty}),\beta(x)(\frac{b}{\mu_1}+\delta),\gamma(x))<1$ for some small $\delta>0$. Then, due to Lemma 3.1, there are $\lambda_0^{\delta}>0$ and $\psi(x)>0$ in $(g_{\infty}, h_{\infty})$ such that

$\left\{ \begin{array}{lll} -\psi_{xx}+\alpha\psi_x=\bigr(\beta(x)(\frac{b}{\mu_1}+\delta)-\gamma(x)-\mu_2\bigl)\psi+\lambda_0^{\delta}\psi, \; & x\in(g_{\infty}, h_{\infty}), \\ \psi(x)=0,\; & x=g_{\infty}~\mbox{or}~ h_{\infty}. \end{array} \right. \label{a41}$

For $\delta$ given above, there exists $T_{\delta}>0$ such that $S(x,t)\leq\frac{b}{\mu_1}+\delta$ for $t\geq T_{\delta}$ and $x\in (-\infty, \infty)$. Let $\overline{I}(x,t)$ be the unique solution of the problem

$\left\{ \begin{array}{lll} \overline{I}_t-\overline{I}_{xx}+\alpha\overline{I}_x=\bigr(\beta(x)(\frac{b}{\mu_1}+\delta)-\gamma(x)-\mu_2\bigl)\overline{I}, \; & g_{\infty}<x<h_{\infty}, t>T_{\delta}, \\ \overline{I}(g_{\infty}, t)=0, \overline{I}(h_{\infty},t)=0, \; & t>T_{\delta},\\ \overline{I}(x, T_{\delta})=I_0(x, T_{\delta}),\; & g_{\infty}<x<h_{\infty}. \end{array} \right. \label{Hbb}$

Using the comparison principle (Lemma 2.5) with $\overline{S}=\frac{b}{\mu_1}+\delta$ yields

$0\leq I(x,t)\leq\overline{I}(x,t)\leq Me^{-\frac{\lambda_0^{\delta}}{2}(t-T_{\delta})}\psi(x), ~g(t)\leq x\leq h(t), t\geq T_{\delta},$

for some large $M>0$. Therefore,

$\begin{array}{lll} \lim\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}=0 \end{array}$

(14)

due to $Me^{-\frac{\lambda_0^{\delta}}{2}(t-T_{\delta})}\psi(x)\rightarrow 0$ as $t\rightarrow\infty$. It then follows from the third equations of (4) that

$\lim\limits_{t\rightarrow\infty}\|R(\cdot,t)\|_{C([g(t),h(t)])}=0.$

It remains to show the limit of $S$. Owing to (14), for any $\varepsilon>0$, there exists $T_{\varepsilon}>0$ such that

$0\leq\beta(x)S I\leq \|\beta\|_{L^{\infty}}C_1 I(x,t)\leq\varepsilon, ~~~~~(x, t)\in (-\infty, +\infty)\times [T_{\varepsilon}, \infty),$

here $C_1$ is the upper bound of $S$ defined in Lemma 2.2. Thus, we have $S(x,t)\geq\underline{S}(t)$ in $(-\infty, +\infty)\times[T_{\varepsilon}, \infty)$, where $\underline{S}(t)$ satisfies

$\left\{ \begin{array}{lll} \frac{\mathrm{d}\underline{S}}{\mathrm{dt}}=b-\varepsilon-\mu_1\underline{S}, &t>T_{\varepsilon},\\ \underline{S}(T)=\inf\limits_{(-\infty, +\infty)}S(x, T_{\varepsilon})\geq0.& \end{array} \right. \label{a410}$

It is easy to see that $\underline{S}(t)\rightarrow\frac{b-\varepsilon}{\mu_1}$ as $t\rightarrow\infty$. Therefore,

$\liminf\limits_{t\rightarrow +\infty}S(x,t)\geq\frac{b-\varepsilon}{\mu_1}, ~~~~x\in(-\infty, +\infty).$

Since $\varepsilon$ is arbitrary, we get

$\liminf\limits_{t\rightarrow +\infty}S(x,t)\geq\frac{b}{\mu_1} \mbox{uniformly for}~~x\in(-\infty, +\infty),$

which together with (13) gives

$\lim\limits_{t\rightarrow\infty}S(x,t)=\frac{b}{\mu_1} \mbox{uniformly for}~ x\in(-\infty, +\infty).$

This completes the proof.

Theorem 4.3. Suppose $R_0^F(0)<1$. Then $h_{\infty}-g_{\infty}<\infty$ and

$\lim\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}=0$

provided that $S_0\leq\frac{b}{\mu_1}$ in $(-\infty, +\infty)$ and $\|I_0\|_{C([-h_0,h_0])}$ is sufficiently small.

Proof. Since $R_0^F(0)=R_0^{DA}((-h_0,h_0))<1$, it follows from Lemma 3.1 that there exist $\lambda_0^0>0$ and $\psi(x)>0$ in $(-h_0, h_0)$ such that

$\left\{ \begin{array}{lll} -\psi_{xx}+\alpha\psi_x=\bigr(\beta(x)\frac{b}{\mu_1}-\gamma(x)-\mu_2\bigl)\psi+\lambda_0^0\psi, \; & -h_0<x<h_0, \\ \psi(x)=0,\; & x=\pm h_0. \end{array} \right. \label{a42}$

(15)

We first assert that there exists some constant $M_0>0$ such that

$\begin{array}{lll} x\psi'(x)\leq M_0\psi(x), -h_0\leq x\leq h_0. \end{array} \label{a420}$

(16)

In fact, let $x_1$ be the first stationary point of $\psi(x)$ (i. e. $\psi'(x_1)=0$) when $x$ moves to the right from $-h_0$ to $h_0$, and oppositely $x_2$ the first one from $h_0$ to $-h_0$. It is easy to see that $-h_0<x_1\leq x_2<h_0$. Denoting $y_1=\min\{x_1,0\}$ and $y_2=\max\{x_2,0\}$, we have $-h_0<y_1\leq 0\leq y_2<h_0$, which divides the interval $[-h_0, h_0]$ into three subintervals $[-h_0, y_1), [y_1, y_2]$ and $(y_2, h_0]$.

Noting that for $x \in[-h_0, y_1)$, $x<0$ and $\psi'(x)>0$, we have $x\psi'(x)<0$. Similarly, for $x\in (y_2, h_0]$, $\psi'(x)>0$ and $x\psi'(x)<0$.

Since that $\psi(x)>0$ for $x\in [y_1, y_2]$, we can choose some large $M_0>0$ such that

$x\psi'(x)\leq h_0\|\psi'\|_{L^{\infty}}\leq M_0\min\limits_{[y_1, y_2]}\psi(x)\leq M_0\psi(x),\ x\in [y_1, y_2],$

therefore (16) holds for $M_0\geq (h_0\|\psi'\|_{L^{\infty}})/\min\limits_{[y_1, y_2]}\psi(x)$.

Now we prove that the vanishing happens. Owing to $\lambda_0^0>0$, we can choose some small $\delta>0$ such that

$\begin{array}{lll} \delta(1+\delta)^2+\frac{\alpha h_0}{4}\delta^2+\frac{M_0}{2}(1+\delta)\delta^2+\|\beta\|_{L^{\infty}}\frac{b}{\mu_1}((1+\delta)^2-1)\leq\lambda_0^0. \end{array} \label{a421}$

(17)

Next we define

$\begin{array}{lll} \sigma(t)=h_0\bigr(1+\delta-\frac{\delta}{2}e^{-\delta t}\bigl),\ t>0, \end{array} \label{a422}$

(18)

and

$U(x,t)=\varepsilon e^{\frac{\alpha x}{2}-\frac{\alpha}{2}\frac{xh_0}{\sigma(t)}}e^{-\delta t}\psi\Bigr(\frac{xh_0}{\sigma(t)}\Bigl), -\sigma(t)\leq x\leq\sigma(t),\ t>0.$

Direct calculations show that

$\begin{array}{lll} \sigma'(t)+\mu U_x(\sigma(t), t)&=&\frac{h_0}{2}\delta^2e^{-\delta t}+\mu\varepsilon e^{-\delta t}e^{\frac{\alpha}{2}(\sigma(t)-h_0)}\psi'(h_0)\frac{h_0}{\sigma(t)}\\ &\geq& h_0e^{-\delta t}\bigr(\frac{\delta^2}{2}+\frac{\mu\varepsilon}{h_0}e^{\frac{\alpha}{2}h_0\delta}\psi'(h_0)\bigl). \end{array}$

Similarly,

$-\sigma'(t)+\mu U_x(-\sigma(t), t)\leq h_0e^{-\delta t}\Bigr(-\frac{\delta^2}{2}+\frac{\mu\varepsilon}{h_0}e^{\frac{\alpha}{2}h_0\delta}\psi'(-h_0)\Bigl).$

Selecting $\varepsilon=\frac{\delta^2h_0}{2\mu e^{\frac{\alpha}{2}h_0\delta}}\min\{\frac{-1}{\psi'(h_0)}, \frac{1}{\psi'(-h_0)}\}$ leads to

$\sigma'(t)\geq-\mu U_x(\sigma(t),t) \;\; \mbox{and} \;\; -\sigma'(t)\leq-\mu U_x(-\sigma(t),t).$

By (16), (17) and (18), a routine computation gives rise to the inequality as follows

$\begin{array}{lll} & & U_t-U_{xx}+\alpha U_x-\bigr(\beta(x)\frac{b}{\mu_1}-\gamma(x)-\mu_2\bigl)U \\&=&U\bigr[-\delta+\frac{\alpha}{2}\frac{xh_0}{\sigma^2(t)}\sigma'(t)-\frac{\sigma'(t)}{\sigma(t)}\cdot\frac{xh_0}{\sigma(t)}\psi'\psi^{-1} +\frac{\alpha^2}{4}\bigr(1-\frac{h_0^2}{\sigma^2(t)}\bigl) \\& &~~~+\frac{h_0^2}{\sigma^2(t)}(-\psi"+\alpha\psi')\psi^{-1}-\bigr(\beta(x)\frac{b}{\mu_1}-\gamma(x)-\mu_2\bigl) \bigl] \\&=&U\bigr[-\delta+\frac{\alpha}{2}\frac{xh_0}{\sigma^2(t)}\sigma'(t)-\frac{\sigma'(t)}{\sigma(t)}\frac{xh_0}{\sigma(t)}\psi'\psi^{-1} -\bigr(1-\frac{h_0^2}{\sigma^2(t)}\bigl)\bigr(\beta(x)\frac{b}{\mu_1}-\gamma(x)-\mu_2-\frac{\alpha^2}{4}\bigl) \\& &~~~+\frac{h_0^2}{\sigma^2(t)}\lambda_0^0\bigl] \\&\geq&U\bigr[-\delta-\frac{\alpha}{2}\frac{h_0^2}{\sigma^2(t)}\sigma'(t)-\frac{\sigma'(t)}{\sigma(t)}M_0-\bigr(1-\frac{h_0^2}{\sigma^2(t)}\bigl) \|\beta\|_{L^{\infty}}\frac{b}{\mu_1}+\frac{h_0^2}{\sigma^2(t)}\lambda_0^0\bigl] \\&\geq&U\frac{h_0^2}{\sigma^2(t)}\bigr[-\delta(1+\delta)^2-\frac{\alpha h_0}{4}\delta^2-\frac{M_0}{2}(1+\delta)\delta^2-\|\beta\|_{L^{\infty}}\frac{b}{\mu_1}((1+\delta)^2-1)+\lambda_0^0\bigl] \\&\geq& 0. \end{array} \label{a423}$

(19)

Because of the assumption that $S_0\leq\frac{b}{\mu_1}$ for $x\in (-\infty, +\infty)$, we derive $S(x, t)\leq\frac{b}{\mu_1}$ for $-\infty<x<+\infty, t\geq0$. Therefore, if $\|I_0\|_{L^{\infty}}\leq U(x,0)=\varepsilon e^{\frac{\alpha x}{2}-\frac{\alpha x}{2}\frac{h_0}{\sigma(0)}}\psi(\frac{xh_0}{\sigma(0)})$ for $x\in [-h_0, h_0]$, we can apply the comparison principle (Lemma 2.5) with $\overline{S}=\frac{b}{\mu_1}$ to conclude that $g(t)\geq -\sigma(t), h(t)\leq\sigma(t)$ and $I(x,t)\leq U(x,t)$ for $g(t)\leq x\leq h(t), t>0$. It follows that $h_{\infty}\leq\lim\limits_{t\rightarrow\infty}\sigma(t)=h_0(1+\delta)<\infty,~ g_{\infty}\geq -\sigma(t)>-\infty$ and then $\lim\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}=0$.

Theorem 4.4. Suppose $R_0^F(0)<1$. Then $h_{\infty}-g_{\infty}<\infty$ and

$\lim\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}=0$

provided that $S_0\leq\frac{b}{\mu_1}$ in $(-\infty, +\infty)$ and $\mu$ is sufficiently small.

Proof. Similar to Theorem 4.3, we define

$W(x,t)=M e^{\frac{\alpha x}{2}-\frac{\alpha}{2}\frac{xh_0}{\sigma(t)}}e^{-\delta t}\psi\Bigr(\frac{xh_0}{\sigma(t)}\Bigl), -\sigma(t)\leq x\leq\sigma(t),\ t>0,$

where $M>0$ is large enough such that $\|I_0\|_{L^{\infty}}\leq W(x,0)=Me^{\frac{\alpha x}{2}-\frac{\alpha x}{2}\frac{h_0}{\sigma(0)}}\psi(\frac{xh_0}{\sigma(0)})$ for $x\in [-h_0, h_0]$. Using the same calculation as (19) yields

$W_t-W_{xx}+\alpha W_x-\bigr(\beta(x)\frac{b}{\mu_1}-\gamma(x)-\mu_2\bigl)W\geq 0.$

Additionally, straightforward calculations tell us that

$\sigma'(t)\geq-\mu W_x(\sigma(t),t) \;\; \mbox{and} \;\; -\sigma'(t)\leq-\mu W_x(-\sigma(t),t)$

if $\mu$ is sufficiently small. The result for vanishing is a direct application of Lemma 2.5.

---

5. The spreading of disease

In this section, our aim is to present the sufficient conditions for the spreading. First of all, we give a lemma for the following initial-boundary value problem

$\left\{ \begin{array}{lll} u_t-u_{xx}+\alpha u_x=f(x,t)u,\; & g(t)<x<h(t),\, t>0,\\ u(x, t)=0,\; & x\leq g(t) ~\mbox{or} ~x\geq h(t),\,t>0,\\ g'(t)=-\mu u_x(g(t), t), g(0)=-h_0<0,\; & t>0,\\ h'(t)=-\mu u_x(h(t),t), h(0)=h_0>0, \; & t>0,\\ u(x, 0)=u_0(x), \; & -h_0 <x<h_0, \end{array} \right. \label{a51}$

(20)

where $\alpha>0$ is a constant, $f(x, t)$ is a continuous function, $u_0(x)\in C^2[-h_0, h_0]$, $u_0(\pm h_0)=0$ and $u_0(x)>0, x\in(-h_0, h_0)$.

Lemma 5.1. Suppose the following conditions hold.

$(i)$ There exists a constant $M_1>0$ such that $|f(x,t)|\leq M_1$ for $-\infty<x<\infty$, $t>0$;

$(ii)$ $u(x,t)$, $g(t)$ and $h(t)$ are bounded.

Then the unique solution $(u; g(t), h(t))$ of problem $(20)$ satisfies

$\begin{array}{lll} \lim\limits_{t\rightarrow\infty}\|u(\cdot,t)\|_{C([g(t),h(t)])}=0. \end{array} \label{a52}$

(21)

Proof. Since $f(x,t)$ is bounded, it is well-known that problem (20) admits a unique global solution $(u(x,t); g(t), h(t))$ and $g(t)$ is decreasing, $h(t)$ is increasing. Furthermore, straightening the free boundaries as follows

$y=\frac{2h_0x}{h(t)-g(t)}-\frac{h_0(h(t)+g(t))}{h(t)-g(t)}, ~~~w(y,t)=u(x,t)$

leads to a related problem with the fixed boundaries. Similarly as Lemma 3.2 in [1], it follows that for $0<\nu<1$, there exists a constant $\hat{C}$ that depends on $\nu, h_0, g_0, \|u_0\|_{C^2[-h_0, h_0]}$ and $g_{\infty}, h_{\infty}$ such that

$\|w\|_{C^{1+\nu, \frac{1+\nu}{2}}([-h_0,h_0]\times[\tau,\tau+1])}\leq\hat{C},$

for any $\tau\geq 1$. Noting that $\tau$ is arbitrary and $\hat{C}$ is independent of $\tau$, we can obtain

$\|u(\cdot, t)\|_{C^1([g(t), h(t)])}\leq\tilde{C}, ~~~t\geq 1, \label{a53}$

(22)

which together with the free boundary conditions in (20) yields

$\|h'\|_{C^{\frac{\nu}{2}}([1, \infty))},~~\|g'\|_{C^{\frac{\nu}{2}}([1, \infty))}\leq\tilde{C}, ~~~t\geq 1, \label{a54}$

(23)

for some positive constant $\tilde{C}$.

Next, we prove (21). Arguing by contradiction, we assume that

$\limsup\limits_{t\rightarrow\infty}\|u(\cdot,t)\|_{C([g(t),h(t)])}=\delta>0. \label{a55}$

(24)

Thus, there exists a sequence $\{(x_k,t_k): g(t_k)<x_k<h(t_k), t_k>0\}$ with $t_k\rightarrow\infty$ as $k\rightarrow\infty$ such that $u(x_k, t_k)\geq\frac{\delta}{2}$ for all $k\in\mathbb{N}$. Owing to $-\infty<g_{\infty}<g(t_k)<x_k<h(t_k)<h_{\infty}<\infty$, we can extract a subsequence of $\{x_k\}$, still denoted by it, converges to $x_0\in [g_{\infty}, h_{\infty}]$. Moreover, it follows from (22) that $x_0\in(g_\infty, h_\infty)$. Define

$u_k(x,t)=u(x,t+t_k), ~~~x\in(g(t+t_k), h(t+t_k)), t\in(-t_k, \infty). \label{a560}$

From condition $(i)$, (22) and the standard parabolic regularity, it follows that $\{u_k\}$ has a subsequence $\{u_{k_i}\}$ such that $u_{k_i}\rightarrow\tilde{u}(i\rightarrow\infty)$ and $\tilde{u}$ satisfies

$\tilde{u}_t-\tilde{u}_{xx}+\alpha\tilde{u}_x=f(x, t)\tilde{u}\geq-M_1\tilde{u},~~~(x,t)\in(g_{\infty}, h_{\infty})\times(-\infty, \infty), \label{a56}$

which together with

$\tilde{u}(x_0, 0)=\lim\limits_{k_i\rightarrow\infty}u_{k_i}(x_{k_i}, 0)=\lim\limits_{k_i\rightarrow\infty}u(x_{k_i}, t_{k_i})\geq\frac{\delta}{2},~~ \tilde{u}(h_{\infty}, 0)=0\label{a57}$

gives that $\tilde{u}>0$ in $(g_{\infty}, h_{\infty})\times(-\infty, \infty)$ via the maximum principle. Hence, applying the Hopf boundary lemma at the point $(h_{\infty},0)$ leads to

$\tilde{u}_x(h_{\infty}, 0)\leq-\sigma<0$

for some $\sigma>0$. From (22) and the above fact, we conclude

$u_x(h(t_{k_i}), t_{k_i})=\frac{\partial}{\partial x}u_{k_i}(h(t_{k_i}), 0)\leq-\frac{\sigma}{2}<0$

for all large $k_i$, which together with the Stefan condition implies that

$h'(t_{k_i})\geq\frac{\mu\sigma}{2}>0. \label{a577}$

(25)

On the other hand, (23) and the assumption that $h_{\infty}-g_{\infty}<0$ give rise to

$h'(t)\rightarrow 0 \;\; \mbox{and}\;\; g'(t)\rightarrow 0. \label{a58}$

(26)

Comparing (25) and (26), it yields a contradiction so that (24) doesn't hold, that is, we arrive at (21).

Theorem 5.2. If there exists $t_0\geq 0$ such that $R_0^F(t_0)\geq 1$, then $h_{\infty}-g_{\infty}=\infty$ and

$\limsup\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}>0,\label{a59}$

(27)

namely, spreading happens.

Proof. Since $S$ is bounded, from the second equation in (4), we conclude

$I_t-I_{xx}+\alpha I_x\geq-M_1I$

by $M_1:=\|\beta\|_{L^{\infty}}\cdot\max\{\frac{b}{\mu_1}, \|S_0\|_{L^{\infty}}\}+\|\gamma\|_{L^{\infty}}+\mu_2$. Assuming that $h_{\infty}-g_{\infty}<\infty$ by contradiction, it follows from Lemma 5.1 that

$\lim\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}=0, \label{a510}$

(28)

which together with the first equation in (4) gives

$\lim\limits_{t\rightarrow\infty}S(x,t)=\frac{b}{\mu _1} \mbox{uniformly for} ~x\in(-\infty,\infty).\label{a511}$

(29)

Additionally, we know that there exists $T_0>t_0$ such that

$R_0^F(T_0)=R_0^{DA}\bigr((g(T_0),h(T_0)), \frac{b}{\mu_1}\beta(x), \gamma(x)\bigl)>1 \label{a512}$

(30)

based on the hypothesis $R_0^F(t_0)\geq 1$ and the monotonicity of $R_0^F(t)$ with respect to $t$. By continuity, there exists $\varepsilon_0>0$ sufficiently small ($\varepsilon_0<\frac{b}{\mu_1}$) such that

$R_0^F(T_0,\varepsilon_0):=R_0^{DA}\bigr((g(T_0),h(T_0)), \beta(x)(\frac{b}{\mu_1}-\varepsilon_0), \gamma(x)\bigl)>1. \label{a513}$

(31)

For $\varepsilon_0$ given above, it follows from (29) that there is $T^*>T_0$ such that

$S(x,t)\geq\frac{b}{\mu_1}-\varepsilon_0, x\in(g_{\infty}, h_{\infty}),\ t\geq T^*,$

and the monotonicity of $R_0^F(t)$ implies that

$R_0^F(T^*,\varepsilon_0)=R_0^{DA}\Bigr((g(T^*),h(T^*)), \beta(x)(\frac{b}{\mu_1}-\varepsilon_0), \gamma(x)\Bigl)>1, \label{a530}$

(32)

which together with Lemma 3.1 shows that the principal eigenvalue $\lambda_0^*<0$ for the following problem

$\left\{ \begin{array}{lll} -\psi_{xx}+\alpha\psi_x=\bigr(\beta(x)(\frac{b}{\mu_1}-\varepsilon_0)-\gamma(x)-\mu_2\bigl)\psi+\lambda_0^*\psi, \; & x\in(g(T^*), h(T^*)),\\ \psi(x)=0,\; & x=g(T^*) ~\mbox{or}~ h(T^*), \end{array} \right. \label{a514}$

(33)

and $\psi(x)>0$ in $(g(T^*),h(T^*))$. Now we set

$\underline{u}(x,t)=\delta e^{-\lambda_0^*(t-T^*)}\psi(x),~~~~~x\in(g(T^*), h(T^*)), t\geq T^*,$

where $\delta$ is sufficiently small such that $\underline{u}(x, T^*)=\delta\psi(x)\leq I(x, T^*)$, and in light of (33), we get

$\underline{u}_t-\underline{u}_{xx}+\alpha\underline{u}_x=\bigr(\beta(x)(\frac{b}{\mu_1}-\varepsilon_0)-\gamma(x)-\mu_2\bigl)\underline{u}.\label{a515}$

(34)

Employing the comparison principle with $\underline{S}=\frac{b}{\mu_1}-\varepsilon_0$ in $[g(T^*), h(T^*)]\times [T^*, \infty)$ deduces that

$\|I(\cdot,t)\|_{C([g(t),h(t)])}\geq\delta e^{-\lambda_0^*(t-T^*)}\psi(0)\rightarrow +\infty \;\; \mbox{as} \;\; t\rightarrow\infty.$

This is a contradiction to (28), which concludes that $h_{\infty}-g_{\infty}=\infty$.

Now, we turn to prove (27). If not, then

$\limsup\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}=0,\label{a516}$

(35)

thus, we can obtain (29) again. Following the same procedure, we can prove that (31) and (32) hold for given $\varepsilon_0, T_0, T^*$. Therefore $I$ admits a lower solution u, which is unbounded. This leads to a contradiction to (35), which completes the proof.

Recalling Theorem 4.4, we know that if the expanding capability $\mu$ is sufficiently small, accompanied with other conditions, the disease will vanish. However, another question arises: if $\mu$ is large, what will happen? To answer this question, we need the following lemma. Meanwhile, in order to stress the dependence of the solutions on $\mu$ for problem (4) and (20), we substitute $(I^{\mu}; g^{\mu}, h^{\mu})$ and $(u^{\mu}; g^{\mu}, h^{\mu})$ for $(I; g, h)$ and $(u; g, h)$ respectively in the following lemma and theorem.

Lemma 5.3. Assume that in problem $(20)$, there exists a constant $M_2>0$ such that $f(x, t)\geq-M_2$. Then for any given constant $H>0$, there exists $\mu_{H}>0$ such that when $\mu>\mu_{H}$, the unique solution $(u^{\mu}; g^{\mu}(t), h^{\mu}(t))$ satisfies

$\limsup\limits_{t\rightarrow\infty}g^{\mu}(t)<-H, ~~and~~\liminf\limits_{t\rightarrow\infty}h^{\mu}(t)>H.\label{a517}$

(36)

Proof. This can be proved in a similar way as shown in [38,Lemma 3.2]. It is clear that

$\begin{array}{lll} u^{\mu}(x,t)\geq v^{\mu}(x,t), &p^{\mu}(t)\leq x\leq q^{\mu}(t), ~t>0.\\ g^{\mu}(t)\leq p^{\mu}(t), ~h^{\mu}(t)\geq q^{\mu}(t),&t>0. \end{array} \label{a519}$

(37)

where $(v^{\mu}; p^{\mu}(t), q^{\mu}(t))$ satisfies

$\left\{ \begin{array}{lll} v_t-v_{xx}+\alpha v_x=-M_2v,\; & p(t)<x<q(t),\, t>0,\\ v(x, t)=0,\; & x\leq p(t) ~\mbox{or} ~x\geq q(t),\,t>0,\\ p'(t)=-\mu v_x(p(t),t), p(0)=-h_0<0,\; & t>0,\\ q'(t)=-\mu v_x(q(t),t), q(0)=h_0>0, \; & t>0,\\ v(x, 0)=u_0(x), \; & -h_0 <x<h_0, \end{array} \right. \label{a518}$

(38)

and $(p^{\mu})'(t)<0, (q^{\mu})'(t)>0$ for $t>0$.

We are in a position to prove that for all large $\mu$,

$p^{\mu}(2)\leq-H ~~~\mbox{and}~~~q^{\mu}(2)\geq H. \label{a520}$

(39)

To this end, we first choose smooth functions $\underline{p}(t)$ and $\underline{q}(t)$ with

$\underline{p}(0)=-\frac{h_0}{2}, \underline{p}'(t)<0, \underline{p}(2)=-H,~\mbox{and}~~\underline{q}(0)=\frac{h_0}{2}, \underline{q}'(t)>0, \underline{q}(2)=H.$

We then invoke the following initial-boundary value problem

$\left\{ \begin{array}{lll} \underline{v}_t-\underline{v}_{xx}+\alpha \underline{v}_x=-M_2\underline{v},\; & \underline{p}(t)<x<\underline{q}(t),\, t>0,\\ \underline{v}(x, t)=0,\; & x\leq \underline{p}(t) ~\mbox{or} ~x\geq\underline{q}(t),\,t>0,\\ \underline{v}(x, 0)=\underline{v}_0(x), \; & -\frac{h_0}{2} \leq x\leq\frac{h_0}{2}, \end{array} \right. \label{a521}$

(40)

where the smooth initial value $\underline{v}_0(x)$ satisfies

$\left\{ \begin{array}{lll} 0<\underline{v}_0(x)<u_0(x),~~~-\frac{h_0}{2} \leq x\leq\frac{h_0}{2},\\ \underline{v}_0(-\frac{h_0}{2})=\underline{v}_0(\frac{h_0}{2})=0,~ \underline{v}'_0(-\frac{h_0}{2})>0, ~\underline{v}'_0(\frac{h_0}{2})<0. \end{array} \right. \label{a522}$

(41)

Thus, the standard theory for parabolic equations ensures that (40) admits a unique solution $\underline{v}$, and the Hopf boundary lemma shows that $\underline{v}_x(\underline{p}(t), t)>0$ and $\underline{v}_x(\underline{q}(t), t)<0$ for $t\in[0,2]$.

According to our choice of $\underline{v}_0(x)$, $\underline{p}(t)$ and $\underline{q}(t)$, there exists a constant $\mu_H$ such that for all $\mu>\mu_H$,

$\underline{p}'(t)\geq-\mu\underline{v}_x(\underline{p}(t), t)~~\mbox{and}~~\underline{q}'(t)\leq-\mu\underline{v}_x(\underline{q}(t), t),~~0\leq t\leq2. \label{a523}$

(42)

Obviously,

$\underline{p}(0)=-\frac{h_0}{2}>-h_0=p^{\mu}(0), ~~~~ \underline{q}(0)=\frac{h_0}{2}<h_0=q^{\mu}(0).$

The comparison principle together with (38), (40), (41) and (42) gives rise to

$v^{\mu}(x,t)\geq\underline{v}(x,t), ~p^{\mu}(t)\leq\underline{p}(t), ~q^{\mu}(t)\geq\underline{q}(t),~~\mbox{for}~~\underline{p}(t)\leq x\leq\underline{q}(t), 0\leq t\leq2,$

which implies (39) hold. Hence, owing to (37) and (39), we obtain

$\begin{array}{lll} \limsup\limits_{t\rightarrow\infty}g(t)\leq\lim\limits_{t\rightarrow\infty}p^{\mu}(t)<p^{\mu}(2)\leq -H,\\ \liminf\limits_{t\rightarrow\infty}h(t)\geq\lim\limits_{t\rightarrow\infty}q^{\mu}(t)>q^{\mu}(2)\geq H. \end{array}$

Theorem 5.4. Suppose $R^F_0(0)<1$. Then $h_{\infty}-g_{\infty}=\infty$ and

$\limsup\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}>0 \label{a524}$

(43)

if $\mu$ is sufficiently large, that is, spreading happens.

Proof. It has been proven successfully for the similar result, which adopts the method of constructing a lower solution and can be found in [36,Lemma 3.13]. To more simple, we will apply Lemma 5.3 to prove here. Clearly,

$I_t-I_{xx}+\alpha I_x\geq-M_2I,\label{a525}$

(44)

where $M_2$ is the same as $M_1$ defined in Theorem 5.2 and independent of $\mu$.

Recalling assertion $(i)$ of Theorem 3.2, we can select some $H>0$ such that $R_0^{DA}((-H, H))>1$. For $H$ chosen above, it follows from (44) and Lemma 5.3 that there exists a $\mu_H$ such that when $\mu>\mu_H$,

$\limsup\limits_{t\rightarrow\infty}g^{\mu}(t)<-H ~~\mbox{and}~~\liminf\limits_{t\rightarrow\infty}h^{\mu}(t)>H.\label{a526}$

Combining with the monotonicity of $g^{\mu}(t)$ and $h^{\mu}(t)$ gives that there is $T _0>0$ such that $g^{\mu}(T_0)<-H$, $h^{\mu}(T_0)>H$, thus,

$R_0^F(T_0)=R_0^{DA}((g^{\mu}(T_0), h^{\mu}(T_0)))>R_0^{DA}((-H, H))>1.$

Therefore, for $\mu>\mu_H$, we can use Theorem 5.2 to conclude that $h_{\infty}-g_{\infty}=\infty$ and $\limsup\limits_{t\rightarrow\infty}\|I(\cdot,t)\|_{C([g(t),h(t)])}>0.$

The following result follows directly from the comparison principle (Lemma 2.5), Theorems 4.4 and 5.4, see also the similar proof of Theorem 5.5 in [14].

Theorem 5.5. (Sharp threshold) For fixed $h_0$, $I_0$ and $S_0$ ($S_0\leq\frac{b}{\mu_1}$), there exists $\mu^*\in[0, \infty)$ such that vanishing occurs when $0<\mu\leq\mu^*$, and spreading occurs when $\mu>\mu^*$ .

---

6. Numerical simulation and discussion

In this section, we first carry out numerical simulations to illustrate the impact of expanding capability $\mu$. Fixing some coefficients and functions as follows:

$\begin{array}{lll} \alpha=1.5, ~b=1, ~\mu_1=0.5, ~\mu_2=0.6, ~h_0=1,\\ S_0(x)=1+\frac{1}{2}\sin x, ~~~I_0(x)=\cos(\frac{\pi}{2}x),\\ \beta(x)=1+\frac{2}{1+x^2}(\sin\frac{\pi}{2} x+1), ~\gamma(x)=0.5+\frac{20}{1+x^2}(\cos\frac{\pi}{2} x+1), \end{array}$

we can see that $\beta_{\infty}=1$, $\gamma_{\infty}=0.5$, $S_0(x)\leq\frac{b}{\mu_1}$ and $(H_2)$ holds. Further, we have by (11) that

$R_0^F(0)\leq\frac{\int_{-1}^{1}\frac{b}{\mu_1}\beta(x)\phi^2dx}{\int_{-1}^1\bigr(\frac{\alpha^2}{4}+\gamma(x)+\mu_2\bigl)\phi^2dx} \leq\frac{\frac{b}{\mu_1}\max\limits_{x\in[-1,1]}\beta(x)\int_{-1}^1\phi^2dx}{(\frac{\alpha^2}{4}+\min\limits_{x\in[-1,1]}\gamma(x)+\mu_2)\int_{-1}^1\phi^2dx}\leq\frac{8}{11}<1.$

Thus, the asymptotic behaviors of the solution to problem (4) and the changing of free boundaries are illustrated by choosing different expanding capabilities.

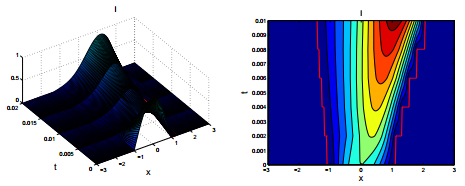
Example 6.1. Fix small $\mu=20$. Theorem 4.4 gives that the solution is vanishing for small $\mu$. We can see from Figure 1 that the disease $I$ tends to extinction quickly, and the free boundaries don't expand.

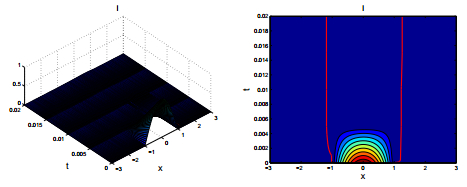
Example 6.2. Fix big $\mu=40$. Theorem 5.4 tells us that the spreading of solution happens if $\mu$ is sufficiently large. Comparing with Figure 1, it is easy to see from Figure 2 that a spatially inhomogeneous stationary endemic state appears and is globally asymptotically stable for bigger $\mu$. The two fronts expand quickly.

In this paper, we consider a reaction-diffusion-advection SIR model (4) with double free boundaries, which describes the left and right fronts of the infected habitat. The model extends the existing models such as (2) for a model without advection and (3) for a simplified SIS model.

We introduce the basic reproduction number $R_0^{DA}$ for system (7) with Dirichlet boundary and the risk index $R_0^F(t)$ for model (4), respectively. Based on the risk index $R_0^F(t)$, we exhibit some sufficient conditions to ensure spreading or vanishing of the disease. Specifically, our results reveal that if $R_0^F(t_0)\geq 1$ for some $t_0$, spreading always happens, namely, the disease will become endemic (Theorem 5.2), and if $R_0^F(\infty)<1$, vanishing always happens, namely, the disease will be controlled (Theorem 4.2). But if $R_0^F(0)<1$, vanishing will happen for the small initial value $I_0$ of infected individuals (Theorem 4.3) or the small expanding capability $\mu$ (Theorem 4.4), however, spreading can also happen for the large $\mu$ (Theorem 5.4).

In our work, three basic reproduction numbers are introduced, one is $R_0$ $(:= \frac{b\beta}{\mu_1(\mu_2+\alpha)})$ for SIR model (2) without advection, one is $R_0^{DA}$ defined by (8) for SIR model with fixed boundaries, another one is $R_0^F(t)$ defined by (11) for SIR model (4) with free boundaries. Their differences and correlations have been discussed in [14,Section 7].

It is worthwhile to point out that our risk index $R_0^F(t)$ is related not only with the advection $\alpha$, but also with the contact transmission rate $\beta(x)$ and recovery rate $\gamma(x)$. In detail, $R_0^F(t)$ increases with $\beta(x)$, and decreases with $\gamma(x)$. These facts suggest that all epidemiological parameters affect the transmission dynamics of disease. Specially, decreasing of $\beta(x)$ or increasing of $\gamma(x)$ can lower the risk index and prevent the further spreading of the disease. For instance, in the control of infectious diseases such as the Ebola epidemics in West Africa ([17]), applying some proper isolation facilities, which can reduce the contact rate, was shown to be a crucial factor in preventing the spread to neighboring countries. Another alternative way is improving medical technical level, which can increase the recovery rate and thus become a vital factor in controlling the spread.

We close this paper by recalling the advection coefficient $\alpha$. To avoid complexity, we begin with a small advection. But big advection, we believe, will cause more complex dynamical behaviors, and interested readers can refer to [4]. We will continue to focus on the dynamics induced by big advection.

---