|
[1]
|
[ H. Duan,R. Ma,X. Xu,F. Kong,S. Zhang,W. Kong,J. Hao,L. Shang, Two-decade reconstruction of algal blooms in China-Lake Taihu, Environ. Sci. Technol., 43 (2009): 3522-3528.
|
|
[2]
|
[ M. Wines,
Spring Rain, Then Foul Algae in Ailing Lake Erie Report of The New York Times, 2013. Available from: http://www.nytimes.com/2013/03/15/science/earth/algae-blooms-threaten-lake-erie.html?&_r=0.
|
|
[3]
|
[ W. McLean and J. Macdonald, CLAS: Colby Liberal Arts Symposium, Lake Erie Algal Blooms 2014. Available from: http://digitalcommons.colby.edu/clas/2014/program/414/.
|
|
[4]
|
[ C. B. Lopez, E. B. Jewett, Q. Dortch, B. T. Walton and H. K. Hudnell, Scientific Assessment of Freshwater Harmful Algal Blooms Interagency Working Group on Harmful Algal Blooms, Hypoxia, and Human Health of the Joint Subcommittee on Ocean Science and Technology. Washington, DC. 2008. Available from: https://www.whitehouse.gov/sites/default/files/microsites/ostp/frshh2o0708.pdf.
|
|
[5]
|
[ E. Beltrami,T. O. Carroll, Modeling the role of viral disease in recurrent phytoplankton blooms, J. Math. Biol., 32 (1994): 857-863.
|
|
[6]
|
[ J. Norberg,D. DeAngelis, Temperature effects on stocks and stability of a phytoplankton-zooplankton model and the dependence on light and nutrients, Ecol. Model., 95 (1997): 75-86.
|
|
[7]
|
[ B. Mukhopadhyay,R. Bhattacharyya, Modelling phytoplankton allelopathy in a nutrient-plankton model with spatial heterogeneity, Ecol. Model., 198 (2006): 163-173.
|
|
[8]
|
[ S. Pal,S. Chatterjee,J. Chattopadhyay, Role of toxin and nutrient for the occurrence and termination of plankton bloom results drawn from field observations and a mathematical model, Biosystems, 90 (2007): 87-100.
|
|
[9]
|
[ T. Saha,M. Bandyopadhyay, Dynamical analysis of toxin producing phytoplankton-zooplankton interactions, Nonlinear Anal-Real., 10 (2009): 314-332.
|
|
[10]
|
[ Y. Lv,Y. Pei,S. Gao,C. Li, Harvesting of a phytoplankton-zooplankton model, Nonlinear Anal-Real., 11 (2010): 3608-3619.
|
|
[11]
|
[ M. Bengfort,U. Feudel,F. M. Hilker,H. Malchow, Plankton blooms and patchiness generated by heterogeneous physical environments, Ecol. Complex., 20 (2014): 185-194.
|
|
[12]
|
[ S. Rana,S. Samanta,S. Bhattacharya,K. Al-Khaled,A. Goswami,J. Chattopadhyay, The effect of nanoparticles on plankton dynamics: A mathematical model, Biosystems, 127 (2015): 28-41.
|
|
[13]
|
[ T. G. Hallam,C. E. Clark,R. R. Lassiter, Effects of toxicants on populations: A qualitative approach Ⅰ. Equilibrium environmental exposure, Ecol. Model., 18 (1983): 291-304.
|
|
[14]
|
[ J. T. Turner,P. A. Tester, Toxic marine phytoplankton, zooplankton grazers, and pelagic food webs, Limnol. Oceanogr., 42 (1997): 1203-1214.
|
|
[15]
|
[ J. Chattopadhyay,R. R. Sarkar,S. Mandal, Toxin producing plankton may act as a biological control for planktonic blooms-field study and mathematical modelling, J. Theor. Biol., 215 (2002): 333-344.
|
|
[16]
|
[ J. Chattopadhyay,R. R. Sarkar,A. El Abdllaoui, A delay differential equation model on harmful algal blooms in the presence of toxic substances, Math. Med. Biol., 19 (2002): 137-161.
|
|
[17]
|
[ R. Pal,D. Basu,M. Banerjee, Modelling of phytoplankton allelopathy with Monod-Haldane-type functional response-A mathematical study, Biosystems, 95 (2009): 243-253.
|
|
[18]
|
[ S. Chakraborty,S. Chatterjee,E. Venturino,J. Chattopadhyay, Recurring plankton bloom dynamics modeled via toxin-producing phytoplankton, J. Biol. Phys., 3 (2008): 271-290.
|
|
[19]
|
[ M. Banerjee,E. Venturino, A phytoplankton-toxic phytoplankton-zooplankton model, Ecol. Complex., 8 (2011): 239-248.
|
|
[20]
|
[ M. M. Mullin,E. F. Stewart,F. J. Fuglister, Ingestion by planktonic grazers as a function of concentration of food1, Limnol. Oceanogr., 20 (1975): 259-262.
|
|
[21]
|
[ J. B. Collings, Bifurcation and stability analysis of a temperature-dependent mite predator-prey interaction model incorporating a prey refuge, B. Math. Biol., 57 (1995): 63-76.
|
|
[22]
|
[ E. González-Olivares,R. Ramos-Jiliberto, Dynamic consequences of prey refuges in a simple model system: more prey, fewer predators and enhanced stability, Ecol. Model., 166 (2003): 135-146.
|
|
[23]
|
[ L. Chen,F. Chen,L. Chen, Qualitative analysis of a predator-rey model with Holling type Ⅱ functional response incorporating a constant prey refuge, Nonlinear anal-real., 11 (2010): 246-252.
|
|
[24]
|
[ T. K. Kar, Stability analysis of a prey-predator model incorporating a prey refuge, Commun. Nonlinear. Sci., 10 (2005): 681-691.
|
|
[25]
|
[ Y. Huang,F. Chen,L. Zhong, Stability analysis of a prey-predator model with Holling type Ⅲ response function incorporating a prey refuge, Appl. Math. Comput., 182 (2006): 672-683.
|
|
[26]
|
[ D. E. Schindler,M. D. Scheuerell, Habitat coupling in lake ecosystems, Oikos, 98 (2002): 177-189.
|
|
[27]
|
[ P. J. Wiles,L. A. van Duren,C. Häse,J. Larsen,J. H. Simpson, Stratification and mixing in the Limfjorden in relation to mussel culture, J. Marine. Syst., 60 (2006): 129-143.
|
|
[28]
|
[ K. S. Cheng,S. B. Hsu,S. S. Lin, Some results on global stability of a predator-prey system, J. Math. Biol., 12 (1981): 115-126.
|
|
[29]
|
[ L. P. Liou,K. S. Cheng, Global stability of a predator-prey system, J. Math. Biol., 26 (1988): 65-71.
|
|
[30]
|
[ S. B. Hsu,T. W. Huang, Global stability for a class of predator-prey systems, SIAM J, Appl. Math., 55 (1995): 763-783.
|
|
[31]
|
[ J. F. Talling, The annual cycle of stratification and phytoplankton growth in Lake Victoria (East Africa), Int. Revue Ges. Hydrobiol., 51 (1966): 545-621.
|
|
[32]
|
[ V. Lakshmikantham,S. Leela, null, Differential and Integral Inequalities: Theory and Applications, Academic press, 1969.
|
|
[33]
|
[ G. Teschl,
Ordinary Differential Equations and Dynamical Systems Am. Math. Soc., 2012.
|
|
[34]
|
[ H. K. Khalil and J. W. Grizzle,
Nonlinear Systems Upper Saddle River: Prentice hall, 2000.
|
|
[35]
|
[ P. Lawrence, null, Differential Equations and Dynamical Systems, , Springer-Verlag, New York, 1991.
|
|
[36]
|
[ Y. A. Kuznetsov, null, Elements of Applied Bifurcation Theory, , Spring-Verlag, New York, 1995.
|










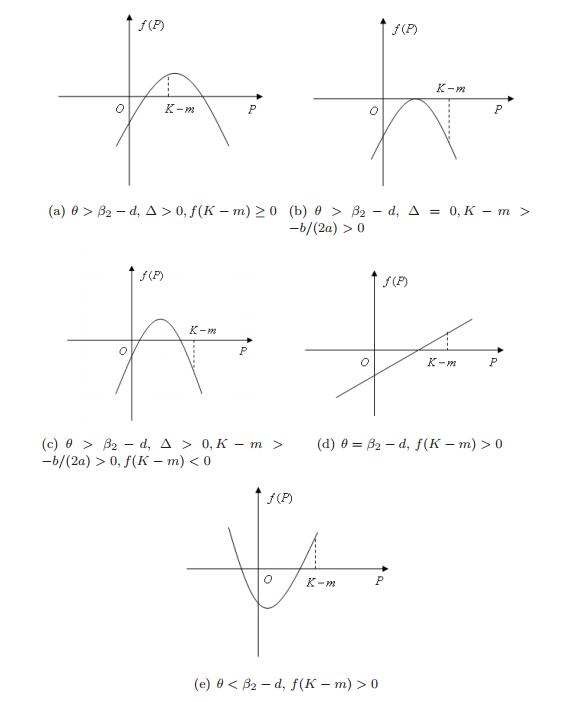
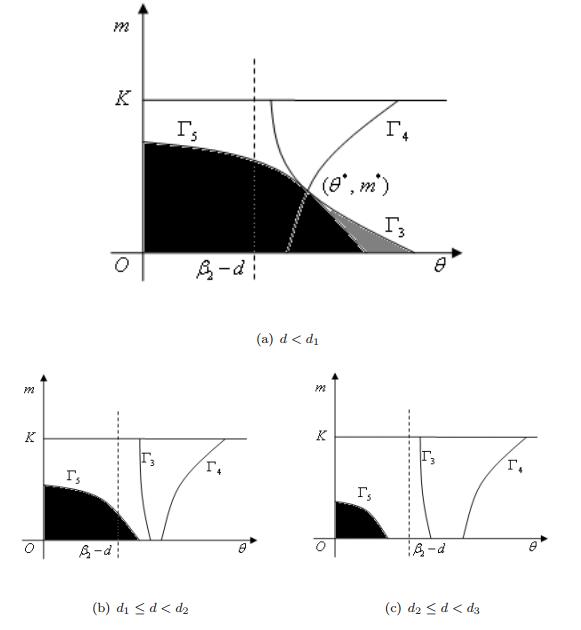
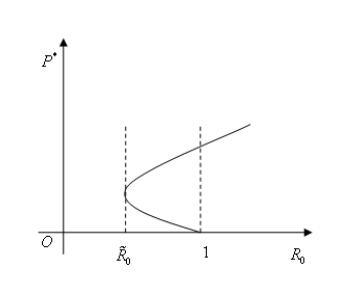
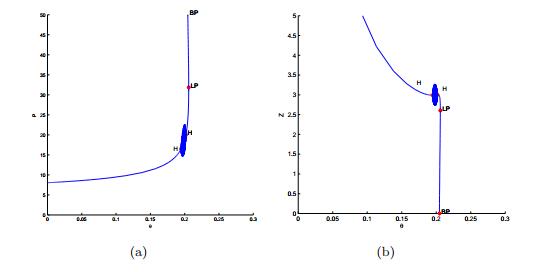
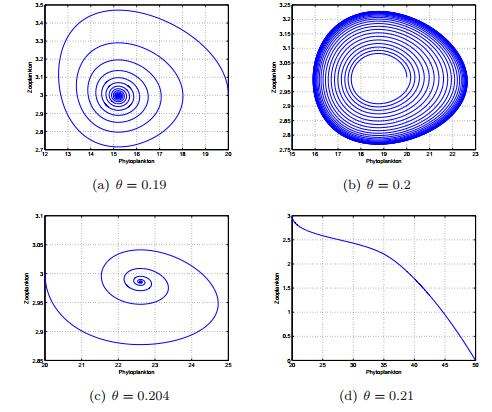

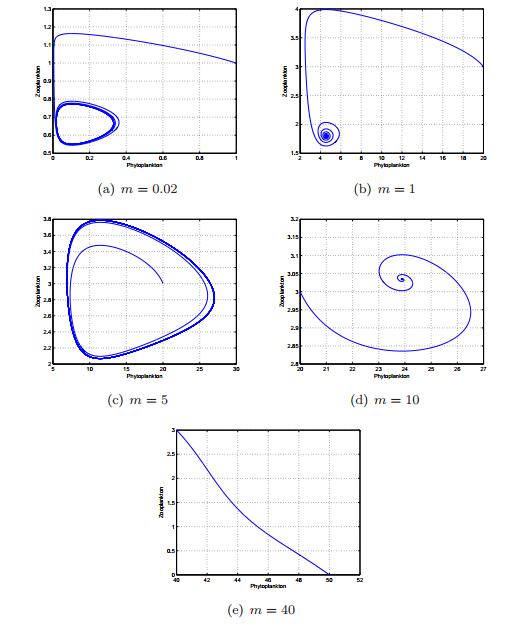
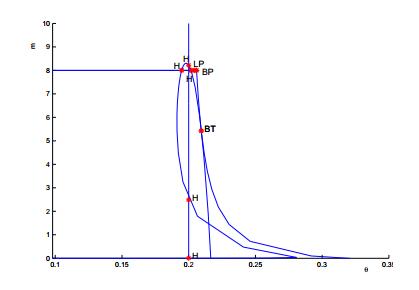
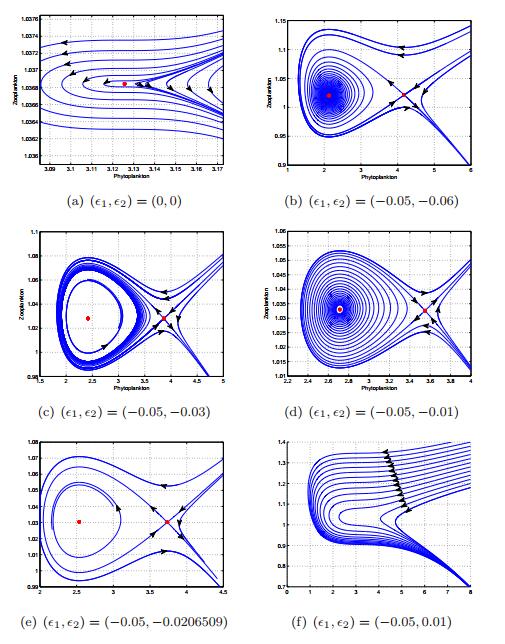
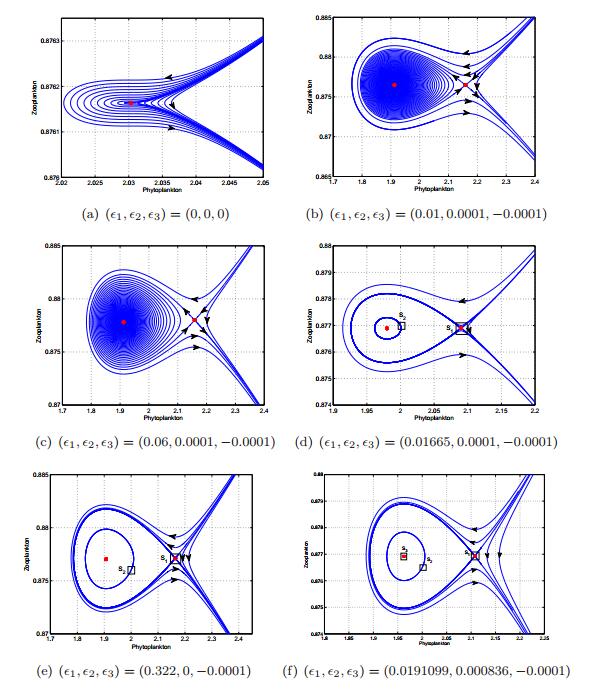
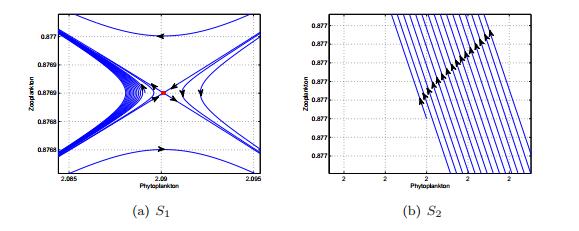
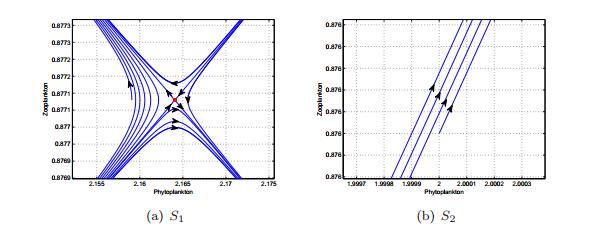
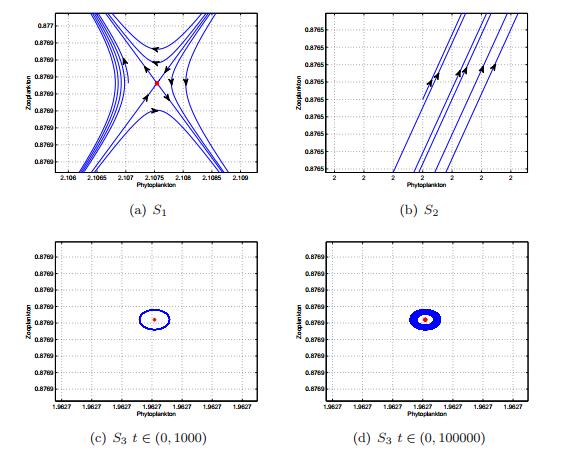


 DownLoad:
DownLoad: