1. Introduction
Experimental and theoretical models have been recently developed to examine fundamental aspects of collective motion exhibited by various biological systems. Following the seminal papers [18]-[17] and works cited therein we suggest that hydrodynamic interactions between the swimmers lead to collective motion when every bacterium interacts with other ones through the viscous environment. The implicit evidences of collective motion were confirmed by reduction in the effective viscosity [16]. The theoretical investigations of collective motion were based on the considering the motion in the framework of mechanical dynamical systems [13]-[20]. While the above presented theoretical and experimental results are related via the effective viscosity of suspension of swimmers, these relation lack simple and direct comparisons of viscosity for experimentally observed sets of bacteria and for simulated ensembles.
In the present paper, we propose a new quantitative criterion of collective behavior. The locations of bacteria are modeled by short segments having a small width randomly embedded in medium without overlapping. First, we theoretically simulate locations of particles called below by disordered sets of bacteria (DB sets for shortness) subjected to local viscous stresses and randomly reacted on hydrodynamic interactions. Second, we calculate the basic statistic moments of the constructed DB sets in terms of the generalized Eisenstein-Rayleigh sums (e-sums for shortness) introduced in [6]. Further, we construct the e-sums (2) for the observed experimental locations (31 film frames) of Bacillus subtilis in a very thin liquid film [18]. As the final step, we compare the e-sums of DB sets and of the experimental locations. The obtained results show a difference between these two sets of e-sums that demonstrates the collective motion of bacteria. We do not explain reasons for the collective motion and refer to [18]-[17], [13]-[20].
Our criterion of the collective behavior is based on a new RVE (representative volume element) theory proposed in [6], on the invariance of the effective transport properties on the conformal mappings [4] and on the algebraic dependence of the viscous lattice sums on the e-sums [6]. The main object of this theory is a set of e-sums systematically investigated in [10], [8], [2], [3], [4], [15]. According to the new RVE theory, the set of the e-sums (see (2) below and general formulas in [6]) determines macroscopically equivalent cells, i.e. cells having the same effective properties (conductivity, viscosity etc). The RVE is chosen as the minimal size cell from all the equivalent cells. The necessary justification of this theory can be found in the above cited works. It is worth noting that the usage of the e-sums implicitly takes into account high order correlation functions without their hard direct computations. In particular, we make simple implementation of the RVE theory [6] which demonstrates its numerical advantages in comparison with expensive computations based on the traditional statistical notion of the RVE.
It is worth noting that the criterion can be applied to various two-phase dispersed media (biological systems, composites etc).
2. Random location of segments
In the present section, we discuss theoretical simulations of elements embedded in a medium. Bacteria are modeled by short segments having non-overlapping thin δ-security coatings. Random locations of segments are generated in the following way. The plane geometry is considered as the complex plane C of the complex variable z=x+iy with standard designations accepted in complex analysis where i denotes the imaginary unit, Re and Im the real and imaginary parts, the bar stands for the complex conjugation.
The complex numbers 1 and i can be considered as the fundamental translation vectors on the complex plane C. We introduce the (0,0)-cell as the square
|
Q(0,0)={z=t1+it2:−12<tk<12(k=1,2)}.
|
The square lattice Q consists of the cells Q(m1,m2):={z∈C:z−m1−im2∈Q(0,0)}, where m1,m2 run over integers.
Consider N non-overlapping segments Γk of length l with the centers bk∈Q(0,0) with the angle of inclination αk∈[−π,π]. (see Fig.1).
The centers bk are considered as random variables distributed in such a way that the segments
|
Γk={z∈C:z=bk±l2eiαkt,0≤t≤1}
|
generate a set of uniformly distributed non-overlapping segments. Theoretically, this distribution can be introduced as the distribution of the variable b=(b1,b2,⋯,bN)∈QN(0,0) with the restrictions |bm−bn|≥δ for m≠n (m,n=1,2,…,N). The separation parameter δ is taken equal to l4. This value refers to the minimum distance between the centers of the bacteria. The choice of the constant 4 is based on the experimentally observed widths of bacteria. It should be noted that the segments Γk belong to the cell Q(0,0) in the double periodic topology when the opposite sides of Q(0,0) are glued by pairs.
The random variable b can be statistically realised for large N by the Monte Carlo method to get numerical results. The following constructive procedure to generate random locations of segments is used. Let a random point b1 is taken in accordance with the uniform distribution in Q(0,0). Next, a random angle α1∈[−π,π] is chosen. Hence, the pair of points z1=b1±l2eiα1 is constructed. This is equivalent to the construction of the first segment Γ1 determined by the point b1 and angle α1. At the next step, we take a random point b2 uniformly distributed in Q∖H1, where H1={z∈C:|z−b1|≤δ}. Further, a random angle α2 is selected and we check whether the segments with the ends z2=b2±l2eiα2 and z1 do not intersect. If it is true, we have the second random segment determined by the point b2 and angle α2. If the segments intersect, we take a random point b2 again in Q∖H1 and randomly select a new random angle α2. In the same way, we take the next point b3 uniformly distributed in Q∖(H1∪H2), where H2={z∈C:|z−b2|≤δ} and so forth. The last random point bN is uniformly distributed in Q∖(⋃N−1k=1Hk) and determines a pair of points zN=bN±l2eiαN with the random angle αN.
Introduce the density segments associated to the conformally invariant conductivity (capacity) [4]
where l is the length of the segment and N the number of segments per representative cell. The algorithm described above generates a probability distribution Uϱ depending on the density. This distribution models the DB sets. In the limit case ϱ=0, the distribution U0 becomes the well known Poisson distribution of points in the square.
In order to study the distributions Uϱ for various densities ϱ we will use the following e-sums [9]
|
e2=1N2N∑k=1N∑m=1E2(bk−bm),epp=(−1)pNp+1N∑m=1|N∑k=1Ep(bm−bk)|2,p=2,3,4.
|
(2)
|
Here, Ep denotes the Eisenstein functions of order p (see Appendix). The values of the basic sums e2, e22, e33 and e44 will be estimated using the Monte Carlo method.
3. Computation of e-sums for DB sets
The theoretical probabilistic distributions corresponding to disordered locations of bacteria are modeled in the previous section. Now, we propose an effective computational tool to properly describe Uϱ.
Let M denote the number of simulated realizations of the unit cell (Monte Carlo experiments) with the random value b. The parameters M and N must be chosen sufficiently large in order to obtain the stable averaged value of the e-sums. Theoretically, it is possible to consider only one experiment (M=1) and to take a huge number N. But computations are less expensive if M is large and N can be not so huge as in the case M=1.
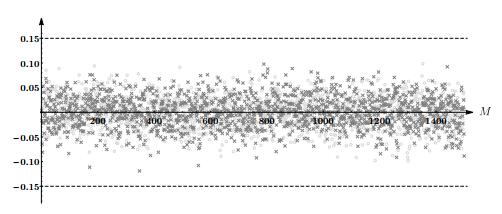
First, we determine the minimal N for which the distribution is characterized in that the angles of the segments will be uniformly distributed over the interval [−π,π]. It is assumed that the segments directions are uniformly distributed if the following inequalities are fulfilled
|
|1NN∑n=1Re[exp(iαn)]|≤0.15and|1NN∑n=1Im[exp(iαn)]|≤0.15,
|
(3)
|
These conditions are satisfied for N=500 (see Fig.2).
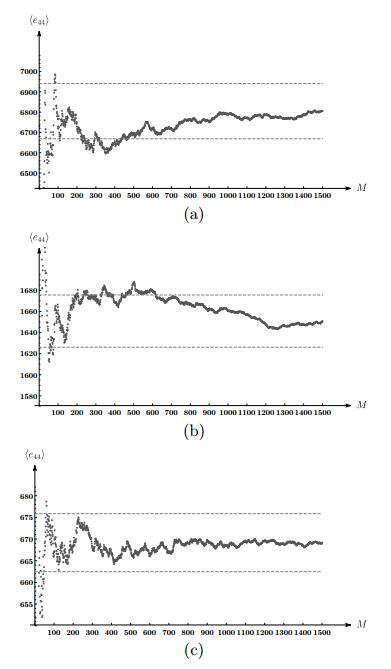
In order to estimate M0=M when the computations become stable we consider the dependence of the mean ⟨e44⟩ on M for M∈[1,1500] experiments. All the sums e2 and epp (p=2,3,4) are estimated, but e44 is characterized by major volatility. Here, ⟨e44⟩ is equal to the mean value of (e44)m calculated for b generated in the m-th numerical experiment, more precisely,
The results are shown in Fig.3. One can observe that errors do not exceed 2% for M>700. Therefore, the computations demonstrate that we have to simulate at least M=800 cells each of them contains at least N=500 segments.
The values e2,e22,e33,e44 are computed for the distributions Uϱ for various densities ϱ. The sum e2 must be equal to π [9] for ideal macroscopically isotropic random locations of segments. This yields the first criterion equation for the macroscopic isotropy of structures. The sums epp (p=2,3,4) describe high order basic terms of the distributions Uϱ. The next terms could describe more precisely Uϱ for higher densities [8].
The average e-sums are selected in Table 1 for the densities ϱ changing from 0.05 to 0.6 with the step 0.05. The algorithm works too slowly for higher densities. The results from Table 1 can be extended by expensive computations to higher densities.
Table 1. The averaged e-sums for various densities.
| ϱ | Re[⟨e2⟩] | ⟨e22⟩ | ⟨e33⟩ | ⟨e44⟩ |
| 0.05 | 3.12977 | 129.053 | −3554.78 | 165787.0 |
| 0.1 | 3.14228 | 68.9110 | −926.015 | 21743.5 |
| 0.15 | 3.13271 | 48.7003 | −424.611 | 6725.43 |
| 0.2 | 3.13447 | 38.8351 | −251.143 | 3037.38 |
| 0.25 | 3.14641 | 33.0394 | −167.170 | 1635.55 |
| 0.3 | 3.13646 | 28.9718 | −121.079 | 1000.09 |
| 0.35 | 3.14165 | 26.3229 | −93.1703 | 672.818 |
| 0.4 | 3.14652 | 24.2258 | −73.9405 | 472.197 |
| 0.45 | 3.14838 | 22.7573 | −61.2791 | 354.635 |
| 0.5 | 3.14157 | 21.4983 | −51.8595 | 274.963 |
| 0.55 | 3.14517 | 20.5061 | −44.5169 | 218.888 |
| 0.6 | 3.13946 | 19.7609 | −39.4423 | 180.827 |
Table 1 contains the fundamental parameters of the uniform non-overlapping distribution Uϱ of segments on the plane. The simulated theoretical distribution describes DB sets when bacteria may affect each other but these interactions are local and do not yield the collective behavior.
4. Collective motion of bacteria
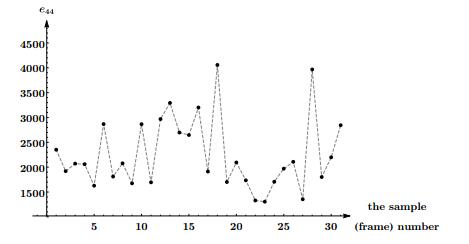
In the present section, we pay attention to experimental results partially presented in [18]. The images of Bacillus subtilis in 31 frames are used in computations. One of the typical frame is displayed in Fig.4.
We use algorithms of image processing and analysis to determine number, centers, angles of inclinations and length of bacteria. The density of bacteria is calculated by formula (1) and oscillates around value 0.15. The results of the image processing and analysis are applied to computation of the values of the experimental e-sums. The results are selected in Table 2.
Table 2. The e-sums for 31 film frames of Bacillus subtilis. The first column contains the number of the film frame, the second column contains the number of bacteria N detected in the frame. The next columns show basic sums.
| no. | N | Re[e2] | e22 | e33 | e44 |
| 1 | 2065 | 3.24113 | 35.3172 | −166.312 | 2351.56 |
| 2 | 2067 | 3.25984 | 36.6725 | −158.136 | 1920.47 |
| 3 | 2066 | 3.19667 | 34.8162 | −164.29 | 2071.58 |
| 4 | 2040 | 3.29149 | 35.4505 | −149.94 | 2060.21 |
| 5 | 2064 | 3.27662 | 33.9367 | −141.591 | 1627.76 |
| 6 | 2056 | 3.42917 | 37.4054 | −190.248 | 2867.12 |
| 7 | 2026 | 3.34495 | 35.6335 | −157.051 | 1811.85 |
| 8 | 2030 | 3.13718 | 34.0681 | −169.746 | 2077.70 |
| 9 | 2039 | 3.21947 | 34.6973 | −148.317 | 1675.23 |
| 10 | 2044 | 3.06423 | 37.2784 | −177.122 | 2865.54 |
| 11 | 2023 | 2.95417 | 32.9400 | −157.421 | 1695.34 |
| 12 | 2014 | 3.09097 | 36.1141 | −208.578 | 2967.78 |
| 13 | 2027 | 3.00734 | 36.0749 | −215.528 | 3292.64 |
| 14 | 2034 | 3.16291 | 35.3946 | −194.029 | 2697.51 |
| 15 | 2059 | 3.21142 | 35.7572 | −175.982 | 2647.37 |
| 16 | 2016 | 3.19012 | 36.9914 | −200.469 | 3200.68 |
| 17 | 2016 | 3.30939 | 35.3018 | −163.073 | 1911.99 |
| 18 | 2057 | 3.22744 | 38.7036 | −243.944 | 4057.40 |
| 19 | 2055 | 3.18527 | 35.9201 | −144.187 | 1701.75 |
| 20 | 2071 | 3.31315 | 37.6613 | −152.177 | 2094.90 |
| 21 | 2066 | 3.2770 | 33.6304 | −131.371 | 1735.46 |
| 22 | 2073 | 3.3854 | 35.1252 | −129.436 | 1330.40 |
| 23 | 2040 | 3.24423 | 33.6249 | −126.809 | 1305.79 |
| 24 | 2080 | 3.30177 | 36.0663 | −159.988 | 1707.04 |
| 25 | 2077 | 3.19037 | 34.2243 | −168.806 | 1970.43 |
| 26 | 2065 | 3.39291 | 39.0489 | −186.748 | 2108.54 |
| 27 | 2062 | 3.17936 | 34.0767 | −138.028 | 1354.70 |
| 28 | 2024 | 3.11102 | 40.2420 | −202.873 | 3966.32 |
| 29 | 2068 | 3.12904 | 33.4322 | −155.213 | 1801.78 |
| 30 | 2059 | 3.28145 | 36.8591 | −176.772 | 2198.46 |
| 31 | 2042 | 3.24301 | 37.0932 | −208.055 | 2844.27 |
In order to compare the distributions of DB sets with the distribution of bacteria we have made theoretical calculation of 31 samples. Because of the average number of bacteria in the frame is about 2050, the minimum distance between the centers of the bacteria is 14 of their length and density of bacteria equals about 0.15, the theoretical calculations have been carried out for the following parameters N=2050, ϱ=0.15 and δ=l4. The length l=0.017108 is normalized to the normalized unit area of the cell. The results of the calculations are shown in Table 3.
Table 3. The e-sums calculated for 31 samples of DB sets. The parameters of distribution are N=2050, ϱ=0.15 and δ=l4.
| no. | Re[e2] | e22 | e33 | e44 |
| 1 | 3.17987 | 46.6427 | −393.453 | 6565.85 |
| 2 | 3.07985 | 50.6260 | −515.407 | 9617.15 |
| 3 | 3.36286 | 58.2470 | −629.653 | 11184.9 |
| 4 | 3.31838 | 47.8645 | −380.243 | 5763.63 |
| 5 | 3.01309 | 47.7780 | −435.587 | 6984.50 |
| 6 | 3.14305 | 47.8691 | −400.298 | 6207.25 |
| 7 | 3.20741 | 50.5550 | −433.739 | 6256.86 |
| 8 | 3.20946 | 45.6877 | −348.511 | 4868.42 |
| 9 | 3.08756 | 50.2205 | −485.495 | 8630.89 |
| 10 | 3.14825 | 51.9186 | −498.135 | 7884.83 |
| 11 | 3.15232 | 50.4770 | −407.538 | 5794.05 |
| 12 | 2.97260 | 48.3467 | −415.332 | 6423.79 |
| 13 | 3.18407 | 48.6382 | −406.544 | 6317.61 |
| 14 | 3.12623 | 43.5618 | −332.846 | 5012.32 |
| 15 | 2.96333 | 47.0048 | −403.513 | 6158.98 |
| 16 | 3.13992 | 49.2681 | −428.006 | 6764.48 |
| 17 | 3.16460 | 48.0914 | −402.791 | 6347.72 |
| 18 | 3.09493 | 53.3020 | −483.722 | 7700.97 |
| 19 | 3.12330 | 50.4108 | −415.444 | 6743.15 |
| 20 | 3.21182 | 49.3165 | −410.478 | 6876.66 |
| 21 | 3.21308 | 50.4445 | −476.521 | 8126.50 |
| 22 | 2.97221 | 48.6954 | −441.899 | 7384.68 |
| 23 | 3.23927 | 51.1514 | −466.984 | 6864.76 |
| 24 | 3.11142 | 43.8766 | −362.591 | 5776.80 |
| 25 | 2.84798 | 44.1550 | −383.563 | 5705.14 |
| 26 | 3.09189 | 44.8430 | −373.888 | 6020.28 |
| 27 | 3.11219 | 44.5645 | −331.345 | 4733.94 |
| 28 | 3.05673 | 50.1022 | −490.807 | 8516.17 |
| 29 | 3.09775 | 48.5431 | −416.398 | 6597.56 |
| 30 | 2.99318 | 47.1511 | −432.571 | 6636.21 |
| 31 | 3.01481 | 47.5799 | −400.869 | 6078.16 |
5. Conclusion
Comparing the results shown in the Tables 2 and 3 for the observed and theoretical distributions of bacteria, we can see that values of the corresponding e-sums differ. Therefore, the observed locations of bacteria are not fitted with the simulated disordered locations. We can conclude that the behavior of the bacteria is not disordered, hence, we suggest that it is collective. An exception is the values of e2 which is close to π≈3.14 for the DB sets and the observed locations (see Table 4). This demonstrates averaged isotropy of the bacteria motion for the considered data.
Table 4. Comparison of the averaged e-sums for the observed bacteria locations with the e-sums computed for the DB sets (ϱ=0.15) from Table 2 and Table 3.
| Re[⟨e2⟩] | ⟨e22⟩ | ⟨e33⟩ | ⟨e44⟩ |
| averaged e-sums for theoretical distributions | 3.11721 | 48.6107 | −425.941 | 6791.75 |
| standard deviation of the e-sums for theoretical distributions | 0.107542 | 3.02546 | 60.3803 | 1366.42 |
| averaged e-sums for distributions of bacteria | 3.22092 | 35.7922 | −169.75 | 2255.47 |
| standard deviation of the e-sums for distributions of bacteria | 0.108139 | 1.73937 | 27.9609 | 717.895 |
In order to see that the theoretical and observed distributions are essentially different, we compare averaged basic sums (see Table 4) from Table 2 and Table 3. It is worth noting that changes of the parameters (δ, M etc) do not essentially impact onto deviations of the e-sums of DB sets. Moreover, the DB sets have significantly higher values epp (p=2,3,4) than the observed ones (c.f., the bold line in Table 1 and the averaged data from Table 4).
The above analysis of collective behavior can be considered as the first application of the RVE theory [6] which will be extended in the future. In particular, we plan to study dynamical parameters of the bacteria distributions in time using the data displayed in Fig.5.
Appendix
Following [6], [7] we present constructive formulae for the Eisenstain-Rayleigh sums Sm the Eisenstain functions Em corresponding to square lattice Q (see section 2).
The Eisenstein--Rayleigh lattice sums Sm can be easily calculated through the rapidly convergent series (43) and recurrent formulae (44) from paper [7]. For the square array, we have S2=π=3.14159, S4=3.15121, S8=4.25577, S12=3.93885. Only the sums Sm (m=2; m=4,8,12,16,…) do not vanish for the square array.
The Eisenstein functions [21] are related to the Weierstrass function ℘(z) [1] by the identities
|
E2(z)=℘(z)+S2,Em(z)=(−1)m(m−1)!dm−2℘(z)dzm−2,m=3,4,….
|
(5)
|
Every function (5) is doubly periodic and has a pole of order m at z=0. For shortness, it is convenient to redefine the Eisenstein functions in (2) at zero as Ep(bk−bm):=Sp for k=m.
Acknowledgments
We thank Alexei Sokolov who kindly presented the experimental results partially reported in [18] and Leonid Berlyand for stimulated discussion during his visit to Kraków and VM's visits to Penn State University.
The authors thank the anonymous reviewer for valuable comments and suggestions to improve the paper.









 DownLoad:
DownLoad: