1. Introduction
Semiconducting oxide nanostructures are an excellent choice of materials for a wide range of applications due to the versatility in their properties. The feasibility of tuning the physical properties in these oxides arises from the common presence of oxygen vacancies and the variety of crystal structures that semiconducting oxides can adopt that combine in some cases several oxidation cation states. These wide band gap materials are very suitable hosts for optically active impurities, what make them particularly attractive for optical applications. In addition to that, semiconducting oxides find applications in gas sensors, photocatalysis and photovoltaic devices. Moreover, a variety of synthesis methods have been employed to grow single and complex nanostructures based on oxides in the last decade, with the purpose of incorporating them as building blocks in novel devices [1]. Some oxide nanomaterial-based devices have already demonstrated an improvement in their performance, in comparison with their thin film or bulk based counterparts. Examples can be found in highly sensitive chemical sensors, laser emitters based on nanowires, or high efficient solar cells, among others [2,3]. A variety of oxide nanomaterials (e.g. ZnO or SnO2) that include nanowires, nanobelts and other elongated morphologies has been obtained by several synthesis methods [4,5]. In our group we use a thermal evaporation method that enables the fabrication of semiconducting oxide nanostructures through the vapor-solid (VS) mechanism [6]. An important issue addressed in recent research is the problem of effective doping of nanomaterials and its consequences on nanodevices performance. Thermal diffusion is one of the mainstream of doping in semiconductor technology. In this work, we take advantage of the thermal evaporation method to obtain doped semiconducting oxide nanomaterials in just one-step process during the synthesis route. We report that the presence of impurities during the growth implies not only the doping of the nanomaterial, but also that they can bring about profound morphological changes in the final architecture. In this work, we consider the consequences of Cr and Sn incorporation in Ga2O3, Sb2O3 and Zn2GeO4 nanowires. Cr ions are optically active and display a strong red luminescence in Ga2O3 nanowires. Sn impurities have been revealed as self-catalysts that considerably enhance the nanowires yield production in the three oxides investigated. Besides the morphology and structural characterization, their optical properties have been assessed by photoluminescence (PL) and cathodoluminescence (CL). In particular, the results show that these oxide nanomaterials are promising candidates for optical microcavities since they exhibit a rather good waveguiding behavior and optical confinement.
2. Materials and Method
2.1. Semiconducting oxides
The materials of this work belong to the family of transparent conductive oxide materials (TCOs). Here we summarize the main features of the binary semiconducting oxides relevant for the purpose of this work.
2.1.1. Ga2O3
The most stable phase of gallium oxide is the monoclinic phase, also known as the b-Ga2O3 phase. It can be considered as a cubic-distorted lattice in which Ga atoms occupy both octahedral and tetrahedral positions in an anionic oxygens lattice. On the other hand, gallium oxide has the widest band gap among the TCOs, with a value of 4.9 eV. In spite of this high value, the presence of oxygen vacancies provides a certain amount of delocalized electrons that are responsible for the electronic conductivity. Hence, undoped Ga2O3 usually shows n-type conductivity and luminescence in the ultraviolet-blue region [7,8]. Most of the works on Ga2O3 refer to thin films and their applications as gas sensor, taking advantage of the tunable electronic conductivity by changing the oxygen vacancies concentration. In this work, we will report the consequences of doping with Cr and Sn in the formation of complex Ga2O3 nanostructures.
2.1.2. Sb2O3
Antimony oxide is a less known oxide with potential applications in sensors, optical devices, or flame-retardants, among others [9]. This oxide exhibits several stable phases: cubic and orthorhombic Sb2O3 and orthorhombic Sb2O4 that combines two oxidation cation states. One interesting feature of this oxide is that the optical band gap depends on the crystalline phase. Cubic Sb2O3 has a band gap of 3.7 eV while for orthorhombic Sb2O3 is 3.2 eV. Phase transformations of antimony oxide have been reported at temperatures in the range of 400-700 ºC under suitable atmospheres [10]. In this work, we will report the fabrication of micro- and nanotriangles, and micro- and nanorods, with the cubic and orthorhombic phases, respectively, depending on the substrates used: pure Sb, Sn doped or Cr doped Sb substrates.
2.1.3. Zn2GeO4
Zn germanate, with a band gap of 4.4 eV is a ternary oxide of the family of germanates. This family is attracting a lot of attention due to merging optical transparency and electrical conductivity in an excellent way [11]. Zn2GeO4 microrods show hexagonal, trigonal or general prismatic habits in accordance with their rhombohedral crystal structure. The high refractive index of this material enables the fabrication of optical microcavities for the visible light. In this work, we discuss the presence of optical resonances in the frame of the optical confinement in Zn2GeO4 microstructures. In addition, the incorporation of Sn during the growth process leads to an enhancement of the aspect ratio of the nanostructures.
2.2. Experimental techniques
The nanostructures of the above-mentioned oxides have been obtained by a thermal evaporation method and the growth mechanism is based on a vapor-solid (VS) process. The precursors are placed into an open tubular furnace where the growth takes place. Compacted pellets of the oxides are used as substrates with no need of foreign catalyst. The thermal treatment is carried out under a dynamic atmosphere, usually an Ar gas flow, and produces the evaporation of the species over the sources and the further deposition onto the substrates. The anisotropic growth needed to the formation of elongated nanostructures is driven by the different surface energies of the lattice planes of each crystalline structure, which favors one preferred direction over others. With this method is possible to get very efficiently a high amount of undoped nanostructures of Ga2O3, Sb2O3 and Zn2GeO4 using as starting materials Ga, Sb or Ge plus ZnO, respectively. To dope the nanostructures, tin or chromium oxides have been added to the precursors in order to get doped material in a single stage process. A more detailed description of the growth process can be found in references [6,14,16,19].
The structural and optical properties were assessed by scanning electron microscopy (SEM) advanced modes of operation, such as spatially resolved cathodoluminescence (CL) and electron back scattering diffraction (EBSD); and photoluminescence and Raman spectroscopies in an optical confocal microscope. The equipment used has been a Leica SEM equipped with EDS and CL, an Inspec FEI instrument with EBSD operation mode, and an optical Horiba Jobin Yvon confocal microscope with Raman and micro-photoluminescence techniques. Special attention has been paid to the luminescence of the different morphologies and the possibility to get optical confinement inside the microstructures. The set of doped oxides studied in this work shows optical luminescence bands that span the electromagnetic range, from the ultraviolet to the red light, which is highly interesting for applications.
3. Results and Discussion
3.1. Morphology and microstructure
The intrinsic conductivity of Ga2O3 arises from the oxygen vacancies, usually present as native defects in semiconducting oxides. One of the possible ways to increase the carrier concentration and consequently the electrical conductivity is by doping with donor impurities [12]. A thermal treatment of pure Ga in the presence of oxygen leads to the growth of a high amount of undoped Ga2O3 nanowires, as Figure 1a shows. The substrate was a compacted gallium oxide pellet and the temperature window is in the range 1100 - 1500 ºC. Sn impurities would behave as donors in Ga2O3 host. Figure 1b shows the result of the growth process when we add tin oxide powders to the pure Ga precursor in order to get Sn doped Ga2O3 nanowires. The figure shows the new arrangement of the nanowires in which most of them appear having lateral branches coming out from main wires. It is noticeable that primary and secondary wires form mostly square angles, what implies preferred growth direction for the nanowires according to their crystal structure. Besides, some previous works have confirmed an effective increase of electrical conductivity of two orders of magnitude in Sn doped nanowires [13]. The last example of doping inducing changes in morphology is Cr-Sn codoping [14]. Here we show the results when Cr and Sn are added to the source materials to get a co-doping of Ga2O3 nanowires. Figure 1c shows the crossing wires structure that appear after the thermal treatment. In this case, we have obtained the growth of both Ga2O3 and SnO2 nanowires crossing each other forming an branch-like shape. In a previous work, we have characterized the structural properties by EBSD in the SEM and EXAFS (Grenoble synchrotron) at the junction point [15]. These results showed a good crystallinity of both oxide lattices, and a slight local distortion of the Ga bonds at the crossing areas.
A study of the influence on morphology by doping with Sn and Cr has been carried out on Sb2O3 nanostructures as well. This oxide has particular features since it presents more than one stable phase at room temperature, as described above. Figure 2a shows a representative SEM micrograph of micro- and nanotriangles of Sb2O3 obtained on pure Sb substrates at 400 ºC. XRD and EBSD measurements have confirmed that the crystal structure corresponds to the cubic phase (senarmontite) of Sb2O3 [16]. On the other hand, Sb2O3 micro-rods with the orthorhombic phase (valentinite) have been obtained by adding some amount of tin oxide to the antimony substrate (figure 2b) after thermal treatments at temperatures between 450-550 ºC [17]. These micro-rods have transversal dimensions in the range of 1-10 µm with a rectangular cross-section. In addition, the incorporation of chromium oxide into the Sb substrate favors as well the stabilization of the orthorhombic phase in the form of nanorods. Figure 2c shows the high amount of nanorods formed on the antimony pellet. It should be mentioned that the orthorhombic phase of Sb2O3 has a laminar character, because of the van der Waals bonds between (020) oxygen planes within the unit lattice. Actually, the stacking of very thin layers of Sb2O3 forms the microrods of Fig 2b. The growth direction of the rods has been identified as the [001] [18]. In terms of growth mechanisms, it seems that adding Sn or Cr impurities promotes the formation of rods at the micro- and nanoscales, respectively.
Finally, we have successfully grown ternary oxide nanostructures with the thermal evaporation method [19]. Here we present some results concerning zinc germanate. In this case, the source materials were a mixture of pure Ge, ZnO and carbon in a 2:1:2 ratio. Undoped Zn2GeO4microrods were obtained at 800 ºC after 8 hours (Figure 3a). Most of the microrods show an hexagonal cross-section with lateral side of about 1-2 µm. For undoped material, the growth yield was rather low, and following the previous results of Sn doping effect on the synthesis of Ga2O3 and Sb2O3 oxides (shown above), we added some tin oxide into the precursors and pursued further with the thermal process. The results confirmed that Sn addition promotes the growth of nanorods, as Figure 3b shows, with characteristic transversal dimensions in the range of hundreds of nanometers.
3.2. Luminescence and optical resonances
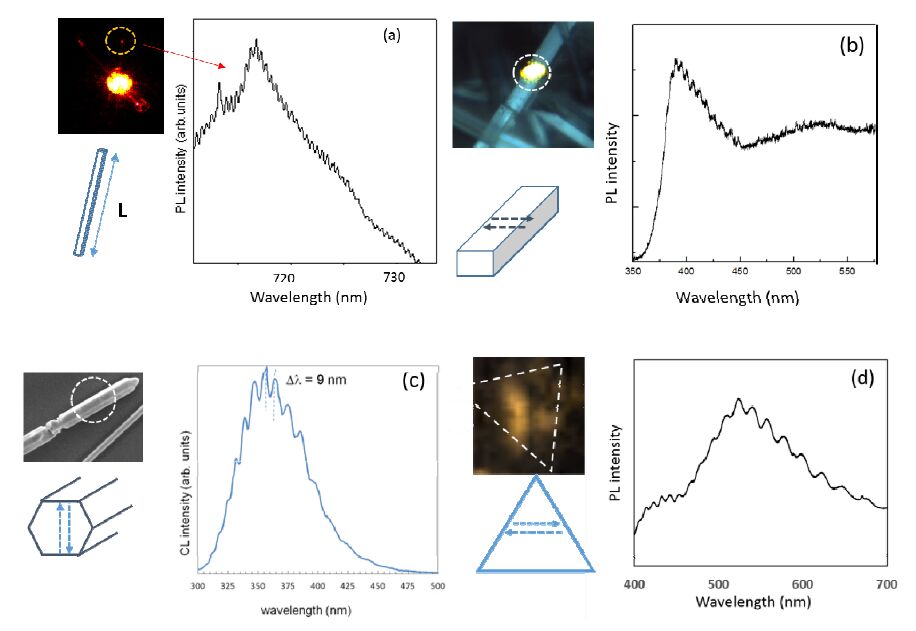
Metal oxides usually are oxygen deficient with a considerable amount of oxygen vacancies that play a major role as native defects, either as single point defects or forming complexes, e.g VO-VGa in Ga2O3. These defects induce localized energy levels within the wide band gap, which varies from 3.2 to 4.9 eV, in the case of the oxides investigated in this work. PL and CL emission bands of native defects are usually broad bands composed of more than one component, which implies that several recombination paths are involved in the origin of the luminescence. In the less studied oxides, there is still controversy about the origin of some components, e.g, Sb2O3 and Zn2GeO4. Here we report luminescence bands arising from: i) near band edge emission, ii) native defects related to oxygen vacancies, and iii) optically active impurities (Cr3+) in nanostructures made of orthorhombic Sb2O3; cubic Sb2O3 and Zn2GeO4; and Ga2O3, respectively. In addition, the obtained oxide microstructures exhibit wave guiding behavior of either an external light source or internally generated light [20,21]. There is some optical confinement of the excited luminescence within the micro- and nanostructures, which is feasible due to several factors, such as the high crystal quality and smooth flat surfaces of the structures. These features prevent optical losses when light propagates through the microstructures. Figure 4 summarizes the results of the luminescence measurements in these oxides. Optical resonances are observed in all cases, what suggests that these microstructures can be potential optical microcavities for light wavelengths ranged from 300 nm to 700 nm.
Figure 4a shows the PL spectrum, recorded at the exit point of a Cr doped Ga2O3 microwire of 90 µm length, with the maximum at 690 nm. Cr impurities are responsible for a strong red emission originated from Cr 3+ ions in the gallium oxide lattice [21]. Radiative recombination from the R lines of Cr3+ ions are very efficient in Cr doped Ga2O3 nanowires in comparison with Cr doped bulk material. The PL spectrum corresponds to the Cr emission along with a set of maxima separated around 1 nm. The inset shows the micro-photoluminescence image of two crossing Cr doped Ga2O3 wires obtained under laser excitation at the crossing point between the wires. The luminescence was taken at room temperature; hence, there is strong contribution of the phonon coupling to the R lines emission leading to a broad emission band. We have measured the separation between wavelength maxima, Dl, for wires of different lengths where optical resonances were present. The Dlobtained scales linearly with the inverse of the wire length, in accordance with the Fabry-Perot (FP) law [22]. Therefore, the Cr doped Ga2O3 wire behaves as an optical microcavity where the wire ends act as reflecting mirrors for the red light generated by Cr
ions and guided through the microstructure.
In principle, we could design the shape and size of an oxide optical microcavity suitable to achieve optical resonances for a certain wavelength interval. In addition to FP resonances, whispering gallery modes (WGM) have also been reported in some oxides microwires, such as ZnO or In2O3, because of internal reflections within the microstructures [23]. In the case of microrods with a well-defined cross-section geometry, such as rectangles or hexagons, it is possible that reflections between parallel sides in the rectangles or hexagons originate FP optical resonances because of constructive interference conditions. We have observed optical resonances in rectangular rods of Sb2O3 and in hexagonal rods of Zn2GeO4 in the wavelength range of 350-500 nm, as it can be seen in Figures 4b and 4c, respectively. In the case of Sb2O3, the luminescence is related to the near band edge emission, as the orthorhombic phase has a reported band gap of 3.2 eV. Reflections between the faces perpendicular to the laser irradiation are the responsible for the optical resonances [17]. In the case of Zn2GeO4 microrods, the emission comes from native defects, and its origin is still unclear. The observed resonances match with FP condition of reflections between parallel sides of the hexagonal cross-section [19]. Finally, figure 4d shows optical resonances resulting from optical confinement in Sb2O3 microtriangles. The inset of figure 4d shows the mapping of the micro-photoluminescence of one triangle highlighted with a dashed line to guide the eye. Three clear maxima of intensity with triangular symmetry are observed. The PL spectrum recorded at one of these maxima shows a rather broad native defect emission band with overlapped resonances. Now, the optical path inside the triangles partially agrees with the WGM condition of internal reflection among the triangle edges [16]. Further work is needed in order to elucidate the alternative optical paths that could be responsible of optical resonances.
4. Conclusion
The role of Sn and Cr impurities in the growth of several oxide nanostructures (Ga2O3, Sb2O3 and Zn2GeO4) has been presented and discussed. The thermal evaporation method used enables to obtain doped oxide nanomaterials in one-step treatment. As a result, besides the desired modification of optical or electrical properties, we have observed some changes in the morphology of the micro- and nanostructures. Sn doping of Ga2O3 promotes the formation of branched nanowires and in the case of Cr-Sn co-doping, crossing wires of Ga2O3/SnO2 have been produced. The only addition of Cr does not modify the formation of nanowires, which may eventually behave as optical microcavities for the red light generated by Cr3+ ions. Antimony oxides microstructures with cubic and orthorhombic phases have been obtained by the thermal method. In this case, the addition of Sn and Cr to the antimony substrate has favored the formation of micro- and nanorods, respectively. Optical resonances in the green region have also been recorded for microrods with the suitable transversal sizes. Finally, undoped Zn2GeO4 microrods have been obtained that show optical confinement of emitted light in the blue region. The effect of Sn doping in this ternary oxide is a change of the aspect ratio of the nanostructures. The incorporation of Sn into the precursors brings about Zn2GeO4 nanorods with smaller transversal sizes than those of the undoped ones. Hence, we would suggest that Sn impurities have been revealed as a key element to increase the production yield of nanowires and nanorods in these three oxides investigated so far.
Acknowledgments
This work has been supported by MINECO (Projects MAT 2012-31959, MAT 2015-65274R and CSD 2009-00013). The authors also acknowledge EAA Grants (NILS project 008-ABEL CM-2013).
Conflict of Interest
The authors declare no conflict of interest.










 DownLoad:
DownLoad: