We consider a two-strain pathogen model described by a system of reaction-diffusion equations. We define a basic reproduction number R0 and show that when the model parameters are constant (spatially homogeneous), if R0>1 then one strain will outcompete the other strain and drive it to extinction, but if R0≤1 then the disease-free equilibrium is globally attractive. When we assume that the diffusion rates are equal while the transmission and recovery rates are heterogeneous, then there are two possible outcomes under the condition R0>1: 1) Competitive exclusion where one strain dies out. 2) Coexistence between the two strains. Thus, spatial heterogeneity promotes coexistence.
1.
Introduction
The role of partial differential equations (PDEs) is fundamental in modeling and analyzing engineering biological processes that evolve over time and space within bioreactors. PDEs provide a robust mathematical framework for describing the spatial and temporal distribution of critical variables, such as nutrient concentrations, microbial populations, and metabolic byproducts. By solving these equations, it is possible to predict the dynamic behavior of these variables, facilitating the optimization of bioreactor design and operational parameters in complex and specific applications. This predictive capability is essential for enhancing process efficiency, achieving precise control over bioprocesses, and maximizing the yield of desired bioproducts. Anaerobic digestion (AD) is a well known biotechnology for waste and wastewater treatment, in which the metabolic activities of specific microorganisms are used to convert complex organic substrates into a value-added gaseous product. During the AD process, complex organic materials are progressively degraded into simpler organic compounds, until a methane rich biogas is obtained as the final product. The biogas can be further utilized for clean energy generation in accordance to environmental policies. Consequently, AD can be considered one of the leading technologies in the context of biorefining systems. Moreover, it is important to account for additional by-products usually contained in the residual non-gaseous effluent, i.e., digestate of the AD process. The digestate is usually rich in nutrients and micro-elements, and it can be successfully used as a fertilizer for agricultural scopes [1,2]. However, some digestate constituents are able to negatively affect the composition of soils and lead to undesired environmental impacts. In some cases, additional treatments are recommended, such as filtration procedures [3], to reduce the content of polluting components or to recover dissolved compounds from the liquid fraction of the digestate. The correct management of digestate, from its generation to the final disposal, represents a crucial point for a sustainable application of the AD process. Its correct use and utilization allow to fulfill the objectives of the Kyoto Protocol and EU Policies concerning organic waste disposal and renewable energy production.
Based on the solid content of the fed bio-waste, AD can be performed in dry, semi-dry, or wet conditions. In dry AD, the total solids (TS) content is higher than 15%, while in semi-dry AD, the TS content ranges between 10 and 15%. Indeed, the most frequently adopted wet AD is used for diluted bio-wastes with a TS content lower than 10% [4]. Over the last decades, high attention has been devoted to the dry AD as its application leads to several advantages compared to wet systems. Small reactor volume, low water addition, easy management of digested by-products, and reduced pre-treatment requirement and nutrient loss are crucial design aspects of dry AD [5,6].
The most used configuration for AD processes are continuously stirred tank reactor (CSTR) and plug-flow reactor (PFR). CSTR is an ideal hydrodynamic model where perfect mixing is hypothesized. For this reason, the concentration of soluble and particulate compounds is supposed to be homogeneous in each point of the reactor [7]. In a real-scale AD plant, this ideal condition is warranted by continuous mixing systems; the more efficient is the mixing system, the closer is the real-scale reactor to the CSTR model. The PFR is characterized by a preferential axial direction in which a continuous flow of waste is forced to pass. The PFR scheme is constituted by a cylindrical/tubular shape reactor where the concentration of different components is a spatial variable in the axial direction. Conversely, soluble and particulate compound concentrations along the radial direction are supposed to be homogeneous. For this reason, the total volume of a PFR can be schematized as an infinite number of in series CSTR [8]. This leads to higher average substrate concentrations and related conversion rates, which could be beneficial for bioreactor design and performances.
In real-scale AD plants, CSTR configuration is commonly used for wet AD [9], while PFR is adopted for dry AD due to the higher viscosity of the medium and the consequent complexity of mixing procedures [10]. The implementation of wet or dry systems has similar costs in terms of investment and management. On the other hand, the two systems are substantially different from an environmental point of view. Typically, wet AD leads to the consumption of around 1m3 of fresh water per ton of waste, e.g., the organic fraction of municipal solid waste (OFMSW), while the water demand of dry AD reactors is ten-fold lower. For this reason, the volume of digestate produced by dry AD processes is several-fold lower than that generated by wet AD systems [6].
1.1. Modeling of AD
Due to the complex biological interaction occurring in AD processes, the role of mathematical modeling is crucial for the development of management/optimization tools able to predict methane production in full-scale applications. The anaerobic digestion model 1 (ADM1) [11] is one of the most popular mathematical models for the prediction of AD dynamics in wet conditions. From its first publication in 2002, several authors were inspired by the ADM1 approach and proposed different modifications to account for specific mechanisms occurring in the AD process or to include relevant phenomena that were neglected in the original version. For instance, the variation of kinetics and stoichiometric parameters due to different pressure levels in AD bioreactors has been recently addressed in [12]. Mathematical models of wet AD are typically based on ordinary differential equation (ODE) systems [13]. Since each state variable only depends on time, they are homogeneous in the reactor domain. On the other hand, the mathematical problem of PFR is described by a PDE system, where the state variables are functions of space and time. This aspect is relevant as it highly increases the complexity of the mathematical modeling of dry AD processes. The effects of turbulence, dispersion, and accumulation of particles in bioreactors strongly affect dry AD performance, as these phenomena are naturally characterized by great uncertainty levels. For this reason, it is possible to state that the modeling of dry AD is a less explored field than wet AD. Some authors avoided to solve the complete PDE system by schematizing the PFR as a number of n in series CSTR [8,14,15]. Other attempts considered a fixed velocity inside the reactor [16] or coupled computational fluid dynamics analysis with a steady-state kinetic model described with ODE [17].
Recently, Panaro et al. [18] proposed an original one-dimensional mathematical model for dry AD in PFR systems. The model was based on mass balance principles for selected state variables resulting in a non-linear PDE system. The convective velocity of the substrate moving along the reactor represented a further unknown, and the model was able to consider the mass/volume variation of the waste along the reactor. Indeed, the solids conversion in gaseous compounds led to a relevant mass variation in dry AD, which in wet systems is negligible due to the high quantity of water in the system. In the same work, the velocity variation was obtained under two main hypotheses: i) the density of the waste substrate moving along the reactor was supposed constant over time, and ii) the volume fractions of the bio-components constituting the treated substrate were constrained to sum up to the unity. These statements implied that the mass of the substrate mixture was constant along the reactor, and the mass reduction of volatile solids (VS) due to the degradation processes was continuously balanced by the variation of velocity. Under these hypotheses, the crucial role of relatively low convective velocity as well as the contextual effect of diffusion and biological reactions in a PFR was addressed. It represents the first mathematical model able to completely describe the bio-physics of the dry anaerobic conversion accounting for the reactor geometry, substrate characteristics, and microbial activities and interactions.
1.2. Quantification of uncertainty and sensitivity analysis
In many mathematical models of biosystems, global sensitivity analysis (GSA) plays a critical role by identifying key parameters that significantly impact model outputs. This analysis helps in simplifying complex models by focusing on the most influential variables, thereby making the models more manageable and interpretable. GSA also quantifies the impact of uncertainties in input parameters, providing insights into the robustness and reliability of model predictions. Additionally, GSA guides model validation and calibration by highlighting discrepancies between model outputs and experimental data, leading to more accurate and predictive models.
In mathematical models including several governing equations, the role of model parameters is crucial to capture specific real world dynamics [19]. To better fit the experimental data, adequate calibration procedures are required, and sensitivity analysis (SA) methods, e.g., GSA techniques, are considered powerful tools to obtain a meaningful screening of model parameters relevance [20]. Indeed, several works explored the input space along mono-dimensional corridors, e.g., local sensitivity analysis (LSA), with a consequent neglect of a significant part of the space of parameters. In their literature review, the authors noticed that 42% of the cited papers do not satisfy the requirements to properly explore the space of input parameters. It is clear that the introduction of high-quality practices and standard procedures is essential to the fields of SA and uncertainty quantification (UQ).
Despite many mathematical models focused on the AD process, only a few studies include GSA. The majority of available works focused on local procedures, thus neglecting more exhaustive global techniques [21]. Several examples of LSA procedures can be found in literature. Tartakovsky et al. [22] used relative sensitivity functions to reduce the number of parameters of an ADM1-based model of an up-flow anaerobic sludge blanket (UASB) reactor; Noykova and Gyllenberg [23] used a similar approach in the case of a mathematical model for an anaerobic process influenced by substrate inhibition; Bernard et al. [24] performed a LSA for an AD process model in an upflow fixed bed reactor (FBR) using sensitivity coefficients evaluated for the chosen output variable; and Vavilin et al. [25] adopted a similar approach for a distributed model of solid waste AD in batch and continuous reactors. They identified the key parameters by changing their baseline values by a certain percentage. Similarly, Lin and Wu [26] used the least-square (LS) method for the parameters of an AD model including the degradation of phenolic compounds. However, these works are based on analysis that overlook the effect of the possible interactions between parameters on model outputs.
On the other hand, only a few works focused on the GSA of AD models, and they were all related to wet AD in CSTR. Solon et al. [27] performed a GSA on the ADM1 implemented in the context of the benchmark simulation model no. 2 (BSM2) using the standardized regression coefficients method and the Morris' elementary effects screening method. They tested different reactor configurations and concluded that sensitivity results were more accurate when AD was performed at a low sludge retention time (SRT) and mesophilic conditions (around 35\si{\celsius}). In the open-loop version of the BSM2, a GSA study on the ADM1 using Monte Carlo (MC) tests and linear regression was proposed [28]. They focused on the reduction of computational time and on the optimal number of simulations to achieve an acceptable sensitivity analysis result. They highlighted the importance of the numerical solver optimization and stated that the optimal number of simulations to warrant an accurate GSA result depends on the number of investigated parameters, that should be multiplied by 50. Zonta et al. [29] used a Bayesian SA tool to evaluate the variance-based SA index in a ADM1-based model accounting for inhibitory phenomena. Carrera-Chapela et al. [30] developed a simplified mathematical model for the AD process to account for hydrogen sulphide generation and related gaseous emissions. They carried out a GSA using ANOVA decomposition and determined the higher sensitive parameters on the model output by changing the inlet flow and the substrate concentration in the reactor. Based on the sensitivity profiles, they selected the less influenced parameters using a collinearity analysis.
To the best of our knowledge, there are no examples of GSA related to PDE models describing dry AD in PFR. Indeed, the objective of the present work is to apply GSA and UQ techniques to perform an exhaustive GSA of the model presented in [18], as it is uniquely able to account for the effective mass variation occurring during the anaerobic biological conversion in PFR. The screening of model parameters represents a helpful reference for further calibration and validation works related to mathematical modeling of dry AD, in particular for real-scale PFR applications. Moreover, the adopted GSA technique allowed to highlight the most influencing aspects affecting model outputs and results. The present work is organized into six main sections. The complete model of dry anaerobic digestion in PFR is recalled in Section 2, and the model parameters and QoI selection for SA and UQ studies are introduced in Section 3. Moreover, that section outlines the test case and the databases used for simulations. Section 4 describes the Morris' screening and the surrogate-based SA, which are the adopted methods for UQ and SA. Section 5 synthesizes the main results of the study, and Section 6 contains remarks and future perspectives.
2.
Model of plug-flow reactor
The one-dimensional mathematical model proposed in [18] describes the evolution of soluble and particulate components in a PFR. The state variables represent the concentrations of these components and are functions of time t and space, where z represents the spatial coordinate, which is oriented along the reactor axis and directed from the inlet to the outlet section. For each state variable, a convection-diffusion-reaction equation describes the transport, along the reactor, and the related bio-chemical transformation. The convective and diffusive fluxes are characterized by the velocity v(z,t) and by a constant diffusion coefficient D along the z direction, respectively. The feeding waste substrate was composed by different components Xi with the same density ρ(z,t)=ρ. Specifically, it was constituted by water X1, particulate inert X2, biodegradable X3 and non-biodegradable X4 VS, microbial biomass X5, and additional dissolved compounds (i.e., soluble acetic acid S1 and soluble methane S2). The produced biogas was supposed to be constituted of methane gas G, and it was collected in the head-space of the reactor.
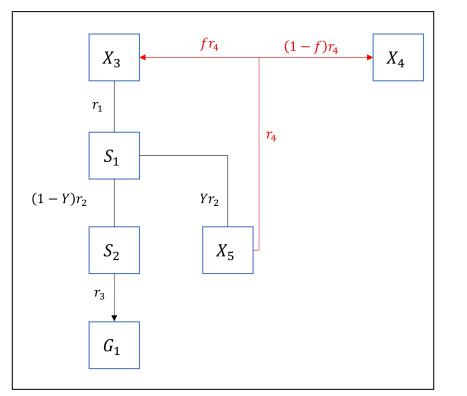
The kinetic scheme describing the bio-conversion processes occurring in dry AD is reported in Figure 1. The degradation of the biodegradable VS fraction X3 in soluble acetic acid S1 is regulated by the kinetic rate r1, which considers the disintegration process as the rate-limiting step for acetic acid generation; S1 is further consumed through the non-linear Monod-type kinetic rate r2 producing both soluble methane S2 and microbial biomass X5; the microbial biomass decay r4 leads to the production of further biodegradable X3 and non-biodegradable X4 VS; finally, soluble S2 and gaseous G methane is regulated by a gas-transfer law with the kinetic rate r3. Note that the only microbial biomass explicitly considered as a particulate component in the model is X5, representing methanogenic bacteria using acetate S1 for methane production.
The convection-diffusion-reaction equations related to each compound constitute the non-linear PDE systems (2.1) and (2.2):
where:
● X=(X1,...,X5);
● S=(S1,S2);
● FX,h(z,t,X,S,G), h=1,...,5, is the reaction term of the compound Xh;
● FS,l(z,t,X,S,G), l=1,2, is the reaction term of the dissolved compound Sl.
● FX,1(z,t,X,S,G)=FX,2(z,t,X,S,G)=0;
● FX,3(z,t,X,S,G)=fr4−r1;
● FX,4(z,t,X,S,G)=(1−f)r4;
● FX,5(z,t,X,S,G)=Yr2−r4;
● FS,1(z,t,X,S,G)=m(r1−r2);
● FS,2(z,t,X,S,G)=m(1−Y)r2−r3;
● D is the diffusion coefficient;
● r1=k1X3;
● r2=k2X5S1/(K1+S1);
● r3=k3(S2−RTKHG);
● r4=k4X5;
● m is the conversion factor of VS in COD [gCOD g−1VS];
● Y is the yield of biomass on substrate;
● f is the fraction of dead microbial biomass converted in biodegradable substrate;
● k1 is the rate of volatile solids X3 consumption, with the dimension of [T−1];
● k2 is the Monod maximum specific uptake rate for the acetic acid [T−1];
● K1 is the half-saturation constant [M L−3] for the acetic acid;
● k3 is the gas-liquid transfer coefficient [T−1];
● R is the gas law constant [L2 T−2 Θ−1];
● T is the operating temperature [Θ];
● KH is the Henry's law coefficient [L2 T−2];
● k4 is the first-order decay rate of the microbial biomass X6 [T−1].
The velocity displacement in the preferential direction of the reactor constitutes a further unknown of the problem, and the equation describing its variation is derived by assuming, for any time and space:
Equation (2.3) implies that the total mass of the waste (composed of water, inert, VS, and microbial biomass) is constant over time. This results in varying the convection velocity along the reactor. Its variation depends on the kinetics of the mixture's compounds. To keep the mass constant, the velocity variation must balance the VS consumption.
By summing Eq (2.1) on h=1,...,5 and considering Eq (2.3),
In addition, the mass balance on the head-space volume Vgas=AgasL leads to an additional differential equation describing the dynamics of the gaseous methane G(t) (Eq (2.5)):
where A is the constant cross-sectional area occupied by the treated substrate. Equation (2.5) accounts for the total gas-transfer rate in the PFR. The ratio between A and the volume of gas Vgas connects the gas-transfer kinetic rate to the volume of the treated substrate.
Finally, boundary and initial conditions are prescribed according to Eqs (2.6) to (2.13):
The value v0 in Eq (2.6) can be obtained by fixing the hydraulic retention time (HRT) of the components moving along the reactor:
In general, HRT refers to the mean residence time of a certain substrate within a biological reactor. This concept, usually used in CSTR, is equally applicable to PFR, wherein the HRT is intrinsically linked to the convective velocity of all compounds traversing the reactor. As a consequence, the HRT in a PFR can be defined as a function of the physical dimensions (L) and flow dynamics within the reactor system. In Eqs (2.7) and (2.8), Xh,IN and Sl,IN are the concentrations of water or particulate components, and dissolved compounds in the incoming flow rate, respectively.
It is important to emphasize that, unlike conventional ADM1-based models, the only microbial biomass described in the present model is methanogenic bacteria that utilize acetate as the organic source for methane production. This approximation can appear highly limiting, as it fails to account for the various fermentation pathways and associated byproducts accumulating in an AD reactor. Specifically, the inability to predict the dynamics of all classical anaerobic species restricts the determination of crucial compounds, such as volatile fatty acids, which are known to cause pH inhibition processes affecting system dynamics. Nevertheless, when limited information is available about microbial species in an AD bioreactor, the model can still successfully reproduce real-case experimental data. An illustrative example is provided in [18], where model parameters were adjusted to replicate lab-scale experimental data, with Tables 1 and 2 listing all the parameters used for data fitting and related boundary conditions.
3.
Uncertainty sources, quantities of interest, and databases
In the presented mathematical model, the state variables whose dynamics are described by the system of Eqs (2.1)–(2.3) and (2.5), coupled with boundary (2.6)–(2.10) and initial conditions (2.11)–(2.13), depend on a significant set of parameters. As recently reported [18], the knowledge about model responses to the variation of parameters is crucial for calibration and validation procedures based on real-world data. In the present investigation, seven different parameters have been selected as reported in Table 1. The first group includes i) the first-order kinetic constant for the conversion process of biodegradable VS in acetic acid k1, ii) the Monod maximum specific uptake rate for acetate k2, iii) the first-order decay rate for the microbial biomass k4, iv) the half-saturation constant K1, and v) the yield of biomass on substrate Y linked to bio-chemical processes. The second group is constituted by vi) the gas-transfer coefficient k3, and vii) the diffusion coefficient D, which was assumed constant for all the components. For the input parameters, uniform distributions were assumed in their physically meaningful literature range [11,16].
3.1. Quantity of interest
The PFR model describes the AD process evolving in time t∈(0,τ) and space x∈(0,L). It also accounts for the already mentioned key variable G(t), which is the biologically produced methane described as a function of time, Xh(z,t), h=1,...,5, and Sl(z,t), l=1,2, which are spatially distributed state variables. To gain a deeper understanding of how uncertain inputs influence the behavior of the PFR model, it is crucial to concentrate on a select set of scalar outputs.
A specific quantity of interest (QoI) has been considered in this study; denoting with y the time integral from t=0 and t=τ of the total methane volume accumulated in the head-space of the reactor at normal temperature and pressure conditions, it is possible to obtain the equation
where:
− G(t) is the gaseous methane concentration expressed in gCOD l−1gas;
− T0 and P0 represent the values of temperature and pressure at normal conditions;
− 64 is a stoichiometric coefficient expressing the grams of COD per mole of methane.
The selection of the QoI is strictly connected to the main objective AD process: to realize an efficient biological treatment for the waste organic compounds fed to the PFR by producing methane. Hence, the main goal of the present analysis is the reduction of the uncertainty related to this specific model output.
3.2. Description of test case
To achieve useful information and significant datasets for the SA, a test case was built for numerical simulations. The test case was based on experimental evidence and procedures aimed at maximizing the methane production from AD in a real PFR. Indeed, many experimental studies focused on the measured methane yield variation when different feeding or environmental conditions were applied to bioreactors, such as different organic loading rates (OLR) or solid contents, different pretreatment on the organic substrate, and different working temperature [31]. These parameters can strongly affect bioreactor design and performances, as well as uncertainty quantification results. In the present study, the more frequent parameters adopted for real-scale PFR were selected. More precisely, OLR is a measure of the organic compounds fed to the bio-reactor, evaluated as the ratio between the concentration of VS in the inlet flow and the HRT, which represents the average treatment time of fed components in the AD process. All these aspects were fundamental to the test case definition.
Table 2 reports the value of the defined geometric and operational parameters adopted in this study. These parameters include the PFR length L, the cross-sectional area A, the reactor head-space volume Vgas, the HRT, the inlet convective velocity v0, the OLR, and the temperature T. The conversion coefficient of VS in COD was fixed at m=1.5 gCOD g−1VS, while the fraction of dead microbial biomass converted in biodegradable substrate was set at f=0.2. The composition of the feeding substrate was chosen in accordance to lab-scale experiments and is reported in Table 3. The initial substrate consisted of a mixture of biodegradable, non-biodegradable, and microbial biomass solids, the latter constituting the microbial biomass required as the inoculum for the anaerobic process. Initial and boundary conditions used for simulations are summarized in Table 4. The simulation time was fixed to 120 d, as it is a common practice to suppose that the reactor stabilization is achieved when three HRT have been performed by the PFR in the same working conditions (HRT=40 d).
3.3. Experimental designs and databases
By using a design of experiments, the input space ZΘ∈Rd (hypercube) of uncertain parameters (d=7 is the number of parameters investigated) was discretized. In this way, N realizations of the parameters θi were defined. The PFR model was treated as a "black box" to generate N functional outputs y. The functional outputs were further analyzed, and useful statistics were obtained. The ensemble was compiled into a database DN:
where y(l)=F(θ(l)) is the integration of the PFR model F obtained by fixing the lth set of input parameters θ(l).
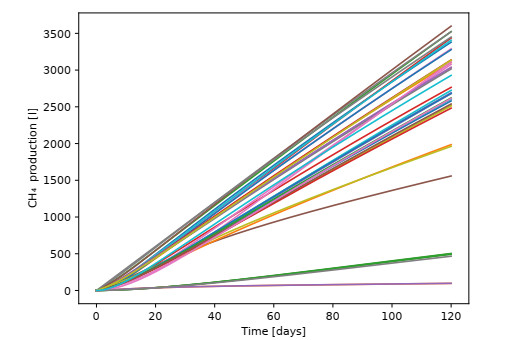
In this study, the parameter set used to carry out the screening θMorris consisted of NM=400 samples. It was generated using the random algorithm proposed in [32]. For the surrogate-based study, quasi-Monte Carlo sampling methods were selected to compile two different databases of size N=210. Halton's sampling was used to generate the first database, which was utilized as a training set. Faure's sampling was used to generate the second database, or validation database. Indeed, the latter was used to investigate the precision of various surrogate techniques. Table 5 summarizes the compiled databases. Remarkably, the considered PFR model features significant non-linearities for the QoI y when θ varies in ZΘ. Figure 2 portrays 40 representative PFR model output snapshots sampled from the Morris database.
4.
Surrogate-based SA
A two-phase SA was conducted on the PFR model: 1) the more rapid preliminary screening process using the elementary effect test (EET), proposed by Morris in [32]; and 2) the exhaustive surrogate-based GSA (4.2), aimed to achieve more accurate results. All GSA computations were pursued with the Python package OpenTURNS [33] (see www.openturns.org). Moreover, the PFR model was developed and integrated in the MATLAB platform. An original software, based on the finite difference upwind method, was used for numerical simulations. The method is conditionally stable and it was implemented according to [18].
4.1. Morris' scheme screening
According to Morris [32], an effective screening sensitivity measure for identifying a model's most significant parameters is the elementary effect (EE). Based on the computation of incremental ratios (the EEs), whose mean is used to measure global sensitivity, the method determines the overall significance of each input parameter on the QoI. The analysis was conducted by adopting randomized single-variable experiments, i.e., One-At-Time (OAT). These involve systematically changing one variable at a time while keeping others constant, with the order of changes randomized to reduce bias and better understand the impact of each variable on the outcome. Initially, the input parameters were initially assumed to be uniformly distributed within [0,1], and then their distributions were mapped from the unit hypercube to their corresponding distributions.
For a given value of θi∈θ, the elementary effect EEi can be expressed as:
where δ∈{1nl−1,1−1nl−1}, nl is the number of levels, θ∗=(θ∗1,…,θ∗d) is a random value in the hypercube Zθ such that the point (θ∗+eiδ) still maps to a point in Zθ for each i∈1,…,d, and ei is a zero valued vector except for its ith component ei=1. For each input parameter θi, the empirical distribution of elementary effects EEi was derived, with a random sampling of θ, s.t. EEi∼Fi, and its mean μi, and standard deviation σi were used as sensitivity measures. Moreover, the correction to the μi introduced in [34] was adopted. To avoid eliminating increments of different signs, their alternative measure employs the absolute value of the EEs instead of the mean μi. Their measure can be written as:
To avoid large databases of experiments and/or simulations, it is a common practice to sample r elementary effects from each Fi and constructing r trajectories of (d+1) points in the input parameter space, which provides d elementary effects. The total cost of the experimental set is thus r(d+1) model evaluations. Apart from the mean (and its eventual corrections), standard deviation of the EEs provides useful information. It may constitute a proxy of the level of interaction between the parameters and it allows to understand if a certain factor has non-linear effects on the QoI.
4.2. Surrogate modeling
An emulator (also known as metamodel, or surrogate model) of the PFR model described in Section 2 was built by adopting two distinct algorithms: i) the generalized polynomial chaos (gPC) expansion, and ii) the Gaussian process (GP) model. Indeed, gPC-expansion and GP model are robust and widely spread techniques, which are well described in literature. In particular, the mathematical setting is detailed in [35,36] and the previous work of Roy et al. [37]. Both approaches created a surrogate for the QoI y using a (finite) sum of basis functions:
The Halton's training database DN with N=210 (see Section 3.3) was used to determine the coefficients {γα}α∈A and the basis functions {Ψα}α∈A in Eq (4.3). The coefficients can be determined using different methods.
Three different algorithms were tested in the present work: two variations of the gPC-expansion and an application of the GP. While performing a polynomial chaos, the basis functions of Eq (4.3) are multivariate orthonormal polynomial functions (see e.g., [38]). The two implementations of gPC differ by the rule that determines the finite sum of polynomial basis in Eq (4.3). One variant of gPC, referred to as standard least squares, used a linear truncation scheme to guide the choice of the polynomial basis, while the second attempt, based on least angle regression, employs a sparse strategy for the truncation scheme [39]. Finally, the execution of the GP used the squared exponential (radial basis function) as the correlation kernel [40]. The algorithms to compute a gPC-expansion and GP surrogate are reported in [41] and adapted for the specific application. For the GP surrogate, the radial basis function (RBF) kernel was used according to [35].
5.
Results
5.1. Morris' screening
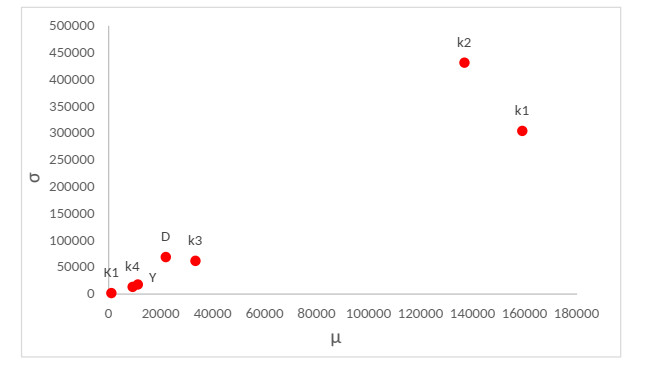
Figure 3 and Table 6 summarize the results of Morris' screening procedure applied to the QoI y. The parameters were classified in three groups in terms of relevance. First, the most relevant parameters for the specific QoI are the kinetic constant related to the conversion process of the biodegradable VS in acetic acid k1 and the Monod maximum uptake rate of acetic acid k2. These results were expected from a biological point of view, as k1 affects the kinetics of the disintegration process, which is one of the most limiting bio-process in AD, and determines the conversion rate of the substrate in intermediate products [42]. Moreover, k2 directly affects the methane production rate and is recognized as one of the most influencing parameter in AD modeling [43]. However, the results suggest that it could be appropriate to focus future research on the disintegration kinetics modeling occurring in this case, and take into account the particle size distribution of biodegradable components as in Panaro et al. [44].
A second group made of physical parameters includes k3, and D, which are sufficiently relevant in determining the QoI value. The gas-transfer coefficient k3 regulates the amount of soluble methane released in the gas-phase from the reactor environment. Of course, its low value leads to a small amount of soluble methane transferred in the gas-phase. When the value of k3 exceeds a specific threshold, all the methane is released in the gas-phase and the value of the gas-transfer coefficient becomes negligible with respect to the QoI. It is clearly important to notice that this observation is due to the atmospheric pressure level considered for the PFR. Indeed, pressure and consequent gas-transfer conditions are critical factors influencing the overall efficiency of the biogas generation process. Elevated pressures can enhance the solubility of gases, thereby potentially increasing the contact between microorganisms and substrates, which can lead to higher methane yields. However, excessively high pressures may also inhibit microbial activity and disrupt the delicate balance of microbial communities, ultimately reducing methane production [12]. Therefore, optimizing pressure conditions is essential for maximizing methane output while maintaining the stability and performance of PFR. Regarding the diffusion coefficient, it was unexpected for D to be so less important than biological parameters for the specific QoI, as the PFR model reproduces convective-diffusive-reactive phenomena. This observation highlighted the crucial role of kinetic coefficients when modeling the effect of diffusion on the process development. Indeed, it has been demonstrated that diffusion strongly affects the hydrolysis of complex material in dry AD processes [45,46]. The one-dimensional structure of the PFR model leads to neglecting the influence of different values of the diffusion coefficient along other directions, which can affect the determination of the QoI in 2D and 3D models. In these cases, a more relevant relationship between the diffusion and the rate of conversion of substrates in methane could emerge, as different diffusion processes in the other directions may influence acids and by-products distribution in the PFR [47]. Moreover, a different formulation of kinetics parameters including the effect of the diffusion coefficient in such particular environment could be proposed for future works.
The last qualitative information obtained through the Morris' screening was that the group of parameters consisting in the half-saturation constant K1, the microbial biomass decay rate k4, and the yield of biomass on substrate Y present very small sensitivities. The roles of the half-saturation constant and the yield of biomass on substrate are not emerging in the qualitative preliminary screening. Indeed, when K1 assumes very small values, the consumption kinetic of the acetic acid becomes linear, which means that the methane production process is more efficient. The yield of biomass on substrate Y determines the amount of acetic acid that becomes methane and, even if it varies among 0 and 1, it is expected to influence methane production. These aspects required a deeper investigation with the quantitative variance based GSA.
5.2. Estimation of the error
Metamodels of the PFR model for UQ and SA must be evaluated for their ability to reproduce model variability. Indeed, it is possible to compute the a posteriori approximation error resulting from the surrogate model by
where y(l) is the lth element of the training set, ˆy(l) is the corresponding prediction (gPC or GP), and N=210 (see Table 5). It is noteworthy that this estimator of the metamodel error is prone to issues of overfitting, which could result in a severe underestimation of the mean square error [39]. Furthermore, since the GP model interpolates the training set points, it is guaranteed to achieve ϵemp=0 when noise-free kernels are used. For any surrogate model, algorithm, and configuration that were tested, the ratio of the empirical error, ϵemp, to the empirical mean of the QoI, ¯y, calculated over the Halton dataset, remains consistently below 4.0×10−3.
To avoid the aforementioned limitations, the surrogates were validated by employing the Q2 predictive coefficient, a cross-validation error metric that utilizes an independent dataset derived from Faure's low discrepancy sequence, as reported in Table 5. In Eq (5.2), this coefficient is described as
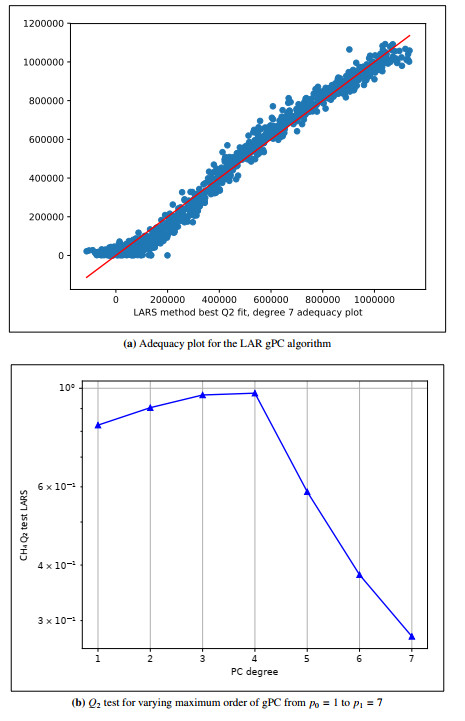
where ¯y denotes the empirical mean calculated from Faure's validation set (Nfaure=210). The Q2 predictor coefficient (with 1 as the target value) provides a normalized estimation of the generalization error, which quantifies the surrogate model's error when evaluating points that are not included in Halton's training set, thereby offering a measure of the model's predictive performance on unseen data [48]. The closer Q2 approaches 1, the better the surrogate replicates the PFR dynamical system. By applying the Q2 indicator, it is possible to rank surrogate models based on their ability to reproduce the PFR model dynamics. When the g-PC technique is applied, the surrogate model characterized by a total polynomial order P demonstrates superior accuracy, yielding the most precise results compared to other adopted models with different polynomial orders. In this study, the polynomial order P ranged from 1 to 7.
Figure 4(a) presents the adequacy plots, which illustrate the performance of the metamodel by comparing it with the actual forward model F runs, using points from the design of experiment (DoE) to assess how well the metamodel approximates the forward model. By plotting the Q2 values in Figure 4(b), the robustness of the LAR-gPC algorithm is illustrated. When P>4, the dimensionality of the underlying statistical model hinders the convergence. As a final note, Table 7 provides a comprehensive overview of the error estimators associated with the various surrogate techniques that have been applied, detailing the measures used to evaluate the accuracy and reliability of each technique.
5.3. Quantitative GSA
Variance decomposition-based analysis is usually performed using Sobol' indices [49,50]. These allow to quantify the weight of the uncertainty of a single input parameter, considered as an independent variable with respect to the other parameters, based on the variance of the QoI y. By indicating the variance of the output random variable y and the variance linked to the variability of the ith parameter as V(y) and Vi(y), respectively, the first-order Sobol' index Si, referred to the ith parameter of Θ, is defined as:
Indeed, Si values ranges between 0 and 1. To account for parameter interactions while defining the measure of the ith input parameter contribution on the output variance, the total Sobol' index STi is defined as:
Consequently, STi≥Si by definition. By observing the difference between the first-order and the total indices, it is possible to detect the presence of these interactions. In the case of the GP-surrogate approach, the Sobol' indices were obtained through a stochastic process, with Martinez's formulation employed as a stable and reliable estimator to ensure precision and robustness in the calculation of these indices [51]. The first-order and total Sobol' indices are derived directly from the gPC coefficients for the LAR gPC expansion. As an example, the first-order Sobol index is expressed as:
where σy is the empirical output sample STD (see [35,36]).
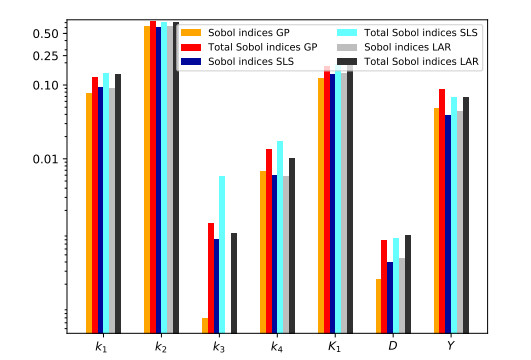
The first-order and total Sobol' indices obtained by the three algorithms are shown in Figure 5. Based on the Q2 error, the GP surrogate was the best-performing algorithm, so the SA and UQ results related to this algorithm were discussed. A comparison of first-order and total Sobol' indices reveals interactions between factors. It is noteworthy that the range of parameters utilized in the investigation can significantly influence the analysis outcomes. To mitigate errors, the parameters were selected based on a comprehensive review of various anaerobic digestion models that examine the bioconversion of different substrates under anaerobic conditions [52,53,54]. The specific ranges of these parameters are detailed in Table 6. Considering the specific QoI (methane production), Sobol' indices analysis confirmed the Morris screening results for k2. Both the Sobol' index and the total Sobol' index of the Monod maximum uptake rate k2 were higher than all the other parameters. As expected, the kinetic constant k1 maintained its relevance, while the half-saturation constant K1 and the yield Y gained positions on k3, k4, and D. As already remarked, the half-saturation constant K1 and the yield Y directly affect the acetic acid maximum consumption rate and the consumed acetic acid, respectively. As a result of the Morris screening, the QoI was not affected by the variation in these parameters. However, quantitative SA highlighted their effects. Finally, the small sensitivities of the microbial decay rate kinetic constant k4, and physical parameters k3 and D were confirmed by the quantitative SA with Sobol' indices.
5.4. Uncertainty quantification
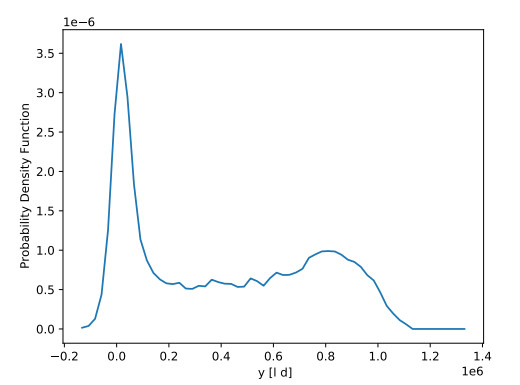
Based on the Q2 error estimator, the analysis was restricted to the surrogate model that provides the highest level of accuracy, such as the Gaussian process metamodel. To achieve a comprehensive statistical characterization of the QoI, including its statistical moments and PDF, a Monte Carlo random sampling method was employed to sample the uncertain input space ZΘ with a sample size of 10,000 members, followed by the evaluation of the GP surrogate model to analyze the resulting data. The mean, standard deviation, skewness, and kurtosis of the QoI, computed from such Monte Carlo samples are given in Table 8.
Figure 6 presents the QoI PDF related to the CH4 net production. Relevant information can be inferred from both the shape of the distribution and its higher-order moments, as these elements collectively provide insight into the underlying characteristics and behavior of the data. Depending on the model parameter values and the initial conditions, the two different peaks revealed a high probability of having a small amount of produced methane (corresponding to the failure of the system) and a medium-high probability of reaching high methane production. Indeed, when the input parameter vector is characterized by unfavorable values, with slow conversion of the biodegradable COD in acetic acid or slow conversion of the acetic acid, it is very difficult to reach a valuable methane production. On the other hand, when the vector of parameters is characterized by a favorable combination of input factors with respect to the reactor working conditions, there is a good chance to achieve relevant methane productions. The PDF drops to zero, after the value of approximately 1×106[lCH4⋅d]. This result highlights that it is impossible to produce more methane in the corresponding period of time with the used values of HRT, v0, and OLR. This revealed the significant limitation due to the operational conditions influencing the performance of the PFR.
6.
Conclusions
Using non-intrusive techniques, UQ and GSA techniques were adopted on a novel dry AD model in a PFR. The model depends on a conspicuous set of input parameters and, up to now, had lacked rigorous studies serving as bases for the application of effective calibration an validation procedures. GSA application leads to identifying which parameters most significantly influence model outputs, thereby guiding targeted adjustments and ensuring that model predictions are robust and reliable. On the other hand, UQ addresses the inherent uncertainties in model inputs and parameters, providing a comprehensive understanding of the range and likelihood of possible outcomes, which is essential for accurate model validation and for making informed decisions in any biotechnological application. The use of these techniques was aimed at predicting the overall effect of uncertainty of the input parameters on CH4 production, which represents the value-added product achievable from this bio-tecnology. The identification of the most sensitive parameters upon which the dry AD process depends, and the identification of the uncertainty associated with their variation within reasonable ranges, represent an initial step in reducing the process-related uncertainty.
The Morris screening test and the quantitative sensitivity analysis with Sobol' indices showed, with a good accordance, that the net methane concentration is mostly sensitive to the values of the conversion parameter related to the particulate biodegradable volatile solids in acetic acid k1, and to the kinetic parameter describing the acetic acid uptake k2. The relevance of the half-saturation constant K1 and the yield of biomass on substrate Y were highlighted by the quantitative sensitivity analysis through the Sobol' indices. The selected QoI was less sensitive to other biochemical and physical parameters. According to the presented results, it is possible to claim that in 1-D PFR models, the role of the diffusion coefficient is negligible with respect to more relevant kinetic parameters. It is important to emphasize that the primary objective of the present study was to investigate the bioconversion of acetic acid into methane in a PFR. Consequently, microbial species responsible for acetic acid accumulation, along with other common metabolic species such as sulfate-reducing bacteria, have been excluded from consideration. A natural progression of this research would involve developing an extended mathematical model that includes a broader range of microbial species and associated parameters. An analytical study of this extended model, combined with the application of SA and UQ techniques, could provide valuable insights into the most influential metabolic processes under these more comprehensive conditions.
Finally, the present analysis revealed the crucial role of UQ for adequate calibration procedures and further validation of such complex mathematical models. These routines, ranging from simple screening analysis to more complex and computationally demanding variance-based metamodel analysis, constitute a robust asset for modelers, designers, and managers of anaerobic reactors. For the performance evaluation of a dry AD process, the group of more sensitive parameters are those connected to the kinetic description of the biological process, leading to the contextual waste substrate degradation and methane production in anaerobic reactors.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work has been partially developed in the context of D.D. n. 1377 on June 5, 2017, additional PhD fellowships for 2017/2018 academic year, course XXXIII within the framework of the "Programma Operativo Nazionale Ricerca e Innovazione (PON RI 2014/2020) Action I.1 - Innovative PhDs with industrial characterization".
VL acknowledges the project "FBIOMA-Fermentative BIOhydrogen production MAthematical modeling" (CUP: E63C22004130001).
MRM acknowledges support from the National Research Center for Agricultural Technologies - Agritech, funded by the European Union NextGenerationEU (PIANO NAZIONALE DI RIPRESA E RESILIENZA PNRR, Missione 4 Componente 2 Investimento 1.4 - D.D. 1032 17/06/2022, Project code CN00000022) The present work has been performed under the auspices of the GNFM of INdAM.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: