1. Introduction
In the presence of the growing global demand for energy, renewable energy provides the most promising solutions. Amongst all other renewable energy resources, solar energy is the most plentiful and permanent till date. There are two types of line-focusing collector systems in CSP plants: Parabolic troughs collector (PTC) and Linear Fresnel collector (LFC). PTC solar thermal power plants use thermal oils as heat transfer fluids (HTFs). This technology has witnessed several improvements over the last several decades. Using water instead of thermal oil as HTF results in higher overall system efficiency and lower costs. Under specified operating conditions, it is found that the levelized electricity costs (LEC) of the DGS is 10% lower than indirect steam generation [1].
Direct steam generation (DSG) parabolic trough collector (PTC) solar thermal power plants can work in three different basic operating modes, namely: once-through, recirculation and injection modes. In Once-through mode; the feed-water is preheated, evaporated, and converted into superheated steam as it circulates from the inlet to the outlet of the parabolic trough collector (PTC) field. A water injector is placed in front of the last parabolic trough collector (PTC) to control the outlet steam temperature. This mode is the simplest and its main issue is the controllability of the outlet superheated steam. In Injection mode, water is injected at several points along the parabolic trough collector (PTC) row. The main drawback is its complexity and high operating costs [7]. In Recirculation mode, a water-steam separator is placed at the end of the evaporation section of the parabolic trough collector (PTC) row. In this separator, excess water is recirculated to the field inlet and mixed with pre-heated water. This guarantees good wetting of the absorber tube. In the separator, the remaining steam is used to feed the superheating section. This operating scheme is highly controllable but also increases parasitic load due to the water-steam separator [8].
Direct steam generation (DSG) technology faces real technical challenges due to phase changes that affect the heat transfer fluid (HTF). The water experiences phase changes while it circulates through linear focusing solar field. The existence of a two-phase flow involves uncertainties regarding stability, controllability of the process, and the gradient temperatures in the pipes. Several theoretical models have been applied to describe the behaviour of a DSG process [9,10,11,12]. It is found that estimating pressure drop based on the correlations of Friedel [13] and Chisholm [14] are suitable for designing DSG solar fields and implementing simulation tools. Several software tools have been used to implement simulation models for DSG in parabolic-troughs [15,16,17,18,19]. Regardless of the significant number of models found in the literature for DSG in parabolic-trough collectors, there is a lack of an efficient model that accurately describes phase changes during the process and allows rigorous optimizations.
Typical two-phase flow patterns in horizontal pipes are: bubbly, interment, stratified and annular [2]. In bubbly, intermittent and annular flows, the pipe wall is well-wetted; therefore, a high temperature gradient between the top and the bottom of the pipe is avoided when the pipe is heated from one side. On the other hand, when pipe is heated from one side for stratified two phase flow, there is a steep temperature gradient between the top and bottom which causes thermal stress and bending that may break the pipe. It has been reported by many researches that non uniform wetting can be significantly reduced by titling the absorber tubes [20,21].
Water is considered perfectly an ideal heat transfer fluid. The using of steam as heat transfer fluid allows operating at high temperature and pressure as opposed to thermo-oil. As a result of that, the efficiency of the steam cycle increases. The objective of this study is to develop more realistic approach that accurately predicts the performance of DSG in evacuated absorber tube (receiver). Furthermore, determine the main types of the flow patterns in the saturated region, and determine the heat transfer coefficient for each type of flow patterns.
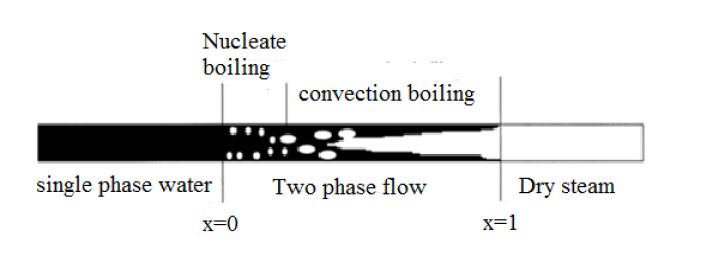
The single-phase flows are divided into laminar and turbulent flows, equally as important as also the two-phase flows are divided into flow patterns Figure 1 illustrates the flow patterns in the two-phase region in a horizontal pipe during evaporation. There are four main flow patterns in the two-phase region in horizontal pipes: stratified, annular, bubbly, and intermittent. The flow pattern depends on the superficial velocities of liquid and vapor in the mixture of the two-phase flow, mass flow rate (m), heat flux (q), pressure (P), and channel geometry. There is no direct method to determine the pattern of two phase flow. Furthermore, there is no universal agreement among researchers on all possible flow patterns.
The most common patterns of two-phase flow in horizontal pipes can be summerized as follows;
· Bubbly flow pattern: In this flow pattern, the shear forces are dominant and this occurs when the bubbles of vapor appear in the fluid, the bubbles tend to distribute homogeneously. Commonly, the bubbly flow pattern is related with high flow rates in horizontal pipes.
· Plug flow pattern: In this flow pattern if the bubbles of vapor collide at this moment the plugs (larger bubbles) can appear. The plug flow pattern is defined by plugs (large bubbles) flowing in the upper half of the pipe.
· Stratified flow pattern: In this flow pattern at low velocities, the liquid phase and vapor phase are separated. Due to gravity the liquid is at bottom and the vapor is at the top of the horizontal pipe.
· Stratified-wavy flow pattern: In this flow pattern if the velocity of the vapor increases with respect to the velocity of fluid, an example of the stratified-wavy flow pattern in the evaporation process, waves can appear in the interface between both phases.
· Intermittent flow pattern: In this flow pattern if the velocity of the vapor increases even more, the size of the waves increase and become larger and wet the top of the horizontal pipe. The Intermittent flow pattern can be seen as interment waves, if a cross-sectional area of the pipe is analyzed.
· Slug flow pattern: In this flow pattern the slugs of liquid are formed and this happens when the waves contact the pipe from the upper side. A liquid film is formed when the vapor at high velocity pushes the slug through the pipe.
· Annular flow pattern: In this flow pattern at higher velocities, the liquid film that created by slugs covers the pipe from the inside, where the vapor flows in the center of the pipe. The thickness of the liquid film in the upper part of the pipe is smaller than the thickness of the liquid film in the lower part of the pipe due to gravity. If the waves are still present, the droplets of liquid can appear in the gas core. The annular flow pattern is the predominant flow regime in evaporators because the convective heat transfer coefficients are the highest in the annular flow pattern.
· Mist flow pattern: This flow pattern is also called droplet flow, because droplets exist in the superheated vapor flow, even after the liquid film has dried out.
2. Theory
In this study, a subcooled water is fed into single evacuated pipe (absorber tube) with known mass flow rate and temperature. The absorber tube made of steel is evacuated (covered with glass) to reduce the heat losses to ambient (surroundings). The heat transfer modes (conduction, convection and radiation) and their equations are used to predict thermal performance of the system. End effects are negligible since the length of steel pipe is larger than the length of its diameter. The view factor between steel pipe and glass pipe is assumed to equal unity. The incident solar radiation on absorber tube is considered uniform along the length of glass-covered tube.
The thermodynamic properties of water-steam are calculated and evaluated based on International Association for the Properties of Water and Steam IAPWS Standard. IAPWS has been widely accepted and used by researchers and industrial sectors [3]. The equations are programmed and integrated into the developed Matlab code.
Subcooled water enters the absorber tube and its temperature increases along the length of the absorber tube. When the temperature of the water equals to the saturation temperature, nucleate boiling begins. Adding more heat increases the quality which leads to changing in the patterns of flow to convective boiling or forced convective vaporization as shown in Figure 2. Further increase of quality leads to higher values of heat transfer coefficient [4]. As water mixture flows downstream, dry out occurs. At this point, the heat transfer coefficient decreases because the decrease of thermal conductivity of steam.
The heat transfer coefficient hsingle phase (W/m2 k) for the single phase either liquid phase or steam phase inside the absorber tube is given as [5]:
|
$\text{h}single phase\text{=0}\text{.0235 R}{{\text{e}}^{\text{0}\text{.8}}}\text{ P}{{\text{r}}^{\text{0}\text{.48}}}\text{ }\left( \frac{{{\text{K}}_{\text{W}}}}{\text{D}} \right)$
|
(1)
|
where Re is Reynolds number, Pr is Prantdl number, Kw is the thermal conductivity, and D is the inner diameter. The heat transfer coefficient depends on the type of the flow in two phase region. Taitel and Dukler's map is used in this study for determining the flow patterns [6]. The total pressure drop ΔPtotal in the absorber tube depends on the momentum losses, the pressure head losses and the friction losses:
|
$\Delta \text{Ptotal=}\Delta {{\text{P}}_{\text{fric}}}\text{+}\Delta {{\text{P}}_{\text{mom}}}\text{+}{{\text{P}}_{\text{static}}}$
|
(2)
|
Neglecting momentum changes and the elevation changes, Equation (2) reduces to
|
$\Delta \text{Ptotal=}\Delta {{\text{P}}_{\text{fric}}}$
|
(3)
|
It is worth mention that Equation (3) is valid for both two phase and single phase flow. The pressure drop in the two phase region is predicted using the separated model flow. These models assume that the phase velocity of liquid phase and vapor phase is constant in the cross-section that occupied by the phase. Friedel correlation is used to predict the pressure drop in the two phase region [7].
The pressure drop for two phase flow is given as [7]:
|
$\Delta {{\text{P}}_{\text{fric}}}\text{=}\Delta {{\text{P}}_{\text{L}}}.{{\varphi }^{2}}$
|
(4)
|
where ΔPL is the pressure drop for liquid phase and calculated from:
|
$\Delta {{\text{P}}_{\text{L}}}\text{=4}{{\text{f}}_{\text{L}}}\text{ }\left( \frac{\text{L}}{{{\text{D}}_{\text{i}}}}\text{ } \right){{\text{G}}^{\text{2}}}\text{ }\left( \frac{\text{1}}{\text{2L}} \right)$
|
(5)
|
where Di is the inner diameter and G is the mass velocity and equals the mass flow rate per unit area. The friction factor for liquid (fL) and the Reynold number for liquid (ReL) are calculated from:
|
${{\text{f}}_{\text{L}}}\text{=}\frac{\text{0}\text{.079}}{{{\text{R}}_{\text{e}}}^{\text{0}\text{.25}}}\text{ }$
|
(6)
|
|
$\text{R}{{\text{e}}_{\text{L}}}\text{=}\frac{{{\rho }_{\text{L}}}\text{ }{{\text{V}}_{\text{L}}}\text{ D}}{{{\mu }_{L}}}\text{ }$
|
(7)
|
where μL is the liquid dynamic viscosity and Փ is the two phase flow multiplier given as:
|
${{\varphi }^{\text{2}}}\text{ =E+}\frac{\text{3}\text{.24FH}}{\text{(F}{{\text{r}}_{\text{H}}}^{\text{0}\text{.045 }}\text{ W}{{\text{e}}_{^{\text{L}}}}^{\text{0}\text{.035}}\text{ }}$
|
(8)
|
The Froude number FrH equals:
|
$\text{F}{{\text{r}}_{\text{H}}}\text{=}\frac{{{\text{G}}^{\text{2}}}}{\text{(g }{{\text{d}}_{\text{i}}}\text{ }\rho \text{ }{{\text{H}}^{\text{2}}}\text{ )}}$
|
(9)
|
The factors E, F and H are calculated as follows:
|
$\text{E=(1-x}{{\text{)}}^{\text{2}}}\text{+}{{\text{x}}^{\text{2}}}\text{ }\left( \frac{{{\rho }_{\text{L}}}\text{ }{{\text{f}}_{\text{G}}}}{{{\rho }_{\text{G}}}\text{ }{{\text{f}}_{\text{L}}}} \right)$
|
(10)
|
|
$\text{F=}{{\text{x}}^{\text{0}\text{.78}}}\text{ (1-x}{{\text{)}}^{\text{0}\text{.224}}}$
|
(11)
|
|
$\text{H=}{{\left( \frac{{{\rho }_{\text{L}}}}{{{\rho }_{\text{G}}}}\text{ } \right)}^{\text{0}\text{.91}}}\text{ }{{\left( \frac{{{\mu }_{G}}}{{{\mu }_{\text{L}}}}\text{ } \right)}^{\text{0}\text{.19}}}{{\left( \text{1-}\frac{{{\mu }_{G}}}{{{\mu }_{\text{L}}}}\text{ } \right)}^{\text{0}\text{.7}}}$
|
(12)
|
The liquid weber number WeL is given as:
|
$\text{W}{{\text{e}}_{\text{L}}}\text{=}\left( \frac{{{\text{G}}^{\text{2}}}\text{ }{{\text{d}}_{\text{i}}}}{\sigma \text{ }\rho \text{ H}} \right)$
|
(13)
|
The homogeneous density ρH as function of vapor quality (x) is:
|
${{\rho }_{\text{H}}}\text{=}\left( \frac{\text{x}}{{{\rho }_{\text{G}}}}\text{ +}\frac{\text{1-x}}{{{\rho }_{\text{L}}}}\text{ } \right)$
|
(14)
|
3. Numerical Techniques
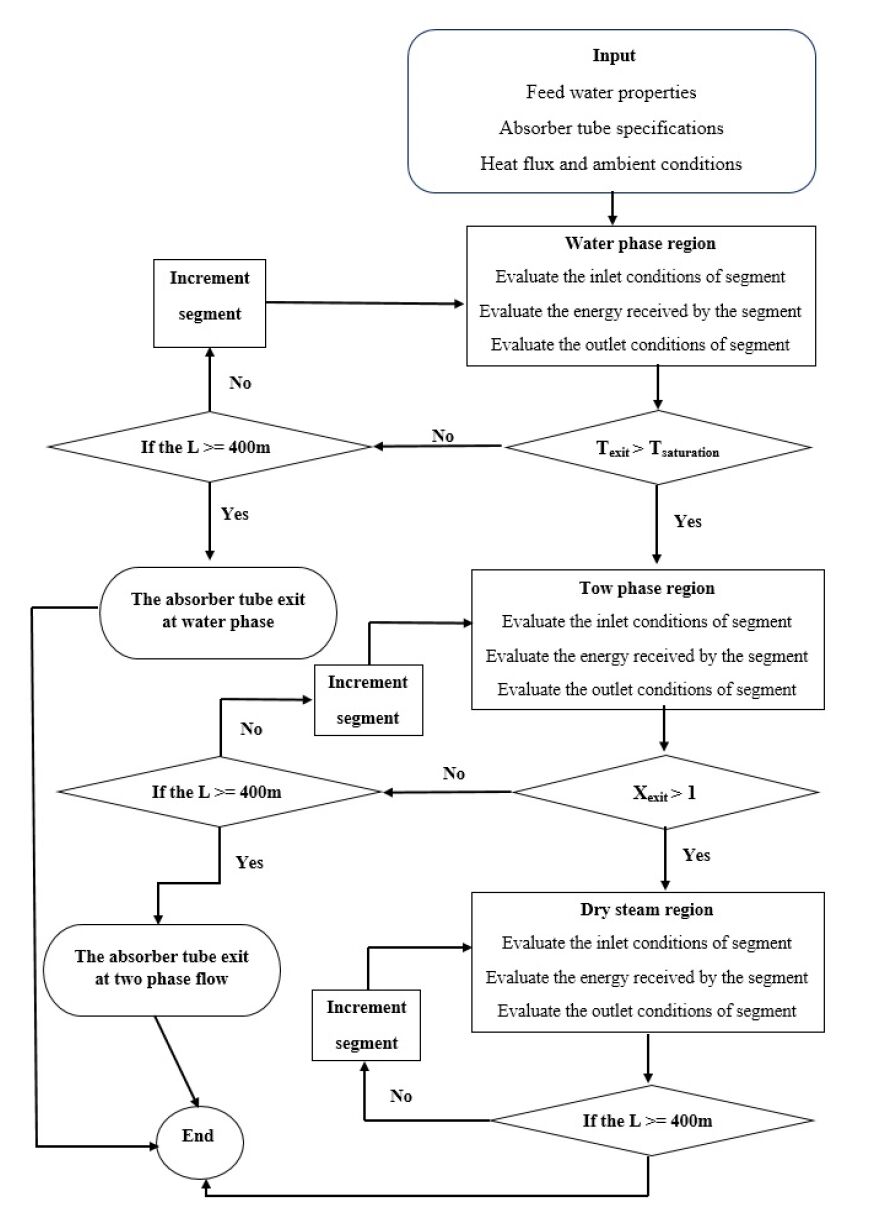
Finite element discretization is used to analyze a system of single pipe covered by glass material in which the subcooled undergoes heating and evaporation process. The absorber tube is divided into n segments. Energy and momentum are applied on each element to calculate the outlet conditions based on the inlet conditions for each segment. For known properties at inlet, and assuming the pressure at the exit of the segment (I), the average pressure between the inlet and outlet of the segment (I) is:
|
$\text{P(I)= }\frac{{{\text{P}}_{\text{i}}}\text{(I)+}{{\text{P}}_{\text{i+1}}}\text{(I)}}{\text{2}}\text{ }$
|
(15)
|
The enthalpy at the exit of the segment (I) is calculated as:
|
${{\text{H}}_{\text{i+1}}}\text{(I)=}\frac{\text{Q}(\text{I})\text{+}(\dot{m}\times \text{ }{{\text{H}}_{\text{i}}}\text{(I) )}}{{\dot{m}}}$
|
(16)
|
The average enthalpy between the inlet and outlet of the segment (I) is calculated by:
|
$\text{H(I)= }\frac{{{\text{H}}_{\text{i}}}\text{(I)+}{{\text{H}}_{\text{i+1}}}\text{(I) }}{\text{2}}\text{ }$
|
(17)
|
The velocity of vapor phase VG(I) and liquid phase VL(I) are calculated as:
|
${{\text{V}}_{\text{L}}}\text{(I)= }\frac{\text{X(I) }\times \dot{m}}{\text{A }\times \text{ }{{\rho }_{\text{L}}}\text{(I)}}\text{ }$
|
(18)
|
|
${{\text{V}}_{\text{G}}}\text{(I)=}\frac{\text{ }[\text{ 1-X(I) }]\text{ }\times \dot{m}}{\text{A }\times \text{ }{{\rho }_{\text{G}}}\text{(I)}}$
|
(19)
|
where A is the cross-section area of the steel pipe. Knowing VG(I), VL(I), and the gas and liquid properties allows calculating new value of Pi+1(I) based on pressure drop. The calculation of pressure drop is given in appendix A. An iteration scheme is run to until the convergence is reached for the outlet pressure of the segment Pi+1(I). This previous procedure is carried out for the subcooled region, superheated region and liquid-vapor region. In single phase region the temperature of the segment T(I) is computed as follows; initially, T(I) is assumed, then the heat rate absorbed by the steel pipe Q(I) is evaluated, the enthalpy at the exit Hi+1(I) of the segment (I) and the average enthalpy H(I) of the segment (I) are calculated by Equation (23) and (24). Knowing the average pressure and the enthalpy, the temperature at segment I can be determined by run iteration until convergence. An external iteration is carried out to that satisfy the exit pressure at the outlet of the absorber tube.
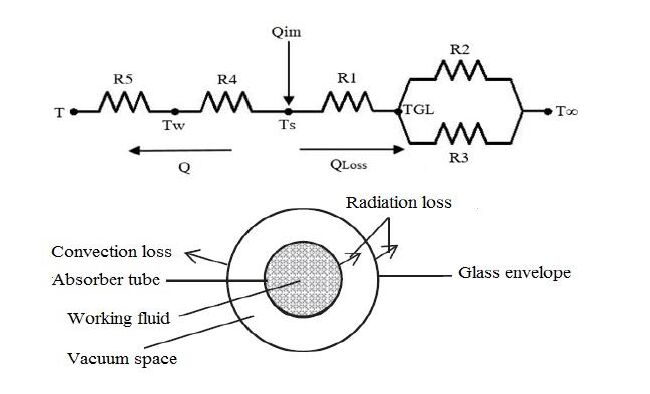
Figure 3 show the electrical analog used to calculate the absorbed heat rate Q(I). As shown in Figure 6, the heat transfer by radiation is absorbed by the steel pipe and then is transferred to the liquid via conduction and convection heat transfer. Appendix B summarized the equation for evaluating all thermal resistances.
The amount of the heat absorbed Q(I) depends on the radiant heat flux Qim and water temperature T(I). Applying heat balance for segment (I):
|
${{\text{Q}}_{\text{im}}}\text{=Q(I)+}{{\text{Q}}_{\text{Loss}}}$
|
(20)
|
|
${{\text{Q}}_{\text{im}}}\text{=}\left( \frac{{{\text{T}}_{\text{s}}}\text{-T}\infty }{{{\text{R}}_{\text{123}}}}\text{ } \right)\text{+}\left( \frac{{{\text{T}}_{\text{s}}}\text{-T}}{{{\text{R}}_{\text{45}}}}\text{ } \right)$
|
(21)
|
where Ts is the surface temperature of steel pipe, R45 is the equivalent resistance of R4 and R5, R123 is the equivalent resistance of R1, R2 and R3, T∞ is the ambient temperature and T is the temperature of water inside the steel pipe. Equation (21) can be used to determine the surface temperature. Water temperature T is computed from the iteration process of pressure drop. The total heat transferred to the water can be evaluated after determining Ts as:
|
$\text{Q=}{{\text{Q}}_{\text{im}}}\text{-}\left( \frac{{{\text{T}}_{\text{s}}}\text{-T}}{{{\text{R}}_{\text{123}}}\text{ }} \right)$
|
(22)
|
Figure 4 shows the flowchart of the numerical algorithm.
4. Numerical solution validation
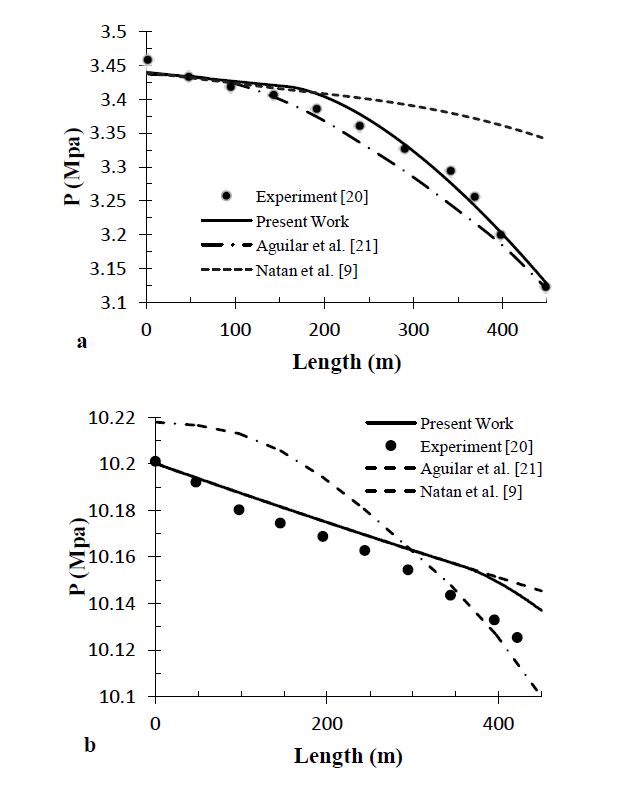
The present numerical solution is validated against experimental data of DISS system located at the Plataforma Solar de Almería (Tabernas, Spain) [20]. Table 1 shows the experimental data that were used for the validation.
Table 1. DISS operating conditions.
| Description
|
Magnitude |
| Day
|
Win (kg/s) |
Tin ( °C) |
Pin (Mpa) |
Q |
| 0.615 |
249.3 |
10.2 |
887.26 |
14/05/2003
|
| 0.581 |
198.1 |
3.47 |
865.02 |
21/05/2003
|
Figure 5 shows a comparison between the experimental and other authors models and present numerical pressure profile for 10 and 3 MPa. As can be seen in Figure 5, our present solution matches well with experimental data. Furthermore, the present numerical solution outperforms results of Natan et al. [9] and Aguilar et al. [21].
5. Results and Discussion
Simulation code is developed to investigate thermal properties of water along the pipe. The length of the absorber and the radiant heat flux impinging along the pipe are kept fixed for entire simulations to 450 m, 1000 W/m respectively. The inlet temperature is 25 °C, and the inclinations angle (β) is 10° are kept fixed as well. The mass flow rate of the water at the inlet equals to 0.12 kg/s, the pressure at the outlet equals to 3 MPa. Table 2 represents the specifications of the absorber tube used in this study.
Table 2. Absorber tube specifications.
| Absorber tube length |
450 m
|
| Absorber tube outer diameter |
0.058 m
|
| Absorber tube inner diameter |
0.025 m
|
| Glass pipe outer diameter |
0.058 m
|
| Glass pipe inner diameter |
0.0564 m
|
| The thickness of glass pipe |
0.0016 m
|
| The emissivity of glass pipe |
0.9
|
| Steel pipe outer diameter |
0.028 m
|
| Steel pipe inner diameter |
0.025 m
|
| The thickness of steel pipe |
0.003 m
|
| The emissivity of steel pipe |
0.87
|
| Steel pipe thermal conductivity of steel pipe steel pipe steel pipe |
18 W/m K
|
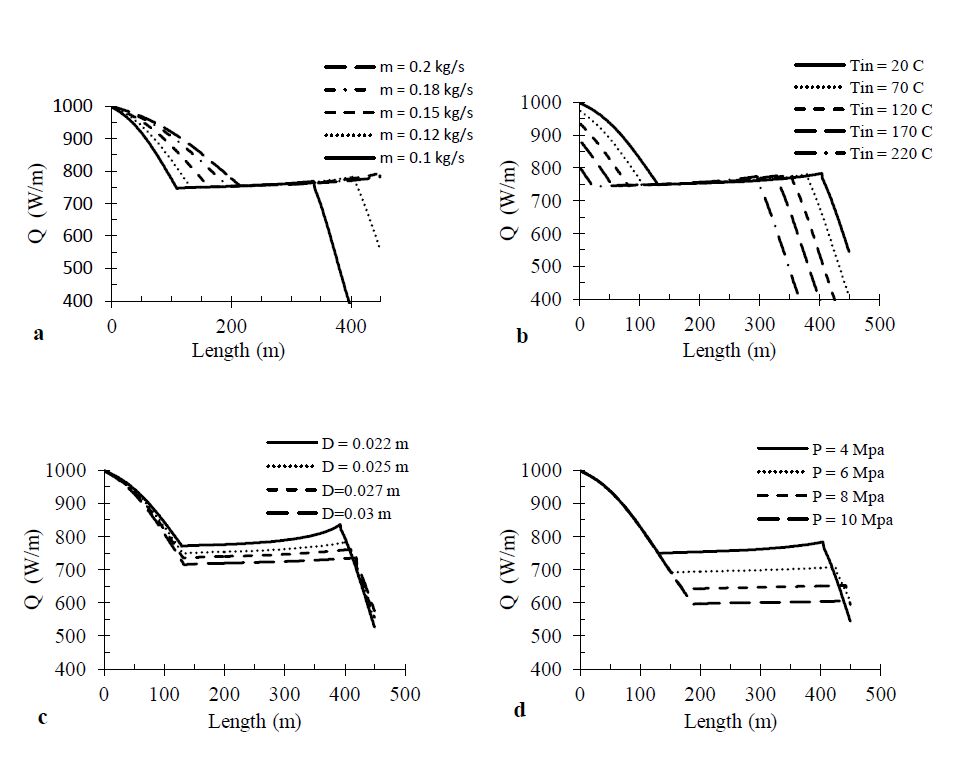
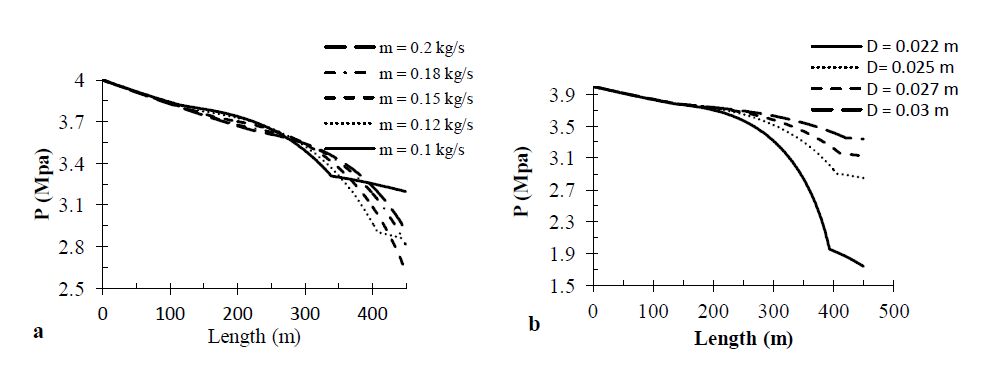
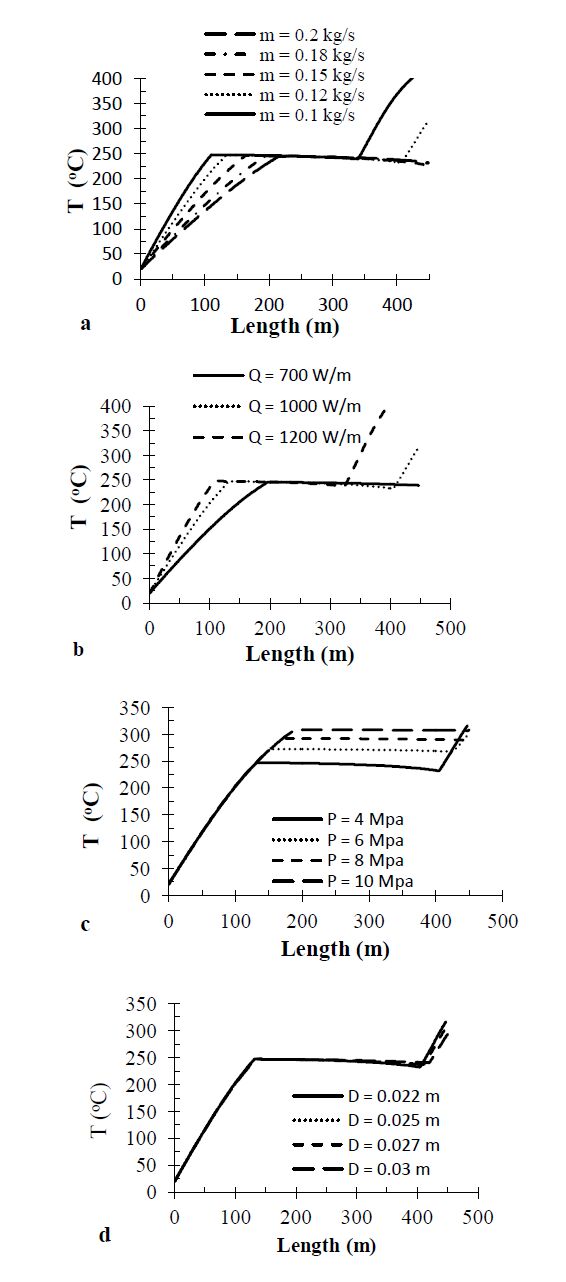
The numerical simulations yield results for the distribution of the pressure, the heat absorbed, temperature, enthalpy and the quality along the pipe length. Figure 6 shows the heat absorbed (Q) by the absorber tube at different parameters (mass flow rate, pressure temperature and diameter) along the length of the pipe. Results shown in Figure 6 show that the heat absorbed increases with increasing mass flow rate and decreasing absorber diameter. Furthermore, the heat absorbed decreases when the temperature decreases and pressure increases. Figure 7 shows pressure drop at different mass flow rate and inner diameters along the absorber tube. The pressure drop (ΔP) of the water inside the absorber tube decreases with the length (L) of the pipe as expected due to friction and static head. It is worth mentioning that the pressure drop of water is calculated in the three regions; water region, two phase region and dry steam region. Figure 7 shows the temperature and the saturation temperature vs. the length of the absorber tube. The temperature of the water equals to the saturation temperature in the two phase region. In the single phase region, the temperature of water depends on the pressure and enthalpy. The saturation temperature depends on the pressure only. Figure 8 shows the water temperature at different parameters along the absorber tube. As seen in Figure 8, the temperature increases with decreasing mass flow rate.
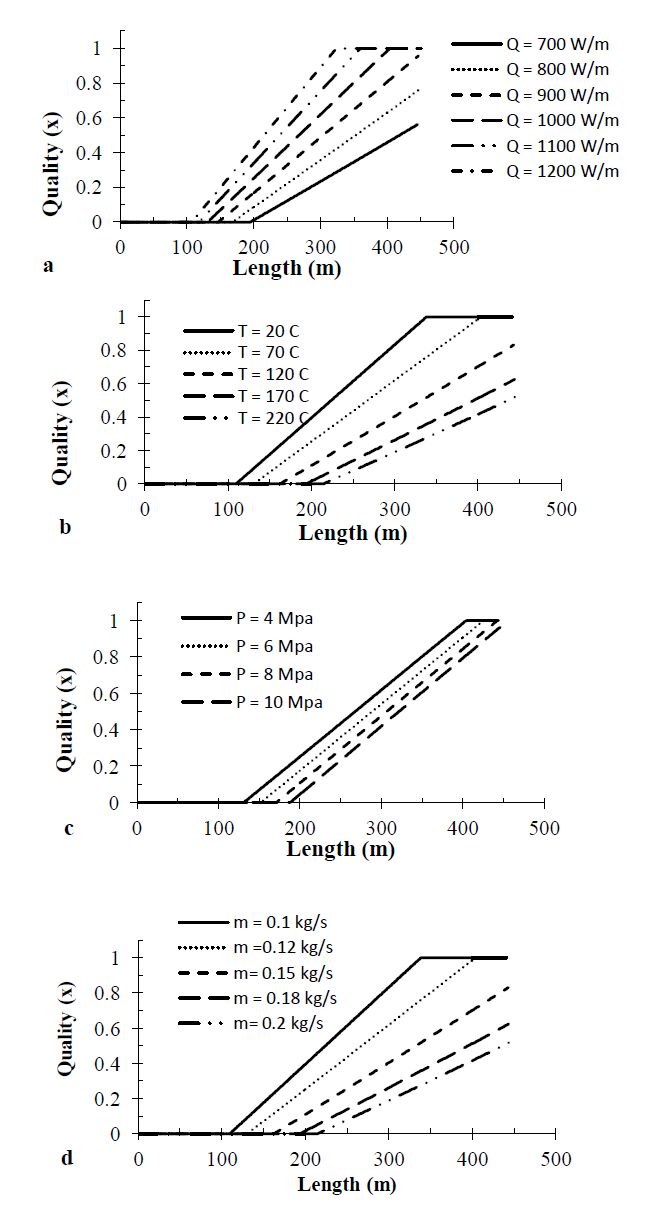
Figure 9 shows the variation of quality of the vapor along absorber tube. The water temperature increases quite fast in single phase region and when the evaporation process starts (two phase region) the temperature decreases slightly due to the decreases of the pressure with the length of pipe. When the evaporation process is completed, the temperature of the steam increases again and the water inside the absorber tube is in the form of superheated steam. The heat absorbed by the absorber tube decreases with the increasing in the pipe length, the reason for this is that the temperature of the water inside the steel pipe increases with length of absorber tube and as a result of that the heat losses to the surrounding increase.
6. Conclusion
The direct steam generated by solar radiation falling on absorber tube (evacuated tube) is analyzed. Two phase flow resulted from evaporation process is considered. The IAPWS-IF97 standards for single phase (liquid or steam) and for two phase (liquid and vapor) are used to calculate and compute the properties of water in single phase region and in two phase region. The amount of heat absorbed by the absorber tube is calculated for single phase and two phase using a suitable heat transfer model. Furthermore, the pressure drop inside the absorber tube is calculated for single phase and two phase using the best model that predict the pressure drop in the single phase flow region and two phase flow region. The Matlab program is used to simulate the system and the parameters such as Q, T, X, P, and Tsat that result from the simulation are discussed in details. It is found that present numerical solution matches very well experimental data of the DISS system of Plataforma Solar de Almería for pressure profiles. Moreover, the results obtained by present numerical models are more accurate than other those predicted by other numerical models found in literature.
Conflict of Interest
The authors declare there is no conflict of interest.










 DownLoad:
DownLoad: