For a time-delayed reaction-diffusion equation of age-structured
single species population, the linear and nonlinear stability of
the traveling wavefronts were proved by Gourley [4] and
Li-Mei-Wong [8] respectively. The stability results,
however, assume the delay-time is sufficiently small. We now prove
that the wavefronts remain stable even when the delay-time is
arbitrarily large. This essentially improves the previous
stability results obtained in [4, 8]. Finally, we point out
that this novel stability can be applied to the age-structured
reaction-diffusion equation with a more general maturation rate.
1.
Introduction
Mathematical modeling becomes an essential tool in the description and analysis of diseases dynamics [1,2]. In the last decades, many models have been used to understand the dynamics of infectious diseases with the purpose of controlling them [3,4]. In this context, the choose of the variables that characterize population dynamics, as the epidemiological state of individual, the tracking of the relevant biological processes, for example, how infection is transmitted, and the decision about the type of model to be used among the available options such as discrete models [5,6], ordinary differential systems [7,8,9,10], age-structured PDE [10,11,12,10,13,14], delay differential systems [15,16,17,18], stochastic models [19,20,21], and etcetera, depend on the main question addressed.
Vaccination is the one of the most efficient way to halt disease transmission through promoting population immunity [22,23]. The designed of vaccination strategies are based on the type of the infectious agent (viruses, bacteria, fungi, protozoa, or worms) and always search for risk groups [24], thresholds such as the proportion of the population to vaccinate [24,2], and the optimum age for vaccination [14,25], with the aim of optimize disease control. The duration of immunity promoted by vaccination and its efficacy determine the number of doses and the interval among them to ensure that the individuals are protected. For example, recently, human papillomavirus (HPV) vaccination moves from a 3–dose schedule to a 2–dose schedule [26]. The change in vaccination schedule was due to evidences that the antibody response generated after 2 doses is enough to prevent virus infection [27]; besides vaccination cost is significantly reduced in this 2 dose–scheme. HPV vaccination target-individuals between 9 to 14 years age because exposure to infection is higher at younger ages with a peak after the debut of sexual activity [28]. To prolong the immunity conferred by certain vaccines, it is sometimes necessary to update them. It is easier to focus on the individuals that are already vaccinated to incite them to update their vaccine. Indeed, these individuals are already known and easier to encourage to be vaccinate again.
For kids, the immunizations schedule depends on where they live, the child's health, the type of vaccine, and also which vaccines are available. For example, the DTaP vaccine (diphtheria, tetanus and acellular pertussis) is applied at 2, 4, 6, 15 months, and 4 years old [29]. For influenza, starting after six months old, the flu vaccine is recommended every year as the main virus that are circulating change and evolve [29]. According to WHO (World Health Organization), a collaborative global vaccination program was able to eradicate smallpox in 1980. But currently, diseases like whooping cough, polio, measles, and rubella that were controlled or almost eradicated are appearing again because of vaccine refusals, under-vaccination, waning immunity, less effective immunizations, and imported cases [30,31].
The duration of protection provided by any mechanism (vaccination is one of them) plays an important role on the evolution and control of epidemics. Although a lot of models in the literature address one or several questions related to vaccination, few of them considered the lost of immunity [23,32,33], and to our knowledge, no one considered the already vaccinated individuals that need to update their vaccine. Mathematical models of vaccination have been studied since 1760 [34,35,36,37,38,39]. To our knowledge, D. Bernoulli [34] proposed the first mathematical model of vaccination. He studied the impact of smallpox vaccination on the life expectancy of the immunized population. The works of [35,36,37,39] deal with age structured models of vaccination. They considered vaccine-induced temporary or permanent immunity. They studied the asymptotic behavior of the steady states. Recently, [38] have considered a model of vaccination with temporary immunity described by a delay differential system. The delay represents the length of immunity period. However, the population of individuals that update their vaccine at the end of their period of protection has never been explicitly incorporated in these models. It is sometimes difficult to reach a reasonable percentage of people to vaccinate in the total population to halt the disease transmission. Therefore, It would be interesting to combine vaccination of a part of total population with a proportion of individuals that were previously vaccinated.
With this in mind, we propose a new mathematical model that take into account the temporary protection and the specific individuals that are at the end of their previous period of protection. The model is an extension of the classical Kermack and McKendrick model [9] which includes a compartment of individuals with a temporary protection. Although, the model is formulated as a direct disease transmission model, it can be adapted to take into account the saturation in the transmission rate observed in vector-borne diseases. The epidemic model is present in section 2. Thus, we reduce the model (section 3) by using the method of characteristics to a delay differential-difference system. We present also some results about the existence, uniqueness, positivity and uniform boundedness of the solutions. Section 4 is devoted to the study of the existence of the steady states: disease-free and endemic. Section 5 concerns the computation of the basic reproduction number R0 of the model and its comparison with the R0 of the classical Kermack-McKendrick model. In Section 6, the local asymptotic stability of the steady states is established. In section 7, we establish the uniform persistence of the infected individuals. In section 8, we show that if R0>1, then the endemic steady state is globally asymptotically stable, and if R0<1, then the disease-free steady state is globally asymptotically stable. Finally, section 9 summarizes the main results and conclusion.
2.
Mathematical model
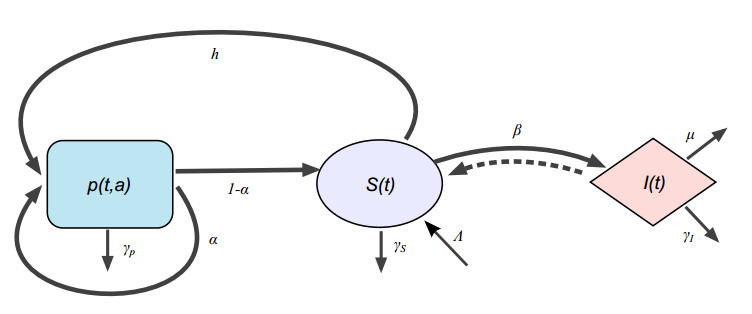
The epidemiological model splits the total population N in four classes: susceptible (S), infected (I), recovered (R) and protected individuals (P). It is an extension of the classical SIR Kermack and McKendrick model [9] that includes a compartment of protected individuals with limited duration τ. Let p:=p(t,a) be the age distribution of the population of protected individuals (the age in this model is the time since an individual is temporarily protected). So, the total number of protected individuals at time t is
The model is given by
The evolution of the density of the protected individuals is given by
The boundary condition is
The system is combined with nonnegative initial conditions
All the parameters of the model are nonnegative constants, and they are described in Table 1. The parameter α∈(0,1) represents a specific protection rate which corresponds to the individuals that get protected again at the end of the previous period of protection. These individuals may represent a population of volunteers or a specific age group, for example children, that are always vaccinated. Figure 1 provides a schematic representation of the epidemiological model.
3.
Reduction to a differential-difference system
Using the characteristics method, see for instance [40], we obtain, for t>0 and a∈[0,τ],
We put
Then the expression of p(t,a) becomes, for t>τ and a∈[0,τ],
Consequently,
Finally, we obtain the following system
By doing a translation in time (t↦t−τ), we can consider the initial conditions
By adding the equations of S, I, R and P, we show that the total population N=S+I+R+P satisfies
where
It follows that
P and R depend on S, I and u. However, the equations of S, I and u are independent on P and R. Then, we can focus on the reduced system
which is completed by the initial conditions
System (3.2)–(3.3) is a coupled system of differential and difference equations with discrete delay.
Remark 1. The particular case when τ=0 reduces the system (3.2) to the classical Kermak and McKendrick model [9] given by
Let us introduce C:=C([−τ,0],R), the space of continuous functions on [−τ,0] and C+:=C([−τ,0],R+), the space of nonnegative continuous functions on [−τ,0]. Throughout this paper, we assume Λ, γS, h, γp, τ, μ, γI, β≥0, α∈(0,1), S0≥0, I0≥0, ϕ∈C+. The existence and uniqueness of nonnegative solutions of (3.2)–(3.3) can be obtained as in [41]. Also, we observe that by the method of steps we can solve the system (3.2)–(3.3) in each interval [kτ,(k+1)τ], for k=0,1,….
Consider the auxiliary linear homogeneous difference equation
where the function ut∈C is defined, for t≥0 and u∈C([−τ,+∞),R), by ut(θ)=u(t+θ) for θ∈[−τ,0], and the operator D:C→R is given, for ψ∈C, by
Remark that
with ‖ψ‖=supθ∈[−τ,0]|ψ(θ)|. The condition (3.5) says that the zero solution of the linear difference equation (3.4) is globally asymptotically stable [42].
Now, we deal with the nonnegativity of the solutions of the system (3.2).
Proposition 1. All the solutions (S,I,u) of the system (3.2) with nonnegative initial conditions are nonnegative. Furthermore, (S,I) has a continuous first derivative for all t>0 and u is continuous for all t≥−τ if and only if the initial condition (S0,I0,ϕ) satisfies the compatibility condition
Proof. Let (S,I,u) be a solution of (3.2) associated to the initial condition (S0,I0,ϕ)∈R+×R+×C+. We first prove the nonnegativity on the interval [0,τ], and we apply the same reasoning by steps on each interval [kτ,(k+1)τ], for k=1,2…. For t∈[0,τ], we have t−τ∈[−τ,0]. Then, the system (3.2) becomes
The idea is to extend the analogous result known for ODE to our system as established in ([43], Theorem 3.4). We have the following implications
and
This implies S(t)≥0 and I(t)≥0 for t∈[0,τ]. Then, u(t)=hS(t)+αe−γpτϕ(t−τ)≥0, for t∈[0,τ]. Hence, one just repeats the same argument by steps. We conclude that S, I and u are nonnegative on [0,+∞). We obtain a nonnegative piecewise solution (S,I,u) of (3.2). We can easily prove that (S,I) has a continuous first derivative for all t>0 and u is continuous for all t≥−τ if and only if ϕ(0)=hS0+αe−γpτϕ(−τ).
Next, we investigate the boundedness of the solutions of (3.2). We propose to prove the following result.
Proposition 2. The solutions of the system (3.2) are uniformly bounded.
Proof. Let (S,I,u) be the solution of (3.2) associated to the initial condition (S0,I0,ϕ)∈R+×R+×C+. First, one can observe from (3.1) that
Then, S and I are uniformly bounded. Moreover, for t>0, we have (see [44] or Lemma 3.5 in [45])
with ν>0, C>0. This implies that u is bounded. On the other hand, we have from the equation of u
Then,
This complete the proof.
4.
Existence of steady states
In this section, we establish the existence of the steady states of the system (3.2). Let (S∗,I∗,u∗) be a steady state of (3.2). Then,
The third equation of (4.1) implies that
From the second equation of (4.1), we have for μ+γI>0 and β>0
Suppose that I∗=0. Then, S∗ satisfies the following equation
Consequently, we obtain for γS+h−(αγS+h)e−γpτ>0,
Remember that α∈(0,1). Then by assuming γS+h>0, we have γS+h−(αγS+h)e−γpτ>0. We put, for γS+h>0,
So, under the condition γS+h>0, (S0,0,u0) is always a steady state of (3.2). It describes the disappearance of the epidemic. We will refer to this steady state as the disease-free steady state.
Suppose now that I∗>0. Then, S∗=(μ+γI)/β with μ+γI>0 and β>0. We have
Moreover, the first equation of (4.1) implies that
In fact, I∗ is given by the following expression
Then, the existence of a positive steady state is equivalent to
We set
We will refer to this steady state as the endemic steady state.
We summarize the existence of steady states in the following result.
Theorem 4.1. Assume that (4.3) holds. Then, the system (3.2) has two distinct steady states: a disease-free steady state (S0,0,u0), which is given by (4.2), and an endemic steady state(¯S,¯I,¯u), which is given by (4.4). If (4.3) does not hold, then (S0,0,u0) is the only steady state.
In the next section, we derive the basic reproduction number R0. We study also the influence of some parameters on this threshold.
5.
The basic reproduction number R0
The number R0 is defined as the average number of secondary infections that occur when one infective individual is introduced into a completely susceptible population. By dividing the equation of I(t), in the system (3.2), by (μ+γI)I we get
The fraction β/(μ+γI) can be interpreted as the number of contacts per infected individuals during their infectious period that lead to the transmission of the disease. If
the disease persist, otherwise, it disappears. Then, the basic reproduction number of the disease is defined by
Remark that the condition (4.3) is equivalent to R0>1. Then, the existence of the endemic stable state is guaranteed by the condition R0>1. In comparison with the classical Kermack-McKendrick SIR epidemic model, the new parameters in our model are h, α and τ. In the next proposition we study the behavior of R0 in terms of these new parameters.
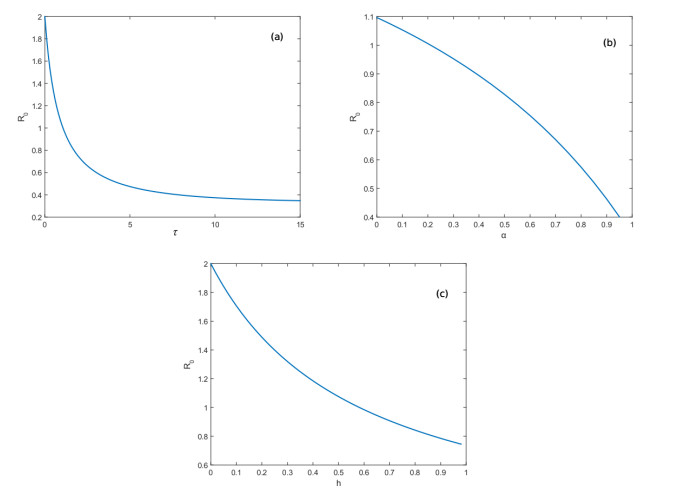
Proposition 3. R0 is a decreasing function with respect to h, α and τ. Furthermore,
where m:=h∈J:=[0,+∞)↦R0(h), m:=α∈J:=[0,1]↦R0(α) or m:=τ∈J:=[0,+∞)↦R0(τ), and
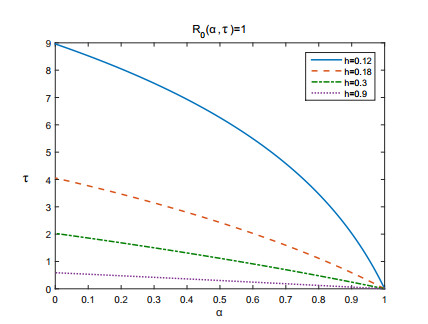
We remark that infm∈JR0(m) is in fact minm∈JR0(m) for h and α. The proof of this proposition is easy, so we drop the details. The behavior of R0 as a function of τ,α and h is shown in Figures 2 and 3.
Remark 2. Observe that:
● If τ=0 or h=0, then R0 becomes
which is the basic reproduction number associated to the classical Kermack-McKendrick model (see Remark 1). If we increase τ or h, R0 decreases until the value minm∈JR0(m), m=τ or h, which is given in Proposition 3 (see Figures 2 and 3).
● If α=0, then R0 becomes
We can decrease R0 by increasing α until the threshold given by minα∈JR0(α) (see Figures 2 and 3).
6.
Local asymptotic stability
The purpose of this section is to study the local asymptotic stability of each steady state in the cases R0<1 and R0>1. We use the results in [44] to linearize the differential-difference system (3.2) about the steady states and to derive the characteristic equations. As we will often vary the delay τ to study the stability of the steady states, we consider when it is necessary the dependence of R0 in terms of the parameter τ, R0:=R0(τ).
The linearized system of (3.2) (see [44]) about any steady state (S∗,I∗,u∗) is given by
We can check (see [44]) that the characteristic equation of this system is
Remark 3. Let τ>0. The characteristic equation (6.1) has the form
Then, any sequence of distinct roots {λn} of this last equation satisfies limn→+∞|λn|=+∞. Furthermore, this sequence approaches the roots of the equation
which are given by
As α∈(0,1), we conclude that all the branches of eigenvalues that appear from infinity have negative real parts.
6.1. Local asymptotic stability of the disease-free steady state
The linearized system of (3.2) about the equilibrium (S0,0,u0) is
and the characteristic equation is given by
The following proposition deals with the instability of disease-free steady state.
Proposition 4. Assume that R0>1. Then, there exists a positive real root of (6.2), and the steady state (S0,0,u0) is unstable.
Proof. From the characteristic equation (6.2), we have the following eigenvalue
Clearly, this eigenvalue is real and positive when R0>1. The proof is complete.
Suppose now that R0<1. Then,
Thus, the local stability of (S0,0,u0) is determined by the sign of the real part of λ∈C satisfying
We have the following theorem.
Theorem 6.1. Assume that R0<1. Then, all roots of the characteristic equation (6.2) have negative real parts, and the steady state (S0,0,u0) is locally asymptotically stable.
Proof. Our approach is to see the stability of (S0,0,u0) when the delay is equal to zero and, by using the continuity and Remark 3, we check if the stability can be lost by the appearance of a pure imaginary roots. We consider in this proof R0 as a function of τ∈[0,+∞)↦R0(τ). Setting τ=0 with R0(0)<1, there exists only one root of (6.3) given by λ=−γS which is negative. We conclude that (S0,0,u0) is locally asymptotically stable when τ=0.
Hence, we look for purely imaginary roots ±iω, ω∈R. Remark that if λ is a root of (6.3) then its conjugate ¯λ is also a root of (6.3). Then, we can look for purely imaginary roots iω with ω>0. We put
Then, by separating real and imaginary parts in (6.3), we obtain
This last system is equivalent to
It follows, by taking cos2(ωτ)+sin2(ωτ)=1, that
We can observe that ρ−(γS+h)<0 and 1−η>0, which is absurd. Then, no ±iω satisfying (6.3) exist. Hence, when R0(τ)<1 all roots of (6.2) have negative real parts. Then, (S0,0,u0) is locally asymptotically stable.
6.2. Local asymptotic stability of the endemic steady state
In this section, we show the local asymptotic stability of the endemic steady state. We assume that
The linearized system of (3.2) about (¯S,¯I,¯u) is given by
The characteristic equation of this system is given by
To study the local asymptotic stability of the endemic steady state, we use the same technique as for the disease-free steady state. We consider again R0 as a function of τ∈[0,+∞)↦R0(τ). We have the following lemma.
Lemma 6.2. For τ=0 and under the condition R0(0)>1, the characteristic equation (6.1) has only roots with negative real parts.
Proof. As τ∈[0,+∞)↦R0(τ) is a decreasing function, the assumption R0(0)>1 implies that R0(τ)>1, for all τ≥0. For τ=0, the characteristic equation (6.1) becomes
It is clear that all coefficients of the above equation are positive. Then, the Routh-Hurwitz criterion implies that all the roots have negative real parts. This is corresponding, when R0(0)>1, to the local asymptotic stability of (¯S,¯I,¯u). The previous lemma states that (¯S,¯I,¯u) is locally asymptotically stable for τ=0. Using this assertion and Remark 3, we show in the following theorem that the eigenvalues of (6.4) stay in the left half plane for all τ>0 with R0(τ)>1.
Theorem 6.3. Assume that R0(τ)>1. Then, all roots of (6.1) have negative real parts, and the steady state (¯S,¯I,¯u) is locally asymptotically stable.
Proof. As in the proof of Theorem 6.1, we show that no purely imaginary roots λ=±iω, ω∈R exist. It is sufficient to look for purely imaginary roots iω with ω>0. Then, by separating real and imaginary parts in (6.4), we obtain
where
It follows, from the system (6.5), that ω satisfies
This implies that
Remember that 1−(αc)2>0. We put
Then, x=ω2>0 satisfies
If D is nonnegative, then the Routh-Hurwitz criterion implies that no positive real roots of (6.6) exist.
Suppose that D is negative. The discriminant of (6.6) is given by
It is clear that D−2b<0. On the other hand, we have
and
We conclude that D+2b>0, and then Δx<0. Consequently, there is no real root of (6.6). In all cases, no x:=ω2 exits.Consequently, the equation (6.4) has no imaginary root iω. This means that no stability switches occurs. Hence, all roots of (6.4) have negative real parts. Then, the steady state (¯S,¯I,¯u) is locally asymptotically stable.
7.
Uniform persistence
In all this section, we assume that
This condition implies that the steady state (S0,0,u0) is unstable. The instability of the disease-free steady state is not in contradiction with the existence of a nonnegative initial condition for which
We therefore need to prove the persistence of the component I of infected individuals [46] (we will prove in fact the uniform persistence), that ensures survival of the infected individuals. First, we prove the following uniform weak persistence result.
Lemma 7.1. Assume that R0>1. Then, there exists a constant ϵ>0 such that for any initial condition (S0,I0,ϕ)∈R+×R+∗×C+
Proof. Assume that
where
We can choose ϵ>0 sufficiently small such that
where
Remark that S0>S0ϵ>0, for all ϵ>0. With the choice of ϵ>0 satisfying (7.2), we are going to show that (7.1) holds true. On the contrary, suppose that lim supt→+∞I(t)≤ϵ. Then, there exists a sufficiently large Tϵ>0 such that I(t)≤ϵ for all t≥Tϵ. Then, we have for all t≥Tϵ
We will use a comparison principle. Then, we consider the following problem
The system (7.4) has a unique steady state (S0ϵ,u0ϵ), with S0ϵ given by (7.3) and
The corresponding R0 is given by (7.2). We will use the following result.
Lemma 7.2. Under the assumption (7.2) and for all initial condition (S0,ϕ)∈R+×C+, we have (S+ϵ(t),u+ϵ(t))→(S0ϵ,u0ϵ) as t→+∞.
Proof. See the proof of Theorem 8.1.
On the other hand, we can choose a sufficiently small ˜ϵ>0 such that
In the same time, we can choose a large T′˜ϵ>Tϵ such that S+ϵ(t)>S0ϵ−˜ϵ, for all t≥T′˜ϵ. Furthermore, by comparison principle we have S(t)≥S+ϵ(t)>S0ϵ−˜ϵ, for all t≥T′˜ϵ. Let ξ>0 be sufficiently small such that
Multiplying the equation of I(t) by e−ξt and integrating from T′˜ϵ to +∞, we obtain
This is a contradiction with (7.6). Hence (7.1) holds true.
In the next result, we use Lemma 7.1 to prove the following stronger result about the uniform strong persistence of infected individuals. The idea is based on the paper [47].
Theorem 7.3. Assume that R0>1. Then, there exists a constant 0<ϵ′≤ϵ, where ϵ is given by Lemma 7.1, such that for any initial condition (S0,I0,ϕ)∈R+×R+∗×C+
Proof. From Lemma 7.1, we have lim supt→+∞I(t)>ϵ. Then, there exists an increasing positive sequence {ηk}+∞k=0, ηk→+∞ such that I(ηk)>ϵ.
We prove Theorem 7.3 by contradiction. Suppose that for all ϵ′∈(0,ϵ] there exists an initial condition (S0,I0,ϕ)∈R+×R+∗×C+, such that
Then, there exist a positive increasing sequence {tk}+∞k=0 and a positive decreasing sequence {μk}+∞k=0 such that tk>ηk, limk→+∞μk=0 and
Then, I(tk)<μk<ϵ. By the continuity of I, there exists a sequence {νk}+∞k=0, νk∈(ηk,tk) such that
Let {Ik}+∞k=0 and {Sk}+∞k=0 be the sequences such that Ik:=I(νk)=ϵ and Sk:=S(νk)∈R+. The sequence {Ik}+∞k=0 is constant and since the sequence {Sk}+∞k=0 is uniformly bounded, it follows that there exist a convergent subsequences of {Ik}+∞k=0 and {Sk}+∞k=0 (denoted again {Ik}+∞k=0 and {Sk}+∞k=0) and ρ∈R+ such that Ik=ϵ and limk→+∞Sk=ρ. Let consider the following problem
For each initial condition ϕ∈C:=C([−τ,0],R), the difference equation (7.9) has a unique solution w, which is continuous on (0,+∞). Let {uk}+∞k=0 be the functional sequence in C defined by uk(θ):=w(νk+θ), θ∈[−τ,0], with νk>τ, for k large enough (we make a translation of k to have νk>τ for all k∈N). Then,
From the Proposition 2, we have the uniform boundedness of the sequence {uk}+∞k=0. For θ,θ′∈[−τ,0], we have
where nk:=⌊νk/τ⌋. Since ϕ is uniformly continuous on [−τ,0], the inequality (7.10) implies that the sequence {uk}+∞k=0 is equicontinuous. Hence, it follows from the Ascoli-Arzela theorem that there exists u∗∈C+ such that limk→+∞uk=u∗ (otherwise, we can choose a convergent subsequence).
Let consider now the solution of (3.2) with the initial condition S0=ρ, I0=ϵ and ϕ=u∗∈C+. We denote this solution by (S∞,I∞,u∞). From Lemma 7.1, there exists σ>0 and we can find 0<m<ϵ (because I∞ is positive), such that
Next, we prove that we obtain a contradiction. For each k∈N, we put ˜Ik(t):=I(νk+t), t>0. From (7.11), the continuity and the fact that
we have (recall that limk→+∞μk=0), for k large enough
On the other hand, for ˜tk:=tk−νk, we have from (7.7) and (7.8) that
We distinguish three cases, if σ<˜tk, then the second inequality in (7.13) gives ˜Ik(σ)<ϵ which contradicts the first inequality in (7.12). If σ=˜tk, then the first inequality in (7.12) contradicts the first inequality in (7.13). If ˜tk<σ, then the second inequality in (7.12) gives ˜Ik(˜tk)>μk which contradicts the first inequality in (7.13). Consequently, there exists ϵ′∈(0,ϵ] such that for any initial condition (S0,I0,ϕ)∈R+×R+∗×C+,
This completes the proof.
8.
Lyapunov functional and global asymptotic stability
In this section, we construct Lyapunov functionals to prove that the disease-free steady state is globally asymptotically stable when the basic reproduction number R0<1 and that the unique endemic steady state is globally asymptotically stable when R0>1.
8.1. The global asymptotic stability of the disease-free steady state
In this part, we assume that R0<1 and we prove the global asymptotic stability of the disease-free steady state (S0,0,u0) of the system (3.2):
The solutions of this system satisfy, for all t>0,
By the comparison principle, we have S(t)≤S+(t) and u(t)≤u+(t) for all t>0, where (S+,u+) is the solution of the following problem
The system (8.1) has a unique steady state (S0,u0), where S0 and u0 are the first and third components of the disease-free steady state of the system (3.2). In the next result, we show that the steady state (S0,u0) of (8.1) is globally asymptotically stable.
Theorem 8.1. The unique steady state (S0,u0) of (8.1) is globally asymptotically stable.
Proof. We put, for t>0,
Then, we get the linear differential-difference system
Let's consider the following Lyapunov functional
defined by
This functional satisfies, for ν1(s)=s2/2 and ν2(s)=((1/2)+τϑ)s2, the inequalities
Moreover, the system (8.2) is input-to-state stable (see [44,48], for the definition and some properties of the notion of input-to-state stable). More precisely, there exist constants C>0 and σ>0 such that the solution (ˆS,ˆu) of (8.2) satisfies
The above estimation is an immediate consequence of ([42], Theorem 3.5, page 275). By differentiating the function t↦V(ˆS(t),ˆut) along the solution (ˆS,ˆu) of the system (8.2), we obtain, for t>0
We want to find ϵ>0 such that
We consider ddtV(ˆS,ˆut)+ϵˆS2(t) as a second order polynomial function of ˆS(t). We compute the discriminant
and the expression
It is clear that we can choose ϵ>0 small enough such that
We conclude that
Hence (0,0) is a globally asymptotically stable steady state of (8.2) (see, [44,48]). This completes the proof of Theorem 8.1.
Let ϵ>0 and consider the set
Lemma 8.2. For any sufficiently small ϵ>0, the subset Ωϵ of R+×R+×C+ is a global attractor for the system (3.2).
Proof. The solutions of (3.2) satisfy, for all t>0,
By the comparison principle, we have S(t)≤S+(t) and u(t)≤u+(t) for all t>0, where (S+,u+) is the solution of the system (8.1). Theorem 8.1 shows that S+(t)→S0 and u+(t)→u0 as t→+∞. This convergence implies that Ωϵ is a global attractor for the system (3.2) in R+×R+×C+. This completes the proof.
Thanks to Lemma 8.2, we can restrict the global stability analysis of the disease-free steady state of (3.2) to the set Ωϵ.
Theorem 8.3. Assume that R0<1. Then, the disease-free steady state (S0,0,u0) of (3.2) is globally asymptotically stable.
Proof. It suffices to consider the solutions in Ωϵ for any sufficiently small ϵ>0. We then have, for t>0,
Since R0<1, we can choose ϵ>0 such that the right-hand side of the above inequality is negative. This implies that limt→+∞I(t)=0.
From the above result, we see that for any ϵ>0, there exists a Tϵ>0 such that I(t)≤ϵ for all t≥Tϵ. We then have, for t>Tϵ
Then, we have S(t)≥Sϵ(t) and u(t)≥uϵ(t) for all t≥Tϵ, where (Sϵ,uϵ) is the solution of the following problem
As in the proof of Lemma 7.1 and Theorem 8.1, we can show that Sϵ(t)→S0ϵ and uϵ(t)→u0ϵ as t→+∞, where (S0ϵ,u0ϵ) is the steady state of (8.3), given by (7.3) and (7.5). Then, there exists a ˜Tϵ>Tϵ>0 such that, for t≥˜Tϵ,
Since ϵ>0 is arbitrary, S0ϵ→S0 and u0ϵ→u0 as ϵ→0, we have that limt→+∞S(t)=S0 and limt→+∞u(t)=u0. Recalling from Theorem 6.1 that (S0,0,u0) is locally asymptotically stable. Then, it is globally asymptotically stable. This completes the proof.
8.2. The global asymptotic stability of the endemic steady state
In this section, we assume that
Let (¯S,¯I,¯u) be the endemic steady state. This equilibrium satisfies ¯S>0, ¯I>0 and ¯u>0. Let ˜S(t):=S(t)−¯S and ˜u(t):=u(t)−¯u. Then, the system (3.2) transforms to
Note that β¯S=μ+γI.
Theorem 8.4. Assume that R0>1. Then, the steady state (¯S,¯I,¯u) is globally asymptotically stable.
Proof. Let consider the following Lyapunov function
defined by
where
We point that the function
satisfies G(I0)≥0 for all I0>0 and G(I0)=0 if and only if I0=¯I. This observation means that W(S0,I0,u0)=0 if and only if (S0,I0,u0,)=(0,¯I,0).
We set
Then, the derivative of t↦W(˜S(t),I(t),˜ut) along the solution trajectory is given by
Since c>0, we obtain
with
Then, the function t↦W(˜S(t),I(t),˜ut) is nonincreasing and we have
Furthermore, by integration (8.5), we get
The both sides of the inequality (8.6) are nondecreasing functions. Then, the limits exist and satisfy
As the function ˜S′(t) is uniformly bounded ˜S(t) is uniformly continuous. Then, the Barbalat's Lemma [49] applied to the function t↦∫t0˜S2(s)ds, shows that
Using [45], Lemma 3.5, we obtain
Then, the expression of the function W implies that
Furthermore, the function ˜S(t) is bounded and differentiable, then the fluctuations Lemma implies that there exists a sequence tk→+∞ such that limk→+∞˜S′(tk)=0. Then, the first equation of (8.4), implies that limk→+∞I(tk)=¯I. The continuity of the function G gives limk→+∞G(I(tk))=G(¯I)=0. Then, W∗=0. From the properties of the function G, we conclude that
This prove the global asymptotic stability of (¯S,¯I,¯u).
9.
Discussion
In this work, an epidemiological SIR model with a class of age structured temporary protected individuals is presented. A coupled system of differential-difference equations with delay is derived from this model by using the method of the characteristics. We followed the same idea as in our recent work [44]. The model presents two steady states: disease-free and endemic. The condition for the existence and the asymptotic behavior of these steady states (local and global asymptotic stability) are discussed. The global asymptotic stability was proved by using Lyapunov functions. In summary, if R0<1 the disease-free steady state is globally asymptotic stable, otherwise if R0>1, which ensures also its existence, the endemic steady state is globally asymptotic stable. The threshold R0 is the well-known "basic reproduction number of the disease". Comparing the new R0 with the one obtained by the classical Kermack-McKendrick model, the new parameters h, α and τ decrease the R0 value, which means that the disease is easier to control when protection, through vaccination or drugs, is take into account (Figures 2 and 3). This emphasize the importance of the compliance with the adopted control strategies. The parameters h, τ and α are, respectively, the protection rate, the duration of the temporary protection phase, and the specific protection rate at the end of the previous period of protection. Keeping one of the three parameters fixed and varying the others, we can observe that if one parameter decrease, the other has to increase to keep the transmission of the disease under control. In all cases, control is achieved if R0(m)<1, with m=h, α or τ, (Figures 2 and 3). Finally, we showed that when short immunity is considered, the fraction of individuals that update their vaccine at the end of their period of protection has an important impact on disease dynamics.
Acknowledgments
CPF acknowledges Grant 18/24058-1 from São Paulo Research Foundation (FAPESP). Part of this research was developed during the visit of Dr Adimy to IBB/UNESP by PROPG 02/2018. We also want to thank the anonymous referees for their careful reading that helped us to improve the manuscript.
Conflict of interest
The authors declare no conflicts of interest.









 DownLoad:
DownLoad: