1. Introduction

Flocculants are widely used in various industrial fields, such as wastewater treatment, low-cost harvest of microalgae, dewater of activated sludge and downstream process of fermentation industries ^[1,2,3,4]. The flocculating agents are divided into three groups: inorganic flocculants such as aluminum sulfate, chemically synthetic flocculants such as polyacrylamide derivatives, and bioflocculants. Several evidences suggest that inorganic flocculants and chemically synthetic flocculants are toxic to humans and environment. For example, aluminum salts are suspected of inducing Alzheimer’s disease ^[5]. Polyacrylamides, a common type of chemically synthetic flocculant, which monomers are found to be both neurotoxic and strong human carcinogens ^[1]. Bioflocculants are extracellular polymeric substances (EPS) produced by microorganisms during their growth, such as glycoproteins, polysaccharides, proteins and nucleic acids ^[6,7]. Therefore, bioflocculants are advantageous over inorganic flocculants and chemically synthetic flocculants due to their nontoxic, harmless and biodegradable properties ^[3,6,8]. However, the high production cost relative to inorganic and synthetic flocculants is a major bottleneck for the commercial application of bioflocculant ^[9,10,11].

To reduce the production cost of bioflocculant, screening high yield strains, optimizing fermentation conditions, using mutational methods to obtain more efficient mutants and expanding their application fields are the main current research directions ^[12,13,14]. In addition, since exploring low-cost substrates is also a way to reduce the production cost, various wastewaters were used as cheap carbon source, such as potato starch wastewater ^[15,16], palm oil mill effluent ^[17,18], dairy wastewater ^[13], chromotropic acid wastewater ^[10] and brewery wastewater ^[19]. Agricultural wastes, such as rice stover and corn stover are rich in lignocelluloses, whose hydrolysates or untreated materials have been applied as non-expensive carbon sources to produce bioflocculants ^[20,21,22]. So far, several bioflocculant-producing strains have been reported, such as Bacillus circulans ^[23], Bacillus licheniformis ^[24], Serratia ficaria ^[25], Klebsiella mobilis ^[13], Halomonas sp. ^[26], Vagococcus sp. ^[27] and Bacillus toyonensis ^[28]. But bioflocculants produced by these strains are cation-dependent. Cations stimulate the flocculating activity by neutralizing the residual negative charge of functional groups and by forming the bridges between particles ^[29]. However, the addition of cations always causes secondary pollution and increase the production cost. Therefore, some cation-independent bioflocculants were explored to avoid the secondary pollution. For example, the bioflocculants produced by Aspergillus flavus ^[30], Chryseobacterium daeguense W6 ^[9], Enterobacter sp. ETH-2 ^[31], Klebsiella pneumonia, Bacillus sp. F19 ^[7] have been found to be cation-independent. The flocculating mechanism of these cation-independent bioflocculants has been reported as charge neutralizing and adhesion mechanisms ^[31,32,33]. However, until now, the yield of reported cation-independent bioflocculants is low. Therefore, screening novel strains which can produce a high yield of cation-independent bioflocculants is still needed.

In this study, an alkali-tolerant strain Microbacterium esteraromaticum C26, which can produce high yield of cation-independent bioflocculant, was isolated from activated sludge. The findings showed that Microbacterium esteraromaticum C26 could produce 4.92 g/L cation-independent bioflocculant BF-C26 under optimized conditions (3 g/L glucose as carbon source and 10 g/L peptone as nitrogen source). The highest flocculating rate of 94.82% was achieved at the condition of 4 mg/L bioflocculant BF-C26, 30 °C and pH 8.23, without addition of any cation. Therefore, Microbacterium esteraromaticum is reported for the first time as a bioflocculant producing strain, which can produce a high yield of cation-independent bioflocculant.

---

2. Materials and Method

---

2.1. Isolation of bioflocculant-producing strain

The bioflocculant-producing strains were isolated from activated sludge, which was obtained from a wastewater treatment plant of Nehe city in Heilongjiang province, China. One gram of sludge sample was suspended and serially diluted using 0.9% NaCl solution. The diluted solution was then loaded on the screening medium which contained glucose 0.5 g/L, starch 0.5 g/L, yeast extract 0.5g/L, peptone 0.5 g/L, casein 0.5 g/L, K₂HPO₄ 0.3 g/L and MgSO₄·7H₂O 0.05 g/L, with initial pH7.2. After 24 h of cultivation at 30 °C, all the colonies present on the plates were purified. Each isolated strain was inoculated into a 150 mL flask containing 50 mL liquid screening medium and incubated at 200 rpm, 30 °C. Then the flocculating rate of each fermentation broth was determined. Strains with high flocculating ability were selected for further studies.

---

2.2. Measurement of cell growth and flocculating activity

The cells were cultured in the liquid medium and sampled after 24 h culture. The cell growth (biomass yield) was analyzed by measuring OD₆₀₀ of the sample of 24 h using a spectrophotometer (Unic-7200) with medium as the baseline. The flocculating activities were measured by calculating the flocculating rate according to a previous study ^[33]. Briefly, the bioflocculant was added into 60 mL kaolin clay suspension (5 g/L) and adjusted to different concentrations. Then the solution was stirred with rapid mixing for 2 min, followed by slow mixing for 1 min. After settling for 1 min, the absorbance (OD₅₅₀) of the supernatant sample was measured by a spectrophotometer (Unic-7200). A control experiment added with water was measured in the same manner. The flocculating rate was calculated according to the following equation: Flocculating rate = (A – B)/A × 100%, where B is the absorbance of the sample at 550 nm and A is the absorbance of the control at 550 nm.

---

2.3. Identification of strain C26

The 16S rRNA sequence was analyzed to identify the strain C26. The cells were cultured overnight. The genomic DNA was extracted using Genomic DNA Mini Kit (Invitrogen). The 16SrRNA of strain C26 was then obtained by PCR amplification using forward primer (5’-GAG AGT TTG ATC CTG GCT CAG-3’) and reverse primer (5’-CTA CGG CTA CCT TGT TAC GA-3’). The PCR product was purified using a PureLink PCR Purification Kit (Invitrogen) and sequenced by Sangon Biotech Company. The sequencing results were compared to the 16S rRNA sequences available in the GenBank from the National Center for Biotechnology Information (NCBI) Database.

---

2.4. Production and extraction of the bioflocculant

Production of the bioflocculant was performed in 500 mL flasks containing 100 mL fermentation medium with 200 rpm shaking at 30 °C. The composition of the optimal fermentation medium was as follows: glucose 3 g/L, peptone (Aoboxing Biotech Co., LTD, total nitrogen content 14.5%) 10 g/L, K₂HPO₄ 0.3 g/L, MgSO₄·7H₂O 0.05 g/L and pH 8.1. After 24 h incubation, the fermentation broth was centrifuged at 12000 rpm, 4 °C for 30 min to remove the cells. The supernatant was collected and mixed with two volumes of cold absolute ethanol to precipitate the bioflocculant. The resulting precipitate was collected by centrifugation at 10000 rpm, 4 °C for 5 min, washed by 75% ethanol and lyophilized to obtain bioflocculant BF-C26.

---

2.5. Characteristics of bioflocculant BF-C26

The total polysaccharides of BF-C26 were measured using the phenol-sulfuric acid method with glucose as the standard sample ^[34]. The total protein content was measured by the Bradford method with bovine serum albumin as the standard ^[35].

---

2.6. Flocculating properties of BF-C26

To analyze the flocculating properties of bioflocculant BF-C26, the effects of metal ions, temperature, pH and bioflocculant dosage on flocculating activity were determined. To test the effect of metal ions on the flocculating rate, 1 mL 10 g/L FeCl₃, AlCl₃, MgCl₂, MnCl₂, BaCl₂, CaCl₂ KCl and NaCl solution was introduced into the 60 mL flocculating system, then the flocculating activity was determined. The dosage of bioflocculant was varied from 1 to 20 mg/L. The pH of the kaolin suspension was adjusted using HCl and NaOH in the range from 3.04 to 11.12. The temperature of kaolin suspension was adjusted from 5 to 80 °C.

---

3. Results and Discussion

---

3.1. Isolation and identification of bioflocculant-producing strain

A bioflocculant-producing strain C26, with high flocculating activity, was isolated from an activated sludge sample. The C26 cells were Gram negative, rod shaped and aerobic bacteria. The colony of C26 was circular and moist. The 16S rRNA of strain C26 was sequenced after PCR amplification and compared with sequences deposited in NCBI database. In total 1420 bp of 16S rRNA of C26 was determined. The highest level of 16S rRNA sequence similarity to Microbacterium esteraromaticum was 99%. Therefore, strain C26 and its biofloculant product were named as Microbacterium esteraromaticum C26 and BF-C26, respectively. Previous study reported that Microbacterium esteraromaticum is able to form aggregates with the non-flocculating strain Acinetobacter johnsonii ^[36]. In this study, it was shown for the first time that Microbacterium esteraromaticum C26 could produce a cation-independent bioflocculant.

---

3.2. The effects of initial pH of fermentation medium on BF-C26 production

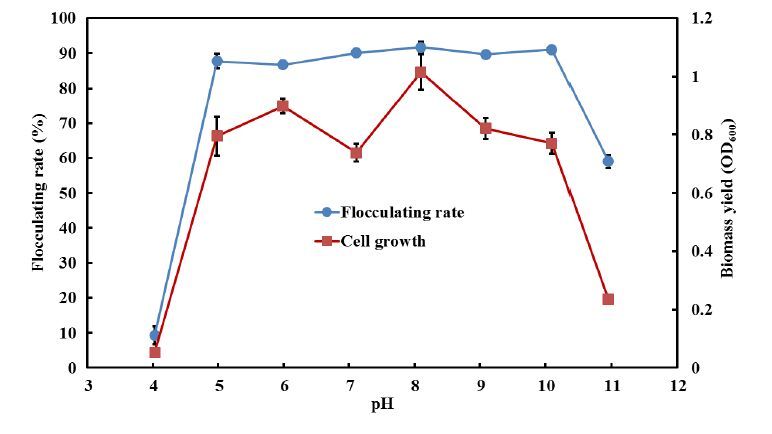
The initial pH of the fermentation medium plays an important role, which can influence the electric charge of the cells and the oxidation–reduction potential, nutrient assimilation and enzymatic reaction of bioflocculant producing strains ^[3]. Consequently, the effects of initial pH of the medium in a range from 4.0 to 10.9 on the cell growth and BF-C26 production were analyzed. As shown in Figure 1, the strain C26 produced bioflocculant BF-C26 in the initial pH range from 5.0 to 10.1, over 90% of flocculating activity was achieved from pH 7.1 to 10.1, and the highest flocculating rate was achieved at initial pH 8.1, which indicated that Microbacterium esteraromaticum C26 is an alkali-tolerant strain. Therefore, initial pH 8.1 was selected in the following experiments.

---

3.3. Effects of carbon, nitrogen sources and ratio of carbon to nitrogen source on BF-C26 production

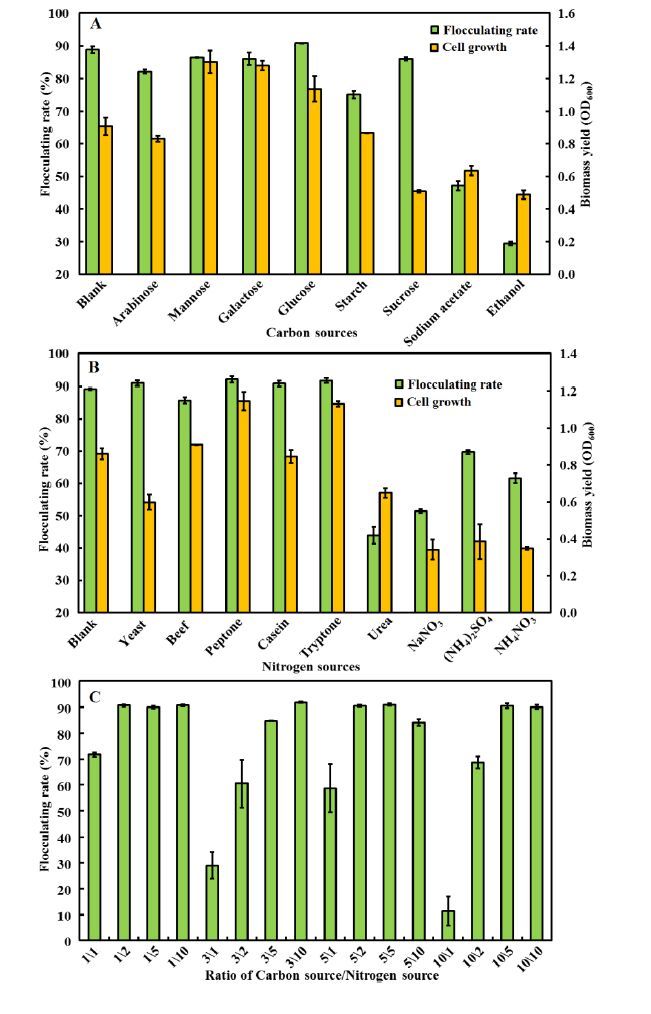
Carbon and nitrogen sources are important for the bioflocculant production and cell growth. The preferred carbon sources, nitrogen sources and the ratio of carbon source to nitrogen source lead to the maximum flocculating activity in the shortest incubation time ^[3,8]. Therefore the effects of various carbon sources, nitrogen sources and the ratios of carbon source to nitrogen source on the BF-C26 production were then analyzed. As shown in Figure 2A, flocculating rate of over 85% was achieved when mannose, galactose, glucose and sucrose were used as carbon sources, and the highest flocculating rate of 90.8% was observed when glucose was used as the carbon source. Therefore the glucose was used as the optimal carbon source in the following experiments.

Figure 2B shows the influences of different nitrogen sources on the production of BF-C26 when glucose was used as carbon source. Among the nitrogen sources investigated, all inorganic nitrogen sources resulted in poor cell growth and flocculating activity. Compared with inorganic nitrogen sources, organic nitrogen sources including yeast, beef, peptone, casein hydrolysate and tryptone were significantly better sources for BF-C26 production. Peptone was selected as the nitrogen source in the following experiments because it was favorable for both cell growth and BF-C26 production. The ratio of carbon source to nitrogen source can significantly enhance the yield of bioflocculant ^[3]. So the effects of the ratio of carbon source to nitrogen source (glucose/peptone) were determined. As shown in Figure 2C, the flocculating activity increased with the increase of peptone amount when the medium contained same concentration of glucose, and high ratio of carbon source to nitrogen source inhibited the production of BF-C26 and resulted in poor flocculating activity. The highest flocculating rate of 91.9% was achieved when C26 cells were cultured in the medium containing 3g/L glucose as carbon source and 10 g/L peptone as nitrogen source.

---

3.4. Time curse of cell growth and BF-C26 production

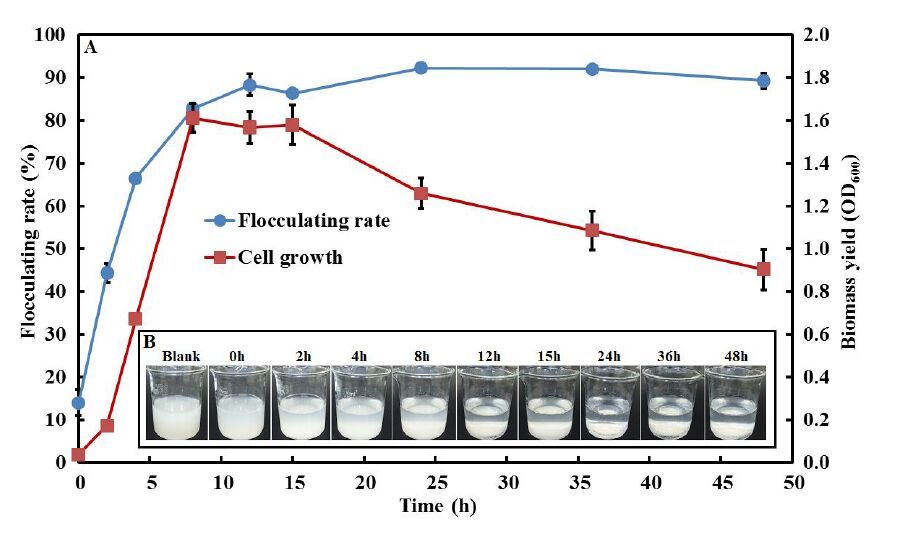
Previous studies revealed that different strains produced bioflocculant at different growth phases. The bioflocculants produced by Serratia ficaria ^[25], Bacillus sp. F19 ^[7], Proteus mirabilis TJ1 ^[6] and Enterobacter aerogenes ^[37] reached its maximum flocculating activity in early stationary phase. Bioflocculant produced by Chryseobacterium daeguense W6 reached highest flocculating activity in the death phase in which the cell lysed and the intracellular substance was released ^[9]. The bioflocculant production of Aspergillus parasiticus and Bacillus licheniformisparalleled cell growth, indicating that the bioflocculant was formed during cell growth ^[38,39]. In this study, the time course of cell growth and BF-C26 production was analyzed. As shown in Figure 3, similar to most extracellular bioflocculant, the BF-C26 was produced in the early growth stage. It can be seen that the cell growth (OD₆₀₀) increased sharply in the first 8 h, and the flocculating activity of BF-C26 showed good correspondence to the cell growth profile, indicating that the bioflocculant was secreted during cell growth. After 24 h incubation, cell growth entered into the death phase, the flocculating activity further increased to 92.27% of 24 h, and decreased after 24 h. Therefore, the fermentation broth of 24 h incubation was collected for BF-C26 extraction and the yield of BF-C26 under optimized condition was 4.92 g/L. Although the purity of the bioflocculant BF-C26 was not currently estimated, we estimated the composition of BF-C26 as being 52.8% protein and 28.1% polysaccharide. Bioflocculant BF-C26 was a cation-independent bioflocculant (As we discussed in the following results). Table 1 summarized the yields and the components of cation-independent bioflocculant reported previously. Comparatively, Microbacterium esteraromaticum C26 produced higher yield of cation-independent bioflocculant.

---

3.5. Effects of metal ions, temperature, pH and dosage on the flocculating activity

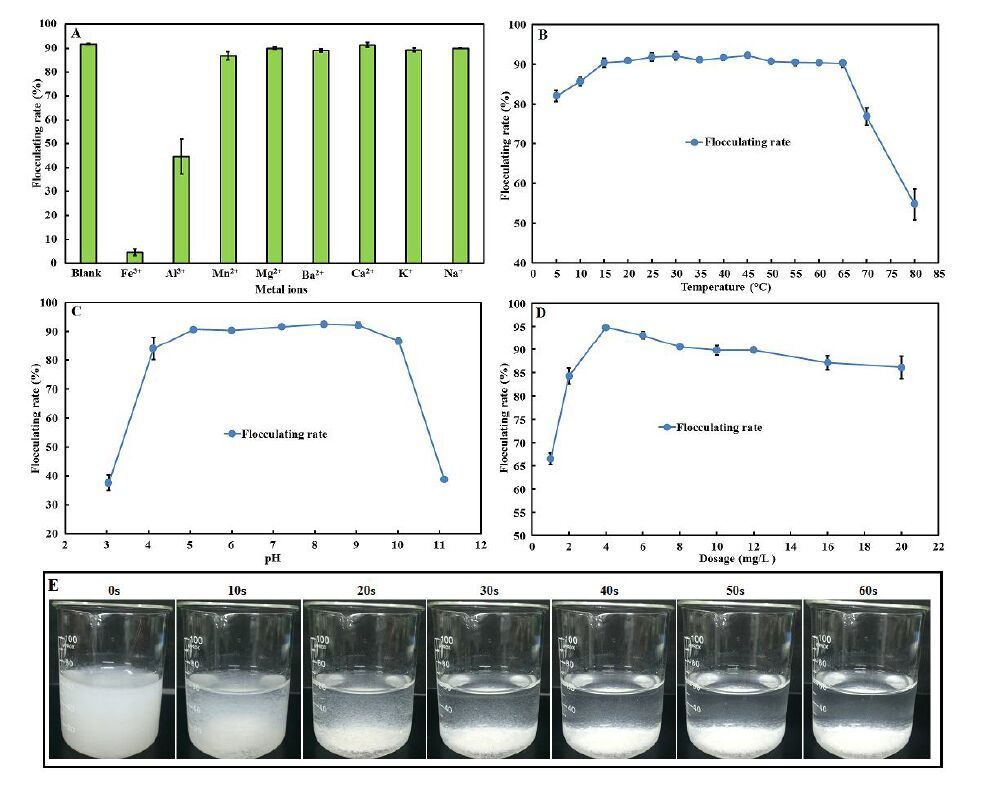
The effects of metal ions, temperature, pH value and bioflocculant dosage on the flocculating activity were evaluated. As shown in Figure 4A, none of the tested cations enhanced the flocculating activity of BF-C26. In addition, the presence of Fe³⁺ and Al³⁺ significantly decreased the flocculating rate from 91.86% to 4.68% and 44.64%, respectively. Similar results were reported previously ^[7,25]. Cations are important for the flocculation process of extracellular polysaccharide bioflocculants. For example, the bioflocculant WF-1 generated by Enterobacter aerogenes required the presence of Zn^{2+ [37]}. The flocculating ability of bioflocculant secreted by Pseudomonas aeruginosa ^[42], Aspergillus parasiticus ^[38] and Staphylococcus cohnii ssp. ^[17] depended strongly on cations. Cations stimulate the flocculating activity by neutralizing and stabilizing the residual negative charge of functional groups, and by forming the bridges between particles ^[29]. In this study, the addition of metal ions had no positive effects on flocculating activity of BF-C26, indicating that BF-C26 is a cation-independent bioflocculant, which could avoid secondary pollution and reduce the cost caused by the addition of metal ions.

The temperature is also an important factor influencing the flocculating activity. Figure 4B shows the flocculating rate of different temperatures. It can be seen that BF-C26 achieved more than 80% flocculating activity in a temperature range from 5 to 65 °C and the highest flocculating activity of 92.18% was observed at 30 °C. However, the flocculating rate decreased significantly when the temperature was higher than 65 °C, indicating that BF-C26 is heat-sensitive. This could be explained by the main components of BF-C26 being a complex of polysaccharides and proteins. The effects of pH on flocculating activity were also investigated. The pH of kaolin clay solution was adjusted with HCl and NaOH, and then the flocculating activity was measured. As shown in Figure 4C, over 90% flocculating activity was obtained in the pH range of 5.09 to 9.05, extremes of pH lead to lower flocculating activity, and the highest flocculating rate of 92.55% was achieved at pH 8.23. The flocculating rate over 90% was achieved in a dosage range of 1 to 20 mg/L, and the highest flocculating rate of 94.82% was observed when 4 mg/L BF-C26 was added (Figure 4D). The solution with lower or higher BF-C26 dosage showed poor flocculating activity. This can be explained by the bridging phenomenon in the colloid system is insufficient when the BF-C26 dosage was lower than 4mg/L. When BF-C26 dosage was higher than 6 mg/L, the decrease of flocculating activity was due to the repulsion between particles, which caused by the excessive addition of charged bioflocculant. The similar relationship between bioflocculant dosage and flocculating activity was observed in other extracellular bioflocculants ^[33,43].

The time-course images of kaolin clay suspension flocculated by bioflocculant MBF-C26 was shown in Figure 4E. It can be seen that the kaolin clay particles settled at the bottom of the beaker. In previous studies, the flocs formed by cation independent bioflocculant from Enterobacter sp. ETH-2 were observed using microscopy ^[31]. And the photomicrographs of flocs formed by cation independent bioflocculants produced by Aspergillus flavus and Chryseobacterium daeguenseW6 were observed using scanning electron microscopy ^[32,33]. These images suggested that the kaolin clay particles were bridged together by cation independent bioflocculant and formed tight packed structure. So the bioflocculant BF-C26 showed good potential to flocculate other suspension, however, until now, only kaolin clay was flocculated by bioflocculant BF-C26 in this study. In future work, the application field of this cation independent bioflocculant will be explored.

---

4. Conclusion

A novel cation-independent bioflocculant BF-C26 was produced by an alkali-tolerant strain Microbacterium esteraromaticum C26, which was reported for the first time as a bioflocculant-producing strain in this study. High yield of 4.92 g/L cation-independent bioflocculant BF-C26 was achieved at the optimal condition: 3 g/L glucose, 10 g/L peptone and initial pH 8.1. The bioflocculant BF-C26 was a complex of 52.8% proteins and 28.1% polysaccharides. The highest flocculating rate of 94.82% for kaolin suspension was achieved when 4 mg/L BF-C26 was added into the kaolin suspension at pH 8.23 and 30 °C.

---

Acknowledgments

This research was supported by National Natural Science Foundation of China (31300054), Youth Fund of the Natural Science Foundation of Jiangsu Province of China (BK20130228), Natural Science Foundation of Xuzhou City (KC15N0014), Grants from Natural Science Foundation by Jiangsu Normal University (13XLR032), Jiangsu student’s innovation and entrepreneurship training program (201513988006Y) and Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).

---

Conflict of interest

All authors declare no conflicts of interest in this paper.

---