We present a system of four nonlinear differential equations to model the use of virotherapy as a treatment for cancer. This model describes interactions among infected tumor cells, uninfected tumor cells, effector T-cells, and virions. We establish a necessary and sufficient treatment condition to ensure a globally stable cure state, and we additionally show the existence of a cancer persistence state when this condition is violated. We provide numerical evidence of a Hopf bifurcation under estimated parameter values from the literature, and we conclude with a discussion on the biological implications of our results.
1.
Introduction
Coronavirus disease 2019 (COVID-19) is a contagious disease caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The virus was first identified in Wuhan, China, in December 2019, and it quickly spread to other parts of mainland China and many other countries [1]–[6]. Due to the rapid spread of the virus with consequences worldwide, the World Health Organization (WHO) declared a public health emergency of international concern on January 30, 2020, and a pandemic on March 11, 2020 [7],[8]. The transmission of COVID-19 has become a global health threat. As of April 17, 2020, there was a total of 2,230,439 COVID-19 cases reported worldwide, with 150,810 deaths and 564,210 recovered cases [9]. According to the WHO's COVID-19 global report, over 21.2 million people had been infected with the virus as of August 16, 2020, with over 761,779 deaths [10]. Moreover, till October 14, 2021, more than 239,426,728 cases of infection and at least 4,878,373 deaths have been confirmed in Africa, Asia, Europe, North America, Oceania, South America and Antarctica. This has become one of the deadliest pandemics in history according to the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU) [11].
Studying and analyzing complex infectious disease models are difficult tasks and require some computational tools and mathematical approaches. In systems biology, mathematical presentations and computational simulations are effective tools and will help further understanding and future predictions about model dynamics. The models of COVID-19 are complicated, and they are required some mathematical tools to improve interventions and healthcare strategies. Recently, several studies about COVID-19 were suggested based on mathematical tools and computational simulations to understand this pandemic and its control approaches. In [12]–[14], the SEIR model was modified by several researchers to understand the impacts of social distancing, rapid testing, vaccination and contaminated objects in controlling the spread of COVID-19. One of the most important key elements in the spreading of COVID-19 is the basic reproduction number (also called basic reproductive ratio). This quantity, denoted by R0, represents the number of secondary infections induced by a single primary infection in a population where everyone is susceptible [15]. According to developed techniques of mathematical epidemiology models, R0 plays an important role for understanding epidemiological ideas and identifying key critical parameters for such models, and R0 may have different values for reported cases of coronavirus. According to a published study, the basic reproduction number was computed using incidence data in the city of Jakarta from March 3, 2020, to May 10, 2020. The median value of R0 was about 1.75 during the first interval. After the rigorous social distancing implemented, this value was about 1.22. In addition, the basic reproduction number has been calculated for different infectious disease models. Consequently, this quantity was calculated for a mathematical model of the CD8+ T-cell response to human T cell leukemia/lymphoma virus type I (HTLV-I) infection, given in [16].
According to published studies given in [14],[17],[18], the concept of sensitivity analysis has been presented to detect model sensitive parameters, including local sensitivities for each model state with respect to model parameters. Such sensitivities are computed by using three different methods: non-normalization, half-normalization and full-normalization. Accordingly, there was another method of sensitivity analysis given in [19]. They suggested the partial rank correlation coefficient (PRCC) technique to determine how the glioma-immune model output is affected by changes in specific parameter values.
Optimal control analysis is another effective method to identify the model critical parameters and to suggest control strategies. This technique has been used with the COVID-19 pandemic for deriving control policies. Recently, this technique has been used to find some control strategies for the COVID-19 pandemic in Indonesia, given in [20]. Then, there was a study about mathematical modeling with optimal control analysis for the spread of the COVID-19 pandemic with a case study of Brazil and cost-effectiveness; this was given in [21]. More recently, there was another approach that suggested a mathematical model with optimal control to highlight the negative impact of quarantine on diabetic people, with cost-effectiveness, presented in [22]. The reader can also find more relevant works about different approaches and mathematical models of the COVID-19 pandemic and its control strategies in [23]–[29].
Although there are many mathematical models that have been suggested for prediction of the COVID-19 pandemic, such models can be further improved and analyzed in terms of real data. Calculating the basic reproduction number with local sensitivities can improve the model outcomes further. An issue that has not been considered enough is elasticity of basic reproduction number with respect to model parameters. This helps us to identify the most critical model parameters in spreading this disease. Another issue of modeling such phenomena is validating the model results. Therefore, comparing the model predictions with real data can also indicate the accuracy and reliability of such models.
Estimating the model initial parameters for the suggested SEIR model is an important step forward in this study compared to the other existing studies about the confirmed cases of COVID-19 in the Kurdistan Region of Iraq. Therefore, we suggest the Metropolis–Hastings (MH) algorithm to estimate such model parameters, and then we use them in computational simulations. Such estimated parameters can also provide a good agreement between the model results and the daily infected cases. Another novelty here is the data collection of COVID-19 infected cases in the area that provides the future predictions and interventions. Accordingly, we have collected the daily confirmed cases of COVID-19 from January 10, 2021, to March 22, 2021. The collected real data here give us a great understanding about this disease in the area and suggested more interventions and strategies to control this pandemic. Interestingly, identifying the critical model parameters based on sensitivity and elasticity methods becomes another novelty for the suggested SEIR model.
This paper has some contributions. The main contribution is suggesting the simplified SEIR model for COVID-19 disease to predict the spreading of the disease in the Kurdistan Region of Iraq. We use this model to compare the model results and the daily infected cases more easily and correctly. Another contribution here is identifying the model critical parameters. Consequently, we suggest the local sensitivity methods to calculate the model sensitivities between the model variables and parameters. Additionally, the elasticity between the basic reproduction number, R0, and model parameters are also calculated and helps to identify the key critical parameters in spreading this disease.
The organization of this paper is as follows. In Section 2, we construct the SEIR model based on our assumptions and model transmissions. Using the next generation matrix, we derive the formula of the basic reproduction number, calculate the elasticity between R0 and model parameters and show the model local sensitivities based on the estimated values, as discussed in Section 3. We perform our computational model simulations of daily infected cases in Section 4. Finally, some conclusions and suggestions are given in Section 5.
2.
A mathematical model of the spread of the COVID-19 pandemic
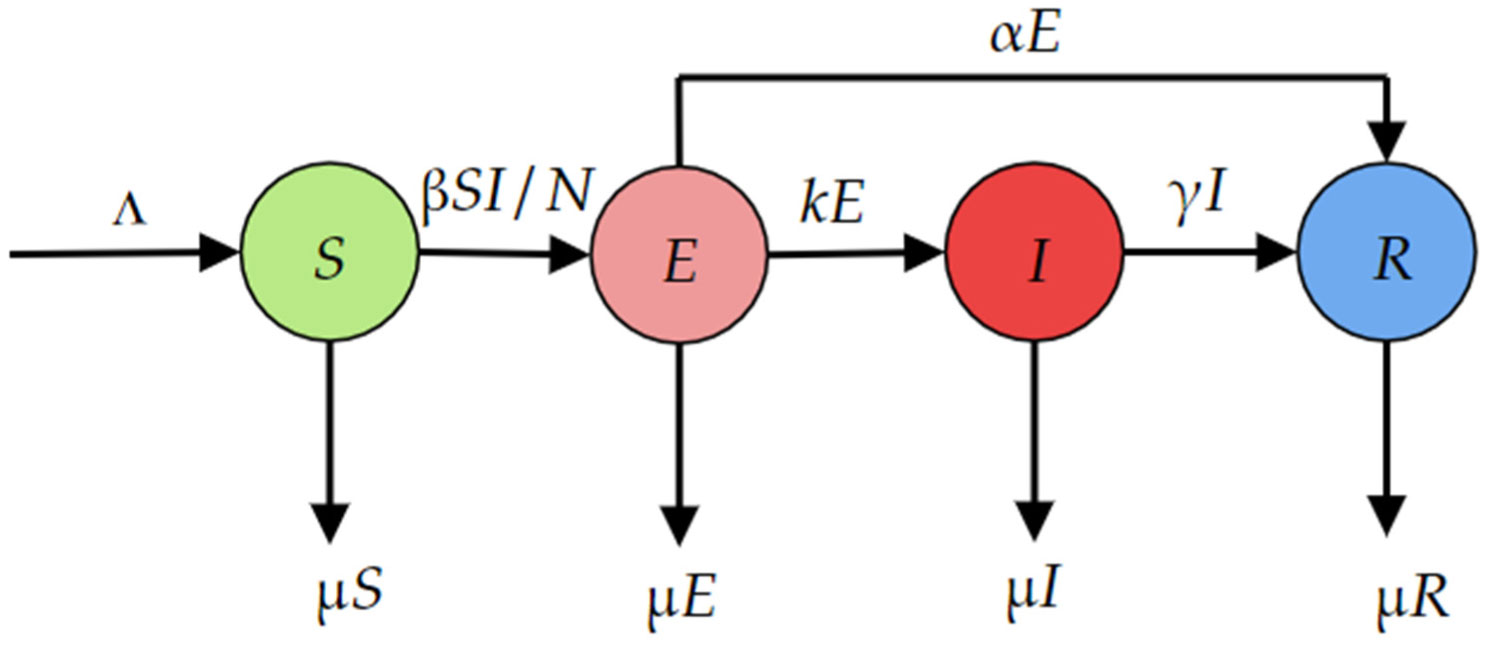
Many infectious disease models have been suggested to understand the transmission rates of COVID-19. The SEIR model has been commonly applied in many infectious diseases. This model consists of four compartments, namely, susceptible S(t), exposed E(t), infected I(t) and recovered R(t) individuals. Several authors modified the SEIR model for studying the transmission of pathogens. Among them, in [30], a modified SEIR model was used to describe the 2009 influenza A (H1N1) pandemic within local regions in Japan. It was also used for the Ebola epidemic occurring in the West African nations of Guinea, Liberia and Sierra Leone [31]. In this paper, we use the SEIR model for COVID-19 disease that describes the spreading of COVID-19 in the Kurdistan Region of Iraq. Accordingly, we develop the previously published work given in [32], and we add a parameter that shows a rate of recovery of the individuals from the exposed class. The model network of SEIR shown in Figure 1 includes various compartments with their transmissions. The model compartments and transmission rates are defined in Table 1.
The chemical reactions of the model can be expressed as follows:
Furthermore, all parameters and initial states with their biological meanings are shown in Table 1. We use the concepts of standard chemical kinetics and the mass action law to derive a system of non–linear ordinary differential equations [33],[34]. Then, the system of nonlinear ordinary differential equations takes the following form:
with non-negative initial conditions S(0) = S0 > 0, E(0) = E0 > 0, I(0) = I0 > 0, R(0) = R0 ≥ 0. All parameters are defined as contact rates between individual categories.
3.
Methods
Infectious disease models cannot be well understood only by biological techniques. Model analysis techniques and computational simulations can serve a great role in predicting and analyzing the model dynamics and identifying critical model parameters. Recently, some techniques of model analysis have been applied such as sensitivity and elasticity methods. They are useful tools to determine which variable or parameter is sensitive to a specific condition [12],[17],[18]. Calculating the basic reproduction numbers at the equilibrium points can also provide a great environment to discuss infectious disease models more widely and accurately [13],[14]. Here, in this study, we focus on three important techniques of model analysis: basic reproduction numbers, local sensitivity and elasticity methods. More details about the suggested techniques are discussed in the following sections.
3.1. Next generation method
In epidemiology, the next-generation matrix is used to derive the basic reproduction number for a compartmental model of the spread of infectious disease. This method was proposed by Diekmann et al. (1990) [35] and van den Driessche and Watmough (2002) [36]. One of the most important parameters for epidemiological models is the basic reproduction number [37]. Using Equation 2, we can easily derive R0 at an equilibrium point E0. The suggested model here includes two infected states, E and I, and two uninfected states, S and R. Let X be a vector of infected classes and Y be a vector of uninfected classes. They are shown below:
To find equilibrium points for the model, let us set the right-hand side of Equation 2 equal to zero. Then, the equilibrium points are obtained. The first equilibrium is the COVID-19-free equilibrium point, which is represented by
The second type of equilibrium is called the endemic equilibrium point. It is given below:
where S′,E′,I′,R′ are positive and defined as follows:
Using the next generation method, we have the vector functions
Then, the Jacobian matrices for M, G at E0 are given below:
Since W is a non-singular matrix, W−1 can be calculated:
Therefore, the basic reproduction number is the spectral radius of HW−1. Thus, the basic reproduction number for Equation 2 is
3.2. Elasticity of R0
The concept of elasticity for infectious disease models has an effective role in determining the sensitivity between R0 and the model parameters. For calculating such coefficients, the following main formula is used:
where ω is the set of all parameters. Using Equation 5, we can calculate the elasticity index of R0 for each model parameter. They are given below:
Using the estimated parameters, we can compute the model elasticity; see Table 2.
The results given in Table 2 show the positive and negative signs for the model elasticity. These give us the direct or indirect relations between R0 and the model parameters. For example, this coefficient is positive for the set of parameters {Λ, k, β}. This means that when these parameters, {Λ, k, β}, are increased, the value of R0 is also increased, and this virus spreads further. On the other hand, the signs of {γ, α, µ} are negative. This means that the value of the basic reproduction number can be reduced by increasing such parameters. Interestingly, β is the most significant positive parameter that can be utilized to reduce R0. For example, if the value of β is decreased by 10%, then the basic reproduction number will be reduced to R0 = 0.52886708. Furthermore, reducing the contact rate between individuals can impact the number of infected people from the disease.
3.3. Sensitivity analysis
The concept of local sensitivity analysis is another step forward for studying infection disease models and identifying the model critical elements. This is simply used for determining the sensitivity of each model species with respect to the model parameters. This method was recently considered in [14],[17],[18],[38]. Assume that there are p compartments (yi for i = 1,2,...,p) and q parameters (bj for j = 1,2,...,q) in an infectious disease model. The model balanced equations are represented by the following system of differential equations:
where y∈ℝp, b∈ℝq. The model sensitivities can be computed with three different techniques: non normalizations, half normalizations and full normalizations.
The full-normalization sensitivities are given as follows:
The half-normalization sensitivities are defined as follows:
The non-normalization sensitivities can be expressed as follows:
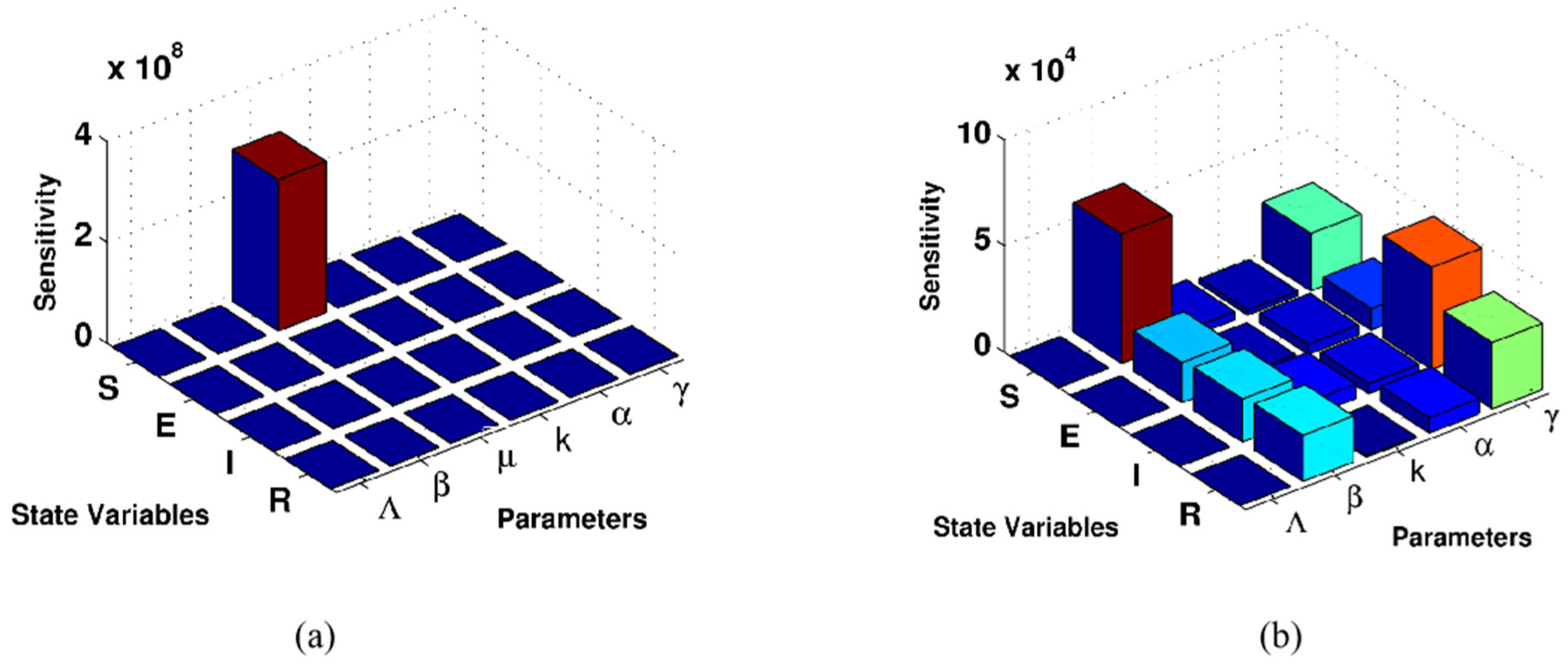
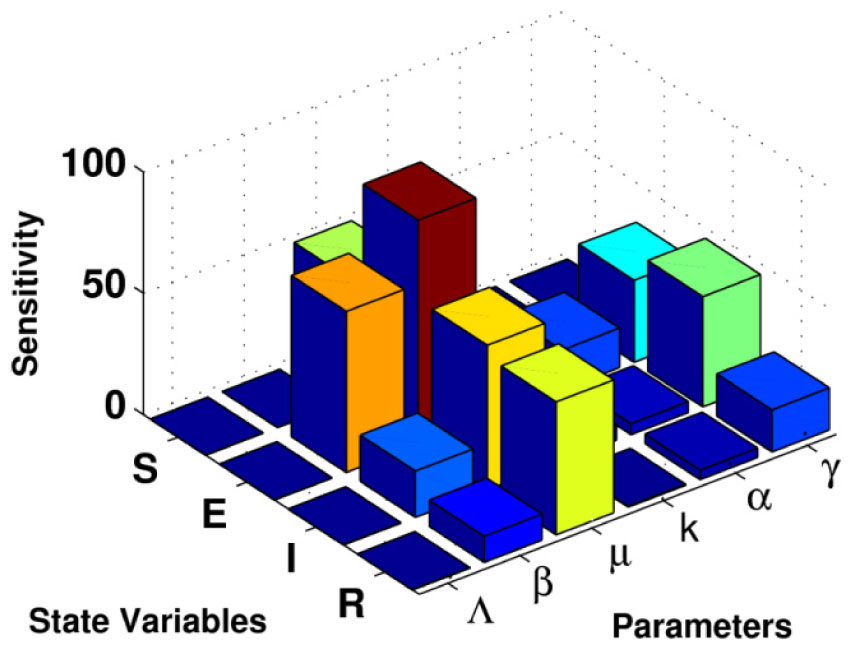
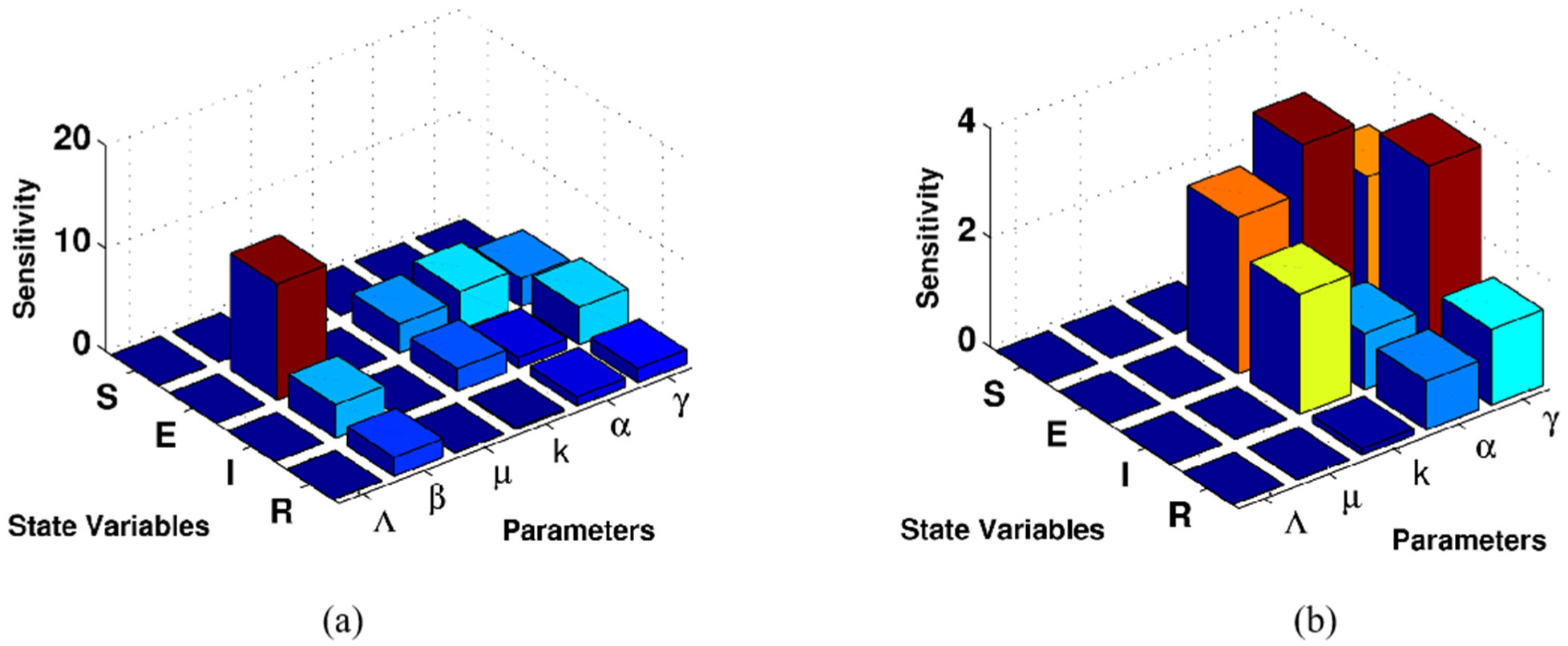
where Syibj stands for sensitivity for each variable yi with respect to each parameter bj. We apply the idea of local sensitivity for the proposed COVID-19 model (Equation 2). The model initial populations are S0 = 6 × 106, E0 = 105.26, I0 = 1027 and R0 = 1027, and the model estimated parameters are α = 0.23, k = 0.34, γ = 0.08, β = 0.17, µ = 0.00003, and Λ = 182.46. They are used in computational simulations using SimBiology Toolbox for MATLAB. The results provide a wide range of means of identifying the key critical model parameters. According to the non-normalization technique, susceptible individuals, S, are very sensitive to the natural death, µ. This is clearly shown in Figure 2a. In addition, all model states are also sensitive to these parameters: {β, α, γ} (see Figure 2b). This means that natural death rate, infection rate, natural recovery rate and transition rate between exposed individuals and recovered individuals have a great impact on the model populations, while the rate of natural birth has less impact on the model states. In addition, using the half-normalization method shows that the most sensitive parameter for all model states is the natural death µ. In addition, the exposed and infected individuals are also very sensitive to the set of parameters {β, γ}; see Figure 3. According to the full-normalization technique shown in Figure 4, the model parameters {Λ, µ} are the less critical model parameters, whereas the remaining model parameters are the most sensitive parameters. Interestingly, all model results here provide a wide range of means of studying such models biologically and give more suggestions. This is because identifying critical model parameters helps us to further model improvements and suggest control strategies and vaccination programs.
4.
Computational simulations and discussions
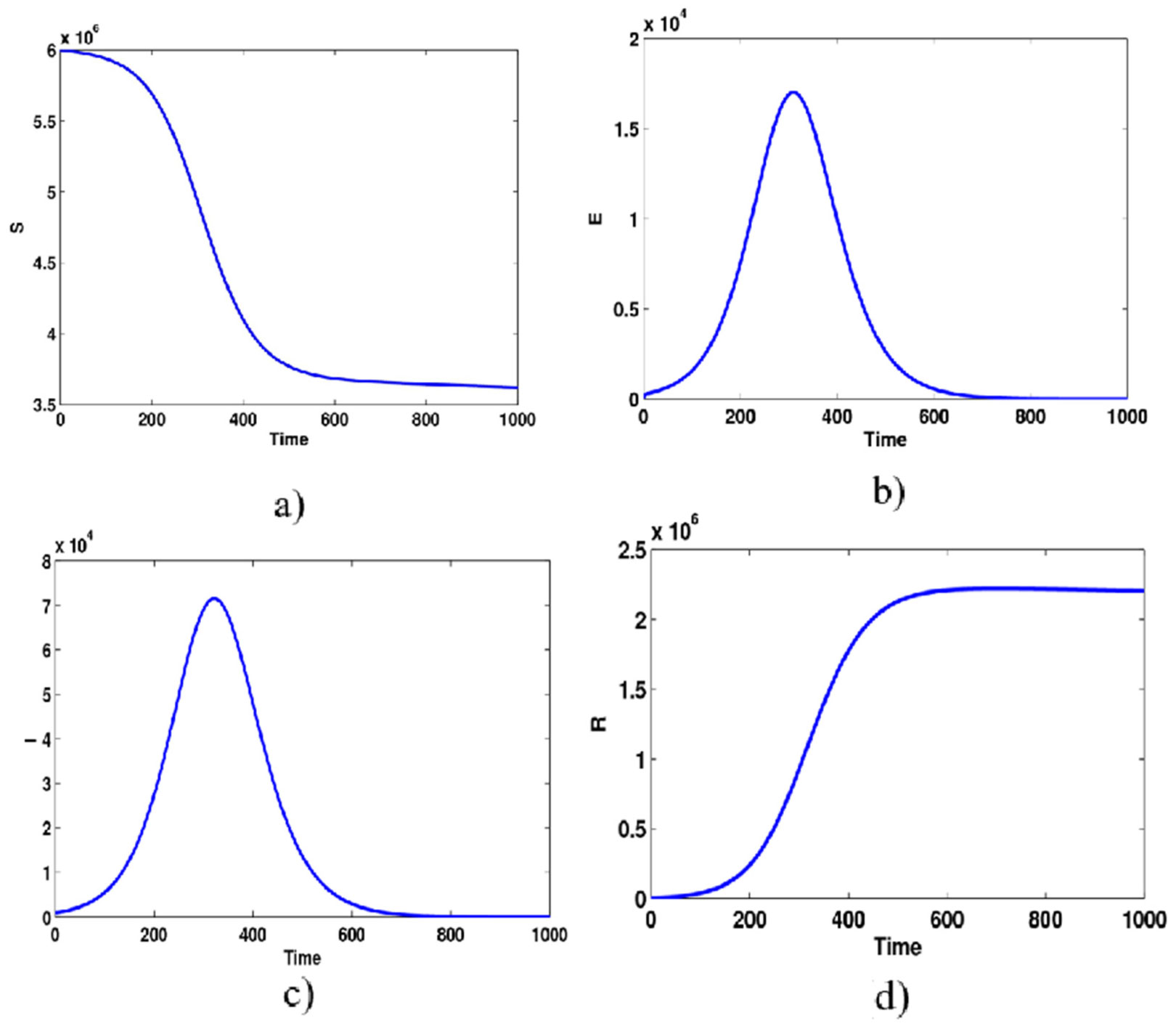
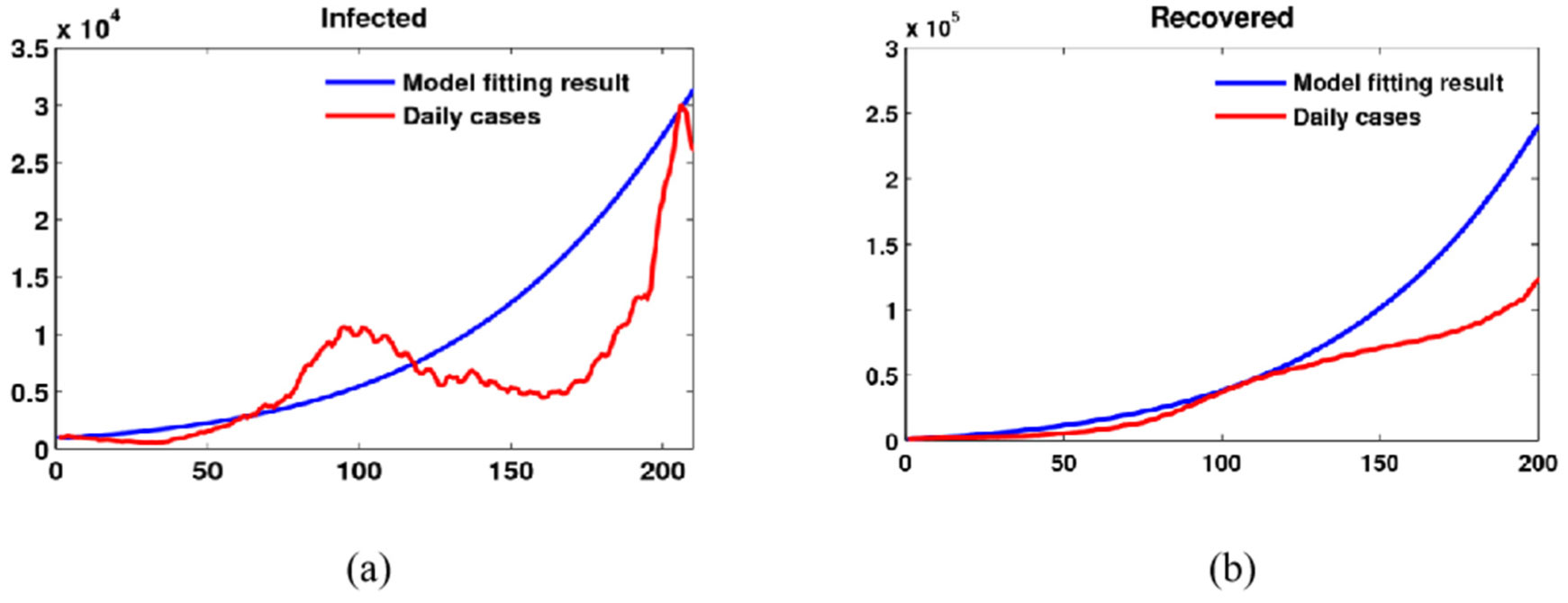
Computational techniques are effective tools and frequently required to analyze some complex infectious disease models. The estimated parameter values and initial populations are obtained from the real data in the Kurdistan Region of Iraq given in the Appendices. The model estimated parameters are α = 0.23, k = 0.34, γ = 0.08, β = 0.17, µ = 0.00003, Λ = 182.46, and the model initial variables are S0 = 6 × 106, E0 = 105.26, I0 = 1027, R0 = 1027. Using System Biology Toolbox (SBedit) in MATLAB, we determine the numerical approximate solutions of the model (Equation 2); see Figures 5 and 6. Numerical simulations are calculated in two-dimensional planes. All model computational results here are very interesting and provide some biological aspects. Firstly, it can be seen that Figure 5 shows the model dynamics of susceptible, exposed, asymptomatic infected and recovered people. We have noticed that the number of healthy people decreases gradually and becomes stable after 500 days, while the dynamics of recovered people increases and then becomes more flat after 500 days as well. Then, from 200 to 600 days, the numbers of exposed and infected individuals change dramatically. More interestingly, Figure 6 shows the comparison of total populations between the real data cases shown in Table 3 and the model equations given in Equation 2. For example, the total populations of infected people for the model equations and real data are given in Figure 6a. Then, Figure 6b shows the total populations of recovered individuals for model equations and real data. The results show good agreement between the real data and the model results. Finally, it is clear that our model results are fitted for the confirmed cases in Kurdistan. This means that the suggested model here can further be used to predict and give more control strategies.
5.
Conclusions
Control strategies and preventions for the COVID-19 pandemic may not be well understood only by healthcare techniques and biological concepts. Mathematical models and computational simulations have been widely used for further improvements and identifying the model critical parameters. Therefore, identifying such parameters becomes an issue that can be further studied, and more techniques can be proposed. Sensitivity of model parameters helps international efforts to suggest more control strategies and preventions. Accordingly, the suggested SEIR model in this study plays an effective role in identifying the model critical elements using elasticity and sensitivity of R0. Thus, the model sensitivities were calculated using three different techniques: non normalizations, half normalizations, and full normalizations. The results showed that the most effective parameters for spreading this disease are contact rate among people, transition rate from exposed class to the infected class and natural recovery rate. Interestingly, identifying the model critical parameters here will help to suggest further interventions and control strategies in the Kurdistan Region of Iraq. The suggested SEIR model can be further developed and can have added more transmission rates between model states. For example, the vaccination compartment with its contact rates can be added to the model. This helps to study this disease more widely and accurately. Further techniques of model analysis such as optimal control will also be applied to the model to find more control strategies.









 DownLoad:
DownLoad: