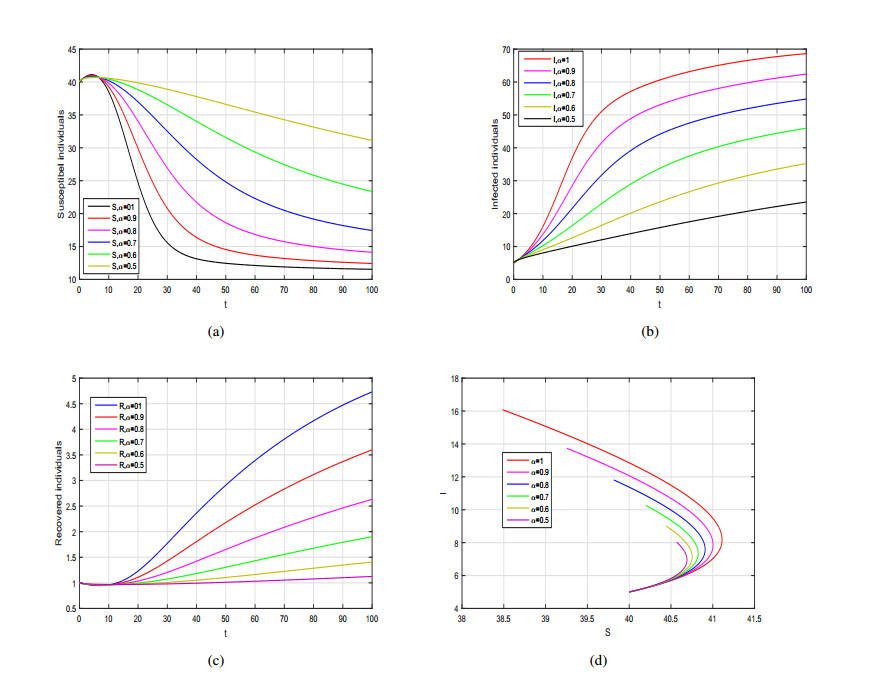
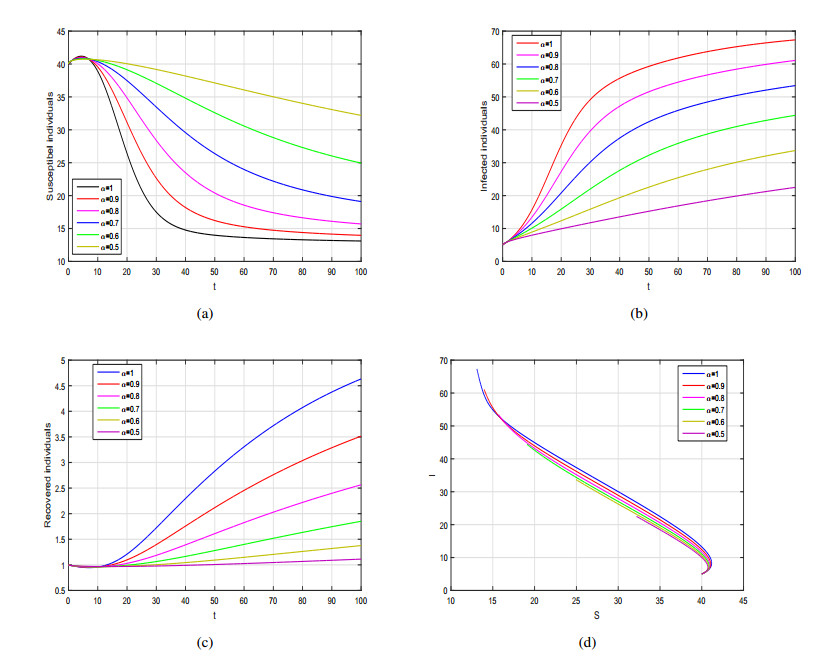
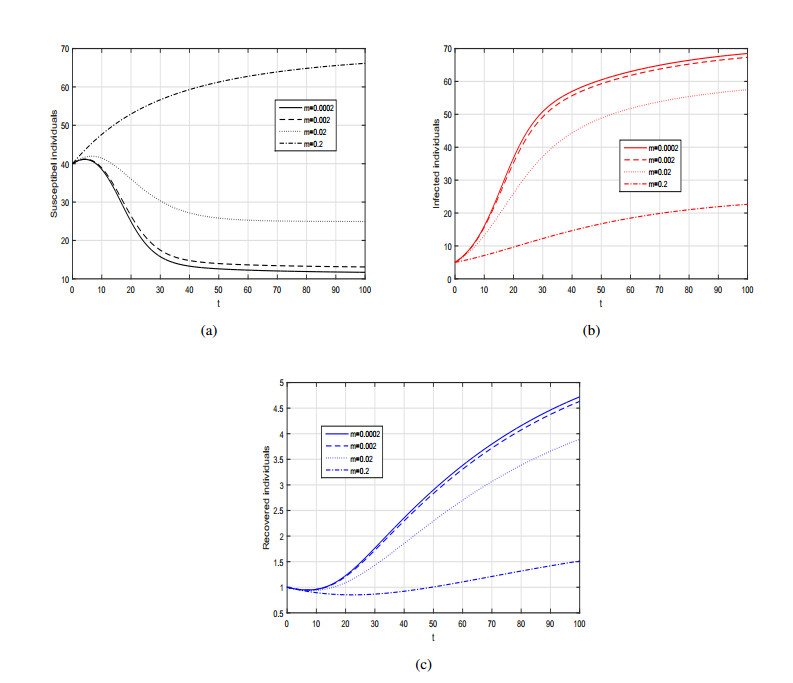
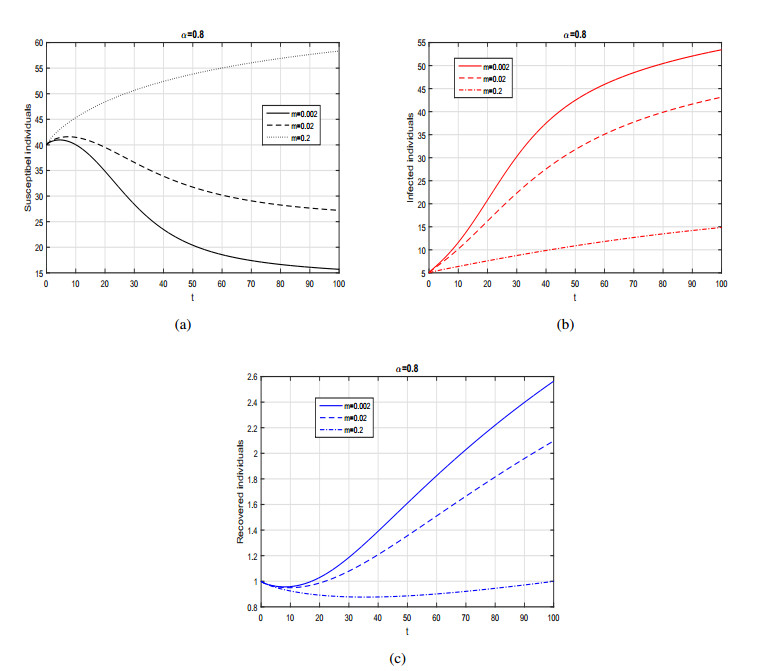
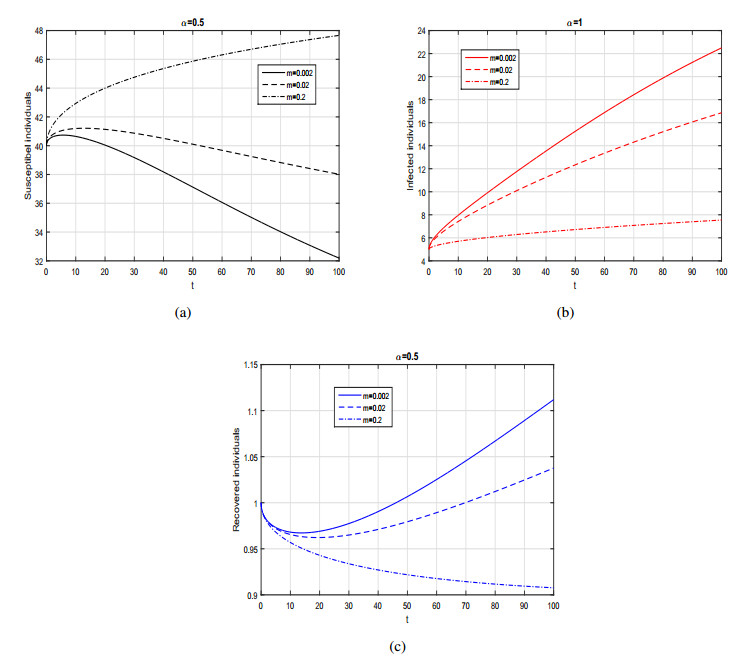
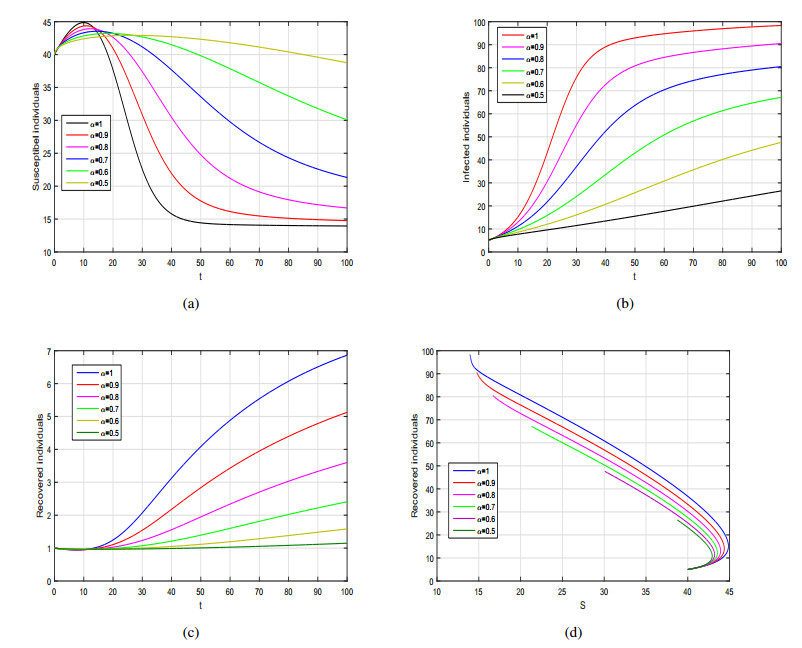
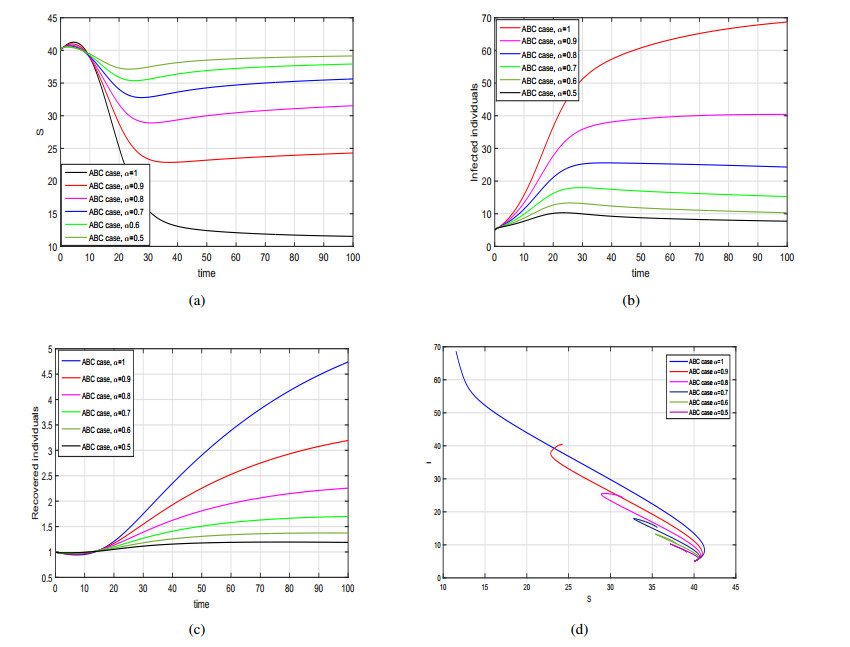
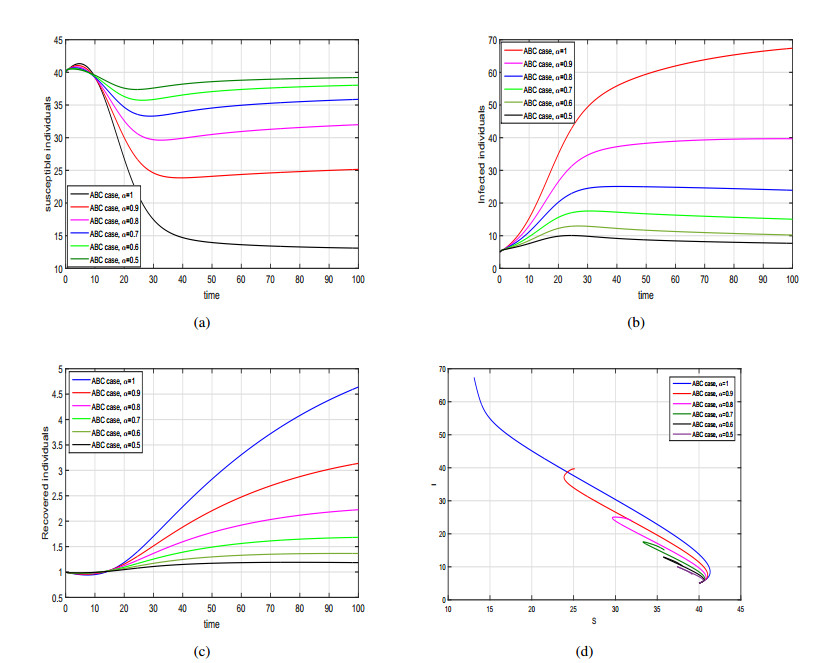
The purpose of this work is to present the dynamics of a fractional SIR model with generalized incidence rate using two differential derivatives, that are the Caputo and the AtanganaBaleanu. Firstly, we formulate the proposed model in Caputo sense and carried out the basic mathematical analysis such as positivity, basic reproduction number, local and global dynamics of the disease free and endemic case. The disease free equilibrium is locally and globally asymptotically stable when the basic reproduction number is less than 1. We also show that the SIR fractional model is locally and globally asymptotically stable at endemic state when the basic reproduction number greater than unity. Further, to analyze the dynamics of Caputo model we provide some numerical results by considering various incidence rates and with different fractional order parameters. Then, we reformulate the same model using the Atangana-Baleanu operator having nonsingular and non-local kernel. We prove the existence and uniqueness of the Atangana-Baleanu SIR model using PicardLindelof approach. Furthermore, we present an iterative scheme of the model and provide graphical results for various values of the fractional order α. From the graphical interpretation we conclude that the Atangana-Baleanu derivative is more prominent and provides biologically more feasible results than Caputo operator.
1.
Introduction
Poroelastic materials play an important role in various fields such as geophysics [1,2,3], biomechanics, chemical engineering [4,5], and materials science [6,7]. The physical process in porous media is usually described by a poroelasticity model. In homogeneous isotropic linear elastic porous media, the governing equations for the quasi-static poroelasticity model are given as
where
Here u and p represent the displacement vector of solid and the pressure of solvent, σ(u) is the (effective) stress tensor, vf is the volumetric solvent flux, and Eq (1.4) is so-called Darcy's law. I denotes the d×d identity matrix and ε(u) is the Green strain tensor. f is the body force and ϕ is the source term. The permeability tensor K=K(x) is assumed to be symmetric and uniformly positive definite in the sense that there exist positive constants K1 and K2 such that K1|ζ|2≤K(x)ζ⋅ζ≤K2|ζ|2 for a.e. x∈Ω and ζ∈Rd. The parameters μf,α and c0 are the solvent viscosity, Biot-Willis constant and constrained specific storage coefficient, respectively. λ and μ (Note that we use μ instead of 2μ in (1.3), as often seen in the literature, to simplify the notation) are Lamé constants, which can be computed from the Young's modulus E and Poisson ratio ν as
Much effort has been carried out for the above poroelasticity model. Biot [1] proposed the three-dimensional consolidation theory, providing important theoretical support for the development of the poroelasticity model. Showalter [8] showed the well-posedness of a weak solution of a linear poroelasticity model. Phillips and Wheeler proposed and analyzed a continuous-in-time linear poroelasticity model [9] and a discrete-in-time linear poroelasticity model [10] with the continuous Galerkin mixed finite element method (MFEM) in space. After that, a discontinuous Galerkin MFEM for the model is also developed [11]. The nonconforming FEM was studied for the linear poroelasticity model [12,13], and the MINI and stabilized P1−P1 elements were employed to solve the linear poroelasticity model [14]. Ju et al. [15] developed parameter-robust numerical algorithms for the Biot model and applied the algorithms to simulations of brain edema. Yi [16] studied two kinds of locking phenomena (Poisson locking and pressure oscillation) in linear poroelasticity and proposed a new family of MFEM to overcome them. To reveal the underlying deformation and diffusion processes of the original model, Feng et al. reformulated the linear poroelasticity model to a fluid-fluid coupled system and proposed a multiphysics MFEM to overcome the locking phenomena [17]. One can refer to more numerical methods for solving the poroelasticity model, such as the Galerkin least square methods [18,19], two-field finite element method [20,21], four-field finite element method[22,23], finite volume method [24], and Weak Galerkin finite element method [25,26].
In practical problems, the model parameters have different ranges, such as the Poisson ratio ν=0.1∼0.3 and the permeability K=10−14∼10−16m2 in geophysics [6]. This requires us to construct numerical methods to be robust for the selection of model parameters. Following the idea of [17], we first reformulate the original problem into a four-field by introducing some auxiliary variables. After that, we discretize the four-field problem by the backward Euler method in time and design the coupled and decoupled algorithms by using MFEM with P2−P1−P1−P1 element pairs in space. The inf-sup condition is proved to be uniformly independent of the physical parameters, and the optimal convergence rates both in space and time are also obtained for the proposed algorithms. It is pointed out that, for the decoupled algorithm [17], there exists the constraint τ=O(h2) on the mesh size h and time step τ while performing the error estimates. But there is no constraint on h and τ for the decoupled algorithm arising from our four-field problem. The reason is that the decoupled algorithm ensures that the variables p,ξ, and η are in the same time layer, thereby avoiding the use of inverse inequality. To improve computational efficiency and achieve high-accuracy in time, we further design a two-step backward differentiation formula (BDF2) Galerkin algorithm, which combines the MFEM with P2−P1−P1 element pairs for the space variables. The corresponding stability and error estimates of the BDF2 algorithm are performed, and the optimal convergence rate in time is also obtained in Theorem 7. Numerical tests are also provided to verify that our proposed algorithms are robust for selection of ν and K, overcome the Poisson locking in stress field and nonphysical oscillation in the pressure field, and have the optimal convergence rates. In addition, our algorithms are also used to simulate the brain edema. The numerical results on pressure are consistent with the experimental results [27]. The influence of the Poisson rate ν on the displacement of brain tissue and maximum pressure is investigated, which shows that the values of ν have little influence on the maximum pressure, and the maximum tissue deformation becomes smaller as ν gets bigger.
The remainder of this paper is organized as follows: In Section 2, the original problem is equivalently transformed into a four-field problem, and the four-field problem is also proved to satisfy the inf-sup condition. In Section 3, the coupled and decoupled algorithms with the Euler method are proposed for the four-field problem, and the error estimates are also presented. In Section 4, the BDF2 algorithm for the poroelasticity problem is also designed, and the stability analysis and error estimates are established. In Section 5, numerical examples are provided to verify that the algorithms are robust with respect to the key physical parameters, reach the optimal convergence rates, and overcome the locking phenomenon. In Section 6, the algorithms are applied to simulate the brain edema. Finally, we draw a conclusion to summarize the main results of this paper.
2.
Analysis of the model
2.1. Model reformulation
The standard function space notations are adopted; their precise definitions can be found in [28,29,30]. In particular, (⋅,⋅) and ⟨⋅,⋅⟩ denote respectively the standard L2(Ω) and L2(∂Ω) inner products, where Ω⊂Rd(d=2,3) is a bounded polygonal domain with the boundary ∂Ω. For any Banach space B, we let B=[B]d, and use B′ to denote its dual space. We also introduce the function spaces
Define the space of infinitesimal rigid motions by RM={r:=a+b×x;a,b,x∈Rd}. As in [28,30,31], RM is the kernel of the operator ε, i.e., r∈RM if and only if ε(r)=0. Hence, we have
Denote L2⊥(∂Ω) and H1⊥(Ω) respectively by the subspaces of L2(∂Ω) and H1(Ω), which are orthogonal to RM, and are given as,
It follows from [17,32] that there exists a constant ck>0 such that
To close the above system (1.1)–(1.4), here we set the following boundary and initial conditions:
By introducing the variables q=divu,η=c0p+αq,ξ=αp−λq, one has
with
Thus, the problem (1.1)–(1.4) can be equivalently written as
Remark 1. We point out that the following results with respect to the pure Neumann condition can be extended to the case of the pure Dirichlet condition or mixed Dirichlet-Neumann condition. If the boundary condition (2.3) is replaced by a pure Dirichlet condition or the mixed Dirichlet-Neumann condition, there is no need to introduce the space H1⊥(Ω) for the variable u.
2.2. Inf-sup condition
We here consider an equidistant partition of the time interval [0,T] with a time step τ=T/N and tn=nτ (n=1,2,⋯,N), where N∈N. The focus of this section is on the proof of the inf-sup condition, which will hold uniformly independently of physical parameters. To do that, we first discretize the time-dependent problem (2.7)–(2.10) with (2.3)–(2.5) by the backward Euler method and BDF2 scheme in time to make it a static problem in each time step. Note that the discussion on inf-sup condition is similar for the backward Euler method and BDF2 scheme. Below, we mainly consider the backward Euler method. By the backward Euler method, the weak formulation of problem (2.7)–(2.10) with (2.3)–(2.5) reads: ∀(v,φ,ω,ψ)∈H1(Ω)×L2(Ω)×L2(Ω)×H1(Ω), ∃(u,ξ,η,p)∈H1⊥(Ω)×L2(Ω)×L2(Ω)×H1(Ω) such that
where ˜ϕ(x,tn)=τϕ(x,tn)+η(x,tn−1) and ˜ϕ1=τϕ1.
Define
Taking Λ=H1⊥(Ω)×L2(Ω)×L2(Ω)×H1(Ω) and ξ0 as the mean-value zero part of ξ, we define
where δ0 is a positive constant, u∈H1⊥(Ω), ξ∈L2(Ω), η∈L2(Ω) and p∈H1(Ω).
The following theorem shows that A is invertible and the inverse is a map from Λ′ to Λ.
Theorem 1. There exists a constant β>0 for the problem (2.11)–(2.14), independent of μ,κ2,κ3 and Kτ/μf, such that the following inf-sup condition holds:
Proof. To prove (2.16), we need to prove the following inequalities: ∀(0,0,0,0)≠(u,ξ,η,p)∈Λ, ∃(v,φ,ω,ψ)∈Λ such that
where β1 and β2 are positive constants and independent of μ,κ1,κ2,κ3 and Kτ/μf.
Suppose that (0,0,0,0)≠(u,ξ,η,p)∈Λ is given. It follows from the theory of the Stokes equation that there exists a constant β0>0, depending only on the domain Ω, and w∈H1⊥(Ω) such that
Taking v=u−δ0w, ϕ=ξ, ω=η, ψ=p in (A(u,ξ,η,p),(v,φ,ω,ψ)), we have
Using Young's inequality and (2.17), we have
Inserting (2.19) into (2.18), using (2.17) and choosing θ0=δ0=β−20μ−1, we obtain
Noting that
and using (2.21) in (2.20), we have
It is easy to check that
Combining (2.22) and (2.23), the (2.16) holds and β=1/(8(1+μ12δ120β0)). The proof is complete. □
Theorem 1 shows that the bilinear form (A(⋅),⋅) is coercive. Moreover, it is easy to check that (A(⋅),⋅) is bounded. According to the Lax-Milgram theorem, there exists a unique solution (u,ξ,η,p)∈Λ for the linear system (2.11)–(2.14). Thus, there holds the following theorem:
Theorem 2. There exists a unique weak solution to problem (2.7)–(2.10) with (2.3)–(2.5). Likewise, there exists a unique weak solution to problem (1.1)–(1.4) and (2.3)–(2.5).
3.
MFEM with backward Euler method
3.1. Coupled and decoupled algorithms
Let Th be a quasi-uniform triangulation or rectangular partition of Ω with maximum mesh size h, and ˉΩ=∪K∈ThˉK. In this part, we use the backward Euler method in time discretization. For a smooth function v defined on [0,T], we denote dtvn=(vn−vn−1)/τ.
A number of stable mixed finite element spaces (Xh,Mh) have been presented in the literature [33]. A typical example is the following so-called Taylor-Hood element (cf. [33,34]):
Finite element approximation space Wh for p and η variables can be chosen independently; any piecewise polynomial space is acceptable provided that Wh⊃Mh. A convenient choice is Wh=Mh.
Define
If the problem (2.11)–(2.14) is discretized by the finite element spaces Vh,Mh, and Wh, then the discrete counterpart is to find (uh,ξh,ηh,ph)∈Vh×Mh×Wh×Wh such that
Set Λh=Vh×Mh×Wh×Wh, and define the operator Ah:Λh→Λ′h arisen from (3.2)–(3.5). Then we have the following theorem:
Theorem 3. For the problem (3.2)–(3.5), there exists a constant β>0, independent of μ,κ2,κ3, and Kτ/μf, such that the following inf-sup condition holds:
We omit the proof of Theorem 3, since it is completely analogous to the proof of Theorem 1. Moreover, Theorem 3 implies that Ah is invertible and the inverse is a map from Λ′h to Λh with operator norm independent of the parameters.
Below, we assume f,f1, ϕ, and ϕ1 all are independent of t. Note that all the results can be easily extended to the case of time-dependent source functions.
Now, we consider the fully discrete MFEM for the problem (2.7)–(2.10) with (2.3)–(2.5) based on the backward Euler method, which involves the coupled (i.e., Algorithm 1) and decoupled (i.e., Algorithm 2) algorithms. The coupled algorithm solves four unknowns simultaneously based on problem (2.7)–(2.10). The decoupled algorithm only solves two subproblems. Noting that problem (2.7) and (2.8) can be regarded as a generalized Stokes problem for a given η and problem (2.9) and (2.10) is a coupled problem associated with the diffusion problem, we can solve a generalized Stokes problem for u and ξ by using the solution of η at the previous time-step. After that, we solve the diffusion problem for η and p.
3.2. Error estimates
To derive the error estimates of the MFEM, we define L2(Ω)-projection Qh:L2(Ω)→Xkh by
where Xkh:={ψh∈C0;ψh|K∈Pk(K)∀K∈Th}, k is the degree of piecewise polynomial on K.
Next, for any φ∈H1(Ω), we define the elliptic projection Sh:H1(Ω)→Xkh as
and for any v∈H1(Ω), we define its elliptic projection Rh:H1(Ω)→Vkh as
where Vkh:={vh∈C0;vh|K∈Pk(K),(vh,r)=0∀r∈RM}.
It follows from [28] that for any 0≤s≤k, Qh,Sh and Rh satisfy
Furthermore, we introduce the following error notations:
Also, we denote
Then we present the error estimates for the coupled and decoupled algorithms by the following theorems.
Theorem 4. Let {(unh,ξnh,ηnh,pnh)}n≥0 be solutions of the coupled algorithm (i.e., Algorithm 1). Then it holds
Theorem 5. Let {(unh,ξnh,ηnh,pnh)}n≥0 be solutions of the decoupled algorithm (i.e., Algorithm 2). Then for the case c0>0 and λ<∞, it holds
The proof of the aforementioned theorems follows a similar approach to that of [17, Theorem 3.7]; thus, further details are omitted here. Our primary focus is on the constraint condition τ=O(h2) in the error estimates for the algorithm with θ=0 [17]. This constraint arises because the choice of the test function ψh results in the variables p,ξ, and η being in different time layers, which in turn leads to the application of an inverse inequality in the estimation of the right-hand side term. To address this issue, a straightforward solution is to select an appropriate test function ψh that ensures the variables p,ξ, and η reside in the same time layer. To do that, we first examine the following error equations:
which are derived from the fourth equation of Algorithm 2 and the continuous problem (2.10) the fourth equation of Algorithm 2 and the continuous problem (2.10). Based on Algorithm 2, we can define η−1h by
Setting ωh=dtGnη,ψh=Znp in (3.16) and (3.17) separately after lowering the super index n+1 to n, applying the summation operator τ∑ln=0 to both sides of (3.17) and utilizing the fact that G−1η=0, there holds
Note that the choice of ψh=Znp is critical. Unlike the setting in [17], where ψh=ˆZnp:=κ1Zn+1ξ+κ2Znη is employed, selecting ψh=Znp eliminates the need to apply the inverse inequality to bound a gradient term (as seen in [17, estimate (3.52)]). Instead, we only need to apply the Cauchy-Schwarz and Young inequalities to the last term on the right-hand side of (3.18) to derive
where ϵ∈(√2κ2κ3,+∞) is a positive constant from Young inequality.
Additionally, we point out that:
(i) The aim of ϵ∈(√2κ2κ3,+∞) is to ensure the signs of terms κ2−κ1ϵ2τ2∑ln=0‖dtGnη‖2L2(Ω) and (κ34−κ12ϵ)τ2∑ln=0‖dtGnη‖2L2(Ω) to be positive. In addition, for the case of λ→+∞, there does not exist the term κ1τ2∑ln=0(dtGn+1ξ,dtGnη) in error estimates. For the case of c0=0, it has a similar discussion for the term κ1τ2∑ln=0(dtGn+1ξ,dtGnη).
(ii) For the decoupled algorithm, it does not exist the constraint on the time step τ and mesh size h.
4.
MFEM with BDF2 scheme
4.1. BDF2 algorithm and stability analysis
We now consider the BDF2 scheme in time discretization for the problem (2.7)–(2.10) with (2.3)–(2.5). For a smooth function v defined on [0,T], we denote
Based on (4.1), we introduce the BDF2 fully discrete scheme in Algorithm 3.
The next lemma establishes a discrete energy inequality for the BDF2 algorithm.
Lemma 4.1. Let {(unh,ξnh,ηnh)}n≥0 be defined by the BDF2 algorithm. Then it holds
where C3=C3(ck,ca,cb,cp,μ,κ3,κ2,T,K,μf).
Proof. Setting vh=dtu1h in (4.2), φh=dtξ1h in (4.3) and ψh=p12h in (4.4), we get
Adding (4.10)–(4.12), there holds
Using the Cauchy-Schwarz inequality, triangle inequality, (2.2), (4.32), trace inequality, Poincaré inequality, and Young inequality, we can bound the right-side terms of (4.13) as follows:
where ca is a positive constant related to Trace inequality.
Substituting (4.14)–(4.19) into (4.13), we have
Next, setting vh=Dtun+1h,φh=ξn+1h and ψh=pn+1h in (4.5)–(4.7), we obtain
Adding (4.21)–(4.23) and using the fact of
we have
Applying the summation operator τ∑ln=1 to both sides of (4.25), there holds
Similar to (4.13), we can bound the first four terms of the right side of (4.26) as follows:
Substituting (4.27)–(4.30) into (4.26) and using (4.20) for the resulting inequality, we can deduce that (4.9) holds. The proof is complete. □
4.2. Error estimates
In this subsection, we consider the optimal convergence analysis of the BDF2 algorithm. Before that, we have the following estimate for the BDF2 algorithm.
Theorem 6. Let \{(\mathbf{u}_h^{n}, \xi_h^{n}, \eta_h^{n})\}_{n\geq 0} be defined by the BDF2 algorithm. Then there exists a positive constant C_{4} independent of mesh size h and time step \tau such that
Proof. First, it is easy to check that there exists a positive constant c_{b} such that
For n\geq 1 , at t = t_{n+1} , we have for (2.7)–(2.10) that
Moreover, we have from (2.7)–(2.10) at t = t_{0} and t = t_{1} that
where v(t_{\frac{1}{2}}) = (v(t_{0})+v(t_{1}))/2 .
Subtracting (4.2)–(4.4) from (4.36)–(4.38), there holds
where
Using the definitions of the projection operators \mathcal{Q}_{h}, \mathcal{S}_{h}, \mathcal{R}_{h} for (4.39)–(4.41), we have
Setting \mathbf{v}_{h} = d_{t}Z_{\mathbf{u}}^{1} in (4.42), \varphi_{h} = d_{t}G_{\xi}^{1} in (4.43) and \psi_{h} = Z_{p}^{\frac{1}{2}} in (4.44), we get
Adding (4.45)–(4.47), there holds
Then, we bound the fourth to tenth terms on the right side of (4.48). Using the Cauchy-Schwarz inequality, triangle equality, and (4.32), Poincaré and Young inequalities, we have
Substituting (4.49)–(4.55) into (4.48) and using (3.11)–(3.13), the facts of Z_{\mathbf{u}}^{0} = \mathbf{0}, \; G_{\xi}^{0} = 0 , and G_{\eta}^{0} = 0 , we find there exists a positive constant \widetilde{C} = \widetilde{C}\big(\|\mathbf{u}\|_{L^{\infty}(t_{0}, t_{1};H^{2}(\Omega))}, \|\xi\|_{L^{\infty}(t_{0}, t_{1};H^{2}(\Omega))}, \|\eta\|_{L^{\infty}(t_{0}, t_{1};H^{2}(\Omega))}, \\ \|\eta_{ttt}\|_{L^{2}(t_{0}, t_{1};L^{2}(\Omega))}, c_{b}, \mu, \kappa_{3}, c_{p}, \mu_{f}, K_{1}, \kappa_{2}, \kappa_{1}\big) such that
Next, we show the error estimate at t = t_{n+1} . Subtracting (4.5)–(4.7) from (4.33)–(4.35), it holds
where
Setting \mathbf{v}_{h} = D_{t}Z_{\mathbf{u}}^{n+1} in (4.57), \varphi_{h} = G_{\xi}^{n+1} in (4.58) after using the operator D_{t} to both sides of (4.58), \psi_{h} = Z_{p}^{n+1} in (4.59), using (4.24) and adding the result equation, we get
Applying the summation operator \tau\sum_{n = 1}^{l} to both sides of (4.60), there holds
Now, we begin to estimate the first four terms on the right side of (4.61). For the first term, it is easy to check that
Applying the Cauchy-Schwarz inequality, (4.32), triangle and Young inequalities to (4.62), we have
For the second term, using the Canchy-Schwarz and Young inequalities, we obtain
Applying the Canchy-Schwarz inequality, Poincaré inequality, Young inequality, and the fact of
to the third term, there holds
Similar to the first term, we can bound the fourth term as follows:
Substituting (4.63)–(4.66) into (4.61), using the facts of Z_{\mathbf{u}}^{0} = \mathbf{0}, \; G_{\xi}^{0} = 0, \; G_{\eta}^{0} = 0 , (4.56), (3.11)–(3.13), there exists a positive constant \widehat{C} = \widehat{C}(c_{b}, \mu, \kappa_{3}, \mu_{f}, K_{1}, c_{p}, \kappa_{2}) such that
Applying the Gronwall inequality to (4.67), one has that (4.31) holds. The proof is complete. □
Furthermore, we state the main result of this part by a theorem.
Theorem 7. There exists a positive constant C_{5} independent of h and \tau such that the solution of the BDF2 algorithm satisfies the following error estimates:
Proof. Using (3.11)–(3.13), the relation p = \kappa_{1}\xi+\kappa_{2}\eta , Theorem 6, (4.56), and the triangle inequality on
one can see that (4.68) and (4.69) hold. The proof is complete. □
5.
Numerical tests
Here the \mathbf{P}_{2}-P_{1}-P_{1}-P_{1} element pairs are employed for the coupled algorithm and decoupled algorithms, and \mathbf{P}_{2}-P_{1}-P_{1} element pairs are employed for the BDF2 algorithm. To verify the robustness of our algorithms with respect to parameters, we compute the spatial errors and convergence rates of the variables \mathbf{u} and p for different values of Poisson rates and permeability tensor separately. In the meantime, we show the effectiveness of our algorithms in overcoming the Poisson locking as \nu\rightarrow 0.5 . After that, to illustrate that there is no nonphysical oscillation in the pressure field, we use the decoupled algorithm to test a Barry-Mercer problem. Finally, we use the following examples to compute the convergence rates for the above proposed algorithms in subsections 5.1, 5.2, and 5.4.
Example 1. Let \Omega = (0, 1)^2 , \Gamma_1 = \{(1, x_2); 0\leq x_2\leq 1\} , \Gamma_2 = \{(x_1, 0); 0\leq x_1\leq 1\} , \Gamma_3 = \{(0, x_2); 0\leq x_2\leq 1\} , \Gamma_4 = \{(x_1, 1); 0\leq x_1\leq 1\} and T = 1 . The boundary and initial conditions are
The exact solutions of (1.1)–(1.4) and (2.3)–(2.5) are p = t\sin(\pi x_{1})\cos(\pi x_{2}) and
5.1. The robustness on the Poisson ratio \nu
We first test the robustness of the coupled and decoupled algorithms on the Poisson ratio \nu by fixing \alpha = 1 , \mu_{f} = 1 , E = 2.8\text{e}3 , K = 1 e-7 \mathbf{I} , and c_{0} = 0.2 for \nu = 0.49 and \nu = 0.4999999 , respectively.
Tables 1 and 2 show the spatial errors and convergence rates of the coupled algorithm for \nu = 0.49 and \nu = 0.4999999 , respectively. Numerical results show that the H^{1} convergence rates of \mathbf{u} and the L^{2} convergence rates of p are all approaching 2 . The L^{2} convergence rates of \mathbf{u} are around 3 . The H^{1} convergence rates of p are around 1 . It can be concluded that the convergence rates of \mathbf{u} and p are optimal, which is consistent with Theorem 4.
For the decoupled algorithm, we also take \nu = 0.49 and \nu = 0.4999999 separately to observe the convergence rates of \mathbf{u} and p . Tables 3 and 4 show that the convergence rates of all variables are optimal.
Thus, Tables 1–4 imply the coupled and decoupled algorithms are robust on the Poisson rate \nu .
Table 5 reports the CPU time for both the coupled and decoupled algorithms. The results indicate that the decoupled algorithm significantly outperforms the coupled one in terms of runtime, demonstrating its superior efficiency.
5.2. The robustness on the permeability tensor K
We now test the robustness of the algorithms with respect to the permeability tensor K by fixing \alpha = 1 , \mu_{f} = 1 , E = 2.8\text{e}3 , \nu = 0.49 , and c_{0} = 0.2 for K = 1\mathbf{I} and K = 1 e- 4\mathbf{I} , respectively.
For the cases of K = 1\mathbf{I} and K = 1 e- 4\mathbf{I} , Tables 6 and 7 exhibit the spatial errors and convergence rates of \mathbf{u} and p for the coupled algorithm. The convergence rates of \mathbf{u} with respect to H^{1} norm and L^{2} norm are all around 3 and 2 separately. The convergence rates of p with respect to H^{1} norm and L^{2} norm are all around 2 and 1, respectively. This implies that the coupled algorithm is robust for K .
Again, for the cases of K = 1\mathbf{I} and K = 1 e- 4\mathbf{I} , we compute the convergence rates of \mathbf{u} and p by the decoupled algorithm. Tables 8 and 9 show that the convergence rates of \mathbf{u} and p are optimal, which is consistent with the results in Theorem 5 and shows that the decoupled algorithm is robust for K .
5.3. The investigation of nonphysical oscillation on pressure field
We now verify that there is no nonphysical oscillation in the pressure field for the proposed algorithms. For brevity, we only consider the decoupled algorithm. The benchmark problem for the poroelasticity model is given as follows:
Example 2. (Barry-Mercer problem) Again we take \Omega = (0, 1)^2 and T = 1 . The boundary segments \Gamma_{j}(j = 1, 2, 3, 4) are defined in Example 1. The source functions \mathbf{f} = 0 and \phi = 0 , and the boundary and initial conditions are
where
Set \alpha = 1 , \mu_{f} = 1 , E = 2.8 e 3 , \nu = 0.4 , K = 1 e- 8\mathbf{I} , and c_{0} = 0 . For the case of c_{0} = 0 , low permeability K , and small time step \tau , it will lead to \mathrm{div}\mathbf{u}^{1}\approx 0 for the discrete form of Eq (1.2). If using \mathbf{P}_2-P_1 element pairs to solve the original problem, there exists the nonphysical oscillation in the pressure field at a very short time see Figure 1. But Figure 2 shows that there is no nonphysical oscillation in the pressure field for the decoupled algorithm with \mathbf{P}_2-P_1-P_1-P_1 element pairs. In addition, the arrows near the boundary match very well with the inner arrows in Figure 3. This implies that the decoupled algorithm is locking-free and stable.
5.4. The convergence rates of BDF2 algorithm
We here test the convergence rates for the BDF2 algorithm by fixing \alpha = 1 , \mu_{f} = 1 , E = 2.8 e 3 , K = 1 e- 7\mathbf{I} and c_{0} = 0.2 for \nu = 0.49 and \nu = 0.4999999 , respectively.
Tables 10 and 11 show the spatial errors and convergence rates of the BDF2 algorithm for \nu = 0.49 and \nu = 0.4999999 , respectively. The numerical results show that the H^{1} convergence rates of \mathbf{u} and the L^{2} convergence rates of p are all approaching 2 . The L^{2} convergence rates of \mathbf{u} are around 3 . The H^{1} convergence rates of p are around 1 . This implies that the BDF2 algorithm has the optimal convergence rates for the different values of \nu .
6.
Numerical simulation of brain swelling
In this section, the coupled and decoupled algorithms with \mathbf{P}_2-P_1-P_1-P_1 element pairs and BDF2 algorithm with \mathbf{P}_2-P_1-P_1 element pairs are used to simulate brain swelling caused by brain injury. Since the coupled and decoupled algorithms present almost the same result, we only report the simulation result based on the coupled algorithm. For more details about \Omega, \; \Gamma = \Gamma_{1}+\Gamma_{2} , source functions, boundary conditions, and the values of parameters, one can see [15]. Here we list the required information, which is obtained from [15]. The \Omega is a 2D cross-section of a 3D model of the brain (see Figure 4), and the values of parameters are shown in Table 12. The injured area is marked with a yellow line in the right-hand figure of Figure 4.
Moreover, the source functions are \mathbf{f} = \mathbf{0}, \; \phi = 9 e- 3\; \text{ml}/{\rm min} , and the boundary conditions are
Figures 5 and 6 show the simulation results of the coupled and BDF2 algorithms for an injured brain with respect to \nu = 0.35, \; 0.49 . From Figure 5, one can see that the maximum pressures of the coupled algorithm are 3025.17 Pa and 3025.69 Pa separately, which are consistent with that in [27]. And Figure 6 illustrates the similar facts for the BDF2 algorithm by the values of maximum pressures ( 3028.13 Pa and 3025.87 Pa). In addition, the brain tissue can deform due to the influence of the total stress. In our simulation, the values of maximum tissue deformation are 0.99342 mm and 0.048082 mm for the coupled algorithm and 1.0018 mm and 0.048174 mm for the BDF2 algorithm, respectively. It is easy to find that the change of \nu has little influence on the maximum pressure, and the maximum tissue deformation becomes smaller as \nu gets bigger. When the Poisson ratio is approaching 0.5 , the brain tissue is nearly incompressible such that the tissue deformation is very small. Moreover, from Table 13, the execution time of the CPU of the coupled algorithm is longer than the BDF2 algorithm; thus the latter has higher computational efficiency.
7.
Conclusions
In this paper, we transform the poroelasticity model into a four-field problem by introducing the new variables and discuss the inf-sup condition about the four-field problem. Besides, we design the coupled and decoupled algorithms for the four-field problem and perform the error estimates. Optimal convergence is obtained in space and time. It can be observed that there is no constraint on mesh size and time step in error estimates. Then we introduce the BDF2 algorithm and perform stability analysis and error estimates. Furthermore, some numerical examples are presented to verify the theoretical results. More importantly, we successfully apply the algorithms to simulate the brain edema and observe the influence on the maximum tissue deformation and maximum pressure.
Author contributions
Peizhen Wang: Conceptualization, investigation, writing-original draft; Wenlong He: Validation; Yajuan Di: Writing-review, editing. All authors have read and approved the final version of the manuscript for publication.
Use of Generative-AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No.11901197) and the Young Teacher Foundation of Henan Province (Grant No.2021GGJS080). The numerical simulations have been done on the supercomputing system in the Supercomputing Center of Wuhan University.
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: