Fractal approximation of chaos game representations using recurrent iterated function systems

1.   Introduction

Fractal-based analysis provides a framework to investigate self-similar and scale-invariant patterns. Fractal-generating systems can model complex objects using simple self-referential rules with few parameters ^[2]. A simple method for generating fractals called the chaos game was introduced in ^[4] which involved repeatedly iterating a set of contractive mappings in order to compute the approximation of a fixed point. A more generalized framework was introduced in ^[3] that could produce more complex patterns. Chaos game representation is a method to visualize one-dimensional sequences first introduced to investigate multi-scale structures in DNA ^[9]. The chaos game representations of many different DNA samples were shown to be self-similar and scale-invariant ^[11]. This motivates the study of fractal properties in chaos game representations more rigorously.

Chaos game representation has been used for the characterization and classification of species ^[5], protein structure prediction methods ^[6,17], and the analysis of whole genomes ^[1,16]. Multifractal analyses of chaos game representation have also been investigated ^[7,13,18,19] with some wavelet analysis ^[10]. However, there does not seem to be much work done on drawing a comparison between recurrent iterated function systems and chaos game representation. Such work may contribute to the theoretical basis for fractal-based methods of analysis and modelling of DNA.

The paper is organized as follows. Section 2 recalls the definition of chaos game representation, describes a method for generating fractal objects, and introduces the method for approximating chaos game representations. Section 3 discusses numerical experiments investigating fractal scaling properties and approximation errors. Section 4 concludes with a discussion of possible applications and further directions.

2.   Method

In this section, we describe both chaos game representation and recurrent iterated function systems. We then introduce the method for approximating the former with the latter.

2.1.   Chaos game representation

Chaos game representation (CGR) ^[9] is a method of visualizing one-dimensional sequences used to investigate local and global structures in DNA. Consider the sequence $\{s_i\}_{i = 1}^{M}$ where the element $s_i$ may be one of $N$ possible symbols. The method is as follows:

1. Consider a regular $N$-gon and associate each vertex with a unique symbol

2. Initialize a set $S = \emptyset$

3. Read off the sequence. For each element in the sequence, add to the set $S$ the midpoint between the previous point and the vertex associated with the current element. Use the center of the polygon as an initial seed to compute the points in $S$.

4. Plot $S$

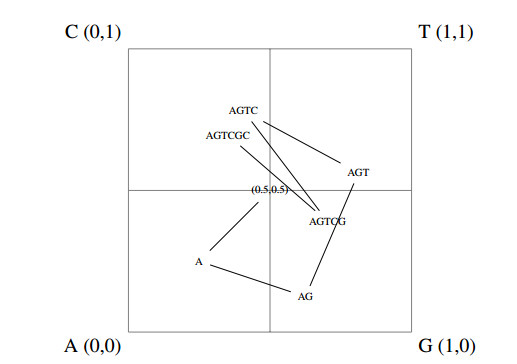
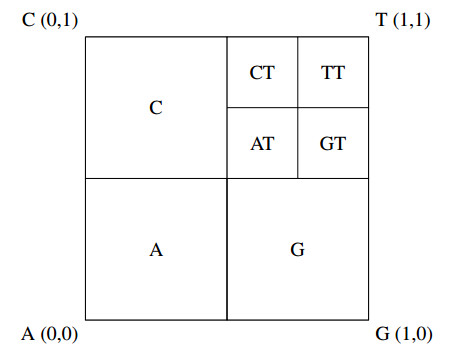
In the case of DNA, the sequence is a finite list of nucleotides $\{A, G, T, C\}$ which are chosen to be associated with the points $\{ (0, 0), (1, 0), (1, 1), (0, 1) \}$, respectively. CGR is thus supported on a unit square and each nucleotide is represented by a corner. Note that for any subquadrant (or cell) at a fixed resolution, i.e. when the unit square is divided into a non-overlapping grid of size $1/i \times 1/i$ for resolution level $i \in \mathbb{Z}^+$, there is a subsequence of length $i$ associated with that grid cell. See Figure 1 for subquadrants of resolution $i = 1, 2$ and their associated subsequence codes.

Thus, a point in $(0, 0.25)\times(0, 0.25)$ is an element in the sequence with symbol `A' that is preceded by another `A' nucleotide and the subquadrant can be coded with the sequence `AA'. Similarly, a point in the subquadrant $(1/2, 5/8)\times(1/2, 5/8)$ is generated by a symbol `T' preceded by the subsequence/code `AA'. So, for example, the points generated by the last element of the two sequences `AAGAATC' and 'CAATC', i.e. the symbol `C', will both have previous points from the subquadrant $(1/2, 5/8)\times(1/2, 5/8)$ (since they are both at least preceded by `AAT') even though they may be reads from different regions of the DNA sequence. Specifically, the points will be in the subquadrants (of different resolution) addressed by the codes `AAGAATC' and `CAATC' contained in the quadrant $(0, 1/2)\times(1/2, 1)$, respectively. Every point in the set generated by the CGR method may be viewed as a member of some subquadrant at resolution $i$ and from this subquadrant's unique code the subsequence preceding the element associated with the point may be recovered (Figure 2).

Figure 3 shows the CGRs of Cannabis sativa chloroplast genomes taken from four different regions around the world: Dagestani, Russia ^[15]; Cargmagnola, Italy ^[15]; Yoruba, Nigeria ^[14]; Cheungsam, Korea ^[14]. There is a diagonal-dominant pattern that is self-similar in different quadrants and subquadrants. The self-similarity across scales motivates the use of fractals to approximate CGR.

2.2.   Recurrent iterated function systems

Recurrent iterated function systems (RIFS) ^[3] are a natural generalization of iterated function systems ^[4]. Iterated function systems provide a method for constructing fractals as the attractive fixed-point of a contractive operator defined on a complete metric space. We recall the definition of a RIFS in generality from ^[8].

Definition 2.1. An $N$-map RIFS is defined as $(G, \{ f_i : \mathbb{X} \rightarrow \mathbb{X} \}_{i = 1}^N)$ where $G = (V, E)$ is a directed $N$-vertex graph with vertices $V$ and edges $E$, and $\{f_i\}_{i = 1}^N$ is a set of contractive transformations defined on $\mathbb{X}$ the set of all non-empty compact subsets of a complete metric space $\mathcal{X}$. Note that the convention of expressing $x \in \mathbb{X}$ as a union of $N$ separate sets $\bigcup_{i = 1}^{N} x_i = x \in \mathbb{X}$ is adopted. This decomposition is done in order to ``combine" the parallel action of the $N$ contractive transformations. Each vertex $v_i \in V$ is associated with a transformation $f_i$. Each edge $e_{ij} \in E$ represents the connection from $v_i$ to $v_j$ associated with the transformations $f_i$ and $f_j$. We represent the graph $G$ using its adjacency matrix $M$ where $M_{ij}$ is the edge $e_{ij}$.

We first introduce deterministic fractals generated by a RIFS and then consider so-called random fractals generated by a RIFS with probabilities.

Definition 2.2. Given a RIFS $(G, \{f_i\}_{i = 1}^N)$, the Hutchinson operator $T:\mathbb{X} \to \mathbb{X}$ is the collective action of the transformations on $x$ given by

where

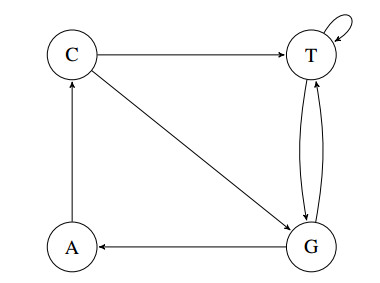
Example Consider the $4$-map RIFS $(G, \{f_i\}_{i = 1}^4)$ where $G$ is the graph as in Figure 4 and $\{f_i\}$ is a set of contractive transformations. The Hutchinson operator defined by such a RIFS is given by

The action of the Hutchinson operator is thus the union of transformations given the connectivity of the vertices on the graph $G$. By ^[3], $T$ is contractive and thus there exists a unique attractive fixed point $\bar{x}$ that satisfies the self-referential equation

whose self-similarity motivates the description of the attractor $\bar{x}$ as a fractal. The set $\bar{x}$ is invariant under $T$. Such attractors are called deterministic fractals. Denote the $n$th composition of the operator $T$ as $T^{\circ n}$, e.g. $(T \circ T)(x) \equiv T^{\circ 2} (x)$, $(T \circ T \circ T)(x) \equiv T^{\circ 3} (x)$, etc. The dynamic of a RIFS and the iteration of its Hutchinson operator on any initial set $x$ may thus be written as the limit of compositions

The attractor $\bar{x}$ of a RIFS may be approximated by the chaos game method ^[8] which generates $N$ sequences of points for an initial $x^{(0)} \in \mathbb{X}$ using the recurrence relation

Thus $\bar{x} \approx \cup_{i = 1}^{t} x^{(i)}$ for some stopping iteration $t$.

Definition 2.3. A RIFS $(G, \{f_i\}_{i = 1}^N)$ may also be probabilistic, generating attractor sets that are called random fractals. Let G be a weighted directed graph where $p_{ij}$ denotes the weight of the edge $e_{ij}$ and $\sum_{j = 1}^N p_{ij} = 1$ $\forall i = 1...N$. The adjacency matrix $M$ of the graph $G$ thus contains the elements $M_{ij} = p_{ij}$.

Definition 2.4. The probabilistic Hutchinson operator can thus be expressed as

where

and $P \sim U[0, 1]$ is a uniform random variable with $\mathit{\boldsymbol{1}}_{\{P \leq p_{ij} \}}$ an indicator variable.

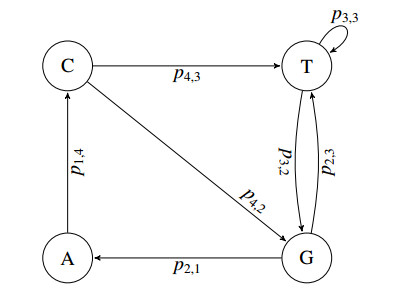
Example We revisit the previous example. Consider the $4$-map RIFS $(G, \{f_i\}_{i = 1}^4)$ where $G$ is the graph as in Figure 5 and $\{f_i\}$ is a set of contractive transformations. Depending on the observed values of the random variable $P$, one possible set of the first three iterations of the chaos game may have the forms:

The iteration of a Hutchinson operator defined by a RIFS with probabilities is related to a Markov process. For an initial state $x^{(0)} = \bigcup_{i = 1}^N x_i^{(0)}$, the next set of values $x^{(t+1)}$ is obtained by randomly selecting the actions from a set of transformations $f_j$ with probability $p_{ij}$ given the previous transformation $f_i$ for each of the $x_i$. The initial transformation for each set $x_i$ is its index $i$, i.e. $x_i^{(1)}$ is obtained by randomly applying a transformation $f_j$ with probability $p_{ij}$ onto the set $x_i^{(0)}$ and the $f_j$ becomes the most recent transformation applied to that $i$th set. From this point forward we consider RIFS with probabilities.

Example Consider the 3-map RIFS $(G, \{f_i\}_{i = 1}^3)$ on the unit square $\mathcal{X} = [0, 1]\times[0, 1]$ where $\{f_i\}_{i = 1}^3$ is a set of affine transformations

and the $3$-vertex graph G is described by the right stochastic adjacency matrix

The chaos game for $x^{(0)} = \begin{bmatrix}0.5\\0.5\end{bmatrix}$ and $t = 10^6$ is shown in Figure 6.

Example Consider the 5-map RIFS $(G, \{f_i\}_{i = 1}^5)$ on the unit square $\mathcal{X} = [0, 1]\times[0, 1]$ where $\{f_i\}_{i = 1}^5$ is a set of affine transformations

and the $5$-vertex graph G is described by the right stochastic adjacency matrix

The chaos game for $x^{(0)} = \begin{bmatrix}0.5\\0.5\end{bmatrix}$ and $t = 10^6$ is shown in Figure 6.

2.3.   CGR approximation

We define the CGR approximating models in both deterministic and random settings by constraining the general RIFS model above.

Let $\mathbb{X}$ be the set of non-empty compact subsets of the unit square $\mathcal{X} = [0, 1]\times[0, 1]$. Let the nucleotide symbols $\{A, G, T, C\}$ be denoted by the indices $i \in \{1, 2, 3, 4\}$ corresponding to the graph vertices (i.e. the corners given by the unit square $\{ (0, 0), (1, 0), (1, 1), (0, 1) \}$, respectively). Define the four non-overlapping contractive transformations $\{f_i : \mathbb{X} \rightarrow \mathbb{X} \}_{i = 1}^4$

That is, $f_1, f_2, f_3, f_4$ correspond to taking the midpoint of each point in a set with the corners $(0, 0), (1, 0), (1, 1), (0, 1)$ when a nucleotide $A, G, T, C$ is read, respectively. Note that this is a fairly strong constraint on the general RIFS framework as the transformations need not share a domain but is the natural analogue to CGR.

We first define the approximating model in the deterministic setting.

Definition 2.5. Let $G$ be a complete 4-vertex directed graph with a loop on every vertex. The deterministic approximating model is thus the RIFS given by $(G, \{f_i\}_{i = 1}^4)$. The CGR of a sequence is thus approximated by generating a chaos game approximation of the RIFS attractor such that the total number of points is equivalent to the length of the sequence.

We define the approximating model in the random setting by using the sequence to compute the edge weights of the graph.

Definition 2.6. Let $G$ be a weighted complete 4-vertex directed graph with a loop on every vertex, represented by a right stochastic adjacency matrix $M \in \mathbb{R}^{4\times4}$. The matrix entries $M_{ii'}$ representing edge weights are computed as the probability of a nucleotide $i$ being followed by a nucleotide $i'$ in the DNA sequence. These probabilities are obtained by computing the proportion of adjacent pairs $ii'$ that appear in the sequence. Thus the entry $M_{ii'}$ represents the likelihood of the nucleotide $i'$ following the nucleotide $i$ in the DNA sequence. The random approximating model is thus the RIFS given by $(G, \{f_i\}_{i = 1}^4)$. Again, the CGR of a sequence is approximated by generating a chaos game approximation of the RIFS attractor. The use of probabilities allows for local variation that better approximates CGR by using known information.

3.   Numerical results

In this section, we discuss numerical experiments investigating the fractal properties of CGR and RIFS attractor approximations.

3.1.   Approximating Cannabis sativa CGR

The RIFS attractor approximations of the Cannabis sativa CGRs are shown in Figure 7. There is a self-similar diagonal-dominant pattern as in Figure 3, however the distribution of this pattern is more uniform. This implies that there are smaller-scale visual structures (corresponding to longer subsequence patterns) that are not captured by the RIFS approximation. This information may be encoded by extending the RIFS as a higher-order Markov chain keeping track of the sequence of previous transformations applied to each set and computing the proportion of longer nucleotide subsequences in the DNA (e.g. $ii'i''$ where $i$, $i'$, $i''$ are nucleotides). The error images are shown in Figure 8. The diagonal-dominant error pattern may be a result of the RIFS attractor not encoding the smaller scale features but still capturing the larger scale diagonal patterns.

The Dagestani and Carmagnola sequences differ by only 16 single nucleotide polymorphisms ^[15] and the Yoruba and Cheungsam sequences are also nearly identical ^[14]. Thus the adjacency matrices computed for the four different DNA sequences are equal (up to four significant digits) and given by

The RIFS approximations between different DNA samples of Cannabis sativa are thus nearly identical with any difference being a result of the stochasticity of the chaos game. For this reason we only consider the results of the DNA sample from Dagestani as the other sequences produce similar results.

3.2.   Image approximation errors

We consider the image approximation errors of the RIFS attractor to the CGR as seen in Figure 8. Table 1 compares the average $l^1$ and $l^2$ distances as well as the structural similarity index (SSIM) and peak signal-to-noise ratio (PSNR) between 1000 fractal approximations computed by chaos game and the chaos game representation for an image of size $1024 \times 1024$. The poor approximation errors are a result of errors at the local level. That is, since only the subsequences of length 2 were used to encode the fractal generating system, global structures were captured with more accuracy than local structures. To capture these local structures, a system would need to incorporate the statistics for the frequency of longer subsequences. This may be a weakness of using image based methods to compare the approximations as encoding smaller scale local structures would require comparing larger images. In particular, images may suffer from aliasing as the pixel size determines the scale of resolution for the smallest subquadrant, and that subquadrant may indeed contain several points from the generated set. It is for this reason that measures on sets may be preferable, and would extend naturally into the iterated function system framework.

3.3.   Box counting

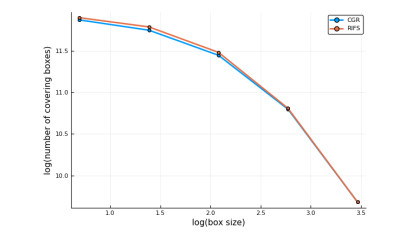
The box counting method ^[2] is applied to the Dagestani Cannabis sativa in order to investigate how similar both CGR and RIFS approximations are to each other in terms of fractal scaling. Boxes sized in powers of 2 are used in a fixed grid scan for $4096\times4096$ sized images. The number of boxes which contain a non-empty subset of the sets of points are counted. The log-log relationship between the box size and number of boxes covering the set are plotted in Figure 9 and suggests that both images have similar fractal scaling. The curve for the RIFS is given by the average of 1000 chaos games run for 150000 iterations each. The slightly higher number of covering boxes for the RIFS attractor at smaller box sizes is a result of the more uniformly distributed diagonal-dominant pattern across scales. The global patterns of the attractor are more present at the smaller scales than is the case with CGR. Conversely, the slightly lower number of covering boxes for the CGR implies that there is more local variation than in the RIFS attractor. The similarity in the box-counting dimension implies that there is a similar amount of overlap in the plots of the points. Since each box size can be associated with a subquadrant, this implies that at each resolution corresponding to a box size there has been an accurate amount of information approximated by the RIFS attractor. For instance, a box of size 8 pixels implies that the subquadrant resolution is $i = 4096/8 = 512$ and thus the common degree of overlap between the two images at this resolution suggests that the RIFS has partially encoded for elements in the sequence preceded by subsequences of length 512 despite issues with flexibility in local variation.

3.4.   Wavelet multiresolution analysis

In order to compare the self-similarities at different scales, a wavelet multiresolution analysis (MRA) ^[12] is used to decompose the CGR and RIFS approximation into a multiscale representation using the Haar wavelet basis. The Haar wavelet basis is chosen since the support of the basis functions are analogous to the unique subsequence corresponding to a subquadrant on the unit square in the CGR. That is, the Haar wavelet basis is chosen because it has support on contracted and translated versions of the unit square which corresponds to subquadrants of different resolutions. The MRA of the approximation error is shown in Figure 10. The MRA of the CGR and RIFS approximation for the Dagestani Cannabis sativa are shown in Figures 11 and 12. The MRA of the RIFS approximation is more uniformly distributed with the diagonal-dominant pattern more prominent across all scales. Both have similar Haar wavelet decompositions demonstrating that the RIFS approximation has captured the multi-scale structure of the sequence. The diagonal-dominant structure visible at all four resolutions indicates that it is a pattern exhibited in subsequences of the DNA up to length four.

The similarity in wavelet MRA profile implies that the RIFS attractor and CGR have similar scale-space representations. That is, both sets of points have the same self-similar structure at different scales. This is supported by the measurements of the box-counting dimension. Due to the uniqueness of subquadrants at a fixed resolution being associated with a subsequence, small-scale self-similar structures in the MRA imply patterns in the frequency of different nucleotides following large subsequences. It is for this reason that the Haar basis is chosen. In particular, the address of a wavelet coefficient in the MRA is associated to a particular subquadrant and so can be coded by the corresponding subsequence. For example, a wavelet coefficient at the fourth decomposition level can be uniquely associated to a subquadrant of resolution $i = 4$ and a subsequence of length 4. Thus the interpretation of the similarity in MRA profiles should be that the introduced method incorporates information at a resolution of $i = 2$ but the generated fractal contains accurate information and patterns at greater levels of resolution. Note that these small-scale wavelet patterns (of level 4) and their associated patterns in large subsequences (of length 4) were captured by the statistics of small subsequences (of length 2). This is demonstrative of the robustness of fractal-based methods for investigating scale-invariant structures.

Lastly, the wavelet MRA of the error suggests that there is information at higher resolutions not being encoded. This may be improved by extending the RIFS to encode the probabilities of longer subsequences, i.e. using a higher order Markov chain process to model the fractal attractor.

4.   Conclusion

The chaos game approximation of a recurrent iterated function system attractor can well approximate the global structures produced by the chaos game representation of DNA sequences, although the lack of encoding for larger subsequence statistics in the fractal generation results in poor local approximations. The attractor and chaos game representation have similar fractal scaling and wavelet multiresolution analysis profile. This method of approximating DNA sequence representations may offer a way to investigate mutations and genetic variation. The CGR of a mutated DNA sequence can be approximated and the fractal-generating system providing a latent space of parameters in which to compare with a referent sequence. This system may be extended to include information at smaller visual scales and thus encode information relating to larger sequence scales.

Genomic applications for the proposed framework include imputation of unknown sequence reads and the construction of a phylogeny of Cannabis. Imputation may be done by encoding the statistics of the known reads and generating the unknown nucleotides by playing the chaos game given the preceding known subsequence. For instance, a single nucleotide polymorphism (SNP) may be imputed by considering the preceding subsequence at the unknown location and using the center point of the corresponding subquadrant as a `seed' to bias the generation of the next element in the sequence. Such a method may also be useful when codon information relating to protein production is available, using the codon subsequence to extend the seed to higher resolution subquadrants. Additionally, statistics from both the positive and negative strands may be incorporated to make use of all known data. The construction of a phylogeny as in ^[11] would offer a latent space representation to compare different strands of Cannabis. These representations may then be correlated with phenotypic expressions (such as seeds, flower size, crystalline cannabinoids, etc.). Such analysis may help to inform agricultural practices, e.g. helping to select which plants to breed together if a certain phenotype is desired. Of particular interest is the correlation of the psychoactive substances in Cannabis with the parameters encoded by the fractal generating system. Indeed, such an application of fractal-based analysis would be in line with the original motivations for the construction of fractal generating systems where the parameters are suggested to encode for biological mechanisms ^[2].

The proposed iterated function system framework has several weaknesses that may be addressed by further research. Firstly, the generation of these sets of points does not necessarily induce a corresponding sequence since there are in fact $N$ subsets being generated in parallel. Secondly, the error in approximation is subject to the stochasticity of the RIFS and thus is in turn subject to the quality and availability of known sequence information. Lastly, there lacks the flexibility to control the local structure of the generated sets which would be important for capturing genetic variation and mutations. These drawbacks may be addressed by the use of $V$-variable fractals ^[2], a further generalization of iterated function systems. $V$-variable fractals make accessible the generation of families of fractals from a code space in which genomic analysis may be done. The integer parameter $V$ prescribes the number of distinct patterns that may be present at any level of resolution. Thus in the case of $V$ DNA samples, a $V$-variable fractal generating system may be constructed that allows for the selection of which of the $V$ sets of statistics (from the DNA sequences) will be used to generate the next point in the chaos game. Given $V$ sequences, all the statistics may be incorporated into a single family of fractals by constructing a $V$-variable fractal generating system where the permissible patterns at different resolutions are given by the $V$ sequences; the selection of which set of statistics to use at the resolution may then be informed by biologically plausible hypotheses. For example, in the case of phasing genomes, a $V = 2$ $V$-variable fractal generating system may be constructed where the two distinct patterns (and sets of statistics) are given by the paternal and maternal sequences. Similarly, when dealing with positive and negative DNA strands, a $V = 2$ $V$-variable fractal generating system may be constructed where the two patterns are given by the positive and negative strands. Alternatively, a reference sequence and a mutated sequence may be used to construct a $V = 2$ $V$-variable fractal generating system where the presence of patterns is distributed across scales to capture local variation informed by the mutated sequence with the global structure of the fractal mostly informed by the reference sequence. Thus, $V$-variable fractals would offer a robust generalization of the proposed framework that offers flexibility in local variation as well as a code space addressing the generated fractals to use as a latent space representation of sequences.

Acknowledgments

The author would like to thank Edward Vrscay for his insightful direction, Giang Tran for her support and discussions, Eunice Chan for her introducing chaos game representations, and the CAIMS 2018 Annual Meeting for their feedback.

Conflict of interest

The author declares no conflict of interest in this paper.