Dynamic modeling of discrete leader-following consensus with impulses

1.   Introduction

One of the most important topic in multi-agent systems is the consensus algorithm. In these systems, agents interact with each other via a communication topology and only employ local information. As a result, in order to drive them to accomplish tasks, a control law is required. It is connected with the driving a team of agents to reach an agreement on a certain issue by negotiating with their neighbors. In more details, each agent receives information from the set of other agents in the group and then all agents adjust their own information states depending on the information received from other agents. The goal is to reach an agreement. This behavior is widespread in the nature. A consensus algorithm describes the information transfers between agents and varies depending on the application and the model. In the literature, many different consensus algorithms have been proposed (see for example, ^[4,11,17]). The virtual leader is a special agent whose motion is independent of all the other agents and thus is followed by all the other ones. Such a problem is commonly called leader-following consensus problem ^[12,24]. Many different types of such kind of problems are studied recently, for instance those based on nearest-neighbor rules ^[15], bounded confidence ^[9], a virtual leader ^[18]. Note most studied models for neural networks are continuous ones which is connected with the continuous behavior of any agent in the neural networks. The continuous time networks are usually discretized when they are used for the sake of computer-based simulation or experimentation. Unfortunately, the dynamic of the continuous-time networks cannot be preserved by discretization, as it is mentioned in ^[14]. It proves the application of discrete models ^[7,9,13,16]. The applied technique and methods for the discrete-time case are, however, different from the continuous-time case. Note one of the main property of the solution of difference equations ^[1,2,3,8] is that it is a sequence of numbers defined on the initially given discrete set of points. In the case there are impulses they connect these numbers at the current point and at the previous one (or ones). Some properties of first order difference equations with impulses are studied by some authors, see for example ^[10].

Sometimes the interactions between multi-agents are changed instantaneously. Then the model is called impulsive model. Some neural networks with instantaneous changes are studied for stochastic neural networks in ^[21,22,23], for stochastic differential equations in ^[19,22]. In this paper we set up the discrete-time model of a multi-agent system consisting of agents and the leader. Differently than the existing models, such as ^[9,13], we consider the case of two interacting topologies, one is determining the interactions between the agents including the leader, the second one is determining the instantaneous switching interactions of the agents with the leader at some initially given times. Sufficient conditions ensuring both local and global leader-following consensus are found. By intensive application of computer simulation the influence of the impulses on the discrete leader-following consensus is illustrated and the necessity and effectiveness of the obtained conditions are shown.

2.   Description of the discrete model with impulses

Let $\mathbb{Z}_+$ denote the set of all nonegative integers. Let the increasing sequence $\{n_k\}_{k = 1}^{\infty}: n_k\in\mathbb{Z}_+$, $\lim\limits_{k\to \infty}n_k = \infty$, be given and $n_0 = 0$.

In this paper, we consider a discrete-time multi-agent system consisting of N agents and the leader. The dynamics of each agent labeled $i, \ i = 1, 2, \dots, N,$ is given by the difference equation

where $x_i(n)$ and $u_i(n)$ represent the state and the control input at time $n$, respectively. Function $f: \mathbb{Z}_+\times\mathbb{ R}\to \mathbb{ R}$ describes the intrinsic, generally nonlinear, dynamics. The leader, labeled as $i = 0$, for multi-agent system (1) is an isolated agent described by

Let the control protocol be based on two interaction topologies and be given by:

where $\delta(0) = 1$ and $\delta(n) = 0$ for $n\not = 0$, $\Delta(0) = 0$ and $\Delta(n) = 1$ for $n\not = 0$. $a_{ij}\geq 0, \ (i, j = 1, 2, \dots, N)$ are entries of the weighted adjacency matrix $A$, $d_i\geq 0$, $(i = 1, \, 2, \, \dots, \, N)$ are entries of the adjacency matrix $D$ associated with the graph, modeled the first interaction topology in the multi-agent systems, $B_{i n_k}\in \mathbb{ R}$ ($i = 1, \, 2, \, \dots, \, N$, $k = 1, \, 2, \, \dots$) are the diagonal elements of the matrix $B_{n_k}$ associated with the graph, modeled the second interaction topology, and $\gamma$ is a real constant.

Definition 2.1. Multi-agent system (1) and (2) under control law (3) is said to achieve

$-$ the local leader-following consensus if there exists $\varepsilon > 0$ such that for any initial values $x_i(n_0)\in \mathbb{ R}:$ $|x_i(n_0)-x_0(n_0)|\leq \varepsilon$, $i = 0, \, 1, \, 2, \, \dots, \, N$ the corresponding solution to (1) and (2) satisfies $\lim\limits_{n\to\infty}|x_i(n)-x_0(n)| = 0$ for $i = 1, 2, \dots, N$.

$-$ the leader-following consensus if a solution to (1) and (2) satisfies $\lim\limits_{n\to\infty}|x_i(n)-x_0(n)| = 0$ for $i = 1, \, 2, \, \dots, \, N$ for any initial values $x_i(n_0)\in \mathbb{ R}$, $i = 0, \, 1, \, 2, \, \dots, \, N$.

Then the system (1), (2) where $u_i(n)$ is given by (3) could be written as a system of impulsive difference equations

Remark 2.1. The model (4) is a generalization of the studied in ^[13] discrete leader consensus problem with one interacting topology. The system (4) models the case of two interacting topologies: The first one (described by the first and the second equations in (4)) is determining the interactions between the agents including the leader; the second one (described by the third equation in (4)) is determining the instantaneous switching interactions of the agents with the leader at some initially given times.

Denote $e_i(n) = x_i(n)-x_0(n), \ i = 1, 2, \dots, N,$ and rewrite the system of difference equations (3) in the form

where $F(n, u) = f(n, u)-f(n, x_0(n))$ and $e_i^0 = x_i^0-x_0^0$.

Denote

Introduce the quadratic $n$ dimensional matrix $\mathcal{L}$ with elements $l_{ii} = \sum_{j\not = i}a_{ij}$ and $l_{ij} = -a_{ij}, \ i\not = j$ and the quadratic $n$ dimensional matrix $D$ with elements $d_{ii} = d_i$ and $d_{ij} = 0, \ i\not = j$.

In our further study we will use the following discrete inequality which is an analog to the classical Gronwall's inequality:

Lemma 2.1. (^[5]) Let $\{x_n\}_{n = n_0}^\infty$ and $\{b_n\}_{n = n_0}^\infty$ be sequences of real numbers with $b_n\geq 0$ which satisfies

Then for any integer $n\geq n_0$ the inequality $x_n\leq a\prod\limits_{k = n_0}^{n-1}(1+b_k)$ holds.

2.1.   Leader-following consensus of (5)

Theorem 2.1. Let the following conditions be satisfied:

1. There exists $\varepsilon > 0$ such that function $f: \mathit{\mathbb{ N}}\times\mathit{\mathbb{ R}}\to \mathit{\mathbb{ R}}$ and $|f(n, u)-f(n, v)|\leq L|u-v|$ uniformly in $n$ for $u, v\in S(\varepsilon)$.

2. The inequality $L+M\leq 1$ holds where $M = |\gamma|\sqrt{|\gamma l_{max}|}$, $\gamma_{max}$ is the eigenvalue of matrix $C\ C^T$ with the maximal modulus, $C = \mathcal{L}+D-\frac{1}{\gamma}I$, $I$ is the unit $n$ dimensional matrix.

3. For all $k = 1, 2, \dots$ the inequality $\max\limits_{i = 1, \, 2, \, \dots\, , \, N}|1-B_{i, n_k}|\leq 1-L$ holds.

Then under control law (3) multi-agent system (1) and (2) with initial values $x_i^0\in S(\varepsilon)$, $i = 1, \, \dots, \, N$, achieves the local leader-following consensus.

Remark 2.2. Under the condition 1 of Theorem 2.1 it follows that for any $u\in S(\varepsilon)$ the inequality $|F(n, u)| = |f(n, u)-f(n, x_0(n))|\leq L|u-x_0(n)|$ holds.

Proof. Let the initial values $x_i^0\in S(\varepsilon)$, $i = 1, \, \dots, \, N$, i.e., $|e_i(0)|\leq \varepsilon$, $i = 1, \, 2, \, \dots, \, N$. Then according to (5) and Remark 2.2 we get

i.e., $e_i(1)\in S(\varepsilon), \ i = 1, \, 2, \, \dots, \, N$.

Using induction we prove $e_i(n)\in S(\varepsilon), \ n = 1, \, 2, \, \dots, \, n_1$.

Then from the second equation in (5) with $k = 1$ we obtain

By induction we prove that $e_i(n)\in S(\varepsilon)$ for all $n\in \mathbb{ Z}$, $i = 1, 2, \dots, N$.

Then from (5) for any $n = 1, \, 2, \, \dots, \, n_1$ we get

where $e = (e_1, e_2, \dots, e_N)$ and $F(n, e) = (F_1(n, e_1), \, F_2(n, e_2), \, \dots, \, F_N(n, e_N))$. Therefore,

or

Thus, by the discrete analogue of Gronwall's inequality (see, Lemma 2.1), we get

From the second equation in (5) with $k = 1$ we get

Similarly, for $n = n_1+1, \, n_1+2, \, \dots, \, n_2$ we get

From the second equation in (5) with $k = 2$ we get

Applying induction and the conditions 2 and 3 of Theorem 2.1 we obtain $\lim\limits_{n\to \infty}||e(n)|| = 0$.

Theorem 2.2. Let the conditions 2 and 3 of Theorem 2.1 be satisfied and the function $f:\mathit{\mathbb{ N}}\times\mathit{\mathbb{ R}}\to \mathit{\mathbb{ R}}$ be Lipshitz with a constant $L$ w.r.t. its second argument in $\mathit{\mathbb{ R}}$.

Then under control law (3) multi-agent system (1) and (2) achieves the leader-following consensus.

The proof of Theorem 2.2 is similar to the one of Theorem 2.1 and we omit it.

3.   Examples

In this section we will present several examples to illustrate the effectiveness and the necessity of the obtained conditions. All examples are computer realized. The algorithms for calculating the state trajectories lead to delays in computations if CAS Wolfram Mathematica is used. Thus, by the help of the programming language C$_{++}$ we obtain the values of the state trajectories in quicker way. The graphs are generated by CAS Wolfram Mathematica.

Now we will study a group of 4 followers and the leader with two interacting topologies. The first one $\mathcal{G}$ and the second one $\mathcal{F}$ determining the switching interactions with the leader at times $n_k$, $k = 1, \, 2, \, \dots$, where the weighted adjacency matrix $A$, the diagonal matrix $D$, giving the leader adjacency matrix associated with $\bar{\mathcal{G}}$ and the diagonal matrix $B_k$, giving the leader adjacency switching matrix associated with $\bar{\mathcal{F}}$ are given by

the intrinsic dynamics is described by $f(n, x) = 0.1\ln(1+x^2)$ and the constant $\gamma = 0.2$. Then $L = 0.1$ and $M \approx 0.84$, i.e., conditions 1 and 2 of Theorem 2.1 are satisfied.

We will study different case for this system illustrating the above theory.

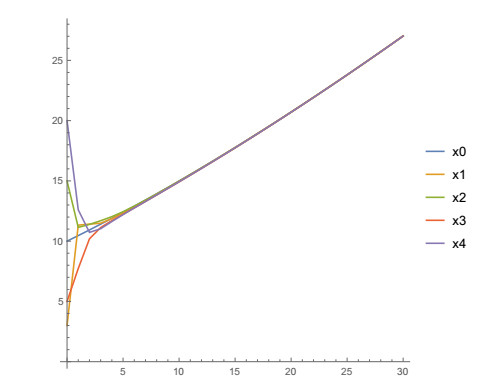
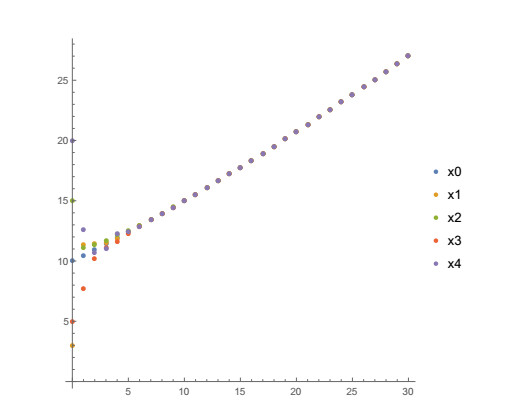
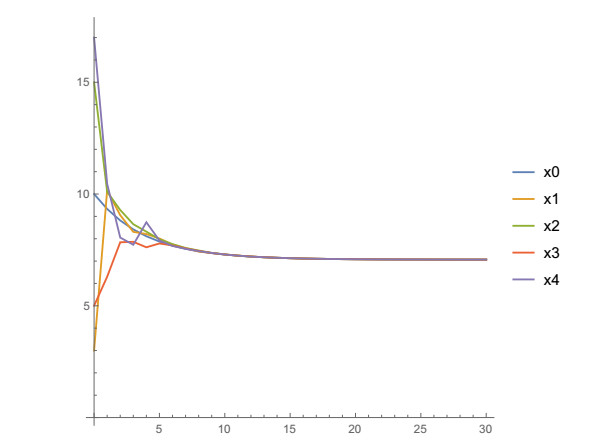
Example 1. (The multi agent system without impulses). Let the initial values be $x_0^0 = 10$, $x_1^0 = 3$, $x_2^0 = 15$, $x_3^0 = 5$, $x_4^0 = 20.$ Consider

According to Theorem 2.2 the leader-following consensus is achieved. The state trajectories $x_i(n)$, $i = 0, \, 1, \, 2, \, 3, \, 4$ and $n = 0, \, 1, \, 2, \, \dots, \, 30$ are shown in Figure 1 (discretely) and Figure 2 (continuously) and its values for $n = 1, \, 2, \dots, \, 12$ are shown in Table 1. From Table 1 and Figures 1 and 2 it could be seen that the state trajectory $x_i(n)$ of any agent approaches the state trajectory $x_0(n)$ of the leader.

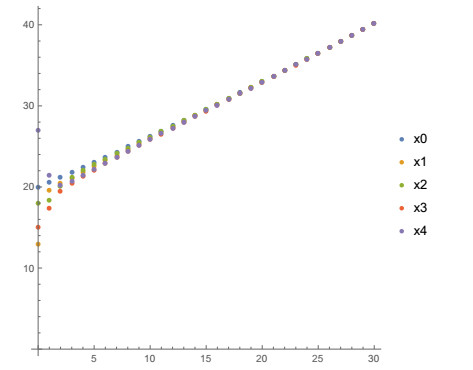
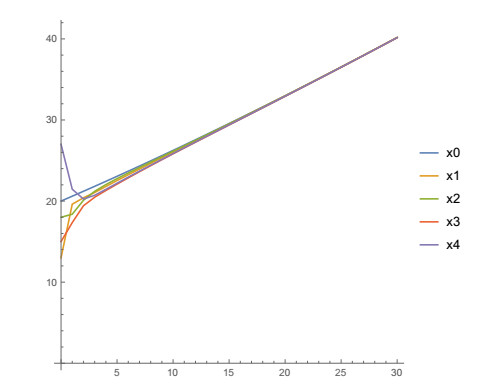
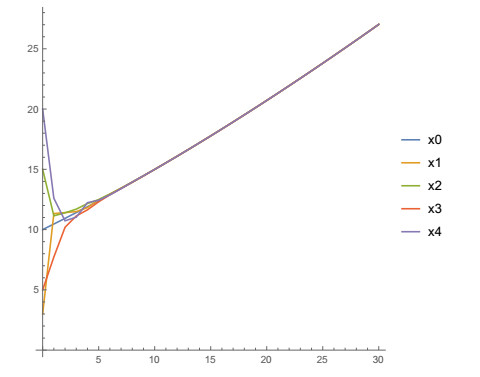
Let's change the initial conditions, i.e., $x_0^0 = 20, x_1^0 = 13, x_2^0 = 18, x_3^0 = 15, x_4^0 = 27.$ The state trajectories $x_i(n)$, $i = 0, \, 1, \, 2, \, 3, \, 4$ and $n = 0, \, 1, \, 2, \, \dots, \, 30$ are shown in Figures 3 and 4. Again the state trajectory $x_i(n)$ of any agent approaches the state trajectory $x_0(n)$ of the leader.

Example 2. (Instantaneous changes of the behavior of the followers with small jumps). Now we will consider the case when the followers at same times change their behavior instantaneously, i.e., in a form of impulses. Let the points of impulses be $n_k = 4k-1$, $k = 1, \, 2, \, \dots$ and the model be

where $B_{i, k} = 1.9, \ i = 1, \, 4, \ B_{i, k} = 0.9, \ i = 2, \, 3, \ k = 1, \, 2, \, 3, \, \dots$ and the initial values are $x_0^0 = 10$, $x_1^0 = 3$, $x_2^0 = 15$, $x_3^0 = 5$, $x_4^0 = 20.$

Then $L+|1-B_{i, k}| = 1$, i.e., condition 3 of Theorem 2.1 is satisfied. According to Theorem 2.1 the leader-following consensus is achieved. The state trajectories $x_i(n)$, $i = 0, \, 1, \, 2, \, 3, \, 4$ and $n = 0, \, 1, \, 2, \, \dots, \, 30$ are shown in Figure 5 (discretely) and Figure 6 (continuously) and its values for $n = 1, \, 2, \, \dots, \, 12$ are shown in Table 2. From Table 2 and Figures 5 and 6 it could be seen that the state trajectory $x_i(n)$ of any agent approaches the state trajectory $x_0(n)$ of the leader.

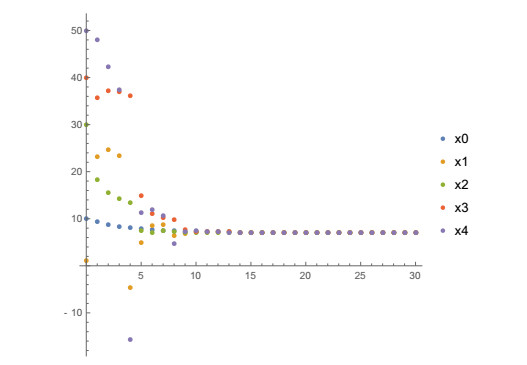
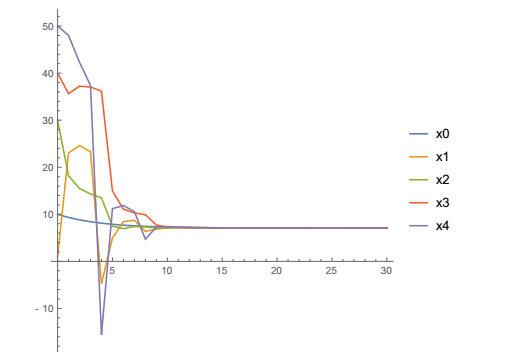
Example 3. (Instantaneous changes of the behavior of the followers with at least one large jump). Now we will consider the case when the followers at same times change their behavior instantaneously, but at least one of them has a large jump.

Consider (15) with the following initial values $x_0^0 = 10, x_1^0 = 3, x_2^0 = 15, x_3^0 = 5, x_4^0 = 20$, $B_{1, k} = 1.9$, $B_{i, k} = 0.1$, $i = 2, \, 3$, $k = 1, \, 2, \, 3, \, \dots$ and $B_{4, k} = 4k.$

Then the condition 3 of Theorem 2.1 is not satisfied because $L+\max\limits_{i = 1, \, 2, \, 3, \, 4}|1-B_{i, k}| = 4k-0.9 > 1$.

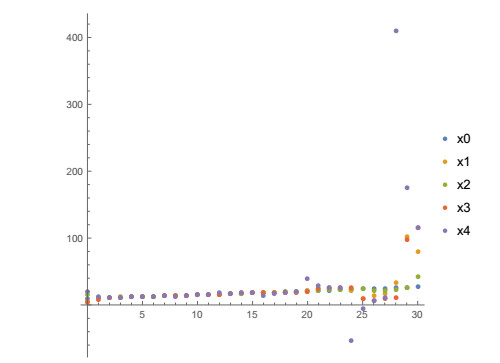
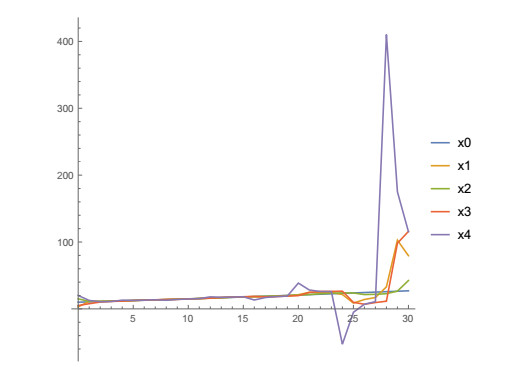
The state trajectories $x_i(n)$, $i = 0, \, 1, \, 2, \, 3, \, 4$ and $n = 0, \, 1, \, 2, \, \dots, \, 30$ are shown in Figure 7 (discretely) and Figure 8 (continuously) and its values for $n = 1, \, 2, \, \dots, \, 12$ are shown in Table 3. From Table 3 and Figures 7 and 8 it could be seen that the state trajectory $x_4(n)$ of the agent with large jumps does not approach the state trajectory $x_0(n)$ of the leader.

Therefore, the condition 3 of Theorem 2.1 is a necessary condition to achieve leader-following consensus.

Example 4. (Necessity of small Lipschitz constant). Now we change the intrinsic dynamics to $f(n, x) = 0.1\frac{x^2-20x}{15}e^{\frac{-n}{4}}$. Let $x_0^0 = 10$, $C = 4$ and $U^* = [6, 14]$. Then $\max\limits_{x\in U^*}\sum\limits_{n = 0}^\infty |f(n, x)| = 0.1\max\limits_{x\in [6, 14]}\Big(\frac{x^2-20x}{10}\Big)\sum\limits_{n = 0}^\infty e^{\frac{-n}{4}}\leq 0.1*\frac{100}{15}*\frac{e^{0.25}}{-1 + e^{0.25}} < 4$ and according to Lemma 5 ^[13] $|x_0(n)-10|\leq 4$. Now let $\varepsilon = 3.5$ and let $x\in S(3.5)$, i.e., $|x-x_0(n)|\leq 3.5$. Then $|x-10|\leq |x-x_0(n)|+|x_0(n)-10|\leq 7.5$ and therefore, $2 \frac{x-10}{10}\in [-1, 1]$ for $x\in [2.5, 17.5]$. Then $L = 0.1$.

Now, consider the initial values such that $|x_i^0-10|\leq 3.5$, i.e., $x_0^0 = 10$, $x_1^0 = 3$, $x_2^0 = 15$, $x_3^0 = 5$ and $x_4^0 = 17$.

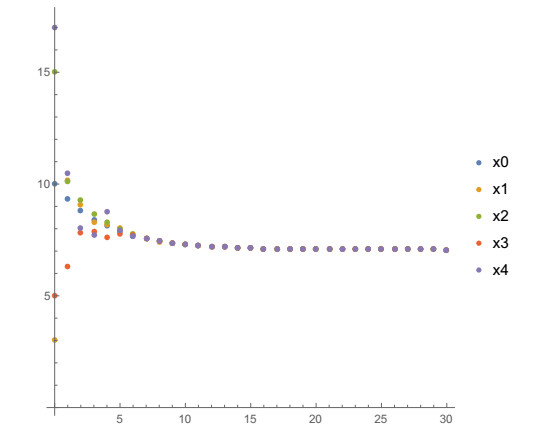
The state trajectories $x_i(n)$, $i = 0, \, 1, \, 2, \, 3, \, 4$ and $n = 0, \, 1, \, 2, \, \dots, \, 30$ are shown in Figure 9 (discretely) and Figure 10 (continuously) and its values for $n = 1, \, 2, \, \dots, \, 12$ are shown in Table 4. From Table 4 and Figures 9 and 10 it could be seen that the state trajectories $x_i(n)$, $i = 1, \, 2, \, 3, \, 4$ approach the state trajectory $x_0(n)$ of the leader, i.e., the local leader consensus is achieved and $x_i(n)\in S(3.5)$ for $i = 1, \, 2, \, 3, \, 4$ and $n\in\mathbb{ Z}$.

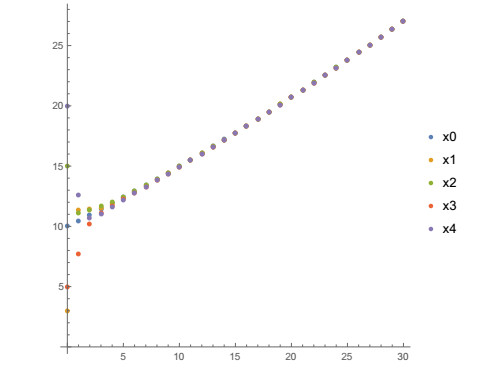
Note that for $x\not \in [2.5, 17.5]$ the function is locally Lipschitz but the Lipschitz constant does not satisfy condition 2 of Theorem 2.1. Let, for example, consider the following initial values $x_0^0 = 10, x_1^0 = 1, x_2^0 = 30, x_3^0 = 40, x_4^0 = 50$.

The state trajectories $x_i(n), i = 0, \, 1, \, 2, \, 3, \, 4$ and $n = 0, \, 1, \, 2, \, \dots, \, 30$ are shown in Figure 11 (discretely) and Figure 12 (continuously) and its values for $n = 1, \, 2, \, \dots, \, 12$ are shown in Table 5. From Table 5 and Figures 11 and 12 it could be seen that the state trajectories $x_i(n)$, $i = 1, \, 2, \, 3, \, 4$ are in the enough small tube around the leader only for large values of time.

4.   Conclusion

A discrete model of a multi-agent system with a virtual leader, whose motion is independent of all the other agents, is studied. It is modeled the case when at initially known time-points the interactions between multi-agents are changed instantaneously. We consider the case of two interacting topologies, one is determining the interactions between the agents including the leader, the second one is determining the instantaneous switching interactions of the agents with the leader. Several sufficient conditions ensuring both local and global leader-following consensus are obtained. These results are illustrated on particular examples by intensive application of computer simulation. The influence of the impulses on the discrete leader-following consensus is shown and the necessity of some of the obtained conditions is illustrated.

Acknowledgments

K. Stefanova is supported by National Program ``Young Scientists and Postdoctoral Candidates'' of Ministry of Education and Science, Bulgaria.

Conflict of interest

The authors declare no conflict of interest.