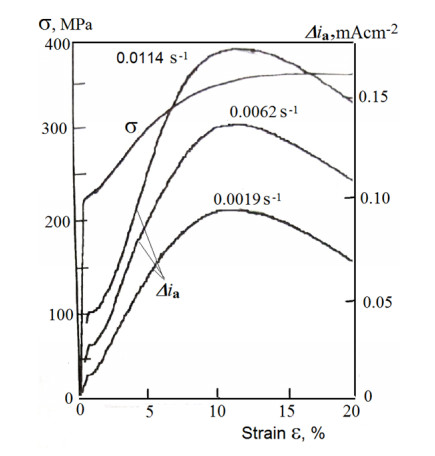
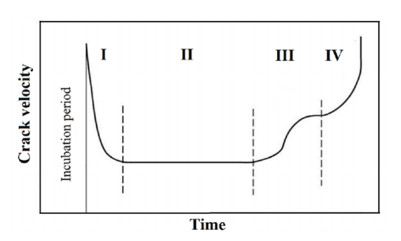
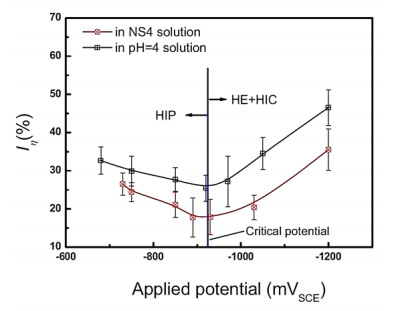
The review presents brief theoretical foundations of the mechanochemical and chemomechanical surface effects (MCE and CME) associated with corrosion-mechanical destruction of metals, considers the results of various scientific publications that studied the mechanochemical behavior of steels in near-neutral pH media, and analyzes the application of the results of such studies with the purpose of their practical use in the stress corrosion cracking (SCC) prevention. The article attempts to summarize the results of modern experimental studies and numerical modeling of mechanochemical and chemomechanical processes occurring on the surface of pipe steels and at the tip of the crack under the simultaneous effects of stresses/strains and corrosion media. The influence of these processes on the mechanism and kinetics of corrosion cracking of pipe steels in near-neutral aqueous solutions is discussed. The criteria for the quantitative assessment of the influence of MCE and CME on the SCC of pipeline steels are considered. The analysis of research methods for the study of MCE and CME, was carried out with the aim of further developing a unified methodological approach to assessment and quantification in predicting SCC in neutral media.
1.
Introduction
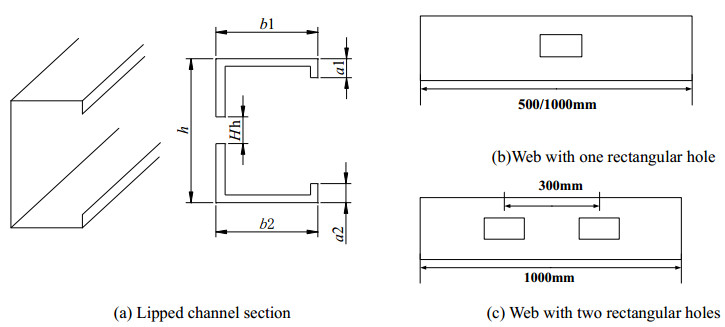
The CFS lipped channel sections have been widely used in buildings as walls, floors, and ceilings due to their high strength-to-weight ratio and ease of construction. However, the holes often appear in the web because of the installation of electrical, plumbing, and heating conduits for such lipped channel sections. The occurrence of holes in the web would decrease the cross-section area, stiffness and the constraint for the flange, which makes such sections prone to be distortional buckling.
In the literature, the distortional buckling of CFS members has been investigated by most researchers. Based on the studies conducted by Schafer et al. [1,2] and Yao et al. [3,4], the design methods of distortional buckling were given in the AISI 100-2016 [5] and GB50018 [6], respectively. Meanwhile, some significant work has been reported on the reduction in strength of channel sections having openings covering web crippling by Uzzaman et al. [7,8,9,10] and Lian et al. [11,12,13,14], shear by Pham [15], Pham et al. [16], Keerthan et al. [17,18], and Pham et al [16], the bending of beam by Moen et al. [20] and Zhao et al. [21], and the deep learning-based prediction by using Deep Belief Network by Fang et al. [22,23].
Recently, Chen et al. [24,25,26] reported experimental and numerical studies on the axial strength of single channels and back-to-back channels with edge-stiffened holes and found that the axial strength of channels with edge-stiffened holes was greater than those of plain channels. Meanwhile, some other work has been reported on the strength of channel sections having edge-stiffened hole covering web crippling by Uzzaman et al. [27,28] and moment capacity by Chen et al. [29].
In the literature, limited work has been reported on distortional buckling of CFS channels with holes in the web. The compression tests of 24 short and intermediate CFS lipped channel columns with and without slotted web holes showed that the presence of slotted hole caused a slight decrease in the ultimate capacity [30]. For lipped channel columns with web stiffener, numerical and experimental studies were carried out to analysis the effects of holes on the failure mode and load-carrying capacity by Yao and Wu [31]. The results demonstrated that the holes led the change of bucking mode and decreased the ultimate strength. The effects of holes on the buckling behavior of CFS channels under axial compression were studied by Macdonald et al. [32,33], and it was found that the ultimate failure load of the channels under compression varied greatly with the presence of holes. Zheng and Yu [34] reported the distortional buckling behavior of the CFS channel with web openings by using ANSYS finite element software, and the influence of the transverse and longitudinal hole spacing, the hole size, and the shape of the hole on the distortional buckling.
In order to develop the design method of effective width method and direct strength method for the axially-compressed member with holes, the calculated method of buckling coefficient and elastic buckling capacity for the member with holes has been studied by some researchers. The equivalent modulus method is used to calculate the elastic buckling stress of CFS members with slotted holes by Zhou and Yu [35]. According to finite element analysis, the modified formula of the distortional buckling coefficient for axially-compressed member with circular hole was given by Yao et al. [36]. The simplified methods to predict the local, distortional, and global critical elastic buckling loads of CFS columns with holes were developed based on theoretical and FE analysis [37]. Based on experiments and theoretical analysis, the modified direct strength methods were proposed by Moen and Schafer [38] and Yao and Rasmussen [39] for calculating the distortional buckling capacity of CFS members with web openings under axial compression. In terms of the design standards, the American Iron and Steel Institute (AISI) [5] do not provide sufficient effective width design rules for determining the distortional buckling strength of CFS channels with holes because the reduced effective width method is only suitable to members with relatively small holes in these codes. The direct strength method is given in AISI for determining distortional buckling strength of CFS channels with holes, but the elastic buckling capacity of members with holes need to be calculated by using finite element method or complicated formula. Meanwhile, there is no design provision about distortional buckling for the perforated members in the Chinese code [6].
As mentioned previously literatures, some works considered the distortional buckling behavior and design method of the CFS channels with holes have been reported. Nevertheless, limited work considered the distortional buckling has been reported on columns with large holes under axial compression by using effective width method. Thus, this paper reports 44 new distortional buckling experiments on the axial strength of CFS lipped channels with rectangular holes in the web. A nonlinear elasto-plastic FE model was then developed and validated against the test results in terms of ultimate strength and buckling modes. Using the validated FE model, a parametric study involving 16 models was conducted to investigate the effects of sections, hole size, and number of holes on the axial strength of such columns. The proven FEM was used to develop the distortional buckling coefficient equation of CFS lipped channel section under axial compression considering the effect of holes. Finally, the prediction method of ultimate strength of CFS lipped channels with holes in the web considering distortional buckling was proposed and the design strengths were compared against both the test and FEA results.
2.
Experimental investigation
2.1. Test specimen
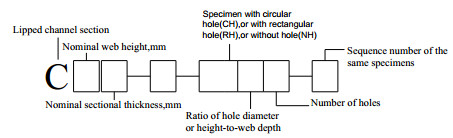
This test employed 44 CFS lipped channel sections under axial compression. There were 8 nonperforated members and 36 members with rectangular holes. The definitions of geometric parameters of specimen and the location and spacing of holes are illustrated in Figure 1. Four cross-sections were selected. The nominal thicknesses of the specimens are 0.8 and 1.0 mm. The heights of the rectangular holes are 0.2, 0.4, and 0.6 to the web depth. The ratio of length-to-width (Lh/Hh) of rectangular hole is equal to 2. The length of specimens is 500 and 1000 mm. The hole spacings are 300 mm for members with two rectangular holes. The labeling rule of all specimens is defined in Figure 2. For example, the label "C8008-05-RH21-1" defines the specimen as follows: C indicates the section is a lip channel section column; 8008 means that the nominal height of the web and the nominal thickness of section are 80 and 0.8 mm, respectively; RH21 represents that the section has a rectangular hole and the ratio of the height of the rectangular hole to the height of the web is 0.2; 1 represents the sequence number of the same specimens. The nominal and measured dimensions of all specimens are tabulated in Table 1.
2.2. Material properties
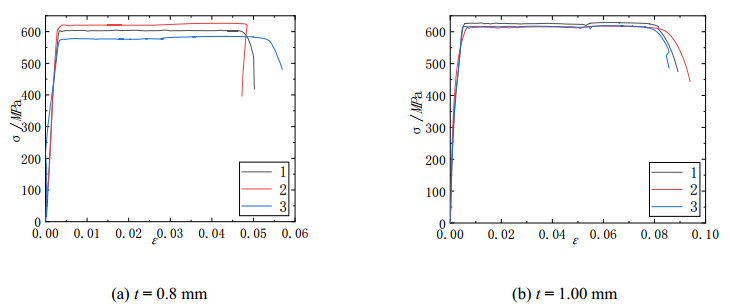
Steel sheets of grade LQ550 with two kinds of thicknesses were selected to manufacture the specimens. 3 tensile coupon tests of steel sheets with different thicknesses were conducted to determine the material properties based on Chinese specification "Tensile tests of metallic materials Part 1: test methods at room temperature" (GB/T228.1-2010)
[19]. The stress-strain curves of coupons for every kind of steel plates are shown in Figure 3. The measured average material properties including the static 0.2% proof stress (f0.2), initial Young's modulus (E), ultimate strength (fu), and ultimate strain (εu) are listed in Table 2.
2.3. Initial geometric imperfections
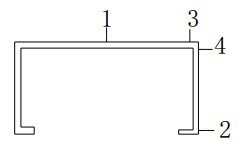
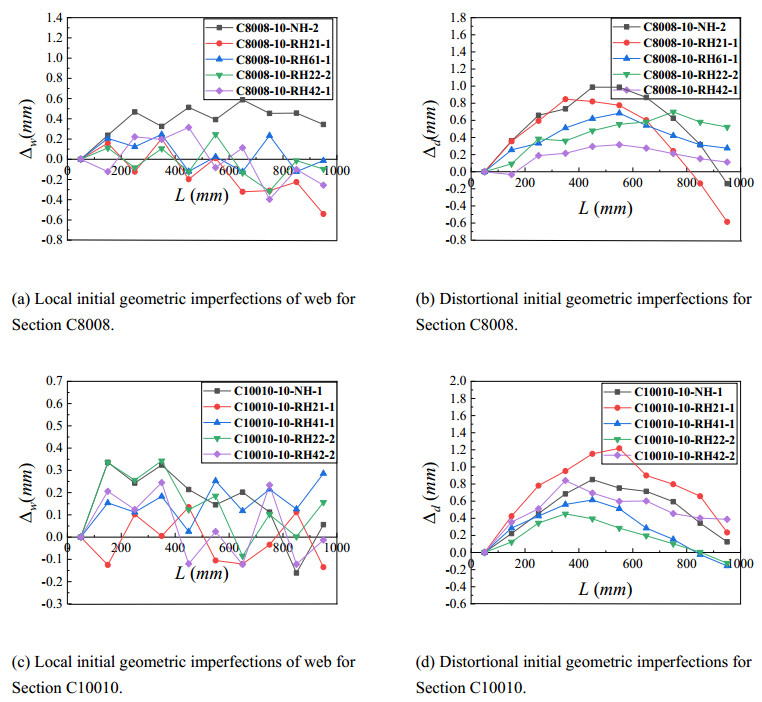
The initial geometric imperfection resulted from forming and transportation has a great influence on the buckling behavior of CFS members. So the initial imperfections of all specimens along the longitudinal direction were measured before test. The interval of longitudinal location measured was 150 mm. The measuring locations of cross-section are illustrated in Figure 4, including the initial local imperfection calculated by locations 1 and 3 and the initial distortional imperfection predicted by locations 2 and 4. The initial local and distortional geometric imperfections of Section C8008 and Section C10010 are depicted in Figure 5. The initial imperfections indicated that the imperfections of the CFS lipped channel columns had no obvious laws along the longitudinal direction. The maximum initial geometric imperfection magnitudes (Δmax) for all specimens are listed in Table 2.
2.4. Test rig and procedure
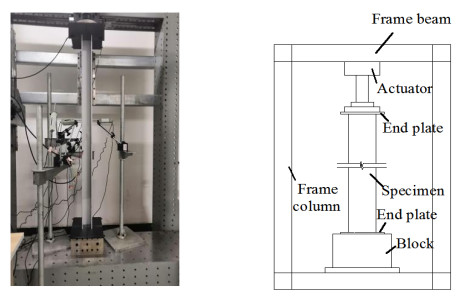
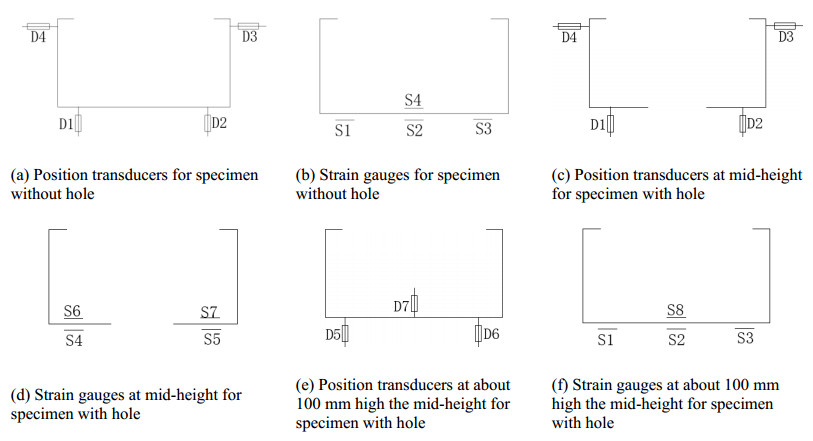
The reaction frame system and a 500 kN hydraulic jack were used to apply axial compression load on all specimens as shown in Figure 6. The upper actuator and lower pedestal were fitted with 250 mm × 200 mm × 8 mm thick steel platen ground flat and parallel. The column specimens put directly on the steel platen as they were compressed. Friction between the column ends and the steel platens were the only lateral forces that restrained the column cross-section under load. A load cell measured the applied compression force on each specimen. The displacement transducers and strain gauges were adopted to capture the displacement, deformation, and stress of the specimens during the loading process as illustrated in Figure 7. For specimens without hole, four position transducers (Figure 7(a)) were used to record the lateral deformations and four strain gauges (Figure 7(b)) were arranged to measure the stress of web. These instrumentations are set at the mid-height of the stud column. At the mid-height of all specimens with hole, four position transducers (Figure 7(c)) and four strain gauges (Figure 7(d)) were positioned. At the web about 50 mm higher the mid-height of specimens with hole, Three position transducers and four strain gauges were employed as depicted in Figure 7(e), (f). A position transducer was set at the upper end plate of the specimens to measure the vertical displacement under axial load for all specimens.
3.
Test results
3.1. Failure buckling mode
The buckling failure modes of 44 axial compression specimens are shown in Table 3, where L represents local buckling, D represents distorted buckling. Pt, Pa,
Pc are the test result, finite element analysis result, and calculated result by using proposed method, respectively.
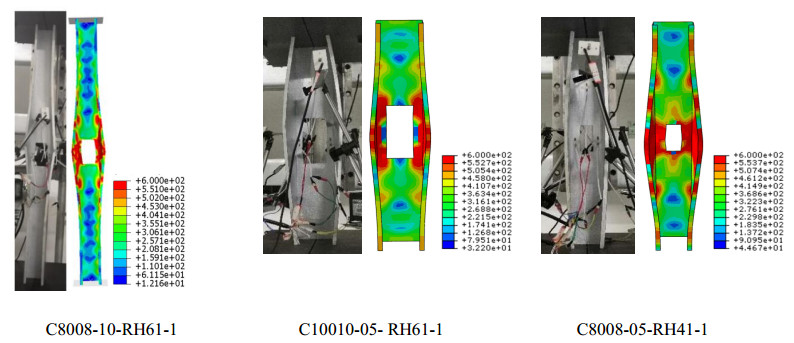
It can be found from Table 3, the local buckling occurred firstly for the Section C8008 with the length of 500 mm (Figure 8(a)). With the increase of load, the distortional buckling appeared sequentially (Figure 8(b)). Finally, the specimens failed with the interaction of local and distortional buckling (Figure 8(c)). For Section C10010 with the length of 500 mm, the distortional buckling occurred firstly (Figure 9(a)). Then the deformation of distortional buckling was more and more obvious with the increase of load (Figure 9(b)). The specimens failed with distortional buckling (Figure 9(c)). For Sections C10010 and C8008 with the length of 1000 mm, the local buckling occurred at the web firstly (Figure 10(a)). Then the distortional buckling appeared with the increasing of load (Figure 10(b)). Finally the specimens suffered with interaction of local and distortional buckling (Figure 10(c)).
3.2. Load-strain curves
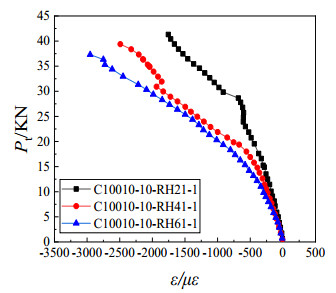
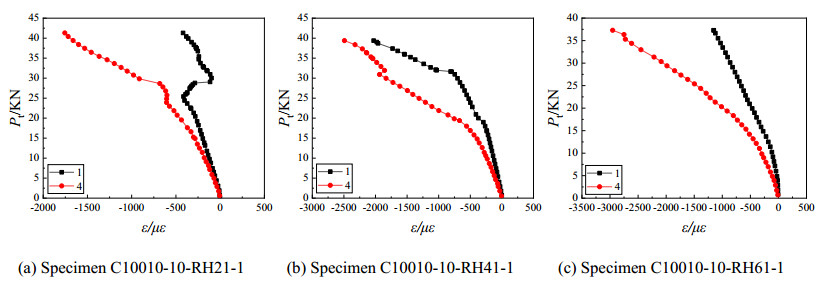
The comparison on load-strain curves at the plate adjacent to hole (Point 4) for specimen C10010 with the length of 1000 mm and different hole sizes is shown in Figure 11. It can be seen from Figure 11, the strain gradually increases with the increase of the hole size, which indicates that the stress concentration is more obvious with the increase of hole size.
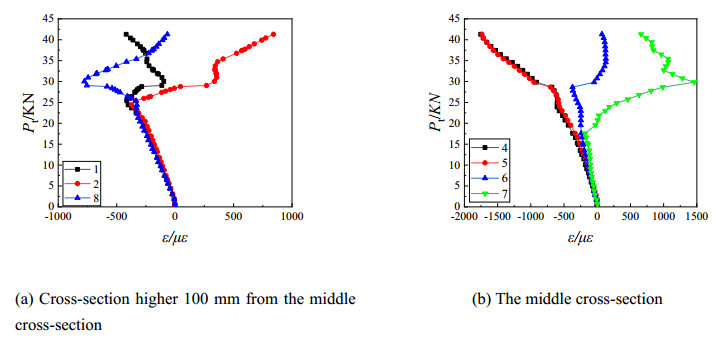
Figure 12 shows the load-strain curves of the specimen C10010-10-RH21-1 at two cross-sections. For the cross-section which is higher than middle cross-section, it can be seen from Figure 12(a), the strains of all points increases linearly before the load of the specimen reaches 24 kN. The strain changes abruptly after the load exceeds 24 kN which indicates that the local buckling occurs for the web. For the middle cross-section, it can be seen from Figure 12(b), the strain changes abruptly when the load reaches 15 kN which indicates the local buckling occurs at the plate adjacent to hole. The above comparison shows that the presence of hole lets the local buckling occur early.
The comparisons on load-strain curves between the plate adjacent to hole (Point 4) and the position higher 100 mm along the longitudinal direction (Point 1) for the Section C10010 with the length of 1000 mm and different hole sizes are shown in Figure 13. It can be seen from Figure 13, the strain of the plate adjacent to hole is larger than that of the position higher 100 mm along the longitudinal direction because of the stress concentration resulted from the hole. Larger the hole size is, larger the stress concentration is.
3.3. Load capacities and load-displacement curve
The load-carrying capacities of all specimens are shown in Table 3. As can be seen from Table 3, the load-carrying capacities for Sections C8008 and C10010 with the length of 500 mm and hole size Hh/h of 0.2, 0.4 and 0.6 decrease by 2.2, 6.33, 16.28% and 1.75, 4.16, 15.8% compared with the specimens without hole, respectively. The load-carrying capacities for Sections C8008 and C10010 with the length of 1000 mm and hole size Hh/h of 0.2, 0.4 and 0.6 decrease by 0.6, 4.8, 13.9% and 1.3, 3.1, 8.2% compared with the specimens without hole, respectively. It indicates that the load-carrying capacity of the specimen decreases obviously with the increase of the hole size. It indicates that the load-carrying capacity of the specimen decreases obviously with the increase of the hole size. For the specimens with the length of 100 mm and two rectangular holes, the same conclusion can be obtained.
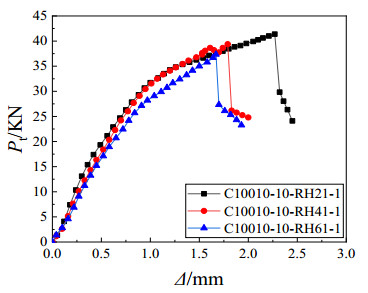
Figure 14 shows the load-axial displacement curves of the Section C10010 with the length of 1000 mm for different hole sizes. It can be seen from Figure 13 that the load-carrying capacity and the ductility of the specimen decrease with the increasing of the hole size.
4.
Verification of finite element models
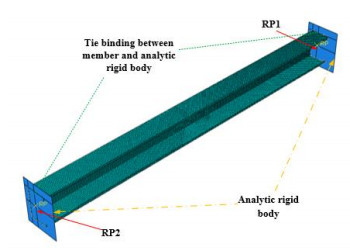
The finite element program ABAQUS [20] was used to simulate the distortional buckling modes and behavior of the specimens and conduct a further parametric analysis on the CFS lipped channel axially-compressed columns with rectangular holes. The finite element model is shown in Figure 15. The S4R shell element was selected for modeling column and the analytical rigid body element was used for modeling the upper and lower end steel plates of the specimens. The dimensions of the cross sections measured before the tests were used in the FEM. The mesh size of 5 mm × 5 mm was selected to model specimens. The ideal elasto-plastic model based on the material properties obtained from the coupon tests shown in Table 2 was used in FEM. The end constraint conditions of the test plate were all fixed, by constraining the five degrees of freedom of the reference point RP1 at the upper end plate (2 translation degrees of freedom and 3 rotational degree of freedom, releasing UZ degrees of freedom to control displacement) and the six degrees of freedom of the reference point RP2 at the lower end plate. In fact, the fixed end constraint conditions developed in the paper had a few different with the test because a litter movement or rotation can be observed at the failure stage for the specimen ends. But the effect of this error on the buckling mode and the load carrying capacity can be ignored in the finite element analysis. The measured dimensions of specimens (see in Table 1) were all included in the models. The analysis procedure included two phases: Firstly, an eigenvalue buckling analysis was performed to find the most probable elastic buckling mode of the specimen. The measured maximum magnitude of the initial geometric imperfections shown in Table 1 was applied to the first eigen-mode to produce the geometric imperfection of FEM. Secondly, nonlinear analysis considering both material nonlinear and geometric nonlinear was carried out by using the arc-length method to analyze the failure modes and ultimate load-carrying capacity of the specimen.
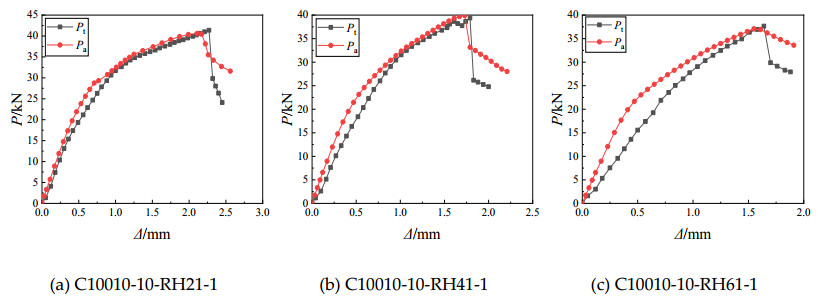
The buckling failure mode and load-carrying capacities of all specimens obtained from the finite element analysis are shown in Table 3. It can be seen from Table 3 that the buckling modes of the specimens obtained from the finite element analysis are consistent with the experimental buckling mode. The maximum error of the load-carrying capacity between the test and the finite element analysis results is 6%. The mean value and the corresponding coefficient of variation of ratio of the test result and the finite element analysis result are 0.99 and 0.023, respectively. The comparison on load-axial displacement curve and buckling mode of the finite element analysis and test for the specimen C10010-10-RH61-1 are shown in Figures 16 and 17, respectively. By the above-mentioned comparison, the load-carrying capacities, the failure modes, and load-displacement curves obtained from FEA show good agreement with the test results. Therefore, the FEM developed in this study for the axially-compressed members with rectangular hole in the web has been well validated with the tests.
5.
Finite element parametric study
The proven finite element model was used to analysis on the buckling behavior and ultimate load-carrying capacity of Sections SS89 and SS7510 with different hole sizes and lengths which are widely used in engineering. The section dimensions of the columns with holes, the buckling modes and the ultimate load-carrying capacities obtained from the finite element analysis were shown in Table 4, and G represents the overall buckling.
It can be seen from Table 4 that the ultimate load-carrying capacity gradually decreases with the increase of the hole size. Larger the hole size is, lower the ultimate load-carrying capacity is. For example, the ultimate load-carrying capacity of the Section SS89 with the length of 1000 mm and the hole size Hh/h of 0.7 decreases by 18% compared with that of the Section SS89 with the length of 1000 mm without hole. At the same time, it can be found that the buckling mode of the members with large holes may change from interaction of local and distortional buckling to interaction of local, distortional, and overall buckling due to the reduction of the rotational constraint of the web to the flange and the bending stiffness.
6.
Modified design method for axial columns with rectangular holes in the web
6.1. Proposed method
The load-carrying capacity of the axially-compressed member with rectangular holes can be calculated by using effective width method in Chinese code GB50018-2002. The calculation formula is shown in Eq (1):
where, φ is the overall buckling coefficient of the axially-compressed member; Ae is the effective area of the cross section, which should be calculated by the effective width of the cross section be. The effective width of the web can be predicted according to the suggested method in reference [21]. The effective width of flange is calculated by using the Eq (2), and the buckling coefficient takes into account the influence of the hole. For single rectangular hole and multi-rectangular holes, k1 = δ1k and k2 = δ2k are used to calculate the buckling stability, respectively. k is the buckling coefficient of flange without hole in the web, while k1 and k2 are buckling coefficients of flange with single hole and multi holes in the web.
6.2. Modified distortional buckling coefficient of compression members with web holes
Since the hole in the web reduces the rotational constraint stiffness of web to flange, members with holes in the web are prone to occur distortional buckling than the members without hole. The distortional buckling stress and coefficient decrease because of the presence of hole. The finite element is used to analyze the elastic distortional buckling stress of axially-compressed member with rectangular holes in the web. The analysis parameters include hole size, hole spacing and number of holes.
6.2.1. Single rectangular hole
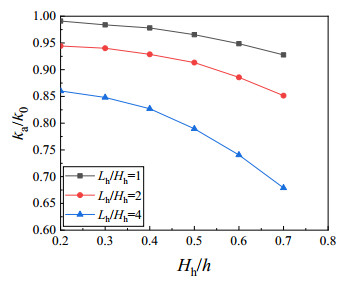
In order to ensure the occurrence of distortional buckling for the member with rectangular hole, the section dimensions of the member were selected as h = 100 mm, b = 65 mm, a = 10 mm, t = 1.5 mm and l = 1200 mm. The distortional buckling half wavelength of this member was 400 mm. A single rectangular hole was in the middle of the web, and the ratio of hole height to web height (Hh/h) changed from 0.2 to 0.7. The ratio of hole length to hole height (Lh/Hh) was set as 1, 2 and 4, respectively. The comparison between the distortional buckling coefficient of members with holes (ka) and the distortional buckling coefficient of members without holes (k0) is shown in Figure 18. It can be seen from Figure 18 that the distortional buckling coefficient decrease with the increase of Lh/Hh and Hh/h which indicates that Lh/Hh and Hh/h have important effect on the distortional buckling coefficient.
6.2.2. Multiple rectangular holes
1) A single hole and multiple holes in a distortional buckling half wave
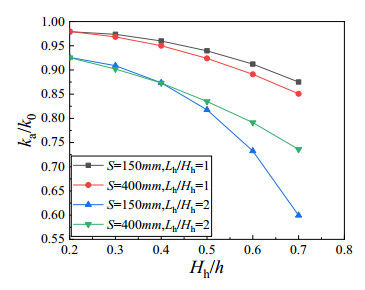
The section of the finite element analysis is the same as the section of the member with single rectangular hole. Three rectangular holes are equally separated from the middle of the member to both ends. The size of the hole Hh/h changes from 0.2 to 0.7, and Lh/Hh is 1 and 2. The hole spacing is 150 mm when holes are set in a distorted buckling half-wave. The hole spacing is equal to the distorted buckling half-wavelength of the member when holes are set in different half-waves. The variation of ka/k0 is shown in Figure 19. It can be seen from Figure 19 that Lh/Hh has a great influence on the distortional buckling coefficient, while the single hole or multiple holes in a distortional buckling half wave have little influence on the distortional buckling coefficient.
2) Effect of hole spacing
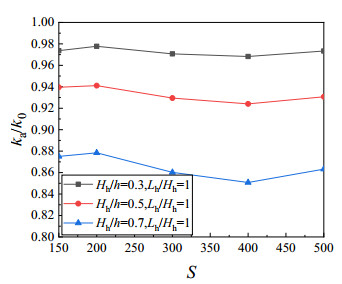
When the number of holes is 3, Lh/Hh is equal to 1, the hole spacing changes from 150 to 500 mm, and the hole size Hh/h is 0.3, 0.5 and 0.7, the ratio of the distortional buckling coefficient ka to the distortional buckling coefficient k0 varies with the hole spacing as shown in Figure 20. It can be seen from Figure 20 that ka/k0 changes with hole spacing basically similar. With the increase of hole spacing,
ka/k0 increases firstly and then decreases. When the hole spacing reaches 400 mm (half wavelength of distortional buckling), ka/k0 is the minimum. Therefore, the distorted buckling coefficient of the member with holes spacing equaling to the distortional buckling half wavelength can be conservative taken as the distortional buckling coefficient of the cold-formed thin-wall steel channel section with rectangular holes in the web.
6.2.3. Calculation method of distortional buckling coefficient
1) Axially-compressed member with single rectangular hole in the web
The distortional buckling coefficient of members with holes can be calculated using formula k1 = δ1k, where k is the distortional buckling coefficient of the axially-compressed member without holes, δ1 is the reduction coefficient of distortional buckling coefficient which can be calculated by using formula (3) obtained from above finite element analysis as shown in Figure 17.
2) Axially-compressed member with multiple rectangular holes in the web.
The distortional buckling coefficient of members with holes can be calculated using formula k2 = δ2k, where δ2 is the reduction coefficient of distortional buckling coefficient which can be calculated by using Eq (4) obtained from above finite element analysis as shown in Figures 18 and 19.
6.3. Comparison of design capacity with test and FEA data
The load-carrying capacities of specimens were calculated by using the suggested reduction coefficient of distortional buckling coefficient as shown in Table 3. The mean value and the coefficient of variation of the ratio of test and calculated capacity Pt/Pc were 1.05 and 0.029, respectively. The load-carrying capacities were calculated by using the suggested reduction coefficient of distortional buckling coefficient for the common Sections SS89 and SS7510 as shown in Table 4. The mean and the coefficient of variation of the ratio of Pa/Pc of the finite element analysis and the calculated results are 1.07 and 0.014, respectively. The results show that the proposed method is safe and reliable to calculate the load-carrying capacity of the lipped channel section with holes in the web under axial compression.
7.
Conclusions
1) Forty-four CFS lipped channel sections with and without rectangular holes in the web were conducted under axial compression. The specimens displayed distortional buckling or interaction of distortional and local buckling. The load-carrying capacity of specimens with holes was lower than that of specimens without holes. The load-carrying capacities of specimens gradually decreased with the increase of the size of holes.
2) The finite element program ABAQUS was used to simulate the buckling modes and ultimate capacities of test specimens. The analysis results were in good agreement with the test results. The compared results show that the finite element model is feasible to analyze the distortional buckling behavior and load-carrying capacity of the axially-compressed member with holes in the web. The proven finite element model was used to analyze the distortional buckling behavior of the common cross-sections used in engineering. The analysis results show that the load-carrying capacity decreases with the increase of the hole size and the buckling mode would be affected by the hole.
3) The elastic distortional buckling behavior and buckling coefficient of CFS lipped channel section with holes under axial compression was analyzed by using finite element. Based on the finite element analysis results, a reduction method for the distortional buckling coefficient of axially-compressed members with rectangular holes in the web was developed.
4) Based on the reduction formulas of distortion buckling coefficient and effective width method, the load-carrying capacities of axially-compressed members with rectangular holes in the web were calculated. The comparison between the experimental results and the finite element analysis results shows that the developed calculation method has great accuracy and applicability.
Conflict of interest
The author declares that there is no conflict of interest regarding the publication of this paper.
Acknowledgments
This research was funded by National Natural Science Foundation Projects of China, grant number 51868049, Natural Science Foundation Projects of Jiangxi Province in China, grant number 20181BAB206040, and Department of Education Science and Technology Projects of Jiangxi Province in China, grant number GJJ180932 and GJJ170983.









 DownLoad:
DownLoad: