Citation: Qiu-bo Wang, Chao Xu, Yi-bao Jiang, Xian Zhang, Jin-shui Yao, Cong-de Qiao, Qin-ze Liu, Yuan-hong Zhang. The synthesis of conjugated polymers with different length side chains and the effect on their nanoparticles[J]. AIMS Materials Science, 2018, 5(4): 770-780. doi: 10.3934/matersci.2018.4.770
| [1] | Gaurav Gupta, Varun Danke, Tamoor Babur, Mario Beiner . Morphology orientation of comb-like polymers with rigid backbones under the influence of shear fields. AIMS Materials Science, 2017, 4(4): 970-981. doi: 10.3934/matersci.2017.4.970 |
| [2] | Laura J. Weiser, Erik E. Santiso . Molecular modeling studies of peptoid polymers. AIMS Materials Science, 2017, 4(5): 1029-1051. doi: 10.3934/matersci.2017.5.1029 |
| [3] | Sergey V. Belim . Study of ordering in 2D ferromagnetic nanoparticles arrays: Computer simulation. AIMS Materials Science, 2023, 10(6): 948-964. doi: 10.3934/matersci.2023051 |
| [4] | Harold O. Lee III, Sam-Shajing Sun . Properties and mechanisms of iodine doped of P3HT and P3HT/PCBM composites. AIMS Materials Science, 2018, 5(3): 479-493. doi: 10.3934/matersci.2018.3.479 |
| [5] | Yong X. Gan . A review of electrohydrodynamic casting energy conversion polymer composites. AIMS Materials Science, 2018, 5(2): 206-225. doi: 10.3934/matersci.2018.2.206 |
| [6] | Silvia Colodrero . Conjugated polymers as functional hole selective layers in efficient metal halide perovskite solar cells. AIMS Materials Science, 2017, 4(4): 956-969. doi: 10.3934/matersci.2017.4.956 |
| [7] | Saviska Luqyana Fadia, Istie Rahayu, Deded Sarip Nawawi, Rohmat Ismail, Esti Prihatini, Gilang Dwi Laksono, Irma Wahyuningtyas . Magnetic characteristics of sengon wood-impregnated magnetite nanoparticles synthesized by the co-precipitation method. AIMS Materials Science, 2024, 11(1): 1-27. doi: 10.3934/matersci.2024001 |
| [8] | Abdullah Ahmed Ali Ahmed, Abdullah Mohammed Al-Hussam, Abdu Mohammed Abdulwahab, Ahmed Nasser Ahmed Ali Ahmed . The impact of sodium chloride as dopant on optical and electrical properties of polyvinyl alcohol. AIMS Materials Science, 2018, 5(3): 533-542. doi: 10.3934/matersci.2018.3.533 |
| [9] | Aruna P. Wanninayake, Benjamin C. Church, Nidal Abu-Zahra . Effect of ZnO nanoparticles on the power conversion efficiency of organic photovoltaic devices synthesized with CuO nanoparticles. AIMS Materials Science, 2016, 3(3): 927-937. doi: 10.3934/matersci.2016.3.927 |
| [10] | Nataly Arrieta-Sandoval, Juan Francisco Hernández Paz, Imelda Olivas-Armendáriz, Laura Elizabeth Valencia-Gómez, Claudia Alejandra, Rodríguez González . Silver nanoclusters stabilized with PVP-BSA conjugate: Optical properties approach. AIMS Materials Science, 2024, 11(1): 173-199. doi: 10.3934/matersci.2024010 |
Over the past ten years, conjugated polymer nanoparticles (CPNs) have attracted more attentions because of their merits in comparison to organic fluorescence dyes and quantum dots, such as higher absorption coefficients, good photostability, low toxicity and good biocompatibility [1,2]. These features are widely applied in biological fields including pH sensing, metal ions and temperature sensing [3,4,5,6], molecular imaging of tissues and biomarkers of disease [7,8], photodynamic therapy of tumors [9,10], immediate activation of nerve cells, and photothermal therapy of cancer [11,12] and so on. In general, CPNs consist of one or more types of conjugated polymers (CPs), and they supplied photoelectric properties. Therefore, a complete CPNs preparation process is divided into two steps including the synthesis of CPs and the preparation of nanoparticles.
In the polymerization methods of CPs, palladium catalyzed coupling (Suzuki coupling) [13], Sonogashira coupling [14], Heck coupling [15] and Wittig–Horner [16] reactions are widely used in the preparation of PFP, PPE and PPV. CPNs can be obtained by the methods such as nano-precipitation [17,18], microemulsion [19,20] and self-assembly [21,22] based on the synthetized CPs.
As we all know, the different structure and morphology of CPNs will supply diverse performances. The influencing factors include the structure of CPs and the above preparation methods, and the former can be subdivided into the effects of main chains, side chains and substituent groups. A main chain is the most important part of CPs, which determines the basic physical and chemical properties. At present, the designs of the main chain structure are the focus of most work [23]. Side chains play a crucial role in improving the molecular weight, solubility and processability of polymers [24,25]. Therefore, the research showed that flexible side chains other than the main chain have a large influence on the optical properties of CPs, which can change the intermolecular forces and steric hindrance, affecting the effective conjugate chain length and energy band, absorption and emission [26,27]. Some researches about conjugated polymer side chain engineering have been reported [28,29]. The studies were mainly focused on the effect of different alkyl side chains to polymer solubility, the influence of the side chain spacer length to the charge transfer and the tuning of the branch position of the side chain to the properties of CPs [26,30,31]. For all we know, the studies on the effects of different length side chains on the properties of CPs and their nanoparticles are still scarce. Therefore, in this work, we synthesized four hydrophobic CPs by Wittig–Horner reaction and their CPNs by nano-precipitation method with different length side chains, and studied the effects of different length side chains on the optical properties of CPs and their nanoparticles.
Carbazole and N, N-dimethyl formamide were purchased from Fuyu fine chemical, Tianjin, China. Hydroquinone and 1-bromo-ethylhexane were purchased from Macklin Biochemical, Shanghai, China. Bromoethane, bromo-n-butane, bromo-n-octane, bromo-n-hexadecane and Polystyrene-maleic anhydride (PSMA) with molecular weight of 18,000 were purchased from Aladdin, Shanghai, China. Other chemicals were AR grade and purchased from the commercial corporation without further purification.
1H NMR (400 MHz) spectra were determined and recorded using a Bruker Avance spectrometer, and TMS was used as the internal standard. The sample was grinded with KBr to form pellets, then Fourier transform infrared spectroscopy (FTIR) was measured on a Thermo IS10 spectrometer. UV and Fluorescence spectra were measured and recorded on Shimadzu UV-3600 UV spectrophotometer and Hitrchif-7000 fluorescence spectrometer, respectively. Transmission Electron Microscope (TEM) images were recorded through JEM-2100 electron microscope. Dynamic light Scattering (DLS) was carried out on a Malvern Zetasizer Nano ZS analyzer.
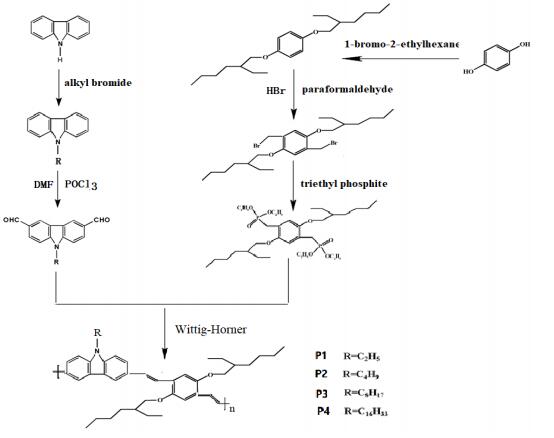
9-ethyl-3, 6'-diformyl-carbazole (Monomer 1a), 9-butyl-3, 6'-diformyl-carbazole (Monomer 1b), 9-octyl-3, 6'-diformyl-carbazole (Monomer 1c) and 9-cetyl-3, 6'-diformyl-carbazole (Monomer 1d) and 1, 4-phosphonic acid diethyl ester-2, 5-(1-methyl ether-ethylhexane)-benzene (Monomer 2) were obtained according to the previous methods with carbazole and hydroquinone as raw materials, respectively [32,33].
The polymer (P1) was synthesized by Wittig–Horner reaction on the basis of Monomer 1a and Monomer 2 (Scheme 1). The Monomer 2 (0.3 g, 0.45 mmoL) was added to the dry tetrahydrofuran (THF) under nitrogen atmosphere and the potassium tertbutoxide (0.2 g, 1.7 mmoL) dissolved in THF was added dropwise to the mixture and stirred for 30 minutes in ice–water bath. Then the Monomer 1a (0.15 g, 0.59 mmoL) was added at room temperature (r.t.). The reaction mixture was kept stirring for 72 hours at r.t. under nitrogen atmosphere, then poured into the water and extracted with dichloromethane. The solvent was removed by rotary evaporator. The residue was refined by fractional diffusion precipitation with THF and n-hexane. Lastly, the yellow solid was obtained with a yield of 58%. 1H NMR (CDC13, 400 Hz) δ (ppm): 8.25 ppm (d, 2H), 7.75 (m, 2H), 7.55 (t, 2H), 7.35 (d, 2H), 7.35 (m, 2H), 7.25 (m, 2H), 4.38 (s, 2H), 4.0 (m, 4H), 1.95–1.75 (m, 2H), 1.75–1.25 (m, 19H), 1.1–0.85 (m, 12H); IR (KBr) ν/cm−1: 1670 (C = C), 1600 (Ar–C), 1096 (C–O), 960 (CH = CH). Mn = 2.693 × 104 (±1.448%), Mω = 3.279 × 104 (±1.534%), Mω/Mn = 1.218 (±2.109%).
Scheme 1. The synthetic route of P1–P4.The synthetic process of polymers P2, P3 and P4 are similar to that of P1.
P2: Yield, 50%. 1H NMR (CDC13, 400 Hz) δ (ppm): 8.25 (d, 2H), 7.75 (m, 2H), 7.55 (t, 2H), 7.35 (d, 2H), 7.35 (m, 2H), 7.25 (m, 2H), 4.38 (s, 2H), 4.0 (m, 4H), 1.95–1.75 (m, 2H), 1.75–1.15 (m, 23H), 1.15–0.7 (m, 12H); IR (KBr) ν/cm−1: 1685 (C = C), 1598 (Ar–C), 1033 (C–O), 954 (CH = CH). Mn = 2.216 × 104 (±1.016%), Mω = 2.419 × 104 (±1.638%), Mω/Mn = 1.092 (±1.928%).
P3: Yield, 55%. 1H NMR (CDC13, 400 Hz) δ (ppm): 8.25 (d, 2H), 7.75 (m, 2H), 7.55 (t, 2H), 7.35 (d, 2H), 7.35 (m, 2H), 7.25 (m, 2H), 4.38 (s, 2H), 4.0 (m, 4H), 1.95–1.75 (m, 2H), 1.75–1.15 (m, 33H), 1.15–0.7 (m, 12H); IR (KBr) ν/cm−1: 1666 (C = C), 1598 (Ar–C), 1039 (C–O), 960 (CH = CH). Mn = 3.509 × 104 (±3.887%), Mω = 5.032 × 104 (±6.782%), Mω/Mn = 1.434 (±7.817%).
P4: Yield, 46%. 1H NMR (CDC13, 400 Hz) δ (ppm): 8.25 (d, 2H), 7.75 (m, 2H), 7.55 (t, 2H), 7.35 (d, 2H), 7.35 (m, 2H), 7.25 (m, 2H), 4.38 (s, 2H), 4.0 (m, 4H), 1.95–1.80 (m, 2H), 1.80–1.15 (m, 49H), 1.15–0.7 (m, 12H); IR (KBr) ν/cm−1: 1662 (C = C), 1592 (Ar–C), 1031 (C–O), 962 (CH = CH). Mn = 2.127 × 104 (±5.248%), Mω = 2.397 × 104 (±6.724%), Mω/Mn = 1.127 (±8.529%).
The preparation of CPNs Ⅰ–COOH~CPNs Ⅳ–COOH: The stock solutions of CPs (P1, P2, P3, P4) and PSMA in THF were prepared with the concentrations of 1 mg/mL and 2 mg/mL, respectively. 0.5 mL of CPs solutions and 0.1 mL of PSMA were added to 10 mL of THF and mixed. After 5 min, the mixture was quickly poured into 20 mL of ultrapure water in a bath sonicator for 5–10 min. Then THF was removed by rotary evaporator, and the solution was concentrated to 10 mL. The solution of carboxyl functional CPNs Ⅰ–CPNs Ⅳ was obtained through a diameter of 0.22 μm micron filter. The same process was carried out without PSMA to get the nanoparticles of CPNs Ⅰ, CPNs Ⅱ, CPNs Ⅲ and CPNs Ⅳ, respectively.
Some relative parameters including number-average molecular weight (Mn), weight-average molecular weight (Mw), polydispersity index (PDI = Mw/Mn) and degrees of polymerization (DP) were summarized in Table 1. One can see that there were narrower PDI (1.092–1.434) by Wittig–Horner reaction. The molecular weights of P1~P4 were found from 21000 to 35000, and the DPs are from 27 to 51. It was found that Mn, Mw and DP reduced with the rising of side chain length. The possible reason may be that the increased side chain length will generate steric hindrance for the reaction [34,35]. However, P3 (octyl) is exceptional, which may be attributed to the octyl side chain supplying a special interaction with 1-bromo-2-ethylhexane to reduce the steric hindrance.
| Names | CPNs Ⅰ | CPNs Ⅱ | CPNs Ⅲ | CPNs Ⅳ |
| Mn | 2.693 × 104 | 2.216 × 104 | 3.509 × 104 | 2.127 × 104 |
| Mω | 3.279 × 104 | 2.419 × 104 | 5.032 × 104 | 2.397 × 104 |
| PDI | 1.218 | 1.092 | 1.434 | 1.127 |
| Molecular weight of structural units | 607 | 635 | 689 | 801 |
| DP | 44 | 35 | 51 | 27 |
| Particle size (without PSMA) (nm) | 23.00 ± 1.00 | 43.95 ± 2.00 | 32.83 ± 2.00 | 44.79 ± 1.00 |
| Particle size (with PSMA) (nm) | 25.00 ± 1.00 | 42.15 ± 2.00 | 28.03 ± 2.00 | 55.64 ± 1.00 |
| Mn: Number-average molecular weight; Mω: Weight-average molecular weight; PDI: Polydispersity index (Mω/Mn); DP: Degrees of polymerization. | ||||
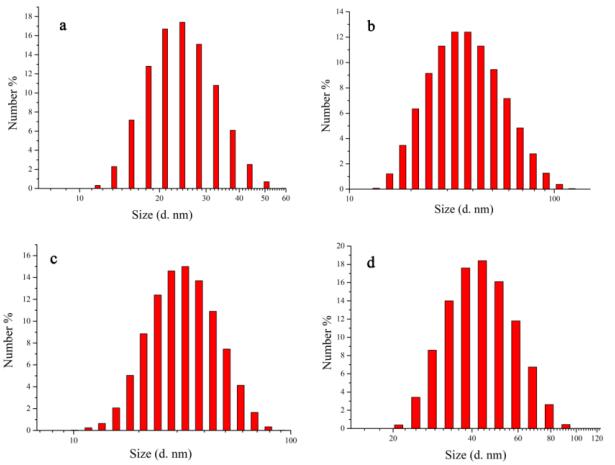
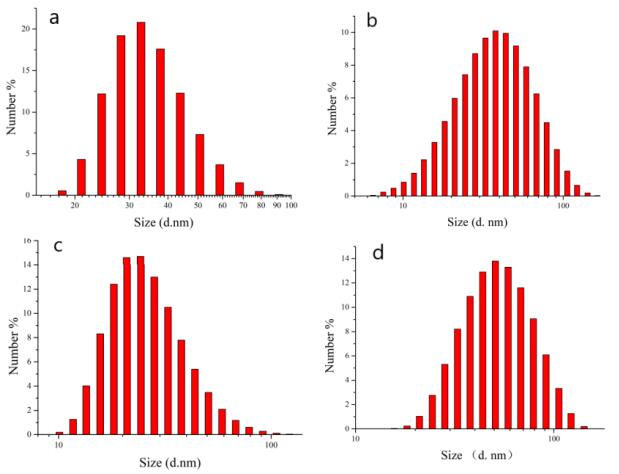
DownLoad: CSVThe CPNs were characterized and analyzed by DLS and TEM. The relative data were listed in Table 1. The sizes of CPNs Ⅰ-Ⅳ are 23.00 nm, 43.95 nm, 32.83 nm, and 44.79 nm in Figure 1, respectively. After adding PSMA, their sizes became 25.00 nm, 42.15 nm, 28.03 nm, and 55.64 nm (Figure 2), respectively.
Figure 1. The particle size of nanoparticles without PSMA was measured by DLS. (a) The DLS measurement of CPNs Ⅰ; (b) The DLS measurement of CPNs Ⅱ; (c) The DLS measurement of CPNs Ⅲ; (d) The DLS measurement of CPNs Ⅳ.
Figure 2. The particle size of nanoparticles with PSMA was measured by DLS. (a) The DLS measurement of CPNs Ⅰ–COOH; (b) The DLS measurement of CPNs Ⅱ–COOH; (c) The DLS measurement of CPNs Ⅲ–COOH; (d) The DLS measurement of CPNs Ⅳ–COOH.It is observed that the sizes of CPNs were almost no change before and after adding PSMA. The possible reason is because of the lesser amount of PSMA (CP:PSMA = 5:1). In addition, thought DPs are decreasing, the nanoparticles size enhanced with the increased side chain length. As discussed above, the special rule of octyl afforded smaller particles size under a higher molecular weights of P3. Moreover, TEM images in Figure 3 showed that the longer side chain increased the flexibility of polymer, which was benefit to form the better nanoparticles morphology with better dispersion and uniform size.
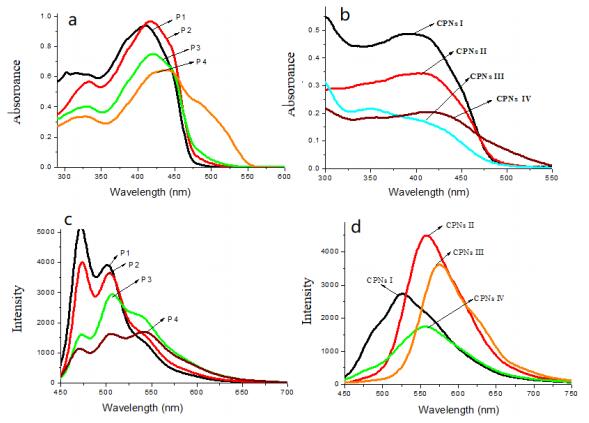
Figure 3. TEM images of CPNs Ⅰ–CPNs Ⅳ: (a) CPNs Ⅰ, (b) CPNs Ⅱ, (c) CPNs Ⅲ, (d) CPNs Ⅳ.The absorption and fluorescence spectra of P1–P4 (1 × 10−5 mol/L) in THF and CPNs Ⅰ–Ⅳ solutions (10 μg/mL) were measured and showed in Figure 4. The relative photophysical data were summarized in Table 2. The quantum yields (Фs) were calculated by the reference method using coumarin307 (Ф = 0.56 in methanol) as the standard according to the literature described [36]. From Figure 4 and Table 2, we can find that the absorption and fluorescence spectra of CPs and CPNs are both red-shifted with the increase of side-chain length, and their Stokes shifts (Δλ) showed the same trend. The reason may be attributed to the enhanced conjugation because of longer side chains [37]. The Фs enhanced with the increased side chain length from 0.25 to 0.40 for CPs and from 0.23 to 0.58 for CPNs. But the values of P3 reached 0.66, which may be affected by the higher DP. In addition, different length side chains of CPs and CPNs supplied various fluorescence colors from green to yellow in Figure 5, but the fluorescence of CPNs is brighter than that of the corresponding CPs. These results indicated that the synthetized CPs and CPNs have better absorbance and fluorescence emission properties.
Figure 4. (a and b): The UV absorption spectra of P1–P4 in THF (10 μmol/L) and CPNs Ⅰ-Ⅳ solution (10 μg/mL); (c and d) The fluorescence emission spectra of P1–P4 in THF (10 μmol/L) and CPNs Ⅰ-Ⅳ solution (10 μg/mL).| λmaxA (nm) | λmaxF (nm) | Δλ (nm) | Ф | |
| P1 | 410 | 472 | 62 | 0.25 |
| P2 | 417 | 473 | 56 | 0.33 |
| P3 | 420 | 507 | 87 | 0.66 |
| P4 | 440 | 542 | 102 | 0.40 |
| CPNs Ⅰ | 397 | 525 | 128 | 0.23 |
| CPNs Ⅱ | 406 | 558 | 152 | 0.42 |
| CPNs Ⅲ | 409 | 557 | 148 | 0.47 |
| CPNs Ⅳ | 415 | 571 | 155 | 0.58 |
| λmaxA is the wavelength of maximum absorption; λmaxF is the wavelength of maximum fluorescence emission; Δλ was stokes shift; Ф is quantum yield. | ||||
DownLoad: CSV
Figure 5. (a) The fluorescence photographs of CPs (Ⅰ–Ⅳ) in THF at 365 nm; (b) The fluorescence photographs of the CPNs Ⅰ–Ⅳ aqueous at 365 nm.In summary, four CPs of different side chains (P1-ethyl, P2-butyl, P3-octyl, P4-hexadecyl) were prepared by Wittig–Horner reaction based on carbazole and hydroquinone with narrow PDI. The DP declined with the increase of the side chain length except P3. The data of DLS, TEM and the absorbance and fluorescence emission showed the increased side chain length of CPs will be benefit to longer wavelength absorbance, better fluorescence and morphology for CPNs. In addition, the nanoparticle size is lightly affected by simply functional group and the side chain length. These results will be benefit to the design of CPs and the preparation of CPNs.
This project was supported by the National Natural Science Foundation of China (NSFC 51403111, 11774188). We are particularly grateful to State Key Laboratory of Crystal Materials in Shandong University for help in fluorescence measuring.
There is no conflict of interest regarding the publication of this manuscript.
| [1] |
Lyu Y, Pu K (2017) Recent advances of activatable molecular probes based on semiconducting polymer nanoparticles in sensing and imaging. Adv Sci 4: 1600481–1600487. doi: 10.1002/advs.201600481
|
| [2] |
Cui Q, Wang X, Yang Y, et al. (2016) Binding-directed energy transfer of conjugated polymer materials for dual-color imaging of cell membrane. Chem Mater 28: 4661–4669. doi: 10.1021/acs.chemmater.6b01424
|
| [3] |
Chan YH, Wu C, Ye F, et al. (2011) Development of ultrabright semiconducting polymer dots for ratiometric pH sensing. Anal Chem 83: 1448–1455. doi: 10.1021/ac103140x
|
| [4] |
Wu PJ, Chen JL, Chen CP, et al. (2013) Photoactivated ratiometric copper(II) ion sensing with semiconducting polymer dots. Chem Commun 49: 898–900. doi: 10.1039/C2CC37848E
|
| [5] |
Zhang P, Lu H, Chen H, et al. (2016) Cationic conjugated polymers-induced quorum sensing of bacteria cells. Anal Chem 88: 2985–2988. doi: 10.1021/acs.analchem.5b03920
|
| [6] |
Wu PJ, Kuo SY, Huang YC, et al. (2014) Polydiacetylene-enclosed near-infrared fluorescent semiconducting polymer dots for bioimaging and sensing. Anal Chem 86: 4831–4839. doi: 10.1021/ac404237q
|
| [7] |
Zhou X, Liang H, Jiang P, et al. (2016) Ultifunctional phosphorescent conjugated polymer dots for hypoxia imaging and photodynamic therapy of cancer cells. Adv Sci 3: 1500155–1500166. doi: 10.1002/advs.201500155
|
| [8] |
Palner M, Pu K, Shao S, et al. (2015) Semiconducting polymer nanoparticles with persistent near‐infrared luminescence for in vivo optical imaging. Angew Chem Int Edit 127: 11639–11642. doi: 10.1002/ange.201502736
|
| [9] |
Zhang D, Wu M, Zeng Y, et al. (2016) Lipid micelles packaged with semiconducting polymer dots as simultaneous MRI/photoacoustic imaging and photodynamic/photothermal dual-modal therapeutic agents for liver cancer. J Mater Chem B 4: 589–599. doi: 10.1039/C5TB01827G
|
| [10] |
Lyu Y, Xie C, Chechetka SA, et al. (2016) Semiconducting polymer nanobioconjugates for targeted photothermal activation of neurons. J Am Chem Sci 138: 9049–9052. doi: 10.1021/jacs.6b05192
|
| [11] |
Cai X, Liu X, Liao LD, et al. (2016) Encapsulated conjugated oligomer nanoparticles for real‐time photoacoustic sentinel lymph node imaging and targeted photothermal therapy. Small 12: 4873–4880. doi: 10.1002/smll.201600697
|
| [12] |
Cheng L, He W, Gong H, et al. (2013) PEGylated micelle nanoparticles encapsulating a non‐fluorescent near‐infrared organic dye as a safe and highly‐effective photothermal agent for in vivo cancer therapy. Adv Funct Mater 23: 5893–5902. doi: 10.1002/adfm.201301045
|
| [13] |
Li K, Liu B (2010) Water-soluble conjugated polymers as the platform for protein sensors. Polym Chem 1: 252–259. doi: 10.1039/B9PY00283A
|
| [14] |
Moon JH, McDaniel W, MacLean P, et al. (2007) Live‐cell‐permeable poly(p‐phenylene ethynylene). Angew Chem Int Edit 46: 8223–8225. doi: 10.1002/anie.200701991
|
| [15] |
Feng X, Yang G, Liu L, et al. (2012) A convenient preparation of multi‐spectral microparticles by bacteria‐mediated assemblies of conjugated polymer nanoparticles for cell imaging and barcoding. Adv Mater 24: 637–641. doi: 10.1002/adma.201102026
|
| [16] |
Khidre RE, Abdou WM (2016) Wittig–Horner reagents: powerful tools in the synthesis of 5- and 6-heterocyclic compounds; shedding light on their application in pharmaceutical chemistry. Turk J Chem 40: 225–247. doi: 10.3906/kim-1502-56
|
| [17] |
Wu C, Jin Y, Schneider T, et al. (2010) Ultrabright and bioorthogonal labeling of cellular targets using semiconducting polymer dots and click chemistry. Angew Chem Int Edit 49: 9436–9440. doi: 10.1002/anie.201004260
|
| [18] |
Wu C, Schneider T, Zeigler M, et al. (2010) Bioconjugation of ultrabright semiconducting polymer dots for specific cellular targeting. J Am Chem Sci 132: 15410–15417. doi: 10.1021/ja107196s
|
| [19] |
Wu C, Hansen SJ, Hou Q, et al. (2011) Design of highly emissive polymer dot bioconjugates for in vivo tumor targeting. Angew Chem Int Edit 50: 3430–3434. doi: 10.1002/anie.201007461
|
| [20] |
Li K, Pan J, Feng SS, et al. (2009) Generic strategy of preparing fluorescent conjugated‐polymer‐loaded poly(dl‐lactide‐co‐glycolide) nanoparticles for targeted cell imaging. Adv Funct Mater 19: 3535–3542. doi: 10.1002/adfm.200901098
|
| [21] |
Howes P, Green M, Levitt J, et al. (2010) Phospholipid encapsulated semiconducting polymer nanoparticles: their use in cell imaging and protein attachment. J Am Chem Sci 132: 3989–3996. doi: 10.1021/ja1002179
|
| [22] |
Yang G, Liu L, Yang Q, et al. (2012) A multifunctional cationic pentathiophene: Synthesis, organelle‐selective imaging, and anticancer activity. Adv Funct Mater 22: 736–743. doi: 10.1002/adfm.201101764
|
| [23] |
Ni D, Yang D, Ma S, et al. (2013) Side chains and backbone structures influence on 4,7-dithien-2-yl-2,1,3-benzothiadiazole (DTBT)-based low-bandgap conjugated copolymers for organic photovoltaics. Front Optoelectron 6: 418–428. doi: 10.1007/s12200-013-0343-9
|
| [24] |
Subramaniyan S, Xin H, Kim FS, et al. (2011) Effects of side chains on thiazolothiazole-based copolymer semiconductors for high performance solar cells. Adv Energy Mater 1: 854–860. doi: 10.1002/aenm.201100215
|
| [25] |
Zhang W, Shiotsuki M, Masuda T (2007) Synthesis and properties of polymer brush consisting of poly(phenylacetylene) main chain and poly(dimethylsiloxane) side chains. Polymer 48: 2548–2553. doi: 10.1016/j.polymer.2007.03.016
|
| [26] |
Zhu L, Jiang C, Chen G, et al. (2017) Side chain engineering: The effect on the properties of isoindigo-based conjugated polymers contain different length and structure alkyl chains on nitrogen atom. Org Electron 49: 278–285. doi: 10.1016/j.orgel.2017.06.035
|
| [27] |
Hwang KH, Kim DH, Min HC, et al. (2016) Effect of side chain position and conformation of quinacridone–quinoxaline based conjugated polymers on photovoltaic properties. J Ind Eng Chem 34: 66–75. doi: 10.1016/j.jiec.2015.10.029
|
| [28] |
Wang YJ, Larsson M, Huang WT, et al. (2016) The use of polymer-based nanoparticles and nanostructured materials in treatment and diagnosis of cardiovascular diseases: Recent advances and emerging designs. Prog Polym Sci 57: 153–178. doi: 10.1016/j.progpolymsci.2016.01.002
|
| [29] |
Kamaly N, Xiao Z, Valencia PM, et al. (2012) Targeted polymeric therapeutic nanoparticles: design, development and clinical translation. Chem Soc Rev 41: 2971–3010. doi: 10.1039/c2cs15344k
|
| [30] | Razzellhollis J, Fleischli F, Jahnke AA, et al. (2017) Effects of side-chain length and shape on polytellurophene molecular order and blend morphology. J Phys Chem C 121: 11675–11679. |
| [31] |
Duan C, Willems REM, Franeker JJV, et al. (2016) Effect of side chain length on the charge transport, morphology, and photovoltaic performance of conjugated polymers in bulk heterojunction solar cells. J Mater Chem A 4: 1855–1866. doi: 10.1039/C5TA09483F
|
| [32] |
Jiang YB, Gao C, Zhang X, et al. (2018) A highly selective and sensitive fluorescence probe with A-π-D-π-A structure for detection of Ag+. J Mol Struct 1163: 33–40. doi: 10.1016/j.molstruc.2018.01.058
|
| [33] |
Zhang X, Sun YM, Yu XQ, et al. (2009) Synthesis and nonlinear optical properties of several new two-photon photopolymerization initiators about dibenzothiophene derivatives. Synthetic Met 159: 2491–2496. doi: 10.1016/j.synthmet.2009.08.057
|
| [34] |
Shin CK, Lee H (2004) Effect of alkyl side-chain length and solvent on the luminescent characteristics of poly(3-n-alkylthiophene). Synthetic Met 140: 177–181. doi: 10.1016/S0379-6779(03)00361-8
|
| [35] |
Lecollinet G, Delorme N, Edely M, et al. (2009) Self-assembled monolayers of bisphosphonates: influence of side chain steric hindrance. Langmuir 25: 7828–7835. doi: 10.1021/la8039576
|
| [36] |
Meng XL, Zhang X, Yao JS, et al. (2013) Fluorescence and fluorescence imaging of two schiff derivatives sensitive to Fe3+ induced by single- and two-photon excitation. Sensor Actuat B-Chem 176: 488–496. doi: 10.1016/j.snb.2012.10.089
|
| [37] |
Fu B, Baltazar J, Sankar AR, et al. (2014) Enhancing field‐effect mobility of conjugated polymers through rational design of branched side chains. Adv Funct Mater 24: 3734–3744. doi: 10.1002/adfm.201304231
|
| 1. | Qiu-bo Wang, Cui-jiao Zhang, Qian Lu, Zhao-e Liu, Jin-shui Yao, Xian Zhang, A “turn-on” fluorescence platform of detection glutathione using MnO2 nanosheets quenched fluorescent conjugated polymer nanoparticles, 2020, 176, 01437208, 108189, 10.1016/j.dyepig.2020.108189 | |
| 2. | Qiu-bo Wang, Cui-jiao Zhang, Hao Yu, Xian Zhang, Qian Lu, Jin-shui Yao, Hui Zhao, The sensitive “Turn-on” fluorescence platform of ascorbic acid based on conjugated polymer nanoparticles, 2020, 1097, 00032670, 153, 10.1016/j.aca.2019.10.076 | |
| 3. | Zhi-yan Gao, Xian Zhang, Shu Xing, Qian Lu, Jin-shui Yao, Qin-ze Liu, Cong-de Qiao, Rui-xing Xie, Biyan Ding, Conjugated polymer nanoparticles based on carbazole for detecting ferric ion (III) with a large Stokes shift and high sensitivity and the application in cell imaging, 2019, 168, 01437208, 68, 10.1016/j.dyepig.2019.04.030 | |
| 4. | Mariia V. Pavliuk, Sina Wrede, Aijie Liu, Andjela Brnovic, Sicong Wang, Martin Axelsson, Haining Tian, Preparation, characterization, evaluation and mechanistic study of organic polymer nano-photocatalysts for solar fuel production, 2022, 51, 0306-0012, 6909, 10.1039/D2CS00356B | |
| 5. | Agni Puentes Ossa, Diego Julian Rodriguez, Julian Andres Salamanca Bernal, Computational Modeling of Light Scattering in Polymer Nanoparticles for Optical Characterization, 2024, 34, 1909-7735, 63, 10.18359/rcin.7276 |
Figures(6) / Tables(2)
Qiu-bo Wang, Chao Xu, Yi-bao Jiang, Xian Zhang, Jin-shui Yao, Cong-de Qiao, Qin-ze Liu, Yuan-hong Zhang. The synthesis of conjugated polymers with different length side chains and the effect on their nanoparticles[J]. AIMS Materials Science, 2018, 5(4): 770-780. doi: 10.3934/matersci.2018.4.770
| Names | CPNs Ⅰ | CPNs Ⅱ | CPNs Ⅲ | CPNs Ⅳ |
| Mn | 2.693 × 104 | 2.216 × 104 | 3.509 × 104 | 2.127 × 104 |
| Mω | 3.279 × 104 | 2.419 × 104 | 5.032 × 104 | 2.397 × 104 |
| PDI | 1.218 | 1.092 | 1.434 | 1.127 |
| Molecular weight of structural units | 607 | 635 | 689 | 801 |
| DP | 44 | 35 | 51 | 27 |
| Particle size (without PSMA) (nm) | 23.00 ± 1.00 | 43.95 ± 2.00 | 32.83 ± 2.00 | 44.79 ± 1.00 |
| Particle size (with PSMA) (nm) | 25.00 ± 1.00 | 42.15 ± 2.00 | 28.03 ± 2.00 | 55.64 ± 1.00 |
| Mn: Number-average molecular weight; Mω: Weight-average molecular weight; PDI: Polydispersity index (Mω/Mn); DP: Degrees of polymerization. | ||||
DownLoad: CSV| λmaxA (nm) | λmaxF (nm) | Δλ (nm) | Ф | |
| P1 | 410 | 472 | 62 | 0.25 |
| P2 | 417 | 473 | 56 | 0.33 |
| P3 | 420 | 507 | 87 | 0.66 |
| P4 | 440 | 542 | 102 | 0.40 |
| CPNs Ⅰ | 397 | 525 | 128 | 0.23 |
| CPNs Ⅱ | 406 | 558 | 152 | 0.42 |
| CPNs Ⅲ | 409 | 557 | 148 | 0.47 |
| CPNs Ⅳ | 415 | 571 | 155 | 0.58 |
| λmaxA is the wavelength of maximum absorption; λmaxF is the wavelength of maximum fluorescence emission; Δλ was stokes shift; Ф is quantum yield. | ||||
DownLoad: CSV| Names | CPNs Ⅰ | CPNs Ⅱ | CPNs Ⅲ | CPNs Ⅳ |
| Mn | 2.693 × 104 | 2.216 × 104 | 3.509 × 104 | 2.127 × 104 |
| Mω | 3.279 × 104 | 2.419 × 104 | 5.032 × 104 | 2.397 × 104 |
| PDI | 1.218 | 1.092 | 1.434 | 1.127 |
| Molecular weight of structural units | 607 | 635 | 689 | 801 |
| DP | 44 | 35 | 51 | 27 |
| Particle size (without PSMA) (nm) | 23.00 ± 1.00 | 43.95 ± 2.00 | 32.83 ± 2.00 | 44.79 ± 1.00 |
| Particle size (with PSMA) (nm) | 25.00 ± 1.00 | 42.15 ± 2.00 | 28.03 ± 2.00 | 55.64 ± 1.00 |
| Mn: Number-average molecular weight; Mω: Weight-average molecular weight; PDI: Polydispersity index (Mω/Mn); DP: Degrees of polymerization. | ||||
| λmaxA (nm) | λmaxF (nm) | Δλ (nm) | Ф | |
| P1 | 410 | 472 | 62 | 0.25 |
| P2 | 417 | 473 | 56 | 0.33 |
| P3 | 420 | 507 | 87 | 0.66 |
| P4 | 440 | 542 | 102 | 0.40 |
| CPNs Ⅰ | 397 | 525 | 128 | 0.23 |
| CPNs Ⅱ | 406 | 558 | 152 | 0.42 |
| CPNs Ⅲ | 409 | 557 | 148 | 0.47 |
| CPNs Ⅳ | 415 | 571 | 155 | 0.58 |
| λmaxA is the wavelength of maximum absorption; λmaxF is the wavelength of maximum fluorescence emission; Δλ was stokes shift; Ф is quantum yield. | ||||
