1. Introduction
Recent advances in genetic and environmental contributions to autoimmunity suggest that interaction between genetic elements and epigenetic changes caused by environmental agents may be responsible for inducing autoimmune diseases (ADs). Autoimmunity arises when immune responses mounted in the host are directed against self-components as a result of the loss of self-tolerance. ADs may be ether tissues-pecific where unique tissue-specific antigens are targeted, or systemic in which multiple tissues are affected and a variety of apparently ubiquitously expressed autoantigens are targeted [1,2] (Table 1). The affliction of autoimmunity is believed to develop when genetically predisposed individuals encounter environmental agents that trigger it. The environmental agents that are revered in this respect are stress and the viruses [3,4,5,6,7,8,9,10,11,12,13,14,15], which are operatives in this scene as stimuli for the activation of the nuclear factor (NF-KB), a transcription factor which specifically binds promoter DNA to activate target gene expression.
Table 1. Examples of selected human autoimmune diseases (adapted from Ray S et al. [1]).
| Organ specific autoimmune diseases |
| Organ |
Disease(s) |
Self-Antigen |
| Adrenal cells |
Addison's disease |
Cytochrome P-450 antigens |
| Red blood cells |
Autoimmune haemolitic anaemia |
Red blood cell membrane proteins |
| Platelets |
Idiopathic thrombocytopaenic purpura |
Platelet antigens |
| Stomach |
Pernicious anaemia |
Gastric parietal cell antigens |
| Small bowel |
Coeliac sprue (gluten eneteropathy) |
Transglutaminase |
| Thyroid |
Hashimoto's thyroiditis Grave's disease |
Thyroid cell antigens Thyroid-stimulating hormone receptor |
| Muscle |
Myasthenia gravis |
Acetylcholine receptors |
| Pancreatic islets |
Type 1 diabetes |
Beta cell antigens |
| Hepatocytes |
Autoimmune hepatitis |
Hepatocyte antigens (cytochrome P-450 2D6) |
| Bile duct cells |
Primary biliary cirrhosis |
Intra-hepatic bile duct |
| Heart |
Rheumatic heart disease |
Myocardial antigens |
| Kidney/lung |
Goodpasture's syndrome |
Basement membrane antigens |
| Systematic autoimmune diseases |
|
Disease(s) |
Self-Antigen |
| Ankylosing sponkylitis |
Vertebrae |
| Multiple sclerosis |
Brain or white matter |
| Rheumatoid arthritis |
Connective tissue, IgG |
| Systemic lupus erythematosus |
DNA nuclear protein RBC and platelet membranes |
| Scleroderma |
Nuclei, heart, lungs, gastrointestinal tract, kidney |
| Sjogren's syndrome |
Salivary gland, liver, kidney, thyroid |
1.1. NF-ΚB
The transcription factor NF-ΚB is involved in the regulation of a large number of genes that control various aspects of the immune and inflammatory responses. According to Zhu et al. [16], NF-ΚB is a family of structurally related transcription factors. In mammals the NF-ΚB family consists of five members: NF-ΚB1 (p105/50), NF-ΚB2 (p100/52), RelA (p65), RelB, and c-Rel. They all have a structurally conserved N-terminal 300-amino-acid Rel homology domain (RHD), which contains sequences responsible for dimerization, nuclear translocation and DNA binding. Only RelA, RelB and c-Rel have a transactivation domain, which is non-homologous and located at the C-termini of the proteins. The other two NF-ΚB proteins, NF-ΚB1 and NF-ΚB2, lack a transactivation domain but instead contain seven ankyrin repeats, a 33-amino-acid characteristic motif of the inhibitor of NF-ΚB, (IΚB), that mediates protein-protein interactions. The five NF-ΚB proteins above can form 15 transcription factors through homo-or hetero-dimerization [17]: the main activated forms being RelA: p50 and RelB: p52. These NF-ΚB family members play critical roles in a wide variety of biological processes, including immune and inflammatory responses, development, cell growth and apoptosis. In unstimulated cells, the NF-ΚB dimers are sequestered in the cytoplasm by a family of inhibitors called IΚBs (IΚBα, IΚBβ, IΚBε and IΚBγ, IΚBδ, IΚBζ and Bcl-3), which are proteins that contain multiple copies of the sequence ankyrin repeats. By virtue of their ankyrin repeat domains, the IΚB proteins mask the nuclear localization signals of NF-ΚB proteins and keep them sequestered in an inactive state in the cytoplasm [18]. The NF-ΚB dimer becomes activated through degradation of the IΚB following phosphorylation of specific serines in the IΚB proteins by the IΚB-kinase complex (IKK), leading to their ubiquitination and thus allowing the liberation and nuclear translocation of NF-ΚB dimers to induce gene expression.
1.2. Activation of NF-ΚB
The NF-ΚB is recognized as a master transcription factor that responds to diverse stimuli by activating the expression of stress-response genes. Multiple signals, including cytokines, growth factors, engagement of the T cell receptor, bacterial and viral products, various forms of radiation and the oxidative stress, induce NF-ΚB transcriptional activity [19,20,21]. We are particularly interested in, and will limit ourselves to, the mechanism by which NF-ΚB is activated by oxidative stress and the viruses, the latter being represented by the gamma herpesviruses KSHV and EBV.
1.2.1. Oxidative stress-activation of NF-ΚB
In respiring cells, a small amount of consumed oxygen is reduced in a specific way, yielding a variety of highly reactive chemical entities collectively called reactive oxygen species (ROS) or reactive oxidative intermediates (ROIs) and include hydrogen peroxide (H2O2), nitric oxide radical (NO), superoxide anion (O2–) and hydroxyl radical (OH–). A state of moderately increased levels of intracellular ROS is referred to as cellular oxidative stress [19,22]. Oxidative stress is caused by an imbalance between the production of oxidants and/or decreased ability to detoxify those oxidants. ROS activate NF-ΚB by various mechanisms [23,24]. Studies have been made which suggest that IΚBα phosphorylation and degradation might be the step that is responsive to oxidative stress. NF-ΚB activation has been suggested to be regulated by the levels of oxidants inside cells [22]. Thus it is observed that H2O2, a ROS, regulates NF-ΚB activation through alternative phosphorylation of IΚBα. While typically IΚBα is usually phosphorylated on serines 32 and 36, which leads to its ubiquitination and degradation, ROS H2O2 affects the phosphorylation of IΚBα on tyrosine Tyr42 or other tyrosine residues, and IΚBα may or may not be degraded as part of the process [25,26,27,28,29]. IKK is not required in this case, and IΚBα phosphorylation may be mediated by kasein Kinase II as well as a tyrosine kinase. Degradation of IΚBα may not be necessary in this case because Tyr42-phosphorylated IΚBα is bound by the SH2 domains of p85α regulatory subunit of PI3K, thus unmasking NF-ΚB and allowing it to translocate to the nucleus [30,31,32]. PI3K as well as c-Src have been implicated in alternative phosphorylation of IΚBα.
1.2.2. Viral activation of NF-ΚB, installment of viral latency
NF-ΚB activation is imperative for latent infection of gamma herpesviruses. KSHV infection activates IKKβ and IKKε to enable host NF-ΚB activation and KSHV latent infection. Biochemical and genetic experiments identified RelA as a key player downstream of IKKβ and IKKε, i.e., IKKβ and IKKε were essential for phosphorylation of serines S536 and S468 of RelA, respectively [33]. That the expression of the phosphorylation-resistant RelAS536A increased KSHV lytic genes expression and impaired latent infection is further seen as completing evidence. NF-ΚB activation is coordinated by IKKβ and IKKε, which sequentially phosphorylate RelA in a site-specific manner to enable latent infection after KSHV de novo infection. As a further evidential support, knockdown of IKKβ and IKKε impairs NF-ΚB activation and elevates KSHV lytic genes expression resulting in abrogation of the latent infection. Please recall here that RelA is one of the five members of NF-ΚB family that is the most abundantly and ubiquitously expressed and is the transcriptionally active subunit of the predominant RelA: p50 dimer. Post translational modifications of the RelA subunit, e.g., phosphorylation and acetylation, are important means to regulate NF-ΚB-dependent gene expression [34,35,36,37]. Activation of NF-ΚB through viral infection results in the transactivation of the NF-ΚB sitec-ontaining viral promoter, resulting in installment of latency [38].
1.3. Viral latency
In latent infection, the full viral genome is retained in the host, but its expression is dramatically restricted, such that few viral antigens and no viral particles are produced. To qualify as latency, this cryptic form of infection must display two additional properties: persistence and reversibility, i.e., the capacity of the genome, under the appropriate circumstances (e.g., oxidative stress) to be fully reactivated with the production of infectious progeny, (the lytic replication), is the key requirement of latency. It is the property of reversibility that allows latent infections to avoid abortive infection, or a dead end, and instead become an effective mechanism of viral persistence. Efficient establishment of latency allows the viral genome to persist despite the host immune responses to many viral antigens, and in the face of other potentially adverse signals in the microenvironment. When environmental conditions warrant, appropriate signals can trigger the full repertoire of viral gene expression, allowing viral production and spread to resume.
1.3.1. Maintenance of latency
The herpesviruses, alpha, beta and gamma subfamilies are the viruses capable of true latency as described above. In fact all herpesviruses share a propensity to establish latent infection [39,40]. The herpesviruses HBV and KSHV encode multiple viral miRNAs which mimic cellular miRNAs and modulate cellular and viral gene expression [41,42,43,44]. Some of the viral miRNAs have been implicated in maintaining latent infection and altering the balance between latent/lytic infection [45,46]. The first study showing that miRNAs can be encoded in the viral genome was published in 2004 [47]. The unique ability of the herpesviruses to establish long term latent infections means that these viruses need to block protective host innate or adaptive immune responses over the long term while minimizing the expression of potentially antigenic viral proteins, and this is accomplished by the viral miRNAs. Employing quantitative algorithms prediction, the authors, Grey et al. and Lu et al. [48,49] determined that the herpesviruses employ viral miRNAs to suppress expression of their own genes, including their immediate early genes. These authors concluded that these viruses use viral miRNAs-mediated suppression of immediate early genes as part of their strategy to enter and maintain latency. The lytic cascade is reinitiated with the expression of the immediate early genes (RTA, BZLF1 and BRLF1). Multiple viral miRNAs are transcribed during latency. The KSHV encoded miRNAs (miR-K12-9-5p and miR-12-7-5p) have been shown to directly regulate and inhibit the transcription of the master lytic switch protein, the viral immediate early gene known as the replication and transcription activator (RTA), and in this way they contribute to the maintenance of viral latency. They target the expression of RTA at the translational level [50,51,52]. Fang Lu et al. observed that EBV-coded miR-155 attenuates NF-ΚB signaling and stabilizes latent virus persistence [41]. miRNA-155 is important for the stable maintenance of EBV genomes during latent infection. Several latency genes have been observed to influence the activation of NF-ΚB which turns out to be important in the maintenance of latency. EBV encoded latency membrane protein 1 (LMP1) is a potent activator of NF-ΚB signaling pathways and is essential for EBV immortalization of B lymphocytes. Finally, the observations by Lei et al. [53] established that the viral activation of NF-ΚB is essential for the establishment of latency.
1.3.2. Abrogation of latency (the activation of the lytic, replicative phase of infection)
EBV lytic genes are expressed in a temporally regulated cascade. Following the activation, transcription and expression of the lytic master switch RTA, the switch from the latent to the replicative form of EBV infection is mediated by the two immediate early proteins BZLF1 and BRLF1, which are transcription factors that together activate the entire lytic viral cascade of gene expression, ultimately resulting in the production of infectious viral particles [54]. In natural viral life cycle, the differentiation of the cells triggers the abrogation of latency and entrance into the lytic phase of infection. In the situations leading to virus-induced autoimmunity, however, it is cellular stress, in particular for our purpose, oxidative stress that triggers latency termination [5].
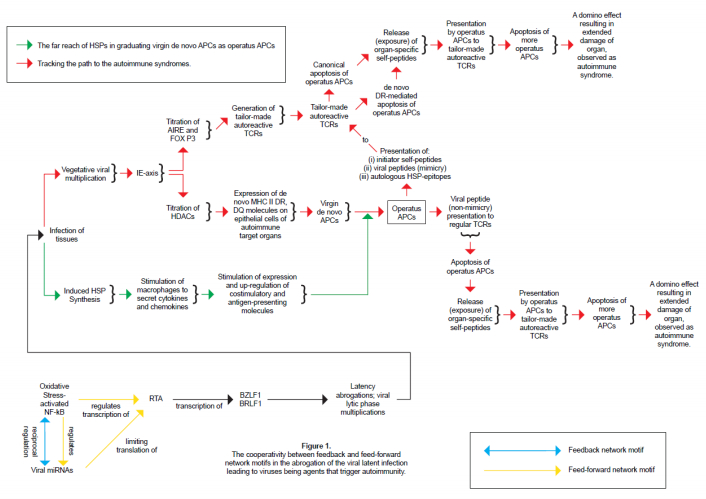
2. The Hypothesis
The switch between latency and lytic replication is regulated by epigenetic factors: (ⅰ) hypomethylation of the promoter of replication and transcription activator, RTA (which, as said above, is essential for the lytic switch) leads to viral reactivation; (ⅱ) histone acetylation induces viral replication by influencing protein-protein associations and transcription factor binding [55]; and (ⅲ) it is the general and established situation that post-transcriptional gene regulation of mRNA turnover and translation is mediated by microRNAs and RNA-binding proteins in events identified as network motifs [56,57,58,59,60]. The network motifs in the images of feedback and feed-forward mechanisms or loops [61] are defined as small gene regulating circuits that occur more often than can be expected by chance. Feed-back motifs are prominent throughout biology: they can be identified when protein-protein interactions are combined with transcriptional interactions [62] or when transcriptional interactions and miRNA-mediated post-transcriptional interactions are involved. We hypothesize that this latter scenario and mode of feedback motif occurs with stress-activated NF-ΚB (a transcription factor) and viral miRNAs: the ensemble being depicted as NF-ΚB <--> miRNA, signifying a reciprocal regulation between the viral miRNA and NF-ΚB in which NF-ΚB regulates viral miRNA and is itself regulated by the same miRNA. NF-ΚB gets directly involved in up-regulation and down-regulation of miRNAs [63]. We suggest that the relationship above induces a down-regulation of the viral miRNA with the consequence that the viral miRNA gets sequestered (titrated out) and neutralized by the RTA site with which it interacts through a process termed "sponging". Equally interacting with the RTA site is the stress-activated NF-ΚB. But the down-regulation of the viral miRNA by NF-ΚB in the feed-back circuit (formula) above accentuates the viral miRNA sponging, making it (the viral miRNA) no longer in excess but reduced to below some minimal proportionate value. This frees the RTA site for the transcription factor NF-ΚB interaction and it results in the activation and transcription of RTA: we say this event spells switching on of the master lytic switch, if you will!
In the situation of feed-forward circuitry, a regulator X regulates the expression of a target Z via a direct or indirect path through a regulator Y, the whole setting represented as X/Z/Y, which in our particular case is translated as "stress-activated NF-ΚB/RTA/viral miRNA". This feed-forward loop reveals a mechanism through which stress-activated NF-ΚB simultaneously activates RTA transcription and limits its translation through activation of the viral miRNA.
In summary, NF-ΚB is unusually activated: its viral activation via serine residues phosphorylation by IKKβ and IKKε leads to viral latency, while activation by oxidative stress (ROS) occurs via tyrosine phosphorylation of IΚBα which then complexes with NF-ΚB and leads to abrogation of the viral latency. To facilitate understanding of the above we abbreviate that "viral activation of NF-ΚB leads to viral latency; while stress activation of the same molecular entity, the NF-ΚB, leads instead to abrogation of the latency". Thus NF-ΚB emerges as the converging focus between stress and the viruses in their efforts as separate environmental agents that trigger autoimmunity. The phosphorylation of particular amino acid residues of a protein molecule modulates that protein's polymorphic conformations, appropriately. For a transcription factor, TF, a given conformation influences its choice of cognate DNA sequence recognition as well as its interaction with a neighboring TF or other proteins and molecules. The transcription factor, NF-ΚB, in particular is reputed to be involved in a battery of regulatory functions [23,64]. We interpret this to mean that as a TF that is variously and differentially phosphorylated, NF-ΚB is capable of assuming or exhibiting a multitude of polymorphic conformations that we choose to call them "derivative isoforms". Thus the virus activation of NF-ΚB that occurs via its phosphorylation by IKKβ and IKKε at serines S536 and S468 generates the derivative isoforms with the potential to activate the transcription of viral latency genes thereby installing and maintaining a latent infection. On the other hand oxidative stress-activation of NF-ΚB occurs via complexation with IΚBα that is phosphorylated at tyrosine Tyr42 and yields derivative isoforms with the attributes that activate the transcription of RTA, the master lytic switch, thereby precipitating abrogation of the viral latency and engendering the lytic cycle phase. The above two alternative involvements of NF-ΚB portray its versatility and sophistication and confirms the difference in mechanism between viral-and stress-activations of NF-ΚB. The revelation of the feedback and feedforward network motifs cited above represents evidence of regulatory circuits involving stress-activated NF-ΚB and viral miRNAs: the feedback mechanism co-accomplishes with the feed-forward loop, in a relation possibly reverberative of a cooperativity, the expression and switching on of RTA, the master lytic switch. This expressed RTA in turn activates the transcription of the immediate early genes BZLF1 and BRLF1: the two transcription factors that mobilize the expression of the whole set of lytic genes, resulting in the procreation of the lytic cascade. Interpret this simply as the activation of NF-ΚB by stress materializes in a dual prong: feedback and feedforward loops that cooperate in the switching on of RTA and thus abrogate the viral latency, consequentially setting in trend or motion the journey of the virus to the triggering of autoimmunity (Figure 1) [65].
Take-home Messages
(1) In man, autoimmunity is an event in which the immune responses mounted in the host are directed against self-components as a result of the loss of self-tolerance. The resulting autoimmune diseases are either tissue-specific when a particular tissue is affected, or systemic when a number of tissues are enrolled.
(2) To happen, autoimmunity requires triggering by environmental factors: the viruses and oxidative stress, in genetically primed individuals. The viruses and stress feature as stimuli for the activation of the transcription factor NF-ΚB.
(3) Post-transcriptional gene regulation of mRNA turnover and translation is mediated by microRNAs and RNA-binding proteins in events identified as network motifs, in the images of feedback and feed-forward mechanisms. The feedback network motif in which transcriptional interactions and miRNA-mediated post-transcriptional interactions are involved occurs with stress-activated NF-ΚB and viral miRNAs in a reciprocal regulation between NF-ΚB and viral miRNAs such that NF-ΚB regulates the viral miRNAs and is itself regulated by the same miRNAs.
(4) NF-ΚB and viral miRNAs compete for RTA site with which they interact. The NF-ΚB regulation of miRNA above is a down-regulation that consequents in miRNA depletion by RTA site in a process called sponging, thus sparing the RTA site for NF-ΚB; this scenario favors NF-ΚB-activated transcription and expression of RTA, the lytic master switch, leading to abrogation of the viral latency and to a lytic replication.
(5) The feed-forward network motif reveals a mechanism through which stress-activated NF-ΚB simultaneously activates RTA transcription and limits its translation through activation of the viral miRNA.
(6) Finally, as Figure 1 displays, the feedback and feed-forward mechanisms cooperate in the switching on of RTA which in turn activates the transcription and expression of the immediate early genes BZLF1 and BRLF1. These two immediate early genes mobilize the expression of lytic genes and thus abrogate the viral latency, consequentially setting in trend the journey of the virus to the triggering of autoimmunity.
Acknowledgments
This investigation was supported by grants from the NSW Health Department. The author would like to thank Professor Schlink for providing the facilities for the investigation. Dr Temajo is particularly grateful to his wife Julianne Temajo for her enlightening suggestions in their learned and civilized discourse.
Conflict of Interest
All authors declare no conflicts of interest in this review.









 DownLoad:
DownLoad: