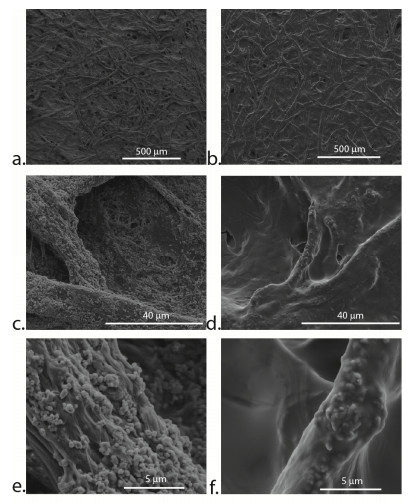
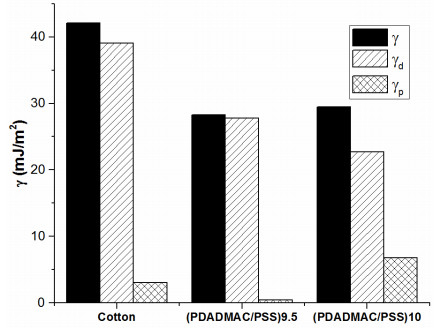
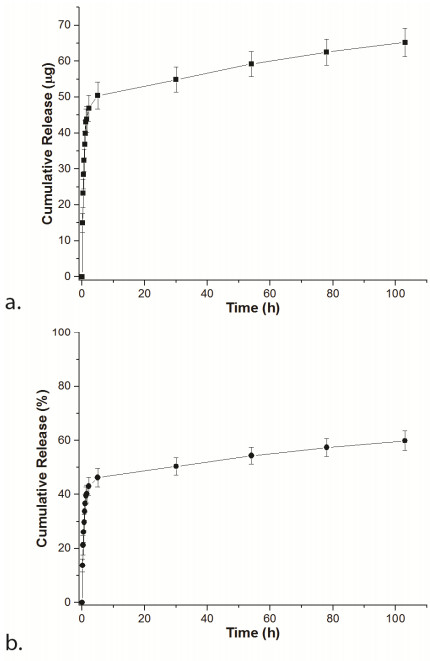
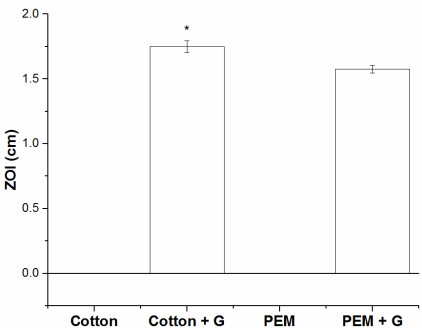
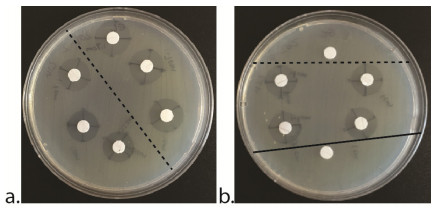
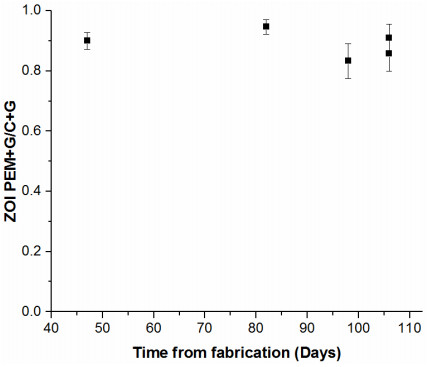
Inkjet printing was used as a novel processing method for the preparation of polyelectrolyte multilayers. Conformal, consistent coatings were formed on a cotton substrate. As a demonstration of a potential application of this processing method, polyelectrolyte multilayers were assembled on cotton for wound dressing. When loaded with gentamicin, these coatings demonstrated burst release of 50% of the loaded gentamicin over the first five hours, followed by consistent release of 0.15 µg/(cm2-h) for at least four days. Significant antimicrobial activity of the gentamicin-releasing polyelectrolyte multilayer-coated cotton was observed, with a zone of inhibition of 1.575 ± 0.03 cm. This result is comparable to the zone of inhibition for cotton soaked in gentamicin (1.75 ± 0.04 cm), indicating that the inkjet printing processing method does not degrade gentamicin. Inkjet printing shows promise as a low cost, versatile option for polyelectrolyte multilayer fabrication. Additionally, as a scalable process, inkjet printed samples exhibited consistent antibacterial function for over three months after preparation.
1.
Introduction
Composite materials have been playing an ever-increasing role in composite structures for automotive, aerospace, wind turbine, spacecraft, sport goods, marine, etc applications. This is due to their high specific strength to weight ratio or high stiffness and strength with low weight, better fatigue behavior, corrosion resistance, resistance to thermal expansions, low creep and good elevated temperature for substituting conventional materials (i.e. steel, aluminum, and other alloy materials) [1,2,3,4,5,6,7,8,9,10,11,12]. Heterogeneous materials have enormous advantages however; structures made of composite materials require special consideration during design in comparison with conventional materials. As for all new ideas, failures of structural materials have been increasing through time as the technological sophistication has become advanced. So that the failure of composite materials have to be studied using both strength and fracture approaches. From the constituents of fiber reinforced composite materials, the fiber directions establish the performance of the structure while the matrices transfer the shear load form fiber to fiber or ply to ply and protect the fibers or plies. The fibers give a relevant reinforcement in fibers’ directions and in case of fabric, in-plane directions [1,13] although mechanical characteristics remain poor in out of plane direction (perpendicular to the fiber directions). Matrices can be polymeric, ceramic, and metallic in types. The polymeric matrices are the most common in composite materials. Polymeric matrices such as epoxies are poor in strength and are applied in non-structural, semi structural and structural engineering applications owing to their low moisture absorption, relatively high modulus, and relatively high-temperature performance however they generally come with an undesirable property of brittleness with relatively poor strength and low fracture resistance because of their structures [14,15].
Homogeneous and heterogeneous materials are not defect free. Conventional materials fail because of manufacturing defects, impurities, dislocations, vacancies/voids, and impurities. Likewise, voids, defects during development process, scratch of fibers, bubbles in matrix, poor bonding between fiber and matrix, environment, curing process degrade the performance of composite materials. Minimizing the causes of degrading factors can help to keep the performance of composite materials. Adding of new ingredients and material development quality controls are becoming essentials to improve the performance of composite materials. Thus improving the poor strength constitutes of the composite materials can help to obtain better overall composite material properties. As fiber reinforced materials have evolved through time, fiber reinforced materials demand advancement along with time intuitive technology. One of the improving mechanisms of composite materials is adding inclusions/nanomaterials. From the fiber reinforced composite materials, laminated composite materials, which are not modified using nanomaterials, are the most common. The enhancements are depending on the application of the bulk materials and the type of nanomaterials. For structural applications, toughening of the matrix has a great impact in increasing the strength in the direction parallel and perpendicular to the axis of the fibers. Stitching, z-pinning and braiding are some of the methods to improve the out of plane properties however, these methods affect the in-plane properties. Toughening of the matrix requires nanofillers, which have various properties.
Nowadays, various types of reinforcing materials including hard and soft particles [13] have enhanced mechanical performances of polymeric matrices. These novel enhancing particles are nano-sized materials (nanoparticles) which can be easily combined with the polymeric matrices and the combined resulting materials are named as nanocomposites. The nanomaterials are significantly larger than individual atoms and molecules but they have high surface area per volume unit compared to macro level materials. And nanocomposites are a class of materials in which one or more phases, with nanoscale dimensions (0D, 1D, and 2D), are embedded in a metal, ceramic, or polymer matrix, which depends on the intrinsic and synergetic properties [12,16]. The general idea behind the addition of the nanoscale second phase is to create a synergy between the various constituents, such that novel properties result capable of meeting or exceeding design expectations [17]. The properties of nanocomposites relay on a range of variables; particularly the matrix reinforcing materials, which can exhibit nanoscale dimensions, loading (percentage by volume, percentage by weight), degree of dispersion, size, shape, and orientation of the nanoscale second phase and interactions between the matrix and the second phase [12,18].
The nanosized materials/nanomaterials can be produced from metals, metallic oxide, silicates, carbon, and polymers. Some of the nonmetallic based nanomaterials are fullerene [12], graphene [17], carbon black [12,17,19], ZnO2, Fe2O3
[20], nanoclays [12,18,21], carbon nanotubes (CNT, SWCNT, MWCNT) [12,18,22,23], CaCO3 [18,20,23], rubber [24], nanocellulose [25], TiO2 [12,20,22]. Besides gold, silver [22,23], iron, cobalt, tungsten, platinum [23], Copper [23,25,26], nickel [27] are some of the metallic type of nanomaterials. Currently, nanoclay, CNT and graphene have been widely used to enhance the various properties of the bulk composite materials.
Nanosized coalesced materials modify the physical/chemical and mechanical properties of the composite materials. Ni nanopillars [27] are very good representative to show how the nanomaterials can change the chemical properties such as the corrosion resistance of the bulk materials, alumina. The development of tungsten-copper composite for radiation resistance application [28] and the biocompatible modification of Fe3O4 for medical application [29] are parts of the application of nanomaterials while nanoclays, carbon nanotubes, rubber, graphene, and carbon blacks are applied in fiber-reinforced plastic for structural application.
The main aspiration of the review is to compile the effects of nanomaterials on the mechanical properties and fracture behavior of the bulk materials for structural applications. Nanomaterials influence composite materials positively if proper loadings, types, and shapes are determined. The review focuses about the proper loadings of common nanomaterials that are used in structural and semi structural fiber reinforced composite materials.
Therefore, the review principally focuses on the influence of nanomaterials related to mechanical properties (such as stiffness and strength), fracture toughness enhancement and influence of nanomaterials concerning the damage initiation/behaviors of composite materials as it will be described in later sections. This review also addresses related factors that affect the effectiveness of nanofillers to obtain the desired mechanical properties of the targeted composite material; the percentage of nanosized coalesced materials by weight, percentage by volume, sizes, shape, morphology, type, interfacial adhesion, compatibility of the nanomaterials/nanofillers are of particular relevance.
2.
Influence of nanomaterials on mechanical properties of composite materials
Mechanical property improvements have resulted major interests in nanocomposites. The mechanical properties fiber reinforced materials depend on the bond between fiber and matrix and the quality of the fiber. The bonding of fiber-matrix can be improved by increasing the contact surface area between the matrix and fiber. The improvement has to be done on nanocomposites that are the outcome of innovative technologies with great potential to create new multifunctional materials, characterized by enhanced physical and mechanical properties and new improved products for various fields of applications [30]. Factors like type, size distribution, agglomeration state/dispersion, chemical deposition, crystal structure, surface area, surface chemistry, surface charge, shape/morphology, dissolution/solubility, physical/chemical properties of nanoparticles affect the property of composite material characteristics [23]. Agglomeration, which is caused by poor dispersion of nanomaterials, may cause dis-homogeneity and, eventually, uncured resin zones while imposing extra energy into the mixing process. The mixing process to achieve fine dispersion under sonication may also cause early curing of the resin, which leads the resultant composite to be brittle [31]. Thus by adding the optimum amount of nanomaterials, the mechanical properties such as tensile strength, flexural strength, modulus of elasticity and the physical properties like thermal stability and barrier properties can be improved remarkably for fiber reinforced plastic type of composite materials [32]. Mechanical properties of nanomaterials may reach the theoretical strength, which are one or two orders of magnitude higher than that of single crystals in the bulk form. The enhancement in mechanical strength is simply due to the reduced probability of defects of nanomaterials and the ability of healing parts of bulk materials, fibers. Thus, in the following subtopics, the influences of various types of nanomaterials (in great extent nanoclay) on the mechanical properties of composite materials are reviewed.
2.1. Effects of nanoclay loadings
One of the nanomaterials type considered quite frequently and relatively inexpensive is nanoclay that stays under the category of silicate. The ability of nanoclay to induce enhancement in the physical, chemical, and mechanical properties of the composite material in comparison with what is possible to obtain from conventionally filled composites is largely reported in literatures [33,34,35]. Clay is a weathering product resulting from the disintegration and chemical decomposition of igneous rocks with the fine texture of particle size. Clay–polymer nanocomposites (CPNC) became one of the important fields of nanotechnology since Toyota applied for first time in the automobile industry [36]. Nanoclay fillers induce great improvement in the mechanical, thermal and barrier properties. Epoxy–clay nanocomposites can be used for many specific applications such as in aerospace, defense, and automobile industries. The materials have been used in high performance structural and functional applications such as laminates and composites, adhesives, sealants, tooling, molding, casting, electronics, and construction. Mechanical properties of polymer–clay nanocomposites depend on the microstructure in which the clay particles are dispersed in the polymer matrix as well as finesse of their dispersion. Generally, the fine dispersion of the clay particles into the polymer matrix yields enhanced tensile modulus, storage, and loss modulus (relevant in case of dynamic loading of viscoelastic materials) and tensile strength [37]. The greatest improvement of the mechanical characteristics of these materials often comes with the exfoliation degree. In the following, the effects of nanoclay loadings are compiled.
Nanoclays are available in various forms, among them, platelet (Cloisite 30B) is one of the most common types. Assaedi, et al. [38] studied the effects of nanoclay (Cloisite 30B) on the mechanical and thermal properties of fly ash geopolymer by adding nanoclay platelets with different loadings such as 1, to 2, and to 3 wt%. The mechanical properties of geopolymer nanocomposites were considerably influenced. The flexural modulus was increased by 15.9%, 25%, and 20.45% with loadings of 1, 2, and 3 wt%, respectively. Similarly, the material’s flexural strength was increased by 13.33%, 24.44%, and 15.55% for the given nanoclay loadings correspondingly. Moreover, the compressive strength and the hardness increased by 5.9%, 23.38%, 8.06%, and by 2.8%, 12.68%, 4.23%, respectively. It is evident that the improvement in the mechanical properties is not linear with the increment of the percentage of nanoclay addition in weight however the maximum effect was identified in correspondence of the 2 wt% addition. On the other side, the addition of 2 wt% nanoclay reduced the porosity and the reduction of porosity significantly increased the nanocomposites’ resistance to water absorption. Furthermore, Assaedi also reported the conditions for the optimum thermal stability of the nanoclay enhancement. Addition of nanoclay in geopolymer affected the material properties as the temperature varied. The thermal stability was determined using thermo-gravimetric analysis (TGA) and the stability was studied in terms of the weight loss percentage as a function of temperature. According to the report, the weight loss decreased at the higher temperature (e.g. 600 to 700 ℃) with the increment in the nanoclay fraction. The highest enhancement to the thermal stability of the geopolymer matrix was reported at loading of 2 wt% of nanoclay. The higher amount of nanoclay concentration caused agglomeration and poor dispersion, which showed the increment of porosity.
Other researchers, Eesaee et al. [39] dealt about natural montmorillonite (CN) and organically modified montmorillonite (CB). The nanoclay improved the mechanical performance of novolac phenolic resin (PF)/woven glass–fiber (GF) composites because of the better nanoclay dispersion, which resulted good interfacial interaction with the matrix. The nanoclay’s loadings were 0.5, 1.5, and wt%. The nanoclay at 2.5 wt% enhanced the elastic modulus up to 38% for CN and 43% for CB. PF/GF composites were submitted to aging processes with various aqueous solutions such as water, brine, and acidic environments and the enhancements improved stiffness from 100% to 250% with respect to the base composite. On the other hand, aging led to the reduction of strength caused by matrix degradation due to hydrolysis and interfacial debonding. Both clays diminished the durability of PF/GF composites and the report resoned out as the hydrophilic nature of the nanoclays.
Hakamy et al. [20] worked on the effect of calcined nanoclay (CNC) on the microstructure and mechanical properties of treated hemp fabric-reinforced cement nanocomposites. The optimum hemp fabric content for these nanocomposites was 6.9 wt% (6 fabric layers). Mechanical properties were improved by the calcined nanoclay (CNC) inclusions. Tests were done with inclusions of 1, 2 and 3 wt% and an optimum replacement of ordinary Portland cement with 1 wt% CNC was observed. The microstructure of composite materials usually showed porosity. Avil et al. [40] observed porosity reduction from the composite materials, which was made up of S2-glass epoxy nanoclay materials because of the nanoclay reactions with the hardener aliphatic amine-(triethylenetetramine) and resins. The porosity decreased by 77.32% at 10 wt% of nanoclay however large amount of concentration results strength degradation.
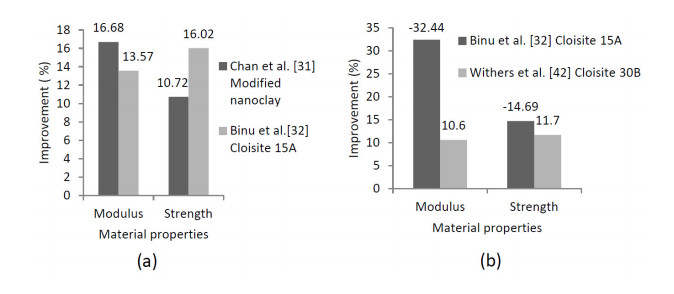
Binu et al. [32] studied the significant effect of nanoclay, Cloisite 15A, on the mechanical properties of glass fiber reinforced polyester for 0.5, 1, 1.5 and 2 wt% nanomaterials. Highest tensile modulus and strength were obtained with the addition of 0.5 and 1 wt% loadings while for 1.5 and 2 wt% nanoclay addition, the modulus value became lower. On the other hand, optimum impact strength and storage modulus were exhibited at 1 wt% loadings. The nanoclay loadings that were considered by John et al. [21], led to substantial improvements in mechanical properties (i.e. tensile, flexural, compressive strengths and moduli). According to the study, the addition of 2 and 4 vol% nanoclay in cyanate-ester syntactic foam registered tensile strength improvement by 63 and 94%, respectively. However, thermal properties were not significantly altered by the addition of nanoclay particles. Glass transition temperature decreased due to the increment in plasticization of the matrix caused by the organic modifier present in the nanoclay. Similarly, Maharsia et al. [41] conducted the hybridizations by using the volume fraction in the range of 2 to 5 vol%. The nanoclay reinforcement of syntactic foams enhanced the tensile strength by 22%. Chan et al. [31] reported another interesting finding. The Araldite GY251 epoxy resin and hardener HY956 in the ratio of 5:1 were used to produce nanoclay/epoxy composites. As indicated in Table 1, the increment in Young’s modulus and tensile strength of a composite sample with 5 wt% are 34% and 25%, respectively. Further increments of the content of nanoclay result in lowering the mechanical properties of the enhanced composites. Withers et al. [42] considered epoxy glass–fiber composites with the organomodified surface, Cloisite 30B nanoclay was dispersed in the epoxy at 2 and 4 wt% levels to improve the mechanical properties. The researchers concluded that the nanoclays apparently toughened the epoxy matrix and strengthened the fiber–matrix interfaces in the composite to achieve the above-mentioned the enhancements of mechanical properties.
The enhancement may vary with the bulk materials as well as the types of nanomaterials. Figure 1 shows the variation of improvements of the material property with the same percentage by weight and with the various nanoclay families. The figure indicates that enhancements of materials are more specific and types of nanomaterials dependent.
Sharma et al. [43] dealt with glass fiber reinforced polymer-clay nanocomposites. Their work showed better dispersion of clay in epoxy for samples with 1 and 3 wt% clay loadings while agglomerates were found in 5 wt% samples. Tensile and bending tests were performed on nanocomposites and the properties showed that with the addition of nanoclay up to 3 wt% the tensile strength increased and a reduction of strength was obtained at a 5 wt% loading while the flexural strength increased with the addition of nanoclay up to 5 wt%. Table 2 summarizes the effective nanoclay loadings and the enhanced mechanical property using quantitative expression.
Loading of nanoclay ranges are of interest not only for mechanical property enhancement but for morphology also has a great impact on the customization of composite materials. Quang et al. [35] worked on morphology and they found that the addition of nanoclay to polymer matrices with a good degree of exfoliation was obtained for concentrations of 6.6 wt% while the mechanical properties, such as Young modulus, were increased of 54%. Wang et al. [44] obtained complex interaction between the aromatic epoxy and clay layer at 1 wt% nanoclay. As a conclusion, all the mentioned articles excluding morphological issue shows that loadings (i.e. the % in weight addition) of nanoclay has to be less than 5 wt%. The conclusion is similar to the summary of other articles, such as Azeez et al. [37] and Ravandi et al. [45]. This implies that the optimal amount of nanoclay should not exceed 5 wt% to enhance mechanical properties.
2.2. Effect of nanomaterials loadings, particle size, and adhesion
Mechanical properties, including Young’s modulus, ultimate tensile strength, ductility, etc, of the epoxy matrix, can be enhanced by loadings of carbon nanotubes, graphene, and silica. According to Domun et al. [33], the carbon nano tube families (CNT), single-walled CNT (SWCNT), double-walled CNT (DWCNT) and multi-walled CNT (MWCNT) modified the mechanical property of epoxy considerably. The Young’s modulus was enhanced by 80 to 130% for CNT additions within the range of 0.04 to 5 wt% and by 94% to 148% for graphene additions within the range of 0.03 wt% to 4.5 wt% respectively. Further silica-enhanced Young’s modulus by 86% to 158% for additions within the range of 0.05 to about 25 wt%. The researchers exhaustively dealt the superposition of the different clusters of nanoparticles that described the possible enhancement of the ultimate tensile strength by 72.5 to 145% for graphene loadings within the range of 0.03 to 3 wt% and by 92% to 130% for CNT loadings within the range of 0.045 to 0.7 wt% respectively. Silica, under a clusters of loadings between 1 and 25 wt% enhanced the ultimate tensile strength by 60% to 132%. Another scholar who worked in carbon based nanomaterials; Giannopoulos [46] studied about the inclusion of fullerene (C60 and C70) to a nylon-12 polymer bulk material to predict the elastic modulus and Poisson’s ratio. The researcher used molecular dynamics (MD) approach and MD-finite element method (FEM) to work out the effects. Four small C60 loadings of 0.5, 1, 1.5, and 2 wt% were tested using FEM models while Six C60 loadings of 1, 1.98 wt%, 2.95, 3.89, 6.79, and 8.35 wt% were tested using MD approach. The result showed an increase in stiffness and a reduction of Poisson’s ratio while C70 fullerene registered a better reinforcing capability. The same researcher, Giannopoulos [47] introduced bone-shaped carbon nanotubes to reinforce polymer nanocomposite via molecular dynamics approach. The bone-shaped nanotube (BSNT) significantly enhanced the stiffness and strength of nanocomposite. The report indicated that BSNT facilitated the upgrading of interfacial binding energy, which led to overall strength of nanocomposite. The BSNT interfacial binding energy increased by 47.9% relative to capped nanotube (CPNT). Giannopoulos et al. [48] developed a hybrid numerical method to predict the mechanical behavior of carbon nanotube reinforced matrix.
Shuvo et al. [49] published another interesting work. Graded nanoclay (nanoclay, montmorillonite clay with modified surface at 15–35 wt% in octadecylamine and 5 wt% aminopropyltriethoxysilane) and non-graded nanoclays were used as reinforcements of polyester. Upon addition of non-graded nanoclay to pure polyester, the tensile strength and modulus decreased by about 30% while with graded nanoclay increased by about 10%. Flexural strength also increased by about 15%. Ghadami et al. [50] studied nanoclay and alumina nanoparticles. The tensile strength of epoxy-clay nanocomposite specimens gradually enhanced by increasing nanoclay up to 5 wt% content with good dispersion process, also the young's modulus of epoxy-nanoclay nanocomposite significantly increased. These results were obtained through the addition of the various wt% of nanoclay in a resin that was made of hot-cured epoxy resin (LY556), anhydride-curing agent (Aradur 917) and imidazole accelerator (DY070). With the addition of alumina nanoparticles higher than 3 wt%, the tensile strength decreased for the specified epoxy resin. This behavior can be explained by the increasing viscosity of uncured compound that causes to trap more porosity during mixing, casting, and finally curing of nanocomposite specimens.
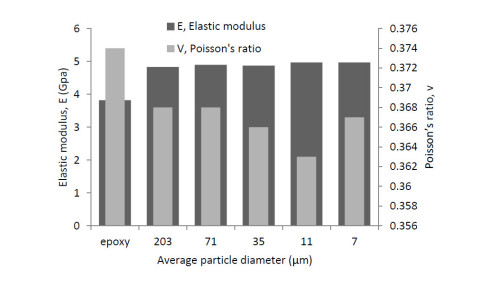
Other researchers, Phong et al [51] observed the effects of loadings made with nano-polyvinyl alcohol (nPVA). Polyvinyl alcohol powder was added to the matrix of a composite reinforced with plain-woven carbon cloth (TR3110M), the matrix was made of epoxy resin (Epikote 828), while modified aliphatic polyamines were used as curing agent. Randomly-aligned web of PVA nano-fibers whose diameter was about 40–80 nm, with four different values of loading percentage, namely 0, 0.03, 0.05 and 0.1 wt%, resulted to affect the strength. In particular, the tensile strength was increased by about 5% with the addition of 0.05 wt% of nPVA. Gantenbein et al. [52] considered the effects of sizes of the particles. The researchers concluded that the increment in the size of the particles affected the enhancement in strength due to lower surface to volume ratio. Similarly, to the size of particles, the distribution of the nanomaterials altered the enhancement of the mechanical properties of bulk material. Iman et al. [53] observed the cross-linking agent, which improved the physicochemical properties such as mechanical, thermal, flame retardancy and dimensional stability. Moreover, Matusik et al. [54] and Awad et al. [55] demonstrated how the improvement of the mechanical parameters could be related to very good particle dispersion. The effects of particle loading and size (in the range 4.5–62 micrometer) on the elastic modulus of epoxy/spherical glass particle composites with low volume fractions of glass beads (10–18 vol%) were studied. the research indicated that the modulus is almost independent on particle size. Strength and toughness exhibited dependency on adhesion quality. Fu et al. [18] observed the adhesion property of nanomaterials. According to the study, adhesion of silica showed magnificent tensile strength at 5 wt% however the tensile strength drastically changed as the loading increased above 5 wt%. Figure 2 shows how the sizes of particles alter the mechanical properties of fiber-reinforced materials. Kitey et al. [56] characterized and tabulated the physical and elastic properties of glass-filled epoxy composite. The study investigated the roll of particle size and filler matrix adhesion. The particle size attenuation gradually squeezed the lateral dimensions of the specimens and increased the longitudinal deformations until the nanofillers diameter approached to 11μm nevertheless the moduli values alteration became insignificant.
3.
Influence of nanomaterials on fracture toughness of composite materials
Failure of composite materials in the out of plane direction is the most concerning types of failure due to the inherent fragility of the epoxy matrix [12,13,14,51,57,58]. The improvements of layered composite material property in the out of plane direction were dealt using different methods such as stitching [45,59,60,61,62,63], 3D weaving, braiding and z-pinning [59,60]. However, while stitching, 3D weaving, braiding, and z-pinning improved the composite fracture toughness considerably, these methods affected negatively the in-plane mechanical properties (tensile strength and stiffness) [45,60]. Alternative methods have been explored in order to obtain improvements in the fracture toughness of composite materials without scarification of the in-plane mechanical properties. Nanomaterials enhancement has been developing to overcome in plane degradations and the technology requires appropriate types of nanomaterials type, loading, shape, and size recommendations.
3.1. Effect of nanomaterials loadings
The fracture toughness behavior of composite materials was improved by various nanomaterials loadings. Maharsia et al. [41] made experiments for syntactic foams. According to their work, the addition of 5 vol% nanoclay particles increased the toughness by 58%. Kim et al. [64] studied the material with modified bisphenol—a type of epoxy resin. The material was used to test the mode I fracture toughness, KIC using 3-point bending method with SENB specimens. The nanoclay (Cloisite 93A) with a loading of only 0.5 up to 3.0 wt% enhanced the KIC value by 20%, up to 50% on average, respectively, at room temperature. However, the toughness decreased as the temperature was increasing and the researchers concluded that the intermolecular forces between polymer networks of the epoxy were more dominant than the toughening effect of the mixed nanoparticles.
The study by Ghadami et al. [50], a material consisting of hot-cured epoxy resin (LY556), with anhydride curing agent (Aradur 917) and imidazole accelerator (DY070) resin, was modified by loading of nanoclay (Cloisite 15A) and Al2O3 nanoparticles with particle size of 100 nm to modify the fracture toughness. The fracture behavior was tested using single-edge-notch specimens in three points bending geometry. The results showed that the nanoclay improved fracture toughness progressively up to 5 wt% addition, while alumina registered maximum improvement at 3 wt%. Increasing the volume fraction of the alumina nanoparticles more than 3 wt% led to a gradual decrement of the fracture toughness. The explanation was the presence of micro-cracks that initiated from undispersed Al2O3 nanoparticles and micro-porosities. Similarly, Wang et al. [65] reported the effects of nano silicon dioxide (nano-SiO2) onto the graphene oxide (GO) through thiol-ene click reaction to improve the material behavior. The fracture toughness of GO-SiO2/epoxy composite was improved by 60.38% relative to the neat epoxy. The improvement is due to the synergetic effect between GO and SiO2.
Further researches instigated the influences of silicates (nanoclays, CaCO3), carbon (fullerene, graphene, CNT, carbon black) and polymer (Rubber, nitrile, nano-cellulose) nonmaterial with respect to the relevant specific subtopic. Specifically, rubber particles have demonstrated to be able to control significantly the enhancement of the fracture toughness.
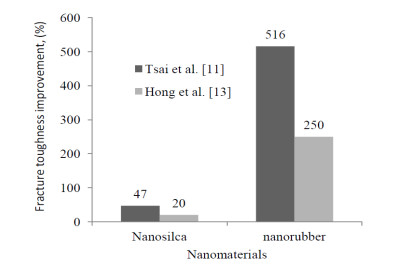
One way for further enhancing the fracture toughness of epoxies could be the use of other toughening mechanisms such as hybrid application of soft particles and rigid fillers as Liang et al. [24] reported. Interlaminar toughness improvement for a carbon fiber/epoxy laminates was achieved by incorporation of nanoparticles by Hong et al. [13]. Two types of nanoparticles were added 40 wt% solgel nanosilica with approximately 20 nm sized SiO2 and nanorubber/bisphenol-A with 25 wt% approximately 100 nm sized core-shell rubbers. Fracture toughness was tested for mode I by means of a double cantilever beam. The toughening effect of rubber was more significant. Laminates with 10 wt% rubber particles improved the highest improvement, 250%, in toughness respect to the base material, while silica modified laminates show a moderate increase in toughness by 20–30%. Hong et al. summarized the toughness transfer mechanism of the nanoparticles modified bulk epoxies in composite laminates by its complicated fiber bridging across the delaminating crack-wake. Therefore, the researchers reasoned out that the toughening effects of rubber cavitations and void expansion in epoxies along with silica particles debonding in epoxies.
Tsai et al. [11] studied the toughness performance of glass/epoxy composites for application of wind blades. The glass/epoxy composite toughness property was enhanced by the addition of silica nanoparticles and rubber particles. In particular, promising results were obtained on the enhancement of mode I fracture toughness. While epoxy with silica (10 wt%) increased the fracture toughness by 47%, epoxy with reactive liquid rubber (CTBN 10 wt%) improved the fracture toughness by 516% while epoxy with core-shell rubber (CSR 10 wt%) enhanced the toughness by 647%. Similarly, the hybrid epoxy with silica (10 wt%) and CTBN(10 wt%) increased fracture toughness by 390%, while epoxy with Silica(10 wt%) and CSR(10 wt%) influenced positively by 442%. For epoxy with silica (20 wt%), the improvement grew up by 84% as Tsai et al. indicated.
Figure 3 shows the fracture toughness improvement and the types of nanomaterials. Both literature used the same weight by percentage and the same family nanomaterials, nanosilca and nanorubber. The work of Tsai et al. [11] became effective either due to the property of bulk material adhesion with nanomaterials or the process of sonication.
3.2. Effect of particle size, adhesion and morphology
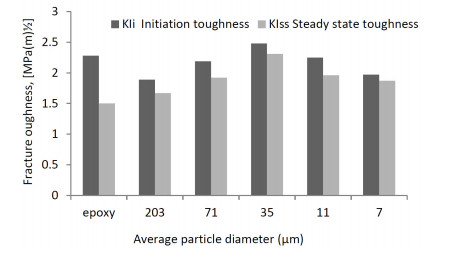
Wetzel et al. [7] studied the loadings and the effects of sizes of particles over toughness both within the nano sizes and out of the nanosized ranges. Thus, addition of Aluminum oxide (Al2O3) with particle size of about 13 nm and of titanium dioxide (TiO2) with particle sizes between 200 and 500 nm (out of nanomaterials range) were done for standard epoxy resin (DER331) cured by a cycloaliphatic amine curing agent in order to improve the fracture toughness. The toughness tests were conducted using compact tension specimens. Filler contents of 5 and 10 vol% Al2O3 increased the fracture toughness by 60% and 120% respectively, while improvements of lower magnitude indicated with TiO2 fillers for the same addition by volumetric percentages. As it was already reviewed for what concerns the mechanical properties, Phong et al. [37] also dealt with the toughness effects of polyvinyl alcohol powder (nPVA). According to the researchers’ process, polyvinyl alcohol powder was added in a composite of plain-woven carbon cloth (TR3110M) with epoxy resin (Epikote 828) that was modified aliphatic polyamines (Japan Epoxy Resins). Randomly–aligned web of PVA nano-fibers with a diameter of about 40–80 nm were loaded in the matrix with different weight by percentages of pristine, 0.03, 0.05 and 0.1 wt%. The result included the material resistance against both the initiation (GIP) and the propagation (GIP) of interlaminar fractures, i.e. the material toughness characteristic in mode I, significantly increased with the addition of 0.1 wt% nPVA by about 65% and 73%, respectively. Kelkar et al. [66] analyzed the effects of stitching, z pinning and nanomaterials’ inclusions about the fracture toughness of composite materials. Addition of alumina nanoparticles (110 nm) which were dispersed using high energy mixing procedures (using ultra sonication, high shear mixing, and pulverization) and nano-fibers, which were manufactured using the electro-spinning technique to woven fiberglass (S2) composite was studied. The process improved interlaminar fracture toughness. The reason was that electrospinning technology relied on the creation of nanofibers with an improved molecular orientation at a reduced concentration of fiber imperfections and crystal defects. The test was conducted with the double cantilever beam scheme in order to identify the interlaminar fracture toughness enhancement (51.7%) and to compare the results with stitching and z-pinning. The fracture toughness increased drastically as the particle diameters decreased [51]. Fu et al. [18] further developed the particle size and fracture toughness relation. They studied the effects of particle’s size and volume fraction on the fracture toughness of alumina trihydrate powder filled epoxy composites at room temperature. They found out that the most important factor is the particle/matrix adhesion, there is also a positive influence of the particles’ size diameter increment on the fracture toughness, however, this trend is not always confirmed if the particles are in the nanosized range and the applied load are characterized by high dynamic rate. However, this does not mean that higher particle loading necessarily leads to higher toughness. According to the authors’ report, optimum value was found at 22 vol% while fracture toughness reduces on either side of this optimum point. Figure 4 presents the effects particles’ size on the fracture toughness initiation and propagation. The figure presents good enhancement of both fracture initiation and propagation at 35μm nanoparticle dimension for weekly bonded fillers.
Domun et al. [33] did the other compiled study related to toughness. The review summarized results for various loadings and nanomaterials types. Based on the authors’ review, nanoclay and nanosilica can increase the fracture toughness by 120% to 270% for 0.7 to 6 wt% loadings, and by 100% to 290% for 0.4 to 20 wt% loadings respectively. Similarly, graphene and carbon nanotube (CNT) enhance fracture toughness by 110% to 300% for 0.04 to 6 wt% loadings and by 100% to 230% for 0.06 wt% to about 3 wt% loadings, respectively. For what concerns the morphological properties of the fractured surfaces, Raja et al. [67] examined a number of surfaces using FESEM and revealed that the nano fly ash has better interaction with matrix than other types of particles, and this leads to better stress transfer and thereby avoiding the formation of cracks. Likewise, Moustafa and Darwish [68] dealt with dispersion and compatibility processes between polymer and nanofiller during the formation of the intercalated and/or exfoliated nanocomposites that leads to better toughening. Unlike strength behavior of enhanced materials, the fracture toughness enhanced at higher loadings. Representative nanomaterials, which can improve the fracture toughness, categorized in quantitative and qualitative expressions as shown in Table 3.
Therefore, nanoclay family enhances both mechanical properties and fracture toughness for 5 wt% loadings, while silica is appropriate up to 20 wt%. At the same time, graphene and CNT enhance both mechanical properties and fracture toughness for about 6 and 3 wt% loadings respectively. However, it is difficult to put a conclusion in such forms because of parameter inconsistency.
4.
Influence of nanomaterials on damages and damage initiations of composite materials
Conclusions of the effects of nanomaterials articulated the degrading concentration/cluster of inclusion in bulk materials. Adding of inclusions more than the recommended volume, weight by percentages leads to decline the intended properties. The reductions of the properties the overall material are due to either agglomeration or large concentration of nanomaterials that is capable to cause damage initiations. Clustered of nanomaterials cause damage initiations whether the loadings are appropriate or not. The reason is that the agglomerated dry region materials fail to transfer shear load from polymer to fiber and vice versa. Damage composite materials due to inclusions are mostly caused by agglomeration. Nanomaterials are required both distributive and dispersive arrangements to enhance the bulk materials. Furthermore, large concentration nanomaterials may cause degradation of mechanical properties such as strength. All strength degradation as the concentrations becomes higher due to poor shears load transfer of matrix and matrix-fiber.
Likely, high surface to volume ratio is one of the main characteristics of nanomaterials because of their sizes and minimized surface defects. This property helps nanomaterials to reflect the stress wave (damage progression) which comes from the other phases. The fillers influenced the damage path either by reflecting or by bridging [26]. Adhesion strengths of polymer composites are enhanced by adding modified clay fillers, which indicates the phenomenon can reduce the failure because of good stress transfer between phases [67,68]. The increment of the particle size may have no significant effects in the process of protection of bulk materials in case of the failure due to the presence of defects on the surface of the filler that may cause initiation of the damage by itself. Particles having irregular shapes (real situation) [69] also can be easily damaged by itself though the bulk property determines the result of the process considerably.
Binu et al. [32] obtained agglomerated 2% nanoclay filled polyester reinforced with glass fiber mat. The authors stated that the agglomerated particles might affect the mechanical properties by initiating early failure. Quaresimin et al. [70] investigated the influence of clay-modified epoxies/glass reinforced laminates about fracture toughness, and interlaminar properties conducted. The result indicated a significant improvement in the fracture toughness and crack propagation threshold of clay-modified epoxy. However, due to the nanofiller morphology, the behavior of clay-modified laminates was still almost comparable with the base laminates.
Zeinedini et al.
[71] described the enhancements of fracture toughness depend on high dispersion of carbon nanotubes (CNT) and CNT declined the fracture toughness at higher loadings of inclusion because of agglomeration. Similarly, Maghsoudlou et al. [72] investigated the effects of interphase, curvature, and agglomeration of single wall carbon nanotube (SWCNT) with bisphenol-F/epoxy resin nanocmposite. The loadings were 0.1, 0.3, and 0.5 wt% and the Young’s modulus was improve up to 0.3 wt%. The property reduced at loadings of higher than 0.3 wt%. The authors reported that there were higher concentration of fillers and local SWCNT fillers agglomerations were observed. The research shows that agglomeration degrades the modulus. Zare et al. [73] dealt influences of nanoparticles agglomeration on the interfacial and tensile properties of nanocomposites. The report indicated interfacial declination because of agglomeration and poor interfacial reduction, which caused lower tensile strength.
Unlike agglomerated nanomaterials which become the cause of damage initiation, well dispersed and appropriate loadings nanomaterials can alter the damage behavior of nanomaterials enhanced fiber reinforced plastic materials. The presences of appropriate nanomaterials loadings can reduce the damage area of fiber reinforced plastic (FRP) composite materials. Rafik et al. [74] examined the impact resistance of hybrid glass fiber reinforced epoxy/nanoclay composite. The experiment was conducted by adding 1.5 and 3 wt% nanoclay at 10, 20, 35, and 50 J impact energy loads. The nanoclay pick loading, 1.5 wt% reduced the damage area by 31%, 66%, 16% and 14% for 10, 20, 35 and 50 J impact loads respectively. Likewise Koricho et al. [8] investigated the effect of hybrid (micro- and nano-) fillers on impact response of glass fiber reinforced plastic (GFRP) composite. The investigation added 1 wt% glass bubble (GB), 1 wt% nanoclay (NC) and 1 wt% hybrid (GB + NC) in GFRP. The report illustrated better damage distribution, which reduced the dye penetration, delamination, and intralaminar crack formation at NC and hybrid inclusions relative to the pristine. 1 wt% NC added panel showed best damage distribution both on back and front faces at 212 J.
Nanomaterials are also effective in the damage behavior of high-speed impact. Domun et al. [75] studied the ballistic characteristics of glass fiber reinforced nanomodified epoxy matrices. According to the report, graphene platelets (GNPs), carbon nanotubes (CNTs), combined hybrid hexagonal boron nitride nanosheets (BNNS)/CNT, and combined boron nitride nanotubes (BNNTs)/GNPs nanoparticles were added to epoxy. The exit velocity improved by 29.8%, 53.9%, 45.2% and 66.3% relative to neat epoxy for nanomaterials GNP, CNT, BNNS + CNT and BNNT + GNP respectively. From visual inspection, BNNS + CNT showed more damage on the rare face of the panel.
Dorigato et al.
[76] discussed about the failure mechanism of composite materials and the authors pointed out the failure mechanism is interfacial debonding. Their specific research investigated the fiber-matrix interfacial adhesion using single-fiber micro-debonding tests. According to the authors report, the addition of nanoclay improved the interfacial shear strength by about 30%. Nanomaterials can improve adhesion of fiber–matrix by increasing wettability and by healing the damaged fiber.
Compatibility is related to morphology of nanomaterials. The more compatible nanomaterials have less effects of damage initiation or degradation of polymers. Gelineau et al. [77] conducted experimental investigation along with modeling to study the effects of modified montmorillonite on elastic and visco-elastic properties of nano-reinforced Poly(lactic acid). The authors’ report indicated the increment of moduli for elastic and visco-elastic materials. Other researchers Mu et al. [78] studied about interface compatibility. According to the report 3.5% enhancement could be at obtained at higher loading, such as 9.6 wt% however at normal condition enhances lower than 5 wt%.
Thus morphology, particle size, interfacial strength, and type of bulk materials influence the damage/failure condition of nanomaterials filled composite. Bandyopadhyay et al. [79] investigated the morphology development and melt-state viscoelastic properties of nylon6/ethylevinyl-alcohol (N6/EVOH) blend composite by adding organoclay. The morphology with the thermal and rheological properties exposed the interfacial adhesion between N6 and EVOH to obtain reactive compatibilization. Likewise, Vo et al. [80] developed 3D finite element model to compute macroscopic elastic properties of a polymer clay nanocomposite. The study considered all morphological parameters such as clay volume fraction, clay’s aspect ratio, contrast of stiffness between clay and polymer matrix, number of clay layers per intercalated block, interlayer distance, interphase’s thickness and stiffness besides the report indicated that partially exfoliated structures are more suitable to predict the polymer clay nanocomposite for even high volume fraction of clay. The compatibility behavior led to the localization of the intercalated silicate layers in the interfacial region. Thus, the studies show that improvement of interfacial adhesion can reduce the damage initiation and degradation of the composite materials.
Thus, good adhesion, compatibility, appropriate loadings, and relatively small size nanomaterials can reduce the damage initiation of the fiber reinforced plastic composite materials unless either agglomerations arise or large concentrations of nanomaterias are added.
5.
Conclusions
The review is to summarize the effect of various types of nanomaterials on the mechanical characteristics of the composite materials with polymeric matrix. Due to lack of detailed research results for specific bulk materials and specific nanomaterials with the report of all the relevant parameters, it is difficult to establish a general conclusion about the influence of nanoparticles on the mechanical properties and fracture behavior of composite materials. In addition, property variations of nanomaterials may happen due to manufacturing, sonication, curing, and modification processes.
However, particular conclusions can be drawn from the above discussion.
➢ Composite strength and toughness are strongly affected by loadings (wt% and vol%), particle size, particle/matrix adhesion, morphology.
➢ Strength depends on effective stress transfer between filler and matrix, and toughness/brittleness is controlled by adhesion. Higher amount of nanomaterials loadings reduce the shear load transfer between matrix and fiber. Likewise, agglomerations cause damage initiation, which can lead to overall materials failure. Strengths of the composite materials are improved at lower loadings however, fracture toughness can be improved at higher concentration when it is compared with strength enhancement. The sizes of nanomaterials have impacts in modification of FRP composite. As the size of the nanomaterials increase, their surface become large and the probability of defects increase. The important parameter in load transferring between matrix and fiber is high surface area to volume ratio. The purposes of nanomaterials are not only wetting the fiber but also heal the defected surfaces of the fiber.
➢ Different properties may not be achieved at the same time with certain nanomaterials loading. The nano loadings and types have to be chosen to avoid achieving certain property with other properties scarification. Furthermore, each type of nanomaterials has specific enhancement roles. Addition of nanoclay for the enhancement of the mechanical properties and fracture toughness both become effective at the same time for low percentage in weight (i.e. lower than 5wt%) of particle loadings, especially when particle dispersions are fine and, sometimes, modification helps to enhance the adhesion property with the bulk materials. Though morphological changes increase the enhancements above 5 wt% good improvements are obtained at lower fractions of nanoclay.
➢ Graphene and CNT enhance mechanical properties with a very low percentage by weight; however, fracture toughness can be enhanced relatively with a higher amount of loadings. Nevertheless, all the other parameters should be considered for better results. Bone shaped carbon nanotubes are a modified form of CNT and helps to have better adhesion processes.
➢ Nanosilica particles can enhance fracture toughness and mechanical properties in a better way with loadings up to 22.5 and 25 wt%, respectively.
➢ Nanomaterials may affect the bulk negatively unless they are treated properly. It includes avoiding agglomeration, appropriate thermal condition, curing the combined materials, loadings, etc. the large size, poor compatibility, and poor adhesions enhances the damage initiations of the composite materials.
Generally, the addition of nanomaterials in composite materials enhance the mechanical properties, fracture toughness if the application type, suitable process, loadings, size, type of nanomaterials are implemented appropriately. If not it could be the cause of damage and it may influence the bulk material’s behavior in an unsatisfactory way or even detrimentally. On the other hand, the review helps the researchers to some extent giving a guide on how the nanomaterials can be selected for the fracture toughness and main mechanical properties of heterogeneous materials.
Conflict of interests
The authors declare no conflict of interest.









 DownLoad:
DownLoad: