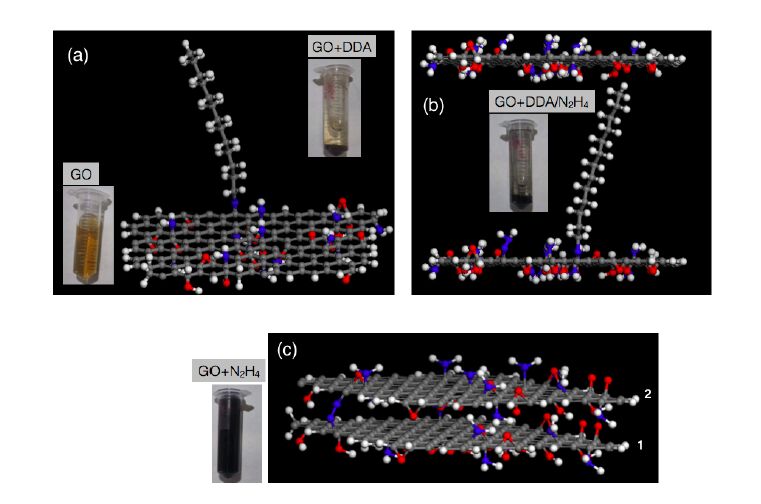
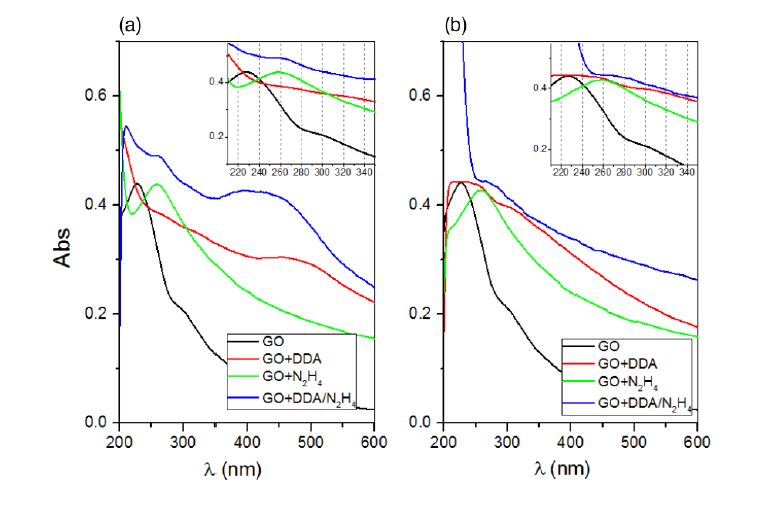
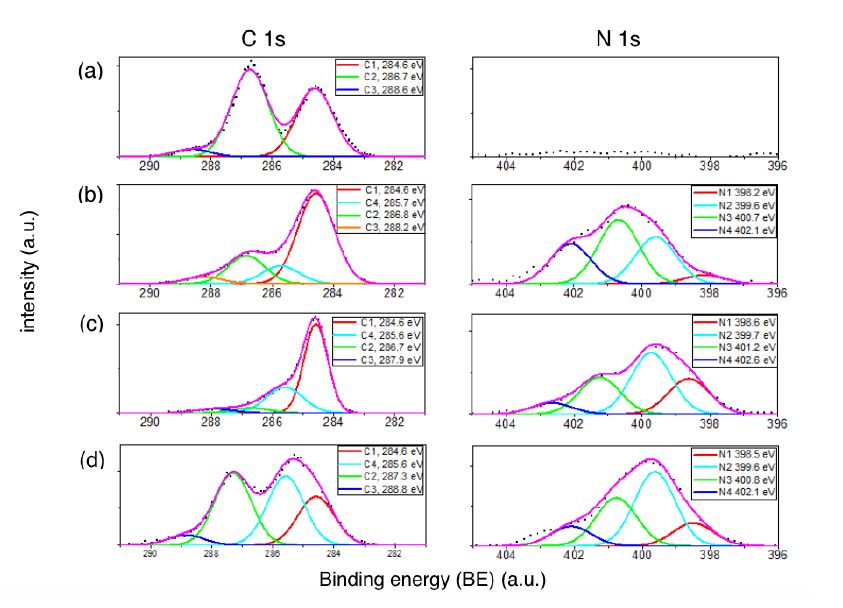
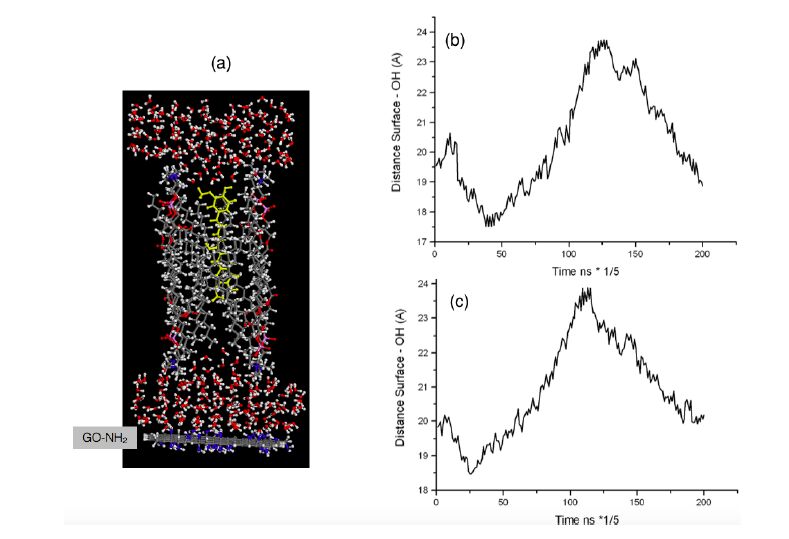
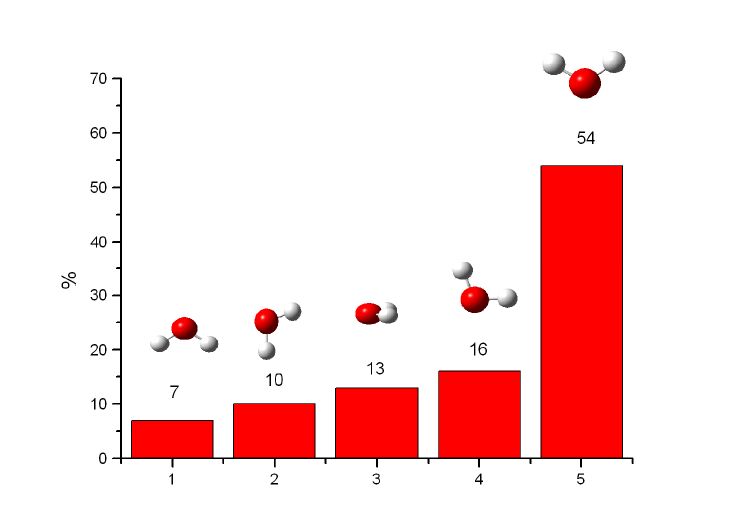
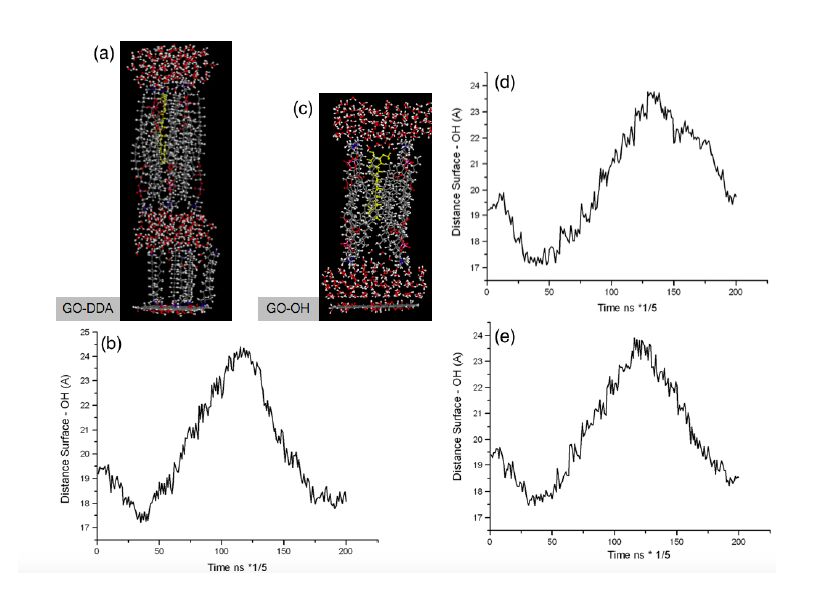
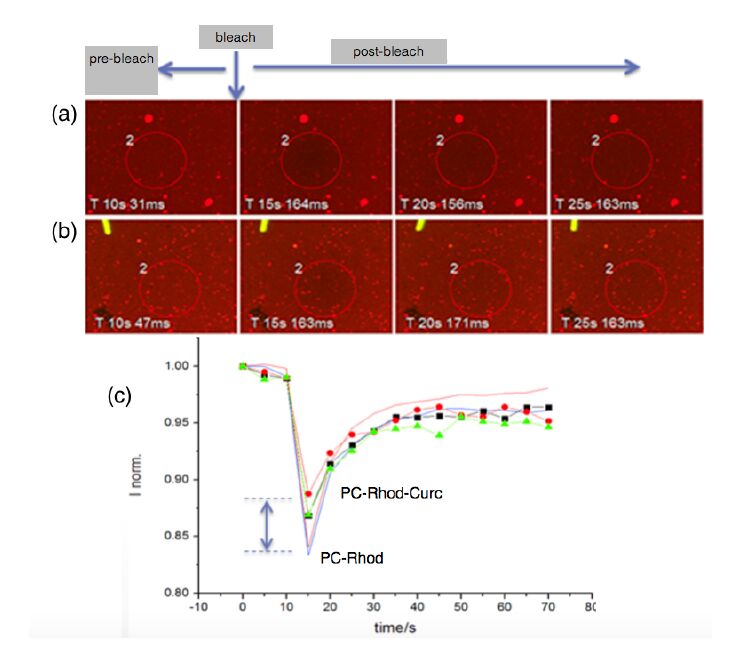
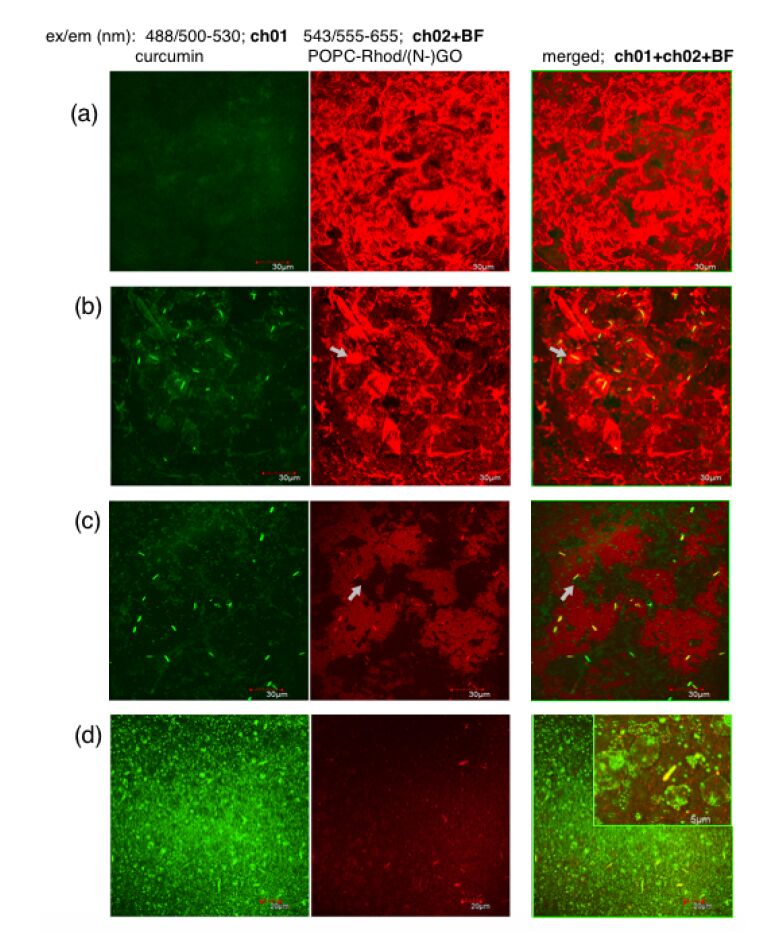
In this study, we present a comparison between graphene oxide (GO) and nitrogen-doped GO (N-GO) in terms of spectroscopic properties and biomolecule-binding potentiality features. Specifically, GO nanosheets, both in aqueous dispersion and in solid state, were successfully modified with different amino-containing moieties, in order to obtain graphene-based nanostructures able to respond to chemical stimuli (e.g., pH) and with tunable surface properties. The physisorption of dye-labelled lipid vesicles loaded with curcumin, was scrutinised both theoretically and experimentally. The energetics of the hybrid lipid membrane-curcumin-GO interface at different pH values, representative respectively of physiological (7.4) and pathological (5.5) environment, were estimated by molecular dynamics (MD) simulations. The GO and GO-N samples characterization by Raman, fluorescence, and UV-vis spectroscopies, as well as confocal microscopy demonstrated promising features of the (N-)GO/lipid platforms for fluorescence imaging and drug delivery applications.
1.
Introduction
Two-dimensional elliptic [1] boundary value problems
with
where Ω=[a,b]×[c,d] and f(t,s),g(t,s),h(t,s) on Ω, can be used in many scientific areas, such as electrostatics, mechanical engineering, magnetic fields, thermal fields and brain activity detection[2].
Floater [3,4,5] proposed a rational interpolation scheme. In [6], a linear rational collocation method was presented for the lower regular function. Wang et al.[7,8,9,10] successfully solved initial value problems, plane elasticity problems, incompressible plane problems and non-linear problems by collocation method. The linear barycentric rational collocation method (LBRCM) to solve nonlinear parabolic partial differential equations[11], biharmonic equation [12], fractional differential equations[13], telegraph equation [14], Volterra integro-differential equation [15] and heat conduction equation[16] have been studied.
In the following, we introduce the barycentric formula of a one dimensional function. Let
and
In order to get the barycentric formula, Eq (1.4) is changed into
and
which means wj=1/l′(tj).
For Eq (1.2), we get
which means
For the case uniform partition, we get
For the case the nonuniform partition is chosen, we take the second Chebyshev point [7] a
with
For the barycentric rational function, we first set
where
and
Combining (1.14) and (1.15), we have
where
and Jk={i∈I;k−d⩽i⩽k}. By taking p(t)=1, we have
and then have
Combining (1.16), (1.19) and (1.13), we get
where ωj is defined as in (1.17).
In this paper, based on linear barycentric rational interpolation of one dimension, we construct a barycentric rational interpolation of a two-dimensional Poisson equation. In order to get the discrete linear equation of a two-dimensional Poisson equation, the equidistant nodes and second kind of Chebyshev points were chosen as collocation point. For the general area, a domain decomposition method of the barycentric rational collocation method is also presented.
2.
Differentiation matrices of Poisson equation
Let a=t1<⋯<tm=b,h=b−am and c=s1<⋯<sn=d,τ=d−cn with mesh point (ti,sj),i=1,2,⋯,m;j=1,2,⋯,n. Then, we have
on [a,b], and
where
and
wi,vj is the weight function defined as (1.6) or (1.17); see [17].
We have
Then, we have
where C(2)ij=L″i(tj), and
ui=[ui1,ui2,⋯uin]T,fi=[fi1,fi2,⋯,fin]T=[fi(si),fi(s2),⋯,fi(sn)]T. With the help of the matrix form, the linear equation systems can be written as
and D(2)ij=M″i(sj),
Then, we have
and
where
and ⊗ is the Kronecker product of the matrices. The Kronecker product of A=(aij)m×n and B=(bij)k×l is defined as
where
and the node of tensor is (ti,sj),i=1,2,⋯,m;j=1,2,⋯,n. Then, matrix A and B can be can be changed to (m×n) column vectors as
and then we get relationship of the partial differential equation and differential matrix as
3.
Domain decomposition method of barycentric rational collocation method for Poisson equation
Consider the generalized elliptic boundary value problems as
with boundary condition
where β(t,s) is the diffusion coefficient, and ∇=(∂∂t,∂∂s) is the gradient operator.
Taking the rectangle domain Ω into two sub-rectangle domains Ωi,i=1,2, the boundary of the domain is Γ, and the boundary of Ωi,i=1,2, is Γ0. Suppose β(t,s)∈CΩ and the interface conditions of Γ0 are
Suppose β(t,s) is not continuous on Ω and the interface conditions of Γ0 are
In the following, we take the two sub-domain Ωi,i=1,2, (t1,i,s1,j), the function u1,ij=u(t1,i,s1,j); (t2,i,s2,j),i=1,2,⋯,m2;j=1,2,⋯,n2 and u2,ij=u(t2,i,s2,j).
On the sub-domain of Ω1, the barycentrix function is defined as
where R1,i(t),R1,j(s) are defined as (2.3) and (2.4).
Equation (3.1) can be written as
Taking Eq (3.3) into Eq (3.4), we have
Taking (t1,i,s1,j) on the sub-domain of Ω1, we have
As we have used
Take the notation
The matrix equation of (3.5) can be written as
where C1(1),C1(2),D1(1),D1(2) are the one order and two order differential matrices, and Im1,In1 are the identity matrices. Then, we write
Similarly in the sub-domain Ω2, we get the matrix equation
and
Combining Eq (3.14) and Eq (3.16), we get
Then, we have
and
Points of the boundary are 2(m1+m2−2)+n1+n2. Sb denotes the number of the domain, and boundary points are denoted as (tbk,sbk),k∈Sb. The boundary condition can be discrete, as
where l=0,1,⋯,m0, and
Define
Take as the matrix equation
The discrete boundary condition condition can be given as
The matrix equations of (3.40) and (3.41) are
4.
Numerical examples
Example 1. Consider
with f(t,s)=t2−2; its analytic solutions are
where Ω=[−1,1]×[−1,1].
In Table 1 convergence rate is O(hd1+1) with d1=d2=2,3,4,5. In Table 2, for the Chebyshev nodes, the convergence rate is O(τd2+2) with d1=d2=2,3,4,5.
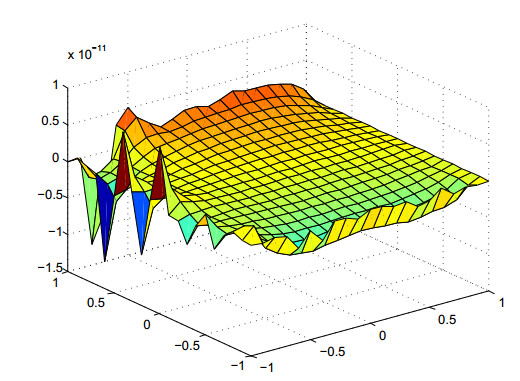
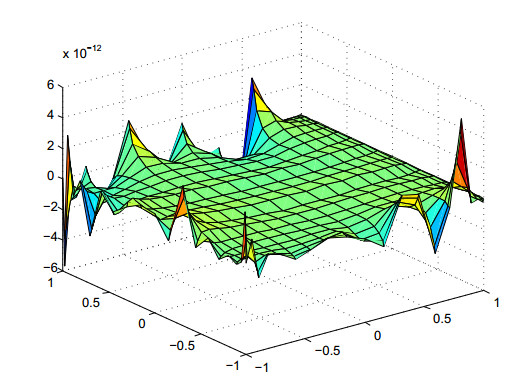
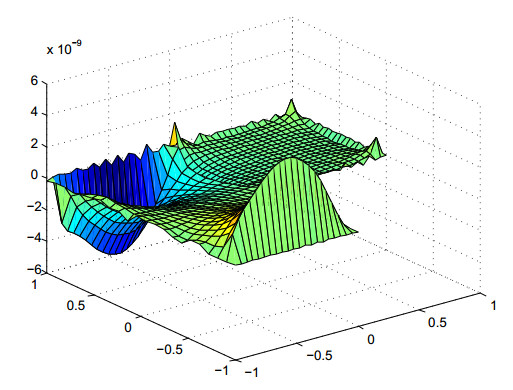
Figure 1 shows the error estimate of equidistant nodes, and Figure 2 shows the error estimate of Chebyshev nodes.
Example 2. Consider
with f(t,s)=3sin(t+s). Its analytic solutions are
where Ω=[−1,1]×[−1,1].
Table 3 shows the convergence is O(hd1+1) with d1=d2=2,3,4,5. In Table 4, for the non-uniform partition with Chebyshev nodes for d1=d2=2,3,4,5, the convergence rate is O(τd2+2).
We choose m=20;n=20;d1=9;d2=9 to test our algorithm.
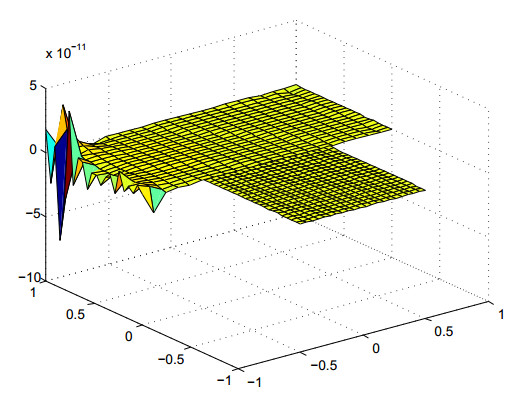
Figure 3 shows the error estimate of equidistant nodes, and Figure 4 shows the error estimate of Chebyshev nodes.
Example 3. Consider the Poisson equation △u=−2sin(πt)cos(πs),(t,s)∈Ω and Ω=Ω1⋃Ω2={t,s:−1<t<1,−1<s<1}⋃{t,s:0<t<1,0<s<1}. Its analytic solutions are
with the boundary condition
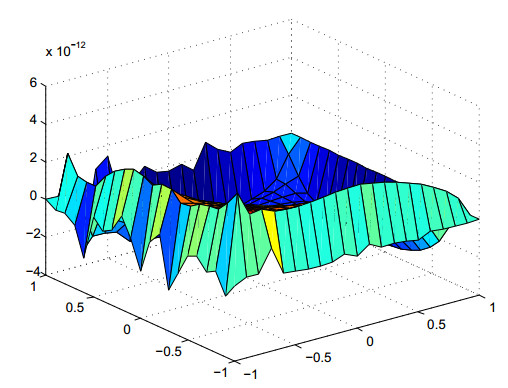
We choose m1=m2=20;n1=n2=20;d1=9;d2=9 to test the domain decomposition method of the barycentric rational collocation method. Figure 5 shows the errors under equidistant nodes. From Figure 5 we know that the error can reach 10−7 with 21 collocation points.
Example 4. Consider △u(t,s)=6ts(t2−s2−2),(t,s)∈Ω and Ω=Ω1⋃Ω2={t,s:−1<t<1,−1<s<1}⋃{t,s:−0.5<t<0.5,−1<s<0}. Its analytic solutions are
with condition
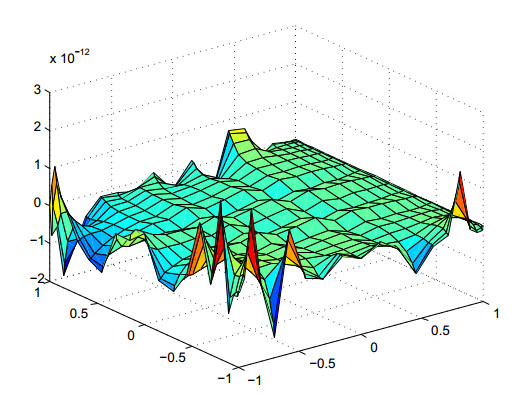
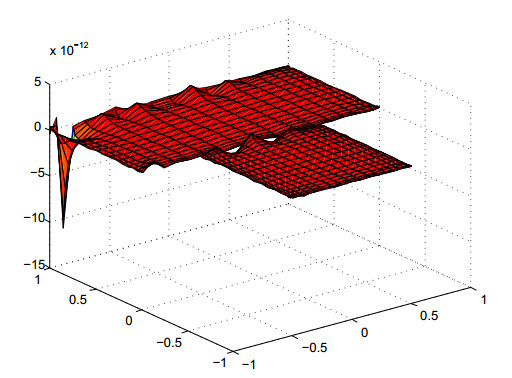
We choose m1=m2=20;n1=n2=20;d1=9;d2=9 on each Ωi,i=1,2, to test the domain decomposition method of the barycentric rational collocation method. Figure 6 shows the error estimate of equidistant nodes, and Figure 7 shows the error estimate of Chebyshev nodes. The error of both equidistant nodes and Chebyshev nodes can reach 10−11, which shows the accuracy of our algorithm.
Acknowledgments
The work of Jin Li was supported by the Natural Science Foundation of Shandong Province (Grant No. ZR2022MA003) and Natural Science Foundation of Hebei Province (Grant No. A2019209533).
The authors also gratefully acknowledge the helpful comments and suggestions of the reviewers, which have improved the presentation.
Conflict of interest
The authors declare that there are no conflicts of interest.









 DownLoad:
DownLoad: