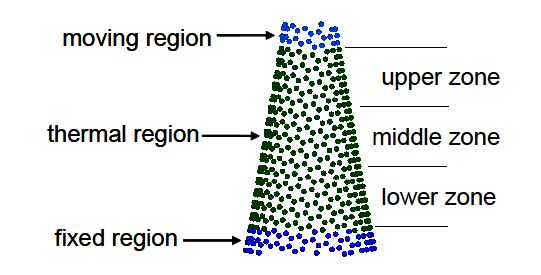
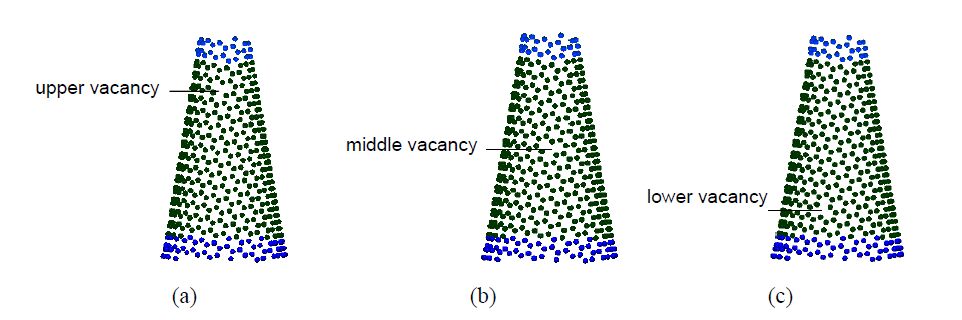
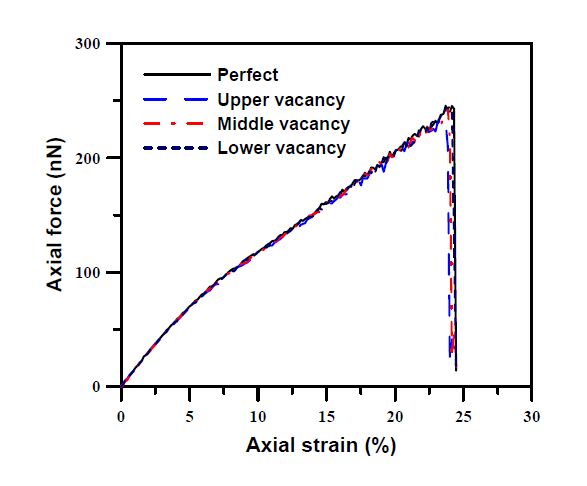
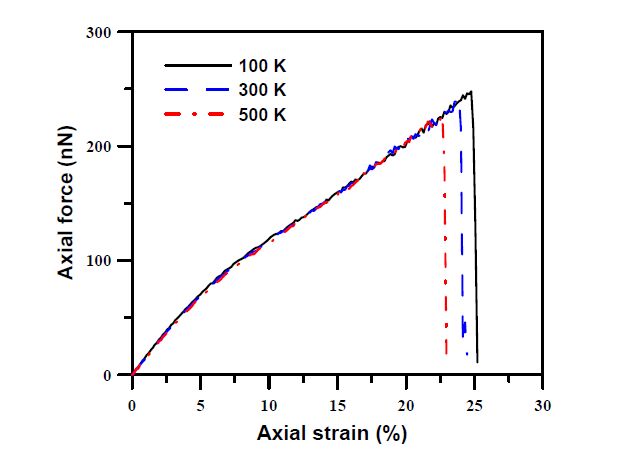
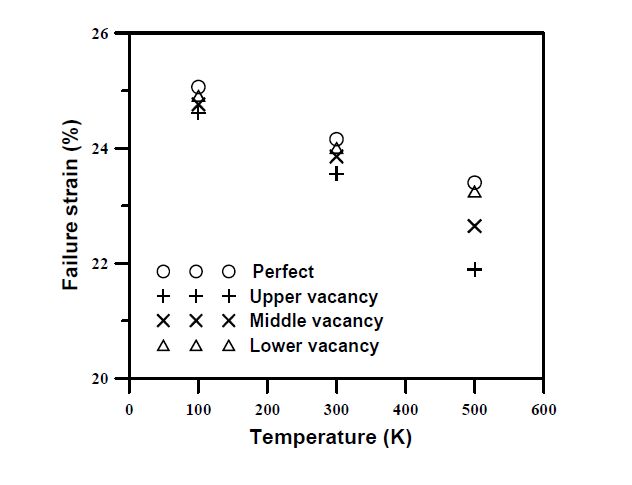
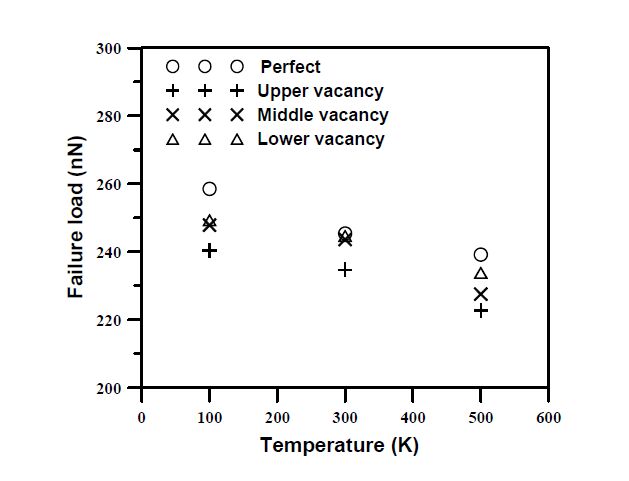
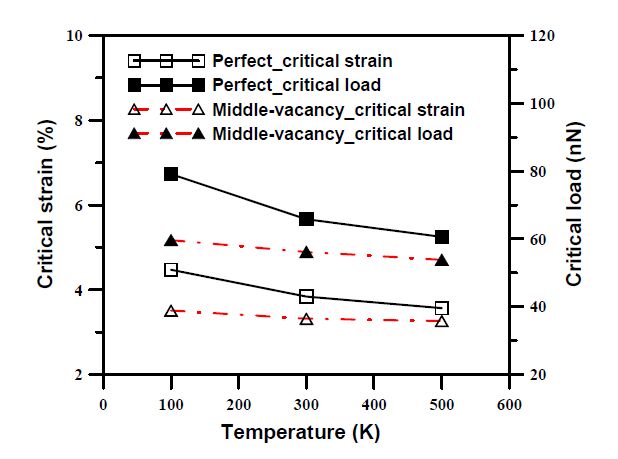
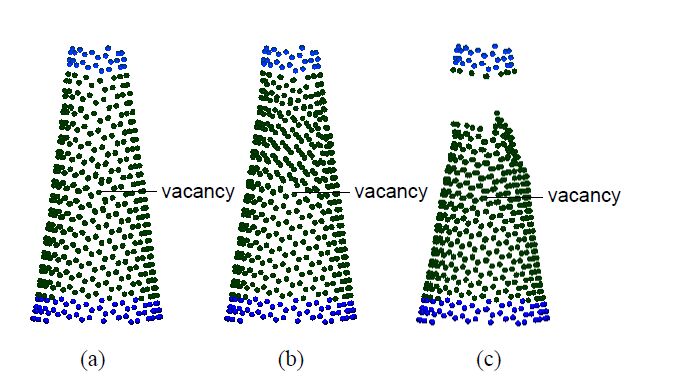
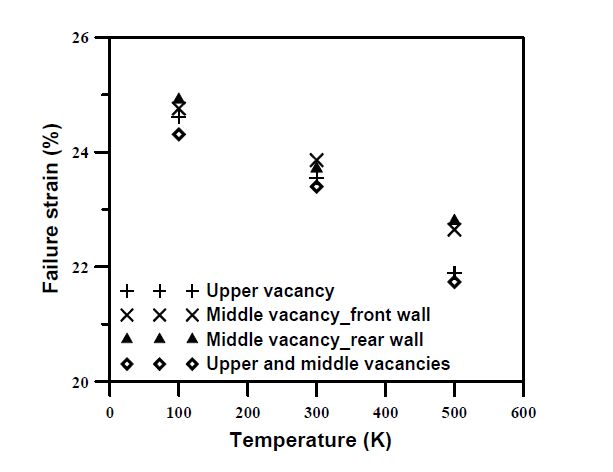
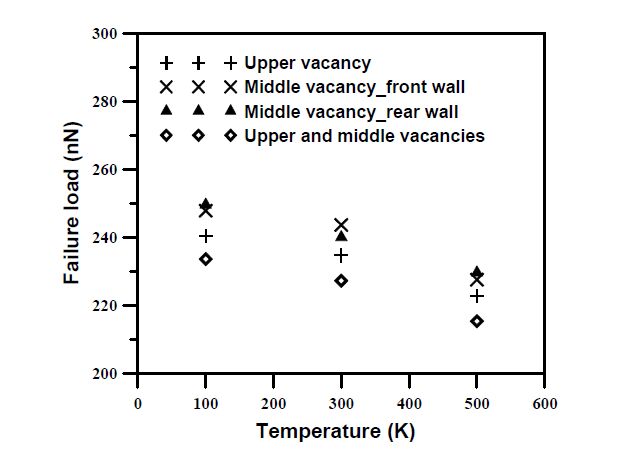
Influences of vacancy defects on tensile failure of open-tip carbon nanocones

1.   Introduction

The Schrödinger-Virasoro algebra is an infinite-dimensional Lie algebra that was introduced (see, e.g., [10]) in the context of non-equilibrium statistical physics. In [21], the author give a representation of the Schrödinger-Virasoro algebra by using vertex algebras, and introduced an extension of the Schrödinger-Virasoro algebra. To be precise, for $\varepsilon\in\{0,\frac{1}{2}\}$, the Schrödinger-Virasoro algebra $\mathcal{SV}(\varepsilon)$ is a Lie algebra with the $\mathbb{C}$ basis

and Lie brackets

The Lie algebra $\mathcal{SV}(\frac{1}{2})$ is called the original Schrödinger-Virasoro algebra, and $\mathcal{SV}(0)$ is called the twisted Schrödinger-Virasoro algebra. Recently, the theory of the structure and representations of both original and twisted Schrödinger-Virasoro algebra has been investigated in a series of studies. For instance, the Lie bialgebra structures, (bi)derivations, automorphisms, 2-cocycles, vertex algebra representations and Whittaker modules were investigated in [9,11,14,15,21].

Post-Lie algebras were introduced around 2007 by B. Vallette [22], who found the structure in a purely operadic manner as the Koszul dual of a commutative trialgebra. Post-Lie algebras have arose the interest of a great many authors, see [4,5,12,13]. One of the most important problems in the study of post-Lie algebras is to find the post-Lie algebra structures on the (given) Lie algebras. In [13,18,20], the authors determined all post-Lie algebra structures on $sl(2, \mathbb{C})$ of special linear Lie algebra of order $2$, the Witt algebra and the W-algebra $W(2,2)$ respectively.

In this paper, we shall study the graded post-Lie algebra structures on the Schrödinger-Virasoro algebra. We only study the twisted Schrödinger-Virasoro algebra $\mathcal{SV}(0)$, the case for the original Schrödinger-Virasoro algebra $\mathcal{SV}(\frac{1}{2})$ is similar. For convenience we denote $\mathcal{S} = \mathcal{SV}(0)$. It should be noted that the commutative post-Lie algebra structures on $\mathcal{S}$ already are given by [11], we will consider the general case.

Throughout this paper, we denote by $\mathbb{Z}$ the set of all integers. For a subset $S$ of $\mathbb{Z}$ and a fixed integer $k$, denote $S^* = S\setminus \{0\}$, $S_{>k} = \{t\in S|t>k\}$, $S_{<k} = \{t\in S|t<k\}$, $S_{\geqslant k} = \{t\in S|t\geqslant k\}$ and $S_{\leqslant k} = \{t\in S|t\leqslant k\}$. We assume that the field in this paper always is the complex number field $\mathbb{C}$.

The paper is organized as follows. In Section 2, we give general results on post-Lie algebras and some lemmas which will be used to our proof. In Section 3, we completely characterize the graded post-Lie algebra structures on Schrödinger-Virasoro algebra $\mathcal{S}$. In Section 4, by using the post-Lie algebra structures we characterize the forms of the homogeneous Rota-Baxter operator on $\mathcal{S}$.

2.   Preliminaries

We will give the essential definitions and results as follows.

Definition 2.1. A post-Lie algebra $(V,\triangleright,[,])$ is a vector space V over a field $k$ equipped with two $k$-bilinear products $x\triangleright y$ and $[x,y]$ satisfying that $(V,[,])$ is a Lie algebra and

for all $x,y\in V$, where $\langle x,y\rangle = x\triangleright y-y\triangleright x$. We also say that $(V,\triangleright, [,])$ is a post-Lie algebra structure on the Lie algebra $(V,[,])$. If a post-Lie algebra $(V,\triangleright, [,])$ satisfies $x\triangleright y = y\triangleright x$ for all $x,y\in V$, then it is called a commutative post-Lie algebra.

Suppose that $(L,[,])$ is a Lie algebra. Two post-Lie algebras $(L,[,],\triangleright_{1})$ and $(L,[,],\triangleright_{2})$ on the Lie algebra $L$ are called to the isomorphic if there is an automorphism $\tau$ of the Lie algebra $(L,[,])$ satisfies

Remark 1. The left multiplications of the post-Lie algebra $(V,[,],\triangleright)$ are denoted by $\mathcal{L}$, i.e., we have $\mathcal{L}(x)(y) = x\triangleright y$ for all $x,y\in V$. By (2), we see that all operator $\mathcal{L}(x)$ are Lie algebra derivations of the Lie algebra (V, [, ]).

Lemma 2.2. [15] Denote by $Der(\mathcal{S})$ and by Inn$(\mathcal{S})$ the space of derivations and the space of inner derivations of $\mathcal{S}$ respectively. Then

where $D_1,D_2, D_3$ are outer derivations defined by

3.   The graded post-Lie algebra structures on the Schrödinger-Virasoro algebra

Since the Schrödinger-Virasoro algebra $\mathcal{S}$ is graded, we suppose that the post-Lie algebra structure on the Schrödinger-Virasoro algebra $\mathcal{S}$ to be graded. Namely, we mainly consider the post-Lie algebra structure on Schrödinger-Virasoro algebra $\mathcal{S}$ which satisfies

for all $m,n\in\mathbb{Z}$, where $\phi$, $\varphi$, $\chi$, $\psi$, $\xi$, $\theta$ are complex-valued functions on $\mathbb{Z}\times\mathbb{Z}$.

We start with the crucial lemma.

Lemma 3.1. There exists a graded post-Lie algebra structure on $\mathcal{S}$ satisfying (3)-(9) if and only if there are complex-valued functions $f, g, h$ on $\mathbb{Z}$ and complex numbers $a,\mu$ such that

Proof. Suppose that there exists a graded post-Lie algebra structure satisfying (3)-(9) on $\mathcal{S}$. By Remark 1, $\mathcal{L}(x)$ is a derivation of $\mathcal{S}$. It follows by Lemma 2.2 that there are a linear map $\psi$ from $\mathcal{S}$ into itself and linear functions $\alpha, \beta, \gamma$ on $\mathcal{S}$ such that

where $D_i, i = 1,2,3$ are given by Lemma 2.2. This, together with (3)-(9), gives that

Let

where $a^{(m)}_{i}, b^{(m)}_{i}, c^{(m)}_{i}, d^{(m)}_{i}, e^{(m)}_{i}, f^{(m)}_{i}, g^{(m)}_{i}, h^{(m)}_{i}, x^{(m)}_{i}\in\mathbb{C}$ for all $i\in\mathbb{Z}$. Then by (23)-(31), similar to the proof of [18], we obtain that (10)-(22) hold.

The "if'' part is a direct checking. The proof is completed.

Lemma 3.2. Let $f,g,h$ be complex-valued functions on $\mathbb{Z}$ and $\mu,a\in \mathbb{C}$ satisfying (18) and (20). Then we have

Proof. By letting $m = 0$ in (18) and (20), respectively, we have $nh(n)(1+h(n)) = 0$ and $n^{2}g(n)(1+g(n)) = 0$. This implies (32).

Lemma 3.3. Let $f,g,h$ be complex-valued functions on $\mathbb{Z}$ and $\mu,a$ be complex numbers satisfying (17)-(22). If $f(\mathbb{Z}) = 0$, then we have $\mu = a = 0$ and

Proof. Since $f(\mathbb{Z}) = 0$, we take $m = -n = 1$ in (17) and (19) we have $\mu = 0$ and

By letting $n = 0$ and $m = -1$ in (20) we deduce that $ag(-1) = 0$. This, together with (33), implies $a = 0$. As $\mu = a = 0$, so Equations (18), (20) and (22) become to

We now prove the following four claims:

Claim 1. If $h(1) = 0$, then $h(\mathbb{Z}) = 0$.

By (34) with $n = 1$ we see that $h(m+1) = 0$ for all $m\neq 2$. It follows that $h(\mathbb{Z}\backslash \{3\}) = 0$. Since $h(2) = 0$, by taking $n = 2, m = 1$ in (34) we have $-\frac{3}{2}h(3) = 0$, which implies $h(3) = 0$. We obtain $h(\mathbb{Z}) = 0$.

Claim 2. If $h(1) = -1$, then $h(\mathbb{Z}) = -1$.

By (34) with $m+n = 1$ we see that $h(n) = -1$ for all $n\in \mathbb{Z}$ with $\frac{1-3n}{2}\neq 0$. This means that $h(\mathbb{Z}) = -1$.

Claim 3. If $g(1) = 0$, then $g(\mathbb{Z}^*) = 0$.

By (35) with $n = 1$ we see that $g(m+1) = 0$ for all $m\neq -1$. It follows that $g(\mathbb{Z^*}) = 0$.

Claim 4. If $g(1) = -1$, then $g(\mathbb{Z}^*) = -1$.

By (35) with $m+n = 1$ we see that $g(n) = -1$ for all $n\neq 0$. This means that $g(\mathbb{Z^*}) = -1$.

Now we consider the values of $h(1)$ and $g(1)$ according to (32).

Case i. If $h(1) = g(1) = 0$, then by Claims 1 and 3 we have $h(\mathbb{Z}) = 0$ and $g(\mathbb{Z}^*) = 0$. According to (36) with $n = -1$ and $m = 1$ we know $g(0) = 0$. This means that $g(\mathbb{Z}) = 0$.

Case ii. If $h(1) = g(1) = -1$, then by Claims 2 and 4 we have $h(\mathbb{Z}) = -1$ and $g(\mathbb{Z}^*) = -1$. According to (36) with $n = -1$ and $m = 1$ we see that $1+g(0) = 0$ and so that $g(0) = -1$. This implies $g(\mathbb{Z}) = -1$.

Case iii. If $h(1) = 0$, $g(1) = -1$, then we will get a contradiction. In fact, by Claims 1 and 4, we have $h(\mathbb{Z}) = 0$ and $g(\mathbb{Z}^*) = -1$. From (36) with $m = 2, n = -1$ we see that $g(1) = 0$ which contradicts $g(1) = -1$.

Case iv. If $h(1) = -1$, $g(1) = 0$, then we will also get a contradiction. In fact, by Claims 2 and 3, we have $h(\mathbb{Z}) = -1$ and $g(\mathbb{Z^*}) = 0$. From (36) with with $m = 2$, $n = -1$ we see that $g(1) = -1$ which contradicts $g(1) = 0$. The proof is completed.

Lemma 3.4. Let $f,g,h$ be complex-valued functions on $\mathbb{Z}$ and $\mu,a$ be complex numbers satisfying (17)-(22). If $f{(\mathbb{Z}_{\geqslant2})} = -1, f{(\mathbb{Z}_{\leqslant 1})} = 0$, then $\mu = a = 0$ and $g$, $h$ must satisfy one of the following forms:

(i) $g{(\mathbb{Z})} = h{(\mathbb{Z})} = 0$;

(ii) $g{(\mathbb{Z})} = h{(\mathbb{Z})} = -1$;

(iii) $h{(\mathbb{Z}_{\leqslant 0})} = 0$, $h{(\mathbb{Z}_{\geqslant 1})} = -1$ and

$g{(\mathbb{Z}_{\leqslant-1})} = 0$, $g{(\mathbb{Z}_{\geqslant 1})} = -1$, $g(0) = \hat{\lambda}$ for some $\hat{\lambda}\in \mathbb{C}$.

Proof. By $f{(\mathbb{Z}_{\geqslant2})} = -1, f{(\mathbb{Z}_{\leqslant 1})} = 0$, similar to the proof of Lemma 3.3, we know $\mu = a = 0$. From this, we have by (18), (20) and (22) that

We first prove the following six claims:

Claim 1. If $h(1) = 0$, then $h(\mathbb{Z}) = 0$.

By (37) with $n = 1$ we see that $h(m+1) = 0$ for all $\frac{m}{2}-1\neq 0$ with $m\leqslant 1$. Hence, we deduce that $h(\mathbb{Z}_{\leqslant 2}) = 0$. Note that $h(2) = 0$, by (37) with $n = 2$ we see that $h(m+2) = 0$ for all $\frac{m}{2}-2\neq 0$ with $m\leqslant 1$. We now have $h(\mathbb{Z}_{\leqslant 3}) = 0$. If we repeat this process, we see that $h(\mathbb{Z}_{\leqslant k}) = 0$ for all $k = 1,2,3,\cdots$. Note that $\bigcup_{k\geqslant 1}(\mathbb{Z}_{\leqslant k}) = \mathbb{Z}$, so one has $h(\mathbb{Z}) = 0$.

Claim 2. If $h(-1) = -1$, then $h(\mathbb{Z}) = -1$.

By (37) with $m+n = -1$ we see that $h(n) = h(-1-m) = -1$ for all $\frac{3m}{2}+1\neq 0$ with $m\leqslant 1$. This deduces that $h(\mathbb{Z}_{\geqslant -2}) = -1$. Note that $h(-2) = -1$, by (37) with $m+n = -2$ we see that $h(-m-2) = -1$ for all $\frac{3m}{2}+2\neq 0$ with $m\leqslant 1$. Thus, $h(\mathbb{Z}_{\geqslant -3}) = -1$. If we repeat this process, we see that $h(\mathbb{Z}_{\geqslant k}) = -1$ for all $k = -1,-2,-3,\cdots$. Note that $\bigcup_{k\leqslant -1}(\mathbb{Z}_{\geqslant k}) = \mathbb{Z}$, so one has $h(\mathbb{Z}) = -1$.

Claim 3. If $h(1) = -1$, then $h(\mathbb{Z}_{\geqslant 1}) = -1$.

By (37) with $m+n = 1$ we see that $h(n) = h(1-m) = -1$ for all $\frac{3m}{2}-1\neq0$ with $m\leqslant 1$. This implies $h(\mathbb{Z}_{\geqslant 1}) = -1$.

Claim 4. If $h(-1) = 0$, then $h(\mathbb{Z}_{\leqslant 0}) = 0$.

By (37) with $n = -1$ we see that $h(m-1) = 0$ for all $m\neq -2$ with $m\leqslant 1$. It follows that $h(\mathbb{Z}_{\leqslant 0}\setminus \{-3\}) = 0$. Let $m = -1, n = -2$ in (37), from $\frac{m}{2}\neq n$ we have $h(-3) = 0$. Therefore, we get $h(\mathbb{Z}_{\leqslant 0}) = 0$.

Next, similar to Claims 1 and 3, we from (38) obtain the following claims.

Claim 5. If $g(1) = 0$, then $g(\mathbb{Z}^*) = 0$.

Claim 6. If $g(1) = -1$, then $g(\mathbb{Z}_{\geqslant 1}) = -1$.

Now we discuss the values of $h(1)$ and $h(-1)$. By (32), $h(1), h(-1)\in \{-1, 0\}$.

Case i. When $h(1) = 0$.

By Claim 1 we have $h(\mathbb{Z}) = 0$. According to (39), one has $g(m+n) = 0$ for any $m,n\in \mathbb{Z}$ with $m\neq n$. This implies $g(\mathbb{Z}) = 0$.

Case ii. When $h(-1) = -1$.

By Claim 2 we have $h(\mathbb{Z}) = -1$. According to (39), one has $g(m+n) = -1$ for any $m,n\in \mathbb{Z}$ with $m\neq n$. This implies $g(\mathbb{Z}) = -1$.

Case iii. When $h(1) = -1$ and $h(-1) = 0$.

By Claims 3 and 4 we have $h(\mathbb{Z}_{\leqslant 0}) = 0$ and $h(\mathbb{Z}_{\geqslant 1}) = -1$. This, together with (39), yields $g(m+n) = 0$ for any $m,n\in \mathbb{Z}$ with $m,n\leqslant 0$ and $m\neq n$, and $g(m+n) = -1$ for any $m,n\in \mathbb{Z}$ with $m,n\geqslant 1$ and $m\neq n$. Consequently, we obtain $g{(\mathbb{Z}_{\leqslant-1})} = 0$ and $g{(\mathbb{Z}_{\geqslant 3})} = -1$. By (32), $g(1)\in \{-1, 0\}$. If $g(1) = 0$, then Claim 5 tells us that $g(\mathbb{Z}^*) = 0$ which contracts $g{(\mathbb{Z}_{\geqslant 3})} = -1$. Therefore, we have $g(1) = -1$. From this with Claim 6 we have $g{(\mathbb{Z}_{\geqslant 1})} = -1$. Let $g(0) = \hat{\lambda}$ for some $\hat{\lambda}\in \mathbb{C}$.

It is easy to check that the values of $g$ given in Cases i-iii above are consistent with (38). They give the conclusions (i), (ii) and (iii) respectively. The proof is completed.

Lemma 3.5. Let $f,g,h$ be complex-valued functions on $\mathbb{Z}$ and $\mu,a$ be complex numbers satisfying (17)-(22). If $f{(\mathbb{Z}_{>0})} = -1,f{(\mathbb{Z}_{<0})} = 0 \,$ and $\, f{(0)} = c$ for some $c\in \mathbb{C}$, then there are $\lambda, \hat{\tau}\in \mathbb{C}$ such that $\mu, a$, $g$, $h$ must be one of the following forms:

(i) $a = 0$, $\mu\in \mathbb{C}$ and $g{(\mathbb{Z})} = h{(\mathbb{Z})} = 0$;

(ii) $a = 0$, $\mu\in \mathbb{C}$ and $g{(\mathbb{Z})} = h{(\mathbb{Z})} = -1$;

(iii) $\mu \in \mathbb{C}$, $h{(\mathbb{Z}_{> 0})} = -1$, $h{(\mathbb{Z}_{<0})} = 0$, $h(0) = \lambda$ and $g{(\mathbb{Z}^*_{\geqslant k})} = -1$, $g{(\mathbb{Z}^*_{\leqslant k-1})} = 0$

for some $k\in \{-2,-1,1,2,3\}$, $g(0) = \hat{\tau}$ and $a = 0$ when $k\neq 1$;

(iv) $a = 0$, $\mu\in \mathbb{C}$ and $h{(\mathbb{Z}_{\geqslant t})} = -1$, $h{(\mathbb{Z}_{\leqslant t-1})} = 0$ for some $t\in \mathbb{Z}\setminus\{0,1\}$ and

$g{(\mathbb{Z}_{\geqslant s})} = -1$, $g{(\mathbb{Z}_{\leqslant s-1})} = 0$ for some $s\in \{2t-2,2t-1,2t,2t+1,2t+2\}$.

Proof. Take $m = -n\neq 0$ in (18)-(22), one has

Note that $f{(\mathbb{Z}_{>0})} = -1,f{(\mathbb{Z}_{<0})} = 0 \,$ and $\, f{(0)} = c$ for some $c\in \mathbb{C}$. It is follows by (18), (20) and (22) that

For any $t\in \mathbb{Z}^*$, we first prove some claims as follows.

Claim 1. If $h(t) = 0$, then $h(\mathbb{Z}_{\leqslant t}) = 0$.

In fact, by (44) with $n = t-m$ we deduce $h(t-m) = 0$ for all $m>0$ with $m\neq \frac{2}{3}t$. This implies $h(\mathbb{Z}_{\leqslant t}\setminus\{\frac{1}{3}t\}) = 0$. On the other hand, by (45) with $n = t$ we see that $h(m+t) = 0$ for all $m<0$ with $m\neq 2t$. This gives that $h(\mathbb{Z}_{\leqslant t}\setminus\{3t\}) = 0$. Clearly, $3t\neq \frac{1}{3}t$ since $t\neq 0$. Thereby, we obtain $h(\mathbb{Z}_{\leqslant t}) = 0$.

Claim 2. If $h(t) = -1$, then $h(\mathbb{Z}_{\geqslant t}) = -1$.

This proof is similar to Claim 1 by using (44) and (45). Also, similar to Claims 1 and 2, by (46) and (47) we can obtain the following two claims:

Claim 3. If $g(t) = 0$, then $g(\mathbb{Z}^*_{\leqslant t}) = 0$.

Claim 4. If $g(t) = -1$, then $g(\mathbb{Z}^*_{\geqslant t}) = -1$.

According to (32), by Claims 1 and 2, $h$ must be one of the following forms:

(1) $h(\mathbb{Z}^{*}) = 0$;

(2) $h(\mathbb{Z}^{*}) = -1$;

(3) $h(\mathbb{Z}_{>0}) = -1$, $h(\mathbb{Z}_{<0}) = 0$ and $h(0) = \lambda$ for some $\lambda\in \mathbb{C}$;

(4) $h(\mathbb{Z}_{\geqslant t}) = -1$, $h(\mathbb{Z}_{\leqslant t-1}) = 0$ for some $t\in \mathbb{Z}\setminus\{0,1\}$.

In view of the above result, the next proof will be divided into the following cases.

Case i. When $h(\mathbb{Z}^{*}) = 0$.

By taking $n = 1$ in (40), one has $h(0) = 0$. Hence we see that $h(\mathbb{Z}) = 0$. This together with (48) yields $g(\mathbb{Z}) = 0$. In addition, we have by (43) that $a = 0$.

Case ii. When $h(\mathbb{Z}^{*}) = -1$.

By taking $n = -1$ in (40), one has $h(0) = -1$. Hence we see that $h(\mathbb{Z}) = -1$. This together with (48) yields $g(\mathbb{Z}) = -1$. In addition, by (43) we get $a = 0$.

Case iii. When $h(\mathbb{Z}_{>0}) = -1$, $h(\mathbb{Z}_{<0}) = 0$ and $h(0) = \lambda$ for some $\lambda\in \mathbb{C}$.

By (48) we see that $g(m+n) = -1$ for any $m,n\in \mathbb{Z}$ with $m,n> 0$ and $m\neq n$, and $g(m+n) = 0$ for any $m,n\in \mathbb{Z}$ with $m,n< 0$ and $m\neq n$. Consequently, we obtain $g{(\mathbb{Z}_{\leqslant -3})} = 0$ and $g{(\mathbb{Z}_{\geqslant 3})} = -1$. By (32), $g(i)\in \{-1, 0\}$ for $i\in \{-2,-1,1,2\}$. In view of Claims 3 and 4, we can assume that $g(k) = -1$ and $g(k-1) = 0$ for some $k\in \{-2,-1,1,2,3\}$. In all, by Claims 3 and 4 we get $g(\mathbb{Z}_{\geqslant k}^*) = -1$ and $g(\mathbb{Z}_{\leqslant k-1}^*) = 0$. Next, if $k\in \{-1,-2\}$ then by taking $n = k$ in (41) we have $a = 0$; and if $k\in \{2,3\}$ then by taking $n = k-1$ in (41) we also have $a = 0$. But $a$ can be arbitrary if $k = 1$.

Case iv. When $h(\mathbb{Z}_{\geqslant t}) = -1$, $h(\mathbb{Z}_{\leqslant t-1}) = 0$ for some $t\in \mathbb{Z}\setminus\{0,1\}$.

Note that $t\geqslant 2$ or $t \leqslant -1$, then by taking $n = 1$ in (42) we have $a = 0$. Next, by(48) we see that $g(m+n) = -1$ for any $m,n\in \mathbb{Z}$ with $m,n\geqslant t$ and $m\neq n$, and $g(m+n) = 0$ for any $m,n\in \mathbb{Z}$ with $m,n\leqslant t-1$ and $m\neq n$. Consequently, we obtain $g{(\mathbb{Z}_{\leqslant 2t-3})} = 0$ and $g{(\mathbb{Z}_{\geqslant 2t+1})} = -1$. By (32), $g(i)\in \{-1, 0\}$ for $i\in \{2t-2,2t-1,2t,2t+1\}$. In view of Claims 3 and 4, we can assume that $g(s) = -1$ and $g(s-1) = 0$ for some $s\in \{2t-2,2t-1,2t,2t+1,2t+2\}$. Note that $0\notin \{2t-2,2t-1,2t,2t+1\}$ since $t\neq 0,1$, by Claims 3 and 4 we get $g(\mathbb{Z}_{\geqslant s}) = -1$ and $g(\mathbb{Z}_{\leqslant s-1}) = 0$. The proof is completed.

Lemma 3.6. Let $f,g,h$ be complex-valued functions on $\mathbb{Z}$ and $\mu,a$ be complex numbers. Then (17)-(22) hold if and only if $f,g,h,a,\mu$ meet one of the situations listed in Table 2.

Proof. The proof of the "if" direction can be directly verified. We now prove the "only if" direction. In view of $f$ satisfying (16), by Theorem 2.4 of [10] we know that $f$ is determined by Table 1.

When $f$ takes the form of Case $\mathcal{P}_{1}$ in Table 1, by the results of Lemma 3.3, we see that $\mu,a,g,h$ must satisfy the condition of Cases $\mathcal{W}_{1}^{\mathcal{P}_{1}}$ and $\mathcal{W}_{2}^{\mathcal{P}_{1}}$ in Table 2. From Lemma 3.3, Cases $\mathcal{W}_{1}^{\mathcal{P}_{1}}, i = 1,2$ is easy to say. In the same way, when $f$ takes the form of Case $\mathcal{P}_{2}$ in Table 1, then we obtain the forms of Cases $\mathcal{W}_{1}^{\mathcal{P}_{2}}$ and $\mathcal{W}_{2}^{\mathcal{P}_{2}}$ in Table 2.

When $f$ takes the form of Case $\mathcal{P}_{3}^c$ in Table 1, by the results of Lemma 3.5, we see that $\mu,a,g,h$ must satisfy the one condition of Cases $\mathcal{W}_{i,\mu}^{\mathcal{P}_{3}^c}, i = 1,2$, $\mathcal{W}_{3,\mu}^{\mathcal{P}_{3}^c,k}$, $\mathcal{W}_{4,a,\mu}^{\mathcal{P}_{3}^c,k = 1}$ and $\mathcal{W}_{5,\mu}^{\mathcal{P}_{3}^c,s,t}$ in Table 2. From Lemma 3.5, the results of Cases $\mathcal{W}_{i,\mu}^{\mathcal{P}_{3}^c}, i = 1,2$ are easily obtained; and Case $\mathcal{W}_{3,\mu}^{\mathcal{P}_{3}^c,k}$ satisfies $\mu \in \mathbb{C}$, $h{(\mathbb{Z}_{> 0})} = -1$, $h{(\mathbb{Z}_{<0})} = 0$, $h(0) = \lambda$ and $g{(\mathbb{Z}^*_{\geqslant k})} = -1$, $g{(\mathbb{Z}^*_{\leqslant k-1})} = 0$, for some $k\in \{-2,-1,1,2,3\}$, $g(0) = \hat{\tau}$ with $a = 0$ when $k\neq 1$ and $a$ is arbitrary if $k = 1$; Case $\mathcal{W}_{4,a,\mu}^{\mathcal{P}_{3}^c,k = 1}$ satisfies $\mu \in \mathbb{C}$, $h{(\mathbb{Z}_{> 0})} = -1$, $h{(\mathbb{Z}_{<0})} = 0$, $h(0) = \lambda$ and $g{(\mathbb{Z}_{> 0})} = -1$, $g{(\mathbb{Z}_{< 0})} = 0$ for some $k = 1$, $g(0) = \hat{\tau}$; Case $\mathcal{W}_{5,\mu}^{\mathcal{P}_{3}^c,s,t}$ satisfies $a = 0$, $\mu\in \mathbb{C}$ and $h{(\mathbb{Z}_{\geqslant t})} = -1$, $h{(\mathbb{Z}_{\leqslant t-1})} = 0$ for some $t\in \mathbb{Z}\setminus\{0,1\}$ and $g{(\mathbb{Z}_{\geqslant s})} = -1$, $g{(\mathbb{Z}_{\leqslant s-1})} = 0$ for some $s\in \{2t-2,2t-1,2t,2t+1,2t+2\}$. In the same way, when $f$ takes the form of Case $\mathcal{P}_{4}^c$ in Table 1, then we obtain the results of Cases $\mathcal{W}_{i,\mu}^{\mathcal{P}_{4}^c}, i = 1,2$, $\mathcal{W}_{3,\mu}^{\mathcal{P}_{4}^c,k}$, $\mathcal{W}_{4,a,\mu}^{\mathcal{P}_{4}^c,k = 1}$ and $\mathcal{W}_{5,\mu}^{\mathcal{P}_{4}^c,s,t}$ in Table 2, respectively.

When $f$ takes the form of Case $\mathcal{P}_{5}$ in Table 1, by the results of Lemma 3.4, we see that $\mu,a,g,h$ must satisfy the condition of Cases $\mathcal{W}_{i}^{\mathcal{P}_{5}}, i = 1,2,3$ in Table 2. From Lemma 3.4, the results of Cases $\mathcal{W}_{i}^{\mathcal{P}_{5}}, i = 1,2,$ are easily obtained; and for Case $\mathcal{W}_{3}^{\mathcal{P}_{5}}$, we get $h{(\mathbb{Z}_{\leqslant 0})} = 0$, $h{(\mathbb{Z}_{\geqslant 1})} = -1$ and $g{(\mathbb{Z}_{\leqslant-1})} = 0$, $g{(\mathbb{Z}_{\geqslant 1})} = -1$, $g(0) = \hat{\lambda}$ for some $\hat{\lambda}\in \mathbb{C}$. Similarly, when $f$ takes the form of Case $\mathcal{P}_{k}, k = 6,7,8$ in Table 1, then we obtain the forms of Cases $\mathcal{W}_{i}^{\mathcal{P}_{k}}$, $i = 1,2,3$, $k = 6,7,8$ in Table 2. The proof is completed.

Lemma 3.7. Let $(\mathcal{P}(\phi_{i}, \varphi_{i}, \chi_{i}, \psi_{i}, \xi_{i}, \theta_{i}), \triangleright_{i})$, $i = 1, 2$ be two algebras with the same linear space as $\mathcal{S}$ and equipped with $\mathbb{C}$-bilinear products $x\triangleright_{i}y$ such that

for all $m, n\in\mathbb{Z}$, where $\phi_{i}, \varphi_{i}, \chi_{i}, \psi_{i}, \xi_{i}, \theta_{i}$, $i = 1, 2$ are complex-valued functions on $\mathbb{Z}\times\mathbb{Z}$. Furthermore, let $\tau:\mathcal{P}(\phi_{1}, \varphi_{1}, \chi_{1}, \psi_{1}, \xi_{1}, \theta_{1})\rightarrow\mathcal{P}(\phi_{2}, \varphi_{2}, \chi_{2}, \psi_{2}, \xi_{2}, \theta_{2})$ be a linear map determined by

for all $m\in\mathbb{Z}$. In addition, suppose that $(\mathcal{P}(\phi_{1},\varphi_{1},\chi_{1},\psi_{1},\xi_{1},\theta_{1}),[,],\triangleright_{1})$ is a post-Lie algebra. Then $(\mathcal{P}(\phi_{2},\varphi_{2},\chi_{2},\psi_{2},\xi_{2},\theta_{2}),[,],,\triangleright_{2})$ is a post-Lie algebra and $\tau$ is an isomorphism on post-Lie algebras if and only if

Proof. Clearly, $\tau$ is a Lie automorphism of $\mathcal{S}$. Suppose $(\mathcal{P}(\phi_{2},\varphi_{2},\chi_{2},\psi_{2},\xi_{2},\theta_{2}),[,], \triangleright_{2})$ is a post-Lie algebra and $\tau:\mathcal{P}(\phi_{1},\varphi_{1},\chi_{1},\psi_{1},\xi_{1},\theta_{1}) \rightarrow \mathcal{P}(\phi_{2},\varphi_{2},\chi_{2},\psi_{2},\xi_{2},\theta_{2})$ is a post-Lie isomorphism. Then we have

for $i = 1,2$. This tell us that that (49) holds. Conversely, we first suppose that (49) hold. Then, by using Lemma 3.1 and $(\phi_{1},\varphi_{1},\chi_{1},\psi_{1},\xi_{1},\theta_{1},[,],\triangleright_{1})$ is a post-Lie algebra, we know that there are complex-valued functions $f_{1},g_{1},h_{1}$ on $\mathbb{Z}$ and complex numbers $a_1,\mu_{1}$ satisfying (10)-(22) with replacing $(\phi,\varphi,\chi,\psi,\xi,\theta,f,g,h,\mu,a)$ by $(\phi_{1},\varphi_{1},\chi_{1},\psi_{1},\xi_{1},\theta_{1},f_1,g_1, h_1,\mu_1,a_1)$. Next, let $f_{2}(m) = f_{1}(-m)$, $g_{2}(m) = g_{1}(-m)$, $h_{2}(m) = h_{1}(-m)$, $\mu_{2} = -\mu_{1}$ and $a_{2} = a_{1}$, then we see that (10)-(22) hold with replacing $(\phi,\varphi,\chi,\psi,\xi,\theta,f,g,h,\mu,a)$ by $(\phi_2,\varphi_2,\chi_2,\psi_2,\xi_2,\theta_2,f_1,g_1, h_1,\mu_1,a_1)$. By Lemma 3.1, $\mathcal{P}(\phi_2,\varphi_2,\chi_2,\psi_2,\xi_2,\theta_2)$ is a post-Lie algebra.

The remainder is to prove that $\tau$ is an isomorphism between post-Lie algebra. But one has

and $\tau(H_{m}\triangleright_{1}I_{n}) = \tau(H_{m})\triangleright_{2}\tau(I_{n}) = 0$, $\tau(I_{m}\triangleright_{1}H_{n}) = \tau(I_{m})\triangleright_{2}\tau(H_{n})$ = 0, $\tau(I_{m}\triangleright_{1}I_{n}) = \tau(I_{m})\triangleright_{2}\tau(I_{n})$ = 0. The proof is completed.

Theorem 3.8. A graded post-Lie algebra structure on $\mathcal{S}$ satisfying (3)-(9) must be one of the following types, for all $m, n\in \mathbb{Z}$ (in every case $I_{m}\triangleright H_{n} = H_{m}\triangleright I_{n} = I_{m}\triangleright I_{n} = 0$),

$(\mathcal{W}_1^{\mathcal{P}_1} ):$ $L_m \triangleright_1^{\mathcal{P}_1} L_n = 0$, $L_m \triangleright_1^{\mathcal{P}_1} H_n = 0$, $L_m \triangleright_1^{\mathcal{P}_1} I_n = 0$, $H_m \triangleright_1^{\mathcal{P}_1} L_n = 0$, $H_m \triangleright_1^{\mathcal{P}_1} H_n = 0$, $I_m \triangleright_1^{\mathcal{P}_1} L_n = 0$;

$(\mathcal{W}_2^{\mathcal{P}_1} )$: $L_m \triangleright_2^{\mathcal{P}_1} L_n = 0$, $L_m \triangleright_2^{\mathcal{P}_1} H_n = 0$, $L_m \triangleright_2^{\mathcal{P}_1} I_n = 0$, $H_m \triangleright_2^{\mathcal{P}_1} L_n = (\frac{n}{2}-m)H_{m+n}$, $H_m \triangleright_2^{\mathcal{P}_1} H_n = (n-m)I_{m+n}$, $I_m \triangleright_2^{\mathcal{P}_1} L_n = -mI_{m+n}$;

$( \mathcal{W}_1^{\mathcal{P}_2} ):$ $L_m \triangleright_1^{\mathcal{P}_2} L_n = (n-m)L_{m+n}$, $L_m \triangleright_1^{\mathcal{P}_2} H_n = (n-\frac{m}{2})H_{m+n}$, $L_m \triangleright_1^{\mathcal{P}_2} I_n = nI_{m+n}$, $H_m \triangleright_1^{\mathcal{P}_2} L_n = 0$, $H_m \triangleright_1^{\mathcal{P}_2} H_n = 0$, $I_m \triangleright_1^{\mathcal{P}_2} L_n = 0$;

$(\mathcal{W}_2^{\mathcal{P}_2}):$ $L_m \triangleright_2^{\mathcal{P}_2} L_n = (n-m)L_{m+n}$, $L_m \triangleright_2^{\mathcal{P}_2} H_n = (n-\frac{m}{2})H_{m+n}$, $L_m \triangleright_2^{\mathcal{P}_2} I_n = nI_{m+n}$, $H_m \triangleright_2^{\mathcal{P}_2} L_n = (\frac{n}{2}-m)H_{m+n}$, $H_m \triangleright_2^{\mathcal{P}_2} H_n = (n-m)I_{m+n}$, $I_m \triangleright_2^{\mathcal{P}_2} L_n = -mI_{m+n}$;

$(\mathcal{W}_{i,a,\mu,\lambda}^{\mathcal{P}^{c}_3,s,k,t}): \ i = 1,2,3, 4,5$

$L_m \triangleright_{i}^{\mathcal{P}_3^c} L_n = \left\{{ \begin{array}{cc} (n-m)L_{m+n}, & m> 0,\\ -ncL_n,& m = 0,\\ 0, & m<0; \end{array}} \right.$

$L_m \triangleright_{i}^{\mathcal{P}_3^c} H_n = \left\{ { \begin{array}{cc} (n-\frac{m}{2})H_{m+n}, & m> 0,\\ (-nc+\mu) H_n, & m = 0,\\ 0, & m<0; \end{array}} \right.$

$L_m \triangleright_{i}^{\mathcal{P}_3^c} I_n = \left\{ { \begin{array}{cc} nI_{m+n}, & m> 0,\\ (-nc+2\mu) I_n, & m = 0,\\ 0, & m<0; \end{array}} \right.$

$\ \ \quad H_m \triangleright_{i}^{\mathcal{P}_3^c} L_n = \delta_{i,2}(\frac{n}{2}-m)H_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +(\delta_{i,3}+\delta_{i,4}) \begin{cases} (\frac{n}{2}-m)H_{m+n}, & m> 0,\\ -\frac{n}{2}\lambda H_{n}, & m = 0,\\ 0, & m< 0; \end{cases}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,5} \begin{cases} (\frac{n}{2}-m)H_{m+n}, &m\geqslant t ,\\ 0, & m\leqslant t-1 ; \end{cases}$

$\ \ \quad H_m \triangleright_{i}^{\mathcal{P}_3^c} H_n = \delta_{i,2}(n-m)I_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +(\delta_{i,3}+\delta_{i,4}) \begin{cases} (n-m)I_{m+n}, & m> 0,\\ -n\lambda I_{n}, & m = 0,\\ 0, & m< 0; \end{cases}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,5} \begin{cases} (n-m)I_{m+n}, &m\geqslant t ,\\ 0, & m\leqslant t-1 ; \end{cases}$

$\ \ \quad I_m \triangleright_{i}^{\mathcal{P}_3^c} L_n = \delta_{i,2}(-m)I_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,3} \begin{cases} -mI_{m+n}, &m\geqslant k ,\\ 0, & m\leqslant k-1 ; \end{cases}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,4} \begin{cases} -mI_{m+n}, & m> 0,\\ naI_{n}, & m = 0,\\ 0, & m<0; \end{cases}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,5} \begin{cases} -mI_{m+n}, & m\geqslant s,\\ 0, & m\leqslant s-1; \end{cases}$

$(\mathcal{W}_{i,a,\mu,\lambda}^{\mathcal{P}_4^{c},s,k,t}): \ i = 1,2,3, 4,5$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_4^{c}} L_n = \left\{{ \begin{array}{cc} (n-m)L_{m+n},& m< 0,\\ -ncL_n,& m = 0,\\ 0, & m>0; \end{array}} \right.$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_4^{c}} H_n = \left\{{ \begin{array}{cc} (n-\frac{m}{2})H_{m+n},& m< 0,\\ (-nc+\mu)H_n,& m = 0,\\ 0, & m>0; \end{array}} \right.$

$\ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_4^{c}} I_n = \left\{ { \begin{array}{cc} nI_{m+n}, &m< 0,\\ (-nc+2\mu) I_n, &m = 0,\\ 0, & m>0; \end{array}} \right.$

$H_m \triangleright_{i}^{\mathcal{P}_4^{c}} L_n = \delta_{i,2}(\frac{n}{2}-m)H_{n+m}$

$\ \qquad \qquad \quad \ \ \ \ +(\delta_{i,3}+\delta_{i,4})\begin{cases} 0, & m > 0,\\ -\frac{n}{2}\lambda H_{n}, & m = 0,\\ (\frac{n}{2}-m)H_{m+n}, & m< 0; \end{cases}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,5}\begin{cases} 0, & m\geqslant t ,\\ (\frac{n}{2}-m)H_{m+n}, & m \leqslant t-1 ; \end{cases}$

$H_m \triangleright_{i}^{\mathcal{P}_4^{c}} H_n = \delta_{i,2}(n-m)I_{n+m}$

$\ \qquad \qquad \quad \ \ \ \ +(\delta_{i,3}+\delta_{i,4})\begin{cases} 0, & m > 0,\\ -n\lambda I_{n}, & m = 0,\\ (n-m)I_{m+n}, & m< 0; \end{cases}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,5}\begin{cases} 0, & m\geqslant t ,\\ (n-m)I_{m+n}, & m \leqslant t-1 ; \end{cases}$

$I_m \triangleright_{i}^{\mathcal{P}_4^{c}} L_n = \delta_{i,2}(-m)I_{n+m}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,3}\begin{cases} 0, & m \geqslant k ,\\ -mI_{m+n}, & m \leqslant k-1 ; \end{cases}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,4}\begin{cases} 0, & m > 0,\\ naI_{n}, & m = 0,\\ -mI_{m+n}, & m< 0; \end{cases}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,5}\begin{cases} 0, & m \geqslant s,\\ -mI_{m+n}, & m\leqslant s-1; \end{cases}$

$(\mathcal{W}_{i}^{\mathcal{P}_5}): \ i = 1,2,3,$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_5} L_n = \left\{{ \begin{array}{cc} (n-m)L_{m+n}, & m\geqslant 2,\\ 0, & m \leqslant 1; \end{array}} \right.$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_5} H_n = \left\{{ \begin{array}{cc} (n-\frac{m}{2})L_{m+n}, & m\geqslant 2,\\ 0, & m \leqslant 1; \end{array}} \right.$

$\ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_5} I_n = \left\{ { \begin{array}{cc} nI_{m+n}, & m \geqslant 2,\\ 0, & m\leqslant 1; \end{array}} \right.$

$H_m \triangleright_{i}^{\mathcal{P}_5} L_n = \delta_{i,2}(\frac{n}{2}-m)H_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,3}\begin{cases} 0, & m\leqslant 0,\\ (\frac{n}{2}-m)H_{m+n}, & m \geqslant 1; \end{cases}$

$H_m \triangleright_{i}^{\mathcal{P}_5} H_n = \delta_{i,2}(n-m)I_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,3}\begin{cases} 0, & m\leqslant 0,\\ (n-m)I_{m+n}, & m \geqslant 1; \end{cases}$

$I_m \triangleright_{i}^{\mathcal{P}_5} L_n = \delta_{i,2}(-m)I_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i,3}\begin{cases} 0, & m\leqslant 0,\\ -mI_{m+n}, & m \geqslant 1; \end{cases}$

$(\mathcal{W}_{i}^{\mathcal{P}_6}):\ i = 1,2,3,$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_6} L_n = \left\{{ \begin{array}{cc} (n-m)L_{m+n}, & m\leqslant 1,\\ 0, & m \geqslant 2; \end{array}} \right.$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_6} H_n = \left\{{ \begin{array}{cc} (n-\frac{m}{2})H_{m+n}, & m\leqslant 1,\\ 0, & m \geqslant 2; \end{array}} \right.$

$\ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_6} I_n = \left\{ { \begin{array}{cc} nI_{m+n}, & m \leqslant 1,\\ 0, & m \geqslant 2; \end{array}} \right.$

$H_m \triangleright_{i}^{\mathcal{P}_6} L_n = \delta_{i, 2}(\frac{n}{2}-m)H_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i, 3}\begin{cases} (\frac{n}{2}-m)H_{m+n}, & m \leqslant 0,\\ 0, & m \geqslant 1; \end{cases}$

$H_m \triangleright_{i}^{\mathcal{P}_6} H_n = \delta_{i, 2}(n-m)I_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i, 3}\begin{cases} (n-m)I_{m+n}, & m \leqslant 0,\\ 0, & m \geqslant 1; \end{cases}$

$I_m \triangleright_{i}^{\mathcal{P}_6} L_n = \delta_{i, 2}(-m)I_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i, 3}\begin{cases} -mI_{m+n}, & m \leqslant -1,\\ 0, & m \geqslant 0; \end{cases}$

$(\mathcal{W}_{i}^{\mathcal{P}_7}):\ i = 1,2,3,$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_7} L_n = \left\{{ \begin{array}{cc} (n-m)L_{m+n}, & m\leqslant -2,\\ 0, & m \geqslant -1; \end{array}} \right.$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_7} H_n = \left\{{ \begin{array}{cc} (n-\frac{m}{2})H_{m+n}, & m\leqslant -2,\\ 0, & m \geqslant -1; \end{array}} \right.$

$\ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_7} I_n = \left\{ { \begin{array}{cc} nI_{m+n},& m \leqslant -2,\\ 0, & m \geqslant -1; \end{array}} \right.$

$H_m \triangleright_{i}^{\mathcal{P}_7} L_n = \delta_{i, 2}(\frac{n}{2}-m)H_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i, 3} \begin{cases} (\frac{n}{2}-m)H_{m+n}, & m \leqslant 0,\\ 0, & m \geqslant 1; \end{cases}$

$H_m \triangleright_{i}^{\mathcal{P}_7} H_n = \delta_{i, 2}(n-m)I_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i, 3} \begin{cases} (n-m)I_{m+n}, & m \leqslant 0,\\ 0, & m \geqslant 1; \end{cases}$

$I_m \triangleright_{i}^{\mathcal{P}_7} L_n = \delta_{i, 2}(-m)I_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i, 3} \begin{cases} -mI_{m+n}, & m \leqslant -1,\\ 0, & m \geqslant 0; \end{cases}$

$(\mathcal{W}_{i}^{\mathcal{P}_8}):\ i = 1,2,3,$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_8} L_n = \left\{{ \begin{array}{cc} (n-m)L_{m+n}, & m\geqslant -1,\\ 0, & m \leqslant -2; \end{array}} \right.$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_8} H_n = \left\{{ \begin{array}{cc} (n-\frac{m}{2})H_{m+n}, & m\geqslant -1,\\ 0, & m \leqslant -2; \end{array}} \right.$

$\ \ \ \ \ \ \ L_m \triangleright_{i}^{\mathcal{P}_8} I_n = \left\{{ \begin{array}{cc} nI_{m+n}, & m\geqslant -1,\\ 0, & m \leqslant -2; \end{array}} \right.$

$H_m \triangleright_{i}^{\mathcal{P}_8} L_n = \delta_{i, 2}(\frac{n}{2}-m)H_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i, 3} \begin{cases} 0, & m \leqslant 0,\\ (\frac{n}{2}-m)H_{m+n}, & m \geqslant 1 \end{cases}$

$H_m \triangleright_{i}^{\mathcal{P}_8} H_n = \delta_{i, 2}(n-m)I_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i, 3} \begin{cases} 0, & m \leqslant 0,\\ (n-m)I_{m+n}, & m \geqslant 1 \end{cases}$

$I_m \triangleright_{i}^{\mathcal{P}_8} L_n = \delta_{i, 2}(-m)I_{m+n}$

$\ \qquad \qquad \quad \ \ \ \ +\delta_{i, 3} \begin{cases} 0, & m \leqslant 0,\\ -mI_{m+n}, & m \geqslant 1 \end{cases}$

where $c,a,\mu,\lambda\in\mathbb{C}$, $k\in \{-2,-1,1,2,3\}$, $t\in \mathbb{Z}\setminus\{0,1\}$ and $s\in \{2t-2,2t-1,2t,2t+1,2t+2\}$. Conversely, the above types are all the graded post-Lie algebra structures satisfying (3)-(9) on $\mathcal{S}$. Furthermore, the post-Lie algebras $\mathcal{W}^{\mathcal{P}_{3}^c,s,k,t}_{i,a,\mu,\lambda}$, $\mathcal{W}^{\mathcal{P}_{5}}_{j}$ and $\mathcal{W}^{\mathcal{P}_{6}}_{j}$ are isomorphic to the post-Lie algebras $\mathcal{W}^{\mathcal{P}_{4}^c,s,k,t}_{i,a,\mu,\lambda}$, $\mathcal{W}^{\mathcal{P}_{7}}_{j}$ and $\mathcal{W}^{\mathcal{P}_{8}}_{j}$, $i = 1,2,3,4,5$ and $j = 1,2,3$ respectively, and other post-Lie algebras are not mutually isomorphic.

Proof. Suppose that $(\mathcal{S},[,],\triangleright)$ is a class of post-Lie algebra structures satisfying (3)-(9) on the Schrödinger-Virasoro algebra $\mathcal{S}$. By Lemma 3.3-3.5, there are complex-valued functions $f$, $g$, $h$ on $\mathbb{Z}$ and complex numbers $\mu,a$ such that one of $26$ cases in Table 2 holds. From this with Lemma 3.1, we obtain $26$ classes of graded post-Lie algebra structures on $\mathcal{S}$. We claim that $h(0) = \lambda$ and $g(0) = \hat{\tau}$ in $\mathcal{W}_{i,a,\mu,\lambda}^{\mathcal{P}_{j}^c,s,k,t}, j = 3,4$ and $i = 1,2,3,4,5$ and $g(0) = \hat{\lambda}$ in $\mathcal{W}^{\mathcal{P}_{j}}_{i}$, $j = 5,6,7,8$ and $i = 1,2,3$. We claim that $g(0) = \hat{\lambda}$ and $g(0) = \hat{\tau}$ will not appear in every structures, when $m = 0$, for example, in Case $\mathcal{W}^{\mathcal{P}_{5}}_{i}$, $i = 1,2,3$, then $I_{m}\triangleright_{3}^{P_{5}}L_{n} = 0 \hat{\lambda} I_{0+n} = 0$, one has $I_{m}\triangleright_{3}^{P_{5}}L_{n} = 0$ for $m \leqslant 0$, and in Case $\mathcal{W}^{\mathcal{P}_{3}^c,s,k,t}_{i,a,\mu,\lambda}$, $i = 1,2,3,4,5$, then $H_{m}\triangleright_{3,\lambda}^{P_{3}}L_{n} = -(\frac{n}{2}-0)\lambda H_{0+n} = 0$, one has $H_{m}\triangleright_{3,\lambda}^{P_{3}}L_{n} = -\frac{n}{2}\lambda H_{n}$ for $m = 0$. Hence we can obtain $26$ classes of graded post-Lie algebra structures on $\mathcal{S}$ listed in the theorem.

Conversely, every type of the $26$ cases means that there are complex-valued functions $f$ and $g$, $h$ on $\mathbb{Z}$ and complex numbers $a,\mu$ such that (10)-(15) hold and, the Equations (16)-(22) are easily verified. Thus, by Lemma 3.1 we see that they are the all graded post-Lie algebra structures satisfying (3)-(9) on the Schrödinger-Virasoro algebra $\mathcal{S}$.

Finally, by Lemma 3.7 with maps $L_{m}\rightarrow-L_{-m}$, $H_{m}\rightarrow-H_{-m}$, $I_{m}\rightarrow-I_{-m}$ we know that the post-Lie algebras $\mathcal{W}^{\mathcal{P}_{3}^c,s,k,t}_{i,a,\mu,\lambda}$, $\mathcal{W}^{\mathcal{P}_{5}}_{j}$ and $\mathcal{W}^{\mathcal{P}_{6}}_{j}$ are isomorphic to the post-Lie algebras $\mathcal{W}^{\mathcal{P}_{4}^c,s,k,t}_{i,a,\mu,\lambda}$, $\mathcal{W}^{\mathcal{P}_{7}}_{j}$ and $\mathcal{W}^{\mathcal{P}_{8}}_{j}$, $i = 1,2,3,4,5$ and $j = 1,2,3$ respectively. Clearly, the other post-Lie algebras are not mutually isomorphic. The proof is completed.

4.   Application to Rota-Baxter operators

The Rota-Baxter algebra was introduced by the mathematician Glen E. Baxter [2] in 1960 in his probability study, and was popularized mainly by the work of Rota [G. Rota1, G. Rota2] and his school. Recently, the Rota-Baxter algebra relation were introduced to solve certain analytic and combinatorial problem and then applied to many fields in mathematics and mathematical physics (see [6,7,19,23] and the references therein). Now let us recall the definition of Rota-Baxter operator.

Definition 4.1. Let $L$ be a complex Lie algebra. A Rota-Baxter operator of weight $\lambda\in\mathbb{C}$ is a liner map $R:L\rightarrow L$ satisfying

Note that if $R$ is a Rota-Baxter operator of weight $\lambda\neq0$, then $\lambda^{-1}R$ is a Rota-Baxter operator of weight 1. Therefore, one only needs to consider Rota-Baxter operators of weight $0$ and $1$.

4.1.   Rota-Baxter operators of weight $1$

In this section, we mainly consider the homogeneous Rota-Baxter operator $R$ of weight 1 on the Schrödinger-Virasoro $\mathcal{S}$ given by

for all $m\in\mathbb{Z}$, where $f,g,h$ are complex-valued functions on $\mathbb{Z}$.

Lemma 4.2. (see [1]) Let $(L, [,])$ be a Lie algebra and $R:L\rightarrow L$ a Rota-Baxter operator of weight 1. Define a new operation $x\triangleright y = [R(x),y]$ on L. Then $(L,[,],\triangleright)$ is a post-Lie algebra.

Theorem 4.3. A homogeneous Rote-Baxrer operator $R$ of weight 1 satisfying (51) on the Schrödinger-Virasoro $\mathcal{S}$ must be one of the following types

$(\mathcal{R}_1^{\mathcal{P}_1} ):$ $R(L_m) = 0, R(H_n) = 0, R(I_n) = 0;$

($\mathcal{R}_2^{\mathcal{P}_1}$): $R(L_m) = 0, R(H_n) = -H_n, R(I_n) = -I_n;$

$( \mathcal{R}_1^{\mathcal{P}_2} ):$ $R(L_m) = -L_m, R(H_n) = 0, R(I_n) = 0;$

$( \mathcal{R}_2^{\mathcal{P}_2}):$ $R(L_m) = -L_m, R(H_n) = -H_n, R(I_n) = -I_n;$

($\mathcal{R}_1^{\mathcal{P}_3^c}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m>0, \\ cL_{0}, \ \ & m = 0,\\ 0, & m< 0; \end{cases}$ $R(H_n) = 0,$ $R(I_n) = 0;$

($\mathcal{R}_2^{\mathcal{P}_3^c}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m>0, \\ cL_{0}, \ \ & m = 0,\\ 0, & m< 0; \end{cases}$ $R(H_n) = -H_n,$ $R(I_n) = -I_n;$

($\mathcal{R}_{3,\hat{\tau},\lambda}^{\mathcal{P}^{c}_{3},k}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m>0, \\ cL_{0}, \ \ & m = 0,\\ 0, & m< 0; \end{cases}$ $R(H_n) = \begin{cases} -H_{n}, \ \ & n> 0, \\ \lambda H_{0}, \ \ & n = 0,\\ 0, & n< 0; \end{cases}$

$\quad R(I_n) = \begin{cases} -I_{n}, \ \ & n\geqslant k, \\ \hat{\tau} I_{0}, \ \ & n = 0,\\ 0, & n\leqslant k-1; \end{cases}$

($\mathcal{R}_{5}^{\mathcal{P}^{c}_{3},s,t}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m>0, \\ cL_{0}, \ \ & m = 0,\\ 0, & m< 0; \end{cases}$ $R(H_n) = \begin{cases} -H_{n}, \ \ & n\geqslant t, \\ 0 , \ \ & n\leqslant t-1; \end{cases}$

$R(I_n) = \begin{cases} -I_{n}, \ \ & n\geqslant s, \\ 0, \ \ & n\leqslant s-1; \end{cases}$

($\mathcal{R}_1^{\mathcal{P}_4^{c}}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m< 0,\\ cL_{0}, \ \ & m = 0,\\ 0, & m>0; \end{cases}$ $R(H_n) = 0,$ $R(I_n) = 0;$

($\mathcal{R}_2^{\mathcal{P}_4^{c}}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m< 0,\\ cL_{0}, \ \ & m = 0,\\ 0, & m>0; \end{cases}$ $R(H_n) = -H_n,$ $R(I_n) = -I_n;$

($\mathcal{R}_{3,\hat{\tau},\lambda}^{\mathcal{P}^{c}_{4},k}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m< 0,\\ cL_{0}, \ \ & m = 0,\\ 0, & m>0; \end{cases}$ $R(H_n) = \begin{cases} 0, \ \ & n> 0, \\ \lambda H_{0}, \ \ & n = 0,\\ -H_{n}, \ \ & n<0 ; \end{cases}$

$R(I_n) = \begin{cases} 0, \ \ & n\geqslant k, \\ \hat{\tau} I_{0}, \ \ & n = 0,\\ -I_{n}, \ \ & n\leqslant k-1 ; \end{cases}$

($\mathcal{R}_{5}^{\mathcal{P}^{c}_{4},s,t}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m>0, \\ cL_{0}, \ \ & m = 0,\\ 0, & m< 0; \end{cases}$ $R(H_n) = \begin{cases} 0, \ \ & n\geqslant t, \\ -H_n, \ \ & n\leqslant t-1; \end{cases}$

$R(I_n) = \begin{cases} 0, \ \ & n\geqslant s, \\ -I_n, \ \ & n\leqslant s-1; \end{cases}$

($\mathcal{R}_1^{\mathcal{P}_5}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m\geqslant 2,\\ 0, \ \ & m\leqslant 1; \end{cases}$ $R(H_n) = 0,$ $R(I_n) = 0;$

($\mathcal{R}_2^{\mathcal{P}_5}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m\geqslant 2,\\ 0, \ \ & m\leqslant 1; \end{cases}$ $R(H_n) = -H_n,$ $R(I_n) = -I_n;$

($\mathcal{R}_{3,\hat{\lambda}}^{\mathcal{P}_5}$): $R(L_m) = \begin{cases} -L_{m}, \ \ & m\geqslant 2,\\ 0, \ \ & m\leqslant 1; \end{cases}$ $R(H_n) = \begin{cases} 0, \ \ & n\leqslant 0,\\ -H_{n}, \ \ & n\geqslant 1; \end{cases}$

$\qquad\quad R(I_n) = \begin{cases} 0, \ \ & n\leqslant -1,\\ \hat{\lambda} I_{0}, \ \ & n = 0,\\ -I_{n}, \ \ & n \geqslant 1; \end{cases}$

($\mathcal{R}_1^{\mathcal{P}_6}$): $R(L_m) = \begin{cases} -L_{m}, & m \leqslant 1,\\ 0, \ \ & m\geqslant 2; \end{cases}$ $R(H_n) = 0,$ $R(I_n) = 0;$

($\mathcal{R}_2^{\mathcal{P}_6}$): $R(L_m) = \begin{cases} -L_{m}, & m \leqslant 1,\\ 0, \ \ & m\geqslant 2; \end{cases}$ $R(H_n) = -H_n,$ $R(I_n) = -I_n;$

($\mathcal{R}_{3,\hat{\lambda}}^{\mathcal{P}_6}$): $R(L_m) = \begin{cases} -L_{m}, & m \leqslant 1,\\ 0, \ \ & m\geqslant 2; \end{cases}$ $R(H_n) = \begin{cases} -H_{n}, & n \leqslant 0,\\ 0, \ \ & n\geqslant 1 ; \end{cases}$

$\qquad\quad R(I_n) = \begin{cases} -I_{n}, & n \leqslant -1,\\ \hat{\lambda} I_{0}, \ \ & n = 0,\\ 0, \ \ & n\geqslant 1 ; \end{cases}$

($\mathcal{R}_1^{\mathcal{P}_7}$): $R(L_m) = \begin{cases} -L_{m}, & m\leqslant -2 ,\\ 0, \ \ & m\geqslant -1; \end{cases}$ $R(H_n) = 0,$ $R(I_n) = 0;$

($\mathcal{R}_2^{\mathcal{P}_7}$): $R(L_m) = \begin{cases} -L_{m}, & m\leqslant -2,\\ 0, \ \ & m\geqslant -1; \end{cases}$ $R(H_n) = -H_n,$ $R(I_n) = -I_n$;

($\mathcal{R}_{3,\hat{\lambda}}^{\mathcal{P}_7}$): $R(L_m) = \begin{cases} -L_{m}, & m\leqslant -2,\\ 0, \ \ & m\geqslant -1; \end{cases}$ $R(H_n) = \begin{cases} 0, \ \ & n\geqslant 1,\\ -H_{n}, \ \ & n\leqslant 0; \end{cases}$

$\qquad\quad R(I_n) = \begin{cases} 0, & n\geqslant 1,\\ \hat{\lambda} I_{0}, \ \ & n = 0,\\ -I_{n}, \ \ & n\leqslant -1; \end{cases}$

($\mathcal{R}_1^{\mathcal{P}_8}$): $R(L_m) = \begin{cases} -L_{m}, & m\geqslant -1,\\ 0, \ \ & m\leqslant -2; \end{cases}$ $R(H_n) = 0,$ $R(I_n) = 0$;

$(\mathcal{R}_2^{\mathcal{P}_8} ):$ $R(L_m) = \begin{cases} -L_{m}, & m\geqslant -1,\\ 0, \ \ & m\leqslant -2, \end{cases}$ $R(H_n) = -H_n,$ $R(I_n) = -I_n$;

$( \mathcal{R}_{3,\hat{\lambda}}^{\mathcal{P}_8} ):$ $R(L_m) = \begin{cases} -L_{m}, &m\geqslant -1,\\ 0, \ \ & m\leqslant -2, \end{cases}$ $R(H_n) = \begin{cases} -H_{n}, & n\geqslant 1,\\ 0, \ \ &n\leqslant 0; \end{cases}$

$R(I_n) = \begin{cases} -I_{n}, & n\geqslant 1,\\ \hat{\lambda} I_{0}, \ \ & n = 0,\\ 0, \ \ &n\leqslant -1 \end{cases}$

for all $m,n\in\mathbb{Z}$, where $c,\lambda,\hat{\lambda},\hat{\tau}\in\mathbb{C}$, $k\in \{-2,-1,1,2,3\}$ with $k\neq1$, $t\in \mathbb{Z}\setminus\{0,1\}$ and $s\in \{2t-2,2t-1,2t,2t+1,2t+2\}$.

Proof. In view of Lemma 4.2, if we define a new operation $x\triangleright y = [R(x),y]$ on $\mathcal{S}$, then ($\mathcal{S},[,],\triangleright$) is a post-Lie algebra. By (51), we have

and $I_{m}\triangleright H_{n} = [R(I_{m}),H_{n}] = H_{m}\triangleright I_{n} = [R(H_{m}),I_{n}] = I_{m}\triangleright I_{n} = [R(I_{m}),I_{n}] = 0$ for all $m,n\in\mathbb{Z}$. This means that $(\mathcal{S},[,],\triangleright)$ is a graded post-Lie algebras structure satisfying (3)-(9) with $\phi(m,n) = (m-n)f(m)$, $\varphi(m,n) = (\frac{m}{2}-n)f(m)$, $\chi(m,n) = -nf(m)$, $\psi(m,n) = -(\frac{n}{2}-m)h(m)$, $\xi(m,n) = (m-n)h(m)$ and $\theta(m,n) = mg(m)$.

A similar discussion to Lemma 3.1 gives

From this we conclude that Equations (10)-(22) hold with $a = \mu = 0$. In the same way of Lemma 3.6, we see that $f,g,h$ must satisfy Table 2 with $a = \mu = 0$. This excludes Cases $\mathcal{W}_{4,a,\mu}^{\mathcal{P}^{c}_{3},k = 1}$ and $\mathcal{W}_{4,a,\mu}^{\mathcal{P}^{c}_{4},k = 1}$. Thus, $f$, $g$, $h$ must be of the $24$ cases listed in Table 2 with $a = \mu = 0$, which can yield the $24$ forms of $R$ one by one. It is easy to verify that every form of $R$ listed in the above is a Rota-Baxter operator of weight $1$ satisfying (51). The proof is completed.

4.2.   Remark on Rota-Baxter operators of weight zero and pre-Lie algebras

The natural question is: how we can characterize the Rota-Baxter operators of weight zero on the Schrödinger-Virasoro $\mathcal{S}$? This is related to the so called pre-Lie algebra which is a class of Lie-admissible algebras whose commutators are Lie algebras. Pre-Lie algebras appeared in many fields in mathematics and physics under different names like left-symmetric algebras, Vinberg algebras and quasi-associative algebras (see the survey article [3] and the references therein). Now we recall the definition of pre-Lie algebra as follows.

Definition 4.4. A pre-Lie algebra $A$ is a vector space $A$ with a bilinear product $\triangleright$ satisfying

As a parallel result of Lemma 4.2, one has the following conclusion.

Proposition 1. (see [8]) Let $(L,[\cdot, \cdot])$ be a Lie algebra with a Rota-Baxter operator $R$ of weight 0 on it. Define a new operation $x\triangleright y = [R(x),y]$ for any $x,y\in L$. Then $(L,\triangleright)$ is a pre-Lie algebra.

Using a similar method on classification of Rota-Baxter operators of weight $1$ in the above subsection, by Proposition 1 we can get the forms of Rota-Baxter operators of weight zero when the corresponding structure of pre-Lie algebra are known. For example, consider the homogeneous Rota-Baxter operator $R$ of weight zero on the Schrödinger-Virasoro algebra $\mathcal{S}$ satisfying (51). According to Proposition 1, if we define a new operation $x\triangleright y = [R(x),y]$ on $\mathcal{S}$, then ($\mathcal{S},\triangleright$) is a pre-Lie algebra. By (51), we have Equations (52)-(57) hold. At this point we can apply the relevant results on pre-Lie algebra satisfying (52)-(57). But the classification of graded pre-Lie algebra structures on $\mathcal{S}$ is also an unsolved problem, as far as we know. In fact, we can direct characterize the Rota-Baxter operators of weight zero on the Schrödinger-Virasoro $\mathcal{S}$ satisfying (51) following the approach of [6]. Due to limited space, it will not be discussed here.

Acknowledgments

We would like to express our sincere thanks to the anonymous referees for their careful reading and valuable comments towards the improvement of this article.