1. Introduction
Since the launch of lithium-ion batteries (LIBs) into the market in 1991 [1], LIBs have been widely used in portable electric devices owing to their higher power and energy density compared with other batteries. Recently, the application of LIBs has been expanded to hybrid electric vehicles (HEVs) and battery electric vehicles (BEVs), to exploit their high efficiency energy usage [2]. LIBs have been further proven to be useful in innovative technology, such as smart grids [3,4]. Thus, LIBs are one of the most important devices for a sustainable society. Given that rechargeable batteries, including LIBs, store and deliver electricity through chemical reactions, the batteries degrade with charge-discharge cycles and storage time [5]. The degradation of LIBs has been widely investigated; for anodes, formation of a solid electrolyte interphase (SEI) increases the internal resistance of LIBs [5,6] and metallic lithium deposition on the anode lowers their safety of LIBs [7]. For cathodes, surface film formation increases internal resistance [8,9] and dissolution of transition metal dissolution degrade their capacity [6]. Therefore, the diagnostic technology of LIBs is important, not only for research and development, but also for application in HEVs, BEVs, and smart grids.
Electrochemical impedance spectroscopy (EIS) is a powerful tool for in-situ measurement without having to disassemble the battery. It is also beneficial in that it can separate a complicated reaction process into elementary processes on the basis of the difference in time constants. Hence, the degraded part and degree in a LIB can be interpreted on the basis of the elementary processes by means of EIS. Therefore, EIS has been extensively applied in this field [6,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. However, because information acquired from both the cathode and anode is complex, it is still difficult for impedance analysis to evaluate LIBs accurately. In addition, the recent development of LIBs has made the impedance values smaller and the time constants for the processes closer, which have resulted in the overlapping of the impedance responses [23,24]. Therefore, the cathode and anode should be analyzed separately, before the impedance response of the whole LIB can be assessed. To separate the impedance response of LIBs, many researchers have adopted the approach to use a reference electrode such as lithium foil [25,26], LixAl micro wire [27], LiySn micro wire [28], Li4Ti5O12 or LiFePO4 [29] and lithiated bismuth [30]. However, although a reference electrode should be theoretically inserted between the cathode and anode [22], the insertion of a reference electrode between the cathode and anode may cause difficulties by disturbing the uniform current distribution between the electrodes. However, the impedance response, which is obtained by a reference electrode placed away from the middle of the electrodes, is strongly influenced by the potential gradient [31,32]. Therefore, the edges of cathode and anode must align completely, otherwise the potential gradient away from the opposing electrodes will vary during frequency sweep of input amplitude in impedance measurement.
To accurately determine the impedance of the cathode and anode, we developed a separable cell, which consisted of two electrode sheets that were 70 mm × 70 mm in size, which were compatible to configure a 5 Ah class pouch type LIB cell. The separable cell was mounted in electrode holders with an optional separation gap of electrodes, which enabled a change of electrodes between electrochemical measurements [33]. The possibility to measure an impedance accurately by using a symmetric cell has been explained by Chen et al. [34] and Aurbach et al. [35]. In our previous study [33], the impedance, which was obtained from the symmetric cell of LiCoO2 cathodes with an electrolyte composed of 1.0 mol/dm3 LiPF6 in a 1:1 mixture of ethylene carbonate (EC) and diethyl carbonate (DEC) (1 M LiPF6/EC-DEC) containing less than 20 ppm of H2O without any additives, obviously increased with storage time after the symmetric cell assembly from full cells, while that of graphite anodes did not change, as shown in Fig.2. The degradation of the LiCoO2 cathode was well-investigated by Aurbach et al. [9] by means of inductively coupled plasma mass spectrometry (ICP-MS), X-ray photoelectron spectroscopy, and EIS. According to the literature, the LiCoO2 cathode degrades on its surface rather than its bulk: on the surface, LiF, which is a product of the reaction between LiCoO2 and HF, was detected. However, the conclusion remained that “the presence of HF in solutions may play a major negative role” [9], while cobalt dissolution from LiCoO2 at high voltage was reported by Amatucci et al. [36].
Herein, we investigate the LiCoO2 cathode degradation at the relatively low potential of 3.7 V, which was detected by EIS using theseparable cell, and correlated that with Co dissolution by changing the electrolyte conditions which relates to HF generation.
2. Materials and Method
A full pouch-type LIB cell fabricated in a dry room maintained a dew point below −50 °C in the laboratory used in this work. The full LIB cell was composed of a LiCoO2 cathode with a capacity of 1.5 mA cm−2, and a carbon anode with a capacity of 1.6 mAh cm−2 with the electrode areas of 46.24 cm2 and 49.00 cm2 for cathode and anode, respectively, after being dried in a vacuum at 120 °C for 2 hours. The electrolyte used was 1 M LiPF6/EC-DECcontaining less than 20 ppm of H2O in a polyolefin separator without any additives.
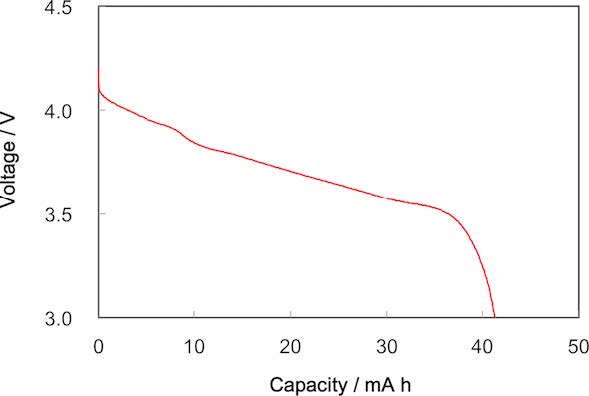
The pouch-type cells were charged and discharged in two initial cycles between 3.0 and 4.2 V at a rate of 0.1 C (7.0 mA) as the aging process to stabilize the cell performance, and were maintained at 4.2 V for 1 h at the end of each charge process before starting the electrochemical investigation or charge/discharge cycling test. All the pouch type cells exhibited an initial discharge capacity of 42 ± 1 mAh at the second cycle during the aging process as shown in Fig.1.
Symmetric cells, which contained two identical electrodes, were configured using two cathode sheets or two anode sheets for the investigation. The two sets of identical cathodes and identical anodes were prepared from two pouch-type cells, which were charged and discharged in pairs. For the EIS analysis of the symmetric cells, the cells were charged up to 3.7 V after the aging process and then EIS was performed.
When opening these two pouch-type cells, which were operated under the same conditions, the cathodes and anodes were taken out from the cell, and were removed from the separators used in the pouch-type cells. To configure the symmetric cells, a separable cell module [33] was used. This module enabled the handling of large electrode sheets, 68 mm × 68 mm for cathodes and 70 mm × 70 mm for anodes. Two sheets of cathodes were mounted to electrode holders that were designed to maintain the shape of the sheets with an electric conducting path from the current collector sheet to the outer lead. The electrode holders mounted with cathodes were faced towards each other with a spacer frame to maintain a 10 mm gap with sealing, and then fresh electrolyte solutions were poured to fill the space between the electrodes to complete the cathode symmetric cell. An anode symmetric cell was also formed in the same manner with two anode sheets obtained from the two whole LIB cells. The reassembling of the cells was performed in a dry Ar-filled glove box. In the present study, four electrolytes were used as the fresh electrolyte solutions, 1 M LiPF6/EC-DEC, 1 M LiClO4/EC-DEC, 1 M LiClO4/EC-DEC with 100 ppm of aqueous HF, and 1 M LiClO4/EC-DEC with 50 ppm of H2O.
The AC impedance spectra were obtained at the open circuit voltage with 20 mV (peak to peak) of an AC signal in the frequency range of 100 kHz to 10 mHz using a potentiostat system (VSP, Bio Logic, Claix, France) with elapsed time from assembly of the symmetric cells. All measurements were performed at room temperature. The impedance spectra are shown as a sum of two identical cathodes and two identical anodes, and all Nyquist plots are aligned with the intersections of the plots and x-axis by subtracting the resistances, which are generally related to the electrolyte solution, electric contacts, and wiring.
The Co concentration in the electrolyte solutions was analyzed by the ICP technique (ICP-MS, Agilent 7700, Agilent Technologies, Santa Clara, CA, United States). A small amount of the electrolyte solutions was extracted from the symmetric cells at each elapsed time from the assembly of the symmetric cells.
3. Results and Discussion
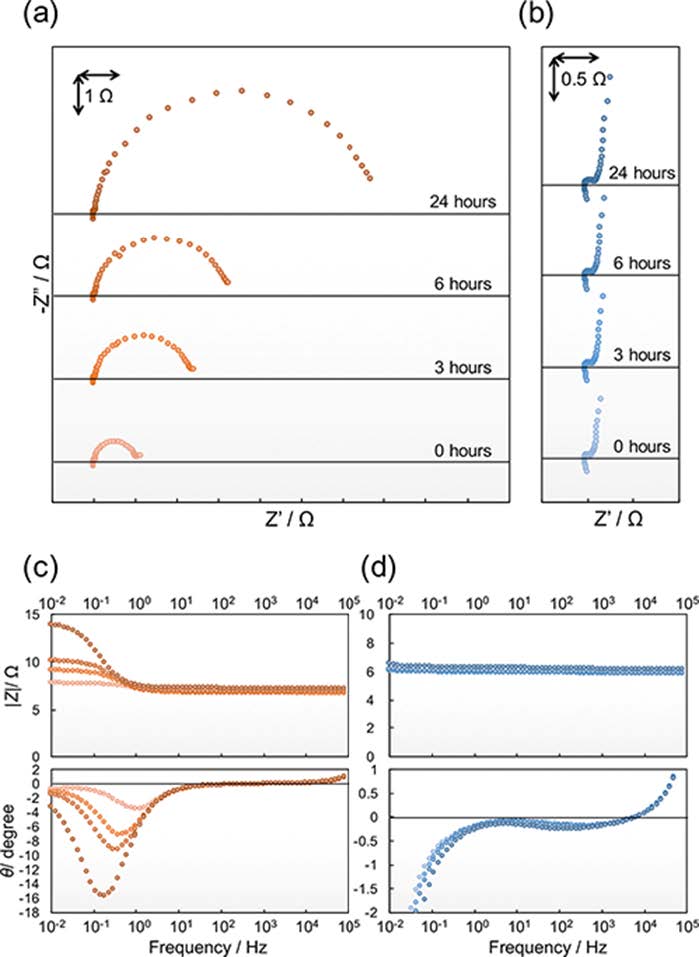
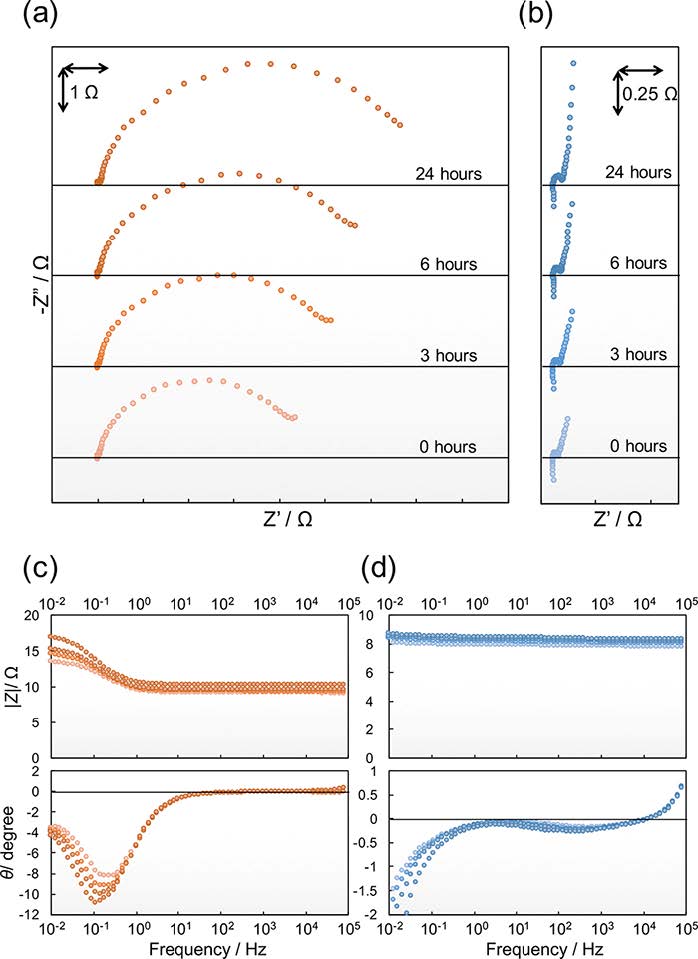
Figure 2 shows the Nyquist and Bode plots of the impedances obtained in 1 M LiPF6/EC-DEC with the elapsed time from assembly of the cathode and anode symmetric cells. The impedance response of the LiCoO2 cathode in the Nyquist plots has two semi-circles with characteristic frequencies observed at approximately 1 kHz and 1 Hz: the former semi-circle is difficult to be determined because of the very small impedance compared with the latter semi-circle and an inductive response at the high frequency region. In the literature, the two semicircles in the cathode were confirmed at a several kHz and a several Hz, which were attributed to lithium migration in the surface film and charge transfer, respectively [37]. As for the impedance of the LiCoO2 cathode, it is revealed that the charge transfer resistance obviously increased with the elapsed time. The increase rate of the charge transfer resistance after 3, 6, and 24 hours are roughly calculated to be 2.4, 3.4, and 7.0, respectively. However, the impedance response of the graphite anode in the Nyquist plots has two semi-circles overlapping whose characteristic frequency was observed at approximately 1 kHz. In our previous work, the overlapping semicircles in the anode contains at least two elemental processes, which are lithium migration in a solid electrolyte interphase (SEI) and charge transfer [38,39]. In contrast to the impedance of the LiCoO2 cathode, the graphite anode impedance with elapsed time was hardlyobserved at the frequency regions in which the lithium migration in a SEI and charge transfer occur. The increase of the LiCoO2 cathode impedance is in accordance with the previous study [9]. The previous study explained that the degradation of the LiCoO2 cathode may be the effect of HF that is generated from the reaction of LiPF6 and H2O as indicated in Eq. (1). Therefore, we selected LiClO4 as a lithium salt instead of LiPF6 to exclude the HF source.
|
PF6- + H2O → HF + PF5 + OH-
|
(1) |
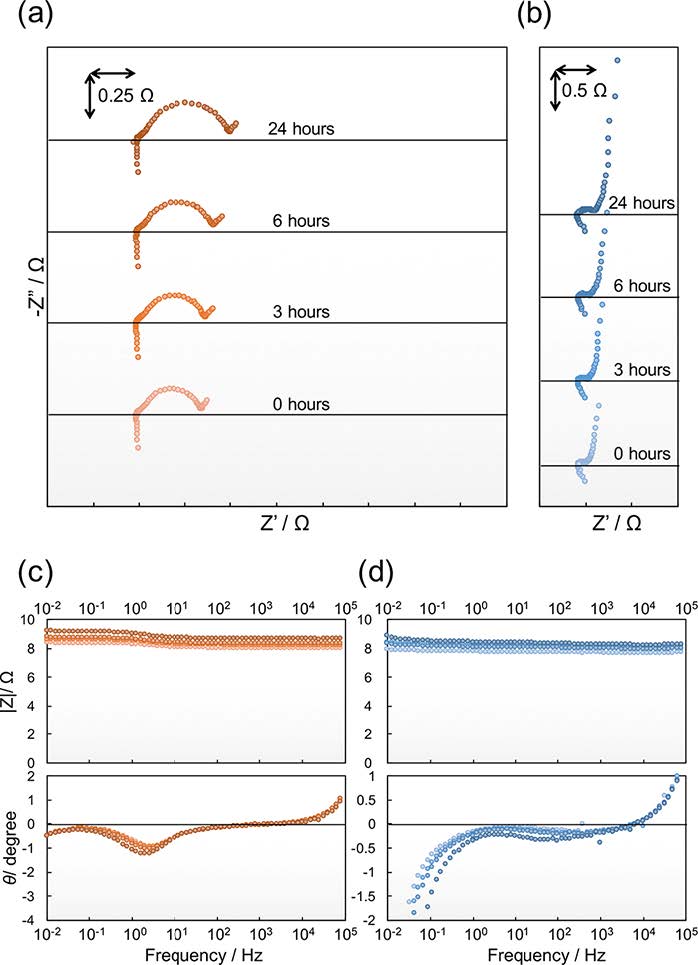
Figure 3 shows the Nyquist and Bode plots of the impedances obtained in 1 M LiClO4/EC-DEC with elapsed time from the assembly of cathode and anode symmetric cells. As was the case with 1 M LiPF6/EC-DEC, the impedance response of the LiCoO2 cathode in the Nyquist plots have two semi-circles whose maxima were observed at approximately 1 kHz and 1 Hz, and the impedance response of the graphite anode in the Nyquist plots have two semicircles overlapping whose maximum was observed at approximately 1 kHz. However, as for the impedance of the LiCoO2 cathode, an increase of the charge transfer resistance with the elapsed time was not confirmed, compared with the case of 1 M LiPF6/EC-DEC. The increase rate of the charge transfer resistance after 3, 6, and 24 hours were roughly calculated to be 1.1, 1.2, and 1.4, respectively. However, the impedance of the graphite anode was not changed at the frequency region in which the lithium migration in a SEI and the charge transfer occur, as was observed in the case of 1 M LiPF6/EC-DEC. Therefore, the difference between 1 M LiPF6/EC-DEC and 1 M LiClO4/EC-DEC for the charge transfer resistance of LiCoO2 is considered to be derived from the effect of HF, as was discussed by Aurbach et al. [9].
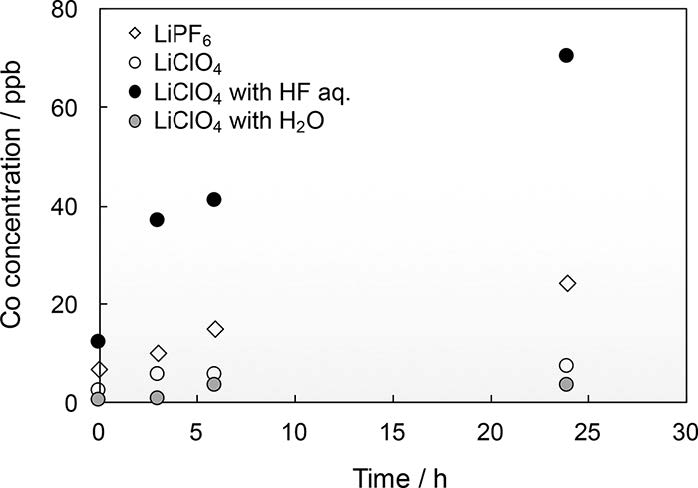
To confirm the effect of HF, we investigated the Co concentration in the electrolyte of the cathode symmetric cells by ICP-MS with the elapsed time. The cobalt concentration variation in the electrolyte of 1 M LiPF6/EC-DEC and 1 M LiClO4/EC-DEC with elapsed time is shown in Figure 4. The effect of HF is clearly confirmed to be responsible for the cobalt dissolution. The cobalt concentration in the electrolyte of 1 M LiPF6/EC-DEC increased with the elapsed time, whereas that of 1 M LiClO4/EC-DEC was approximately constant. The results suggest that the increase of the charge transfer resistance of LiCoO2 strongly relates to the cobalt dissolution by HF. In contrast, X-ray photon spectroscopy of the LiCoO2 cathode surfaces in 1 M LiPF6/EC-DEC and 1 M LiClO4/EC-DEC did not reveal any obvious difference (data not shown). Additionally, according to a paper by D. Aurbach et al. [9], the XRD patterns of LiCoO2 samples cycled or stored at 25 ºC were identical even though the samples possessed different impedances.
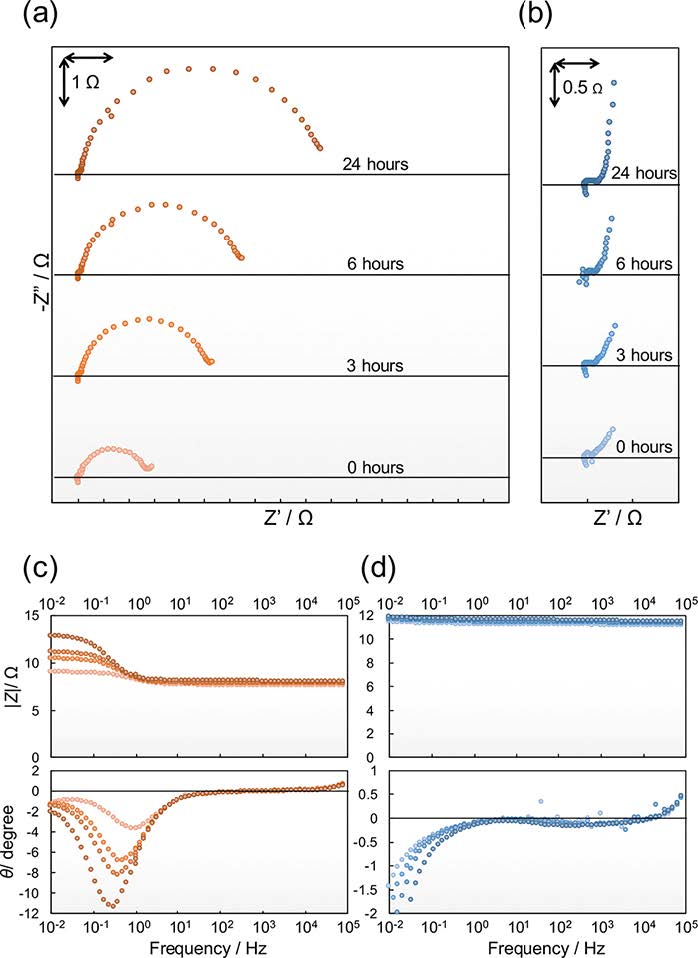
To establish the effect of HF, HF solution was added to the electrolyte of 1 M LiClO4/EC-DEC, in which there are no HF sources. Figure 5 shows the Nyquist and Bode plots of the impedances obtained in 1 M LiClO4/EC-DEC with 100 ppm of aqueous HF with elapsed time from the assembly of the cathode and anode symmetric cells. As was the case with 1 M LiPF6/EC-DEC, the impedance response of the LiCoO2 cathode in Nyquist plots has two semi-circles whose characteristic frequencies were observed at approximately 1 kHz and 1 Hz, and the impedance response of the graphite anode in Nyquist plots have two semi-circles overlapping whose characteristic frequency was observed at approximately 1 kHz. Additionally, as was observed for the impedance of the LiCoO2 cathode, the increase of the charge transfer resistance with the elapsed time was confirmed. The increase rate of the charge transfer resistance after 3, 6, and 24 hours are roughly calculated to be 2.0, 2.4, and 3.6, respectively. Additionally, the cobalt concentration variation in the electrolyte of 1 M LiClO4/EC-DEC with 100 ppm aqueous HF clearly shows the relationship with HF, as shown in Fig.4. The cobalt concentration in the 1 M LiClO4/EC-DECelectrolyte with 100 ppm aqueous HF increased with elapsed time. However, the impedance of the graphite anode was unchanged at the frequency region in which the lithium migration in a SEI and the charge transfer occur. The result confirms the effect of HF to increase the charge transfer resistance of LiCoO2. Here, one should consider the role of the water in the HF solution.
To eliminate a role of the water in the HF solution, distilled water was added to the 1 M LiClO4/EC-DEC electrolyte. Figure 6 shows the Nyquist and Bode plots of the impedances obtained in 1 M LiClO4/EC-DEC with 50 ppm H2O with elapsed time from the assembly of the cathode and anode symmetric cells. As was the case with 1 M LiPF6/EC-DEC and 1 M LiClO4/EC-DEC, the impedance response of the LiCoO2 cathode in the Nyquist plots has two semi-circles whose characteristic frequencies were observed at approximately 1 kHz and 1 Hz, and the impedance response of the graphite anode in the Nyquist plots has two semi-circles overlapping whose characteristic frequency was observed at approximately 1 kHz. As was the case with the 1 M LiClO4/EC-DEC electrolyte, the charge transfer resistance of LiCoO2 was approximately constant. The increase rate of the charge transfer resistance after 3, 6, and 24 hours are roughly calculated to be 1.2, 1.3, and 1.5, respectively. The increase rate of the charge transfer resistance of LiCoO2 in the 1 M LiClO4/EC-DEC electrolyte with H2O was almost the same as that in the 1 M LiClO4/EC-DEC electrolyte. The cobalt concentration in the 1 M LiClO4/EC-DEC electrolyte with H2O was nearly constant, as was the case with the 1 M LiClO4/EC-DEC electrolyte, as shown in Fig.4. Therefore, the result eliminates the suggestion that H2O may affect the increase of the charge transfer resistance of LiCoO2 and cobalt dissolution in the LiClO4 electrolyte system. However, as is the case with the electrolytes, the impedance of the graphite anode was unchanged at the frequency region in which the lithium migration in a SEI and the charge transfer occur.
The cobalt dissolution from the active material of LiCoO2 was reported under storage at a high voltage [36]. However, even under storage at a lower voltage, approximately 3.7 V, the cobalt dissolution arising from HF attack of LiCoO2 was observed, resulting in the increase of the charge transfer resistance of the LiCoO2 cathode.
4. Conclusion
We consider the problem that the charge transfer resistance of LiCoO2, with a potential of approximately 3.7 V, increased in the cathode symmetric cell, which we developed, with 1 M LiPF6/EC-DEC electrolyte. The reason why the charge transfer resistance increased was investigated by EIS and ICP-MS analyses with various electrolyte solutions, which were 1 M LiPF6/EC-DEC, 1 M LiClO4/EC-DEC, 1 M LiClO4/EC-DEC with 100 ppm of aqueous HF, and 1 M LiClO4/EC-DEC with 50 ppm of H2O. The increase of the charge transfer resistance of the LiCoO2 cathode was attributed to the cobalt dissolution from the active material of LiCoO2. The cobalt dissolution from LiCoO2 was revealed to occur even at low potentials in the presence of HF, which is generated from LiPF6 and H2O. The results indicate that avoidance of the HF generation is important for the analysis of LIB electrodes by using the separable cell. Therefore, the usability of the separable cell for the accurate analysis by means of EIS is enhanced.
Acknowledgments
This work was partly supported by the “Research & Development Initiative for Scientific Innovation of New Generation Batteries (RISING)” from the New Energy and Industrial Technology Development Organization (NEDO) of Japan.
Conflict of Interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: