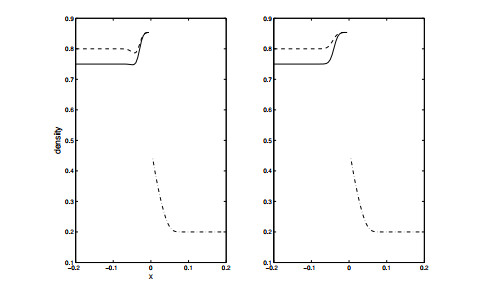
Example 1. Left panel:
Citation: Michael Sebastiano, Xiaolei Chu, Fikret Aydin, Leebyn Chong, Meenakshi Dutt. Interactions of Bio-Inspired Membranes with Peptides and Peptide-Mimetic Nanoparticles[J]. AIMS Materials Science, 2015, 2(3): 303-318. doi: 10.3934/matersci.2015.3.303
| [1] | John D. Towers . An explicit finite volume algorithm for vanishing viscosity solutions on a network. Networks and Heterogeneous Media, 2022, 17(1): 1-13. doi: 10.3934/nhm.2021021 |
| [2] | Boris Andreianov, Kenneth H. Karlsen, Nils H. Risebro . On vanishing viscosity approximation of conservation laws with discontinuous flux. Networks and Heterogeneous Media, 2010, 5(3): 617-633. doi: 10.3934/nhm.2010.5.617 |
| [3] | Giuseppe Maria Coclite, Carlotta Donadello . Vanishing viscosity on a star-shaped graph under general transmission conditions at the node. Networks and Heterogeneous Media, 2020, 15(2): 197-213. doi: 10.3934/nhm.2020009 |
| [4] | Markus Musch, Ulrik Skre Fjordholm, Nils Henrik Risebro . Well-posedness theory for nonlinear scalar conservation laws on networks. Networks and Heterogeneous Media, 2022, 17(1): 101-128. doi: 10.3934/nhm.2021025 |
| [5] |
Giuseppe Maria Coclite, Nicola De Nitti, Mauro Garavello, Francesca Marcellini .
Vanishing viscosity for a |
| [6] | Karoline Disser, Matthias Liero . On gradient structures for Markov chains and the passage to Wasserstein gradient flows. Networks and Heterogeneous Media, 2015, 10(2): 233-253. doi: 10.3934/nhm.2015.10.233 |
| [7] | Wen Shen . Traveling wave profiles for a Follow-the-Leader model for traffic flow with rough road condition. Networks and Heterogeneous Media, 2018, 13(3): 449-478. doi: 10.3934/nhm.2018020 |
| [8] | Giuseppe Maria Coclite, Lorenzo di Ruvo, Jan Ernest, Siddhartha Mishra . Convergence of vanishing capillarity approximations for scalar conservation laws with discontinuous fluxes. Networks and Heterogeneous Media, 2013, 8(4): 969-984. doi: 10.3934/nhm.2013.8.969 |
| [9] | Abraham Sylla . Influence of a slow moving vehicle on traffic: Well-posedness and approximation for a mildly nonlocal model. Networks and Heterogeneous Media, 2021, 16(2): 221-256. doi: 10.3934/nhm.2021005 |
| [10] | Christophe Chalons, Paola Goatin, Nicolas Seguin . General constrained conservation laws. Application to pedestrian flow modeling. Networks and Heterogeneous Media, 2013, 8(2): 433-463. doi: 10.3934/nhm.2013.8.433 |
This paper proposes an explicit finite volume scheme for first-order scalar conservation laws on a network having a single junction. The algorithm and analysis extend readily to networks with multiple junctions, due to the finite speed of propagation of the solutions of conservation laws. For the sake of concreteness, we view the setup as a model of traffic flow, with the vector of unknowns representing the vehicle density on each road. A number of such scalar models have been proposed, mostly differing in how the junction is modeled. An incomplete list of such models can be found in [4,5,6,7,8,11,12,13,14,15,16,18,19]. In this paper we focus on the so-called vanishing viscosity solution proposed and analyzed in [7] and [2]. The junction has
| $ ∂tuh+∂xfh(uh)=0,h=1,…,m+n. $ | (1.1) |
Incoming roads are indexed by
| $ ui∈L∞(R−×R+;[0,R]),i∈{1,…,m},uj∈L∞(R+×R+;[0,R]),j∈{m+1,…,m+n}. $ | (1.2) |
Following [2] we make the following assumptions concerning the fluxes
The study of vanishing viscosity solutions on a network was initiated by Coclite and Garavello [7], who proved that vanishing viscosity solutions converge to weak solutions if
For the convenience of the reader, and to establish notation, we review some relevant portions of the theory of network vanishing viscosity solutions, as described in [2], where we refer the reader for a more complete development. Let
| $ Gh(β,α)={minz∈[α,β]fh(z),α≤β,maxz∈[β,α]fh(z),β≤α. $ | (1.3) |
(Compared to [2], we list the arguments
| $ −Lh≤∂Gh(β,α)/∂β≤0,0≤∂Gh(β,α)/∂α≤Lh,h∈{1,…,m+n}. $ | (1.4) |
Definition 1.1 (Vanishing viscosity germ [2]). The vanishing viscosity germ
| $ m∑i=1Gi(p→u,ui)=m+n∑j=m+1Gj(uj,p→u),Gi(p→u,ui)=fi(ui),i=1,…,m,Gj(uj,p→u)=fj(uj),j=m+1,…,m+n. $ | (1.5) |
The definition of entropy solution requires one-sided traces along the half-line
| $ γiui(⋅)=ui(⋅,0−),i∈{1,…,m},γjuj(⋅)=uj(⋅,0+),j∈{m+1,…,m+n}. $ | (1.6) |
Definition 1.2 (
| $ qh(v,w)=sign(v−w)(fh(v)−fh(w)),h=1,…,m+n. $ | (1.7) |
Given an initial condition
● For each
| $ ∫R+∫Ωh(|uh−c|∂tξ+qh(uh,c)∂xξ)dxdt+∫Ωh|uh,0−c|ξ(x,0)dx≥0. $ | (1.8) |
● For a.e.
Associated with each
| $ kh(x)=kh,x∈Ωh,h∈{1,…,m+n}. $ | (1.9) |
It is readily verified that viewed in this way,
Definition 1.2 reveals the relationship between the set
Definition 1.3 (
● The first item of Definition 1.2 holds.
● For any
| $ m+n∑h=1(∫R+∫Ωh{|uh−kh|ξt+qh(uh,kh)ξx}dxdt)≥0 $ | (1.10) |
for any nonnegative test function
Theorem 1.4 (Well posedness [2]). Given any initial datum
| $ →u0=(u1,0,…,um+n,0)∈L∞(Γ;[0,R]m+n), $ | (1.11) |
there exists one and only one
In addition to the results above, reference [2] also includes a proof of existence of the associated Riemann problem. Based on the resulting Riemann solver, a Godunov finite volume algorithm is constructed in [2], which handles the interface in an implicit manner. This requires the solution of a single nonlinear equation at each time step. The resulting finite volume scheme generates approximations that are shown to converge to the unique
The main contribution of the present paper is an explicit version of the finite volume scheme of [2]. It differs only in the processing of the junction. We place an artificial grid point at the junction, which is assigned an artificial density. The artificial density is evolved from one time level to the next in an explicit manner. Thus a nonlinear equation solver is not required. (However, we found that in certain cases accuracy can be improved by processing the junction implicitly on the first time step.) Like the finite volume scheme of [2], the new algorithm has the order preservation property and is well-balanced. This makes it possible to employ the analytical framework of [2], resulting in a proof that the approximations converge to the unique entropy solution of the associated Cauchy problem.
In Section 2 we present our explicit finite volume scheme and prove convergence to a
For a fixed spatial mesh size
| $ xℓ=(ℓ+1/2)Δx,ℓ∈{…,−2,−1},xℓ=(ℓ−1/2)Δx,ℓ∈{1,2,…}. $ | (2.1) |
Each road
| $ Ωi=⋃ℓ≤−1Iℓ,Iℓ:=(xℓ−Δx/2,xℓ+Δx/2] for ℓ≤−1,Ωj=⋃ℓ≥1Iℓ,Iℓ:=[xℓ−Δx/2,xℓ+Δx/2) for ℓ≥1. $ | (2.2) |
Our discretization of the spatial domain
| $ Uh,sℓ≈uh(xℓ,ts),ℓ∈Z∖{0},Ps≈pγ→u(ts). $ | (2.3) |
We are somewhat artificially assigning a density, namely
Remark 1. We make the association
The initial data are initialized via
| $ Uh,0ℓ=1Δx∫Iℓuh,0(x)dx,h∈{1,…,m+n},P0∈[0,R]. $ | (2.4) |
Note that
| $ {Ps+1=Ps−λ(m+n∑j=m+1Gj(Uj,s1,Ps)−m∑i=1Gi(Ps,Ui,s−1)),Ui,s+1ℓ=Ui,sℓ−λ(Gi(Ui,sℓ+1,Ui,sℓ)−Gi(Ui,sℓ,Ui,sℓ−1)),i∈{1,…,m},ℓ≤−1,Uj,s+1ℓ=Uj,sℓ−λ(Gj(Uj,sℓ+1,Uj,sℓ)−Gj(Uj,sℓ,Uj,sℓ−1)),j∈{m+1,…,m+n},ℓ≥1. $ | (2.5) |
Define
| $ λ(m+n)L≤1. $ | (2.6) |
If all of the
| $ λmax(m,n)L≤1. $ | (2.7) |
Remark 2. The algorithm (2.5) is an explicit version of the scheme of [2]. To recover the scheme of [2] from (2.5), one proceeds as follows:
● first substitute
● then advance each
The equation mentioned above (after substituting
| $ m+n∑j=m+1Gj(Uj,s1,Ps)=m∑i=1Gi(Ps,Ui,s−1). $ | (2.8) |
The implicit portion of the scheme of [2] consists of solving (2.8) for the unknown
Remark 3. The convergence of the scheme (2.5) is unaffected by the choice of
| $ P0ν+1=P0ν−λ(m+n∑j=m+1Gj(Uj,01,P0ν)−m∑i=1Gi(P0ν,Ui,0−1)). $ | (2.9) |
Moreover, we found that this same fixed point iteration approach is a convenient way to solve (2.8) when implementing the implicit scheme of [2]. From this point of view the algorithm of this paper and the algorithm of [2] only differ in whether the first equation of (2.5) is iterated once, or iterated to (approximate) convergence. See Appendix A for a proof that the iterative scheme (2.9) converges to a solution of (2.8).
Remark 4. The CFL condition associated with the finite volume scheme of [2] is
| $ λL≤1/2. $ | (2.10) |
As soon as there are more than a few roads impinging on the junction, our CFL condition (2.6) imposes a more severe restriction on the allowable time step, which becomes increasingly restrictive as more roads are included. One could view this as the price to be paid for the simplified processing of the junction. On the other hand, most of the specific examples discussed in the literature are limited to
Let
| $ ui,Δ=∑s≥0∑ℓ≤−1χℓ(x)χs(t)Ui,sℓ,i∈{1,…,m},uj,Δ=∑s≥0∑ℓ≥1χℓ(x)χs(t)Uj,sℓ,j∈{m+1,…,m+n}. $ | (2.11) |
The discrete solution operator is denoted by
| $ SΔ→u0=(ui,Δ,…,um,Δ,um+1,Δ,…um+n,Δ). $ | (2.12) |
The symbol
| $ Γdiscr=({1,…,m}×{ℓ∈Z,ℓ≤−1})⋃({m+1,…,m+n}×{ℓ∈Z,ℓ≥1}), $ | (2.13) |
and with the notation
| $ Us=(Uh,sℓ)(h,l)∈Γdiscr, $ | (2.14) |
Remark 5. In the case where
Lemma 2.1. Fix a time level
Proof. For
Fix
| $ ∂Ui,s+1−1/∂Ui,s−2=λ∂Gi(Ui,s−1,Ui,s−2)/∂Ui,s−2,∂Ui,s+1−1/∂Ui,s0=−λ∂Gi(Ui,s0,Ui,s−1)/∂Ui,s0,∂Ui,s+1−1/∂Ui,s−1=1−λ∂Gi(Ui,s0,Ui,s−1)/∂Ui,s−1+λ∂Gi(Ui,s−1,Ui,s0)/∂Ui,s−1. $ | (2.15) |
That partial derivatives in the first two lines are nonnegative is a well-known property of the Godunov numerical flux. The partial derivative on the third line is nonnegative due to (1.4) and the CFL condition (2.6).
A similar calculation shows that the partial derivatives of
It remains to show that the partial derivatives of
| $ ∂Ps+1/∂Ui,s−1=λ∂Gi(Ps,Ui,s−1)/∂Ui,s−1,∂Ps+1/∂Uj,s1=−λ∂Gj(Uj,s1,Ps)/∂Uj,s1,∂Ps+1/∂Ps=1−λ(m+n∑j=m+1∂Gj(Uj,s1,Ps)/∂Ps−m∑i=1∂Gi(Ps,Ui,s−1)/∂Ps)≥1−λ(m+n∑j=m+1max(0,f′j(Ps))−m∑i=1min(0,f′i(Ps))). $ | (2.16) |
The first two partial derivatives are clearly nonnegative. For the third partial derivative we have used the following readily verified fact about the Godunov flux:
| $ min(0,f′h(β))≤∂Gh∂β(β,α)≤0≤∂Gh∂α(β,α)≤max(0,f′h(α)), $ | (2.17) |
and thus the third partial derivative is nonnegative due to (1.4) and the CFL condition (2.6).
Remark 6. If all of the fluxes
| $ ∂Ps+1/∂Ps≥1−λ(nmax(0,f′(Ps))−mmin(0,f′(Ps))), $ | (2.18) |
from which it is clear that
Lemma 2.2. Assuming that the initial data satisfies
Proof. The assertion is true for
| $ ˜Uhℓ=0,˜P=0,ˆUhℓ=R,ˆP=R. $ | (2.19) |
It is readily verified that
| $ ˜Uhℓ≤U0,hℓ≤ˆUhℓ,˜P≤P0≤ˆP. $ | (2.20) |
After an application of a single step of the finite volume scheme, these ordering relationships are preserved, as a result of Lemma 2.1. Since
| $ ˜Uhℓ≤U1,hℓ≤ˆUhℓ,˜P≤P1≤ˆP. $ | (2.21) |
This proves the assertion for
Given
| $ Khℓ={ki,ℓ<0 and h∈{1,…,m},kj,ℓ>0 and h∈{m+1,…,m+n}. $ | (2.22) |
and
Lemma 2.3. The finite volume scheme of Section 2 is well-balanced in the sense that each
Proof. For each fixed
Fix
| $ ki−λ(Gi(p→k,ki)−Gi(ki,ki))=ki−λ(fi(ki)−fi(ki))=ki. $ | (2.23) |
Here we have used the definition of
| $ p→k−λ(n∑j=m+1Gj(kj,p→k)−m∑i=1Gi(p→k,ki))=p→k, $ | (2.24) |
where we have applied the first equation of (1.5).
With the notation
| $ Qhℓ+1/2[Us,ˆUs]=Gh(Uh,sℓ+1∨ˆUh,sℓ+1,Uh,sℓ∨ˆUh,sℓ)−Gh(Uh,sℓ+1∧ˆUh,sℓ+1,Uh,sℓ∧ˆUh,sℓ). $ | (2.25) |
Lemma 2.4. Let
| $ m∑i=1ΔxΔt+∞∑s=1∑ℓ<0|Ui,sℓ−ˆUi,sℓ|(ξsℓ−ξs−1ℓ)/Δt+m∑i=1ΔxΔt+∞∑s=0∑ℓ≤0Qiℓ−1/2[Us,ˆUs](ξsℓ−ξsℓ−1)/Δx+m+n∑j=m+1ΔxΔt+∞∑s=1∑ℓ>0|Ui,sℓ−ˆUi,sℓ|(ξsℓ−ξs−1ℓ)/Δt+m+n∑j=m+1ΔxΔt+∞∑s=0∑ℓ≥0Qjℓ+1/2[Us,ˆUs](ξsℓ+1−ξsℓ)/Δx+ΔxΔt+∞∑s=1|Ps−ˆPs|(ξs0−ξs−10)/Δt≥0. $ | (2.26) |
Proof. From the monotonicity property (Lemma 2.1), a standard calculation [9] yields
| $ |Ui,s+1ℓ−ˆUi,s+1ℓ|≤|Ui,sℓ−ˆUi,sℓ|−λ(Qiℓ+1/2[Us,ˆUs]−Qiℓ−1/2[Us,ˆUs]),ℓ≤−1,i∈{1,…,m},|Uj,s+1ℓ−ˆUj,s+1ℓ|≤|Uj,sℓ−ˆUj,sℓ|−λ(Qjℓ+1/2[Us,ˆUs]−Qjℓ−1/2[Us,ˆUs]),ℓ≥1,j∈{m+1,…,m+n},|Ps+1−ˆPs+1|≤|Ps−ˆPs|−λ(m+n∑j=m+1Qj1/2[Us,ˆUs]−m∑i=1Qi−1/2[Us,ˆUs]). $ | (2.27) |
We first multiply each of the first and second set of inequalities indexed by
Lemma 2.5. Suppose that
Proof. The proof that the first condition of Definition 1.2 holds is a slight adaptation of a standard fact about monotone schemes for scalar conservation laws [9].
The proof is completed by verifying the second condition of Definition 1.2. Let
With Lemmas 2.1 through 2.5 in hand it is possible to repeat the proof of Theorem 3.3 of [2], which yields Theorem 2.6 below.
Theorem 2.6. For a given initial datum
We found that if
Initialization of
● Initialize
● Initialize
Example 1. This example demonstrates the appearance of a spurious bump when

Example 1. Left panel:
One can also get rid of the spurious bump by choosing
I thank two anonymous referees for their comments and suggestions.
In this appendix we prove that the fixed point iterations (2.9) converge to a solution of the equation (2.8). Let
| $ ui=Ui,s−1fori=1,…,m,uj=Uj,s1 for j=m+1,…,m+n. $ | (A.1) |
Then (2.8) takes the form
| $ Φout→u(p)=Φin→u(p), $ | (A.2) |
where
| $ Φin→u(p)=m∑i=1Gi(p,ui),Φout→u(p)=m+n∑j=m+1Gj(uj,p). $ | (A.3) |
This notation agrees with that of [2], where it was shown that
With the simplified notation introduced above, the iterative scheme (2.9) becomes
| $ pν+1=pν−λ(Φout→u(pν)−Φin→u(pν)),p0∈[0,R]. $ | (A.4) |
Proposition 1. The sequence
Proof. Note that
| $ 0≤Gi(0,ui),Gi(R,ui)=0,Gj(uj,0)=0,0≤Gj(uj,R). $ | (A.5) |
Thus,
| $ 0≤Φin→u(0),Φin→u(R)=0,Φout→u(0)=0,0≤Φout→u(R). $ | (A.6) |
Define
| $ Ψ→u(p)=Φout→u(p)−Φin→u(p), $ | (A.7) |
and observe that
| $ Ψ→u(0)≤0≤Ψ→u(R). $ | (A.8) |
Define
| $ Π(p)=p−λΨ→u(p). $ | (A.9) |
| $ Π′(p)=1−λΨ′→u(p)≥1−λ(m+n)L. $ | (A.10) |
Thanks to (A.10) and the CFL condition (2.6), it is clear that
| $ 0≤Π(0)≤Π(p)≤Π(R)≤R for p∈[0,R]. $ | (A.11) |
Thus
| $ pν+1=Π(pν),p0∈[0,R]. $ | (A.12) |
We can now prove convergence of the sequence
Now consider the case where
| $ pν+1−pν=Π(pν)−Π(pν−1)=Π(pν)−Π(pν−1)pν−pν−1(pν−pν−1). $ | (A.13) |
Since
| $ sign(pν+1−pν)=sign(pν−pν−1)=…=sign(p1−p0). $ | (A.14) |
In other words, the sequence
| [1] | Alberts B, Johnson A, Lewis J, et al. (2007) Molecular Biology of the Cell, Garland Science: New York. |
| [2] | Brannigan G, Brown FLH (2005) Composition Dependence of Bilayer Elasticity. J Chem Phys 122: 07490. |
| [3] | Shillcock JC, Lipowsky R (2002) Equilibrium structure and lateral stress distribution of amphiphilic bilayers from dissipative particle dynamics simulations. J Chem Phys 117: 5048-5061. |
| [4] | Lipowsky R, Sackmann E (1995) Structure and dynamics of membranes, Handbook of biological physics, Elsevier, Amsterdam. |
| [5] | Petelska AD, Figaszewski ZA (2002) Effect of pH on the Interfacial Tension of Lipid Bilayer Membrane. Biophys J 1561:135-146. |
| [6] |
Cooke IR, Kremer K, Deserno M (2005) Tunable Generic Model for Fluid Bilayer Membranes. Phys Rev E 72: 011506. doi: 10.1103/PhysRevE.72.011506

|
| [7] |
Laradji M, Kumar PBS (2004) Dynamics of Domain Growth in Self-assembled Fluid Vesicles. Phys Rev Lett 93: 198105. doi: 10.1103/PhysRevLett.93.198105

|
| [8] |
Laradji M, Kumar PBS (2005) Domain Growth, Budding, and Fission in Phase Separating Self-assembled Fluid Bilayers. J Chem Phys 123: 224902. doi: 10.1063/1.2102894

|
| [9] |
Ramachandran S, Laradji M, Kumar PBS (2009) Lateral Organization of Lipids in Multi-component Liposomes. J Phys Soc Jpn 78: 041006. doi: 10.1143/JPSJ.78.041006

|
| [10] |
Taniguchi T (1996) Shape Deformation and Phase Separation Dynamics of Two-component Vesicles. Phys Rev Lett 76: 4444-4447. doi: 10.1103/PhysRevLett.76.4444

|
| [11] | Fan J, Han T, Haataja M (2010) Hydrodynamic Effects on Spinodal Decomposition Kinetics in Planar Lipid Bilayer Membranes. J Chem Phys 133: 235101. |
| [12] |
Stanich CA, Honerkamp-Smith AR, Putzel GG, et al. (2013) Coarsening Dynamics of Domains in Lipid Membranes. Biophys J 105: 444-454. doi: 10.1016/j.bpj.2013.06.013

|
| [13] |
Veatch SL, Keller SL (2003) Separation of Liquid Phases in Giant Vesicles of Ternary Mixtures of Phospholipids and Cholesterol. Biophys J 85:3074-3083. doi: 10.1016/S0006-3495(03)74726-2

|
| [14] |
Esposito C, Tian A, Melamed S, et al. (2007) Flicker Spectroscopy of Thermal Lipid Bilayer Domain Boundary Fluctuations. Biophys J 93: 3169-3181. doi: 10.1529/biophysj.107.111922

|
| [15] | Lipowsky R (1992) Budding of Membranes Induced by Intramembrane Domains. J Phys II 2: 1825. |
| [16] |
Bagatolli LA, Gratton E (2001) Direct Observation of Lipid Domains in Free Standing Bilayers Using Two-photon Excitation Fluorescence Microscopy. J Fluorescence 11: 141-160. doi: 10.1023/A:1012228631693

|
| [17] |
Ramachandran S, Komura S, Gommper G (2010) Effects of an Embedding Bulk Fluid on Phase Separation Dynamics in a Thin Liquid Film. EPL 89: 56001. doi: 10.1209/0295-5075/89/56001

|
| [18] |
Ursell TS, Klug WS, Phillips R (2009) Morphology and Interaction between Lipid Domains. Proc Natl Acad Sci U S A 106: 13301. doi: 10.1073/pnas.0903825106

|
| [19] |
Bagatolli L, Kumar PBS (2009) Phase Behavior of Multicomponent Membranes: Experimental and Compuatational Techniques. Soft Matter 5: 3234-3248. doi: 10.1039/b901866b

|
| [20] | Marrink SJ, de Vries AH, Tieleman DP (2009) Lipids on the Move: Simulations of Membrane Pores, Domains, Stalks and Curves. Biochim Biophys Acta Biomembr 1788: 149-168. |
| [21] |
Lipowsky R (2002) Domains and Rafts in Membranes—Hidden Dimensions of Selforganization. J Biol Phys 28: 195-210. doi: 10.1023/A:1019994628793

|
| [22] | Simons K, Vaz WLC (2004) Model Systems, Lipid Rafts, and Cell Membranes. Annu Rev Biophys Biomol Struct 3: 269. |
| [23] |
Barberousse A, Franceschelli S, Imbert C (2009) Computer Simulations as Experiments. Synthese 169: 557-574. doi: 10.1007/s11229-008-9430-7

|
| [24] | Farago O (2003) “Water-free” Computer Model for Fluid Bilayer Membranes. O J Chem Phys 119: 596-605. |
| [25] |
Brannigan G, Brown FLH (2004) Solvent-free Simulations of Fluid Membrane Bilayers. J Chem Phys 120: 1059. doi: 10.1063/1.1625913

|
| [26] | Shillcock JC (2012) Spontaneous Vesicle Self-Assembly: A Mesoscopic View of Membrane Dynamics. Langmuir 28: 541-547. |
| [27] | Tieleman DP, Leontiadau H, Mark AE, et al. (2003) Simulation of Pore Formation in Lipid Bilayers by Mechanical Stress and Electric Fields. J Am Chem Soc125: 6382-6383. |
| [28] |
Damodaran KV, Merz KM (1994) A Comparison of DMPC- and DLPE-based Lipid Bilayers. Biophys J 66: 1076-1087. doi: 10.1016/S0006-3495(94)80889-6

|
| [29] |
Moore PB, Lopez CF, Klein ML (2001) Dynamical Properties of a Hydrated Lipid Bilayer from a Multinanosecond Molecular Dynamics Simulation. Biophys J 81: 2484-2494. doi: 10.1016/S0006-3495(01)75894-8

|
| [30] |
Essmann U, Perera L, Berkowitz ML (1995) The Origin of the Hydration Interaction of Lipid Bilayers from MD Simulation of Dipalmitoylphosphatidylcholine Membranes in Gel and Liquid Crystalline Phases. Langmuir 11: 4519-4531. doi: 10.1021/la00011a056

|
| [31] |
Cooke IR, Deserno M (2005) Solvent-free Model for Self-assembling Fluid Bilayer Membranes: Stabilization of the Fluid Phase based on Broad Attractive Tail Potentials. J Chem Phys 123: 224710. doi: 10.1063/1.2135785

|
| [32] |
West B, Schmid F (2010) Fluctuations and Elastic Properties of Lipid Membranes in the Gel L-beta State: A Coarse-grained Monte Carlo Study. Soft Matter 6: 1275. doi: 10.1039/b920978f

|
| [33] |
Farago O (2008) Mode Excitation Monte Carlo Simulations of Mesoscopically Large Membranes. J Chem Phys 128: 184105. doi: 10.1063/1.2918736

|
| [34] |
Farago O (2010) Fluctuation-induced Attraction between Adhesion Sites of Supported Membranes. Phys Rev E 81: 050902. doi: 10.1103/PhysRevE.81.050902

|
| [35] |
Farago O (2008) Membrane Fluctuations near a Plane Rigid Surface. Phys Rev E 78:051919. doi: 10.1103/PhysRevE.78.051919

|
| [36] | Dutt M, Nayhouse MJ, Kuksenok O, et al. (2011) Interactions of End-Functionalized Nanotubes with Lipid Vesicles: Spontaneous Insertion and Nanotube Self-organization. Current Nanoscience 7: 699-715. |
| [37] |
Dutt M, Kuksenok O, Nayhouse MJ, et al. (2011) Modeling the Self-Assembly of Lipids and Nanotubes in Solution: Forming Vesicles and Bicelles with Transmembrane Nanotube Channels. ACS Nano 5: 4769-4782. doi: 10.1021/nn201260r

|
| [38] |
Dutt M, Kuksenok O, Little SR, et al. (2011) Forming Transmembrane Channels Using End-Functionalized Nanotubes. Nanoscale. 3: 240-250. doi: 10.1039/C0NR00578A

|
| [39] | Dutt M, Kuksenok O, Little SR, et al. (2012) Designing Tunable Bio-nanostructured Materials via Self-assembly of Amphiphilic Lipids and Functionalized Nanotubes. MRS Spring 2012 Conference Proceedings; 1464. |
| [40] | Ludford P, Aydin F, Dutt M (2013) Design and Characterization of Nanostructured Biomaterials via the Self-assembly of Lipids. MRS Fall 2013 Conference Proceedings; 1498. |
| [41] | Koufos E, Dutt M (2013) Design of Nanostructured Hybrid Inorganic-biological Materials via Self-assembly. MRS Spring 2013 Conference Proceedings; 1569. |
| [42] |
Smith KA, Jasnow D, Balazs AC (2007) Designing Synthetic Vesicles that Engulf Nanoscopic Particles. J Chem Phys 127: 084703. doi: 10.1063/1.2766953

|
| [43] | Goetz R, Lipowsky R (1998) Computer Simulations of Bilayer Membranes: Self-assembly and Interfacial Tension. J Chem Phys 108: 7397-7409. |
| [44] | Kranenburg M, Venturoli M, Smit B. (2003) Phase Behavior and Induced Interdigitation in Bilayers Studied with Dissipative Particle Dynamics. J Phys Chem 41: 11491. |
| [45] |
Kranenburg M, Laforge C, Smit B (2004) Mesoscopic Simulations of Phase Transitions in Lipid Bilayers. Phys Chem Chem Phys 6: 4531-4534. doi: 10.1039/b410914g

|
| [46] | Yamamoto S, Maruyama Y, Hyodo S (2002) Dissipative Particle Dynamics Study of Spontaneous Vesicle Formation of Amphiphilic Molecules. J Chem Phys 116: 5842. |
| [47] |
Yamamoto S, Hyodo S (2003) Budding and Fission Dynamics of Two-Component Vesicles. J Chem Phys 118: 7937-7943. doi: 10.1063/1.1563613

|
| [48] |
Stevens MJ, Hoh JH, Woolf TB (2003) Insights into the Molecular Mechanism of Membrane Fusion from Simulation: Evidence for the Association of Splayed Tails. Phys Rev Lett 91: 188102. doi: 10.1103/PhysRevLett.91.188102

|
| [49] | Stevens MJ (2004) Coarse-grained Simulations of Lipid Bilayers. Chem Phys 121: 11942-11948. |
| [50] | Arkhipov A, Yin Y, Schulten K (2009) Membrane-bending Mechanism of Amphiphysin N-BAR Domains. Biophys J 97: 2727-2735. |
| [51] |
Shih AY, Arkhipov A, Freddolino PL, et al. (2006) A Coarse-grained Protein-lipid Model with Application to Lipoprotein Particles. J Phys Chem 110: 3674-3684. doi: 10.1021/jp0550816

|
| [52] |
Marrink SJ, Risselada HJ, Yefimov S, et al. (2007) The MARTINI Forcefield: Coarse-grained Model for Biomolecular Simulations. J Phys Chem B 111: 7812-7824. doi: 10.1021/jp071097f

|
| [53] | Wang Z, Frenkel DJ (2005) Modeling Flexible Amphiphilic Bilayers: A Solvent-free Off-lattice Monte Carlo Study. Chem Phys 122: 234711. |
| [54] |
Brannigan G, Philips PF, Brown FLH (2005) Flexible Lipid Bilayers in Implicit Solvent. Phys Rev E 72: 011915. doi: 10.1103/PhysRevE.72.011915

|
| [55] |
Noguchi H, Takasu M (2001) Self-assembly of Amphiphiles into Vesicles: A Brownian Dynamics Simulation. Phys Rev E 64: 041913. doi: 10.1103/PhysRevE.64.041913

|
| [56] |
Noguchi H (2002) Fusion and Toroidal Formation of Vesicles by Mechanical Forces: A Brownian Dynamics Simulation. J Chem Phys 117: 8130-8137. doi: 10.1063/1.1510114

|
| [57] |
Katsov K, Mueller M, Schick M (2004) Field Theoretic Study of Bilayer Membrane Fusion I Hemifusion Mechanism. Biophys J 87: 3277. doi: 10.1529/biophysj.103.038943

|
| [58] | Schick M (2012) Membranes: A Field-theoretic Description. Encyclopedia of Biophysics. Roberts, G.C.K., Ed., Springer-Verlag: Berlin Heidelberg. |
| [59] |
May S, Kozlovsky Y, Ben-Shaul A, et al. (2004) Tilt Modulus of a Lipid Monolayer. Eur Phys J E 14: 299-308. doi: 10.1140/epje/i2004-10019-y

|
| [60] |
May S (2000) A Molecular Model for the Line Tension of Lipid Membranes. Eur Phys J E 3: 37-44. doi: 10.1007/s101890070039

|
| [61] |
Lee WB, Mezzenga R, Fredrickson GH (2008) Self-consistent Field Theory for Lipid-based Liquid Crystals: Hydrogen Bonding Effect. J Chem Phys 128: 074504-074510. doi: 10.1063/1.2838624

|
| [62] | Ginzburg VV, Balijepalli S (2007) Modelling the Thermodynamics of the Interaction of Nanoparticles with Cell Membranes. Nano Lett 7: 3716-3722. |
| [63] |
Ayton G, Voth GA (2002) Bridging Microscopic and Mesoscopic Simulations of Lipid Bilayers. Biophys J 83: 3357-3370. doi: 10.1016/S0006-3495(02)75336-8

|
| [64] |
Wang ZJ, Deserno MA (2010) Systematically Coarse-grained Solvent-free Model for Quantitative Phospholipid Bilayer Simulations. J Phys Chem B 114: 11207. doi: 10.1021/jp102543j

|
| [65] |
Wang ZJ, Deserno M (2010) Systematic Implicit Solvent Coarse-graining of Bilayer Membranes: Lipid and Phase Transferability of the Force Field. New J Phys 12: 095004. doi: 10.1088/1367-2630/12/9/095004

|
| [66] |
Ge Z, Li Q, Wang Y (2014) Free energy Calculation of Nanodiamond-Membrane Association—The Effect of Shape and Surface Functionalization. J Chem Theory Comput 10: 2751-2758. doi: 10.1021/ct500194s

|
| [67] | Reid CVL, Ricci M, Silva PHJ, et al. (2014) Lipid tail protrusions mediate the insertion of nanoparticles into model cell membranes. Nat Commun 5: 4482. |
| [68] |
Wong-Ekkabut J, Baoukina S, Triampo W, et al. (2008) Computer simulation study of fullerene translocation through lipid membranes. Nat Nanotechnol 3: 363-368. doi: 10.1038/nnano.2008.130

|
| [69] |
Li Y, Chen X, Gu N (2008) Computational Investigation of Interaction between Nanoparticles and Membranes: Hydrophobic/Hydrophilic Effect. J Phys Chem B 112: 16647-16653. doi: 10.1021/jp8051906

|
| [70] |
Huang C, Zhang Y, Yuan H, et al. (2013) Role of Nanoparticle Geometry in Endocytosis: Laying Down to Stand Up. Nano Lett 13: 4546-4550. doi: 10.1021/nl402628n

|
| [71] |
Shi X, Bussche AVD, Hurt RH, et al. (2011) Cell entry of one-dimensional nanomaterials occurs by tip recognition and rotation. Nat Nanotechnol 6: 714-719. doi: 10.1038/nnano.2011.151

|
| [72] |
Illya G, Lipowsky R, Shillcock JC (2006) Two-component membrane material properties and domain formation from dissipative particle dynamics. J Chem Phys 125: 114710. doi: 10.1063/1.2353114

|
| [73] |
Groot RD, Warren PB (1997) Dissipative Particle Dynamics: Bridging the gap between atomistic and mesoscopic simulation. J Chem Phys 107: 4423-4435. doi: 10.1063/1.474784

|
| [74] |
Chou H, Tsao HK, Sheng YJ (2006) Morphologies of multicompartment micelles formed by triblock copolymers. J Chem Phys 125: 194903. doi: 10.1063/1.2390716

|
| [75] |
Ortiz V, Nielsen SO, Discher DE, et al. (2005) Disipative Particle Dyanmics simulations of polymerosome. J Phys Chem B 109: 17708-17714. doi: 10.1021/jp0512762

|
| [76] | Boek ES, Coveney PV, Lekkerkerker HNW, et al. (1997) Simulating rheology of dense colloidal suspensions using dissipative particle dynamics. Phys Rev E 55: 3124-3131. |
| [77] | Spenley NA (200) Scaling laws for polymers in dissipative particle dynamics, Europhys Lett 49: 534-540. |
| [78] |
Fan XJ, Phan-Thien N, Chen S, et al. (2006) Simulating flow of DNA suspension using dissipative particle dynamics. Phys Fluids 18: 063102. doi: 10.1063/1.2206595

|
| [79] |
Chem S, Phan-Thien N, Fan XJ, et al. (2004) Dissipative particle dynamics of polymer drops in periodic shear flow. J Non-Newtonian Fluid Mech 118: 65-81. doi: 10.1016/j.jnnfm.2004.02.005

|
| [80] |
Arai N, Yasuoka K, Zeng XC (2013) A vesicle cell under collision with a Janus or homogeneous nanoparticle: translocation dynamics and late-stage morphology. Nanoscale 5: 9089-9100. doi: 10.1039/c3nr02024j

|
| [81] |
Yang K, Ma Y (2010) Computer simulation of the translocation of nanoparticles with different shapes across a lipid bilayer. Nat Nanotechnol 5: 579-583. doi: 10.1038/nnano.2010.141

|
| [82] |
Ding H, Tian W, Ma Y (2012) Designing Nanoparticle Translocation through Membranes by Computer Simulations. ACS Nano 6: 1230-1238. doi: 10.1021/nn2038862

|
| [83] |
Chen X, Tian F, Zhang X, et al. (2013) Internalization pathways of nanoparticles and their interaction with a vesicle. Soft Matter 9: 7592-7600. doi: 10.1039/c3sm50931a

|
| [84] |
Arnarez C, Uusitalo JJ, Masman MF, et al. (2015) Dry Martini, a Coarse-Grained Force Field for Lipid Membrane Simulations with Implicit Solvent. J Chem Theory Comput 11: 260-275. doi: 10.1021/ct500477k

|
| [85] | Hall BA, Chetwynd AP, Sansom MSP (2011) Exploring Peptide-Membrane Interactions with Coarse-Grained MD Simulations. Biophys J 100: 1940-1948. |
| [86] |
Gkeka P, Sarkisov L (2010). Interactions of Phospholipid Bilayers with Several Classes of Amphiphilic α-Helical Peptides: Insights from Coarse-Grained Molecular Dynamics Simulations. J Phys Chem B 114: 826-839. doi: 10.1021/jp908320b

|
| [87] | Allen MP, Tildesley DJ (2001) Computer simulations of liquids, Clarendon Press, Oxford. |
| [88] |
Koufos E, Muralidharan B, Dutt M (2014) Computational Design of Multi-component Bio-Inspired Bilayer. AIMS Materials Science 1: 103-120. doi: 10.3934/matersci.2014.2.103

|
| [89] |
Milletti F (2012) Cell-Penetrating Peptides: Classes, Origin, and Current Landscape. Drug Discov Today 17: 850-860. doi: 10.1016/j.drudis.2012.03.002

|
| [90] |
Aydin F, Ludford P, Dutt M (2014) Phase segregation in bio-inspired multi-component vesicles encompassing double tail phospholipid species. Soft Matter 10: 6096-6108. doi: 10.1039/C4SM00998C

|
| [91] |
Aydin F, Uppaladadium G, Dutt M (2015) The Design of Shape-Tunable Hairy Vesicles. Colloids Surf B Biointerfaces 128: 268-275. doi: 10.1016/j.colsurfb.2015.01.049

|
| [92] |
Monticelli L, Kandasamy SK, Periole X, et al. (2008) The MARTINI Coarse-Grained Force Field: Extension to Proteins. J Chem Theory Comput 4: 819-834. doi: 10.1021/ct700324x

|
| [93] |
Feller SE, Pastor RW (1999) Constant surface tension simulations of lipid bilayers: The sensitivity of surface areas and compressibilities. J Chem Phys 111: 1281-1287. doi: 10.1063/1.479313

|
| 1. | Nicola De Nitti, Enrique Zuazua, On the Controllability of Entropy Solutions of Scalar Conservation Laws at a Junction via Lyapunov Methods, 2023, 51, 2305-221X, 71, 10.1007/s10013-022-00598-9 | |
| 2. | Michael Herty, Niklas Kolbe, Siegfried Müller, Central schemes for networked scalar conservation laws, 2022, 18, 1556-1801, 310, 10.3934/nhm.2023012 | |
| 3. | Markus Musch, Ulrik Skre Fjordholm, Nils Henrik Risebro, Well-posedness theory for nonlinear scalar conservation laws on networks, 2022, 17, 1556-1801, 101, 10.3934/nhm.2021025 | |
| 4. | Michael Herty, Niklas Kolbe, Siegfried Müller, A Central Scheme for Two Coupled Hyperbolic Systems, 2024, 6, 2096-6385, 2093, 10.1007/s42967-023-00306-5 | |
| 5. | Dilip Sarkar, Shridhar Kumar, Pratibhamoy Das, Higinio Ramos, Higher-order convergence analysis for interior and boundary layers in a semi-linear reaction-diffusion system networked by a $ k $-star graph with non-smooth source terms, 2024, 19, 1556-1801, 1085, 10.3934/nhm.2024048 | |
| 6. | Sabrina F. Pellegrino, A filtered Chebyshev spectral method for conservation laws on network, 2023, 151, 08981221, 418, 10.1016/j.camwa.2023.10.017 |