1.
Introduction
Brucellosis, a zoonotic disease, is a natural epidemic disease that is not only prevalent among livestock and humans but also widely spread in wild animals [1,2]. There are human and animal brucellosis in most countries of the world, and high-risk areas of epidemics are mainly distributed in developing countries, such as Syria, Jordan, Zambia, Mongolia [3,4,5,6]. It has brought huge losses to the livestock industry worldwide and serious health problems to livestock-related practitioners, there are hundreds of thousands of new cases reported annually [6,7,8]. Infected domestic and wild animals and their excreta are the main source of infection, it is contact and pathogen infection which are the main modes of brucellosis transmission [9]. Human brucellosis is rarely transmitted to susceptible animals, and there is no infection between people reported [10,11]. Therefore, it is the eradication of animal brucellosis that is the only way to solving human health problem, and understanding the mechanisms and risk factors of the spread of brucellosis is one of the first problems that must be solved.
Brucellosis is transmitted to susceptible individuals mainly by contact with infectious individuals or by sucking pathogens from the environment [8]. In animals, the transmission of brucellosis mainly occurs between sexually mature animals, young animals may also be infected, but generally do not have any clinical manifestations and serological tests are usually non-positive, and the infection between young animals is so little as to be almost invisible [12]. In other words, sexually mature animals are very susceptible to brucellosis, latent infections may be found in young animals, but they are generally resistant [9]. It is important that many infected animals have a longer incubation period and that these animals remain serologically non-positive during this period. That is to say, latent animals may not be infectious and it is almost impossible to be found through detection, which is an important risk factor in the elimination of brucellosis [9]. Therefore, the impact of these mechanisms on brucellosis is worthy to be studied using mathematical models.
Statistical methods such as descriptive statistics, correlation analysis and time series analysis have been widely used for quantitative assessment of risk management measures for brucellosis, among which is very worthy of concern about the study of bison, elk and livestock brucellosis (see [13,14,15,16,17]). Theoretical studies on the impacts of the transmission mechanisms of brucellosis and applied studies on the assessments of risk management measures have also been studied using the kinetic model (see [18,19,20,21,22]). Especially in recent years, many kinetic models with indirect transmission have been established to analyze brucellosis transmission (see [23,24,25,26,27]). Although there have been many studies on brucellosis, there are still many transmission mechanisms and risk factors that are not considered in existing models. For example, infected individuals may have no infectivity in the early stage, during which time is different; and animals that are not sexually mature are hardly infected with direct and indirect modes [9]. Therefore, in the present work, a multi-stage dynamic model with distributed time delay is proposed involving the above risk factors and general nonlinear incidences. The existence and uniqueness of the endemic equilibrium is analyzed, and the local and global asymptotic stability of equilibria is proved.
The rest of this manuscript is constructed as follows. The dynamic model with distributed time delay and some preliminary results are given in Section 2. In Section 3, the content of research is the global dynamics of the disease-free equilibrium. The global stability of the equilibrium of persistent infection are analyzed in Section 4. In Section 5, the stability results are further explained by numerical simulation. A summary and further discussion is proposed in Section 6.
2.
The model and preliminary results
According to the transmission mechanisms of animal brucellosis, we classify animal population into three compartments: The young susceptible compartment $ S_1(t) $, the adult susceptible compartment $ S_2(t) $ (sexually mature), the infected compartment $ I(t) $. Similar to the definition in literature [25], $ B(t) $ can be defined as the concentration or number of pathogens in the environment. Some explanations and assumptions about the kinetic model are listed as follows. (Ⅰ) Since brucellosis can cause abortion and significantly reduce the survival rate of young animals, we suppose that infected animals have no birth rate. (Ⅱ) The supplementary rate of young susceptible animal population $ S_1(t) $ is mainly derived from birth and import, it is assumed that the supplementary rate is $ A+bS_2(t) $. (Ⅲ) Usually, there are two different stages for infected animals, which are no infection force in the early stage and are infectious carriers when infected animals begin to shed brucella. Therefore, we make use of a delay $ \tau $ to describe the time from a susceptible individual to a infectious individual, and since the length of this time is varied, thus the delay $ \tau $ is a distributed parameter in the interval $ [0, h] $, where $ h $ is the maximum value of the delay. As a result, the susceptible class $ S_2(t) $ is reduced due to infection at the rate $ S_2 g(B)+S_2\int_0^{h} \rho(\tau)f(I(t-\tau))e^{-(\mu_2+c)\tau}d\tau $. (Ⅳ) Since the infected animal sheds the pathogen after the time $ \tau $, then the pathogen shedding rate of the infected animal is $ \int_0^{h}\rho(\tau)h(I(t-\tau))e^{-(\mu_2+c)\tau}d\tau $. (Ⅴ) In animal breeding, only the basic ewes breed newborns, and adult animals are widely used for slaughter or trade, then the birth rate $ b $ of adult animals is assumed to be less than the elimination rate $ \mu_2 $ of adult animals. Therefore, the modelling for animal brucellosis is given through the following distributed time-delay system:
Here, $ b $ is the birth rate of adult animals. $ \mu_1 $ and $ \mu_2 $ are the elimination rates of young and adult animals, respectively. $ \sigma_1 $ is the transfer rate from young susceptible individuals to sexually mature individuals. The culling rate is defined by $ c $ and $ d $ is the decay rate of the pathogen. $ f(I) $ and $ g(B) $ are contact and indirect infection rates, respectively. $ \rho(\tau) $ is a distributed function, it is non-negative, continuous and $ \int_0^{h} \rho(\tau)d\tau = 1 $.
The initial conditions for system (2.1) are given as follows:
Here, $ C $ denotes the Banach space $ C([-h, 0], \Re^4) $ of continuous functions mapping the interval $ [-h, 0] $ into $ \Re^4 $ with the sup-norm $ \|\phi\| = \sup_{x\in[-h, 0]}|\phi_i(x)|, i = 1, 2, 3, 4 $ for $ \phi\in C $. The nonnegative cone of $ C $ is defined as $ C_+ = C([-h, 0], \Re_+^4) $.
In order to make epidemiological significance for system (2.1), $ f, g $ and $ h $ are assumed to be second-order continuous differentiable functions and satisfy the following hypotheses:
$ (H_1) $ $ f(0) = g(0) = h(0) = 0 $ and $ f(I), g(B), h(I) > 0 $ for $ I, B > 0 $;
$ (H_2) $ $ f'(I), g'(B) > 0 $ and $ f''(I), g''(B)\leq0 $ for $ B, I\geq0 $;
$ (H_3) $ $ h'(I) > 0 $ and $ h''(I)\leq0 $ for $ I\geq0 $.
The function $ f $ may be $ \beta I^p $ or saturation incidences $ k\ln(1+\frac{\lambda I}{k}) $ and $ \frac{\beta I^p}{1+kI^p} $ with constants $ \beta, p, \lambda, k > 0 $ [28,29]. The pathogen infection rate $ g $ may be $ \frac{\lambda B}{1+TB} $ or $ \eta(1-e^{-\alpha B}) $ with constants $ \lambda, \eta, \alpha > 0 $ and $ T\geq0 $ [30]. The function $ h $ may be $ kI $ with constants $ k > 0 $ [31].
It is easy to verify that the system (2.1) always has a disease-free equilibrium $ E_0 = (S_1^0, S_2^0, 0, 0) $, where
The reproduction number of sytem (2.1) is given by the following expression:
where $ n = \int_0^{h}\rho(\tau)e^{-(\mu_2+c)\tau}d\tau $. $ e^{-(\mu_2+c)\tau} $ denotes the probability of survival from a newly infected susceptible individual to an infectious individual. $ n $ is the total survival rate of infected individuals. $ f_I(0) $ is the infection rate by an infectious individual. $ g_B(0) $ is the infection rate of brucella. $ \frac{1}{\mu_2+c} $ is the average life span of infected individual. $ \frac{h_I(0)}{d} $ represents the total number of brucella shed by infectious individuals. Therefore, based on the explanation in the literature [26], $ R_0 $ relies on direct and indirect infection and can be divided into two parts $ R_{01} $ and $ R_{02} $.
In the next section, we establish that the solution of system (2.1) is non-negative and bounded and analyze the uniqueness of the equilibrium point of persistent infection. The following qualitative results indicate the nonnegativity and boundedness of the solution of system (2.1) with initial conditions (2.2).
Theorem 2.1. $ (S_1(t), S_2(t), I(t), B(t)) $ is the solution of system (2.1) with the initial conditions (2.2), then $ S_1(t), S_2(t), I(t), B(t) $ are nonnegative and ultimately bounded.
Proof. Since $ (\dot{S_1}(t)+\dot{S_2}(t)) = A > 0 $ for $ t\in[0, +\infty) $ when $ S_1(t) = S_2(t) = 0 $, it implies that $ S_1(t)+S_2(t)\geq0 $ for all $ t\in[0, +\infty) $. Therefore, if $ S_1(t) = 0 $, then $ S_2(t)\geq0 $ and $ \dot{S_1}(t) = A+bS_2 > 0 $, so that $ S_1(t)\geq0 $. We denote
and
From the last three equations in (2.1), it can conclude that
and
for all $ t\geq0 $. Thus, $ S_1(t), S_2(t), I(t), B(t)\geq0 $ for $ t\geq0 $.
We now analyze the boundedness of the solution of system (2.1). In fact,
where $ \mu = \min\{\mu_1, \mu_2-b\} $.
Hence, $ \limsup_{t\rightarrow\infty}(S_1(t)+S_2(t)+I(t))\leq \frac{A}{\mu} $, it implies that $ \limsup_{t\rightarrow\infty}I(t)\leq \frac{A}{\mu} $ and $ \limsup_{t\rightarrow\infty}B(t)\leq \frac{n}{d}h(\frac{A}{\mu}) $. Therefore, $ S_1(t), S_2(t), I(t), B(t) $ are ultimately bounded.
Since the solution of system (2.1) is nonnegative and ultimately bounded, the set
is positively invariant for system (2.1).
In order to analyze the uniqueness of the positive solution of system (2.1), the following lemma is given:
Lemma 2.1. Assume that conditions $ (H_1)-(H_{3}) $ are satisfied, the functions $ \frac{f(I)}{I} $, $ \frac{h(I)}{I} $, $ \frac{g(B)}{B} $ and $ \frac{g(h(I))}{I} $ are monotonic decreasing for $ I, B > 0 $.
Proof. Since $ f''(I)\leq0 $, it shows that $ f'(I) $ is monotonic decreasing, it follows that
and
That is to say, $ \frac{f(I)}{I} $ is a monotonically decreasing function. On the basis of the above method, it can show that $ \frac{h(I)}{I} $ and $ \frac{g(B)}{B} $ are also monotonic decreasing. Noting that
It can deduce that
Therefore, $ \frac{g(h(I))}{I} $ is also monotonic decreasing.
For system (2.1), the endemic equilibrium $ E_* = (S_1^*, S_2^*, I^*, B^*) $ can be derived from the following algebraic equations:
By direct calculation, it can be written as
where $ m(S_2) = \frac{A\sigma_1-(\mu_2(\mu_1+\sigma_1)-b\sigma_1)S_2}{\mu_1+\sigma_1} $ and $ H(I) = \frac{n}{d}h(I) $.
Let us define
Similar to the method of analysis in literature [26], using Lemma 2.1, the following result can be summarized:
Theorem 2.2. Assume that conditions $ (H_1)-(H_3) $ hold. Then there is a unique positive solution $ E_* = (S_1^*, S_2^*, I^*, B^*) $ of system (2.1) if and only if $ R_0 > 1 $.
3.
Stability of the disease-free equilibrium
In this section, we show that the global stability of the equilibrium point $ E_0 $ of system (2.1) is independent of the initial value. The following conclusions are first obtained.
Lemma 3.1. Assume that conditions $ (H_1)-(H_{3}) $ hold. The disease-free equilibrium $ E_0 $ is locally asymptotically stable if $ R_0\leq1 $ and is unstable if $ R_0 > 1 $.
Proof. The characteristic equation at $ E_0 $ is
where
It follows from (3.1) that
That is,
It follows that
where $ H_1(\lambda) = (\lambda+\mu_1+\sigma_1)(\lambda+\mu_2)-b\sigma_1 $. Since $ \mu_1+\sigma_1+\mu_2 > 0 $ and $ \mu_2(\mu_1+\sigma_1)-b\sigma_1 > 0 $, then $ H_1(\lambda) $ consists of two roots which are negative real parts. Therefore, we only analyze the distribution of the roots of the following equation:
Assume now that $ R_0 > 1 $, then
Hence $ H_2(\lambda) $ has at least one positive root in $ [0, +\infty) $, then $ E_0 $ is unstable if $ R_0 > 1 $.
From (3.2), we have
or
Next, considering the case $ R_0\leq1 $. If $ \lambda = x+yi $ is a solution of (3.3), one shows that $ x < 0 $. Otherwise, $ x\geq 0 $ implies
and thus
this is a contradiction to (3.3). Therefore, all roots of Eq (3.3) have no zero and positive real parts when $ R_0\leq1 $, this shows that $ E_0 $ is locally asymptotically stable.
Theorem 3.1. Assume that conditions $ (H_1)-(H_{3}) $ are established. If $ R_0\leq1 $, the disease-free equilibrium $ E_0 = (S_1^0, S_2^0, 0, 0) $ of system (2.1) is globally asymptotically stable.
Proof. Since the functions $ \frac{f(I)}{I} $, $ \frac{g(B)}{B} $ and $ \frac{h(I)}{I} $ are decreasing, then we have
Define
We find $ a_1 = R_0 $ and define a Lyapunov functional $ L $ as follows:
where
and
Then the derivative of $ L_1 $ along the positive solutions of system (2.1) is
Calculating the derivative of $ L_2(t) $ along the solutions of system (2.1), one obtains
Similar to the above-used method, it can obtain that
Combining the Eqs (3.4), (3.5) and (3.6), it follows that
Similar to the analysis of Theorem 1 in the literature [32], it follows from Lemma 3.1 that the disease-free equilibrium $ E_0 $ is globally asymptotically stable by LaSalle's Invariance Principle [33].
4.
Stability of the endemic equilibrium
According to Lemma 3.1, the disease-free steady state solution $ E_0 $ is unstable when $ R_0 > 1 $. Using Theorem 4.2 in [34], the uniform permanence of system (2.1) can be proven, the process is ignored here. In this following section, by constructing a Lyapunov functional, the global stability of the equilibrium of persistent infection is proved. We first analyze its local stability.
Lemma 4.1. Assume that conditions $ (H_1)-(H_{3}) $ are ture, If $ R_0 > 1 $, the endemic equilibrium $ E_* $ of system (2.1) exists and is locally asymptotically stable.
Proof. For system (2.1), the characteristic equation at $ E_* $ is
where $ H_3(\lambda) = \lambda+nf(I^*)+g(B^*)+\mu_2 $, $ H_4(\lambda) = \lambda+\mu_2+c-\Gamma(\lambda)S_2^*f_I(I^*) $. By simple calculation, one obtains
or
where
Noting that from Lemma 1
Assume $ \lambda = x+yi $ is a solution of (4.1). If $ x\geq0 $, we then have
and
where $ M_1 = x+\mu_2-\frac{b\sigma_1(x+\mu_1+\sigma_1)}{(x+\mu_1+\sigma_1)^2+y^2} > 0 $, $ M_2 = y+\frac{b\sigma_1y}{(x+\mu_1+\sigma_1)^2+y^2} $. So it concludes that
which is a contradiction to (4.1). Therefore, the Eq (4.1) can not have any roots with a nonnegative real part, this implies that $ E_* $ is locally asymptotically stable if $ R_0 > 1 $.
Theorem 4.1. Assume that conditions $ (H_1)-(H_{3}) $ hold. If $ R_0 > 1 $, the endemic equilibrium $ E_* = (S_1^*, S_2^*, I^*, B^*) $ of system (2.1) is globally asymptotically stable.
Proof. Define
Finding the time derivative of $ L_1 $ along the positive solutions of system (2.1) gives
By the Eq (2.4), we get
Since the function $ \nu(x) = 1-x+\ln x $ is nonpositive for $ x > 0 $ and $ \nu(x) = 0 $ if and only if $ x = 1 $, so we define
A direct calculation shows that
Define
Calculating the time derivative of $ L_3(t) $, one obtains
For system (2.1), the following Lyapunov functional is considered:
From (4.2), (4.3) and (4.4), we can get
where
and
it follows from (4.5), (4.6) and (4.7) that
By Lemma 2.1, it can conclude that
The equality $ \frac{dL}{dt} = 0 $ suggests that $ \frac{S_1^*}{S_1} = 1 $, $ \frac{S_1S_2^*}{S_1^*S_2} = 1 $, $ \frac{f(I)}{f(I^*)} = 1 $ and $ \frac{g(B)}{g(B^*)} = 1 $, it implies that $ E_* $ is the maximum invariant set of system (2.1) in the set $ \{\frac{dL}{dt} = 0\} $. Using Lemma 4.1, the endemic steady state $ E_* $ is globally asymptotically stable.
5.
Numerical analysis
By choosing a specific kernel function and some infection functions, system (2.1) can be evolved into different dynamic models with time delays. In this section, some such examples are used to further illustrate theoretical results.
Example: Consider the kernel function $ \rho(\tau) = \delta(\tau-\tau_0) $, where $ \delta $ is the Dirac delta function. Then system (2.1) can be rewritten as
Where $ A, b, \mu_1, \mu_2, \sigma_1, \alpha, \beta, c, k $ and $ d > 0 $, $ g(B) = \alpha B $ and $ h(I) = kI $. If $ f(I) = \beta I $, it is easy to verify that $ f(I), g(B) $ and $ h(I) $ satisfy the assumptions $ (H_1)-(H_3) $. Therefore, the basic reproduction number of system (5.1) can be defined as
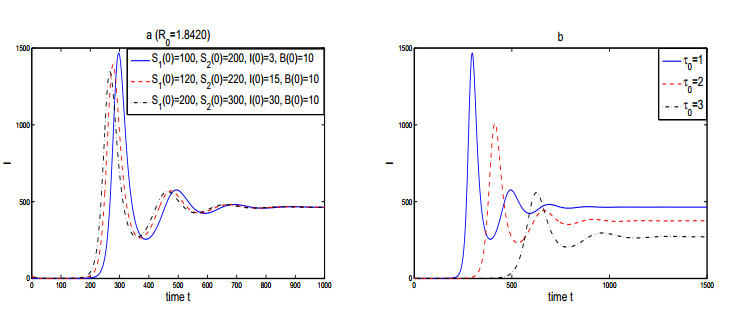
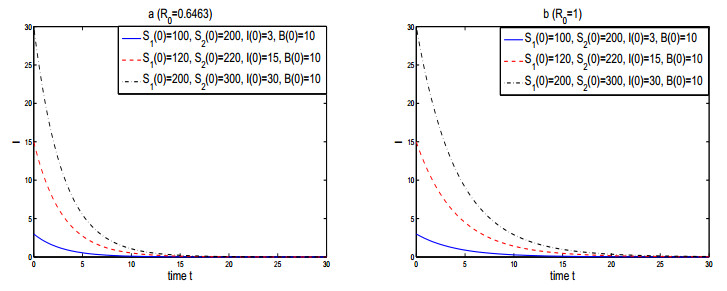
In this case, if $ R_0\leq1 $, the disease-free equilibrium is globally asymptotically stable and the endemic equilibrium is also globally asymptotically stable if $ R_0 > 1 $ (see Figures 1 and 2). As is shown in Figure 2, initial values and time delays can not change dynamic properties of system (2.1) when $ R_0 $ is greater than one or less than or equal to one. However, from Figure 2b, it is easy to find that time delay $ \tau_0 $ has a significant impact on the positive equilibrium of system (5.1).
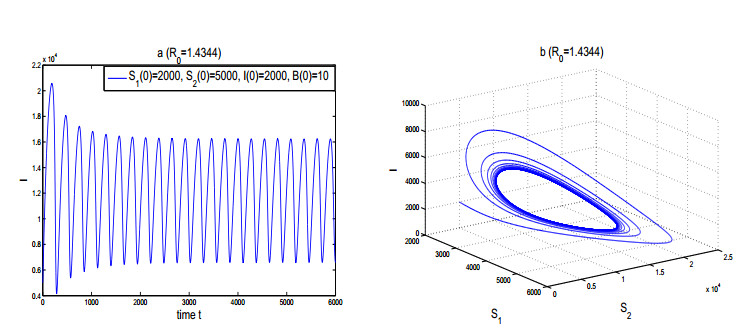
If $ f(I) = \beta I^2 $ [28], then $ f(I) $ does not satisfy hypothesis $ (H_2) $, that is, $ \frac{f(I)}{I} $ is a monotonically increasing function. From Figure 3, it is easy to see that the system (5.1) appears periodic oscillation behavior under certain conditions.
6.
Discussions
In this article, a general $ S_1S_2IB $ dynamics model with distributed time delay for animal brucellosis is formulated. Under the assumptions of general biological significance, the non-negative and boundedness of the solution of system (2.1) is first proved. And then the global dynamics of the steady-state solution of system (2.1) are analyzed by constructing Lyapunov functional, it is found that the dynamic properties of equilibria depend on the basic reproduction number $ R_0 $: If $ R_0\leq 1 $, animal brucellosis will eventually die out regardless of the initial value; and if $ R_0 > 1 $, the spread of animal brucellosis is persistent and it eventually reaches the endemic steady state. These results imply that distributed time delay does not change the dynamic properties of system (2.1) when $ R_0 $ is greater than one or less than or equal to one. Finally, similar to numerical methods in [35,36], the stability results and other dynamic behaviors are further illustrated through numerical simulation, it turns out that the system experiences periodic oscillations if the assumption $ (H_2) $ is not satisfied. In other words, the system (2.1) may exhibit more complex dynamic behaviors if the function $ \frac{f}{I}, \frac{g}{B} $ or $ \frac{h}{I} $ is monotonically increasing. In these cases, the impact of distributed time delay on other dynamical behaviors of system (2.1) is not completely clear, then we leave these for future work.
Acknowledgments
This research is partially supported by the National Youth Science Foundation of China (11501528), the National Sciences Foundation of China(11571324) and the Fund for Shanxi "1331KIRT".
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: