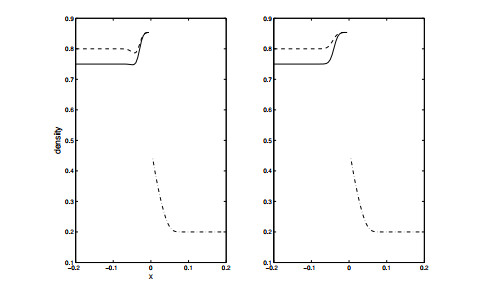
Example 1. Left panel:
Citation: Christopher Talbot, Nico Augustin. Submarine Salt Karst Terrains[J]. AIMS Geosciences, 2016, 2(2): 182-200. doi: 10.3934/geosci.2016.2.182
| [1] | John D. Towers . An explicit finite volume algorithm for vanishing viscosity solutions on a network. Networks and Heterogeneous Media, 2022, 17(1): 1-13. doi: 10.3934/nhm.2021021 |
| [2] | Boris Andreianov, Kenneth H. Karlsen, Nils H. Risebro . On vanishing viscosity approximation of conservation laws with discontinuous flux. Networks and Heterogeneous Media, 2010, 5(3): 617-633. doi: 10.3934/nhm.2010.5.617 |
| [3] | Giuseppe Maria Coclite, Carlotta Donadello . Vanishing viscosity on a star-shaped graph under general transmission conditions at the node. Networks and Heterogeneous Media, 2020, 15(2): 197-213. doi: 10.3934/nhm.2020009 |
| [4] | Markus Musch, Ulrik Skre Fjordholm, Nils Henrik Risebro . Well-posedness theory for nonlinear scalar conservation laws on networks. Networks and Heterogeneous Media, 2022, 17(1): 101-128. doi: 10.3934/nhm.2021025 |
| [5] |
Giuseppe Maria Coclite, Nicola De Nitti, Mauro Garavello, Francesca Marcellini .
Vanishing viscosity for a |
| [6] | Karoline Disser, Matthias Liero . On gradient structures for Markov chains and the passage to Wasserstein gradient flows. Networks and Heterogeneous Media, 2015, 10(2): 233-253. doi: 10.3934/nhm.2015.10.233 |
| [7] | Wen Shen . Traveling wave profiles for a Follow-the-Leader model for traffic flow with rough road condition. Networks and Heterogeneous Media, 2018, 13(3): 449-478. doi: 10.3934/nhm.2018020 |
| [8] | Giuseppe Maria Coclite, Lorenzo di Ruvo, Jan Ernest, Siddhartha Mishra . Convergence of vanishing capillarity approximations for scalar conservation laws with discontinuous fluxes. Networks and Heterogeneous Media, 2013, 8(4): 969-984. doi: 10.3934/nhm.2013.8.969 |
| [9] | Abraham Sylla . Influence of a slow moving vehicle on traffic: Well-posedness and approximation for a mildly nonlocal model. Networks and Heterogeneous Media, 2021, 16(2): 221-256. doi: 10.3934/nhm.2021005 |
| [10] | Christophe Chalons, Paola Goatin, Nicolas Seguin . General constrained conservation laws. Application to pedestrian flow modeling. Networks and Heterogeneous Media, 2013, 8(2): 433-463. doi: 10.3934/nhm.2013.8.433 |
This paper proposes an explicit finite volume scheme for first-order scalar conservation laws on a network having a single junction. The algorithm and analysis extend readily to networks with multiple junctions, due to the finite speed of propagation of the solutions of conservation laws. For the sake of concreteness, we view the setup as a model of traffic flow, with the vector of unknowns representing the vehicle density on each road. A number of such scalar models have been proposed, mostly differing in how the junction is modeled. An incomplete list of such models can be found in [4,5,6,7,8,11,12,13,14,15,16,18,19]. In this paper we focus on the so-called vanishing viscosity solution proposed and analyzed in [7] and [2]. The junction has
| ∂tuh+∂xfh(uh)=0,h=1,…,m+n. | (1.1) |
Incoming roads are indexed by
| ui∈L∞(R−×R+;[0,R]),i∈{1,…,m},uj∈L∞(R+×R+;[0,R]),j∈{m+1,…,m+n}. | (1.2) |
Following [2] we make the following assumptions concerning the fluxes
The study of vanishing viscosity solutions on a network was initiated by Coclite and Garavello [7], who proved that vanishing viscosity solutions converge to weak solutions if
For the convenience of the reader, and to establish notation, we review some relevant portions of the theory of network vanishing viscosity solutions, as described in [2], where we refer the reader for a more complete development. Let
| Gh(β,α)={min | (1.3) |
(Compared to [2], we list the arguments
| \begin{equation} -L_h \le \partial G_h(\beta, \alpha)/\partial \beta \le 0, \quad 0\le \partial G_h(\beta, \alpha)/\partial \alpha \le L_h, \quad h \in \{1, \ldots, m+n\}. \end{equation} | (1.4) |
Definition 1.1 (Vanishing viscosity germ [2]). The vanishing viscosity germ
| \begin{equation} \begin{split} &\sum\limits_{i = 1}^m G_i(p_{ \vec{u}}, u_i) = \sum\limits_{j = m+1}^{m+n} G_j(u_j, p_{ \vec{u}}), \\ &G_i(p_{ \vec{u}}, u_i) = f_i(u_i), \quad i = 1, \ldots, m, \\ &G_j(u_j, p_{ \vec{u}}) = f_j(u_j), \quad j = m+1, \ldots, m+n. \end{split} \end{equation} | (1.5) |
The definition of entropy solution requires one-sided traces along the half-line
| \begin{equation} \begin{split} &\gamma_i u_i(\cdot) = u_i(\cdot, 0^-), \quad i \in \{1, \ldots, m \}, \\ &\gamma_j u_j(\cdot) = u_j(\cdot, 0^+), \quad j \in \{m+1, \ldots, m+n \}. \end{split} \end{equation} | (1.6) |
Definition 1.2 (
| \begin{equation} q_h(v, w) = \mathrm{sign}(v-w)\left(f_h(v)-f_h(w) \right), \quad h = 1, \ldots, m+n. \end{equation} | (1.7) |
Given an initial condition
● For each
| \begin{align} \int_{ \mathbb{R}_+} \int_{\Omega_h} \Bigl(\left|{u_h-c}\right| \partial_t \xi + q_h(u_h, c)\partial_x \xi \Bigr)\, dx\, dt + \int_{\Omega_h} \left|{u_{h, 0}-c}\right| \xi(x, 0) \, dx \geq 0. \end{align} | (1.8) |
● For a.e.
Associated with each
| \begin{equation} k_h(x) = k_h, \quad x \in \Omega_h, \quad h \in \{1, \ldots, m+n\}. \end{equation} | (1.9) |
It is readily verified that viewed in this way,
Definition 1.2 reveals the relationship between the set
Definition 1.3 (
● The first item of Definition 1.2 holds.
● For any
| \begin{equation} \sum\limits_{h = 1}^{m+n} \left(\int_{ \mathbb{R}_+} \int_{\Omega_h} \left\{\left|{u_h - k_h }\right|\xi_t + q_h(u_h, k_h)\xi_x\right\} \, dx \, dt \right) \ge 0 \end{equation} | (1.10) |
for any nonnegative test function
Theorem 1.4 (Well posedness [2]). Given any initial datum
| \begin{equation} \vec{u}_0 = (u_{1, 0}, \ldots, u_{m+n, 0}) \in L^{\infty}(\Gamma; [0, R]^{m+n}), \end{equation} | (1.11) |
there exists one and only one
In addition to the results above, reference [2] also includes a proof of existence of the associated Riemann problem. Based on the resulting Riemann solver, a Godunov finite volume algorithm is constructed in [2], which handles the interface in an implicit manner. This requires the solution of a single nonlinear equation at each time step. The resulting finite volume scheme generates approximations that are shown to converge to the unique
The main contribution of the present paper is an explicit version of the finite volume scheme of [2]. It differs only in the processing of the junction. We place an artificial grid point at the junction, which is assigned an artificial density. The artificial density is evolved from one time level to the next in an explicit manner. Thus a nonlinear equation solver is not required. (However, we found that in certain cases accuracy can be improved by processing the junction implicitly on the first time step.) Like the finite volume scheme of [2], the new algorithm has the order preservation property and is well-balanced. This makes it possible to employ the analytical framework of [2], resulting in a proof that the approximations converge to the unique entropy solution of the associated Cauchy problem.
In Section 2 we present our explicit finite volume scheme and prove convergence to a
For a fixed spatial mesh size
| \begin{equation} \begin{split} &x_{\ell} = (\ell + 1/2) {\Delta} x, \quad \ell \in \{\ldots, -2, -1\}, \\ &x_{\ell} = (\ell - 1/2) {\Delta} x, \quad \ell \in \{1, 2, \ldots\}. \end{split} \end{equation} | (2.1) |
Each road
| \begin{equation} \begin{split} &\Omega_i = \bigcup\limits_{\ell \le -1} I_\ell, \quad I_\ell : = (x_\ell - {\Delta} x/2, x_\ell + {\Delta} x/2] ~\text{ for}~ \ell \le -1 , \\ &\Omega_j = \bigcup\limits_{\ell \ge 1} I_\ell, \quad I_\ell : = [x_\ell - {\Delta} x/2, x_\ell + {\Delta} x/2) ~\text{for }~ \ell \ge 1 . \end{split} \end{equation} | (2.2) |
Our discretization of the spatial domain
| \begin{equation} \begin{split} &U_{\ell}^{h, s} \approx u_h(x_\ell, t^s), \quad \ell \in \mathbb{Z} \setminus \{0\}, \\ &P^s \approx p_{\gamma \vec{u}(t^s)}. \end{split} \end{equation} | (2.3) |
We are somewhat artificially assigning a density, namely
Remark 1. We make the association
The initial data are initialized via
| \begin{equation} \begin{split} &U^{h, 0}_{\ell} = {1\over {\Delta} x} \int_{I_{\ell}} u_{h, 0}(x) \, dx, \quad h \in \{1, \ldots, m+n \}, \\ &P^0 \in [0, R]. \end{split} \end{equation} | (2.4) |
Note that
| \begin{equation} \left\{ \begin{split} &P^{s+1} = P^s - \lambda \left(\sum\limits_{j = m+1}^{m+n} G_j(U_{1}^{j, s}, P^s) - \sum\limits_{i = 1}^m G_i(P^s, U_{-1}^{i, s}) \right), \\ &U_\ell^{i, s+1} = U_\ell^{i, s} - \lambda \left(G_i(U_{\ell+1}^{i, s}, U_{\ell}^{i, s}) - G_i(U_{\ell}^{i, s}, U_{\ell-1}^{i, s}) \right), \quad i \in \{1, \ldots, m \}, \, \, \ell \le -1, \\ &U_\ell^{j, s+1} = U_\ell^{j, s} - \lambda \left(G_j(U_{\ell+1}^{j, s}, U_{\ell}^{j, s}) - G_j(U_{\ell}^{j, s}, U_{\ell-1}^{j, s}) \right), \quad j \in \{m+1, \ldots, m+n \}, \\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \, \, \ell \ge 1.\\ \end{split} \right. \end{equation} | (2.5) |
Define
| \begin{equation} \lambda (m+n) L\le 1. \end{equation} | (2.6) |
If all of the
| \begin{equation} \lambda \max(m, n) L\le 1. \end{equation} | (2.7) |
Remark 2. The algorithm (2.5) is an explicit version of the scheme of [2]. To recover the scheme of [2] from (2.5), one proceeds as follows:
● first substitute
● then advance each
The equation mentioned above (after substituting
| \begin{equation} \sum\limits_{j = m+1}^{m+n} G_j(U_{1}^{j, s}, P^s) = \sum\limits_{i = 1}^m G_i(P^s, U_{-1}^{i, s}). \end{equation} | (2.8) |
The implicit portion of the scheme of [2] consists of solving (2.8) for the unknown
Remark 3. The convergence of the scheme (2.5) is unaffected by the choice of
| \begin{equation} P^{0}_{\nu+1} = P^0_\nu - \lambda \left(\sum\limits_{j = m+1}^{m+n} G_j(U_{1}^{j, 0}, P^0_\nu) - \sum\limits_{i = 1}^m G_i(P^0_\nu, U_{-1}^{i, 0}) \right). \end{equation} | (2.9) |
Moreover, we found that this same fixed point iteration approach is a convenient way to solve (2.8) when implementing the implicit scheme of [2]. From this point of view the algorithm of this paper and the algorithm of [2] only differ in whether the first equation of (2.5) is iterated once, or iterated to (approximate) convergence. See Appendix A for a proof that the iterative scheme (2.9) converges to a solution of (2.8).
Remark 4. The CFL condition associated with the finite volume scheme of [2] is
| \begin{equation} \lambda L \le 1/2. \end{equation} | (2.10) |
As soon as there are more than a few roads impinging on the junction, our CFL condition (2.6) imposes a more severe restriction on the allowable time step, which becomes increasingly restrictive as more roads are included. One could view this as the price to be paid for the simplified processing of the junction. On the other hand, most of the specific examples discussed in the literature are limited to
Let
| \begin{equation} \begin{split} &u^{i, {\Delta}} = \sum\limits_{s\ge 0} \sum\limits_{\ell \le -1} \chi_{\ell}(x) \chi^s(t) U^{i, s}_\ell, \quad i \in \{1, \ldots, m \}, \\ &u^{j, {\Delta}} = \sum\limits_{s\ge 0} \sum\limits_{\ell \ge 1} \chi_{\ell}(x) \chi^s(t) U^{j, s}_\ell, \quad j \in \{m+1, \ldots, m+n \}.\\ \end{split} \end{equation} | (2.11) |
The discrete solution operator is denoted by
| \begin{equation} S^{\Delta} \vec{u}_0 = \left(u^{i, {\Delta}}, \ldots, u^{m, {\Delta}}, u^{m+1, {\Delta}}, \ldots u^{m+n, {\Delta}} \right). \end{equation} | (2.12) |
The symbol
| \begin{equation} \Gamma_{ \text{discr}} = \Bigl(\{1, \ldots, m \}\times\{\ell \in \mathbb{Z}, \ell \le -1 \} \Bigr) \bigcup \Bigl(\{m+1, \ldots, m+n \}\times\{\ell \in \mathbb{Z}, \ell \ge 1 \} \Bigr), \end{equation} | (2.13) |
and with the notation
| \begin{equation} U^s = \left(U_{\ell}^{h, s} \right)_{(h, l)\in \Gamma_{ \text{discr}}}, \end{equation} | (2.14) |
Remark 5. In the case where
Lemma 2.1. Fix a time level
Proof. For
Fix
| \begin{equation} \begin{split} &\partial U^{i, s+1}_{-1}/ \partial U^{i, s}_{-2} = \lambda \partial G_i(U^{i, s}_{-1}, U^{i, s}_{-2})/\partial U^{i, s}_{-2}, \\ &\partial U^{i, s+1}_{-1}/ \partial U^{i, s}_{0} = -\lambda \partial G_i(U^{i, s}_{0}, U^{i, s}_{-1})/\partial U^{i, s}_{0}, \\ &\partial U^{i, s+1}_{-1}/ \partial U^{i, s}_{-1} = 1- \lambda \partial G_i(U^{i, s}_{0}, U^{i, s}_{-1})/\partial U^{i, s}_{-1} + \lambda \partial G_i(U^{i, s}_{-1}, U^{i, s}_{0})/\partial U^{i, s}_{-1}. \end{split} \end{equation} | (2.15) |
That partial derivatives in the first two lines are nonnegative is a well-known property of the Godunov numerical flux. The partial derivative on the third line is nonnegative due to (1.4) and the CFL condition (2.6).
A similar calculation shows that the partial derivatives of
It remains to show that the partial derivatives of
| \begin{equation} \begin{split} &\partial P^{s+1}/\partial U^{i, s}_{-1} = \lambda \partial G_i(P^s, U^{i, s}_{-1})/\partial U^{i, s}_{-1}, \\ &\partial P^{s+1}/\partial U^{j, s}_{1} = -\lambda \partial G_j(U^{j, s}_{1}, P^s)/\partial U^{j, s}_{1}, \\ &\partial P^{s+1}/\partial P^s = 1 - \lambda \left(\sum\limits_{j = m+1}^{m+n} \partial G_j(U^{j, s}_{1}, P^s)/\partial P^s - \sum\limits_{i = 1}^m \partial G_i(P^s, U^{i, s}_{-1})/\partial P^s \right)\\ &\qquad \qquad \quad \ge 1 - \lambda \left(\sum\limits_{j = m+1}^{m+n} \max(0, f'_j(P^s)) - \sum\limits_{i = 1}^m \min(0, f'_i(P^s)) \right). \end{split} \end{equation} | (2.16) |
The first two partial derivatives are clearly nonnegative. For the third partial derivative we have used the following readily verified fact about the Godunov flux:
| \begin{equation} \min(0, f'_h(\beta)) \le {\partial G_h \over \partial \beta}(\beta, \alpha) \le 0 \le {\partial G_h \over \partial \alpha}(\beta, \alpha) \le \max(0, f'_h(\alpha)), \end{equation} | (2.17) |
and thus the third partial derivative is nonnegative due to (1.4) and the CFL condition (2.6).
Remark 6. If all of the fluxes
| \begin{equation} \partial P^{s+1}/\partial P^s \ge 1 - \lambda \left(n \max(0, f'(P^s)) - m \min(0, f'(P^s)) \right), \end{equation} | (2.18) |
from which it is clear that
Lemma 2.2. Assuming that the initial data satisfies
Proof. The assertion is true for
| \begin{equation} \begin{split} \tilde{U}^{h}_{\ell} = 0, \quad \tilde{P} = 0, \\ \hat{U}^{h}_{\ell} = R, \quad \hat{P} = R. \end{split} \end{equation} | (2.19) |
It is readily verified that
| \begin{equation} \tilde{U}_{\ell}^h \le U^{0, h}_\ell \le \hat{U}_{\ell}^h, \quad \tilde{P} \le P^0 \le \hat{P}. \end{equation} | (2.20) |
After an application of a single step of the finite volume scheme, these ordering relationships are preserved, as a result of Lemma 2.1. Since
| \begin{equation} \tilde{U}_{\ell}^h \le U^{1, h}_\ell \le \hat{U}_{\ell}^h, \quad \tilde{P} \le P^1 \le \hat{P}. \end{equation} | (2.21) |
This proves the assertion for
Given
| \begin{equation} K^{h}_\ell = \begin{cases} k^i, \quad & \ell < 0~ \text{ and}~ h\in \{1, \ldots, m \} , \\ k^j, \quad & \ell > 0 ~~\text{and}~~ h\in \{m+1, \ldots, m+n \} .\\ \end{cases} \end{equation} | (2.22) |
and
Lemma 2.3. The finite volume scheme of Section 2 is well-balanced in the sense that each
Proof. For each fixed
Fix
| \begin{equation} k^i - \lambda \left(G_i(p_{ \vec{k}}, k^{i}) - G_i(k^i, k^i) \right) = k^i - \lambda \left(f_i(k^{i}) - f_i(k^i) \right) = k^i. \end{equation} | (2.23) |
Here we have used the definition of
| \begin{equation} p_{ \vec{k}} - \lambda \left(\sum\limits_{j = m+1}^n G_j(k^j, p_{ \vec{k}}) - \sum\limits_{i = 1}^m G_i(p_{ \vec{k}}, k^i) \right) = p_{ \vec{k}}, \end{equation} | (2.24) |
where we have applied the first equation of (1.5).
With the notation
| \begin{equation} Q_{\ell+1/2}^{h}[U^s, \hat{U}^s] = G_h(U^{h, s}_{\ell+1} \vee \hat{U}^{h, s}_{\ell+1}, U^{h, s}_{\ell} \vee \hat{U}^{h, s}_{\ell}) - G_h(U^{h, s}_{\ell+1} \wedge \hat{U}^{h, s}_{\ell+1}, U^{h, s}_{\ell} \wedge \hat{U}^{h, s}_{\ell}). \end{equation} | (2.25) |
Lemma 2.4. Let
| \begin{equation} \begin{split} &\sum\limits_{i = 1}^m {\Delta} x {\Delta} t\sum\limits_{s = 1}^{+\infty} \sum\limits_{\ell < 0} \left|{U^{i, s}_{\ell}-\hat{U}^{i, s}_{\ell}}\right| \left(\xi_{\ell}^{s}-\xi_{\ell}^{s-1} \right)/{\Delta} t\\ &+\sum\limits_{i = 1}^m {\Delta} x {\Delta} t \sum\limits_{s = 0}^{+\infty} \sum\limits_{\ell \le 0} \, Q^i_{\ell-1/2}[U^s, \hat{U}^s] \left(\xi^{s}_{\ell} - \xi^{s}_{\ell-1} \right)/{\Delta} x\\ &+\sum\limits_{j = m+1}^{m+n} {\Delta} x {\Delta} t \sum\limits_{s = 1}^{+\infty} \sum\limits_{\ell > 0} \left|{U^{i, s}_{\ell}-\hat{U}^{i, s}_{\ell}}\right| \left(\xi_{\ell}^{s}-\xi_{\ell}^{s-1} \right)/{\Delta} t\\ &+\sum\limits_{j = m+1}^{m+n} {\Delta} x {\Delta} t \sum\limits_{s = 0}^{+\infty} \sum\limits_{\ell \ge 0} \, Q^j_{\ell+1/2}[U^s, \hat{U}^s] \left(\xi^{s}_{\ell+1} - \xi^{s}_{\ell} \right)/{\Delta} x\\ & +{\Delta} x {\Delta} t \sum\limits_{s = 1}^{+\infty} \, \left|{P^s-\hat{P}^s}\right| \left(\xi_{0}^{s}-\xi_{0}^{s-1} \right)/{\Delta} t \ge 0.\\ \end{split} \end{equation} | (2.26) |
Proof. From the monotonicity property (Lemma 2.1), a standard calculation [9] yields
| \begin{equation} \begin{split} &\left|{U_{\ell}^{i, s+1}-\hat{U}_{\ell}^{i, s+1}}\right| \le \left|{U_{\ell}^{i, s}-\hat{U}_{\ell}^{i, s}}\right|\\ &\qquad \qquad \qquad \qquad - \lambda \left(Q^i_{\ell+1/2}[U^s, \hat{U}^s] - Q^i_{\ell-1/2}[U^s, \hat{U}^s] \right), \quad \ell \le -1, \\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \, \, \, \, i \in \{1, \ldots, m \}, \\ &\left|{U_{\ell}^{j, s+1}-\hat{U}_{\ell}^{j, s+1}}\right| \le \left|{U_{\ell}^{j, s}-\hat{U}_{\ell}^{j, s}}\right|\\ &\qquad \qquad \qquad \qquad - \lambda \left(Q^j_{\ell+1/2}[U^s, \hat{U}^s] - Q^j_{\ell-1/2}[U^s, \hat{U}^s] \right), \quad \ell \ge 1, \\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad j \in \{m+1, \ldots, m+n \}, \\ &\left|{P^{s+1}-\hat{P}^{s+1}}\right| \le \left|{P^{s}-\hat{P}^{s}}\right| - \lambda \left(\sum\limits_{j = m+1}^{m+n} Q_{1/2}^j[U^s, \hat{U}^s] - \sum\limits_{i = 1}^m Q_{-1/2}^i[U^s, \hat{U}^s]\right). \end{split} \end{equation} | (2.27) |
We first multiply each of the first and second set of inequalities indexed by
Lemma 2.5. Suppose that
Proof. The proof that the first condition of Definition 1.2 holds is a slight adaptation of a standard fact about monotone schemes for scalar conservation laws [9].
The proof is completed by verifying the second condition of Definition 1.2. Let
With Lemmas 2.1 through 2.5 in hand it is possible to repeat the proof of Theorem 3.3 of [2], which yields Theorem 2.6 below.
Theorem 2.6. For a given initial datum
We found that if
Initialization of
● Initialize
● Initialize
Example 1. This example demonstrates the appearance of a spurious bump when

Example 1. Left panel:
One can also get rid of the spurious bump by choosing
I thank two anonymous referees for their comments and suggestions.
In this appendix we prove that the fixed point iterations (2.9) converge to a solution of the equation (2.8). Let
| \begin{equation} u_i = U_{-1}^{i, s} for i = 1, \ldots, m , \quad u_j = U_{1}^{j, s} ~\text{for }~ j = m+1, \ldots, m+n . \end{equation} | (A.1) |
Then (2.8) takes the form
| \begin{equation} \Phi_{{\vec u}}^{ \text{out}}(p) = \Phi_{\vec{u}}^{ \text{in}}(p), \end{equation} | (A.2) |
where
| \begin{equation} \Phi_{\vec{u}}^{ \text{in}}(p) = \sum\limits_{i = 1}^m G_i(p, u_i), \quad \Phi_{{\vec u}}^{ \text{out}}(p) = \sum\limits_{j = m+1}^{m+n} G_j(u_j, p). \end{equation} | (A.3) |
This notation agrees with that of [2], where it was shown that
With the simplified notation introduced above, the iterative scheme (2.9) becomes
| \begin{equation} p_{\nu+1} = p_{\nu} - \lambda \left( \Phi_{{\vec u}}^{ \text{out}}(p_{\nu}) - \Phi_{\vec{u}}^{ \text{in}}(p_{\nu}) \right), \quad p_0 \in [0, R]. \end{equation} | (A.4) |
Proposition 1. The sequence
Proof. Note that
| \begin{equation} \begin{split} &0 \le G_i(0, u_i), \quad G_i(R, u_i) = 0, \\ &G_j(u_j, 0) = 0, \quad 0 \le G_j(u_j, R). \end{split} \end{equation} | (A.5) |
Thus,
| \begin{equation} \begin{split} &0 \le \Phi_{\vec{u}}^{ \text{in}}(0), \quad \Phi_{\vec{u}}^{ \text{in}}(R) = 0, \\ & \Phi_{{\vec u}}^{ \text{out}}(0) = 0, \quad 0 \le \Phi_{{\vec u}}^{ \text{out}}(R). \end{split} \end{equation} | (A.6) |
Define
| \begin{equation} \Psi_{ \vec{u}}(p) = \Phi_{{\vec u}}^{ \text{out}}(p) - \Phi_{\vec{u}}^{ \text{in}}(p), \end{equation} | (A.7) |
and observe that
| \begin{equation} \Psi_{ \vec{u}}(0) \le 0 \le \Psi_{ \vec{u}}(R). \end{equation} | (A.8) |
Define
| \begin{equation} \Pi(p) = p - \lambda \Psi_{ \vec{u}}(p). \end{equation} | (A.9) |
| \begin{equation} \Pi'(p) = 1 - \lambda \Psi'_{ \vec{u}}(p) \ge 1 - \lambda (m+n)L. \end{equation} | (A.10) |
Thanks to (A.10) and the CFL condition (2.6), it is clear that
| \begin{equation} 0 \le \Pi(0) \le \Pi(p) \le \Pi(R) \le R ~\text{for}~ p \in [0, R] . \end{equation} | (A.11) |
Thus
| \begin{equation} p_{\nu +1} = \Pi(p_{\nu}), \quad p_0 \in [0, R]. \end{equation} | (A.12) |
We can now prove convergence of the sequence
Now consider the case where
| \begin{equation} \begin{split} p_{\nu+1}-p_{\nu} & = \Pi(p_{\nu}) - \Pi(p_{\nu-1}) \\ & = {\Pi(p_{\nu}) - \Pi(p_{\nu-1})\over p_{\nu} - p_{\nu-1} } (p_{\nu} - p_{\nu-1}). \end{split} \end{equation} | (A.13) |
Since
| \begin{equation} \mathrm{sign}(p_{\nu+1}-p_{\nu}) = \mathrm{sign}(p_{\nu}-p_{\nu-1}) = \ldots = \mathrm{sign}(p_{1}-p_{0}). \end{equation} | (A.14) |
In other words, the sequence
| [1] |
Hudec MR, Jackson MPA. (2007) Terra Infirma: understanding salt tectonics. Earth-Sci Rev 82: 1-28. doi: 10.1016/j.earscirev.2007.01.001

|
| [2] | Frumkin A. (2013) Salt Karst. In: John F. Shroder, Frumkin, A. Treatise on Geomorphology, Vol. 6, Karst Geomorphology, San Diego: Academic Press, 407-24. |
| [3] | Feldens P, Schmidt M, Mücke I, et al. (2016) Expelled subsalt fluids form a pockmark field in the eastern Red Sea. Geo-Mar Lett 1-14. |
| [4] | Zarei M, Raeis E, Talbot, CJ. (2012) Karst development on a mobile substrate: Konarsiah salt, extrusion, Iran. Geol Mag 149 (3): 412-22. |
| [5] | Talbot CJ, (1998) Extrusions of Hormuz salt in Iran. In: Blundell, DJ. & Scott, AC. (Eds.) Lyell: the Past is the Key to the Present. Geological Society of London. Special Publications, 143: 315-34. |
| [6] | Schléder Z, Urai, JL. (2007) Deformation and recrystallization mechanisms in mylonitic shear zones in naturally deformed extrusive Eocene-Oligocene rocksalt from Eyvanekey plateau and Garmsar hills (Central Iran), J Struct Geol 29: 241-55. |
| [7] |
Talbot CJ and Rogers E. (1980) Seasonal movements in an Iranian salt glacier. Science Wash 208: 395-7. doi: 10.1126/science.208.4442.395

|
| [8] | Talbot CJ, Pohjola V. (2009) Subaerial salt extrusions in Iran as analogues of ice sheets, streams and glaciers. Earth-Sci Rev 97: 167-95. |
| [9] |
Talbot CJ, Aftabi P. (2004) Geology and models of salt extrusion at Qum Kuh, central Iran. J Geol Soc London 161: 321-34. doi: 10.1144/0016-764903-102

|
| [10] | Bruthans J, Filippi M, Asadi N, et al. (2009) Surficial deposits on salt diapirs (Zagros Mountains and Persian Gulf Platform, Iran): Characterization, evolution, erosion and the influence on landscape morphology. Geomorphol 107: 195-209. |
| [11] |
Tompkins RE, Shepherd LE. (1979) Orca Basin: Depositional processes, geotechnical properties and clay mineralogy of Holocene sediments within an anoxic hypersaline basin, northwest Gulf of Mexico. Mar Geol 33: 221-38. doi: 10.1016/0025-3227(79)90082-3

|
| [12] |
Pilcher RS, Blumstein RD. (2007) Brine volume and salt dissolution rates in Orca Basin, northeast Gulf of Mexico. AAPG Bull 91: 823-33. doi: 10.1306/12180606049

|
| [13] | Scott E, Peel F, Taylor C, et al. (2001) Deep Water Gulf of Mexico Sea Floor Features Revealed Through 3D Seismic. Offshore Technology Conference. |
| [14] | Barnhart WD, Lohman RB. (2012) Regional trends in active diapirism revealed by mountain range-scale InSAR time series. Geophys Res Lett 39: L08309. |
| [15] | Nibbelink K. (1999) Modeling deepwater reservoir analogs through analysis of recent sediments using coherence, Seismic amplitude, and bathymetry data, Sigsbee escarpment, Green Canyon, Gulf of Mexico. Leading Edge 18(5): 550-61. |
| [16] | Chu D, Gordon R. (1998) Current plate motions across the Red Sea. Geophys J Int 135: 313-28. |
| [17] |
Augustin N, Devey CW, van der Zwan FM, et al. (2014) The rifting to spreading transition in the Red Sea. Earth Planet Sci Lett 395: 217-30. doi: 10.1016/j.epsl.2014.03.047

|
| [18] | Mitchell NC, Ligi M, Ferrante V, et al. (2008) Submarine salt flows in the central Red Sea. Bull Geol Soc Am 122: 701-13. |
| [19] | Feldens P, Mitchell NC. (2015) Salt Flows in the central Red Sea. Chapter 8 in N.M.A. Rasul and O.C.F. Stewart (Eds), The Red Sea. Springer Earth System Science, Berlin. |
| [20] | Manheim F. (1974) Red Sea geochemistry. Initial Rep. Deep Sea Drill. Proj. 23, 975-98. |
| [21] | Pierret MC, Clauer N, Bosch D, et al. (2001) Chemical and isotopic (87Sr/86Sr, δ18O, δD) constraints to the formation processes of Red-Sea brines. Geochim Cosmochim Acta 65: 1259-75. |
| [22] |
Batang ZB, Papathanassiou E, Al-Suwailem A, et al. (2012) First discovery of a cold seep on the continental margin of the central Red Sea. J Mar Syst 94: 247-53. doi: 10.1016/j.jmarsys.2011.12.004

|
| [23] | Brown L. (2014) Texture Shading: A New Technique for Depicting Terrain Relief, Presented at the ICA Mountain Cartography Workshop, 24. April 2014. |
| [24] | Schmidt M, Devey CW, Eisenhauer A. (Eds.). (2011) IFM-Geomar Report. 46: 1-80 Leibnitz- Institute of Marine Science IFM-Geomar. Kiel. |
| [25] | Schmidt M, Al-Farawati R, Al-Aidaroos A,et al. (2013) RV PELAGIA Fahrtbericht/Cruise Report 64PE350/64PE351. GEOMAR Report 5: 1-154. |
| [26] | Augustin N, Schmidt M, Devey CW, et al. (2014) The Jeddah Transect Project: Extensive mapping of the Red Sea Rift. Inter Ridge News 22: 68-73. |
| [27] | Mücke I. (2013) Geophysical and geochemical characterization of pockmarks of the central Red Sea (~19.5°N). Thesis, Faculty of Mathematics and Natural Sciences, Christian-Albrechts-Universität zu Kiel. Referees: Schmidt, M., Feldens, P. 49 pp. |
| [28] | Talbot CJ. (2008) Hydrothermal salt- but how much? Discussion. Marine & Petrol. Geology 25: 191-202. |
| [29] | Maestrelli D, Ali J, Iacopinii D, et al. (2015) Seismic expression of large-scale fluid escape pipes using time lapses seismic surveys: examples from the Loyal Field (Scotland, UK). Rend Online Soc Geol It Suppl. n. 1 al Vol. 37. |
| [30] | Land LA, Paull CK. (2000) Submarine karst belt rimming the continental slope in the Straits of Florida. Geo-Mar Lett 20:123-32. |
| [31] | Fleury, P, Bakalowicz M, de Marsily, G. (2007) Submarine springs and coastal karst aquifers: A review. J Hydrol 339: 279-92. |
| [32] | Bayari CS, Ozyurt NN, Oztan M, et al. (2011) Submarine and coastal karstic groundwater discharges along the southwestern Mediterranean coast of Turkey. Hydrogeol J 19: 399-414. |
| [33] |
Wu S, Bally AW, Cramez C. (1990) Allochthonous salt, structure and stratigraphy of the northeastern Gulf of Mexico, Part 11; Structure. Mar Pet Geol 7: 334-70. doi: 10.1016/0264-8172(90)90014-8

|
| 1. | Nicola De Nitti, Enrique Zuazua, On the Controllability of Entropy Solutions of Scalar Conservation Laws at a Junction via Lyapunov Methods, 2023, 51, 2305-221X, 71, 10.1007/s10013-022-00598-9 | |
| 2. | Michael Herty, Niklas Kolbe, Siegfried Müller, Central schemes for networked scalar conservation laws, 2022, 18, 1556-1801, 310, 10.3934/nhm.2023012 | |
| 3. | Markus Musch, Ulrik Skre Fjordholm, Nils Henrik Risebro, Well-posedness theory for nonlinear scalar conservation laws on networks, 2022, 17, 1556-1801, 101, 10.3934/nhm.2021025 | |
| 4. | Michael Herty, Niklas Kolbe, Siegfried Müller, A Central Scheme for Two Coupled Hyperbolic Systems, 2024, 6, 2096-6385, 2093, 10.1007/s42967-023-00306-5 | |
| 5. | Dilip Sarkar, Shridhar Kumar, Pratibhamoy Das, Higinio Ramos, Higher-order convergence analysis for interior and boundary layers in a semi-linear reaction-diffusion system networked by a k -star graph with non-smooth source terms, 2024, 19, 1556-1801, 1085, 10.3934/nhm.2024048 | |
| 6. | Sabrina F. Pellegrino, A filtered Chebyshev spectral method for conservation laws on network, 2023, 151, 08981221, 418, 10.1016/j.camwa.2023.10.017 |