Concrete has been one of the most common building materials used in construction in the world for many centuries. The manufacturing of concrete plays an important role in the generation of global warming emissions and waste and causes non-renewable resource depletion. This research assesses the environmental impacts of the use of supplementary cementitious materials (SCMs) and engineered nanomaterials (ENMs) (i.e., by-products) as partial replacement of ordinary Portland cement in concrete. It also evaluates the structural performance of the use of construction and demolition waste as partial replacement of natural aggregate in concrete in terms of compressive strength and durability. Results show that the use of SCMs and ENMs reduces the global warming impact (GWI) and the cumulative energy demand (CED) of concrete production without reducing strength and durability. In some cases, it enhances durability and strength. However, there is a tradeoff between durability and strength improvement with the use of reengineered by-products resulting in increased GWI and CED. Although they produce almost the same GWI and CED as those of OPC concrete, improving the use of recycled aggregates as a partial natural aggregate replacement can reduce the use of virgin materials.
1.
Introduction
The building sector is a major contributor to environmental impact [1]. Concrete is one of the most widely used building construction materials and has been extensively used in the world for many centuries. The fabrication of concrete is associated with increased risk of the generation of global warming emissions and wastes and leading to non-renewable resource depletion. Portland cement concrete production is a deeply energy intensive process and results in 5–7% of CO2 emissions [2] which have a crucial effect on global warming. The manufacturing of one tonne of ordinary Portland cement (OPC) discharge approximately one tonne of CO2 to the air [1]. In addition, all processes during the mining to material phase, transportation, construction plant and tool, and operation (heating, cooling, lighting, hot water and home appliances) stages cause high embodied energy consumption [3]. Therefore, it is indispensable to find an environmentally friendly concrete with low emissions which offers high performances in terms of strength and durability.
The addition of supplementary cementitious materials (SCMs), including industrial by-products, as a partial replacement of ordinary Portland cement (OPC) in concrete is the most functional and economic method to reduce the carbon footprint of OPC concrete [4,5]. Additionally, the use of SCMs such as fly ash or ground granulated blast furnace slag (GGBFS) can provide additional sustainability advantages, including raw materials conservation and reuse of industrial by-products [6,7].Waste by-products such as fly ash (FA), GGBFS and silica fume (SF) generated from coal fired power stations, steel industries and silicon and ferrosilicon alloys industries often end their life in landfill, contaminating the soil, but they could potentially replace certain portions of cement OPC due to their pozzolanic properties.
The use of FA, GGBFS and SF has made some progress in facing the challenges of sustainable construction. These SCMs exhibit pozzolanic characteristics which are attributed to the presence of SiO2 and Al2O3. Reacting with calcium hydroxide (CH) during cement hydration, they form additional calcium aluminate hydrate (CAH) and calcium silicate hydrate (CSH). These contribute in forming a denser matrix, providing to better durability and higher strength, for instance, against sulphate attack and alkali silica reaction [8]. As shown by Lye et al. [9] the relative rate of carbonation of FA concrete with respect to the corresponding OPC concrete remains similar under accelerated and natural carbon dioxide exposures. In addition, the use of 20% FA as a cement replacement in reinforced concrete can improve performance against corrosion of steel reinforcement [10]. From a practical point of view, fly ash, GGBFS and SF can replace are between 20–30%, 40–50% and 5–10% of cement, respectively [11,12]. Significant research have been conducted on the use of those SCMs on properties of concrete. And the results show the above replacement levels of FA, GGBFS and SF improved the mechanical, durability and workability properties of concretes [13,14]. However, when FA is used in high volume in concrete it can display negative effects in terms of early age strength due to the pozzolanic characteristics of fly ash particles [11].
In order to overcome this deficiency, solutions have been studied such as the incorporation of very small size pozzolanic materials e.g., silica fume (SF), also known as microsilica, in high volume fly ash (HVFA) systems. Carette and Malhotra [15] observed an increase in the compressive strength of fly ash concrete with the addition of silica fume at all phases of the aging. It was also reported that the inclusion of 10% silica fume makes up for the loss of compressive strength at early age (7 days) and does not affect the service life of fly ash concrete Amudhavalli and Mathew [16] suggested that the optimum 7 and 28-day compressive strength and flexural strength of concrete can be obtained with a silica fume replacement level of 10–15%. Wang et al. [17] found that replacing 25% FA and 5–8% SF both by weight lead to significant improvements in the resistance of concrete against combined freezing-thawing and sulfate attack. In general, fly ash seems to compensate the workability problems related to the use of higher levels of silica fume, while silica fume counterbalances the fly ash concrete low early strength [18].
The use of nano particles has also recently been introduced to improve the strength in many building materials applications, especially in concrete mixtures, because of their extremely small size and very high surface area [19]. Nano materials are described as having very small particles with sizes under 10-9 m, generated from the modification of atoms and molecules in order to produce large scale materials [20]. To date the nanoparticles investigated, include nano silica (SiO2), nano iron (Fe2O3), nano titanium (TiO2), nano alumina (Al2O3) and nano lime. It is suggested that nanoparticles act as a nuclei for cement to accelerate cement hydration and densify the microstructure and the interfacial transition zone (ITZ), thereby reducing permeability [21,22,23]. In recent years, the use of nano-CaCO3 has been introduced in concrete. In general, calcium carbonate can be found in limestone, marble, chalk or produced artificially by combining calcium with CO2 [24]. Among various manufactured nano particles, it has recently been introduced nano-silica (NS) as an advanced pozzolan to enhance the stability and microstructure of cement-based systems [25].
Ultrafine fly ash (UFFA) is one of the recent improvements of micro size pozzolanic materials [26]. UFFA is produced by a patented separation system with an average particle diameter of 1–5 μm and contains 20% more amorphous silica than typical Class F fly ash [27]. Generally, UFFA is produced from pure class F fly ash by grinding and separating ultrafine particles through an air-classification process. The classification system is performed for removing coarse particles by size and weight to retain the finer ash fraction. In some cases, this system not only produces finer material, but it also reduces the carbon content and the variability of constituents in the fly ash [28].
In comparison to OPC production, cement containing UFFA does not require a high energy-intensive process, due to the lower clinker requirement per tonne of cement [29]. Other benefits include reducing the use of natural resources and CO2 emissions. In addition, decreasing the particle size of fly ash increases the amorphous SiO2 content and reduces the amount of SO3, which can prevent the hydration reaction of harmful ions in concrete or mortar [30].
Whilst UFFA is used to replace cement in concrete, Shaikh and Supit [28] suggest that an enhancement of strength and long-term durability of HVFA concretes can be obtained due to the use of micro size UFFA. However, when present at appreciably high levels, UFFA tends to increase the water demand because of the accelerated reaction under fineness and high surface area. As a consequence, UFFA is typically suggested to range from 8% to 12% of the total binder content [31]. Hossain et al. [32] also observed that the replacement of cement with 12% UFFA improved the cracking resistance when compared to ordinary Portland cement concrete and silica fume concrete. Choi et al. [28,33] noted that the compressive strength of concrete increased with the increment of fly ash fineness.
The environmental impact of concrete can be significantly improved by adding large amounts of recycled concrete agammaegates as partial replacement of natural agammaegates in concrete [34]. Because natural agammaegates in concrete occupy almost 70–80% of the volume of concrete. The recycled concrete agammaegates are sourced from old demolished reinforced concrete structures [35]. It is reported that the mechanical and durability properties of concrete decreases with the addition of recycled concrete agammaegates. However, the addition of small amounts of silica fume or other ultrafine SCMs can compensate this deficiency [34]. Currently, a large number of researches is being conducted to make concrete more sustainable by partially replacing OPC and natural agammaegates using industrial wastes and recycled materials [35,36,37].
The purpose of this investigation is to explore the relationship between environmental impacts, such as global warming impact and cumulative energy demand and the use of supplementary cementitious materials (SCMs) and engineered nanomaterials (≤100 nm) [38,39] as partial replacement of ordinary Portland cement. Similarly, the use of construction and demolition waste as partial replacement of natural agammaegate in concrete has been studied. It also examines the way in which these materials can impact the structural performances of concrete, such as compressive strength and durability.
2.
Methodology
A life cycle assessment (LCA) was done to determine the environmental implications of the substitution of conventional concrete with various by-product based concrete mixtures considered following the guidelines outlined in ISO 14040-44 (ISO 2006) guideline: goal and scope, life cycle inventory (LCI), environmental impact assessment and interpretation.
The goal of this LCA is to determine the environmental impacts associated with the manufacturing of conventional and by-products/waste based concrete mixes.
2.1. Functional unit
The functional unit of this study is 1 m3 of concrete. An inventory analysis was performed to estimate the energy and materials used during the mining to material, transportation and manufacturing stages of this amount of concrete.
2.2. System boundary
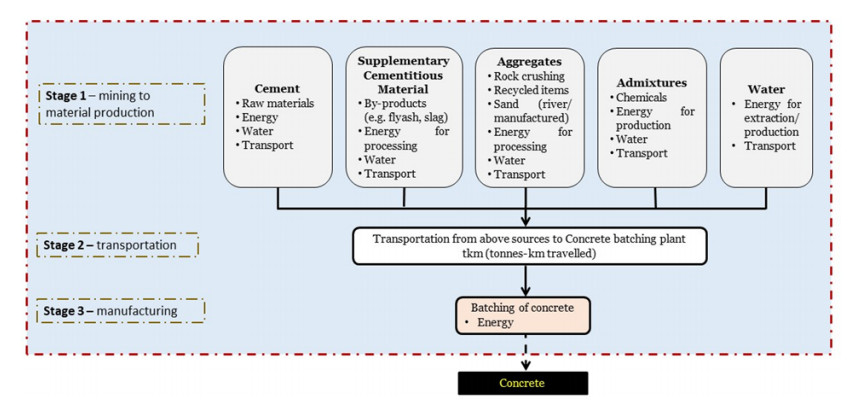
The system boundary of the concrete LCA considered a ‘cradle-to-gate’ approach, up to the manufacturing of the concrete mixes (Figure 1), including the mining of raw materials, the manufacturing and processing of the construction materials, transportation of the materials to the construction site and manufacturing stages of concrete mixtures. All these activities based on Western Australia’s production. The use and disposal/recycling strategy of concrete wastes were excluded from the analysis.
2.3. Life cycle impact assessment methodology
As 23% of the total greenhouse gas (GHG) and 20% of the energy consumption resulted from the construction industry in Australia in 2015 [40], two environmental indicators were selected in order to assess environmental implications of by-product/waste based concrete:
● Cumulative energy demand (CED)
● Global warming impact (GWI)
The CED of a product represents the direct and indirect energy use during all life cycle, including the consumption of energy during extraction, manufacturing, disposal of row material and auxiliary materials and is expressed in megajoules [41]. The GWI (or carbon footprint) is a measure of the exclusive total amount of carbon emission that is directly and indirectly caused by an activity or is collected over stages of a product which is expressed as carbon dioxide equivalent [42].
3.
Life cycle inventory analysis
3.1. Data requirements
Data needed to assess the environmental sustainability were taken from 5 different research papers, made by the same authors, in the same laboratory with similar materials composition (Table 1). The table presents the variations in compositions of both control and alternative concrete mixes and in their structural performance. Two sets (series A and B) of concrete mixtures utilizing two different control concrete (OPC) formulations were analysed.
Materials used in this study are fly ash (FA), slag and silica fume (SF) as a partial replacement for cement having pozzolanic given their cementitious properties. The effect of nanomaterials as nano-silica (NS), nano calcium carbonate (NCC) and ultrafine fly ash (UFFA) as cement replacement was considered. In order to avoid processes associated with the mining of virgin natural agammaegate (NA), construction and demolition waste was used as recycled agammaegate (RA).
3.2. Mix proportion
The amount of materials used in each concrete mix used in this research are shown in the Table 2 and Table 3.
The effect of nanomaterials was evaluated in series A. The mixtures with 40 and 60% of fly ash (respectively A1 and A2), 2% of nano-silica (A3), 2% of nano calcium carbonate (A4), 8 and 12% of ultrafine fly ash (respectively A5 and A6) as partial cement replacement were used to make a comparison with control concrete (A0). The control concrete is a conventional concrete and for the base case ‘0’ means that none of these constituents including natural agammaegates, sand and OPC is either partially or completely replaced with alternative materials, such as wastes, by-products.
Table 2 shows the LCI inputs, including cement, sand, agammaegates, water, transportation and manufacturing energy for series A concrete mixes.
Series B was used to evaluate the environmental implications of construction and demolition (C & D) waste as replacement for virgin agammaegate and the use of SCMs as cementitious material.
Mixtures with 50% of recycled agammaegate (B1), 50% of RA and 50% slag (B2), 40% slag with addition of 10% silica fume and 50% of RA (B3), 50% FA and 35% RA (B4), 50% FA with addition of 10% SF and 35% RA (B5) were used to make a comparison with control concrete (B0).
Table 3 shows the LCI of inputs, including even cement, sand, natural agammaegates, water, super-plasticizer, transportation and manufacturing energy of series B concrete mixes. Since the sources of these LCI input did not specify where the 10 mm or 20 mm coarse agammaegate used this paper considered used 20 mm CA.
3.3. Transportation
The estimation of distance is required to estimate the environmental impacts associated with the transportation of raw materials to the manufacturing plant for concrete production. Approximate distances between the source of materials and the construction site at Curtin University (WA) to evaluate the contribution of transportation are shown in Table 4.
3.4. Concrete manufacturing
Following Biswas et al. [45] and Nath et al. [46] the energy of manufacturing was considered as 0.03 kWh/kg as these studies also estimated the environmental impacts of 1 m3 of concrete.
3.5. Impact assessment
SimaPro 8.4 LCA software was used to calculate global warming impacts (GWI) and cumulative energy demand (CED) [47]. The inputs of LCIs were incorporated into SimaPro 8.4 LCA software, they were linked to relevant libraries (or emission databases). The emission databases for most of these inputs are based on local Western Australian conditions. In the absence of local emission databases, new databases were developed using available raw data for local industries/processes.
The GWI is represented as kg or tonne CO2 equivalent (CO2 –e), all global warming gases are converted to CO2 equivalent GWI emissions following the IPCC (2007) [48]. Accordingly, GPI (GWICO2−e) has been calcaulted as follows.
where, i is the amount of an input
i :1, 2, …..N; type of inputs (e.g., cement, concrete, aluminium, electricity, natural gas).
EFij : Emission factor = Amount of emission of GHG type ‘j’ per kg of input of type ‘i’.
CFj : CF1, CF2, ……. CFM; characterization factors of GHGs (e.g., 1 for CO2, 28 for CH4, 265 for N2O).
Following the cumulative energy consumption method, the total inputs in the life cycle inventory were multiplied by the corresponding embodied energy consumption values to find the total embodied energy consumption (EEtotal) of 1 m3 of concrete mix as shown in Eq 2 [46].
where, EEi :Embodied energy consumption of an input i.
Australian impact assessment in the software was used to convert inputs to global warming impacts and then these impacts are added to determine the total life cycle global warming impacts. Similarly, CED was also calculated using the same method.
Australian emission databases in the Simapro LCA software [47] were available for cement, silica fume, recycled agammaegate, fly ash, slag, sand, electricity, transportation and water. The unit of transportation was considered as tonne-kilometres (tkm) in order to calculate the inputs from transportation. Since local databases for coarse agammaegate, ultrafine fly ash, nano-silica and nano-calcium carbonate are unavailable, these databases were sourced from Shaikh et al. (2019) [48]. The Eco-invent database was used to calculate the emissions to produce plasticizer [49].
4.
Results and discussion
4.1. Cumulative energy demand
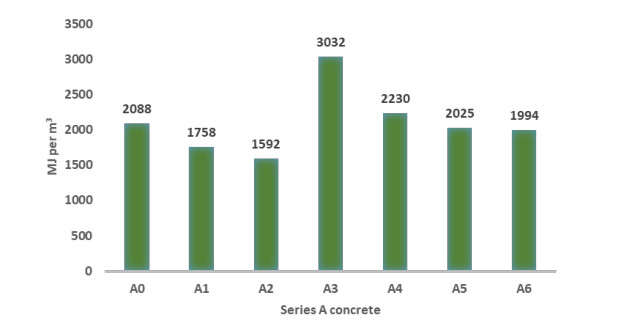
The CED of series A concrete mix range from 1592 MJ to 3032 MJ. Except for A3 and A4, other by-product based concrete mixes performs better than A0 in terms of CED.
Figure 2 shows that the addition of 40% and 60% fly ash in concrete (A1 and A2) significantly decreases the CED by about 16% and 24%, respectively. The CED of the concrete mixes A1 and A2 drop from 2088 MJ for OPC concrete (A0) to 1758 MJ and 1592 MJ, respectively. Nath et al. [41] assessed that embodied energy consumption can be decreased by 8.9% due to the replacement of OPC with 40% FA. However, a cradle-to-gate approach was not used in the analysis that includes the mining to use stages of the product life cycle.
The value of CED dramatically increases due to the incorporation of 2% NS (A3) (3032 MJ). The addition of 2% NCC (A4) produces a similar effect. The CED of concrete mix A4 is 2230 MJ, which is still higher than that of A0 mix. The concrete containing 8% and 12% UFFA as partial cement replacement respectively does not produce noticeable reduction in CED. Mixes A5 and A6 result in 2025 and 1994 MJ, respectively, which are both slightly lower than that of control concrete.
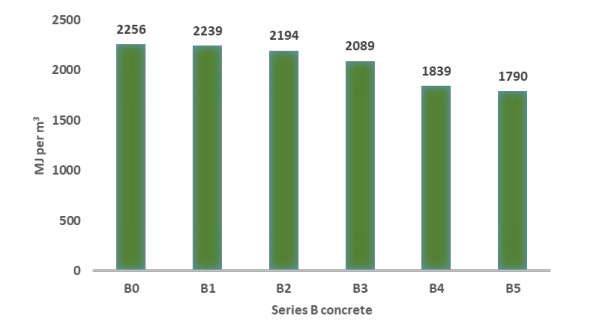
Figure 3 shows that CED of series B concrete mix range from 1790 MJ to 2256 MJ. All by-product based concrete mixes perform better than B0 in terms of CED.
The replacement of 50% RA (B1) does not seem to change the CED. The CED for B1 and B0, is 2239 MJ and 2256 MJ, respectively. There is a slight reduction in CED value for using 50% slag in B2 and 10% SF in B3. The CED values for mixes B1 and B2 are 2194 and 2089 MJ, respectively. A slightly reduction between 3 and 7% of CED can be achieved, when slag was used in addition to silica fume. Tafheem et al. [42] obtained different results, with the same functional unit (i.e., 1 t of concrete) as the one considered in this research. They found that the primary energy of concrete mix using 50% ground granulated blast furnace slag (GGBFS) was 29% less than that of the control concrete. An appreciable reduction in the CED value results was obtained however by introducing 50% FA (B4) and 10% SF (B5). Mixes B4 and B5 produce 1839 MJ and 1790 MJ, respectively, which are 18 and 21% less than that of the mix B0.
4.2. Global warming impact
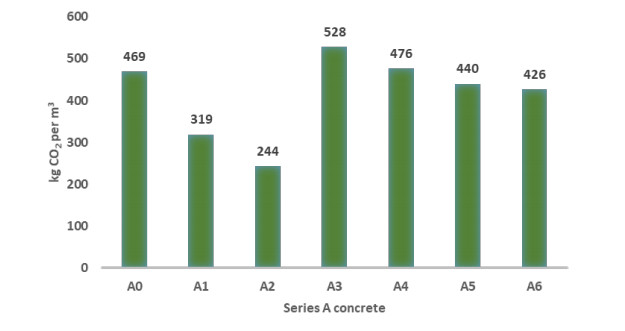
Figure 4 shows that GWI of series A concrete mix range from 244 kg CO2 eq to 528 kg CO2 eq. Except for A3 and A4, other by-product based concrete mixes performs better than A0 in terms of GWI. The results have the same trends provided in the CED analysis shown in the Figure 2.
The GWI of mix A0 is 469 kg CO2 eq, which can be reduced by 32% to 48% by using A1 and A2 concrete mixes (319 and 244 kg CO2 eq). Nath et al. [41] found that carbon footprint of the use of 1 m3 of concrete can be decreased from 345 kg CO2 eq to 269 kg CO2 eq due to the replacement of OPC with 40% FA. Results show how the addition of NS (A3) increased the GWI up to 528 kg CO2 eq. Interestingly, the concrete mixes with higher compressive strength and durability properties showed better environmental performance compared to the concrete mixes with lower structural performance. This is because the use of byproducts in concrete reduces sorptvity and permeability which increases the compressive strength. In addition, the use of by-products as a partial replacement for carbon intensive OPC use reduces the overall GHG emissions.
A similar trend was also observed in the CED value for concrete containing 2% NCC. The GWI in mix A4 was 476 kg CO2 eq, which is 2% higher than the result obtained from ordinary concrete (A0) and 10% lower than that obtained from mix A3. UFFA does not affect concrete mixes A5 and A6 in terms of GWI, which is 440 and 426 kg CO2 eq, respectively.
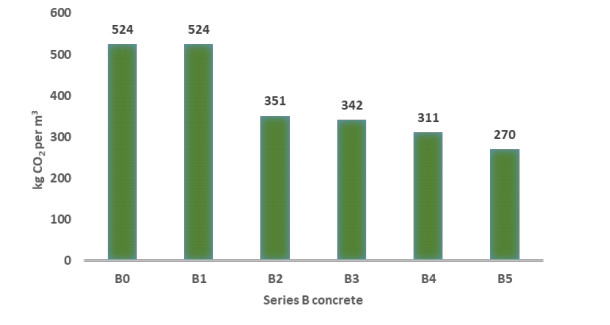
Figure 5 shows that GWI of series B concrete mix range from 270 kg CO2 eq to 524 kg CO2 eq. All by-product based concrete mixes perform better than B0 in terms of GWI.
The replacement of 50% RA does not seem to change GWI. The GWI of B1 and B0 are both 524 kg CO2 eq.
Substantial reduction can be obtained in the mix B2 with 50% slag and mix B3 with 40% and 10% SF. The GWI value of mixes B2 and B3 is 351 and 342 kg CO2 eq, respectively, which is 33 and 35% lower than that of the control concrete. Similar result was obtained by Tafheem et al. [42], which found out that replacing 50% of the Portland cement with ground granulated blast furnace slag (GGBFS) results in 40% reduction in the CO2 emissions, considering 1 t of concrete. A further improvement can be achieved by using 50% FA (mix B4) and 50% FA with 10% SF (mix B5). It can be seen that GWI of mixes B4 and B5 is 311 and 270 kg CO2 eq, which are 41 and 48% lower than that of mix B0, respectively.
In general, it can be seen that the use of ENMs sometime contributes to produce environmental impact which is higher than that of the control concrete and SCMs. This is due to the additional process (i.e., grinding) needed to reduce the size of the particles, which increase the amount of energy required (CED) and the global warming impact produced (GWI). However, due to the large amount of energy (i.e., CO2 emission factor of RA is 0.00563 kg CO2 eq per kg as opposed to NA (0.00477 kg CO2 eq per kg)) consumed in crushing C & D wastes, the substitution of natural agammaegate with recycled agammaegate does not reduce the CED and the GWI, while it contributes to reduce the amount of virgin material mined.
The structural suitability of the concrete mixes have been discussed on the basis of the review of articles [23,29,30,38,39] in the following section.
4.3. Workability
The workability of concrete is quantified in terms of slump according to ASTM C143.
The workability of all concrete mixtures of series A, except mix A6, is reported in the Table 5.
The results show that the addition of 40 and 60% fly ash increases the slump, which results in 160 and 200 mm for mixes A1 and A2, respectively, while the slump for mix A0 is 140 mm. An interesting outcome is given by the addition of nanomaterials, which causes a reduction in the slump value given their large specific surface area which adsorbs more water from concrete mixtures [38]. It can be seen as the slump of mix A3, which contains 2% NS, is 80 mm. In mixes A4 and A5, containing 2% NCC and 8% UFFA, the slump was 140 mm and 120 mm, respectively.
The workability of concrete mixtures B0, B2, B3 and B5 of series B is reported in the Table 6.
As control concrete, mix B0 show 140 mm of slump. In the mixes containing slag the slump increases to 160 and 200 mm for mixes B2 and B3, respectively. However, the addition of fly ash (mix B5) decreases the slump value to 90 mm.
4.4. Compressive strength
Beyond assessing environmental impacts, the compressive strength results from different concrete mixes (as shown in the Table 1) were used to assess the feasibility of using the mixes mentioned above in structural applications. According to Standards Australia Committee BD-002, Concrete Structures (AS 3600:2018) the minimum strength required for structural applications is 20 MPa.
The effect of FA, NS, NCC and UFFA on compressive strength of concrete mixes of series A is shown in the Table 5.
The compression strength of the control mix (A0) is 29 MPa. The addition of 40 and 60% of FA as partial cement replacement decreases the concrete compressive strength. Mixes A1 and A2 result in 26 and 20 MPa, which are 10 and 31% lower than that of mix A0, respectively. However, by adding nano materials, the compressive strength increases compared to the control concrete.
Table 6 presents the compressive strength of concretes containing OPC and FA, slag, SF as partial cement replacement and different percentage of RA as NA replacement of series B mixes.
Results show that compressive strength of B0 concrete mix is 58 MPa. The replacement of NA with RA (B1) reduces the compressive strength to 52 MPa. For mix B2, which contains 50% RA and 50% slag, a reduction in compressive strength to 28% compared with control concrete is noted. The value of compressive strength of mix B2 is 42 MPa. However, the addition of SF increases the compressive strength to 49.5 MPa, which is 18% higher than that of mix B2. A further reduction in compressive strength is caused by the addition of 35% RA as natural agammaegate replacement and 50% FA as cement replacement. Mix B4 has compressive strength of 30 MPa, which is 48% lower than that of the mix B0 control. This is probably because of the fact that the pozzolanic reaction of fly ash is much slower than the hydration of cement, and this has been observed in many previous studies. On the other hand, by adding SF (B5), the compressive strength increases up to 37 MPa, which is 23% higher than the mix B4.
4.5. Sorptivity
Water sorptivity describes water ingress into pores of unsaturated concrete due to capillary suction. It is a function of porosity including pore volumes and continuity of pores within concrete matrix and can be related to permeability. The rate of water absorption of concrete samples with 50 mm in thickness was determined according to ASTM C1585.
Table 5 shows the sorptivity values at 28 days of mixes of series A. The sorptivity of control concrete A0 is 63x10-4 mm/s1/2. The addition of fly ash produces different results depending on the fly ash content. The mix A1, which contains 40% FA has 54x10-4 mm/s1/2 of sorptivity, which is lower than that of control concrete. Whereas, mix A2, which contains 60% FA has 82x10-4 mm/s1/2 of sorptivity, which is higher than that of mix A0. However, an appreciable reduction in the water sorptivity can be obtaining from the addition of ENMs. Mixes with the addition of 2% NS (A3) and NCC (A4) have both 36x10-4 mm/s1/2 of sorptivity, while the addition of UFFA in the mix A5 has a value of sorptivity which is 32x10-4 mm/s1/2. Table 6 shows the sorptivity values at 28 days of mixes of series B. It can be noticed that for this series only two values of sorptivity are reported. The sorptivity of control concrete B0 is 63x10-4 mm/s1/2, which is higher than 50x10-4 mm/s1/2 for mix B5, containing FA and SF.
4.6. Rapid chloride permeability
The performance of concrete against chloride ingress was investigated by means of rapid chloride permeability test (RCPT). The penetration of chloride ions can reach reinforcing steel bars and corrode them rapidly. The lower the total charge passed through the concrete matrix, the higher the resistance to chloride penetration. ASTM C1202 specifies the rating of chloride permeability of concrete based on the charge passed through the specimen during 6 h of testing period. A RCPT value of less than 2000 coulombs is characterized as low chloride permeability, 2000–4000 coulombs is in medium level while higher than 4000 coulombs is defined as high chloride permeability.
Table 5 presents RCPT results of the series A concrete mixtures. The total charge passed in the mix A0 is 3442 coulombs, which is in the medium range. The addition of fly ash produces an increase in the chloride permeability. The value of charge passed in the mixes A1 and A2 was 4995 and 6075 coulombs, which are both higher than A0 and in the range of high chloride permeability. However, results obtained by the addition of ENMs show that the chloride permeability decreases and is in the medium level range. The total charge passed of mixes A3, A4 and A5 was 2497, 3413 and 2775 coulombs, respectively. Table 6 presents RCPT results of the series B concrete mixtures. There is no data availability for all mixes. The total charge passed in the mix A0 is 4400 coulombs, which is in the high-level range.
However, it can be seen how in this case the introduction of FA (B4) and the addition of SF (B5) significantly improve the chloride permeability behaviour. The value of total charge passed is 2200 and 1040 coulombs for mixes B4 and B5, respectively, which represent medium and low level of chloride permeability.
5.
Research limitations
The first limitation concerns the mixes proportion, which have been taken from five different research papers having different compositions. Although these mixes were prepared in the same laboratory at Curtin University, it would have been more appropriate if these mixes had been prepared during the same time.
Another limitation is due to the results of the LCA analysis. It could be a lack of information in the raw materials, energy consumption and impact due to the production cementitious materials. In addition, the data has been taken from other research papers and may not represent exactly the production process used to obtain the materials analysed. Local databases need to be developed by consulting with local industries, which is albeit a time intensive process.
6.
Conclusion
The results of this study suggest that the use of SCMs and nano-materials reduces the GWI and CED of concrete production without reducing strength and durability and in some cases enhancing durability and strength. However, there is a trade-off between durability and strength improvement with the use of re-engineered by-products resulting in increased GWI and CED. Improving the use of recycled agammaegate as a partial natural agammaegate replacement can reduce the use of virgin materials even if it produces almost the same GWI and CED as those of OPC concrete.
Two sets of concrete mixture were studied (Series A and B).
Analysis results of series A indicated that:
● Nanomaterials increase the carbon footprint and energy demand compared with OPC concrete but increase strength and durability performance.
● Ultrafine materials do not show an improvement in terms of GWI and CED but do reduce concrete strength and durability.
● Whilst mix A2 (which contains 60% of fly ash as cement replacement) had the lower GWI and CED results, mix A1 (which contains 40% of fly ash as cement replacement) had a slightly higher GWI and CED than A2, but its compressive strength was around 30% better than that of A2 mix.
From the second analysis (series B) it was found that:
● The use of recycled agammaegate does not reduce GWI and CED compared with OPC, however it does reduce the use of virgin agammaegate resources, which in itself is an important sustainability outcome.
● Using slag and fly ash significantly reduces GWI. However, slag does not reduce CED significantly due to the already high embodied energy in slag, while fly ash does contribute to reduce the CED up to 21%.
● While using slag and fly ash reduces the compressive strength, the introduction of 10% of silica fume enhance compressive strength and contributed to reducing GWI and CED. However, in some areas silica fume is still regarded as a waste product and is not actively marketed for use in concrete [43]. Very recently, Rodella et al. [44] showed that silica fume can be considered a low-cost valid alternative silica source.
In general, it is necessary to find a compromise between environmental and technical performance in the use of unprocessed and processed by-products, because in some cases the enhancement in compressive strength and durability performance might result in an increase of GWI and CED. Using construction and demolition waste as natural agammaegate replacements does not render major positive effects in terms of GWI and CED compared with OPC concrete, but it does contribute importantly to reducing the demand of virgin material.
Acknowledgments
We thank Polytechnic of Turin and Sustainable Engineering Group (SEG) of Curtin University (WA). We declare that we have no actual or potential competing financial interests.
Conflict of interest
The authors declare that there is no conflict of interests.









 DownLoad:
DownLoad: