Water resource policy support system of the Caspian Basin

Amir Hedayati Aghmashhadi; Giuseppe T. Cirella; Samaneh Zahedi; Azadeh Kazemi; Amir Hedayati Aghmashhadi; Giuseppe T. Cirella; Samaneh Zahedi; Azadeh Kazemi

doi:10.3934/environsci.2019.4.242

AIMS Environmental Science

2019, Volume 6, Issue 4: 242-261. doi: 10.3934/environsci.2019.4.242

Previous Article Next Article

Research article

Water resource policy support system of the Caspian Basin

1.
Department of Environmental Science and Engineering, Faculty of Agriculture and Natural Resources, Arak University, Arak, Iran
2.
Faculty of Economics, University of Gdansk, Sopot, Poland
3.
Environmental Management, Islamic Azad University Science and Research Branch, Tehran, Iran

Received: 08 February 2019 Accepted: 06 June 2019 Published: 19 June 2019

Water resource policy support system (WRPSS) is a process that addresses environmental policy and water resource management analyses in conjunction with data interpretation. We examine the use of a WRPSS in Iran’s northern semi-arid region of the Caspian Basin and present how eight human and non-human pressure factors, if automated, would assist in water resource security. The main features of the WRPSS include: (1) water policy modifications suitable to local environmental conditions for water evaluation and (2) development of spatial tools to derive criteria weights. A dynamic, calculative process formulates weight and critical intervals for each pressure parameter provided. The developed knowledge-base ensures the WRPSS record represents a realistic, practicable, and functional system for sound water policy. Such know-how is useful in determining water resource pressure factors in relation to a policy support system (PSS) analysis. WRPSS ensures results are interpreted within the relevant context of maximizing efficiency of water policy goals and PSS interpellation. Results indicate the Caspian Basin’s agricultural water consumption and dam infrastructure are considered most and least important sub-criteria, respectively. Moreover, the sub-basin of Haraz-Ghareh Su is worst off study-wide.

Keywords:

Citation: Amir Hedayati Aghmashhadi, Giuseppe T. Cirella, Samaneh Zahedi, Azadeh Kazemi. Water resource policy support system of the Caspian Basin[J]. AIMS Environmental Science, 2019, 6(4): 242-261. doi: 10.3934/environsci.2019.4.242

Related Papers:

[1]	Qinyan shen, Jiang wang, Liangying zhao . To investigate the internal association between SARS-CoV-2 infections and cancer through bioinformatics. Mathematical Biosciences and Engineering, 2022, 19(11): 11172-11194. doi: 10.3934/mbe.2022521
[2]	Yue Hu, Xiaoqin Mei, Dong Tang . Long non-coding RNA XIST is down-regulated and correlated to better prognosis in ovarian cancer. Mathematical Biosciences and Engineering, 2020, 17(3): 2070-2081. doi: 10.3934/mbe.2020110
[3]	Yongyin Han, Maolin Liu, Zhixiao Wang . Key protein identification by integrating protein complex information and multi-biological features. Mathematical Biosciences and Engineering, 2023, 20(10): 18191-18206. doi: 10.3934/mbe.2023808
[4]	Li-Sha Pan, Zacharia Ackbarkha, Jing Zeng, Min-Li Huang, Zhen Yang, Hao Liang . Immune marker signature helps to predict survival in uveal melanoma. Mathematical Biosciences and Engineering, 2021, 18(4): 4055-4070. doi: 10.3934/mbe.2021203
[5]	Changxiang Huan, Jiaxin Gao . Insight into the potential pathogenesis of human osteoarthritis via single-cell RNA sequencing data on osteoblasts. Mathematical Biosciences and Engineering, 2022, 19(6): 6344-6361. doi: 10.3934/mbe.2022297
[6]	Yutong Man, Guangming Liu, Kuo Yang, Xuezhong Zhou . SNFM: A semi-supervised NMF algorithm for detecting biological functional modules. Mathematical Biosciences and Engineering, 2019, 16(4): 1933-1948. doi: 10.3934/mbe.2019094
[7]	Babak Khorsand, Abdorreza Savadi, Javad Zahiri, Mahmoud Naghibzadeh . Alpha influenza virus infiltration prediction using virus-human protein-protein interaction network. Mathematical Biosciences and Engineering, 2020, 17(4): 3109-3129. doi: 10.3934/mbe.2020176
[8]	Moxuan Zhang, Quan Zhang, Jilin Bai, Zhiming Zhao, Jian Zhang . Transcriptome analysis revealed CENPF associated with glioma prognosis. Mathematical Biosciences and Engineering, 2021, 18(3): 2077-2096. doi: 10.3934/mbe.2021107
[9]	Jian-Di Li, Gang Chen, Mei Wu, Yu Huang, Wei Tang . Downregulation of CDC14B in 5218 breast cancer patients: A novel prognosticator for triple-negative breast cancer. Mathematical Biosciences and Engineering, 2020, 17(6): 8152-8181. doi: 10.3934/mbe.2020414
[10]	Sufang Wu, Hua He, Jingjing Huang, Shiyao Jiang, Xiyun Deng, Jun Huang, Yuanbing Chen, Yiqun Jiang . FMR1 is identified as an immune-related novel prognostic biomarker for renal clear cell carcinoma: A bioinformatics analysis of TAZ/YAP. Mathematical Biosciences and Engineering, 2022, 19(9): 9295-9320. doi: 10.3934/mbe.2022432

Abstract

References

[1]	Mitchell M, Curtis A, Sharp E, et al. (2012) Directions for social research to underpin improved groundwater management. J Hydrol 448: 223–231.
[2]	Conrad SA, Yates D (2018) Coupling stated preferences with a hydrological water resource model to inform water policies for residential areas in the Okanagan Basin, Canada. J Hydrol 564: 846–858. doi: 10.1016/j.jhydrol.2018.07.031
[3]	Hanjra MA, Qureshi ME (2010) Global water crisis and future food security in an era of climate change. Food Policy 35: 365–377. doi: 10.1016/j.foodpol.2010.05.006
[4]	Gu S, Jenkins A, Gao SJ, et al. (2017) Ensuring water resource security in China: The need for advances in evidence-based policy to support sustainable management. Environ Sci Policy 75: 65–69. doi: 10.1016/j.envsci.2017.05.008
[5]	Freund A, Aydin NY, Zeckzer D, et al. (2017) A Decision-Support System for Sustainable Water Distribution System Planning. IEEE Comput Graph Appl 37: 44–55. doi: 10.1109/MCG.2015.120
[6]	Gastélum JR, Valdés JB, Stewart S (2009) A Decision Support System to Improve Water Resources Management in the Conchos Basin. Water Resour Manag 23: 1519–1548. doi: 10.1007/s11269-008-9339-4
[7]	Wilder M (2010) Water governance in Mexico: Political and economic apertures and a shifting state-citizen relationship. Ecol Soc 15: 1–18.
[8]	Rowley HV, Peters GM, Lundie S, et al. (2012) Aggregating sustainability indicators: Beyond the weighted sum. J Environ Manage 111: 24–33. doi: 10.1016/j.jenvman.2012.05.004
[9]	Hedayati Aghmashhadi A (2018) Water Resource Policy Making based on the Pressures Management: Policy, Planning and Management of Water Resource in the Arid and Semi-Arid Regions. Beau-Bassin, Mauritius: LAP Publishing.
[10]	Yu Y, Chen X, Huttner P, et al. (2018) Model based decision support system for land use changes and socio-economic assessments. J Arid Land 10: 169–182. doi: 10.1007/s40333-018-0091-1
[11]	Loucks DP, Kindler J, Fedra K (1985) Interactive Water Resources Modeling and Model Use: An Overview. Water Resour Res 21: 95–102. doi: 10.1029/WR021i002p00095
[12]	Georgakakos AP (2007) Decision support systems for integrated water resources management with an application to the Nile Basin. In: Castelletti A, Soncini-Sessa R, Topics on System Analysis and Integrated Water Resources Management. Amsterdam: Elsevier Science, 99–116.
[13]	Serrat-Capdevila A, Valdes BJ, Gupta HV (2011) Decision Support Systems in Water Resources Planning and Management: Stakeholder Participation and the Sustainable Path to Science-Based Decision Making. In: Jao C, Efficient Decision Support Systems: Practice and Challenges From Current to Future. Rijeka, Croatia: InTech.
[14]	Othman F, Naseri M (2008) Decision Support Systems in Water Resources Management. In: Proceedings of the 9^th Asia Pasific Industrial Engineering Management Systems Conference. Bali, Indonesia : APIEMS 2008, 1772–1780.
[15]	Neuman J (2010) Are We There Yet? Weary Travelers on the Long Road to Water Policy Reform. Nat Resour J 211: 139–166.
[16]	Gutiãrrez RA (2010) When Experts Do Politics: Introducing Water Policy Reform in Brazil. Governance 23: 59–88. doi: 10.1111/j.1468-0491.2009.01467.x
[17]	Lein H, Tagseth M (2009) Tanzanian water policy reforms-between principles and practical applications. Water Policy 11: 203–220. doi: 10.2166/wp.2009.024
[18]	Nhapi I (2009) The water situation in Harare, Zimbabwe: A policy and management problem. Water Policy 11: 221–235. doi: 10.2166/wp.2009.018
[19]	Biswas AK, Tortajada C (2010) Future Water Governance: Problems and Perspectives. Int J Water Resour Dev 26: 129–139. doi: 10.1080/07900627.2010.488853
[20]	Schlueter M, Hirsch D, Pahl-Wostl C (2010) Coping with change: Responses of the Uzbek water management regime to socio-economic transition and global change. Environ Sci Policy 13: 620–636. doi: 10.1016/j.envsci.2010.09.001
[21]	Akter S, Grafton RQ, Merritt WS (2014) Integrated hydro-ecological and economic modeling of environmental flows: Macquarie Marshes, Australia. Agric Water Manag 145: 98–109. doi: 10.1016/j.agwat.2013.12.005
[22]	Hurd BH, Coonrod J (2012) Hydro-economic consequences of climate change in the upper Rio Grande. Clim Res 53: 103–118. doi: 10.3354/cr01092
[23]	Koundouri P, Reppas D, Skianis V (2015) Socio-Economics and Water Management: Revisiting the Contribution of Economics in the Implementation of the Water Framework Directive in Greece. Berlin: Springer, 357–377.
[24]	Lanini S, Courtois N, Giraud F, et al. (2004) Socio-hydrosystem modelling for integrated water-resources management-the Hérault catchment case study, southern France. Environ Model Softw 19: 1011–1019. doi: 10.1016/j.envsoft.2003.11.004
[25]	Słowiński R (1986) A multicriteria fuzzy linear programming method for water supply system development planning. Fuzzy Sets Syst 19: 217–237. doi: 10.1016/0165-0114(86)90052-7
[26]	Huang GH (1998) A hybrid inexact-stochastic water management model. Eur J Oper Res 107: 137–158. doi: 10.1016/S0377-2217(97)00144-6
[27]	Jairaj PG, Vedula S (2000) Multireservoir System Optimization using Fuzzy Mathematical Programming. Water Resour Manag 14: 457–472. doi: 10.1023/A:1011117918943
[28]	Luo B (2003) Adaption to Climate Change through Water Trading under Uncertainty-An Inexact Two-Stage Nonlinear Programming Approach. J Environ Informatics 2: 58–68. doi: 10.3808/jei.200300022
[29]	Maqsood I, Huang GH, Yeomans JS (2005) An interval-parameter fuzzy two-stage stochastic program for water resources management under uncertainty. Eur J Oper Res 167: 208–225. doi: 10.1016/j.ejor.2003.08.068
[30]	Li YP, Huang GH, Nie SL, et al. (2007) ITCLP: An inexact two-stage chance-constrained program for planning waste management systems. Resour Conserv Recycl 49: 284–307. doi: 10.1016/j.resconrec.2006.03.017
[31]	Wu SM, Huang GH, Guo HC (1997) An interactive inexact-fuzzy approach for multiobjective planning of water resource systems. Water Sci Technol 36: 235–242.
[32]	Seifi A, Hipel KW (2001) Interior-Point Method for Reservoir Operation with Stochastic Inflows. J Water Resour Plan Manag 127: 48–57. doi: 10.1061/(ASCE)0733-9496(2001)127:1(48)
[33]	Wang S, Huang GH, Lu HW, et al. (2011) An interval-valued fuzzy linear programming with infinite α-cuts method for environmental management under uncertainty. Stoch Environ Res Risk Assess 25: 211–222. doi: 10.1007/s00477-010-0432-x
[34]	Huang GH (1996) IPWM: An Interval Parameter Water Quality Management Model. Eng Optim 26: 79–103. doi: 10.1080/03052159608941111
[35]	Bender MJ, Simonovic SP (2000) A fuzzy compromise approach to water resource systems planning under uncertainty. Fuzzy Sets Syst 115: 35–44. doi: 10.1016/S0165-0114(99)00025-1
[36]	Simonovic SP, Fahmy H (1999) A new modeling approach for water resources policy analysis. Water Resour Res 35: 295–304. doi: 10.1029/1998WR900023
[37]	Faye RM, Sawadogo S, Mora-Camino F (2005) Flexible management of water resource systems. Appl Math Comput 167: 516–527.
[38]	Lee CS, Chang SP (2005) Interactive fuzzy optimization for an economic and environmental balance in a river system. Water Res 39: 221–231. doi: 10.1016/j.watres.2004.09.013
[39]	Edirisinghe NCP, Patterson EI, Saadouli N (2000) Capacity Planning Model for a Multipurpose Water Reservoir with Target-Priority Operation. Ann Oper Res 100: 273–303. doi: 10.1023/A:1019200623139
[40]	Azaiez MN (2002) A model for conjunctive use of ground and surface water with opportunity costs. Eur J Oper Res 143: 611–624. doi: 10.1016/S0377-2217(01)00339-3
[41]	Pallottino S, Sechi GM, Zuddas P (2005) A DSS for water resources management under uncertainty by scenario analysis. Environ Model Softw 20: 1031–1042. doi: 10.1016/j.envsoft.2004.09.012
[42]	Li YP, Huang GH, Nie SL (2006) An interval-parameter multi-stage stochastic programming model for water resources management under uncertainty. Adv Water Resour 29: 776–789. doi: 10.1016/j.advwatres.2005.07.008
[43]	Nasiri F, Maqsood I, Huang G, et al. (2007) Water Quality Index: A Fuzzy River-Pollution Decision Support Expert System. J Water Resour Plan Manag 133: 95–105. doi: 10.1061/(ASCE)0733-9496(2007)133:2(95)
[44]	Carey M, Baraer M, Mark BG, et al. (2014) Toward hydro-social modeling: Merging human variables and the social sciences with climate-glacier runoff models (Santa River, Peru). J Hydrol 518: 60–70. doi: 10.1016/j.jhydrol.2013.11.006
[45]	Giupponi C, Sgobbi A (2013) Decision Support Systems for Water Resources Management in Developing Countries: Learning from Experiences in Africa. Water 5: 798–818. doi: 10.3390/w5020798
[46]	Soncini-Sessa R, Castelletti A, Weber E (2003) A DSS for planning and managing water reservoir systems. Environ Model Softw 18: 395–404. doi: 10.1016/S1364-8152(03)00035-5
[47]	Li YP, Huang GH, Huang YF, et al. (2009) A multistage fuzzy-stochastic programming model for supporting sustainable water-resources allocation and management. Environ Model Softw 24: 786–797. doi: 10.1016/j.envsoft.2008.11.008
[48]	Spangenberg JH, Douguet J-M, Settele J, et al. (2015) Escaping the lock-in of continuous insecticide spraying in rice: Developing an integrated ecological and socio-political DPSIR analysis. Ecol Modell 295: 188–195. doi: 10.1016/j.ecolmodel.2014.05.010
[49]	Smeets E, Weterings R (1999) Environmental indicators: Typology and overview. Copenhagen: European Environment Agency Press.
[50]	Gabrielsen P, Bosch P (2003) Environmental indicators: Typology and overview. Copenhagen: European Environment Agency Intern. Work. Pap.
[51]	European Environment Agency (2006) EEA Glossary. Brussels: European Commission.
[52]	Voogd H (1983) Multicriteria evaluation for urban and regional planning. Delft: Delftsche Uitgevers Maatschappij B.V.
[53]	Carver SJ (1991) Integrating multi-criteria evaluation with geographical information systems. Int J Geogr Inf Syst 5: 321–339. doi: 10.1080/02693799108927858
[54]	Eastman JR (2012) IDRISI Selva manual. Worcester, MA, USA: Clark University Press.
[55]	Malczewski J (1999) GIS and multicriteria decision analysis. New York: John Wiley and Sons, Inc.
[56]	Shahabi H, Niyazi C (2009) Effecting factors in relief and rescue stations site selection by using weighted linear combination, case study: Saghez-Sanandaj road. In: Proceedings of the Eighth International Conference on Geomatics. Tehran: ICG 2009.
[57]	Burrough PA (1990) Methods of Spatial Analysis in GIS. Int J Geogr Inform Syst 4: 221–223.
[58]	Saaty TL (2001) Fundamentals of the Analytic Hierarchy Process. Dordrecht: Springer, 15–35.
[59]	Deng H (1999) Multicriteria analysis with fuzzy pairwise comparison. Int J Approx Reason 21: 215–231. doi: 10.1016/S0888-613X(99)00025-0
[60]	Boroushaki S, Malczewski J (2008) Implementing an extension of the analytical hierarchy process using ordered weighted averaging operators with fuzzy quantifiers in ArcGIS. Comput Geosci 34: 399–410. doi: 10.1016/j.cageo.2007.04.003
[61]	Linkov I, Satterstrom FK, Steevens J, et al. (2007) Multi-criteria decision analysis and environmental risk assessment for nanomaterials. J Nanoparticle Res 9: 543–554. doi: 10.1007/s11051-007-9211-0
[62]	Alam Tabriz A, Bagherzade Azar M (2009) Combining AHP and TOPSIS Adjusted for supplier selection strategy. Res Manag 6: 149–181.
[63]	Ghodsi Poor H (2010) Analytical Hierarchy Process (AHP). Tehran: Amirkabir University of Technology Press.
[64]	Razmi J, Sadegh Amal Nik M, Hashemi M (2008) Supplier selection techniques using fuzzy analytic network process. Tehran Uni Eng 42: 935–946.
[65]	Leung LC, Cao D (2000) On consistency and ranking of alternatives in fuzzy AHP. Eur J Oper Res 124: 102–113. doi: 10.1016/S0377-2217(99)00118-6
[66]	Hansen HS (2005) GIS-based Multi-Criteria Analysis of Wind Farm Development. In: Hauska H, Tveite H, ScanGis 2005: Proceedings of the Tenth Scandinavian Research Conference on Geographical Information Science. Stockholm: Department of Planning and Environment, 75–87.
[67]	Lee S (2007) Application and verification of fuzzy algebraic operators to landslide susceptibility mapping. Environ Geol 52: 615–623. doi: 10.1007/s00254-006-0491-y
[68]	Kabir S, Edifor E, Walker M, et al. (2014) Quantification of Temporal Fault Trees Based on Fuzzy Set Theory. Springer, Cham, pp 255–264
[69]	Ghosh JK, Bhattacharya D, Sharma SK (2012) Fuzzy Knowledge Based GIS for Zonation of Landslide Susceptibility. In: Zamojski W, Mazurkiewicz J, Sugier J, et al., Proceedings of the Ninth International Conference on Dependability and Complex Systems DepCoS-RELCOMEX. Brunów, Poland: Springer, Cham.
[70]	Dombi J (1990) Membership function as an evaluation. Fuzzy Sets Syst 35: 1–21. doi: 10.1016/0165-0114(90)90014-W
[71]	Keller CP (1995) Geographic information systems for geoscientists: Modelling with GIS. Iny Graeme F. Bonham-Carter, Pergamon, Computer Methods in the Geosciences, Volume 13, 1994, 398 p., incl. bibliographic references and index, US $40.00. Comput Geosci 21: 1110–1112.
[72]	Zimmermann HJ, Zysno P (1980) Latent connectives in human decision making. Fuzzy Sets Syst 4: 37–51. doi: 10.1016/0165-0114(80)90062-7
[73]	Atkinson DM, Deadman P, Dudycha D, et al. (2005) Multi-criteria evaluation and least cost path analysis for an arctic all-weather road. Appl Geogr 25: 287–307. doi: 10.1016/j.apgeog.2005.08.001
[74]	Salari M, Bagherpour M, Wang J (2014) A novel earned value management model using Z-number. Int J Appl Decis Sci 7: 97–119.
[75]	Önüt S, Kara SS, Işik E (2009) Long term supplier selection using a combined fuzzy MCDM approach: A case study for a telecommunication company. Expert Syst Appl 36: 3887–3895. doi: 10.1016/j.eswa.2008.02.045
[76]	Gogus O, Boucher TO (1998) Strong transitivity, rationality and weak monotonicity in fuzzy pairwise comparisons. Fuzzy Sets Syst 94: 133–144. doi: 10.1016/S0165-0114(96)00184-4
[77]	Lin H, Kao J, Li K, et al. (1996) Fuzzy GIS assisted landfill siting analysis. In: Proceedings of the Twelfth International Conference on Solid Waste Technology and Management. Philadelphia, PA, USA: Journal of Solid Waste Technology and Management, 14–17.
[78]	Valizadeh K, Shababi H (2009) Necessities of GIS usage in urban water management at the time of Natural accidents (Case Study: Saqqez City). In: Proceeding of the Fourth International Conference on Geographic Information Systems. Paris: ICGIS.
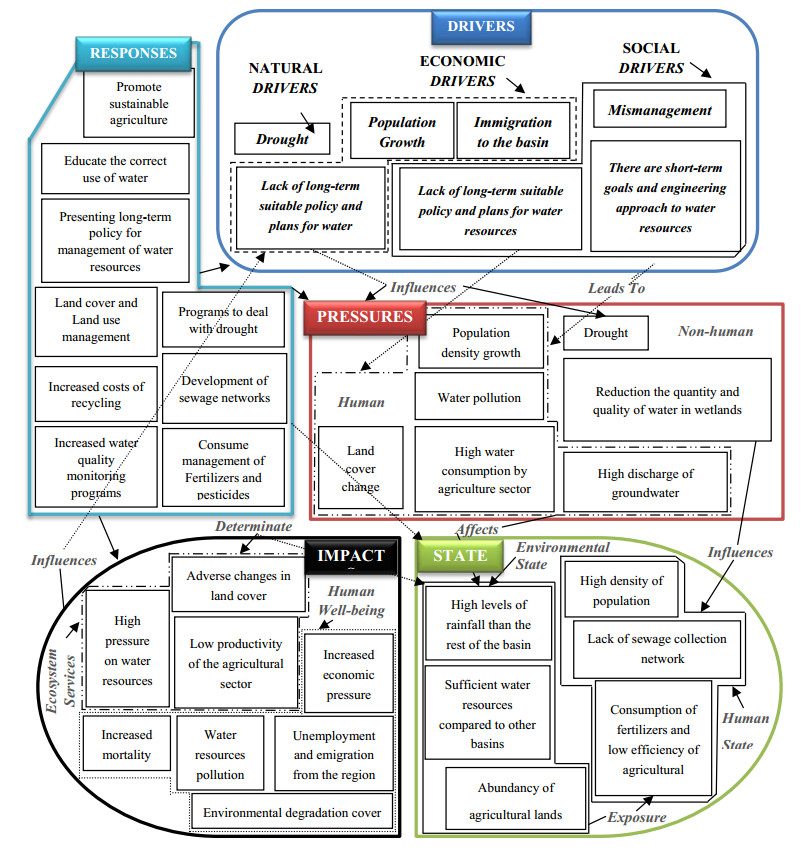
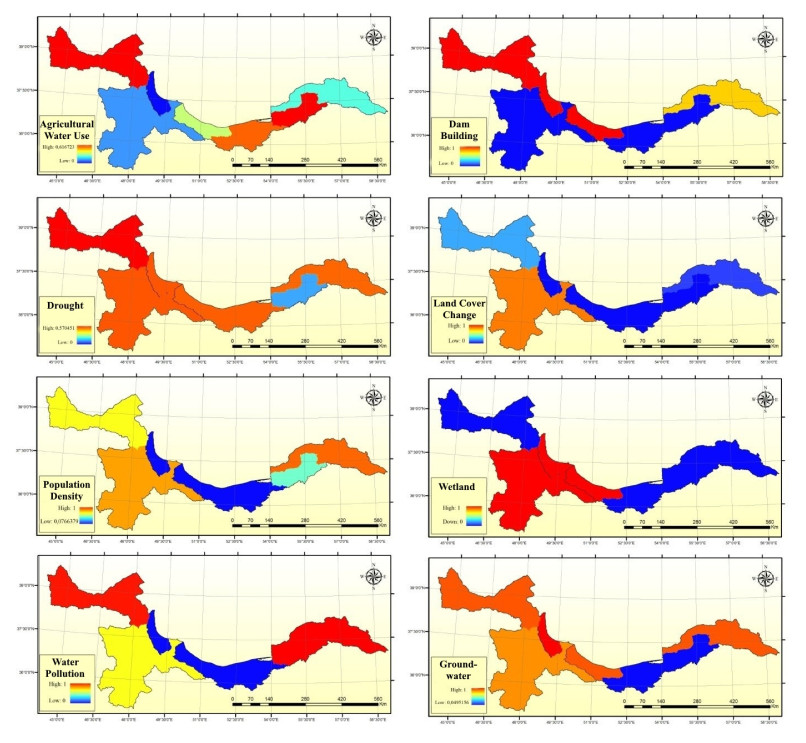
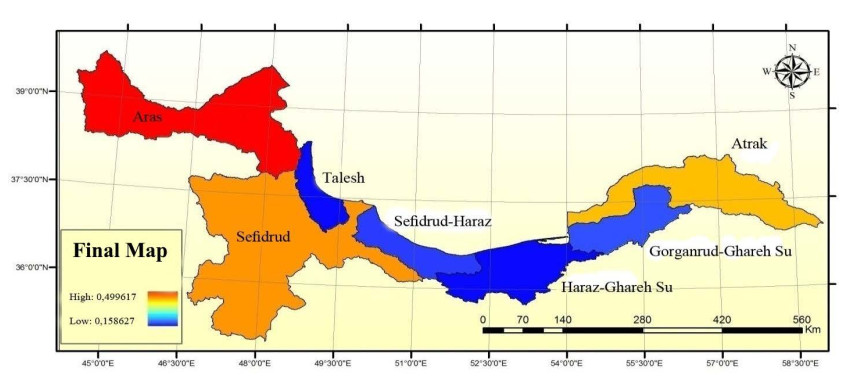
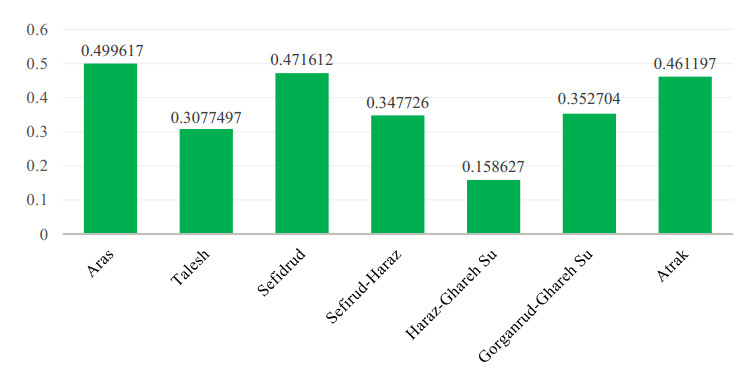
[79]	Ministry of Energy (2013) Water Master Plan Udate in the Aras, Urmia, Talesh, Sefidrud, Sefidrud-Haraz, Haraz-Ghareh Su, Gorganrud-Ghareh Su, Atrak. Ministry of Energy, Water and Abfa Deputy. Tehran: Office of Planning and Abfa Macro Water.
[80]	Statistical Center of Iran (2012) Iran Census of Population and Housing, 2011. Tehran: SCI Press.

This article has been cited by:

1.	Edward A. Rietman, Jacob G. Scott, Jack A. Tuszynski, Giannoula Lakka Klement, Personalized anticancer therapy selection using molecular landscape topology and thermodynamics, 2017, 8, 1949-2553, 18735, 10.18632/oncotarget.12932
2.	Edward A. Rietman, Sophie Taylor, Hava T. Siegelmann, Marco A. Deriu, Marco Cavaglia, Jack A. Tuszynski, Using the Gibbs Function as a Measure of Human Brain Development Trends from Fetal Stage to Advanced Age, 2020, 21, 1422-0067, 1116, 10.3390/ijms21031116
3.	Elizabeth J. Brant, Edward A. Rietman, Giannoula Lakka Klement, Marco Cavaglia, Jack A. Tuszynski, Xu-jie Zhou, Personalized therapy design for systemic lupus erythematosus based on the analysis of protein-protein interaction networks, 2020, 15, 1932-6203, e0226883, 10.1371/journal.pone.0226883
4.	J. James Frost, Kenneth J. Pienta, Donald S. Coffey, Symmetry and symmetry breaking in cancer: a foundational approach to the cancer problem, 2018, 9, 1949-2553, 11429, 10.18632/oncotarget.22939
5.	Edward A. Rietman, John Platig, Jack A. Tuszynski, Giannoula Lakka Klement, Thermodynamic measures of cancer: Gibbs free energy and entropy of protein–protein interactions, 2016, 42, 0092-0606, 339, 10.1007/s10867-016-9410-y
6.	Edward Rietman, Jack A. Tuszynski, 2018, Chapter 8, 978-3-319-74973-0, 139, 10.1007/978-3-319-74974-7_8
7.	Ellen Kure Fischer, Antonio Drago, A molecular pathway analysis stresses the role of inflammation and oxidative stress towards cognition in schizophrenia, 2017, 124, 0300-9564, 765, 10.1007/s00702-017-1730-y
8.	Chang Yu, Edward A. Rietman, Hava T. Siegelmann, Marco Cavaglia, Jack A. Tuszynski, Application of Thermodynamics and Protein–Protein Interaction Network Topology for Discovery of Potential New Treatments for Temporal Lobe Epilepsy, 2021, 11, 2076-3417, 8059, 10.3390/app11178059
9.	Nicolas Carels, Domenico Sgariglia, Marcos Guilherme Vieira Junior, Carlyle Ribeiro Lima, Flávia Raquel Gonçalves Carneiro, Gilberto Ferreira da Silva, Fabricio Alves Barbosa da Silva, Rafaela Scardini, Jack Adam Tuszynski, Cecilia Vianna de Andrade, Ana Carolina Monteiro, Marcel Guimarães Martins, Talita Goulart da Silva, Helen Ferraz, Priscilla Vanessa Finotelli, Tiago Albertini Balbino, José Carlos Pinto, A Strategy Utilizing Protein–Protein Interaction Hubs for the Treatment of Cancer Diseases, 2023, 24, 1422-0067, 16098, 10.3390/ijms242216098
10.	Giulia Pozzati, Jinrui Zhou, Hananel Hazan, Giannoula Lakka Klement, Hava T. Siegelmann, Jack A. Tuszynski, Edward A. Rietman, A Systems Biology Analysis of Chronic Lymphocytic Leukemia, 2024, 4, 2673-7523, 163, 10.3390/onco4030013

Reader Comments

Your name:*

Email:*
© 2019 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)