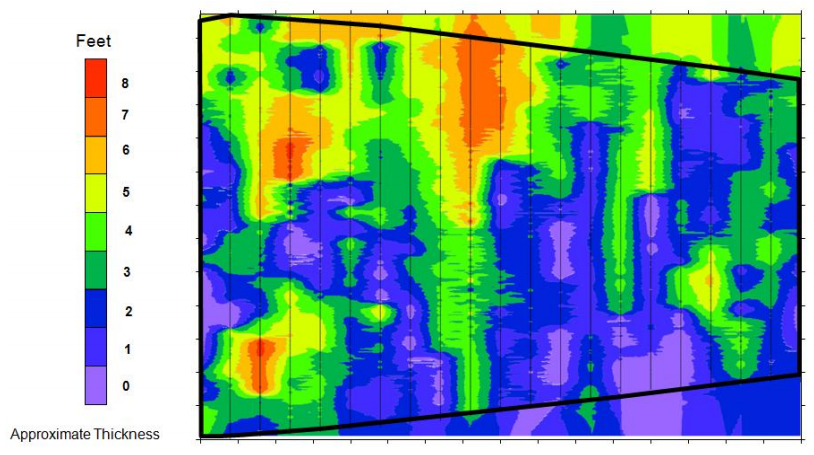
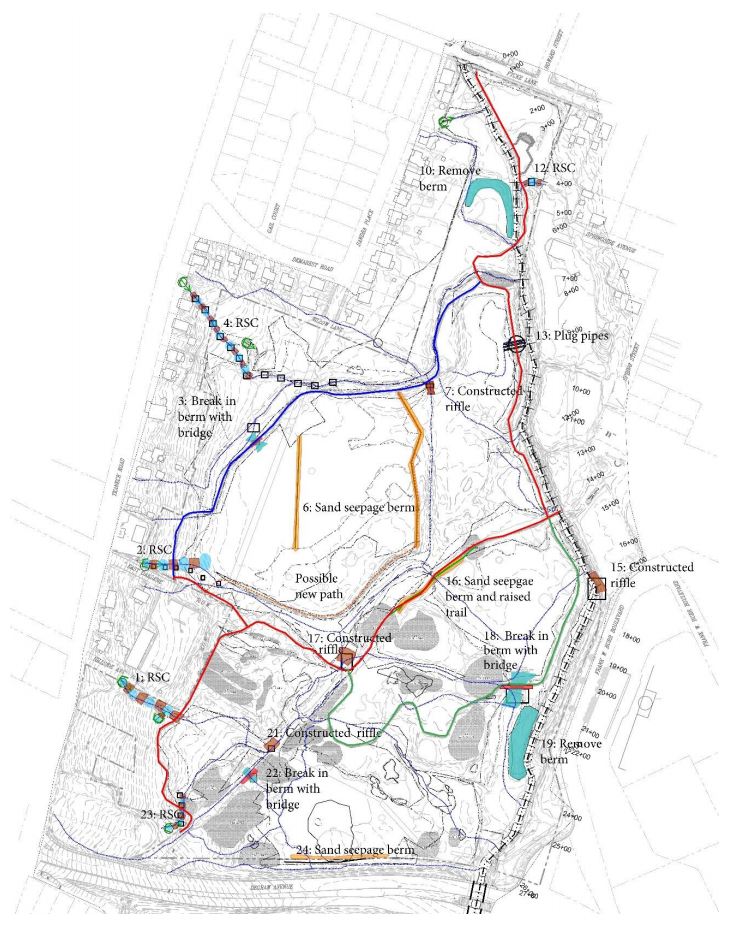
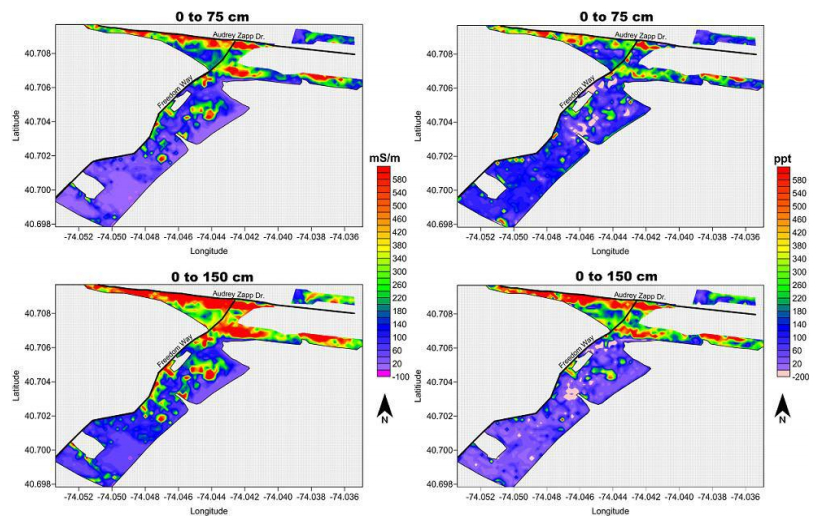
The continuing loss of urban wetlands due to an expanding human population and urban development pressures makes restoration or creation of urban wetlands a high priority. However, urban wetland restorations are particularly challenging due to altered hydrologic patterns, a high proportion of impervious surface and stormwater runoff, degraded urban soils, historic contamination, and competitive pressure from non-native species. Urban wetland projects must also consider human-desired socio-economic benefits. We argue that using current wetland restoration approaches and existing regulatory “success” criteria, such as meeting restoration targets for vegetation structure based on reference sites in non-urban locations, will result in “failed” urban restorations. Using three wetland Case Studies in highly urbanized locations, we describe geophysical tools, stormwater management methods, and design approaches useful in addressing urban challenges and in supporting “successful” urban rehabilitation outcomes. We suggest that in human-dominated landscapes, the current paradigm of “restoration” to a previous state must shift to a paradigm of “rehabilitation”, which prioritizes wetland functions and values rather than vegetation structure in order to provide increased ecological benefits and much needed urban open space amenities.
1.
Practical applications
This approach will be beneficial in developing awareness on how to properly manage the agricultural waste and also its utilization for the synthesis of numerous compounds such as lactic acid, bio-sorbent, biohydrogen, enzyme etc. which serve as a base for developing linkages among industry and sharing new ideas, technologies.
2.
Introduction
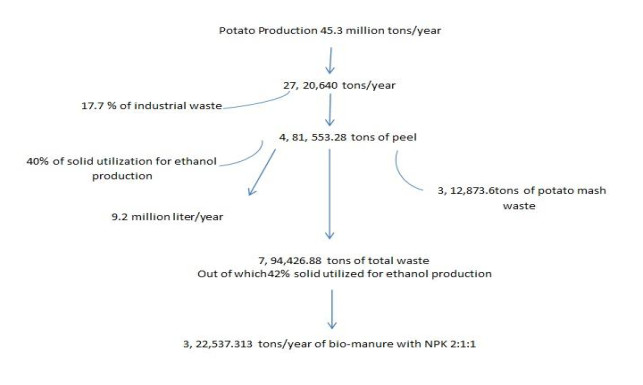
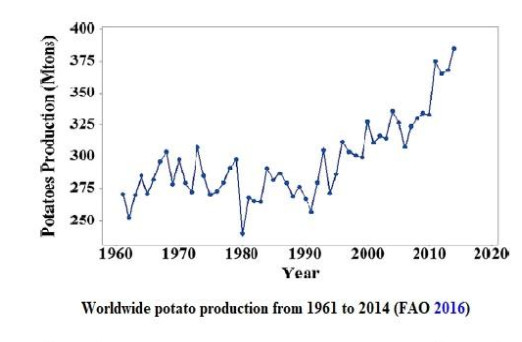
Potato (Solanum tuberosum L.) is ranked among one of the chief crops producing worldwide. As per the statistics of the Food and Agriculture Organization (FAO), the annual production of potato was over 300 million tons in 2016 [1] as shown in Figure 1. Besides, food processing industry is one of the most important businesses worldwide produces a large number of byproducts as organic waste that need to be handled and managed inappropriate way not only to avoid environmental pollution but also extend further apart by contributing towards economic boost from byproduct utilization [2]. Potato peel as a byproduct of food processing industry poses to be totally inexpensive, valuable and affordable starting material for the production of economically important substances, value addition, product extraction including dietary fibre, biopolymers, natural antioxidants, and natural food additives [3]. Industrial processing generates between 70 to 140 thousand tons of peels worldwide annually [4]. Figure 2 illustrates the utilization of potato peel waste.
Traditionally potato peel waste is used for producing low-value animal feed [5], fertilizer or being the raw material of biogas, which causes waste of abundant nutritive materials within it having the properties of antioxidant, antibacterial, apoptotic, chemopreventive and anti-inflammatory [6]. But still, the central dogma of the present study is the proper waste management with the economic feasibility of the processing development [7].
Potato peel is being studied in various manuscripts as an effective feed for animals. Although it has to be treated prior to utilization in animal feed as for non-ruminants feed it is not well suited because of having too much fibre to be digested. On the other side, the same has been used successfully in various studies for the feed of multi-gastric animals. The present review recapitulates applicable endeavours of potato peels exploitation in food as well as nonfood purposes including the extraction, verification and utilization of bioactive components, nutritional aspects, biotechnological usage, livestock feed and other miscellaneous use of potato peels as major potato processing industrial waste.
3.
The composition of potato peel
For a complete understanding of the physicochemical properties of potato peel, it is necessary to focus on its physical and chemical composition. The knowledge of these properties would help in developing an environmentally friendly approach for the utilization of potato peel. Table 1 illustrated different compounds present in potato peel [8,9,10]. Based on geographical cultivation areas, the composition, variety, colour and breed, of potatoes (and thus their peel) varies [11]. Potato peel contains various polyphenols and phenolic acids which are responsible for its antioxidant activities, whereas fatty acids and lipids showed antibacterial activities [12,13]. Potato peel also contains starch (25%), non-starch polysaccharide (30%), protein (18%), acid-soluble and acid-insoluble lignin (20%), lipids (1%) and ash (6%) on dry basis [14]. The lipid fraction includes long-chain fatty acids, alcohols, triglycerides and sterol esters. In addition, lignin units have been found in the cell wall of potatoes [6]. Potato peel is rich in starch (52% dry weight), but the content of fermentable reducing sugar is limited (0.6% dry weight). For this purpose, fermentation of potato peel is not practically possible, thus initial hydrolysis (enzymatic or acidic) of carbohydrates is required to increase the content of fermentable reducing sugar [8]. Elemental analysis of potato peel shows that it contains (in % dry basis): C (43.78 ± 0.15), H (5.96 ± 0.12), N (4.06 ± 0.01) and O (46.21 ± 0.28). The C/N ratio of potato peel is 10.7 and its pH 6.5 [15]. The calorific value of potato peel is 17.37 ± 0.38 (MJ/kg) [6]. Various phenolic acids such as gallic acid (58.6–63.0 mg/100 g), protocatechuic acid (216.0–256.0 mg/100 g), vanillic acid (43.0–48.0 mg/100 g), caffeic acid (278.0–296.0 mg/100 g), chlorogenic acid (753.0–821.3 mg/100 g), p-hydroxybenzoic acid (82.0–87.0 mg/100 g) and p-coumaric acid (41.8–45.6 mg/100 g) are found in the potato peel extract.
These values range from 0.17% to 0.21% (dry weight basis) and show that potato peel has a higher content of lipid than peeled potatoes (0.10%) [8]. Onyeneho and Hettiarachchy [16] had an alike fatty acid composition and have higher quantities of PUFAS (polyunsaturated fatty acids). Variations in the comparative quantities of single fatty acids appeared to be affected by the colour of the potato peel.
4.
Peeling methods and yield percentage
The peeling method has been found to be a critical factor affecting the chemical composition and further utilization suitability of potato peel. As in the steaming method which is applied for the production of dehydrated potatoes, results in more dietary fibre and less starch as compared to the potato peel obtained by abrasion method, used by various potato chip manufacturing industries [17]. In another study, the role of extruded and un-extruded potato peel was studied, as another source of dietary fibre replacing wheat bran and cellulose, for its binding capacity with carcinogenic benzopyrene in digestion model designed in-vitro
[18]. Un-extruded steam potato peels showed the potential to bind more benzopyrene than that of extruded at 110 ℃ with 30% moisture introduced. Additionally, the same binding is lower in abrasion potato peel as compared to steam potato peel. Potato peels with steam peeling were extruded at 110 ℃ to 150 ℃ temperature range and provided with 30 to 35% of moistures, associated with increased lignin and dietary fibre contents with decreased starch. While in abrasion extruded potato peel, the lignin contents were decreased but dietary fibre level remained unaffected with increased soluble non-starch polysaccharides content in both types of peeling due to the extrusion. The insoluble fibre obtained from extruded steam peels, yields with a higher quantity of glucose, was documented to be the potential motive for resistant starch formation. Whereas potato peel from manual peeling produced about 63% of fibre on a dry weight basis, which was further categorized into hemicellulose, lignin, cellulose and pectic substances. The fractions obtained by this gives 7.7% ash, 3.4% pectin, 14.7% protein, 2.2% cellulose, 66.8% starch, 0.9% of reducing sugars and 1.4% of total soluble sugars while each and every component serves as economic currency when extracted [19].
5.
Potato peels—as a source of dietary fiber
5.1. Pharmaceutical application
Dietary fibre is a bulking mediator, enhancing intestinal mobility and faecal hydration. In numerous studies, the benefits of dietary fibres are well documented [20]. Dietary fibre, a broad term, includes various carbohydrates, hemicelluloses, cellulose, pectin, lignin, gum etc. having chief pharmaceutical application as well. Camire, Zhao and Violette [18] documented the insolubility of fibre extracted from potato peel and its ability of binding bile acids during the in-vitro study which contribute as one of the key mechanism in which specific source of dietary fibre potentially reduces the plasma cholesterol. Lazarov and Werman [21] reported the dietary fibres extracted from potato peel showed a hypocholesterolemic effect when experimented with rats, feeding them fibre of potato peels, revealed the fact that rats ultimately showed 40% reduced plasma cholesterol while 30% reduction in hepatic fat cholesterol was detected when compared with controlled rats. Additionally, high levels of low-density lipoprotein (LDL), cholesterol, a high concentration of triglyceride, dyslipidemia, contributed to the agammaegation of blood platelets, increasing the risk for hypertension [22] and cardiovascular diseases (CVD) [23]. In addition, dietary fibres contribute to the lowering of blood glucose level and related health problems in both types of diabetic patients.
Dietary fibre enhances other sugars absorption by altering the emptying time of the gastric system and encourages insulin response as well so that they can be promoted as ant-diabetic drug extracted from potato peel with reduced preparation cost and efficient utilization. Camire, et al. [24] reported the potential effect of potato peel as anti-carcinogenic substance. Potato peel dietary fibres are believed to impart certain protective roles against carcinogenesis and mutagenesis through various mechanisms including the binding of mutagenic and carcinogenic materials, increasing faecal bulk and water absorption, reducing the intestines-transit time, and lowering the faecal pH via fermentation process through intestinal microflora.
The potatoes peel waste has been proved to be an environmentally friendly and economical choice to be considered for use as adsorbents for pharmaceutical effluents treatment [25]. There have been certain toxic compounds as environmental pollutants originated from pharmaceutical preparations that ultimately get penetration into drinking water supplies, groundwater, and surface waters reasoned to inadequate wastewater processing. In this context, activated carbon has been reported to be the most likely adsorbent material with higher adsorption ability for various pollutants (metals and dyes etc.). In another instance, potato peel waste was used for the production of carbon samples after pyrolysis/hydrothermal treatment. Afterwards, with slight modification with oxidation agents and activation with KOH, the above-mentioned substances were used to remove the pharmaceutical compounds (specifically pramipexole and dorzolamide) from the effluents [25].
5.2. Application in the baking industry
In baking industries, dietary fibres extracted from numerous sources have been used in combination with the wheat flour, as almost 50% of potato peel consists of dietary fibre (w/w). Talking about baking industry potato peel fibre (PPF) can contribute to economic boost by serving as a low-cost raw material with superior physical and chemical properties in comparison to wheat bran, studied by. The PPF has been reported to have better water holding capacity with low starch content. Furthermore, some quality defects like musty odour through the use of PPF can be removed by using extruded potato peels [22].
Moreover, Abd-El-Magied [26] reported the effect of potato peel in biscuit processing by using 5 and 10% (w/w) potato peel respectively, replacing wheat flour, were shown to have smaller stack weight with the acceptable sensory score [27]. In another study, muffins with 25% potato peel supplementation resulted in acceptable quality with resistance to compression.
6.
Biotechnological application of potato peels
Potato peel is documented to be an exceptionally low cost and effective substrate for the production of a starch hydrolyzing enzyme, thermo-stable alpha-amylase under controlled solid-state growth conditions, which is broadly employed in various food industries [30]. Moreover, in other studies, potato peel as a low-cost medium has been used to produce alkaline protease and alpha-amylase enzyme with potential application in detergents [31]. Potato peels have found to have specie dependent antimicrobial activity, while in a study the extract of potato peel was reported to be effective against gram-negative bacteria [32]. In another study, potato peel extract was examined for the antimicrobial activity and found to be potentially effective against bacteria as well as fungal species. Compared to streptocycline (antibiotic), potato peel extract effects had significantly against Clavibacter michigenensis and Pseudomonas aeruginosa [33].
Potato peel is also able to hold up the economic growth by producing various extracellular hydrolytic enzymes, by means of Bacillus subtilis. However, in terms of activity and amount, the highest productivity was achieved in a study by using Bacillus amylolequifaciens which were grown over potato peels solid media as compared to various other fruit samples. The mannose enzyme produced, has renowned for its growing interest in the industrial sector for the bioconversion of agro-based industrial residues, by randomly hydrolyzing the hetero-mannans (major softwood hemicellulose) axial chain [34]. Manassas have been experienced in various industrial processes to be effective in the vegetable oil extraction from leguminous seeds, reduces the viscosity of extracts during instant coffee and other oligosaccharide manufacturing, as well as it is significantly used in paper and textile industries.
Potato peel starch waste is proved to be a suitable raw material for industrial fermentation in comparison to other traditional substrates such as syrups and molasses in various cases. While the production of polygalacturonases, proteases and amylases extracted from potato peel waste substrate with the help of Bacillus subtilis have been proved to be a promising application on an industrial scale [35].
6.1. Biogas production
Biogas (CH4) from Potato peel waste is produced by anaerobic fermentation by utilizing starch from peels. The process has advantages as it has low cost and simple method that could be conducted in the same area in situ. It has been reported that each ton of starch waste produces 250 m3 of biogas [35]. In another study, the potential of anaerobically digested Potato peel and its residue of lactic acid fermentation was investigated for methane production. The analytical results revealed the production of 60 to 70% methane. The digester using potato peel fermentation residue as feedstock showed maximum cumulative methane production of 273 Liter/kg with good performance, followed by 239 Liter/kg production by using potato peel waste in the same conditions. Furthermore, et al. [36] initiated potato residue-based biogas fermentation system known as mixture fermentation and reported 0.55 L/GVS biogas production ratio which was much higher as compared to multiple inoculum fermentation of 0.32 L/GVS. Similarly in another study [37] stated that 2.8 kWh per (kgVS) energy was produced and the Carbon oxygen demand (COD) removal treatments were about 61% by the co-digestion of cow manure with potato pulp in a continuously stirred tank reactor (CSTR). Though, with escalating the solid loadings of potato peel fermentation residue feedstock from 6.4–9.1%, the methane production was repressed [38].
6.2. Production of lactic acid
Lactic acid (LA) has considered an important organic acid due to its wide applications in pharmaceuticals, food, cosmetic industry [39]. In general, Lactic acid is synthesized through carbohydrates fermentation with fungi and bacteria. More recently, potato peels serve as an alternative to producing lactic acid by anaerobic fermentation through the inoculation of potato peel waste with undefined mixed culture in a sequencing batch reactor. The set of 0.8 L sequencing batch reactors were employed with solids withholding time of 2 to 4 days, utilizing gelatinized potato peel waste with 30 to 50 g L−1 of solids content range for the optimization of productivity and yield. The maximum LA yields 0.25 g potato peel waste with 125 mg g−1 d−1 as highest productivity achieved. A scale-up sequencing batch reactor analysis employing gelatinized potato peel, with 80 g/L solids content, on the scale of 3 L was used while the highest lactic acid yield of 0.14 g g−1 potato peel waste and 138 mg g−1 d−1 productivity were obtained by 1 d sequencing batch reactor [38]. Liang, McDonald and Coats [6] reported the fermentation of potato peel waste at 35 ℃ to produce ethanol, acetic acid and lactic acid while their numeric data obtained on the 2nd day of the experiment is depicted in Table 3. Moreover, with the wide use of LA in the food industry as well as its application in pharmaceutical, cosmetic and other sectors illustrate it an important industrial stock. While the production of lactic acid from zero-value raw material, potato peel, can significantly improve the economic status of the country.
6.3. Production of polyphenol oxidase enzyme
However, PP has been proved to be an applicable source of polyphenol oxidase enzyme. For the extraction and purification of polyphenol oxidase from PP waste, a two-phase aqueous system can be applied. The two-phase aqueous system is composed of potassium phosphate buffer and polyethene glycol. At optimized experimental conditions, NaCl 2.08 mmol/L, polyethylene glycol 1500 17.62% (w/w) and potassium phosphate buffer 15.11% (w/w) at pH 7 was found. While the yield of 7.8%, a purification factor of 4.5%, and a maximum partition coefficient of 3.7% resulted. After partial purification of polyphenol oxidase from the aqueous two-phase system, further purification of the enzyme was done by the gel chromatography which upsurges the purity up to 12.6 folds. The purified polyphenol oxidase in the study was characterized through sodium-dodecyl-sulfate polyacrylamide-gel electrophoresis, followed by Km value of 3.3 mmol/L and Vmax value 3333 U/mL. Thus, the aqueous two-phase system has been proved to be a smart option to obtain purified polyphenol oxidase enzyme from potato peel waste [35]. Likewise, et al. [49] extracted polyphenol oxidase from PP blended with phosphate buffer of different pH values and concentrations. Triton X-114 (1%) was also added to the extraction medium. At optimal experimental conditions, the maximum specific activity of polyphenol oxidase was obtained as 3572.74 units/mg of protein.
6.4. Bio-oil and biochar production from PP waste
Both biochar and bio-oil were synthesized from the fermentation of PP waste and its residue by employing laboratory-scale auger pyrolyzer at the temperature of 450 ℃. Ultimate and proximate tests of feedstock materials potato peel and its fermentation residues were determined. The bio-oils produced by PP waste and its fermentation residue proved to have a higher level of suberin-derived and lipid components and better absorption performance in comparison to bio-oil produced by hybrid poplar pyrolysis [15].
6.5. Biofertilizer from potato peel
Potato peel has been efficiently used for the synthesis of biofertilizers. PP contains large amounts of proteins and starch, which after degradation by soil microorganisms produce fertilizers with high nitrogen content [40]. Vermicompost prepared from PP earthworms (Pheretima elongate) showed a higher level of the bacterial count than the surrounding soil [41]. The slurry obtained from PP biogas plant (anaerobic digester) is a useful biofertilizer for land application and these replenish nutrients in the soil [42]. Likewise, potato peel, legume peel, cow dung, tulsi leaves and neem leaves were fermented in water for 45 days for the synthesis of biofertilizers. Application of this biofertilizer showed an overall increase in vegetative growth and the physicochemical characteristics of a strawberry fruit [43]. Approx. 7.66, 21.66 and 15 times of nitrogen, phosphorus and potassium content respectively was improved by mixing the residues (obtained by the ethanol production through solid-state fermentation) with the microbes i.e.
Azotobacter chroococcum, Fischerella muscicola, Anabaena variabilis,
Nostoc muscorum, Cylindrospermum muscicola, Azospirillum lipoferum and Aulosira fertilissima in equal ratio [44].
6.6. Production of other enzymes
PP might be used as a substrate for microbial growth in solid-state fermentation (SSF) and is thus useful in the production or synthesis of valuable by-products such as enzymes [45]. Mannanases have been used in numerous industrial processes i.e. viscosity reduction of extracts, synthesized in oligosaccharides and in instant coffee, as well as in the extraction of vegetable oil from leguminous seeds. Potato peel was also used as a carbon source (optimized dose of 14 g/L) for the production of mannanase using Bacillus amyloliquefaciens. The maximum mannanase activity of 105.7 U/mg protein was obtained in this process [46]. Amylases were one of the first enzymes commercially produced by microorganisms. Amylase has a wide application in the textile, food, baking and detergent industries, as well as in the liquidation or saccharification of starch. It is used for the clarification of haze formed in fruits juices or beer, for warp yarn sizing of textile fibres and for the pretreatment of animal feed to improve digestibility. Amylases are produced by Bacillus subtilis, BS9, PB1, Aspergillus niger and Bacillus licheniformis cultivated on Potato peel [45,46,47]. Enzyme activities of 270 U/mL and 600 U/mL, respectively, were obtained by strains of Bacillus licheniformis and Bacillus subtilis [45]. Protease obtained from Bacillus subtilis DM-04 using Potato peel as a substrate exhibited enzyme activity of 400.0 ± 13.0 (U/gd). Protease has major applications in detergent industries as additives. Production of protease by SSF reduces the overall production cost as it does not require any additional supplementation for cocarbon and conitrogen [31]. Cellulolytic (cellulase, xylanase, carboxymethyl cellulose and filter papers) and extracellular (a-amylase, protease, polygalacturonate lyase) enzymes can also be produced using Aspergillus niger and Bacillus subtilis strain 11089 by solid-state fermentation of Potato peel. These enzymes exhibited good enzymatic activities [48]. Polyphenol oxidase is used for removing reactive textile dyes and phenolic contaminants from wastewater, effluents and contaminated soil.
6.7. Biofuels and bio-hydrogen
The demand for the development of tools to access alternative energy sources has gained more attention due to the reduction of oil reserves. Pyrolysis can be one of those tools to access a liquid fuel under atmospheric pressure on a large scale. The liquid fuels i.e. bio-oils are considered more environmentally friendly as compared to the petroleum sources. Such bio-oils are mainly comprised of phenols, aldehydes, organic acids, ketones, esters, furans, alcohols, alkenes and numerous oxygenated complexes. Maloncy, et al. [51] reported that the main idea for this type of environmentally friendly fuel is the transformation of wastes into more valuable energy sources. Thus, Potato peel waste can be converted to the biofuels via pyrolysis. Liang and McDonald [14] stated that the resulting waste obtained after potato peel fermentation were analyzed and explained to represent its possible use as a biofuel. Similarly, another biofuel i.e. bioethanol can also be retrieved by using Potato peel due to the presence of a high amount of starch content. The fermentation of ethanol can occur as a result of the saccharification process. i.e conversion of starch into fermentable sugars. As an alternative to petroleum-derived fuels, bioethanol is considered as an important energy source [52].
As an energy source hydrogen gas also gained the attention as its burning generates a significant amount of energy per unit of weight. The combustion of hydrogen releases environmental friendly gases as compared to the petroleum sources which emit greenhouse gasses in the environment. More recently, the production of bio-hydrogen gas by the use of agricultural waste and microbes has fetched more attention [53,54]. Despite microbes, the combination of photo fermentation followed by the sequential dark fermentation [54] results in more production of biohydrogen gas through the potato’s peel waste as compared to any other fermentation process.
6.8. Production biosorbents
In recent years, potato peel wastes have been employed for the production of bio-sorbents which are used for the treatment of effluents and various other contaminated sources i.e. pigments, dyes, metals. Although, an updated list concerning specifically Potato peel waste is here presented. With almost no cost what-so-ever, potato peel can undergo several treatments leading to materials with specific properties for a precise adsorbate. Numerous studies have been published which prove the efficiency as well as the efficacy of potato peels for this perspective. However, the most recent achievements in this subject are illustrated in Table 2.
7.
Potato peels—as a source of antioxidants
7.1. Potato peels as an antioxidant source in the food industry
In food system, due to the high phenolic contents, potato peel has gained high consideration as a natural antioxidant and is documented to be 10 times more as compared with the levels present in flesh with about 50% of all the polyphenolic contents present in potato tuber. Hence, in food, the potential exploitation of potato peel as an antioxidant has been extensively analyzed. Synthetic antioxidants, particularly BHA (butylated hydroxyanisole) and BHT (butylated hydroxytoluene) were generally utilized to prevent the oxidation. However, Al-Weshahy and Rao [27] reported their concerns about the usage of these synthetic antioxidants which pose a carcinogenic and toxic effect. Synthetic antioxidants may intrude the normal levels of liver enzymes or cause liver swelling. There is an extreme requirement for substitute of synthetic antioxidants. For the first time, the attempt was made to re-use Potato peel waste by extracting natural antioxidants and fortified in food systems. The fats and oils oxidation causes rancid flavour and odours, with a resultant reduction in nutritional quality and safety of food rooted by the production of potentially toxic secondary compounds. Therefore, the addition of antioxidants is a significant stride in processing for the preservation of colour and flavour as well as to prevent nutrient losses.
In addition, quantitatively and qualitatively study was made to asses polyphenolic contents of Potato peel in the methanolic and water extract at 25 ℃ and at 100 ℃ respectively. Methanolic extract of potato peel contains the highest levels of total polyphenolic contents than that of water extract. Im, et al. [55] reported 90% of the phenolic compounds present in potato peels were comprised of chlorogenic acid, having three main isomers, including crypto chlorogenic acid, chlorogenic acid and neo chlorogenic acid [56]. In addition, the Potato peel was analyzed for total polyphenolic contents and antioxidant capacities in another study and extracted with 0.1% of HCL mixture in methanol: water: acetone: (60:10:30, v/v/v). As a result, 177 mg/100 g of total polyphenols of peel weight were found in the Potato peel. As the result, a strong positive association was detected among total polyphenolics in Potato peel extracts and their antioxidant power.
Freeze-dried extract of Potato peel was observed as a natural antioxidant at 500 and 1000 ppm in beef patties for measuring the efficacy of Potato peel extracts against level antioxidants [59]. Freeze-dried Potato peel extract resulted in maximum antioxidant power at 5–6 pH while having less activity at neutral and alkaline pH. Furthermore, freeze-dried Potato peel extracts were heated at more than 80 ℃ for consecutive 30 min results in a significant decrease in antioxidant potential tested with carotene linoleate method. Potato peel extract proved to have antioxidant potential in preventing lipid oxidation in lamb meat which was preserved with radiations [60]. Though, irradiated meat may experience marked oxidative alterations which affect meat sensory quality [61]. Potato peel extract (in the ratio of 0.04%) retards lipid oxidation when added to lamb meat, before the irradiation process, in the same way of butylated hydroxyl toluene (BHT). In another study, Potato peel extract, as a natural antioxidant, showed to avert deteriorations of lipids in food [62]. Potato peel was better in its polyphenolic contents also showing the strongest antioxidant power as compared to sugar beet pulp and sesame cake. Potato peel extract during 60 days of storage of soybean oil (refined) at the temperature of 25 and 45 ℃ was observed as a natural antioxidant. Though, the level of potato peel extract required 8 to 12 times elevated than synthetic antioxidants for controlling the rancidity development cooking oils during storage at high temperature. Potato peel extract can be safely be used as a natural antioxidant to hinder lipid oxidation in fats and oils as well as other food products [63].
7.2. Pharmaceutical applications of potato peel antioxidants
The potato peel potentiality in biological systems as antioxidants has drawn great scientific attention. The aqueous freeze-dried extract of potato peel showed strong suppressing action against lipid peroxidation in liver homogenate of rat introduced by the FeCl2–H2O2 system. Moreover, the potato peel aqueous extract showed high concentration-dependent prevention of deoxyribose (DNA) oxidation. The potency of potato peel extract as antioxidant emphasize over strong superoxide scavenging activity, ion chelating potency and reducing power.
The results of in vitro study suggest the potency of Potato peel to be efficiently used as an ingredient in functional or health foods, to alleviate oxidative potential. In diabetic patients, either with type Ⅱ or type Ⅰ, it is examined that lipid peroxides (LPO) production increases. While it has been recommended that oxidative stress become the major cause for the pathophysiology of diabetes mellitus and is related to hyperglycemia reported in another study [65]. Hyperglycemia causes non-enzymatic protein glycation by Maillard reaction which ultimately alters the energy metabolism resulting in further complication development in diabetic patients [66]. Potato peel affects both antioxidant status and glycemic index in streptozotocin-induced diabetes in male rats [67]. In this study, diabetes-induced rats were fed diet supplemented with potato peel powder for 4 weeks resulted in a significant reduction of glucose level in blood. The addition of potato peel powder in the diet significantly reduced the hypertrophy of both kidney and liver while regularized the activities of serum AST (aspartate aminotransferase) and ALT (alanine aminotransferase) in streptozotocin-induced diabetic rats. Serum enzymes including alanine aminotransferase and aspartate aminotransferase are used for the evaluation of the increased levels of hepatic disorders reflecting acute inflammatory hepatocellular disorders with liver damage [68]. Renal and hepatic lipid oxidation was measured in another study, suggesting potato peel powder supplemented diet cure the eye lens damage linked by diabetic conditions [67]. The antioxidant potential of potato peel extracts was examined as a defensive towards erythrocytes oxidative induced in vitro damage while with the observation of morphological and structural variations in the cell membrane. The 3.93 mg/g of polyphenolics were present in the aqueous extract of potato peel on a dry weight basis [69].
The phenolics present in extract comprised of protocatechuic acid, caffeic acid, gallic acid and chlorogenic acid. A pro-oxidant system was employed in the experiment to stimulate lipid peroxidation in RBCs (red blood cells) of rat and human red blood cell membranes. Potato peel extract of 2.5 mg/mL restrains with 80 to 85% lipid peroxidation with comparable efficiency in both the systems. While potato peel per se did not become the cause of any structural change in erythrocytes, potato peels under experimental conditions potentially retard the H2O2 induced structural changes in rat red blood cells as expressed by using scanning electron microscopy technique [69]. In the same study, the potato peel extract was found to be a significant important defender of human erythrocyte membrane from the damage of oxidation by its strong antioxidant activity. The liver, through its unique metabolic and vascular feature, is more prone to absorb xenobiotics and drugs in high concentration. Detoxification reactions, with both phases, increase substrate hydrophilicity by metabolizing the xenobiotics. Enzymes which metabolize the drugs detoxify many xenobiotics and on the other hand increase or bioactivate the toxicity of others [70]. Bioactivation results in the liver to expose to damage caused by newly formed toxic substances. Hence, liver protective mechanisms are of particular attention because of reactive oxygen species and free radicals which chiefly act in liver diseases occurrence and progression, while antioxidants from Potato peel have been proved to be promising therapeutic agents against the liver damage. In another study, Singh and Rajini [69], a possible protective action of the Potato peel extract against induced hepatic injury was predicted in rats. Before tetrachlorocarbon (CCL4) treatment, the rats were given with the doses of aqueous freeze-dried potato peel extract of 100 mg/Kg of animal’s body weight for seven successive days. Oxidative stress biomarkers and liver enzymes were measured in blood serum or in the liver. The oral dose administration decreased the hepatic damage (induced by the administration of CCl4) observed by measuring alanine aminotransferase (ALT), aspartate aminotransferase (AST) and serum lactate dehydrogenase (LDH) levels in rats treated with CCl4. The malondialdehyde (MDA) (one of the end products of lipid peroxidation in the liver tissue) deterioration and hepatic glutathione (GSH) (an important oxidative stress indicator) level depletion were observed as higher in rats treated with CCl4 as compared to the animals which were pretreated with Potato peel extract. Glutathione peroxidase (GPX), catalase (CAT), superoxidase dismutase (SOD) comprises a jointly helpful team of antioxidant protection towards reactive oxygen species. The super oxidase dismutase is the first antioxidant defence line accelerating the superoxide radical disputation of to H2O2, while H2O2 was converted to water by CAT/GPX. According to this, a measurable defensive increase in super oxidase dismutase activity against the free radicals can stimulate overpoweringly large amounts of H2O2. On the other hand, this would disable the system to hold up the extreme of H2O2, which result in oxidative stress again. Hence, the increase in super oxidase dismutase followed by the reduction of CAT/GPX activity points out the oxidative stress caused by the generation of free radicals [71]. In another study, the noteworthy positive correlation among super oxidase dismutase levels and dosing of Potato peel extract in rats introduced with CCl4 were elucidated. Moreover, histopathological reports reflect that a remarkable degeneration was introduced by CCl4 in focal necrosis. Though, lesions were reduced markedly in pretreated rats with potato peel extract before CCl4 administration.
8.
Conclusions
For an economic boost of developing countries, proper utilization of agriculture wastes must be made effectual in maintaining elevated economic expansion and decreasing poverty. In this regard, potato peel waste can be utilized for the synthesis of numerous compounds such as lactic acid, bio-sorbent, biohydrogen, enzymes, `biogas and biofertilizer which serve as a base for developing linkages among industry and sharing new ideas, technologies and future trails for sustainable economic growth. The potato peel, a zero value material of potato processing industries, is augmented day by day with the ever-escalating consumption of processed potato products. However, it is concluded that the utilization of potato peel waste is the same as converting iron into gold hence boosting economic sector for developing countries.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: