1. Introduction
1.1. Minamata convention on mercury
Mercury (Hydrargyrium = Hg) is highly toxic to humans and the environment and poses a particular threat to the development of fetuses and young children [1,2]. Due to international concern, the United Nations Environment Programme (UNEP) started supporting an intergovernmental negotiating committee in drawing up a global mercury treaty. This resulted in the Minamata Convention on Mercury which was adopted in 2013. By 2016, a total of 128 countries signed and 35 countries ratified the Minamata Convention. The main purpose of this convention is to protect human health and the environment from the anthropogenic emissions of Hg and Hg compounds. One of the goals is the reduction of the use of Hg and Hg compounds before 2020 [3]. Hg is still being used globally although it is considered as one of the top ten chemicals or group of chemicals of major public health concern by the World Health Organization (WHO) [4].
1.2. Mercury in the environment
Hg is a heavy metal that occurs in three main forms: elemental or metallic mercury (Hg0), inorganic mercury (Ⅰ-Hg in e.g., mercuric chloride) and organic mercury (e.g., methylmercury, MeHg). MeHg is formed from Ⅰ-Hg in the aquatic environment by anaerobic bacteria [5]. Hg is emitted into the environment from natural and anthropogenic sources. It occurs in the earth crust and is naturally released into the environment from volcanic activities and weathering of rocks. However, the main cause of Hg release is anthropogenic which can be subdivided into three main sources: (1) release due to mobilization of Hg impurities in raw materials, such as coal burning for heat generation and production of cement and alumina from bauxite; (2) release due to the use of Hg in products and processes, such as small-scale gold mining, and consumer products; and (3) re-mobilization of historically-deposited anthropogenic Hg releases worldwide [6].
1.3. Sources and routes of exposure
Exposure to Hg (all forms) may occur via inhalation, ingestion, or dermal contact. Inhalation exposure of elemental (Hg0) and Ⅰ-Hg occurs mainly through inhalation of ambient air during occupational activities. The respiratory tract is the main absorption route for Hg vapor. After inhalation, Hg0 is efficiently absorbed into the bloodstream. The median (range) absorption was estimated to be 69% (57-73%) based on a human study involving nine volunteers [7] and 79% (75-84%) in another human study with four volunteers [8].
Anthropogenic emissions have resulted in environmental pollution leading to high levels of Hg in fish. MeHg is formed when Ⅰ-Hg is converted by bacteria in the aquatic environment. MeHg bio-accumulates in fish and biomagnifies through the food chain. People are exposed to environmental MeHg through their diet, especially through consumption of contaminated fish, shellfish, and other aquatic species [1], while dermal exposure to MeHg may lead to absorption through the skin. Dermal exposure to Ⅰ-Hg may occur through the use of consumer products that contain Hg, such as skin lightening creams, hair treatment products, and soaps but dermal absorption from these sources is considered unlikely [9,10]. Hursh et al. studied the absorption of Hg vapor through the skin in five male volunteers who held their right hands for 27 to 43 minutes in an airbag containing 203Hg vapor [11]. When the total skin area (of which the forearm skin was assumed to be representative) was compared to the lung as a route of entry for Hg vapor at the same concentration, the rate of uptake was estimated to be 2.2% of the rate of uptake by the lung. For direct skin contact with the liquid phase there are no experimental data to support a quantitative estimate.
1.4. Higher susceptibility and exposure
Subpopulations with higher susceptibility to Hg exposure are fetuses, neonates, and young children because of the sensitivity of their developing central nervous system [12]. In addition to exposure in utero, neonates may be further exposed by consuming contaminated breast milk [13]. Therefore, neonates may experience more severe adverse effects at comparable or lower exposure levels than the general population. The group of people who are at higher risk of Hg vapor exposure is mainly formed by populations from some Asian/Pacific countries and indigenous populations from South America consuming large amounts of fish or marine mammals, individuals with dental amalgams, workers who are occupationally exposed to Hg, and to a lesser extent by individuals who use various consumer products containing Hg, such as some skin lightening creams and soaps [10,14].
1.5. Impact on health
The health effects of Hg exposure in humans vary widely, depending on the chemical form of Hg, the age of the person exposed, the route and duration of exposure, and the dietary patterns of freshwater fish and seafood. Hg primarily affects the central nervous system (CNS), the kidneys and the cardiovascular system. The most prominent health effects of Hg0 toxicity are neurological and behavioral disorders. For Ⅰ-Hg toxicity this is kidney damage, whereas the most prominent health effect of MeHg is damage to the nervous system, especially during its developmental stage.
Developing organ systems are the most sensitive to toxic effects of MeHg [10]. In children, MeHg exposure during pregnancy (in utero) has been associated with developmental delays (e.g., age at first walking), decrease in intelligence (e.g., Intelligence Quotient (IQ) deficit) and behavioral changes (e.g., Attention Deficit Hyperactivity Disorder (ADHD)) [15,16]. Children's cognitive development is the most sensitive endpoint for human MeHg toxicity. In 2007, Axelrad et al. performed a meta-analysis using data derived from neurodevelopmental/cognitive tests, such as the Developmental Test of Visual-Motor Integration (VMI); Wechsler Intelligence Scales for Children, Revised (WISC-R); and Wide Range Assessment of Memory and Learning (WRAML) in studies among children from the Faroe Islands, New Zealand, and the Seychelles [17]. They found a linear association between a 1 mg/g increase in Hg concentration in maternal hair and a decrease of 0.18 IQ points (95% confidence interval: -0.38 to -0.01) [17]. Recently, Jacobsen et al. studied a cohort of 282 Inuit children from whom umbilical cord blood samples had been analyzed for total mercury. They reported an association of prenatal mercury exposure with poorer performance on a school-age assessment of IQ. Children with cord Hg ≥ 7.5 μg/L were four times as likely to have an IQ score < 80, the clinical upper bound cut-off for borderline intellectual disability [18]. A clear association exists between prenatal MeHg exposure and IQ deficits in children, and there is no known safe limit of MeHg [16,19]. More recently, Tratnik et al. studied the association between prenatal exposure to Hg and neurodevelopment of children in a prospective cohort study [20]. They took the genetic polymorphism of apolipoprotein E (Apoe) into account and used the Bayley Scales of Infant and Toddler Development, Third Edition (Bayley-Ⅲ) assessment. Their results showed a negative association between low to moderate Hg exposure in children with normal neurodevelopmental outcome and cognitive and fine motor scores at 18 months of age as assessed by the Bayley-Ⅲ. The decrease in cognitive score was only observed in children carrying at least one Apoe ε4 allele, while the decrease in fine motor scores was independent of the genotype [20].
1.6. Human biomonitoring
The internal dose of chemicals within the general population, various population sub-groups, and individuals can be assessed using human biomonitoring (HBM). With HBM, human exposure to chemicals or their effects can be assessed by measuring these chemicals, their metabolites, or reaction products in human specimens. HBM uses biomarkers-measurable substances or characteristics-in bodily fluids and tissues, such as blood (including cord blood), urine, breast milk, hair, and nails and enables assessing whether or not exposure to a given chemical substance has occurred, to what extent, and how exposure may have changed over time [21]. Thereby, HBM can give precise information on the total internal exposure of an individual at a given point in time.
For the estimation of the internal dose of Hg and its risks to human health, HBM is essential because it reveals whether and to what extent Hg substances were really taken up by humans from the environment. This information cannot be provided by ambient monitoring of air, water, or other environmental samples. HBM can assess the dose really taken up without using worst case scenarios, which regularly leads to overestimation of exposure [21].
In 1999, the German Environmental Agency published guidance values for the interpretation of mercury in urine and blood. Two guidance values (HBM Ⅰ and HBM Ⅱ) were defined. Negative health effects cannot be excluded when the Hg levels are between HBM Ⅰ and HBM Ⅱ. If HBM Ⅱ is exceeded, the risk of adverse health effects is increased and, consequently, there is an acute need for interventions, e.g., exposure reduction measures and the provision of biomedical advice [22].
With this review, we aim to give an overview of the different HBM approaches for long-and short-term exposure to Hg or MeHg in children and adults by discussing: (1) The appropriate selection of biomarkers for assessment of different Hg exposures, and (2) The advantages and limitations of the different biological matrices used in HBM for Hg exposure.
2. Methods
We performed an extensive literature search in PubMed with a search strategy consisting of Medical Subject Headings (MeSH) terms and free text words on August 30, 2016. Search terms were combined for mercury, methylmercury, and biomonitoring, leading to the following search string: (mercury OR methylmercury) AND (human biomonitoring OR hair OR urine OR blood OR cord blood OR exhaled air). We selected humans as species and English, Spanish, and Portuguese as languages. This search strategy resulted in 417 reviews, of which eight reviews were selected by the first author, based on the quality of abstract and title. In addition, valuable information from thirteen online sources and documents from international health authorities (WHO, EPA and UNEP), was adopted to verify consistency with primary sources. The information provided in these secondary sources was compared to our findings in peer-reviewed literature to be able to provide reference to the primary published articles for all information included. We used the format of the biological monitoring application datasheets (BADS) originally developed during the EU/FP7 BIOMONECS project to provide an overview of the different biological media for HBM of Hg and MeHg [23].
3. Results and discussion
HBM of Hg allows the determination of the internal dose of an individual after acute or chronic exposure. Hg can be measured in a variety of biological media. The media used most frequently included hair, blood, cord blood, and urine [19,24]. Nails and cord tissue are also used to study exposures to MeHg [25,26]. An overview of the different biological media for HBM of Hg and MeHg is given in Table 1 and 2.
Table 1. Biological monitoring of Hg0
| Identity |
| Name (parent) |
Mercury |
| UN number |
2809 |
| CAS number |
7439-97-6 |
| Intervention value (AGW in mg/m3) |
- |
| Structure |
Hg |
| Occurrence |
| Chemical state (at 20 °C) |
Heavy liquid + vapor |
| Physical appearances |
Soft, silver-white, shiny fast-moving liquid. Odorless. It is the only metal that is liquid at room temperature[13]. |
| Industrial products |
Thermometers, barometers, batteries, electrical switches, fluorescent lamps etc. |
| Physicochemical properties |
| Molecular weight |
200.59 g/mol |
| Vapour pressure (Pa at 20 °C) |
0.26 |
| Octanol/water partition coefficient (log Po/w) |
No data available |
| Water solubility (in mg/L at 25 °C) |
Negligible |
| Toxicokinetics |
| Uptake by inhalation |
In a study with nine human volunteers, uptake was 69% (range: 57%-73%) after exposure to Hg0 vapors [7]. In another study with four volunteers uptake was 79% (range: 75-84%) [8]. |
| Uptake by skin absorption |
For direct skin contact with the liquid phase there are no experimental data to support a quantitative estimate. Dermal absorption of Hg0 vapor contributed only 2.2% of pulmonary uptake in human volunteers [11]. |
| Uptake via gastrointestinal tract |
Very low ( < 0.01% of ingested Hg0) due to the limited absorption of Hg from the gastro-intestinal tract [27]. |
| Distribution |
Inhaled Hg0 dissolves in the blood and is widely distributed throughout the body. It accumulates in the brain, chest region and kidneys with clearance half-lives of 21, 43 and 64 days, respectively. Some of the Hg0 remains unchanged and readily passes through the blood-brain and placenta barriers. There Hg0 is oxidized and becomes trapped in the brain [28,29,30]. |
| Metabolism |
Hg0 readily crosses through the blood-brain and placenta barrier and remains unchanged. Some of the Hg0 is oxidized by catalases and peroxidases [30]. In the oxidized form Hg can bind to sulfhydryl groups in albumin, globulins, and methallothionein. The main sites of deposition are the kidneys and brain [31]. |
| Excretion via lungs |
Before redistribution of Hg into the tissues a considerable fraction is eliminated via exhalation, with half-lives of 13-25h [29]. |
| Excretion via urine |
About 2.4% of the dose was excreted in urine within 7 days [32]. In another study 8-40% of the dose was excreted in urine after 30 days [7,33]. |
| Excretion via feces |
About 9.2% of the dose was excreted in feces within 7 days [32]. |
| Toxicodynamics |
| Mechanisms of toxicity |
The inhalation of Hg vapor can produce harmful effects on the central and peripheral, nervous, digestive and immune systems, lungs and kidneys, and may be fatal. Inhalation of a high concentration of Hg vapor can lead to the following symptoms, often within hours of exposure: cough, chills, fever, shortness of breath, metallic taste, dysphagia, salivation, weakness, headaches and visual disturbances. Complaints of the gastrointestinal tract include nausea, vomiting and diarrhea. Severe intoxications can lead to respiratory failure, cardiac arrest and death. |
| Classification for carcinogenicity |
Not classified [6,34] |
| Classifications for reprotoxicity |
Not classified [10,35] |
| Classification for sensitizing properties |
Not classified [35] |
| Biological monitoring |
| Biomarkers |
Total Hg in urine |
Total Hg in blood |
Hg vapor in exhaled air |
Total Hg in hair |
| Molecular weight |
200.59 |
200.59 |
200.59 |
200.59 |
| Involved enzymatic metabolism |
- |
The dissolved Hg0 is very lipophilic and easily passes the blood-brain and placenta barrier. Once inside the cell Hg is oxidized via Hg+ into Hg2+ via the hydrogen peroxide-catalase pathway. Hg2+ easily binds to intra-cellular molecules such as enzymes, glutathione, tubulin, transporters and the thiol groups of proteins [13]. |
- |
- |
| Biological material |
Urine |
Venous blood |
Exhaled air |
Hair |
| Type of sample |
Spot urine |
Whole blood or serum/plasma should be separated from each other. |
End-exhaled air |
Scalp hair Isolate ca. 100-150 strands of hair (which is a bundle approximately 0.75-1.0 cm in diameter) about 3 cm in length, from the occipital region of the head [10]. |
| Half life |
63.2 (12.8-98.9) days [7,34] |
1.2 and 10.5 days [7] |
18 (13-25) h [29]; 17h [36] |
No data available |
| Sampling strategy Including time window |
First urine in the morning after awakening. After 10 days for high exposures to 6 months for low exposures [37]. |
First sample to be taken within 24 h following the incident [24]. |
In volunteer studies over a period of three days 7-12% of the dose was recovered in end exhaled-air [36]. |
A lock of hair as thick as a pencil should be cut as close to the scalp as possible from the posterior vertex region of the head. |
| Excretion pattern |
Only 1% of the dose was excreted in urine during 3 days and 8-40% during 30 days [7,33]. |
Excreted as Hg2+in blood. |
Excreted as Hg0 in exhaled air and approximately 7% of the Hg0 inhaled is eliminated by breathing [36]. |
From hair Hg retrieved as MeHg for ca. 90%. Hg in hair is a useful biomarker of long-term exposure to MeHg. Once Hg is incorporated into hair, it remains unchanged [19,38]. |
| Materials |
Urine should be collected in plastic containers that are pre-tested for contamination. |
Heparin-Na or EDTA-2K containing vacutainer tubes. |
Glass pipette or BioVOC. |
Alu-foil blunt tip curved scissors. |
| Transportation |
4 ℃ |
4 ℃ |
Ambient temperature |
Ambient temperature |
| Storage |
The samples must be kept frozen (to be below -20 ℃) to reduce bacterial growth and avoid conversions of the Hg species of interest. |
Total blood or blood fractions can be kept at 4 ℃ for periods of up to 7-10 days. At -20 ℃ or lower for longer periods of storage. |
- |
Store in a sealed zip closable bag at room temperature. Dry dark environment at room temperature |
| Stability |
Thirty-seven days at 5 °C Acidifying the urine sample has been suggested as a means of stabilization prior to storage in a frozen condition [10]. |
Not stable at RT |
Not applicable if analyzed online |
Hair is a strong, stable tissue and is less affected by adulterants or short-term abstinence. |
| Measurement principle |
Cold Vapour-Atomic Absorption Spectrometry (CV-AAS). This method measures THg. It is a development of a cold vapor technique and sometimes utilizes a gold amalgamation device to increase sensitivity and specificity [25,39]. CV-ICP-AES [38]. |
CV-AAS and CV-ICP-AES [38,39,40,41,42] |
RA-915+ atomic absorption Hg spectrometer with an RP-91 attachment unit (Lumex). Operation of the RA-915+ is based on differential Zeeman atomic-absorption spectrometry using high-frequency modulation of light polarization (ZAAS-HFM) [36]. |
Cold Vapour-Atomic Fluorescence Spectrometer (CV-AFS). The method involves digestion of the analyte from hair samples using a 30:70 mixture of sulfuric and nitric acids and subsequent analysis by CV-AFS [43]. |
| Limit of quantification |
For CV-ICP-AES 0.02-5.0 μg/L (calibration curve) and 0.01 μg/L (detection limit) [40] |
For CV-ICP-AES 0.02-5.0 μg/L (calibration curve) and 0.01 μg/L (detection limit) [40] |
2-3 ng/m3-5000 ng/m3 [36] |
0.0006-0.06 μg/g [43] |
| Aliquot for 1 analysis |
5-10 mL |
A minimum of 1-2 mL |
0.7 L exhaled air [35] |
A minimum of 5-10 mg [43,44] |
| Recommended adjustment |
Urinary creatinine |
- |
N.a. if only the last 300-400 mL of an exhalation is collected. |
- |
| Preferred units |
μg Hg/g creat. or μg Hg/L urine |
μg Hg/L blood |
μg Hg/L exhaled air |
μg Hg/g hair |
| Conversion factor |
1 μg/g creat. = 0.564 mmol Hg/mol creat. [45] |
1 μg/L = 5 nmol Hg/L [45] |
1 mg/L = 5 nmol Hg/L [45] |
- |
| BAT (workers) |
25 μg/g creat. [45] |
Not available. |
- |
- |
| BEI (workers) |
20 μg/g creat. prior to shift [45] |
BEI for blood Hg is withdrawn [45] |
- |
- |
| HBM-Ⅰ a |
5 μg Hg/g creat. or 7 ֧/L [22,46] |
5 μg Hg/L blood [10,22,46] |
- |
- |
| HMB-Ⅱa |
20 μg Hg/g creat. or 25 ֧/L [22,46] |
15 μg Hg/L blood [10,22,46] |
- |
- |
| Possible confounders |
Less sensitive to seafood (organic Hg) and fresh dental amalgam fillings [24,45]. |
Sensitive to seafood (organic Hg) and fresh dental amalgam fillings [24,45]. |
Not sensitive to seafood. Sensitive to fresh dental amalgam fillings [24,45]. |
- |
| -: not applicable; a: HBM-Ⅰ value represents the concentration of a substance in human biological material (children and adults) below which-according to the knowledge and judgement of the HBM Commission-there is no risk for adverse health effects and, consequently, no need for action. HBM-Ⅱ represents the concentration of a substance in a human biological material above which-according to the knowledge and judgement of the HBM Commission-there is an increased risk for adverse health effects and, consequently, an acute need for exposure reduction measures and the provision of biomedical advice. The HBM-Ⅱ-value should thus be regarded as an intervention or action level. For values < HBM-Ⅰ no damage to health to be expected according to current knowledge-no need for action; for values between HBM-Ⅰ and HBM-Ⅱ damage to health cannot be excluded with sufficient certainty-repeated sampling and analysis and in the meantime identify potential sources of exposure and reduce exposure adequately; for values > HBM Ⅱ damage to health is possible; immediate action to reduce exposure is required and care by experts in environmental medicine should be provided (source: https://www.umweltbundesamt.de/en/topics/health/commissions-working-groups/human-biomonitoring-commission/reference-hbm-values). |
Table 2. Biological monitoring of MeHga
| Identity |
| Name |
MeHg as in Methylmercury Ⅱ chloride |
| UN number |
2025 |
| CAS number |
115-09-3 |
| Intervention value (AGW in mg/m3) |
- |
| Molecular formula |
CH3-HgCl |
| Occurrence |
| Chemical state (at 20 °C) |
Solid |
| Physical appearances |
White microcrystals or powder |
| Industrial products |
Laboratory chemicals, manufacture of substances |
| Physicochemical properties |
| Molecular weight |
251.1 (MeHgCl) |
| Vapour pressure (mm Hg at 25 °C) |
8.5×10-3 mm Hg at 25 °C [47] |
| Octanol/water partition coefficient (log Po/w) |
0.41 [48] |
| Water solubility (in g/L at 21 °C) |
0.100 [38] |
| Toxicokinetics (parent) |
| Uptake by inhalation |
- |
| Uptake by skin absorption |
MeHg is readily absorbed through the skin. |
| Uptake via gastrointestinal tract |
Approximately 95% of MeHg in fish readily absorbed from the gastrointestinal tract [38]. |
| Distribution |
MeHg is lipophilic (Log Pow = 0.41) and is distributed throughout the body. It readily crosses the blood-brain and placenta barriers. Approximately 1-10% of absorbed oral dose of MeHg is distributed to blood; 90% of blood MeHg is present as MeHg-cysteine complex in erythrocytes [38,48]. |
| Metabolism |
MeHg is slowly demethylated to Hg2+. Tissue macrophages, intestinal flora, and fetal liver are sites of tissue demethylation [38]. |
| Excretion |
The daily excretion of MeHg is about 1% of the human body burden [49]. It is excreted mainly via the bile and feces as MeHg and Hg2+(major route of excretion). MeHg is excreted as a glutathion conjugate. Urine MeHg concentrations do not accurately reflect MeHg exposure. Lactation increases clearance from blood. Circa 16% of Hg in breast milk is MeHg [1,50,51]. In humans, the whole-body half-life of MeHg was estimated to be 70-80 days [52,53,54]. |
| Ecretion via urine |
Urine is a relatively minor route of excretion for MeHg (ca.10%) [38] |
| Excretion via feces |
Major route of excretion is bile and feces. Approximately 90% of MeHg is excreted in feces as Hg2+ [38] |
| Toxicodynamics |
| Mechanisms of toxicity |
The peripheral and central nervous systems and kidney are major target organs. MeHg rapidly passes through the blood brain and placenta barrier. MeHg is converted in the brain and trapped in the form of Hg2+. MeHg poisoning symptoms result primarily from damage to the nervous system. The symptoms are characterized by loss of sensation in the hands and feet and in areas around the mouth, decrease of vision resulting in tunnel vision, ataxia, dysarthria, and hearing loss. Severe poisoning causes blindness, coma and may result in death. There is a latency period of weeks to months, sometimes even more than a year before clinical symptoms are observed. There are no observable symptoms of intoxication during this latency period [1,38]. |
| Classifications for carcinogenicity |
Group 2B: Possibly carcinogenic to humans (Chloromethylmercury) [34]. |
| Classifications for reprotoxicity |
MeHg is reprotoxic. Studies show that MeHg affects the fetus' nervous system [16]. |
| Classifications for sensitizing properties |
- |
| Classifications other |
- |
| Biological monitoring |
| Biomarkers |
Hg in hair |
Hg in blood |
Hg in cord blood |
| Molecular weight |
215.62 (MeHg+) |
215.62 (MeHg+) |
215.62 (MeHg+) |
| Involved enzymatic metabolism |
- |
MeHg is slowly demethylated to Hg2+ in tissue macrophages, intestinal flora and fetal liver [35]. |
- |
| Biological material |
Hair |
Venous blood |
Cord blood |
| Type of sample |
Isolate ca. 100-150 strands of hair (which is a bundle approx. 0.75-1.0 cm in diameter) about 3 cm in length, from the occipital region of the head [10,55]. |
Whole blood or serum/plasma; should be separated from each other [10]. |
Whole blood or serum/plasma; should be separated from each other [10]. |
| Half-life |
The half-life for MeHg in hair ranged from 35 to 100 days, with an average of 65 days [1,56]. |
The half-life for MeHg as measured in blood of humans ranged from 48 to 53 days [54,57,58,59]. |
Unknown |
| Sampling strategy Including time window |
A lock of hair as thick as a pencil should be cut as close to the scalp as possible from the posterior vertex region of the head [60]. |
Mercury blood levels will reflect MeHg exposure but also (primarily) recent exposure to metallic mercury exposure [61]. |
Samples should be collected immediately after birth. |
| Excretion pattern |
Hg in hair is present as MeHg for approx. 90%. Hg in hair is a useful biomarker of long-term exposure to MeHg. Once Hg is incorporated into hair, it remains unchanged [19,38]. |
MeHg is readily absorbed from the gastrointestinal tract. After ingestion, 90% of the MeHg in blood can be primarily found in red blood cells, primarily bound to hemoglobin and some also to plasma proteins [1,38]. |
Unknown |
| Materials |
Alu-foil and blunt tip curved scissors. |
Heparin-Na, EDTA-2K containing vacutainer tubes or BD vacutainer Royal Blue tubes. |
Heparin-Na, EDTA-2K containing vacutainer tubes or BD vacutainer Royal Blue tubes. |
| Transportation |
Ship specimens periodically at ambient temperature. |
At 4 ℃ |
At 4 ℃ |
| Storage |
In sealed zip closable bag at room temperature. Dry dark environment at room temperature. Do not cool or freeze [60]! |
At 4 ℃ for periods of up to 7-10 days. Freeze at -20 ℃ or lower for longer periods of storage. |
At 4 ℃ for periods of up to 7-10 days. Freeze at -20 ℃ or lower for longer periods of storage. |
| Stability |
Hair is a strong, stable tissue and is less affected by adulterants or short-term abstinence [60]. |
Not stable at ambient temperature |
Not stable at ambient temperature |
| Measurement principle |
CV-AAS using a Perkin-Elmer 1100 B spectrometer with a MHS 20 attachment. The amount of MeHg can be calculated as the difference between THg and IHg [62]. CV-AFS [43]. |
CV-ICP-AES [40] CV-AFS [63] GLC-ECD [64,65] |
CV-ICP-AES [40] CV-AFS [63] GLC-ECD [64,65] |
| Limit of quantification |
For CV-AFS the LOQ: 0.0006-0.06 μg/g [43] |
0.01-5.0 μg/L (calibration curve) and 0.01 μg/L (detection limit) for CV-ICP-AES [40] |
0.01-5.0 μg/L (calibration curve) and 0.01 μg/L (detection limit) for CV-ICP-AES [40] |
| Aliquot for 1 analysis |
A minimum of 5-10 mg is required for the hair analysis assay. |
A minimum of 1-2 mL |
A minimum of 1-2 mL |
| Preferred units |
μg MeHg/g hair |
μg Hg/L blood or μg Hg/g blood |
μg Hg/L blood or μg Hg/g blood |
| Conversion factor |
- |
5.35×10-3mmol/L (MeHg+) |
5.35×10-3mmol/L (MeHg+) |
| HBM-Ⅰ b |
- |
5 μg Hg/L blood [10,22,46] |
- |
| HMB-Ⅱb |
- |
15 μg Hg/L blood [10,22,46] |
- |
| Possible confounders |
Bleaching and other chemical hair treatments such as permanent wave [66,67,68]. |
Blood Hg does not provide information solely about MeHg exposure but reflects exposure to other forms of Hg as well [69]. |
Blood Hg does not provide information solely about MeHg exposure but reflects exposure to other forms of Hg as well [69]. |
| -: not applicable; a: Methylmercuric chloride is used experimentally to investigate the effects of MeHg; b: HBM-Ⅰ value represents the concentration of a substance in human biological material (adults, children) below which-according to the knowledge and judgement of the HBM Commission-there is no risk for adverse health effects and, consequently, no need for action. HBM-Ⅱ represents the concentration of a substance in a human biological material above which-according to the knowledge and judgement of the HBM Commission-there is an increased risk for adverse health effects and, consequently, an acute need for exposure reduction measures and the provision of biomedical advice. The HBM-Ⅱ-value should thus be regarded as an intervention or action level. For values < HBM-Ⅰ no damage to health to be expected according to current knowledge-no need for action; for values between HBM-Ⅰ and HBM-Ⅱ damage to health cannot be excluded with sufficient certainty-repeated sampling and analysis and in the meantime identify potential sources of exposure and reduce exposure adequately; for values > HBM Ⅱ damage to health is possible; immediate action to reduce exposure is required and care by experts in environmental medicine should be provided (source: https://www.umweltbundesamt.de/en/topics/health/commissions-working-groups/human-biomonitoring-commission/reference-hbm-values). |
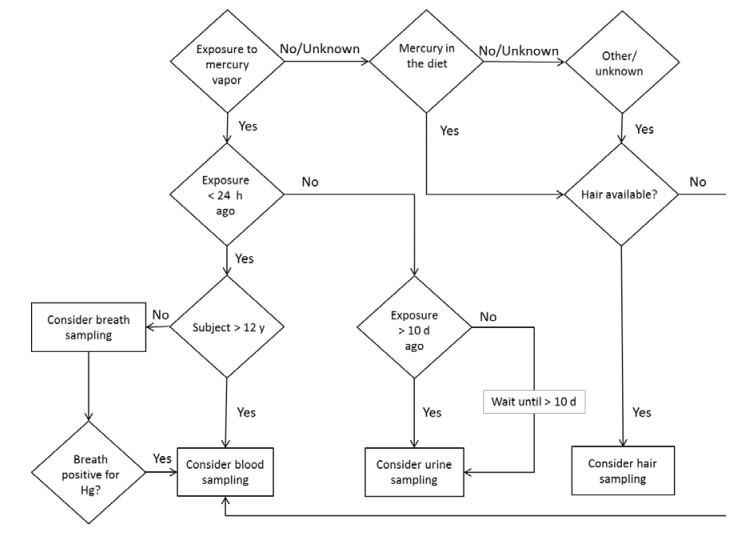
Dependent on the exposure scenario, the most suitable biological medium should be selected for proper measurement of the internal concentration. To assess the appropriateness of each approach, several factors should be considered. The main issues are: source and duration of exposure. The source of exposure determines to a large extent the chemical form of Hg and the route of exposure. The duration of exposure also has implications for the time window for collection of biological materials, e.g., blood or exhaled breath are associated with the fast elimination half-life of Hg0 from the circulation and are most useful when collected within 24 h following exposure [24]. A flow chart to support the decision making process in a HBM Hg study is given in Figure 1.
Table 3 summarizes the advantages and limitations of biological matrices that are commonly used in HBM studies to assess Hg exposure.
Table 3. Possibilities of HBM arranged by biological medium
| Biological medium |
Advantages |
Limitations |
| Blood, serum or plasma |
-Suitable biomarker for recent exposure to Hg vapor [7] -The level of THg in blood reflects recent exposure to both MeHg and Hg vapors [19] |
-Blood THg samples do not provide information regarding historical exposure -Volume limitation -Invasive method of sample collection -Requires a trained medical professional to collect the sample -Background: sensitive to seafood and fresh dental amalgam -Special conditions are required for transport and shipping |
| Cord blood |
-Suitable to study exposure of mother and child (prenatal exposure period) -Non-invasive method of sample collection [10] |
-Only available at birth in maternity care setting -Only available for a specific population -Special conditions are required for transport and storage |
| Urine |
-Suitable biomarker for long-term exposure to Hg 0 [7,33] -Non-invasive method of sample collection that can be performed by self-assessment -There is no volume limitation |
-Composition of urine varies which requires adjustment (e.g., creatinine or osmolality) -Additional test required for volume adjustment -After short-term exposure ( < 24 h) to Hg 0 it is not possible to measure THg in urine. Only if exposure > 10 days ago. There is a latency of 10 days or more which is caused by conversion of Hg 0 to Hg 2+[24,70] -Urine should be collected in plastic containers that are pre-tested for contamination -Special conditions are required for storage and transportation |
| Hair |
-Suitable biomarker for long-term exposure to MeHg, providing information on cumulative exposure to MeHg during previous months [19] -If segmental analysis is performed information on exposure pattern can be obtained -Non-invasive method of sample collection and reasonably well accepted by donors [19] -Minimum training required for personnel to perform sample collection -No special requirements for transport and storage |
-Hair is exposed to the ambient environment and can be contaminated externally -Before analysis the hair should be treated to remove external contamination -Potential variations with subject's hair colour, hair treatment or race. Permanent wave treatment removes Hg from hair [10,66,67] -For bald individuals or neonates it can be difficult to obtain the necessary amount of hair -Sometimes the provision of hair may be hindered by cultural beliefs |
| Exhaled air |
-Suitable biomarker for short-term exposure, especially when (young) children are involved [29] -Non-invasive method of sample collection [36,71] -Allows real-time direct-reading assessment of exposure to Hg 0 vapor |
-Limited to Hg 0 vapor (volatile) -When exhaled air analysis is positive, confirmation by blood testing is recommended for comparison to guidance values -Sensitive to fresh dental amalgam -Transport and storage requires fixation of Hg 0 vapors on a solid sorbent |
3.1. Blood
3.1.1. Advantages of blood
Blood Hg concentrations reflect current and recent exposure to MeHg and/or Hg0 [19].Blood Hg reflects the systemic available Hg that may reach the brain after passing the blood-brain barrier. MeHg is primarily taken up by ingestion as it is very well absorbed from the gastrointestinal tract and is extensively distributed throughout the body [52,54]. This is most noticeable in populations that rely heavily on fish consumption [16]. A directassociation exists between Hg concentrations in human blood and consumption of MeHg contaminated fish [10]. In the absence of mercury vapor exposure the total blood Hg reflects the MeHg level of the fish species as well as the amount of Hg in the contaminated fish consumed. Populations with a diet predominantly consisting of contaminated fish will be exposed to high levels of MeHg. Most of THg in blood consists of MeHg and can be used as a measure of MeHg exposure [55]. Blood MeHg reaches a maximum within 4 to 14 h after exposure and undergoes clearance to other tissues after 20-30 h.
After acute exposure to Hg0, the first sample should be taken within 24 h. If the source of exposure is removed (e.g., a broken thermometer), follow-up blood samples can contribute to reassurance that Hg is eliminated from the body [24]. Well established standard operating procedures (SOPs) are available for blood sampling as well as guidance values for evaluation of the blood Hg concentrations.
3.1.2. Limitations of blood
Blood sampling is invasive for the subjects (usually drawn from a vein) and requires trained staff and proper sterile materials to ensure the samples are collected safely and properly [70]. Blood samples require special conditions for storage and transport. Immediately after collection, blood samples need to be stored at 4 °C in the refrigerator. If the samples are stored for a longer period, they should be frozen. In addition, the provision of blood may be hindered by individual's ethical or cultural beliefs [10].
If (young) children are possibly exposed to mercury vapors, it is crucial to consider that blood collection by venipuncture might be too invasive. The determination of Hg in exhaled air may instead be used as a non-invasive and more child-friendly alternative for initial screening. If a high level of Hg is observed in exhaled air, it might then be useful to consider taking blood samples from these children. Also, irrespective of the age of the individuals in the target population, if repeated sample collection is required, spot urine or exhaled air samples may be preferred by the subjects instead of blood samples [24,36,71]. For exposure to MeHg, exhaled air cannot be used. MeHg exposure in children can be assessed by analysis of Hg in hair.
Fresh dental amalgam and seafood may cause an increased Hg level in blood which is unrelated to exposure from (other) ambient sources of interest. For blood sampling, this can be prevented by asking the subject to avoid fish and seafood consumption 24 h prior to blood collection [28,24].
3.2. Cord blood
3.2.1. Advantages of cord blood
Cord blood Hg concentrations are suitable to study MeHg exposure of pregnant women and fetuses. The prenatal period is a life stage which is characterized by high vulnerability of the fetus to MeHg. The fetal nervous system is very sensitive to the effects of MeHg and can therefore be damaged irreversibly [16,35].
There are several reasons why cord blood is suitable to study or estimate prenatal exposure to Hg. From a toxicokinetic point of view, cord blood THg is suitable to reflect the brain target dose. It is well documented that cord blood Hg levels reflect the in utero MeHg exposure during pregnancy. These levels correlate well with fetal brain concentrations in the final trimester of pregnancy [16]. Several studies showed that the concentration of THg in cord blood is approx. 70% higher than in maternal hair, suggesting active transport of MeHg through the placenta [49,61,72,73]. Previous studies also demonstrated that cord blood THg had a stronger association with health effects than maternal hair THg [74]. Furthermore, biomarkers reflecting the MeHg exposure level in the fetus during gestation are predictors of health effects of MeHg in newborns and young children. Cord blood sample collection at birth is easy and non-invasive for the baby or the mother who has just given birth. Because of the above-mentioned reasons, cord blood is the most desirable biological medium for estimating prenatal exposure [75].
3.2.2. Limitations of cord blood
Cord blood is only available at birth in maternity care settings. Special conditions are required for transport and storage of cord blood samples.
3.3. Urine
3.3.1. Advantages of urine
Urinary THg levels mainly reflect exposure to Hg0 and are suitable to assess long-term THg exposure to Hg0vapor [76]. Urine contains Hg which accumulates in renal tissue and therefore reflects the cumulative dose of Hg in the kidneys [77]. Airborne Hg0 levels below 50 mg/m3 correlate well with urinary THg levels [78].
To estimate the risks associated with Hg exposure, urinary levels of e.g., small-scale gold miners that use THg can be compared to HBM limits published by the German Environmental Agency [22]. Hg levels below 5 mg/g creatinine (HBM-Ⅰ) are considered safe and no health risks are expected [22,46].
Urinary THg among small-scale gold miners, especially those heating Hg0 to remove it from the gold, is potentially elevated. Many studies report urinary THg concentrations above 50 μg/g-creatinine, a urinary concentration at which renal tubular effects are expected to occur, and/or 100 μg/g-creatinine, a urinary concentration above which the probability to develop classical neurological signs of Hg intoxication is high [14].
Compared to blood sampling, urine samples are much easier to collect and useful for self-assessment. Collection of urine samples is less invasive compared to blood samples and better accepted for repeated sample collection. Background urinary THg levels are less sensitive to seafood and fresh dental amalgam [28].
3.3.2. Limitations of urine
Urinary THg provides information about exposure to vapors as well as other forms of Hg [69], but urine is a relatively minor route of excretion for MeHg (ca. 10%) [49]. Therefore, urine is not a suitable biological medium to assess exposure to MeHg. Hair is considered to be the preferred medium for assessment of exposure to MeHg [79] (see section 3.4). Blood is also a good alternative medium to assess MeHg exposure.
Urine THg is not a suitable biomarker after short-term exposure to Hg0 either. A latency period of 10 days or more is caused by conversion of Hg0 to Hg2+, followed by binding with sulfhydryl groups in plasma proteins [80]. The composition of urine varies over time and requires adjustment, e.g., expressing the results per gram of creatinine to account for renal function and differences in hydration [13,81]. This involves an additional step and results in additional costs. Urine should be collected in plastic containers pretested for potential traces of Hg contamination. Study subjects need to be instructed to wash their hands as to avoid contamination when the sample is voided. Bacteria can grow rapidly if urine samples are stored at ambient temperature and may change Hg chemistry. Therefore, urine samples must be kept frozen at -20°C to prevent bacterial growth.
3.4. Hair
3.4.1. Advantages of hair
The use of hair specimens to evaluate Hg exposure is a well-established method in population studies [82], but for the individual patient this method should be used carefully [68].
Exposure to MeHg occurs through the diet and increases with consumption of contaminated fish and seafood [67,83], which is well indicated by the measurement of THg in hair because hair sequesters MeHg during its formation. Measurement of THg in hair provides the cumulative mid-to long-term average exposure during previous months [19,84,85], depending on the length of the hair sample. If a population is constantly exposed to MeHg, the percentage of Hg in the form of MeHg is close to 100% [84]. Speciation studies showed that up to 90% of the THg in hair is in the form of MeHg [19,38].
Hair grows at an approximate rate of 1-1.5 cm per month and segmental analysis can be performed depending on the length of the hair. Analysis of a hair segment collected close to the scalp reflects recent exposure. Further segmental analysis allows study of an exposure pattern over time, e.g., to identify peak exposures of MeHg, such as in seasonal consumption variations. Seasonality of MeHg exposure is highly relevant especially in communities relying on local food sources. McDowell et al. identified in a chronic exposure study, that peak exposures were an important factor to explain adverse health effects [44].
Once Hg is incorporated into hair, it remains unchanged and can provide a history of MeHg exposure. Hg binds to cysteine and remains stable for longer periods [68,86]. Research has shown that maternal hair concentrations of MeHg positively correlate with dietary intake. Cernichiari et al. found that a reasonable correlation existed between maternal THg hair level during pregnancy and Hg concentration in an infant's brain (target tissue) [85]. The incorporation of MeHg into hair follicles is in proportion to its content in blood. Generally, the Hg concentration in hair is 250-300 fold higher than that in blood because sulfur-containing proteins in hair bind to MeHg [19,84]. For comparison of studies using hair or blood as biomarker, the WHO recommends a hair-to-blood ratio of 250 for the conversion of THg hair to whole blood concentration, expressed as mg Hg/g hair to mg Hg/mL blood [72,87].
Ideally, hair samples should be taken from the occipital region near the scalp with Alu-foil using blunt tipped curved scissors made of stainless steel. The manner in which the hair specimen is sampled is associated with the time frame of exposure that can be studied as the distance from the scalp which is directly proportional to the time elapsed since exposure. Hair from the initial 0.5 cm near the scalp reflects on average the last 1-3 weeks before the collection date (the most recent exposure). Therefore, it is very important to cut the hair as close as possible to the scalp and to retain the orientation of the hair strands [10].
The collection of hair is simple, non-invasive and reasonably well accepted by its donors. There are no transportation issues because of the stability of Hg in hair [10,70]. Collected samples can be stored in labeled zip-closable bags at ambient temperature [88]. Therefore, the use of hair as a biomarker for mid-to long-term MeHg exposure is advised.
3.4.2. Limitations of hair
Although the WHO recommends a hair-to-blood ratio of 250, there is some concern about the use of this ratio as it has been shown to vary extensively. Liberda et al. reported a hair-to-blood ratio between 3 and 2845 in a study of 1333 subjects [87], while Yaginuma-Sakurai reported a mean hair-to-blood ratio of 344 ± 54 for 27 subjects [89]. Therefore, using the ratio of 250 to convert hair Hg to blood concentrations may be incorrect, especially at an individual level. When exposure to Hg0 vapor is studied, hair is not a good medium but urine is [10,70,76].
Another limitation of hair for HBM is that hair can be contaminated externally by Hg0 which will distort analysis results. Miners working in artisanal and small-scale gold mining (ASGM) in particular are exposed to Hg vapors when melting a Hg0-containing amalgam complex. However, they sometimes also consume MeHg contaminated fish from these areas. If biomonitoring is considered for this group of workers, it may be important to rule out external contamination. Not washing or pretreating the hair can lead to overestimating the internal hair Hg concentration. With Hg speciation, it is possible to make a distinction between MeHg and Ⅰ-Hg [68]. Recent work indicates that there may be pitfalls concerning the interpretation of THg hair levels, such as the suggestion that direct absorption of Hg0 vapors contributes to THg incorporated in the hair matrix [90].
Sometimes the provision of hair may be hindered by populations' cultural beliefs. Various religious and cultural aspects may play a role in some African or Latin-American populations that are less willing to cooperate with regard to the use of hair [91]. For bald individuals or newborn babies, it may also be difficult to obtain the minimum necessary amount of ca. 100-150 strands of hair that needs to be collected.
Hair structure differs depending on ethnicity and age group and seems to affect the incorporation of Hg. Chemical hair treatments, such as permanent wave remove Hg from hair [66,67,68]. If the hair Hg concentration is used as a dosimeter, these factors should be taken into account.
In short, hair Hg concentration should be used with an understanding of its limitations e.g., distortion of analysis results due to external contamination. An evaluation of the participants' history and health effects is necessary when hair THg analysis is used for individual exposure assessment. Hair is particularly useful for the reconstruction of a pattern of exposure to MeHg over a period of several months on the population level [68,92].Therefore, hair is the preferred medium in many cohort studies assessing mid-to long-term MeHg exposure.
3.5. Exhaled air
3.5.1. Advantages of exhaled air
Exhaled air is a suitable biomarker for short-term exposure to Hg0 vapor. It can serve as an initial screening of a target population e.g., when (young) children are involved in an incident of a broken thermometer and are exposed to the release of Hg0 [24]. It is a non-invasive method of sample collection which makes it child-friendly and it allows real-time direct-reading assessment of exposure to Hg0 vapor. When exhaled air analysis is positive for Hg, confirmation by blood testing is recommended and comparison to guidance values should be performed to know whether an action level (e.g., HBM-Ⅱ) is exceeded. Exhaled air analysis is a well-established method that was validated for humans but so far its use in routine was not reported very often [35]. It is a suitable method for adults and children.
Following a peak exposure, sample collection within 24 h is recommended [24]. The half-life of Hg0 vapor in exhaled air is 18 (13-25) h [29]. Repeated sampling of exhaled air is useful for modeling studies [28]. Exhaled air samples are not sensitive to Hg-compounds originating from seafood [28].
3.5.2. Limitations of exhaled air
Only elemental Hg can be measured because it is volatile. Fresh dental amalgam fillings may cause an increased background level of Hg in exhaled air [28]. Sampling requires special equipment and instructions and storage requires transfer on an adsorption tube. Although exhaled air analysis is a well-established method that was validated for humans it is still not much used in routine.
4. Conclusions and Future Perspectives
HBM is widely used in the field of occupational and environmental health, but can also become useful in case of an unexpected release of Hg. Biological reference and guidance values may be used to evaluate the internal dose and estimate its health impacts. A flow chart can be used to support the decision making process for the most suitable biological medium for HBM of Hg in adults and children.
Blood, urine, and hair are by far the most suitable biological media. Blood is a suitable biomarker for recent or current exposure to both inorganic and organic Hg. Cord blood Hg levels are higher than maternal blood levels, due to an active transport system, and therefore cord blood THg is a better biomarker to study fetal exposure. Urine is a suitable biomarker for long-term exposure to Hg0 vapor. Hair is a suitable biomarker for mid-to long-term exposure to MeHg depending on the hair length. Exhaled air is a suitable biomarker for short-term exposure to Hg0 vapor, especially when (young) children are involved. For adults this method can be useful too.
For populations with dietary exposure to MeHg and additional exposure to Hg0 vapor (e.g., individuals active in artisanal and small gold mining) speciation of Hg with respect to a contribution from inorganic and organic Hg in hair could have added value.
HBM of Hg is a useful tool to support environment and health policy-making because it can provide useful quantitative information regarding the actual exposure of a population to Hg. Furthermore, HBM can provide data regarding the potential health impact and allows preventive action to be taken before adverse effects occur.
Acknowledgements
The authors acknowledge Drs. Jan Quik from the Central Laboratory of the Bureau of Public Health (CL-BOG) in Suriname for fruitful discussion.
Conflict of Interest
The authors declare that there are no conflicts of interest.









 DownLoad:
DownLoad: