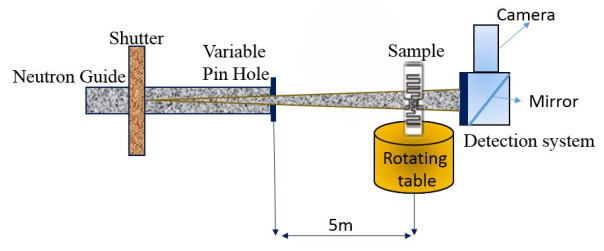
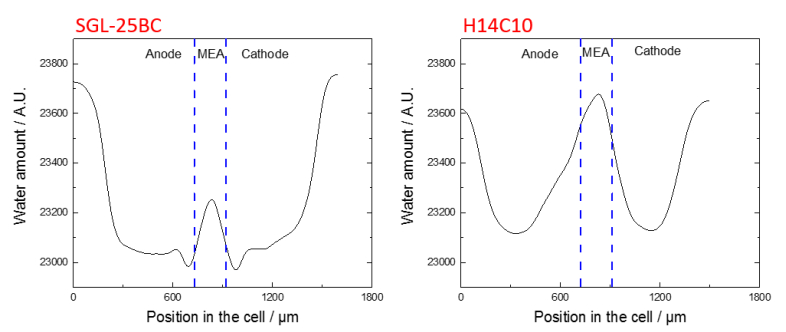
In this feasibility study, high-resolution neutron tomography is used to investigate the water distribution in polymer electrolyte membrane fuel cells (PEMFCs). Two PEMFCs were built up with two different gas diffusion layers (GDLs) namely Sigracet® SGL-25BC and Freudenberg H14C10, respectively. High-resolution neutron tomography has the ability to display the water distribution in the flow field channels and the GDLs, with very high accuracy. Here, we found that the water distribution in the cell equipped with the Freudenberg H14C10 material was much more homogenous compared to the cell with the SGL-25BC material.
1.
Introduction
It has been known that organic nutrients (e.g., nitrogen and phosphorus), light, and inorganic carbon are the important factors that affect the growth of phytoplankton. However, previous competition theory only focused on the interaction between the species and nutrients/light (see, e.g., [7,9]), and neglected the role of inorganic carbon. This is probably due to the complexities including the biochemistry of carbon acquisition by phytoplankton and the geochemistry of inorganic carbon in the ecosystem [10,20]. In the Supplementary Information of [20], the authors proposed a system of ODEs modeling the competition of the species for inorganic carbon and light in a well-mixed water column. Dissolved CO2 and carbonic acid are regarded as one resource (denoted as "CO2"), and bicarbonate and carbonate ions are regarded as another (denoted as "CARB"). The resources "CO2" and "CARB" are stored internally, and they are substitutable in their effects on algal growth [17,20]. On the other hand, uptake rates also includes self-shading by the phytoplankton population, namely, an increase in population density will reduce light available for photosynthesis, and thereby suppressing further carbon assimilation and population growth [20].
It was known that pH and alkalinity are two main factors in the modeling of inorganic carbon [20]. The consumption terms for "CO2" and "CARB" used in [20] include computations of feedbacks that arise from changes in pH and alkalinity during algal growth. In the recent work [17], the authors ignore these latter feedbacks and assume that the parameters in the system are constants, simplifying the complex processes of "CO2" and "CARB" involved. Incorporating the simplifications used in [17], we modify the model presented in the Supplementary Information of [20] and we shall investigate the following chemostat-type model with internal storage:
Here R(t) and S(t) denote the concentrations of "CO2" and "CARB" in the chemostat at time t, respectively. ui(t) denotes the concentration of species i at time t. Qi represents the amount of cell quota of resources R and S per individual of species i at time t. μi(Qi) is the growth rates of species i as a function of cell quota Qi. fRi(R,Qi) (fSi(S,Qi)) is the per capita uptake rate of species i as a function of resource concentration R (S) and cell quota Qi. D is the dilution rate of the chemostat. Each nutrient is supplied at the rate D, and both input concentrations are R(0) and S(0) respectively. Qmin,i denotes threshold cell quota below which no growth of species i occurs. γi(Qi) represents the respiration rate of species i as a function of cell quota Qi. gi(u1,u2) stands for the photosynthetic rate of the species i as a function of u1(t) and u2(t). Following the ideas of model simplifications in [17], we also assume that carbonic acid loses a proton to become bicarbonate at the rate ωr, and the rate of the reverse reaction is denoted by ωs.
One type of the photosynthetic rate of the species i, gi(u1,u2), takes
where mi and ai are the maximal growth rate and half saturation constant of species i, respectively, and
Here we have assumed that the light intensity at each depth is described by Lambert-Beer law [11,14], which states that the amount of light absorbed is proportional to the light intensity (Iin), but decreases with the depth in the water column (z), the background turbidity of the water itself (k0), the specific light attenuation coefficients of the competing species (ki), and the population densities of the species (ui). Assume that zm is the total depth of the water column. Substituting (1.3) into (1.2), then the photosynthetic rate gi(u1,u2) becomes
where
We also note that the other type of the photosynthetic rate gi(u1,u2) takes the form
with
According to [20], we take the growth rate μi(Qi) as follows
where μmax,i is the maximum specific growth rate of species i; Qmin,i is the minimum cellular carbon content required for growth of species i; Qmax,i is the maximum cellular carbon content of species i. From [3,4,5], for i=1,2, the growth rate μi(Qi) can also take the forms :
where (Qi−Qmin,i)+ is the positive part of (Qi−Qmin,i) and μ∞,i is the maximal growth rate at infinite quotas (i.e., as Qi→∞) of the species i.
According to [6,16], for H=R, S and i=1,2, the uptake rate fHi(H,Qi) takes the form:
Here H=R, S represents the concentration of the extracellular resource; ρHi(Qi) represents the maximal uptake rate of the species i; KHi is the half-saturation constant, the resource concentration at which uptake rate is half of the maximal rate. The maximal resource uptake rate, ρHi(Qi), is a decreasing, linear function of quota [8,16], which is defined by
for Qmin,i≤Qi≤Qmax,i. In other words, the maximal rate of resource uptake, ρHi(Qi), varies between upper and lower bounds, ρhighmax,Hi and ρlowmax,Hi, respectively, while quota varies between lower and upper bounds, Qmin,i and Qmax,i, respectively (see, e.g., [8]). Cunningham and Nisbet [1,2] took ρHi(Qi) to be a constant. The authors in [20] put ρhighmax,Hi≡ρmax,Hi, ρlowmax,Hi=0, then ρHi(Qi) becomes
System (1.1) also includes the fact that carbon is lost by respiration. The respiration rate is proportional to the size of the transient carbon pool [20]:
where Qmin,i≤Qi≤Qmax,i, and γmax,i is the maximum respiration rate of species i.
In this whole paper, we always assume that the photosynthetic rate gi(u1,u2) takes the form in (1.2) or (1.4); the functions μi(Qi), fHi(H,Qi), and γi(Qi) satisfy the following assumptions: (i=1,2 and H=R, S)
(C1) μi(Qi) is continuously differentiable for Qi≥Qmin,i, μi(Qmin,i)=0, μi(Qi)≥0 and μ′i(Qi)>0 for Qi≥Qmin,i.
(C2) fHi(H,Qi) is continuously differentiable for H>0 and Qi≥Qmin,i, fHi(0,Qi)=0, fHi(H,Qi)≥0, ∂fHi(H,Qi)∂H>0 and ∂fHi(H,Qi)∂Qi≤0 for H>0 and Qi≥Qmin,i.
(C3) γi(Qi) is continuously differentiable for Qi≥Qmin,i, γi(Qmin,i)=0, γi(Qi)≥0 and γ′i(Qi)>0 for Qi≥Qmin,i.
The rest of the paper is organized as follows. Section 2 is devoted to the study of the single population model. In Section 3, we shall investigate the possibility of coexistence of the two competing species system (1.1). A brief discussion section completes this paper.
2.
Single population model
In this section, we first investigate the extinction and persistence of the single population model. Mathematically, it simply means that we remove equations of Q2 and u2 from (1.1). In order to simplify notation, all subscripts are dropped in the remaining equations and the single population model takes the form:
The specific growth rate G(u) takes the form
where
or
The feasible domain for system (2.1) takes the form
Then it is easy to show that X is positively invariant for system (2.1). Next, we study the boundedness of solutions of (2.1):
Lemma 2.1. Every solution (R(t),S(t),Q(t),u(t)) of system (2.1) exists globally. Furthermore, solutions of (2.1) are ultimately bounded on X.
Proof. By the continuation theorem, it suffices to prove that the solution of system (2.1) is bounded on finite time intervals. Let
Then Θ(t) satisfies
Thus, Θ(t) is bounded on finite time intervals. This fact and the positivity of the solution imply that R(t), S(t), and u(t)Q(t) are bounded on finite time intervals. Since Q(t)≥Qmin, we can also deduce that u(t) is bounded on finite time intervals.
It remains to show that Q(t) is bounded on finite time intervals. Inspired by the ideas in [15,Proposition 3], we will investigate the dynamics of the variable V(t)=12(Q(t))2. By the monotonicity of fN for N=S,R, the inequality x≤12(1+x2), and the fact that Q≥Qmin, it is easy to see that V(t) satisfies
Since R(t) and S(t) in (2.5) are bounded on finite time intervals, we see that V(t) is bounded on finite time intervals, and hence, so is Q(t). Thus, every solution of system (2.1) exists globally.
From (2.4), it is easy to see that
and hence, Θ(t) is ultimately bounded. This together with the positivity of the solution, we deduce that R(t), S(t), and u(t)Q(t) are ultimately bounded. Using the fact Q(t)≥Qmin, we see that u(t) is ultimately bounded. Finally, we show that Q(t) is ultimately bounded. From (2.3), (2.6), and the third equation of (2.1), it follows that there exist τ0>0 and η0>0 such that
Then
where Qη0 is the positive root uniquely determined by
Thus, solutions of (2.1) are ultimately bounded on X since η0>0 is independent of initial values.
In order to find the species-free equilibrium of system (2.1), which corresponds to the absence of species, we put u=0 in (2.1). Then we consider the following system
It is easy to see that (2.7) is a cooperative/monotone system (see, e.g., [18]), and
is the unique equilibrium for (2.7). For a monotone dynamical system, the unique steady state is globally asymptotically stable if and only if every forward orbit has compact closure (see [13,Theorem D]). By Lemma 2.1 and the above discussions, we have the following results:
Lemma 2.2. The unique equilibrium (R∗,S∗) is globally asymptotically stable for (2.7) in R2.
From Lemma 2.2, the species-free equilibrium of system (2.1), which we label E0, is given by
where Q∗ satisfies
The local stability of E0 is determined by the Jacobian matrix of (2.1) at E0, denoted by
where
It is easy to see that the eigenvalues of J0 are j33, μ(Q∗)−D, together with the eigenvalues of the following matrix
Since j33<0 and the eigenvalues of ˜J0 are both negative, we see that the sign of μ(Q∗)−D determines the stability of E0. That is, E0 is locally asymptotically stable if μ(Q∗)−D<0, and unstable if μ(Q∗)−D>0. Thus, we have proved the following result concerning with the local stability of E0:
Lemma 2.3. E0 is locally asymptotically stable if μ(Q∗)−D<0, and unstable if μ(Q∗)−D>0.
2.1. Persistence of system (2.1)
This subsection is devoted to the investigations of persistence of system (2.1).
Theorem 2.4. Assume that (R(t),S(t),Q(t),u(t)) is the unique nonnegative solution of system (2.1), for all t∈[0,∞), with the initial value (R0,S0,Q0,u0)∈X. If μ(Q∗)−D>0, then system (2.1) is uniformly persistent in the sense that there exists a ξ>0 such that
Further, system (2.1) admits at least one positive equilibrium (ˆR,ˆS,ˆQ,ˆu).
Proof. Recall that X is defined in (2.2). Let
and
It is easy to see that both X and X0 are positively invariant for system (2.1), and ∂X0 is relatively closed in X. Furthermore, system (2.1) is point dissipative (see Lemma 2.1). Let Φ(t):X→X be the solution maps associated with system (2.1). Set ˜M∂:={P∈∂X0:Φ(t)P∈∂X0, ∀ t≥0} and ˜ω(P) be the omega limit set of the orbit ˜O+(P):={Φ(t)P:t≥0}. We show the following claim.
Claim: ˜ω(P)={E0}, ∀ P∈˜M∂.
Since P∈˜M∂, we have Φ(t)P∈∂X0, ∀ t≥0. Thus, u(t,P)=0, ∀ t≥0. In view of the first two equations of (2.1), it follows that (R(t,P),S(t,P)) satisfies (2.7), ∀ t≥0. Then Lemma 2.2 implies that
Then, the equation for Q(t) in (2.1) is asymptotic to
From the theory for asymptotically autonomous semiflows (see, e.g., [19,Corollary 4.3]), it follows that limt→∞Q(t,P)=Q∗, where Q∗ is given in (2.8). Hence, the claim is proved.
Let η1:=12(μ(Q∗)−D)>0. Then it follows from the continuity of μ(Q) that there exists σ1>0 such that
Claim: E0 is a uniform weak repeller for X0 in the sense that
Suppose not. Then there exists a P∈X0 such that
Thus, there exists a τ1>0 such that
This and (2.9) imply that
From this inequality and the fourth equation of (2.1), we have
which shows that limt→∞u(t,P)=∞, a contradiction.
Therefore, E0 is isolated in X and ˜Ws(E0)∩X0=∅, where ˜Ws(E0) is the stable set of E0 (see [21]). Since Φt:X→X is point dissipative and compact, we conclude from [21,Theorem 1.1.3] that there exists a global attractor A for Φt in X. By [21,Theorem 1.3.1] on strong repellers, Φt:X→X is uniformly persistent with respect to (X0,∂X0). It follows from [21,Theorem 1.3.6] that there exists a global attractor A0 for Φt in X0 and Φt admits at least one fixed point
Then ˆQ≥Qmin>0, ˆu>0, and (ˆR,ˆS) satisfies
In view of (2.10), we deduce that ˆR>0, ˆS>0. Thus, (ˆR,ˆS,ˆQ,ˆu) is a positive steady-state solution for (2.1). We complete the proof.
2.2. Extinction of system (2.1)
In this subsection, we neglect the effect of respiration and investigate the extinction of system (2.1). Putting the respiration rate to be zero,
Then we have the following result:
Theorem 2.5. Suppose (R(t),S(t),Q(t),u(t)) is the unique nonnegative solution of system (2.1), for all t∈[0,∞), with the initial value (R0,S0,Q0,u0)∈X. Assume that (2.11) holds. If μ(Q∗)−D<0, then system (2.1) is washed out, that is,
Proof. For η>0, we assume that Qη is the unique root of
Recall that Q∗ is the unique root of (2.8). Since
we may find an η2>0 such that
On the other hand, by the continuity, we may find a σ2>0 such that
In view of the assumption (2.11) and the first two equations of system (2.1), it follows that
By the comparison arguments and Lemma 2.2, we have
Then there exists a τ2>0 such that
Then it follows from the third equation of (2.1) that
In view of the first two inequalities of (2.14) and (2.15), we have
Using the comparison arguments, we have
where Qη2 is the unique root of (2.12) with η=η2. Thus, we may find a τ3>0 such that
and hence,
In view of the third inequality of (2.14) and (2.17), we have
By (2.13), (2.18) together with the fourth equation of (2.1), it follows that
Since μ(Q∗)−D<0 and (2.19), we have
Then (R(t),S(t)) is asymptotic to (2.7). By Lemma 2.2 and the theory for asymptotically autonomous semiflows (see, e.g., [19,Corollary 4.3]), it follows that
Similarly, Q(t) is asymptotic to
and limt→∞Q(t)=Q∗, where Q∗ is given in (2.8) with γ(Q)≡0. We complete the proof.
3.
Coexistence for the two-species model
In this section, we shall concentrate on the study of coexistence of system (1.1). The subsequent discussions will reveal that two semi-trivial steady-state solutions of system (1.1), corresponds to the presence of one of the species and the absence of the other species, are not necessarily unique. This makes our analysis more difficult. Fortunately, we can adopt the ideas developed in [12,Section 4] to overcome this difficulty.
The trivial steady-state solution of (1.1), labeled E0, corresponds to the absence of both species. It is given by
where (R∗,S∗) is given in Lemma 2.2, and Q∗i satisfies
where G1(u1)=g1(u1,0) and G2(u2)=g2(0,u2).
In order to determine the semi-trivial steady-state solutions of (1.1), we need the following single population system associated with the growth of species i:
Next, we shall summarize the result of system (3.1). By Theorem 2.4, for i = 1, 2, system (3.1) admits at least one positive equilibrium and we may assume that A_i^{0}\subset\rm{Int}\mathbb{R}_{+}^4 is a global attractor of the semiflows generated by system (3.1), under the condition that \mu_i(Q_i^{*})-D>0. One of the semi-trivial steady-state solutions of (1.1), labeled \mathcal{E}_1, corresponds to the presence of species 1 and the absence of species 2. It is given by
where (\hat{R}_1, \hat{S}_1, \hat{Q}_1, \hat{u}_1)\in A_1^{0} is a positive equilibrium of system (3.1) with i = 1, which is not necessarily unique. Here, \hat{Q}_2 = \hat{Q}_2(\hat{R}_1, \hat{S}_1, \hat{Q}_1, \hat{u}_1) is the root of
Inspired by the arguments in [12,Section 4], we assume that
The other semi-trivial steady-state solution of (1.1), labeled \mathcal{E}_2, corresponds to the presence of species 2 and the absence of species 1. It is given by
where (\check{R}_2, \check{S}_2, \check{Q}_2, \check{u}_2)\in A_2^{0} is a positive equilibrium of system (3.1) with i = 2, which is not necessarily unique. Here, \check{Q}_1 = \check{Q}_1(\check{R}_2, \check{S}_2, \check{Q}_2, \check{u}_2) is the root of
Similarly, we assume
The feasible domain for system (1.1) takes the form
Then it is easy to show that \mathbf{Y} is positively invariant for system (1.1). By the similar arguments in Lemma 2.1, we can show the following result:
Lemma 3.1. Every solution (R(t), S(t), Q_1(t), u_1(t), Q_2(t), u_2(t)) of system (1.1) exists globally. Furthermore, solutions of (1.1) are ultimately bounded on \mathbf{Y}.
Assume that \Psi(t):\mathbf{Y}\rightarrow\mathbf{Y} is the semiflow associated with system (1.1). Let
and
Following the ideas in [12,Section 4], we assume that \mathcal{M}_0 = \{\mathcal{E}_0\},
and
One can easily to use "the method of proof by contradiction" to deduce the following result:
Lemma 3.2. Let \mu_i(Q_i^{*})-D>0, for some i\in \{1, 2\}. Then \mathcal{M}_0 is a uniform weak repeller in the sense that there exists a \delta_0>0 such that
Next, we shall use the strategy in [12,Lemma 4.2] to show the following result:
Lemma 3.3. Let \mu_i(Q_i^{*})-D>0, for each i\in \{1, 2\}. If \mu_2(\hat{Q}_2^{\min})-D>0, then \mathcal{M}_1 is a uniform weak repeller in the sense that there exists a \delta_1>0 such that
Proof. Let
Then
Setting
Define \mathcal{G}:B_1\rightarrow \mathbb{R} by
We may find a \delta_1>0 such that
whenever \phi\in \mathbb{R} with \text{dist}(\phi, B_1)<\delta_1. Since B_1 is compact, it follows that for any \phi\in \mathbb{R} with \text{dist}(\phi, B_1)<\delta_1, there exists \phi_*\in B_1 with \phi_* depending on \phi such that
Thus, we have
whenever \phi\in \mathbb{R} with \text{dist}(\phi, B_1)<\delta_1.
Suppose that (3.5) is not true. Then there exists \mathbf{v}^0\in\mathbf{Y}_0 such that
This implies that
From the first inequality of (3.7), we can choose t_1>0 such that
By (3.6), it follows that there exists \phi_*^t\in B_1 such that
which implies that
From the sixth equation of (1.1), we have
We deduce that \lim_{t\rightarrow \infty}u_{2}(t) = \infty since \epsilon_1>0 and u_{2}(t_1)>0. This contradicts the second inequality of (3.7) and we complete the proof.
By the same arguments in Lemma 3.3, the following result holds:
Lemma 3.4. Let \mu_i(Q_i^{*})-D>0, for each i\in \{1, 2\}. If \mu_1(\check{Q}_1^{\min})-D>0, then \mathcal{M}_2 is a uniform weak repeller in the sense that there exists a \delta_2>0 such that
Now we are in a position to prove the main result of this paper.
Theorem 3.5. Assume that (R(t), S(t), Q_1(t), u_1(t), Q_2(t), u_2(t)) is the unique solution of (1.1) with the initial value (R(0), S(0), Q_1(0), u_1(0), Q_2(0), u_2(0))\in \mathbf{Y}. Let \mu_i(Q_i^{*})-D>0, \ \forall \ i = 1, 2, \mu_2(\hat{Q}_2^{\min})-D>0, and \mu_1(\check{Q}_1^{\min})-D>0. Then system (1.1) is uniformly persistent with respect to (\mathbf{Y}_0, \partial \mathbf{Y}_0) in the sense that there is a positive constant \zeta>0 such that if u_1(0)\neq 0 and u_2(0)\neq 0, we have
Furthermore, system (1.1) admits at least one (componentwise) positive equilibrium.
Proof. Recall that \Psi(t):\mathbf{Y}\rightarrow\mathbf{Y} is the semiflow associated with system (1.1). It is easy to see that \Psi(t)\mathbf{Y}_0\subset\mathbf{Y}_0. Since solutions of the system (1.1) are ultimately bounded (see Lemma 3.1), it follows that \Psi(t) is point dissipative and compact, and hence, \Psi(t) admits a global attractor (see, e.g., [21,Theorem 1.1.3]). Let
and \omega(\mathbf{v}^0) be the omega limit set of the orbit O^{+}(\mathbf{v}^0): = \{\Psi(t)\mathbf{v}^0:t\geq 0\}.
Claim: \bigcup_{\mathbf{v}^0\in M_{\partial}}\omega(\mathbf{v}^0)\subset \mathcal{M}_0\cup \mathcal{M}_1 \cup\mathcal{M}_2.
For any given \mathbf{v}^0: = (R^0, S^0, Q_1^0, u_1^0, Q_2^0, u_2^0)\in M_{\partial}, we have \mathbf{v}^0\in \partial \mathbf{Y}_{0} and \Psi(t)\mathbf{v}^0\in \partial \mathbf{Y}_{0}, \ \forall \ t\geq 0. We discuss the following three subcases:
(ⅰ) If u_1^0 = 0, \ u_2^0 = 0, then we have u_1(t, \mathbf{v}^0) = 0 and u_2(t, \mathbf{v}^0) = 0, \forall\ t\geq0. Thus, it is easy to see that \lim_{t\rightarrow \infty}\Psi(t)\mathbf{v}^0 = \mathcal{E}_0.
(ⅱ) If u_1^0 \neq 0, \ u_2^0 = 0, then we have u_1(t, \mathbf{v}^0)> 0 and u_2(t, \mathbf{v}^0) = 0, \forall\ t\geq0. Then (R(t, \mathbf{v}^0), S(t, \mathbf{v}^0), Q_1(t, \mathbf{v}^0), u_1(t, \mathbf{v}^0)) satisfies system (3.1) with i = 1. Since \mu_1(Q_1^{*})-D>0, it follows from Theorem 2.4 that
will eventually enter the global attractor A_1^{0}\subset\rm{Int}\mathbb{R}_{+}^4, and hence, \Psi(t)\mathbf{v}^0 will eventually enter \mathcal{M}_1.
(ⅲ) If u_1^0 = 0, \ u_2^0\neq 0, then we have u_1(t, \mathbf{v}^0) = 0 and u_2(t, \mathbf{v}^0)> 0, \forall\ t\geq0. Then (R(t, \mathbf{v}^0), S(t, \mathbf{v}^0), Q_2(t, \mathbf{v}^0), u_2(t, \mathbf{v}^0)) satisfies system (3.1) with i = 2. Since \mu_2(Q_2^{*})-D>0, it follows from Theorem 2.4 that
will eventually enter the global attractor A_2^{0}\subset\rm{Int}\mathbb{R}_{+}^4, and hence, \Psi(t)\mathbf{v}^0 will eventually enter \mathcal{M}_2.
The proof of the claim is complete.
By Lemma 3.2, Lemma 3.3 and Lemma 3.4, it follows that for i = 0, 1, 2, \mathcal{M}_i is a uniform weak repeller for \mathbf{Y}_{0} in the sense that there exists \delta_i>0 such that
Note that \mathcal{M}_0, \mathcal{M}_1, and \mathcal{M}_2 are pairwise disjoint, compact and isolated invariant sets for \Psi(t) in \partial\mathbf{Y}_0. Further, each \mathcal{M}_i is isolated in \mathbf{Y} and \mathcal{W}^s(\mathcal{M}_i)\cap \mathbf{Y}_{0} = \emptyset, where \mathcal{W}^{s}(\mathcal{M}_i) is the stable set of \mathcal{M}_i (see [21]). It is easy to see that no subsets of \mathcal{M}_0, \mathcal{M}_1, and \mathcal{M}_2 forms a cycle in \partial\mathbf{Y}_0. By [21,Theorem 1.3.1] on strong repellers, \Psi(t):\mathbf{Y}\rightarrow\mathbf{Y} is uniformly persistent with respect to (\mathbf{Y}_0, \partial\mathbf{Y}_0). It follows from [21,Theorem 1.3.6] that there exists a global attractor \hat{\mathcal{A}}_0 for \Psi(t) in \mathbf{Y}_0 and \Psi(t) has at least one fixed point
Thus, (\tilde{R}, \tilde{S}, \tilde{Q}_1, \tilde{u}_1, \tilde{Q}_2, \tilde{u}_2) is a positive steady-state solution for system (1.1). This completes the proof.
4.
Discussion and conclusion
In this paper, we study the chemostat-type system (1.1) modeling the interactions of two species competing for "CO2" (dissolved CO2 and carbonic acid), "CARB" (bicarbonate and carbonate ions), and light in a spatially homogeneous water column. Our mathematical model presented in this paper is inspired by the recent works [17,20]. In fact, system (1.1) is a modified version of the model in the Supplementary Information of [20], where the specific growth rate of the competing species i depends on their stored cellular carbon content (quota) Q_i. The dynamics of Q_i can be affected by the uptake rates of inorganic carbon, "CO2" (R(t)) and "CARB" (S(t)), photosynthetic activity (g_i(u_1, u_2)), and respiration (\gamma_i(Q_i)). The resources "CO2" and "CARB" are substitutable in their effects on algal growth, which also involves a very complex processes. In order to make our system (1.1) analytically tractable, we have adopted the ideas in [17] to assume that carbonic acid loses a proton to become bicarbonate at the rate \omega_r, and the rate of the reverse reaction is denoted by \omega_s, which simplifies the complex processes of "CO2" and "CARB" involved.
Solutions of both the two-species system (1.1) and its single-species sub-system (2.1) follow mass conservation laws, and are eventually bounded (see Lemma 2.1 and Lemma 3.1). Persistence of a single species depends on the sign of \mu(Q^{*})-D (see Theorem 2.4), where Q^{*} is given in (2.8). Biologically, Q^* represents the quota that a species can obtain when the inorganic carbon concentration is at its long-term upper bound (R^{*}, S^{*}), which is the unique equilibrium for system (2.7) governing the available inorganic carbon in a species-free habitat. Then Theorem 2.4 states that the species can persist if the quota Q^{*} exceeds the quota \hat{Q} required for growth to balance losses (i.e., \mu(\hat{Q}) = D). Thus, the persistence criterion (i.e., \mu(Q^{*})-D>0) summarizes the characteristics of carbon uptake, the growth rate, light availability, and the respiration rate. If the quota Q^{*} is less than the quota \hat{Q}, then we can show that the species population is washed out of the habitat (see Theorem 2.5), where we have ignored the effect of respiration (see the specific assumption (2.11)), due to a technical reason.
In Theorem 2.4, we only show that the single-species model (2.1) admits at least one positive equilibrium if the species can persist by using the theory of uniform persistence. The uniqueness and global stability of positive equilibrium for (2.1) are still open if no extra assumptions are imposed. Thus, two semi-trivial steady-state solutions of the two-species system (1.1), corresponds to the presence of one of the species and the absence of the other species, are not necessarily unique. This makes the investigation of coexistence for the two-species system (1.1) more difficult. Inspired by [12,Section 4], we first define two suitable parameters, \hat{Q}_2^{\min} and \check{Q}_1^{\min} (see 3.3 and 3.4), then we are able to show that the compact attractor \mathcal{M}_1 (on the boundary u_2 = 0), and the compact attractor \mathcal{M}_2 (on the boundary u_1 = 0) are uniform weak repellers for two-species system (1.1) (see Lemma 3.3 and Lemma 3.4) under appropriate conditions depending on \hat{Q}_2^{\min} and \check{Q}_1^{\min}, respectively. Finally, we are able to show that system (1.1) is uniformly persistent, and it admits at least one coexistence (componentwise positive) steady-state solution (see Theorem 3.5) when the trivial steady-state solution, the compact set \mathcal{M}_1, and the compact set \mathcal{M}_2 are all invasible. From biological viewpoints, invasibility will depend on whether the missing competitor obtains sufficiently large quotas (\hat{Q}_2^{\min} or \check{Q}_1^{\min}) to permit a growth rate that exceeds the loss to dilution (D). Then robust coexistence occurs when there is mutual invasibility of both \mathcal{M}_1 and \mathcal{M}_2.
Acknowledgments
Research of F.-B. Wang is supported in part by Ministry of Science and Technology, Taiwan; and National Center for Theoretical Sciences (NCTS), National Taiwan University; and Chang Gung Memorial Hospital (CRRPD3H0011, BMRPD18 and NMRPD5F0543). We would like to express our thanks to Professor Sze-Bi Hsu for the helpful discussions in this paper.
Conflict of interest
All authors declare no conflicts of interest in this paper.














 DownLoad:
DownLoad: