1. Introduction
Currently, the electric power system is confronting many uncertainties. The main source of these uncertainties is penetration of renewable energy sources in power system network. Among these renewable energy sources, photovoltaic (PV) generation and wind energy generation are the dominant sources of uncertainty. Due to randomness nature of uncertainty, it increases the risk associated with electric power system operation modes and further has an influence on load flow analysis. Most of these uncertainties are dependent. This dependence relationship can be linear or non-linear. For example, the loads in the same area can be increased or decrease in a same time due to environmental and social ones. Similarly, the output power of wind energy sources is strongly correlated with the wind speed of neighboring measuring stations [1,2]. On the other hand, the power system highly uncertain due to changing pattern of power demand like the transport (electric mobility) and heat sectors (heat pumps in buildings) [1]. Safeguarding the reliability of the power system is a key enabler for this massive system transformation. For the operation of future power systems, new methods are needed to incorporate the different sources of uncertainty (contingencies, load and renewable energy source forecast errors) during the operational planning stage and to help system operators to steer the system into risk-averse modes of operation [3,4,5].
The probabilistic load flow (PLF) analysis is a tool that can handle uncertainties in the efficient and effective way. The PLF is a steady-state load flow analysis to determine the network parameters by considering uncertainty with input random variables flexibly. The information obtained by PLF analysis is used for power system security assessment, operation and control purpose. In literature, many PLF methods have been used in order to deal with correlated input random variables. In these methods included: Gaussian mixture model method [6,7,8], point estimation method [9,10,11], convolution method [12,13], cumulant method [8,14], unscented transformation [15], and Monte Carlo simulation (MCS) [16,17,18,19]. MCS methods are the most popular methods among all of above methods. It is due to its simplicity and ability to handle complex non-linear problems. Most of the above methods only deal with a linear dependence. Additional, the Persons linear correlation coefficient has been used for measuring the degree of dependence. Most of the nature uncertainties are not linear. This proposed model can handle this non-linear dependence more flexible.
All methods used for PLF can be divided into four categories. These categories are as numerical methods, analytical methods, approximate methods, and hybrid methods [20]. A numerical MCS method with simple random sampling (SRS) has been used frequently for PLF power system problems. MCS with SRS can be express as SMCS. SMCS method has been used as a reference for accuracy comparison in PLF studies [5,8,10,15,21,22,23,24]. From the literature, it is clear that no one method is more accurate than SMCS in term of accuracy. However, it suffers heavy computational burden to achieve the desired accuracy. To overcome computational burden, in literature many methods have been used such as convolution techniques [12,13]. The convolution base methods are also time-consuming due to discrete point problems. Point estimation based methods have lesser computational burden but less accurate. In fact, there are no holistic criteria for PLF evaluation. Always there is a compromise between computational burden and accuracy. But currently, a third moment has been started to overcome computational burden and accuracy problems. This moment is to hybrid methods like combined cumulants and Laplace transform method [25], combine cumulant and Gaussian mixture method [8], cumulant and multiple integral method [26], second order design method [17]. Actually, the accuracy and computational burden of PLF methods highly depend upon the modelling of input uncertainty and sampling techniques.
The contribution in this research work has many aspects included: Almost all of the methods in literature can only deal with a linear correlation between input random variables and have been considered Pearson linear correlation coefficient. This Pearson linear correlation coefficient some time cannot measure the degree of correlation. For example: 1) it cannot measure non-linear dependence between input random variable; 2) it can't measure dependence for those distributions that have not define standard deviation; 3) it is invariant under strictly increasing transformation. To overcome this problem in this work Gaussian Copula theory is proposed that can handle linear and non-linear problems flexibly. By using Copula theory, a desirable correlation can be achieve between input random variables. The other aspect of this work is modelling of input uncertainty. The PV generation and correlated load are used for modelling the input uncertainty. The special in this work real data about PV generation and load are used for accuracy comparison purpose. Additional, the Box-Muller sampling (BMS) and Latin hypercube sampling (LHS) are used for accuracy and computational burden comparison purpose. The SMCS is used for a benchmark for other methods in term of accuracy and computational burden. MCS combine with BMS can be express as BMCS and MCS combine with LHS can be express as LMCS. For three methods, Copula theory is used for capturing the complex stochasticity of correlated loads and PV generation. The modified IEEE 14-bus and IEEE 118-bus test system is used for obtaining results.
The paper is organized as follows. Section 2 describes the modelling of the probability distribution of input random variable included correlated loads and correlated PV generation. Section 3 describes the methodology, and sampling techniques included SRS, BMS, and LHS. Section 4 describes the PLF analysis procedure. Section 5, evaluate the performance analysis of proposed methods. Finally, conclusions are drawn in Section 6.
2. Modelling of input random variables for uncertainty
The accuracy and computational efficiency of PLF analysis usually depending upon three major factors included: a) Uncertainty handing method; b) Accurate power system model; c) Accurate modelling input random variable uncertainty.
2.1. Modelling of correlated loads for uncertainty
There are normally two methods for measurement of correlation between random variable with respect to degree and structure. First one is Pearson's linear correlation coefficient that can only measure the degree of correlation Eq 1. The second one is rank correlation coefficient and Copula theory that can measure the degree as well as the structure of correlation. In this work, Copula theory is proposed to measure the structure as well as the degree of correlation between random variables flexibly. This theory can measure the linear and non-linear correlation between random variables. More, it is invariant under strictly increasing transformation. The correlation matrix for n input random variable is shown in Eq 1 as:
|
Cor_matrix=[1ρ21...ρ1nρ211...ρ2n⋮⋮⋱⋮ρn1ρn2...1]
|
(1)
|
Where ρij is the correlation coefficient and can be calculated as ρij=cov(Wi,Wj)/σiσj where σi and σj is the standard deviation of a random variable Wi and Wj respectively and cov(Wi,Wj) is the covariance. According to Copula theory, it can be express as in Eq 2 for bivariate:
|
F12(w1,w2)=C(F1(w1),F2(w2))
|
(2)
|
Where C is a copula function, according to Sklar theorem [27]. It couples multivariate joint distribution CDF to one dimensional marginal CDFs. F1(w1) and F2(w2) are the marginal CDF of two random variables W1 and W2 respectively. F12(w1,w2) is the joint CDF of these two random variables. C(F1(w1),F2(w2)) is the Copula density function, and it must follow the Sklar theorem property as mention in Eq 3:
|
U∈[0,1]:P(U≤u)=P(F(w)≤u)=P(w≤F−1(u))=F[F−1(u)]=u
|
(3)
|
It can be extended to multivariate as in Eq 4, m is the number of random variables:
|
f(w1,...,wm)=c(F1(w1),...,Fm(wm)).m∏i=1fi(wi)
|
(4)
|
Where C(F1(w1),..,Fm(wm))=∂mC(F1(w1),..,Fm(wm))∂F1(w1).........∂Fm(wm) is the Copula density function for multivariate random variables.
There are many Copula families, but famous one is included elliptical Copula and Archimedean Copula. Here, Gaussian Copula is proposed to measure the dependence between input random variables that belong to Archimedean Copula family. All loads PDFs are modelled as a Gaussian distribution follows the Eq 5:
|
f(x;μ;σ)=1√2πσe−((x−μ)22σ2)
|
(5)
|
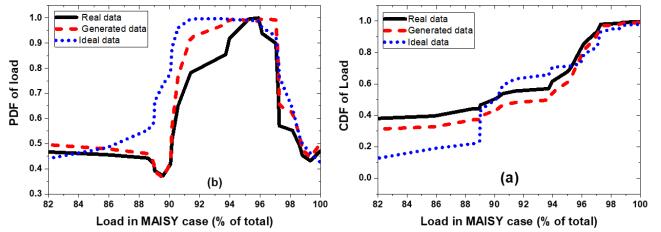
Where x is the required value for which probability distribution function (PDF) needed, μ is the mean value of the load, and σ is the arbitrary value of standard deviation. To show the accuracy of modelled load PDF is compare with actual one day load at MAISY utility customer energy use with per hourly interval available in [28]. Figure 1 shows the PDFs and CDFs of real, generated, and ideal data of loads. Gaussian Copula function is used to establish the desired correlation between different random variables (loads) in the proposed network. The PDFs of multivariate Gaussian distribution with desirable correlation can be found by Eq 6.
|
CGaussR(u)=1√det.Rexp(−12(ϕ−1(u1)....................ϕ−1(ud))T.(R−1−I).(ϕ−1(u1)....................ϕ−1(ud)))
|
(6)
|
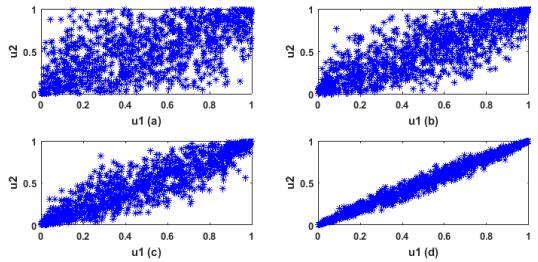
Where R is the correlation matrix belong to [−1,1]d×d, C show the correlation density function, ϕ−1 is the inverse CDF of standard normal distribution, u1,.........,ud is the random variables, d is the number of variables, and I is the identity matrix. The correlation of bivariate function over unit domain from weak to strongly correlated loads with the help of Gaussian Copula is shown in Figure 2.
2.2. PV generation modelling for uncertainty
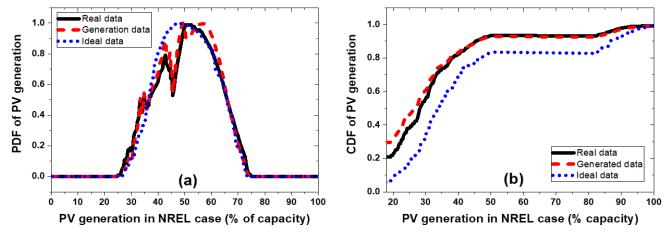
In this work, PV generations are model as a beta distribution with the help of Eq 7. The historical solar power data for integration studies located at California western state is taken to check the accuracy of modelled PV generation available at National Renewable Energy Laboratory (NREL) [29]. One day data (Jun 1, 2006) with a 5-minute interval is taken to check the accuracy of the proposed model.
|
f(x;,α,β)=Γ(α+β)Γ(α)Γ(β)xα−1(1−x)β−1
|
(7)
|
Where x is the observed values or realization, α and β are the shape parameters and always α, β > 0, Ґ is the gamma function. The PDFs and CDFs of real, generated, and ideal values model with the help of Eq 7 are shown in Figure 3.
3. Methodology
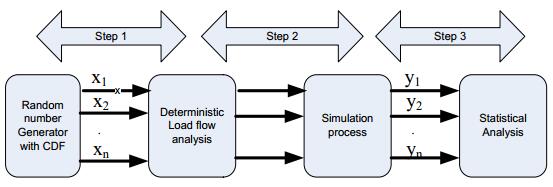
Monte Carlo Simulation is an iterative approach, mostly used for probabilistic load flow analysis. In this approach cumulative distribution function is prepared of a random variable to obtain the uncertainty. To model, the CDF of a random variable is an essential step in this approach. Accurate modelling of CDF give the accurate final results. In this numerical approach, in order to model the uncertainty as a random variable, three basic steps are needed as shown in Figure 4: (1) to model CDF of random variable; (2) to solve the deterministic load flow model; (3) statistical analysis of results.
Monte Carlo Simulation process can be described by Eq 8:
Where in Eq 8–10, X is the vector of input random variable, Y is a vector of output random variables vector, and h is the function of the model under study. The object of study is to obtain PDF of Y at given known PDF of X. T shows the transpose.
3.1. Simple random sampling
Simple random sampling techniques is a theoretical basis technique to design other methods. The variance of the mean of output variable is calculated to find the robustness of sampling techniques [30]. The mean of the sample is calculated as in Eq 11:
Where N is the number of samples, ˉy is the expected value and yi is the output value of ith iteration. The variance of the sample can be obtained as in Eq 12:
|
var(y)=1NN∑i=1(yi−_y)2
|
(12)
|
The variance of the estimating mean can be determined by Eq 13:
3.2. Box-Muller sampling
Box-Muller sampling is also as a sampling technique. In order to determine the sample of given iteration, firstly two random number from uniform distribution in the range of (0, 1) is generated. The sample should be determined by following Eq 14:
|
Si=μi+cos(2πu1)×σi√−2ln(u2)
|
(14)
|
Where,
Si = is the ith sample; µ = mean value of random variable; σ = standard deviation of a random variable; u1 & u2 = uniformly distributed random number in range of (0, 1). For the proposed PLF model, µi and σi are the base load and standard deviation for input variable.
3.3. Latin hypercube sampling
Latin hypercube sampling (LHS) is the type of stratified sampling. It uses to generate a sample of a random variable from entire distribution. In this technique, random variable distribution is divided into equal probability distribution intervals. Each interval is sample exactly once in its entire range of the random variable. In this way, sample value represents the higher sampling efficiency. The sampling procedure is as follows:
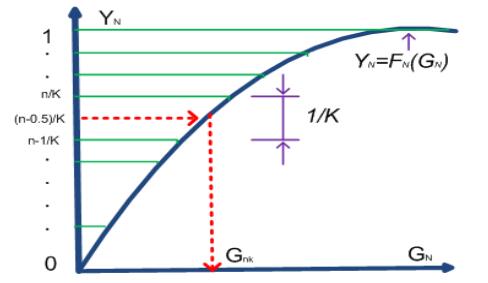
Where in Eq 15, Yn is the CDF of N input random variables such that Gn=G1,........,GN in probability theory, in range Yn = [0, 1]. If the sample size is denoted by K. If the entire range of YN is divided into k non-overlapping intervals than each interval length is equal to 1/k as shown in Figure 5. The sample value is generated from each interval without replacement randomly or midpoint value. In this work, midpoint value is chosen, and this method is call lattice sampling. The sampling value of Gn can be computed by taking the inverse function of Eq 16. The nth sample can be computed as in Eq 16:
The sample values of Gn can be assembled as in Eq 17 in the row of sampling matrix:
From this procedure, the n × k matrix can be obtained.
As described in Section 3.1 the robustness of sampling techniques can be measure on the mean output statistic [30]. Therefore, the mean and variance can be computed by using Eq 11 and Eq 12 respectively. The variance of the estimated mean can be computed with the help of Eq 18:
|
Var(_y)=1Nvar(y)−N−1Ncon(G1,G2)
|
(18)
|
Where con(G1,G2) is the covariance between random variables.
4. Probabilistic load flow evaluations
The deterministic load flow analysis can be described by Eq 19:
Where X is the input vector of nodal active and reactive power injections. Y is the output vector of voltage (V), voltage phase angle (θ), active load flow (Pij), reactive load flow (Qij), h(X) is the load flow function [31]. In case of PLF analysis, correlated nodal loads, PV generation, and conventional generator are the input random variable with their probability distribution functions. The statistical distribution of output variables V, θ, P, and Q are calculated. There are following steps used to perform PLF analysis:
● Prepare the CDF of model correlated loads and correlated PV generations, to set all basic requirement for deterministic load flow analysis, e.g. sample size N.
● To determine the input random variables G.
● To select the desire sampling procedure.
● To generate the sample matrix N × k.
● To set the initial starting point n = 1.
● To perform the deterministic load flow analysis and obtain the values of V, θ, P, Q.
● Set n=n+1; if n<N go to step 6. Otherwise, go to next step.
● To do a statistical analysis of output random variable V, θ, P, Q.
5. Performance evaluation of proposed methods
A series of PLF analysis is carried out to determine the performance of SMCS, BMCS, and LMCS. The PLF analysis is carried out on modified IEEE 14-bus test system and IEEE 118-bus test system. The program is developed with "DIgSILENT PowerFactory (15.1) platform. The simulation was performed on PC with AMD A12-9700P, RADEON R7, 10 COPMPUTE CORES UC+6G, 2.5 GHZ processing speed, and 8 GB RAM". The results obtained by the proposed method are compared with correlated SMCS.
To determine the accuracy of proposed model two error indices are introduced in Eq 20 and Eq 21 [9,10] are adopted.
|
ε∗μ=|μacc−μproμacc|×100%
|
(20)
|
|
ε∗σ=|σacc−σproσacc|×100%
|
(21)
|
Where ε∗μ is an error of the output random variables with * category (* represents V, θ, P, and Q). Second ε∗σ is an error of standard deviation with the * category. The results obtained by the SRS method with a sample size of 20,000 are assumed to be accurate and benchmark. The mean and standard deviation of SMCS method are express as µacc and σacc respectively. Similarly, the mean and standard deviation of proposed methods are express as µpro and σpro respectively. ˉε∗μ and ˉε∗σ are the average error index and average standard deviation error index that determined the distribution convergence of entire system.
To evaluate the convergence of two methods, each method is run 100 times with certain sample size. In this way, 100 values of ε−μ∗ and ε−σ∗ are calculated with four variable categories. For 100 times calculation, two indices are introduced. First one is the mean of the standard deviation error. The second one is the mean of a maximum of error. The standard deviation error is the standard deviation error obtain from 100 calculations for each output categories and denoted by ε∗σ100. The mean of the standard deviation error is the mean of εσ100 each specific type of output random variables and denoted by ˉεσ100. This ˉεσ100 show the stability of two methods. The maximum error of each output random variables are calculated in term of its mean and standard deviation. The mean of maximum of error is calculated is express as ˉεμ,max for each output categories. Similarly, mean of the maximum of error standard deviation is calculated and denoted by ˉεσ,max for each output random variable is calculated. For example, let V1,......,Vn is the voltage magnitude of the n node test system and ε1μ−Vi,......,ε100μ−Vi be the error of Vi after 100 calculationsi=1,.....,n. ThenεViμ,max=max{ε1μ−Vi,.......,ε100μ−Vi},i=1,......,n. For voltage variable mean of the maximum of error is calculated as ε−Vμ−max=1nn∑i=1εViμ−max. Similarly, other variable statistic can be obtain.
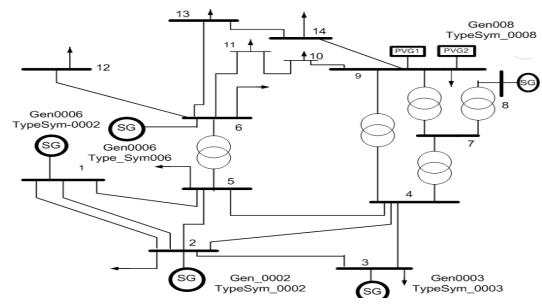
5.1. The modified IEEE 14-bus test system
All deterministic load flow data about this test system is available in [32]. The modified IEEE 14-bus test system is shown in Figure 6. There are total 23 input random variables in this test system. The load distribution is followed Gaussian distribution and discrete, and generator output follows the binomial distribution. The PLF analysis with 20,000 times MCS with SRS sampling consider to be the benchmark for other two methods and consider to be accurate and use to determine the error for other methods as it is usual practice in PLF study [9,10]. Two kinds of correlation is adopted in this test system. First one is between load and other is between active power outputs of PV generations. The constant power factor load model is adopted. The detail load parameters are presented in Table 1.
Table 1. Parameters of loads.
| Node No. |
Mean (p.u) |
StdDev (p.u) |
Power Factor |
| 2 |
0.215 |
0.065 |
0.864 |
| 3 |
0.943 |
0.031 |
0.991 |
| 4 |
0.481 |
0.115 |
0.365 |
| 5 |
0.074 |
0.036 |
0.978 |
| 6 |
0.111 |
0.037 |
0.833 |
| 9 |
0.295 |
0.156 |
0.872 |
| 10 |
0.094 |
0.036 |
0.823 |
| 11 |
0.036 |
0.015 |
0.889 |
| 12 |
0.061 |
0.024 |
0.965 |
| 13 |
0.134 |
0.048 |
0.919 |
| 14 |
0.151 |
0.062 |
0.949 |
All loads are divided into three groups as G1={2,3,4,5,6}, G2={10,11,12,13,14} and {9}. The correlation matrix between G1 is presented in Eq 22 and correlation matrix between G2 is presented in Eq 23. The correlation between same group loads is dependent as shown in Eq 22 and Eq 23 and also correlation between different load groups also dependent with 0.5 correlation coefficient.
|
G1=[10.60.70.50.70.610.70.60.80.70.710.70.80.50.60.710.70.70.80.80.71]
|
(22)
|
|
G2=[10.60.70.50.70.610.70.60.80.70.710.70.80.50.60.710.70.70.80.80.71]
|
(23)
|
Load 9 is correlated with active power output of PV generation available at node 9 with correlation coefficient 0.6. Two PV generation is located at node 9 with installed capacity 0.1 p.u, the active power of PV generation follow the Eq 7 and reactive power assumed to be zero [33,34]. The correlation coefficient matrix between two PV generation and load 9 is presented in Eq 24.
|
GPV−L9=[10.90.60.910.60.60.61]
|
(24)
|
The simulation is change from 100 to 1000 with step size 100. In order to evaluate the performance of SMCS, BMCS, and LMCS error curve are adopted. All the error indices are calculated for all type of output random variables included voltage magnitude, phase angle, active power, and reactive power. The error indices of only active power are consider for presenting the results for all four categories of variables.
5.2. Simulation results analysis of IEEE 14-bus test system
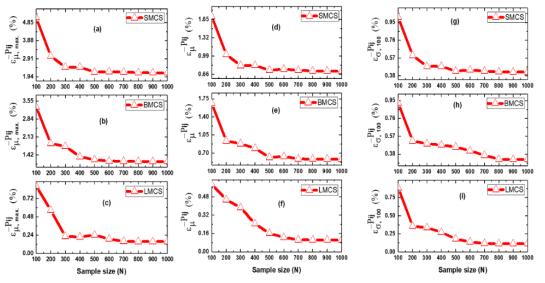
In the simulation analysis, three types are error indices are calculated as average error, mean of the maximum error, and mean of the standard deviation error indices. The average error index determines the distribution convergence degree of the entire system with corresponding output random variable. The other two error indices as mean of the standard deviation error and mean of the maximum of error are determine the stability of the entire method. For obtaining these error indices simulation is performed 100 times for 1000 samples with 100 step size.
The results of Figure 7 (a–c) illustrate the mean of the maximum of error curves with three methods. To present the results only active power through the line 2–3 was considered for IEEE 14-bus test system. It shows the percentage of the mean of maximum of error for 100 sample size to 1000 sample size with 100 step size of three methods SMCS, BMCS, and LMCS. The mean of the maximum of error of three methods SMCS, BMCS, and LMCS was almost 4.88%, 3.56%, and 0.96% respectively with 100 sample size. Similarly, this error index was 2.15%, 1.16%, 0.15% with 1000 sample size. This error index promptly reduces at 200 sample size, after 200 sample size it remains almost constant. Finally, the results of Figure 7 (a–c) shows that LMCS method is more stable method than other two methods. The results of Figure 7 (d–f) illustrate the average error index for three methods. Form these results, it is clearly shown that the LMCS has 0.10% error, but the other two method SMCS and BMCS have 0.71% and 0.58% respectively with 1000 sample size. This show that the LMCS method is best convergence degree for proposed test system rather than other two methods. The results of Figure 7 (g–i) illustrate the mean of the standard deviation error. This show that the LMCS has 0.11% error and other two methods have 0.42% and 0.32% respectively with 1000 sample size. Form these results, it is clearly shown that the LMCS is more stable method than the other two methods.
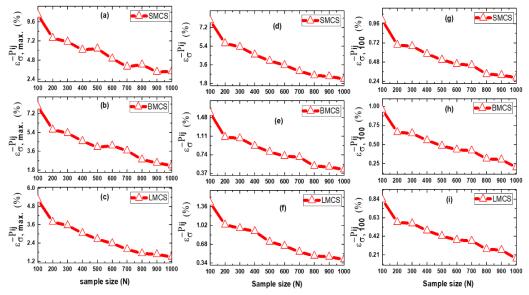
The standard deviation error indices are presented in Figures 8 (a–i). The mean of maximum error of standard deviation is presented in Figure 8 (a–c), average of standard deviation error index is in Figure 8 (d–f), and mean of standard deviation error is in Figure 8 (g–i). All of these indices are calculated with 1000 sample size. The mean of maximum of standard deviation error index of LMCS method was with 1.49%, but the SMCS and BMCS have 3.36% and 2.23%. Similarly, average standard deviation error index of LMCS was 0.40%, but the SMCS and BMCS have 2.23% and 0.44%. Similarly, mean of standard deviation error index of LMCS was 0.16%, but the SMCS and BMCS have 0.28% and 0.20%. All of these results prove that LMCS method is much better than SMCS but almost identical to BMCS method according to distribution convergence and stable point of view.
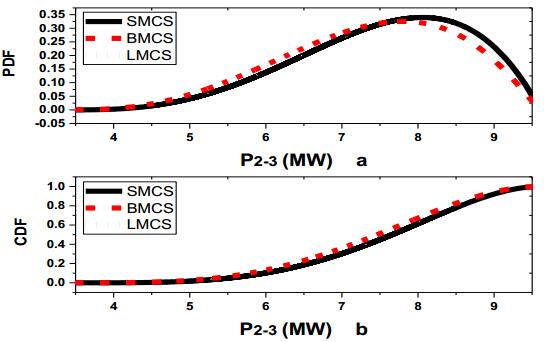
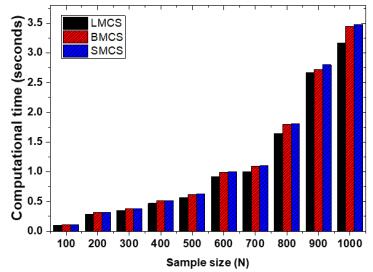
All of the above calculated error indices are for active power output random variable. The remaining three output random variables, i.e. voltage magnitude, phase angle, and reactive power error indices are very similar to this. These are not shown here due to space limitations. All of the remaining output random variable's error indices are calculated and presented in Table 2 with sample size 400. The results of Table 2 show that error indices of all output variable are within 10% with SMCS but with BMCS and ILMCS are within 5%. Additional, the PDF and CDF of active power flow through the line 2–3 are illustrated in Figure 9. From the results of Figure 9, shows that the curves are very close to each other for three methods. All of these curves are calculated with a different sample sizes like SMCS with 20,000 samples and BMCS, and LMCS are with 1000 samples. The accuracy of presented results is almost same but BMCS and LMCS with 1000 sample size. The computational time comparison of three methods is shown in Figure 10. The computational time of SMCS method with sample size 20,000 was 981 s seconds. The computational time for both BMCS and LMCS was almost same like 3.17 s but with 1000 sample size. The computational burden of LMCS was very small for desire accuracy. The results of Figure 10 shows the computational superiority of ILHS with respect to same sample size.
Table 2. Error comparison of IEEE 14-bus test system.
| Method |
SMCS |
BMCS |
LMCS |
Method |
SMCS |
BMCS |
LMCS |
| εvμ(%) |
ˉεvμ,max |
1.022 |
0.018 |
0.012 |
εPijμ(%) |
ˉεpμ,max |
2.151 |
1.164 |
0.156 |
| ˉεvμ |
1.042 |
0.037 |
0.016 |
ˉεpμ |
0.717 |
0.852 |
0.104 |
| ˉεvσ100 |
0.451 |
0.021 |
0.019 |
ˉεpσ100 |
0.421 |
0.323 |
0.115 |
| εvσ(%) |
ˉεvσ,max |
6.451 |
1.882 |
1.667 |
εPijσ(%) |
ˉεpσ,max |
3.365 |
2.235 |
1.490 |
| ˉεvσ |
2.957 |
0.924 |
0.863 |
ˉεpσ |
2.235 |
0.447 |
0.406 |
| ˉεvσ100 |
1.675 |
0.643 |
0.573 |
ˉεpσ100 |
0.285 |
0.201 |
0.167 |
| εθμ(%) |
ˉεθμ,max |
3.056 |
1.568 |
1.235 |
εQijμ(%) |
ˉεQμ,max |
5.689 |
2.235 |
2.035 |
| ˉεθμ |
1.023 |
0.756 |
0.583 |
ˉεQμ |
2.865 |
1.356 |
1.128 |
| ˉεθσ100 |
0.982 |
0.458 |
0.394 |
ˉεQσ100 |
1.225 |
0.754 |
0.586 |
| εθσ(%) |
ˉεθσ,max |
9.985 |
3.895 |
3.128 |
εQijσ(%) |
ˉεQσ,max |
9.972 |
3.365 |
2.864 |
| ˉεθσ |
3.458 |
1.358 |
1.023 |
ˉεQσ |
4.258 |
2.235 |
2.078 |
| ˉεθσ100 |
2.896 |
0.886 |
0.748 |
ˉεQσ100 |
2.458 |
1.423 |
1.358 |
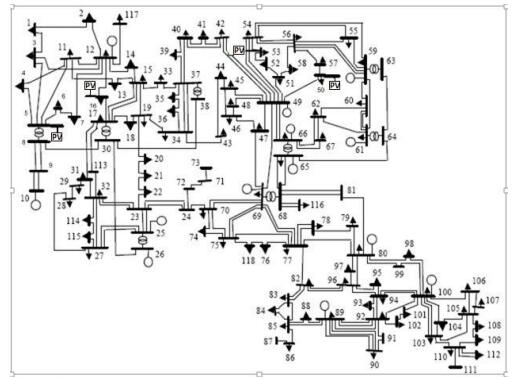
5.3. Modified IEEE 118-bus test system
All of the deterministic data about this test system is available in [32] and also shown in Figure 13. All of the assumption and probabilistic data about this test system is same as in [10,31]. The total input random variables in this test system are 170. The reaming assumption are almost same as in previous test system like loads are follow normally distribution and generator output follow binomial distribution. Four PV generator are located at nodes 5, 16, 50, and 53, respectively with 0.2 p.u installed capacity. The correlation matrix of four PV generation is shown in Eq 25.
|
GPVG4=[10.7000.71000010.7000.71]
|
(25)
|
5.4. The simulation results analysis of IEEE 118-bus test system
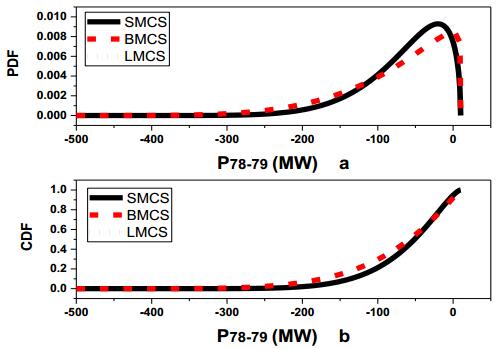
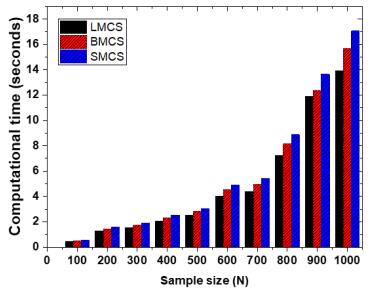
By the simulation study, it is shown that the three types of error indices about four output variables categories were almost same pattern as in IEEE 14-bus test system. These indices are not presented here due to space limitations. The error indices of four categories are presented in Table 3 but with 800 sample size. The results of Table 3 show that the error indices of SMCS are within 10%, with BMCS are within 6%, with LMCS are within 4%. These percentage of error change due to increase input random variables. This conclusion shows that LMCS is more stable and distributed convergent method than the other two methods. The PDF and CDF curves are shown in Figure 11 of active power flow through the line 78–79. From these results, it is shown that LMCS is accurate than BMCS and SMCS but in previous test system BMCS was close to LMCS and SMCS methods. The accuracy of BMCS in term of PDF and CDF are bring down may be due to increase number of input random variables. Additionally, the comparison of the computational time of different sample same is shown in Figure 12. The computational time of SMCS method with sample size 20,000 was 5586 seconds. The computational time for both BMCS and LMCS was almost same like 13.92 s with 1000 sample size. The computational burden of BMCS and LMCS was very small as compare to SMCS for achieving desire accuracy. The results of Figure 12 show the computational superiority of ILHS with respect to same sample size.
Table 3. Error comparison of IEEE 118-bus test system.
| Method |
SMCS |
BMCS |
LMCS |
Method |
SMCS |
BMCS |
LMCS |
| εvμ(%) |
ˉεvμ,max |
0.929 |
0.016 |
0.012 |
εPijμ(%) |
ˉεpμ,max |
1.955 |
1.012 |
0.154 |
| ˉεvμ |
0.947 |
0.032 |
0.016 |
ˉεpμ |
0.652 |
0.741 |
0.103 |
| ˉεvσ100 |
0.410 |
0.018 |
0.019 |
ˉεpσ100 |
0.383 |
0.281 |
0.114 |
| εvσ(%) |
ˉεvσ,max |
5.865 |
1.637 |
1.650 |
εPijσ(%) |
ˉεpσ,max |
3.059 |
1.943 |
1.475 |
| ˉεvσ |
2.688 |
0.803 |
0.854 |
ˉεpσ |
2.032 |
0.389 |
0.402 |
| ˉεvσ100 |
1.523 |
0.559 |
0.567 |
ˉεpσ100 |
0.259 |
0.175 |
0.165 |
| εθμ(%) |
ˉεθμ,max |
2.778 |
1.363 |
1.223 |
εQijμ(%) |
ˉεQμ,max |
5.172 |
1.943 |
2.015 |
| ˉεθμ |
0.930 |
0.657 |
0.577 |
ˉεQμ |
2.605 |
1.179 |
1.117 |
| ˉεθσ100 |
0.893 |
0.398 |
0.390 |
ˉεQσ100 |
1.114 |
0.656 |
0.580 |
| εθσ(%) |
ˉεθσ,max |
9.077 |
5.387 |
3.097 |
εQijσ(%) |
ˉεQσ,max |
9.065 |
5.926 |
2.836 |
| ˉεθσ |
3.144 |
2.181 |
1.013 |
ˉεQσ |
3.871 |
2.943 |
2.057 |
| ˉεθσ100 |
2.633 |
0.770 |
0.741 |
ˉεQσ100 |
2.235 |
1.237 |
1.345 |
6. Conclusion
Due to increasing trend of penetration of renewable energy sources into power system has introduced the uncertainties and dependence factors. The modelling of input random variable for the study of uncertainties and dependence effect on power system operation and planning is a challenge for future. In this paper, a probabilistic load flow analysis is presented for correlated loads and photovoltaic generation. Uncertainty is created with correlated loads and photovoltaic generation. Gaussian Copula theory is proposed to establish the correlation between input random variables. Form the results; it has proved that Copula theory can establish correlation between input random variables flexibly and overcome the restriction of Pearson's correlation coefficient. Additional, it is unconstrained by the marginal distribution type of input random variables. Two methods of sampling has been proposed for analysis purpose. The results obtained by LMCS method is more accurate and efficient. When the input random variables were small, the results obtain by BMCS and LMCS almost have same accuracy and robustness. But when the input random variable has increased BMCS become less accurate as compare to LMCS. As an overall result, LMCS is an efficient sampling method for convergence for entire distribution of input random variable, almost independent of input random variable, and flexible too. The LMCS method has a large potential in order to deal with probabilistic problems with renewable energy sources especially penetration of photovoltaic generation in power system network.
Acknowledgements
This work is supported by the "National Key Research and Development Program (2016YFB0901104), the National Natural Science Foundation of China (51307051), the Fundamental Research Funds for the Central Universities (2014ZP03, 2015ZD01) and the Science and technology projects from State Grid Corporation".
Author contributions
Li Bin and Qi Bing conceived the research idea and designed the simulation setup; Muhammad Shahzad did the remaining work.
Conflicts of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: