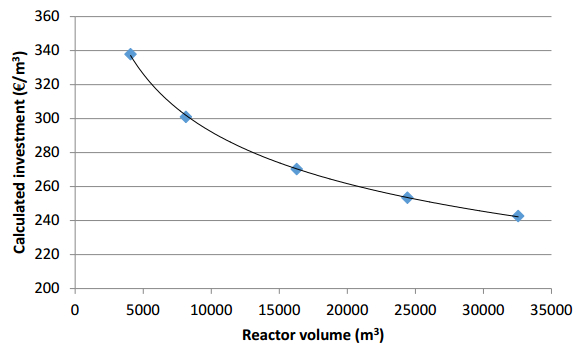
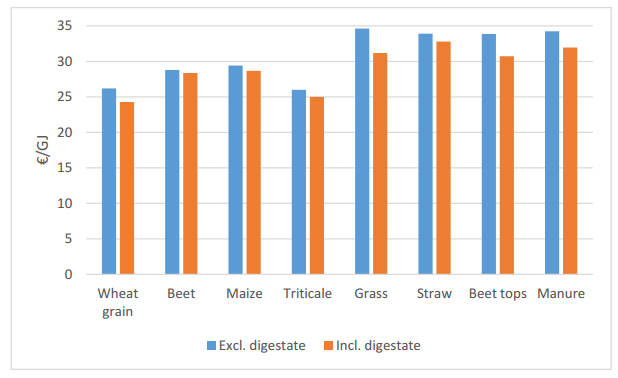
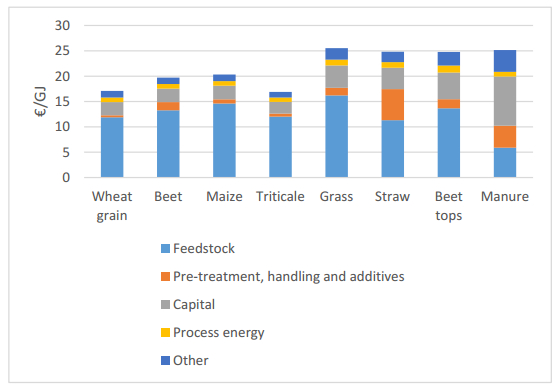
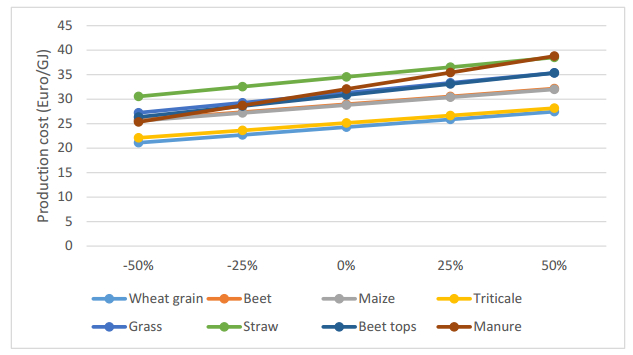
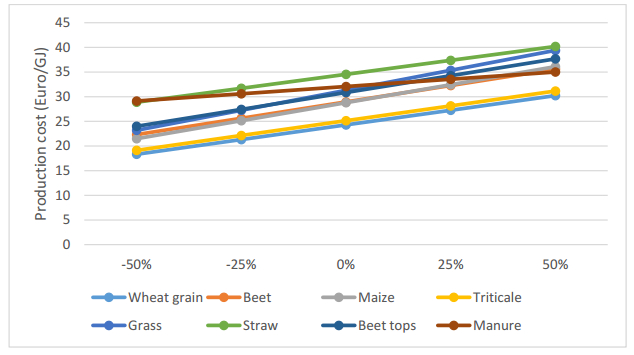
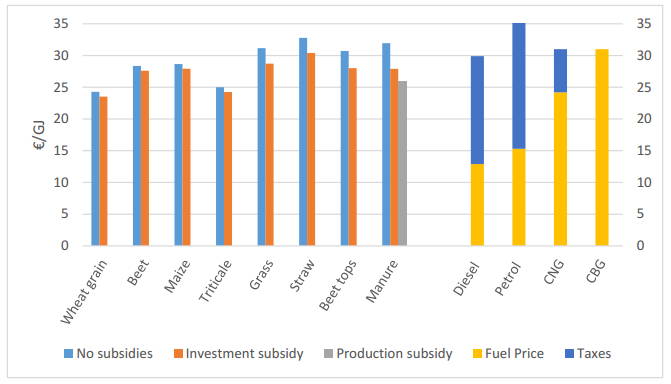
The vast majority of the biofuels presently used in the EU are so called first generation biofuels produced from crops. Concerns of food security, displacement of food crop production and indirect land use change (iLUC) has led to the introduction of measures to reduce the use of first generations biofuels and promote so called advanced biofuels based on feedstock that does not compete with food/feed crops, such as waste and agricultural residues. In Sweden, 60% of the biofuel consumption is already based on waste/residual feedstock, and a unique feature of the Swedish biofuel supply is the relatively large use of biogas for transport, representing 9% of the current use of biofuels. The use of waste/residues dominates the biogas production, but agricultural residues, representing a large domestic feedstock potential, are barely used at present. This could indicate that biofuels from such feedstock is non-competitive compared both to fossil fuels and to biofuels produced from crops and waste under existing policy framework. This study show that without subsidies, the production cost of biogas as biofuel from all non-food feedstocks investigated (grass, crop residues and manure) is higher than from food crops. A shift from food crops to residues, as desired according to EU directives, would thus require additional policy instruments favoring advanced biofuel feedstock. Investment or production subsidies must however be substantial in order for biogas from residues to be competitive with biogas from crops.
1.
Introduction
The three-dimensional reconstruction technology of micro-nano surface topography has been widely studied and applied in many fields such as industrial manufacturing, computer vision reverse engineering [1]. Especially, in the last few decades, optical methods such as coherence scanning interferometry (CSI), phase shifting interferometry (PSI) and focus variation microscopy (FVM) have become increasingly popular for three-dimensional surface reconstruction [2]. During the process of reconstruction, the point cloud contains noise by factors such as the brightness of the ambient light, measuring equipment, object materials and surface texture and man-made factors which will affect the accuracy of reconstruction [3]. Therefore, it is urgent to research an effective point cloud denoising strategy for three-dimensional reconstruction of microscopic measurement as a preprocessing step. However, automatic and effective removal of measurement outliers is challenging since the object surface model is unavailable and the estimate of the object surface shape would be inaccurate in the presence of extensive outliers.
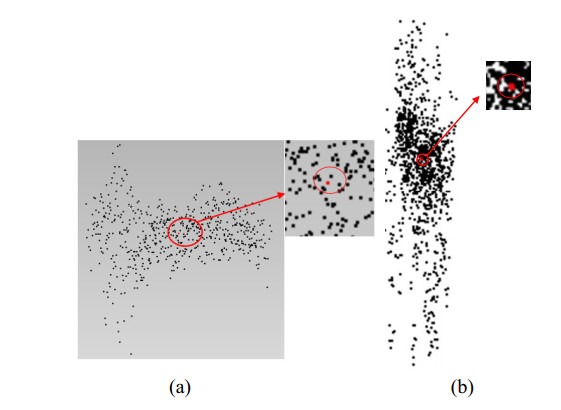
Traditional point cloud denoising algorithms are difficult to filter out the outliers of the point cloud reconstructed during the microscopic measurement process. There two significant reasons that some light during the process of collecting pictures for microscopic measurement and the reflective properties of the material causing different kinds of outliers, such as non-isolated and isolated outliers. Figure 1 shows the point cloud reconstructed by microscopic measurement with isolated outliers and non-isolated outliers.
Because the noise generated during the microscopic measurement is relatively random, and mixed with non-isolated outliers, point cloud filtering methods based on the new method is far from enough. This paper compares the outlier model of the point cloud with the model of the social circle, and studies a robust outlier filtering algorithm based on the social circle. The work has important innovation value and application significance for filtering outliers of ordered point cloud reconstructed by microscopy and improving the accuracy of reconstruction.
2.
Related work
In recent years, a large number of scholars have done in-depth research on point cloud denoising algorithms for improving the accuracy and stability of reconstruction. These filtering algorithms are mainly used to filter outliers for 3D laser scan which is also suitable for point cloud filtering of microscopic reconstruction. For example, since outliers reconstructed by 3D laser scan are usually randomly distributed, Sotoodeh [3] proposed a density-based removal method, which judges whether the point set is a noise point based on the mean value of the closest distance in the K field of the point. However, it is difficult to identify dense outliers depending on local information, so the filtering effect of dense outliers is very poor. For some isolated outliers, Yu [4] performed point cloud denoising through a three-dimensional grid which used a measure of local entropy to update mesh vertices, but this method cannot guarantee convergence, what’s more, it’s not suitable for non-isolated outliers. Some scholars proposed a point cloud outlier filtering algorithm based on statistical distribution [5] which can filtered out outliers quickly, this method performs well in isolated outlier removal, but fails in the non-isolated outlier removal. Wang et al. [6] used the majority voting method to remove non-isolated outliers, but it is not suitable for large-scale point clouds and the robustness is not good. In addition, many filtering algorithms [7,8,9] in image processing can also be applied to filter outliers in point clouds, such as mean filtering [10] and bilateral filtering [11], for example Fleishman et al. [12] applied a bilateral filtering algorithm based on image denoising to the point cloud filtering process, adjusting the position of the vertex according to its normal direction to achieve denoising processing. However, the outliers are not identified, and the original data information is modified while removing the outliers.
Reviewing the development described in afore mentioned studies, it has poor effect on non-isolated outliers which comes from the process of microscopic measurement. Therefore the aim of this work is to develop a fast and effective method to remove the outlier of organized point cloud without modification of non-outlier, besides, the method not only filter out isolate outliers, but also filter out non-isolated outliers. Inspired by social circle [13], an effective solution is proposed removing outlier of organized point cloud. A point is defined as outlier if it lies in exterior of the social circle of all other points [14]. Firstly, a non-outlier needs to be set as the initial point and determine the radius of social circle. Then, the social circle is expanded to iteratively start with the initial point. At last, we save the point which lies in the interior of social circle as the final result.
This study is divided into the following sections. In section 3, we not only begin with the introduction of Focus Variation Technology, but also introduce the algorithm of social circle filtering. Next, in section 4, experiments are carried out to validation of the proposed algorithm. Conclusions are finally addressed in section 5.
3.
Methodology
3.1. Focus variation technology
Focus Variation is also called depth from focus, originally derived from the shape from focus proposed by Nayar [15]. This technology mainly utilizes the small depth of field of the microscope and precision vertical movement equipment. The core idea is to move the object to be measured relative to the microscope, at the same time take a set of sequence pictures, and record height information [16].
As is shown in Figure 2(a), Z axis represents depth information X and Y axis represent pixel. A set of images are captured while the objective of the microscope moves upward (or downward) relative to the surface being measured. As is shown in Figure 2(b), we get sequence of FM (Foucs Measure) images after determining the sharpness of all pixels in sequence of images.
The commonly used focus evaluation algorithm is SML which calculated as follows:
s is the step size, N is the calculation window size, and T is the threshold.
At last, a set of depth information is generated at pixel P(x, y) in sequence of images which is shown in Figure 2(c), we fit the set of depth information. The depth information of measured surface is determined after calculating all pixels in sequence of images. Finally, each pixel is fused according to the position of the corresponding image to obtain an organized point cloud.
3.2. Outlier removing method based on social circle
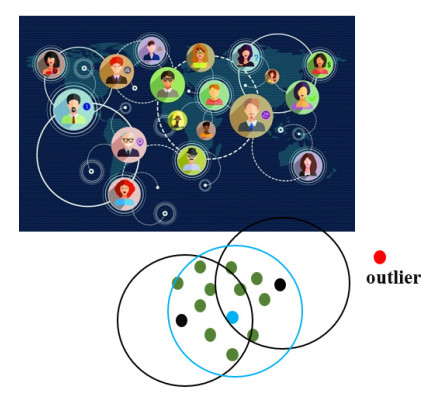
As we know, there are some outliers in the reconstructed point cloud due to some environmental factors, the outlier filtering method proposed in this paper is based on social circle filter. The social circle theory originated from social networks. Users in social networks have a large number of friends, organizing these friends through certain rules is our social circle. Usually, the user's social circle can be described as a self-network clustering problem. Everyone has their own social connections in the society [17]. People are divided into different groups or organizations, within which a man can easily get in touch with the other through friends or friends of friends. However, it is hard for a person to make contact with someone who does not belong to the group. When a person cannot get in touch with people in the circle, then the person can be considered as not belonging to the community, the group will consider him as a stranger. What’s more, Wang [18] proposed an improved density peaks-based clustering method which incorporates both two information of users for social circle discovery in social networks. An illustration of social circle is shown in Figure 3, in this example blue dot is the centeral point of the social circle, blue circle is the initial social circle, black circle represents the expanded social circle, and the red dot represents elements that do not belong to this social circle.
Inspired by which, the concept of the social circle is also can be applied to the outlier removal. The main task of social circle filtering is to define a community and relationship between community members. Through this relationship, we will expand our social circle until the social circle includes all community members, and the members outside the community are outliers point. Our method includes two steps. The first step is to determine the initial point and social circle radius. The second step is to expand the social circle iteratively. The method is detailed as follows.
3.2.1. The acquisition of the initial point
The initial point is very important as it is the beginning point of social circle expansion. Here, the I is taken as a symbol of the initial point. If I is an outlier, the final result will be error. The final point set will lie within the social circle of outlier, which is contrary to our goal. Thus, it is important to determine a reliable non-outlier. In this paper, we find the initial point I through a “vote” strategy.
A square area needs to be determined as the vote area. Here, users need to select a square area T(xi, yi, zi) (I = 0, 1, 2, …)from the original organized point cloud P(xi, yi, zi) (I = 0, 1, 2, …) which comes from FVM. Usually the square area T should not be less than 60 points in the x and y directions when selected. Surely, the larger the selection area, the more accurate the initial point, and try to select the smoother area in the original point cloud P. For each point p of T, it is necessary to calculate the distance between the remaining point and p. Then the vote value of p is calculated for the remaining point through the gaussian function as the following formula shown [19].
Dp(q) is the distance between p and point q. μp is a ratio coefficient which scales Dp(q) into a smaller range. Vp(q) is the vote value of p on q. The reason why we set the μp as the median value of Dp(q) is that μp is inversely proportional to the vote accumulated value difference of adjacent point. Tiny difference may result in a mistaken choice of the initial point. We calculate the vote accumulated value of each point of T and assign it to a matrix M. The size of M is same as T.
The final matrix M stores vote accumulated value of each point of T. Find the max value of matrix M and record its position. The point of the same position in T is the final initial point I. This method is pretty stable. It is still able to give a reliable non-outlier in the case of heavy outlier contamination. Its performance is shown in the follow Figure 4.
The picture tells that this method performs well even if the voting area is heavily polluted by outlier. All points are participated in the voting process. Thus, the final initial point is “fair” for each point. As the outlier is always the minority, their accumulated vote value is always smaller than the non-outlier. In other words, the point which has the max voting accumulated value is always a non-outlier. Therefore our method is able to give a reliable initial point.
3.2.2. The strategy of determining social circle radius
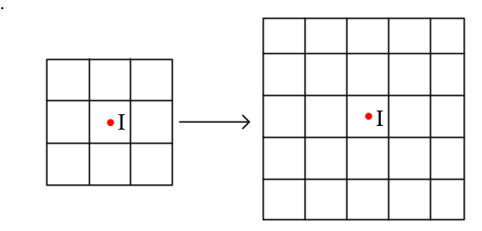
The social circle radius limits the rang of social circle. A larger social circle will increase the possibility that outlier is mistaken for non-outlier. So, it is important to determine a proper social circle radius. The size of search window needs to be set first, the size of search window is inversely proportional to time efficiency. Generally, it is suggested to set a 3×3 window. As the initial point I and the search window size have been determined, the window is expanded in order to get a reliable social circle radius.
As is shown in Figure 5, we expand the window 3×3 and build a new window 5×5, whose radius is the double of original window size. Then, the distance between the initial point I and the rest point is calculated out in the new window. The distance value is assigned to an array B. We sort the array B. The final social circle radius can be obtained through the follow formula.
R is the social circle radius. sort(B(n))8 is the element value at index 8 of sorted array B. The purpose of expand the window is to restrain the outlier disturbance. The outlier may lead to a too large social circle radius. A large radius will weaken the outlier removal performance. We sort the array B and the large distance calculated from outlier will locate in the tail of B. In this way, we exclude the outlier disturbance.
3.2.3. The expansion of social circle
The expansion process of social circle is actually the overlay of social circle. Every point has its own social circle. We combine the social circle of each point and obtain a big group. In the group, each point can get in touch with other points indirectly or directly [17].
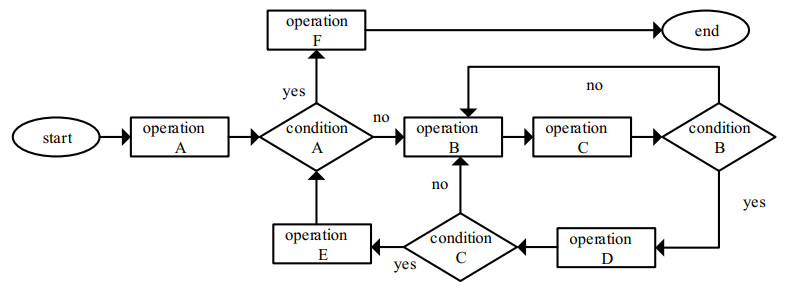
We assume that the input point cloud P, initial point I, search window W and the search radius R is determined, the points within the search radius are used as the initial points in the next iteration, we select the point on the edge of the search window as the initial point to improve calculating effciency. By analogy, continue to iterate the initial point until the final social circle store points which is all connected to the initial point. The algorithm flow is shown in Figure 6.
Operation A: Get the initial point, social circle radius R, search window, create containers V1, V2 for storing three-dimensional points, matrix B with value filled zero which is same size as point cloud P, What ’s more add the initial points to V1.
Condition A: whether V1 is empty.
Operation B: Find the point whose value in the corresponding matrix B is not 0 in the search window.
Operation C: Find the point where the distance between the initial point and the current point is less than the distance from the social circle, and the height of the current point is assigned to the corresponding position in B.
Condition B: whether the current point is at the search window boundary.
Operation D: put the point in V2.
Condition C: whether all points in the search window have been visited.
Operation E: clear V1, add the elements in V2 to V1, and go back to condition A.
Operation F: output the matrix B.
The expansion can be divided into seven steps:
(1) Determine the initial point I of the organized point P, the social circle radius R and search window W.
(2) Create containers V1 and V2 to store three-dimensional points, and add the initial points to V1, what’s more create a matrix B with value filled zero which is same size as P.
(3) Judge whether V1 is empty, if it is, output the matrix B, otherwise take each point in V1 as the initial point and execute steps (4)–(8) cyclically.
(4) For the currently visited point in the search window, determine whether the value of the corresponding position element in B is 0, if it is, execute the next step, otherwise visit the next point.
(5) Calculate the distance between the initial point and the access point. If it is less than the radius of the social circle, the height of the access point is assigned to the corresponding position in B, and perform the next step. Otherwise, visit the next point of the window.
(6) Determine whether the current access point is at the window boundary, if so, put the point in V2.
(7) Judge whether all points in the search window have been visited, if yes, clear V1, add the elements in V2 to V1, and execute step (3), otherwise visit the next point.
Through the above social circle iteration process, matrix B is obtained. The points in A corresponding to values greater than 0 in B are non-outliers. Convert all values greater than 0 in B to three-dimensional points and output the processed points. Finally we get point cloud without outliers.
4.
Experiment and discussions
4.1. The experiment of outlier remove
The principle of our method has been explained in the section 3, we will perform some experiments and discuss the experiment results in this section. A point cloud of metal groove with high outlier is selected as original data. The outlier is non-uniform distribution. We compare our method with another two frequently-used outlier removal methods. They are statistical filter and radius filter which come from Point Cloud Library. They can also remove outlier fast and will not modify the non-outlier. The comparison is conducted in the aspect of time consuming and removal performance. The raw point cloud is shown in Figure 7.
As shown in Figure 7, the degree of outlier contamination differs in different area. The groove area is the most contaminated area. We reimplement the statistical and radius filter so that they are suitable for processing the organized point cloud. Their search window sizes are all set as 5×5(points). We use different combination of parameter to conduct experiment for each method and take the relatively good result as the final output data (Figure 8).
As shown in Figure 8, they have similar performance in the low outlier contaminated area. However, their performance differs a lot in the high outlier contaminated area. The radius filter distinguishes the single outlier well but fails to detect dense outlier cluster. The statistical filter performs better than radius filter, but is hard to detect dense outlier cluster. It is due to the fact that they consider the low local point density and rely on the condition that the local neighborhood of each point contains sufficient data points. So, they cannot remove the dense outlier clusters. Compared with the radius and statistical filter, the social circle filter can not only remove single outlier but also dense outlier cluster. For the high outlier contaminated area, the social circle filter can remove outlier efficiently while the radius and statistical filter perform poorly. Their difference is shown in Table 1 which is corresponding to Figure 8.
As shown in Table 1 and Figure 8, the proposed method keeps more points when outlier is removed. However, the radius and statistical filter keep fewer points while outlier still exists. Besides, the proposed method consumes less time than other two methods.
4.2. Point cloud filtering experiment
The previous experiment intercepted part of the point cloud data for comparison, and then we filtered the entire cloud, and interpolated the filtered part to get final point cloud. The point cloud interpolation method selected in this article unified the use of cubic b-spline curve for patching. The point cloud obtained by the method is not affected by the filtering method. As before, we still compare with statistical removal and radius outlier removal, and we compare the two different occasions, one is a metal groove, the other is a composite material. The raw point cloud is shown as Figure 9.
As shown in Figure 9, both metal grooves and composite material have some outlier. We also use the three filtering methods, and use the same repair method at the same time, and the final output data are shown in the Figures 10 and 11.
It can be seen from Figures 10 and 11 that regardless of whether the outliers are dense or sparse, the quality of the final point cloud data reconstructed by the method of social circle filter is better than that of the traditional methods radius filter and statistical filter, especially when the outliers are dense.
5.
Conclusions
This paper proposes an outlier removal method which is applied for organized point cloud reconstructed by microscopic measurement. With comparison, we found that the method of filtering through social circles can quickly and accurately filter out some outliers without changing the non-outliers, and it is also very robust. The core idea of our method is derived from social circle. It includes three steps. First, an area is selected to determine an initial point. Then, the social circle radius needs to be calculated out. At last, the social circle is iteratively expanded and remove the outlier. Compared with the radius and statistical filter, the experiment result shows that the method proposed in the paper is able to remove outlier robustly and consumes less time.
Acknowledgments
This work was supported by the National Key R & D program of China (2019YFB2006100, 2019YFB1707500), Fundamental Research Funds for the Central Universities (NO. NS2020030), Jiangsu Province Nature Science Fund (BK20191280).
Conflict of interest
The authors declare there is no conflict of interest.










 DownLoad:
DownLoad: