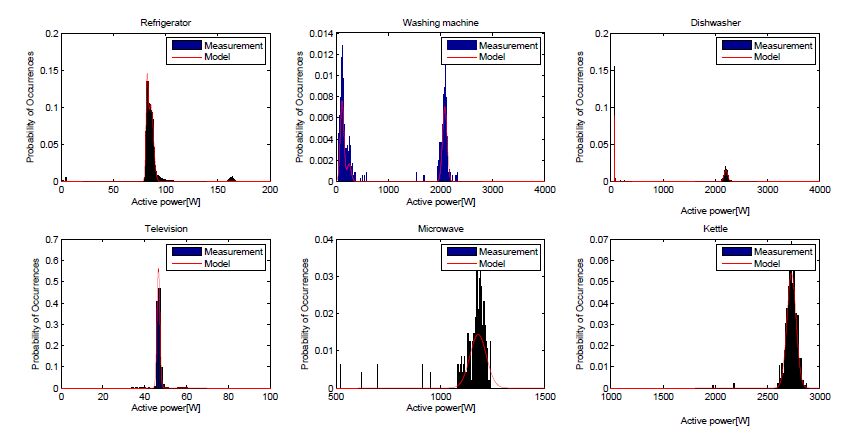
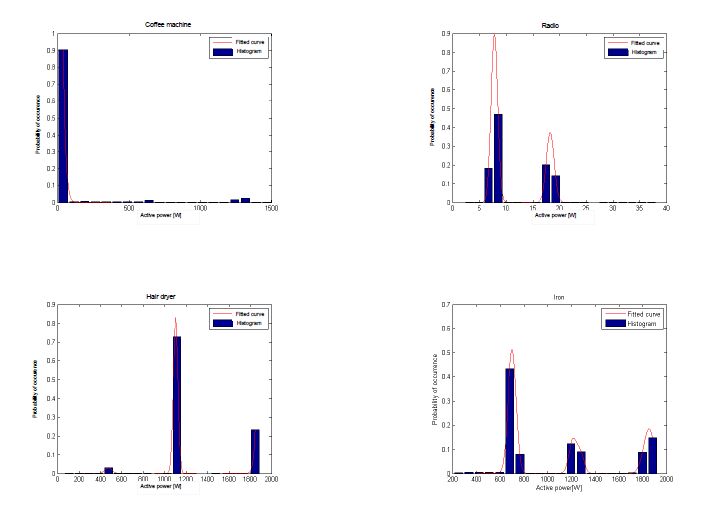
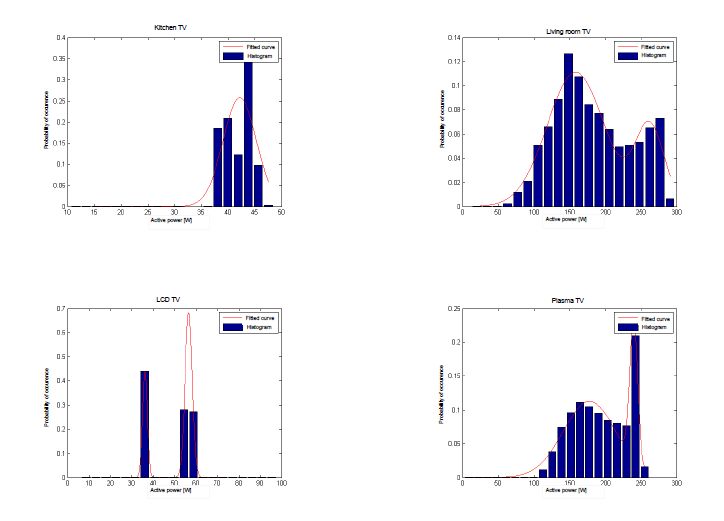
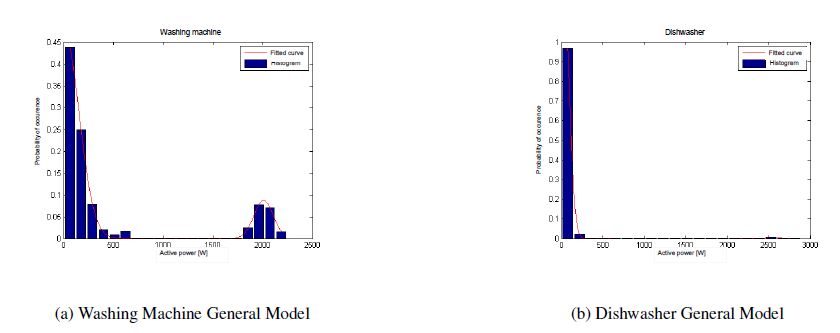
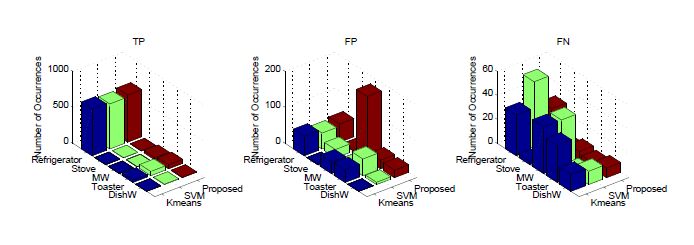
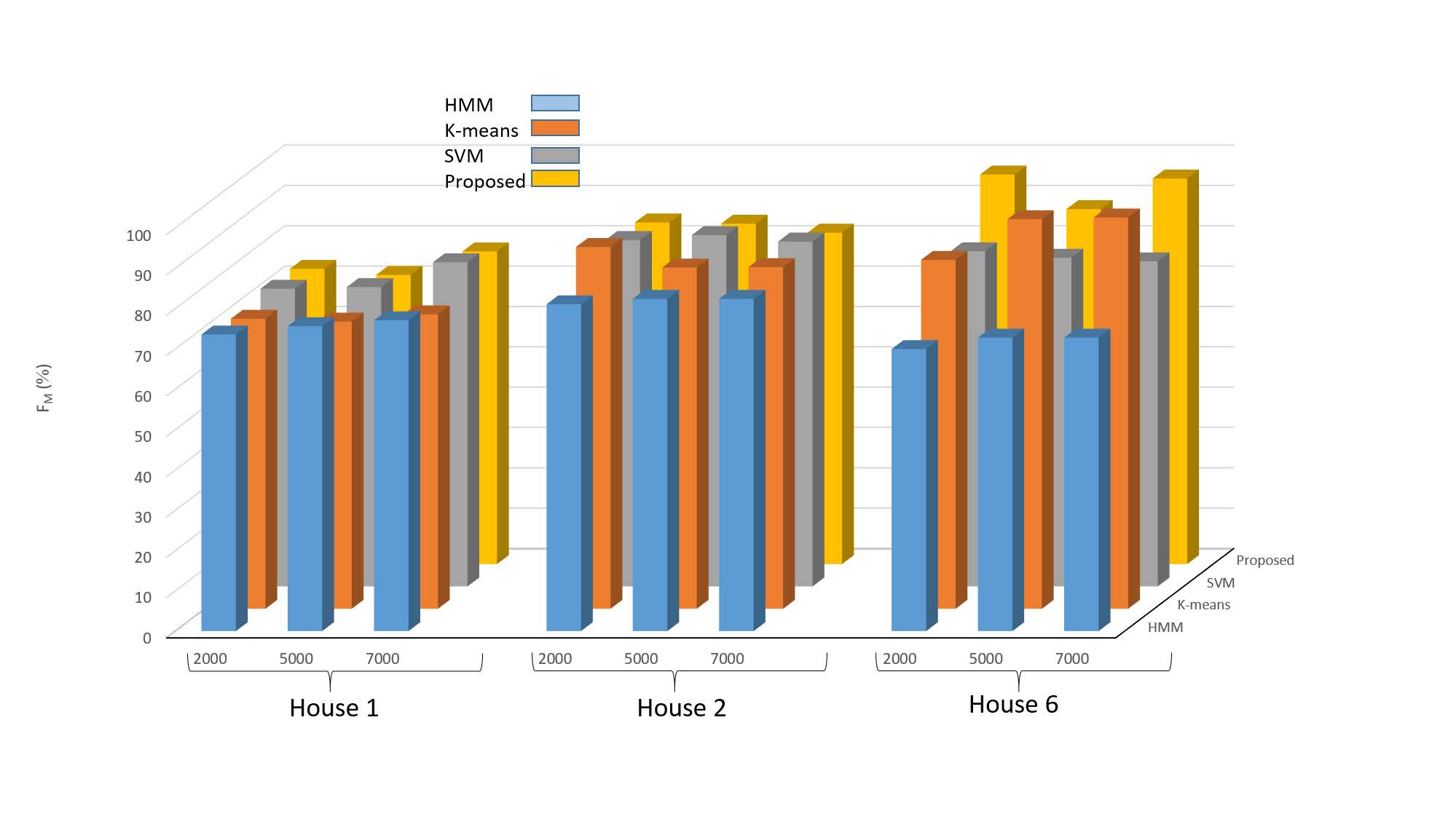
Large-scale smart metering deployments and energy saving targets across the world have ignited renewed interest in residential non-intrusive appliance load monitoring (NALM), that is, disaggregating total household’s energy consumption down to individual appliances, using purely analytical tools. Despite increased research efforts, NALM techniques that can disaggregate power loads at low sampling rates are still not accurate and/or practical enough, requiring substantial customer input and long training periods. In this paper, we address these challenges via a practical low-complexity lowrate NALM, by proposing two approaches based on a combination of the following machine learning techniques: k-means clustering and Support Vector Machine, exploiting their strengths and addressing their individual weaknesses. The first proposed supervised approach is a low-complexity method that requires very short training period and is fairly accurate even in the presence of labelling errors. The second approach relies on a database of appliance signatures that we designed using publicly available datasets. The database compactly represents over 200 appliances using statistical modelling of measured active power. Experimental results on three datasets from US, Italy, Austria and UK, demonstrate the reliability and practicality.
1.
Introduction
Many substantial research efforts have been carried out to use hydrogen as an alternative energy carrier [1]. It is agreed with all environmental issues related to the usage of the conventional fuels such as exhaustion, pollution and climate change [2]. One of the great challenge faced the hydrogen production process is the combination between the energy sustainability and environmental protection. Different hydrogen economic studies have been investigated; it was found that the hydrogen economy offers two main advantages in terms of low greenhouse gases (GHGs) and used as an alternative fuel to reduce the consumption rate of fossil fuels [3,4,5,6,7,8]. Different hydrogen production technologies have been investigated [9,10]. Most of the available world hydrogen is produced by steam methane reforming process. It acts around 80–85% of the total world hydrogen and the remaining is produced by water electrolysis and coal gasification methods [11]. Currently, methane is obviously considered the best choice of fossil fuels due to its availability and low GHGs emissions [12]. Also, hydrogen can be produced by the water electrolysis process which is considered a commercial method [13]. In addition, Hydrogen gas has been generated by thermochemical methods from the biomass process as a renewable and sustainable energy source [14]. Most of the hydrogen production technologies are directly or indirectly utilized fossil fuels, subsequently GHGs are emitted.
Water vapor plasmolysis is mostly considered as a clean hydrogen energy carrier which the hydrogen can be generated without any environmental impact. Plasma is generated using the electrical energy which transformed into electron kinetic energy then water molecules excitation and produce hydrogen and oxygen gas [15,16]. The high productivity and efficiency is behind the continuous interest in hydrogen production using the non-thermal plasma or dielectric barrier discharge plasma (DBD plasma). Hydrogen production from water vapor using plasma has been viewed as a high expensive method, additionally; the efficiency has been registered value of 50% compared with the conventional plasma reactors [15,17]. Plasmolysis has the ability to produce hydrogen 1000 times more than the water electrolysis process due to the multiple excited species are produced by applying plasma, in addition, it was reported that the energy efficiency of the plasma chemical reaction is same as thermos-catalytic and electrolytic methods [18].
Different feed stocks have been utilized in plasma-chemical processes such as methanol, ethanol, kerosene, and water in liquid and vapor state [19,20,21,22,23,24,25,26,27]. The kinetic models of the hydrogen production from water vapor using DBD plasma have been developed [28]. The hypothesis of this study is to simulate the hydrogen production from water vapor plasmolysis over a period of time that will lead to predict the chemical kinetics and compared it with the H2 concentration of the experimental results under the same operating conditions. Two water vapor plasmolysis kinetic models are simulated for a cylindrical type reactor. The simulation analysis was carried out using non-thermal plasma at atmospheric pressure and incorporated with the initial species concentration. The effects of the dissociative attachment reaction on the simulation results of water vapor break down into hydrogen and oxygen gas were evaluated. The species concentrations at steady state were monitored for both simulation models. The hydrogen concentrations results were compared for both tested models and the H2 concentration of experimental results. Also, the H2 conversion rates of both models and experimental results were analyzed.
1.1. Methods of simulation analysis
In this study, the concentrations of product gases of water vapor plasmolysis were simulated and investigated in a cylindrical type DBD plasma reactor using Reaction Engineering Lab of COMSOL Multphysics TM. A few reactions are presented to describe the hydrogen formation from water vapour plasmolysis because we used the water vapour plasmolysis reaction kinetic model suggested by Fahad et al. [28]. The complete reaction mechanism is shown in Table (1). The simulation analysis was carried out for the water vapor decomposition with several mechanisms including dissociative ion attachment and dissociation reaction but without ionization reaction. Also, the simulation is implemented by excluding the dissociative attachment reaction (H-). The first model was excluded (reaction no (2)) in Table (1) to evaluate the effect of the dissociative attachment reaction (H-) on the water vapor dissociation reaction mechanism pathway, while the second one used the full reaction mechanism in Table (1) including the dissociation reaction and the dissociative attachment reaction. However, it was reported that the dissociative attachment reaction (reaction (2)) was an important step for water vapor breakdown using plasma [28].
The experimental species concentrations data are utilized as input data to the simulation models to investigate the water vapour decomposition reaction mechanism pathway. The experimental and simulation results are deeply investigated and compared in section 3. In this reaction mechanism, water vapor is decomposed to generate hydrogen and oxygen molecules after a chain of reactions. The kinetics of H2 formation from water vapor decomposition in a cylindrical type reactor was studied by applying DBD plasma. The water vapor density was determined at the water vapor temperature ranges of 250–350 ℃ using the ideal gas law. This simulation study results were compared with the experimental water vapor decomposition data and the pathway of reactions consists of six chemical reactions.
Many studies have been carried out to model the water vapor decomposition using DBD plasma. The overall water vapor kinetic models and single type plasmo-chemical reactions like ionic collision for the water vapor have been investigated in different studies [15,18,31,32]. A zero dimensional model has been proposed for low density non-stationary discharge gas in water vapor by Avtaeva et al. [31]. The water vapor at very low pressure (133–150 kPa) have been studied, the results showed that the most positive and negative species were H3O+ and OH-, respectively [31]. The effect of dissociative attachment reaction number (2) in table (1) included negative hydrogen a radical (H-) on the hydrogen production in cylindrical reactor was observed on the hydrogen formation kinetics. In the current study, two reaction mechanisms of water vapor dissociation are simulated for hydrogen production with and without the dissociative attachment reaction (H-). The simulation results are compared with the experimental hydrogen concentrations results.
The water vapor plasmolysis dissociation direct decomposition pathway can be expressed as follows [13]:
The primary species of water vapor decomposition are hydrogen and hydroxyl radicals [33]. The dissociation reaction of produced atomic hydrogen and hydroxyl radicals can be written as follows [33,34,35]:
The water vapor decomposition using DBD plasma is formed most of reactive species such as hydroxyl OH, H atoms, and oxygen atoms O-. It was associated that the primary chemical reaction produced species H and OH radicals, then these species react with each other to generate molecular products such as hydroperoxyl HO2 [36]. The chemical reactions pathway included the negative species (OH-, H-, and O-) of water vapor have also been reported [31,32]. Also, it was reported that the following reactions may happen in the water vapor plasmolysis but it has low probability and required a relative high energy [32], therefore, these reactions are not included in the current simulation studies.
The simulation reaction mechanism of water vapor plasmolysis by the dissociative attachment of electrons was included and water vapor dissociation is initiated with the dissociative attachment of an electron (H-). In this simulation study, the effect of dissociative attachment reaction (H-) was investigated on the water vapor decomposition using DBD plasma. The negative hydrogen radical (H-) formed in the full reaction mechanism combines with the electron through electron detachment process as follows:
In the current simulation study, the reaction mechanism model was proposed and analyzed for both different mechanism pathways of the water vapor dissociation. The reaction kinetic models were implemented using Reaction Engineering Lab. (REL) in COMSOL MultiphysicsTM [37]. This package provides an automatic sensing of stiff systems and an adaptive time stepping algorithm with tolerance of 10−6 [38].
1.2. Initial boundary conditions
The initial concentration of water vapor was determined using the ideal gas law at the given water vapor temperature and atmospheric pressure. In this simulation study, water vapor and electrons are the only input reactants to the system. The initial number of electron density was set at 106 m−3 due to cosmic radiation. Furthermore, it was found that the equilibrium electron density values for non-thermal (DBD) plasma vary in a range of (1018–1021 m−3) [39,40]. While it was experimentally reported that the lowest value of electron density was 1017 m-3 [41]. However, the general electron density whole range of (1018–1021 m−3) was applied for both models to investigate the water vapour plasmolysis kinetic behavior. The input plasma voltage ranges of 12–14 kV and pure water vapor flow rate of 0.0104 L/min were used at different water vapor temperatures range of 523–623 K. The hydrogen and oxygen gas species experimental concentrations data were set as input data.
2.
Experimental description and conditions
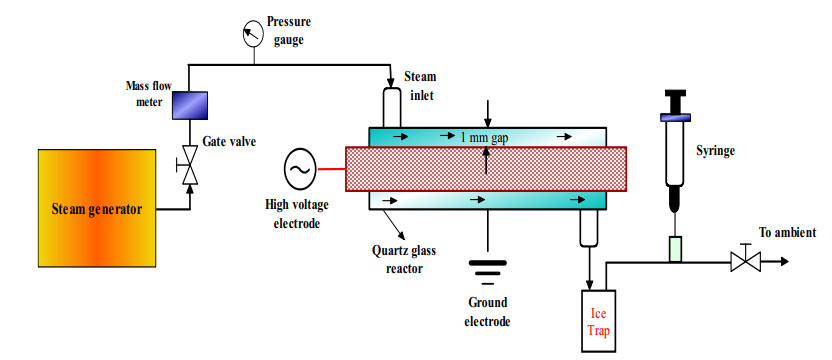
In this study, pure water vapor was decomposed using DBD plasma in a cylindrical type reactor. The DBD plasma was generated between quartz glass and stainless steel surfaces at atmospheric pressure, while the discharge gap between surfaces was 1 mm. The water vapor plasmolysis experiment was carried out at a constant feeding flow rate of 0.0104 L/min, plasma applied voltage of 12–14 kV and temperature ranges of 250–350 ℃. The outlet gas samples are taken after gas separated in the ice trap by using syringe then the hydrogen, oxygen, and nitrogen concentrations are measured by gas chromatography (GC). The plasma reactor volume was 5.296 cm3. The hydrogen concentration was measured using gas chromatography (GC) model type of GC-2014S, SHIMADZU, in addition, the water vapor decomposition experiments were repeated two times. Furthermore, the GC error was estimated before starting the water plasmolysis experiments within ±5% by using standard gas concentrations. The water vapor was generated using the steam generator and the steam flow rate was controlled by mass flow controller while the pressure was monitored using the digital pressure gauges. Figure (1) represents the schematic diagram of the water vapor decomposition process in cylindrical type reactor. The discharge voltage was applied at frequency of 10 kHz. The decomposed gases were separated using the ice trap and the sample was collected using syringe. The current study aims to investigate the hydrogen production from water vapor using DBD plasma. The hydrogen production experiments were carried out using different range of the operational parameters as mentioned above.
3.
Results and discussion
Figure (2) shows the plasma ignition test photos at plasma voltage range of 10–18 kV. The plasma ignition lighting is enhanced with the typical applied voltage increase. The total electrical power input to the DBD plasma is not the same as the total power consumption due to the lag of the voltage phase angle compared to the current phase angle [42]. The applied frequency of DBD plasma was adjusted at 10 kHz, the typical electric plasma power for one oscillation period can be determined as follows [43]:
Where the plasma voltage amplitude is V, the plasma current is I, Z is the impedance, and φ is the phase angle between voltage amplitude and current. Therefore, it was investigated that the power consumption in the DBD plasma is lower than the total plasma power utilized in the water vapor decomposition process. In addition, the total actual power consumed (Ptotal) can be calculated using the current (Ipeak) and voltage (Vpeak) peak values as follow [44]:
The concentration of produced hydrogen gas with time was measured at different water vapor input temperatures and plasma applied voltage ranges of 12–14 kV. It was reported that the negative species (H-) will combine due to their weak cross sections (1 – 6 × 10−18 cm2 per molecule). Furthermore, the electron energies were in a range of 6–12 eV [32].
3.1. Simulation model Ⅰ (without dissociative attachment reaction)
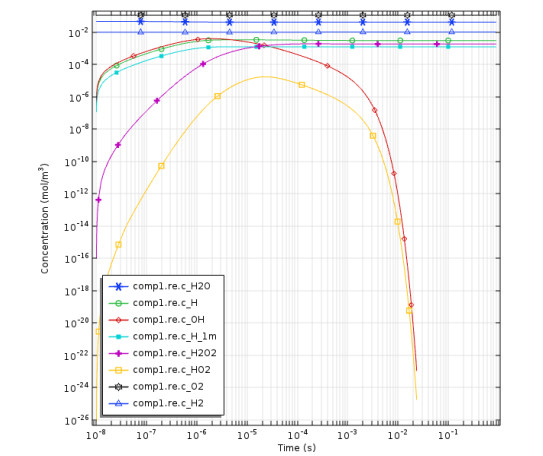
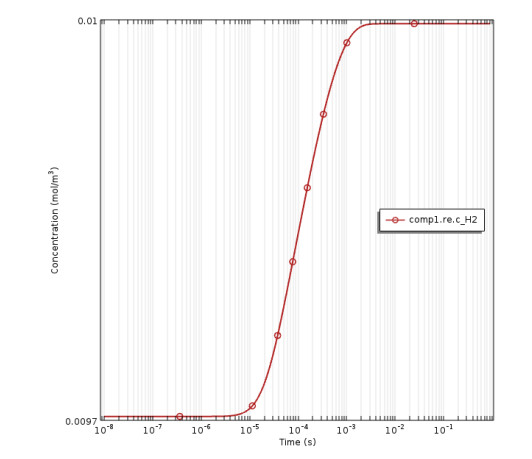
The first simulation analysis was carried out without or by deselecting the dissociative attachment reaction. In this simulation model, the effect of dissociative attachment reaction on the concentration of hydrogen production from water vapor was analyzed by deselecting it from reaction scheme. The simulation results were used the experimental results data and the simulation analysis was carried out at the same operating conditions. The steady state concentration of the water vapor decomposition species without dissociative attachment reaction was introduced in Figure (3). The input species concentrations data of this figure were taken from the experimental data, the experimental outlet hydrogen and oxygen concentrations were measured by GC were also used as a simulation input data. Atypical 99% of the concentrations of water vapor plasmolysis species are found such as H2, O2, OH, etc. at time scale 0.01s [28,45]. In the absence of the dissociative attachment reactions, water vapour concentration is reach to the steady state and more H atoms are generated with the increasing of the electron concentration. Moreover, the recombination of hydrogen atoms is the main source of hydrogen gas. The simulation result of steady state hydrogen gas concentration versus the evolution time is shown in Figure (4). It was clear that the hydrogen concentration increases with the reaction time scale until reach to the steady state. It was found that the hydrogen concentration increased continuously with the reaction time scale. Also, it was reported that the reaction of water vapor plasmolysis should be completed before the ions or gas particles reach to the reactor wall or to the electrode surfaces [38]. Also, different water vapor plasmolysis models have been simulated and the species spectra showed (H, OH, O, etc., ) have been obtained [31,45,46].
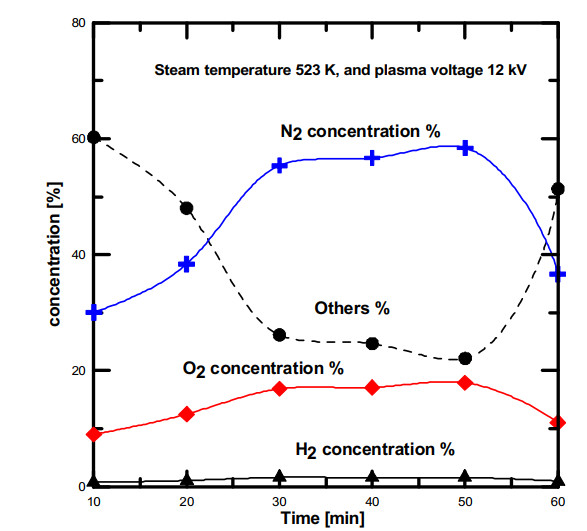
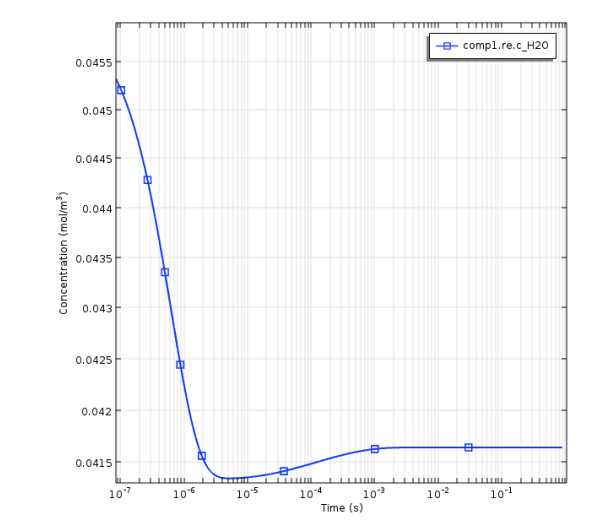
Figure (5) illustrates the water vapour concentration simulation results without the dissociative attachment reaction (H-) over the time. It was clear from the simulation result that the total input water vapours are decomposed into their elements and the concentration of water vapour reach to zero. Although, some of the outlet hydrogen and oxygen gases are recombined in the ice trap by means experimental results showed a condensed water vapor inside the ice trap. Furthermore, this model results did not seem to be accurate because of the water vapour did not completely convert into hydrogen and oxygen in the real experiment. The outlet species concentrations of the experimental results at water vapor temperature of 523 K and plasma voltage of 12 kV are shown in Figure (6). The results of the analyzed gas samples showed the concentration of the following species of (H2, O2, and N2), in addition some of hydrogen and oxygen gas are recombined to compose water inside the ice trap.
It was observed that the nitrogen gas concentration is included in the outlet species because of there are some of air content in the water vapour pathway line, also, it is possible that some of air was entered to syringe during the sample collections [45]. Furthermore, the hydrogen, oxygen, and nitrogen gas concentrations are typically showed the same profile trend, also, it can be concluded that the hydrogen concentration result of water vapour plasmolysis is not affected by air leakage because of the leakage air is not involved in the activated plasma reaction area. Additionally, it was found that the concentrations trend of H2, O2, and N2 decreased at the end of the dissociation time due to more of produced H2 and O2 gas are recombined again to compose water molecules which resulted in the increasing of the concentration of the trend of others. To clarify the effect of water vapor decomposition deselecting the dissociative attachment reaction on the simulation results, a comparison between simulation and experimental results will discuss in the next section.
3.1.1. Comparison between theoretical and experimental results (Model Ⅰ)
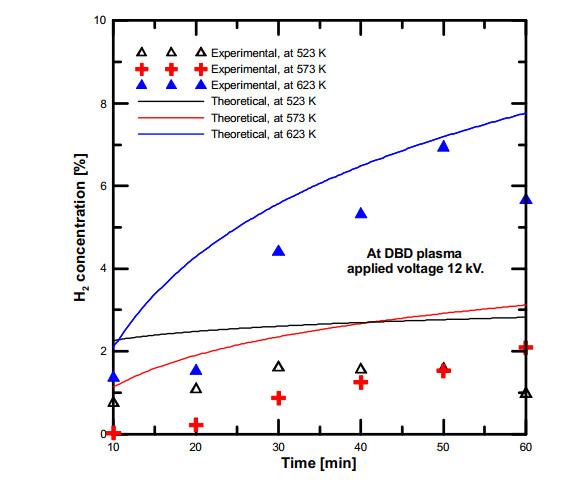
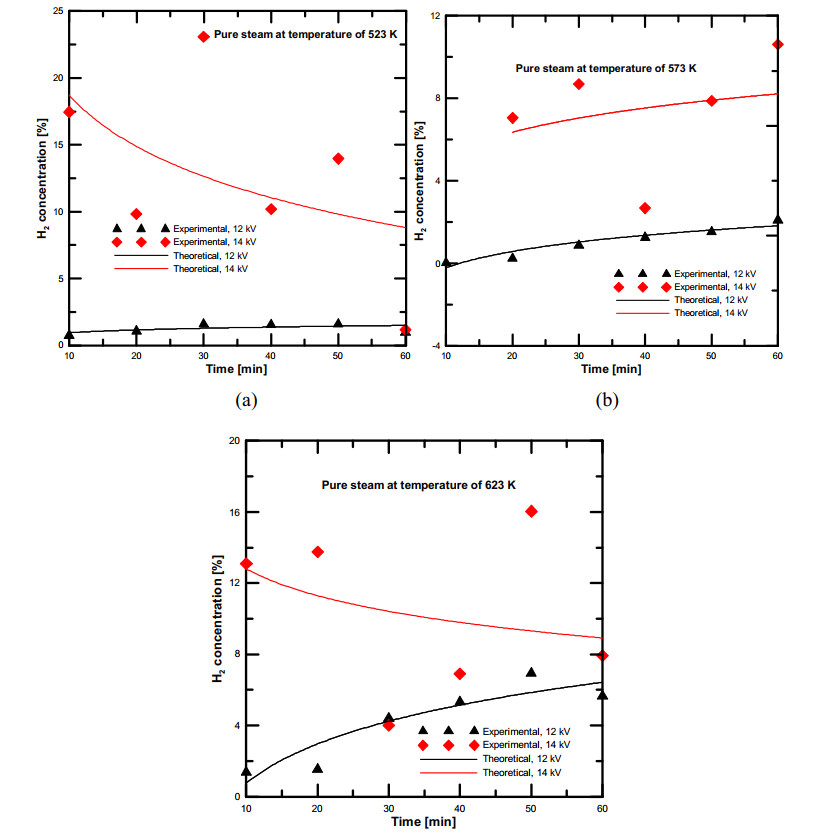
The simulation model of water vapor plasmolysis without dissociative attachment reaction (H-) (reaction (2)) was analyzed and compared with the water vapor decomposition experimental data. Figure (7) shows the effect of inlet water vapor temperature on the hydrogen production concentration over time at plasma applied voltage of 12 kV. The simulation results are obtained at different operating temperatures, it was found that the hydrogen concentration increased with the inlet water vapor temperature at the same plasma applied voltage [16].
Furthermore, the hydrogen concentration of the simulation results without the dissociative attachment reaction was always showed that the H2 concentration was higher than that obtained from the experimental results because of model Ⅰ did not include the H- radicals. As discussed before, the main reason of the decreasing of hydrogen concentration at the end of the dissociation time due to the recombination of H2 and O2 gas inside the ice trap, also, it was reported that some of the separated H2 gas are still remained inside the ice trap.
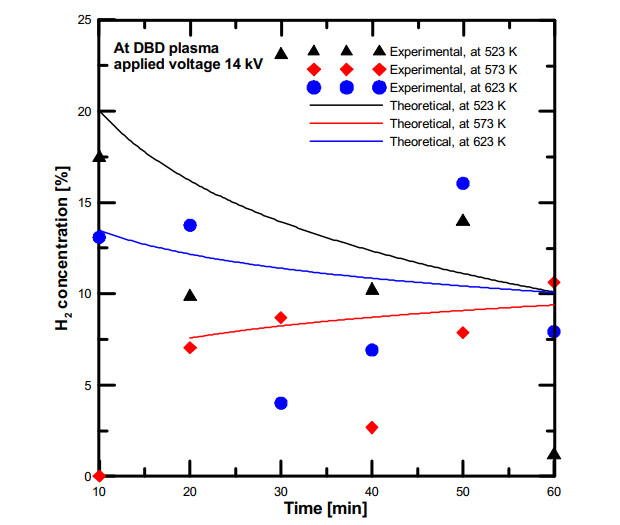
Figure (8) describes the effect of inlet water vapor temperature at plasma applied voltage of 14 kV with time. It was found that the hydrogen concentration decreased with time but the hydrogen concentration values are higher than that obtained from plasma voltage 12 kV. The simulation and experimental results of H2 concentration for low water vapor temperature of 523 K were higher than that obtained from high water vapor temperature due to the syringe sample collection error and the measurement procedures; it is possibly changed due to the change of the measurements accuracy and the separation procedure of the product gases.
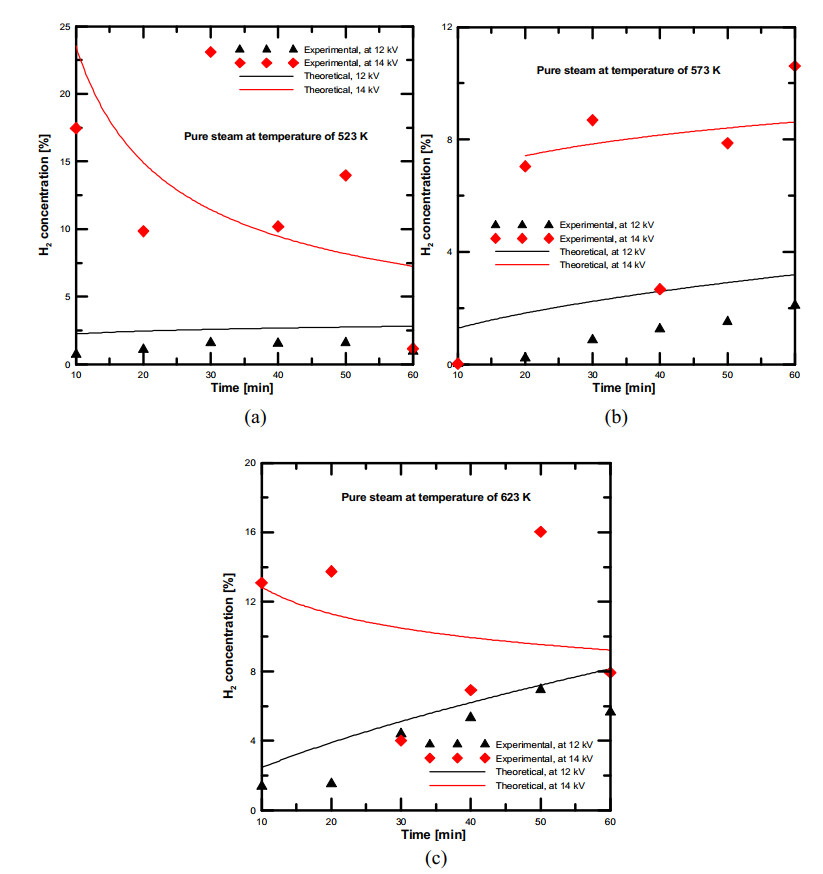
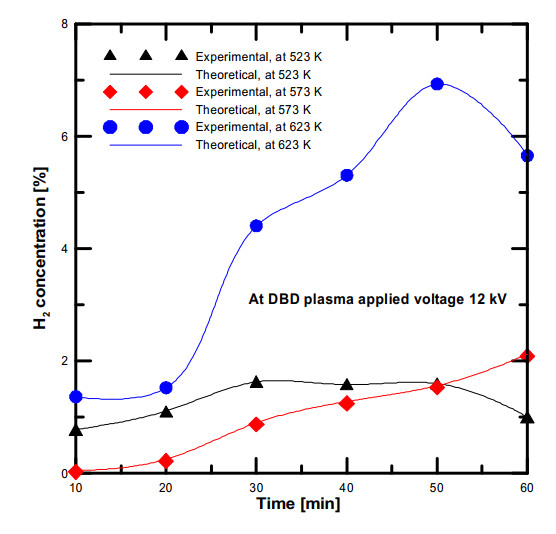
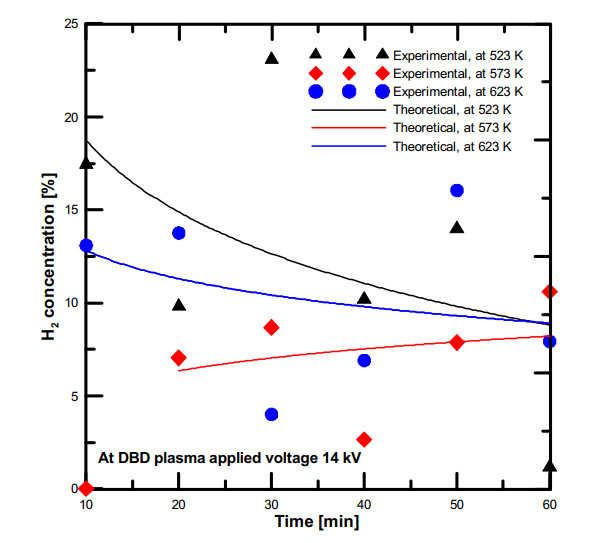
The effect of plasma applied voltage on the hydrogen production from water vapor decomposition using DBD plasma and at constant temperature in ranges of 523–623 K are shown in Figure (9a, b, c). It was found that the hydrogen concentration results of applied voltage 14 kV were higher than 12 kV at the same input temperature. Furthermore, this figure indicates that the simulation of H2 concentration results at plasma voltage of 12 kV were higher than experimental results, while the concentration results at plasma voltage of 14 kV decreased with time scale and also are not same as the simulation results. The simulation results of hydrogen concentration at plasma applied voltage 12 kV were higher than experimental, these results were confirmed the results of deselecting the dissociative attachment (reaction no. (2) in Table (1)) that investigated by Fahad et al. [28]. The dissociative attachment reaction was found that has an important effect on the simulation results of the water vapor dissociation using DBD plasma and the concentration of hydrogen gas is higher than experimental values. From the analysis of simulation and experimental results, it was observed that the H2 concentration results of the simulation model without the dissociative attachment reaction are higher than that obtained from the experimental results, also, the simulation trend profiles are changed according to the H2 concentrations obtained from the water vapour dissociation experiments.
3.2. Theoretical analysis of water vapor decomposition using DBD plasma with dissociative attachment reaction
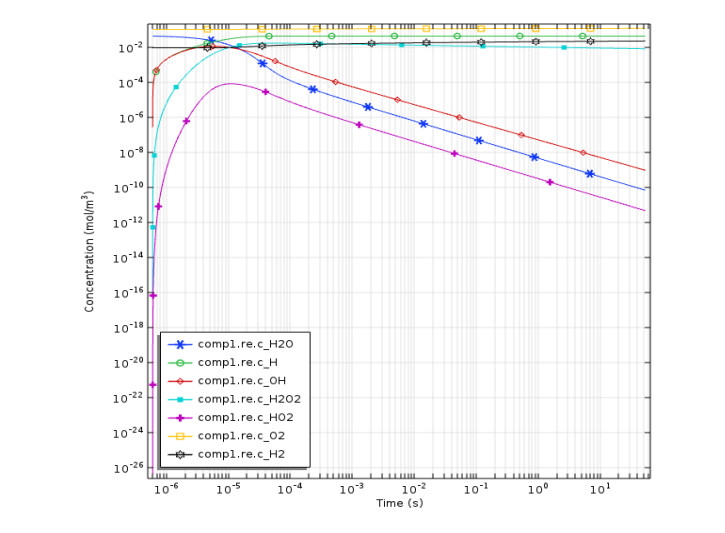
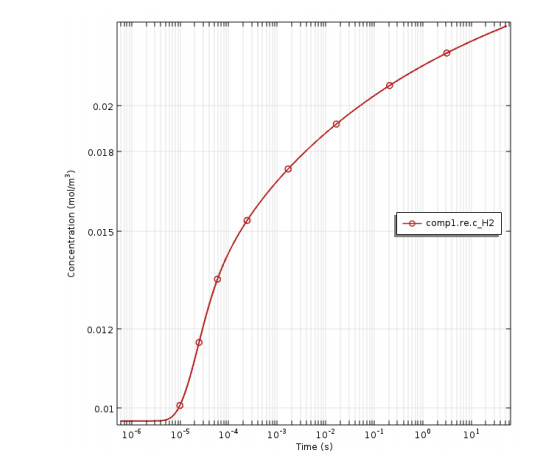
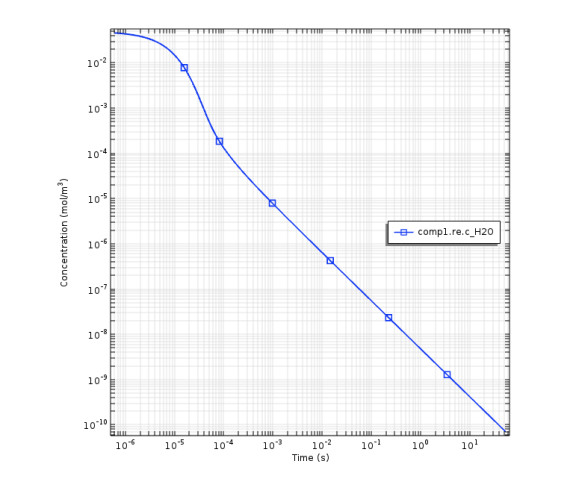
In this simulation model, the full reaction mechanism included the dissociative attachment reaction (H-) was analyzed. The dissociative attachment reaction included H- was utilized to break water vapor molecules by electron impact as a first step of chains of reactions. It could be stated that the hydrogen concentration value dropped by selecting the dissociative attachment reaction [28]. Additionally, it was reported that the dissociative ionization and dissociative excitation reactions have no effect on the kinetics as well as the species concentrations. Figure (10) shows the steady state concentration of the given full reaction mechanism species of H2O, H, OH, H-, H2O2, HO2, O2 and H2 when the dissociative attachment reaction (H-) was used. While e is expressed about the plasma discharge voltage at a frequency of 10 kHz. The concentration results of the species kinetic curves are based on a real water vapor decomposition case used in the simulation of water vapor decomposition without dissociative attachment reaction. Figure (11) indicates that the hydrogen concentration decreased from 0.025 to 0.01 moles/ m3, it was found that the dissociative attachment reaction is an important step in the water vapor dissociation processes. Furthermore, the effect of dissociative attachment reaction (H-) on hydrogen production from water vapor decomposition using DBD plasma was same as the simulation results obtained by Fahad et al. [28]. In addition, the simulation results of steady state water vapor concentration did not reach to zero as shown in Figure (12). It was clear that some of water vapor are not converted into hydrogen and oxygen gas, these simulation result seems to be same as the real water vapor decomposition because of some of the water vapor was remained in the ice trap.
However, the concentration profile results of both simulation models are similar, but in the current simulation study, it was investigated the major products of these reaction mechanisms H2 and O2. Further, the simulation and experimental results were compared in the next section.
3.2.1. Comparison between theoretical and experimental results (Model Ⅱ)
Figure (13) presents theoretical and experimental results of the effect of inlet water vapor temperature on the hydrogen concentration at plasma applied voltage of 12 kV. Compared with the simulation analysis without the dissociative attachment reaction, it was found that the hydrogen concentrations values dropped in a range of 50–62% by applying simulation analysis with dissociative attachment reaction. In addition, it was observed that the simulation results of hydrogen concentrations are nearly same as the experimental data due to add and start the water vapor breakdown with the dissociative attachment reaction. The hydrogen concentration results at different water vapor input temperatures and plasma applied voltage of 14 kV is shown in Figure (14). The results of the simulation and experimental results seem to be same, however, the concentration trend was not similar in both plasma applied voltage for the simulation model with dissociative attachment reaction.
Furthermore, it was found that the hydrogen concentrations of simulation model with dissociative attachment reaction at plasma voltage of 14 kV decreased from the simulation results obtained from simulation model without (H-) radicals in a range of 10–16%. The simulation results of hydrogen concentration obtained at plasma voltage 14 kV are not linearly changed with the water vapor input temperatures because of the effect of plasma high voltage and high electron mobility of decomposed gas, while at plasma voltage 12 kV, the maximum obtained results of H2 concentration at the highest input water vapor temperature. It is possibly changed due to sample collections during the experiment, some of hydrogen gas was not completely separated in the ice trap and some of separated hydrogen was remained inside the ice trap. To clarify the hydrogen concentration at different plasma voltage and at the same water vapor input temperature, Figure (15a, b, c) shows the effect of plasma voltage on the hydrogen concentration of experimental and simulation results with dissociative attachment reaction versus the reaction revolution time. It was found that the simulation results of hydrogen concentration at plasma voltage 14 kV was higher than that obtained from 12 kV at the same input water vapor temperature. The simulation model with the dissociative attachment reaction (H-) showed a good agreement with the water vapor experimental results, it was found that the dissociative attachment reaction to be an important step in water vapor decomposition using DBD plasma. Furthermore, when the simulation was carried out with the dissociative attachment reaction mechanism (H-), the hydrogen concentration dropped to be nearly same as the experimental results. Also, it was observed that the concentration of water molecules did not reach to zero, by means that some of the water vapor molecules are condensed inside the ice trap and did not convert into H2 and O2 gas.
3.3. Comparison between both simulation models reaction mechanism and experimental results
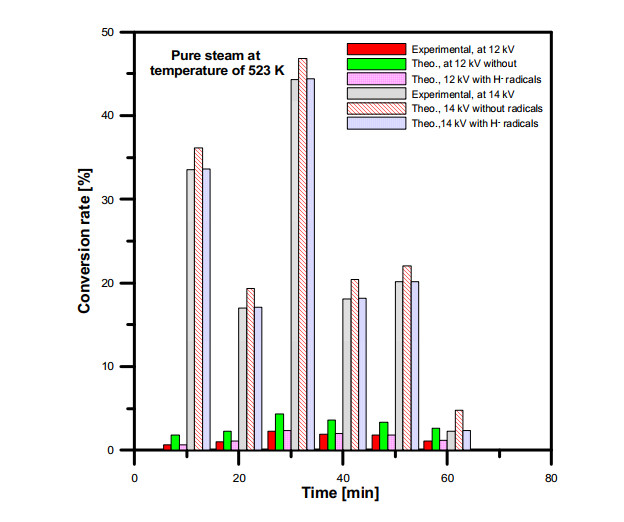
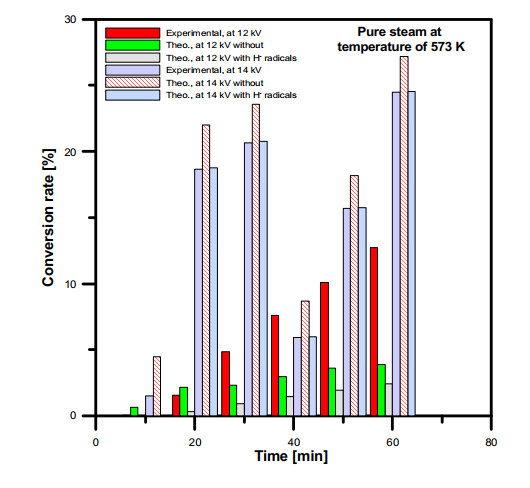
The conversion rate of both simulation models have been evaluated and compared between the water vapor decomposition using DBD plasma experimental results. The conversion rate can be determined according to the following expression: conversion rate [%] = (FH2 [mole/min]/ FinH2O [mole/min]) × 100. Where FH2 is the produced hydrogen gas and FinH2O is the water vapour inlet flow rate. The water vapor was decomposed into their elements hydrogen and oxygen gas using DBD plasma. Figure (16) shows the conversion rate change of the hydrogen production from water vapor at different plasma voltage and at water vapor input temperature 523 K. The conversion rate of the simulation model with the dissociative attachment reaction showed good agreement with the conversion rate of the experimental results compared with the results of the simulation model without dissociative attachment reaction. The comparison between conversion rates of water vapor at input temperature of 573 K is presented in Figure (17). The conversion rate of the simulation models result showed more hydrogen production concentration values than that obtained from the experimental concentration values. In both simulation models, it was found that the dissociative attachment reaction has an important effect as a first step of the water vapor dissociation process using plasma. Furthermore, it was observed that the conversion rate of input water vapor temperature 573 K was lower than the conversion rate of input water vapor temperatures of 523 and 623 K.
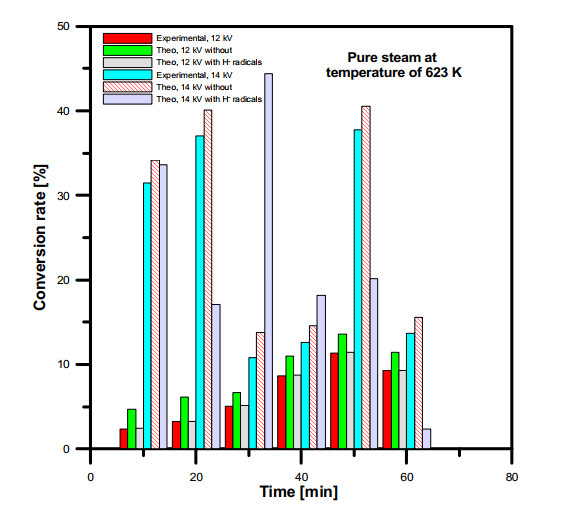
In addition, the conversion rate of input water vapor at temperature of 623 K is shown in Figure (18). The conversion rate results of the simulation model with dissociative attachment reaction seemed to be same in all water vapor input gas temperatures. Furthermore, it was found that the dissociation attachment reaction dominate the water vapor dissociation, in addition the hydrogen concentrations were dropped in both plasma applied voltages to be appeared same as the experimental results.
4.
Conclusions
The simulation results showed that the dissociative attachment reaction and the dissociative reaction of electrons have an important effect on the water vapour breakdown processes. The simulation analysis showed that the hydrogen concentrations obtained from the simulation model with the dissociative attachment reaction were lower than those obtained from the simulation model deselecting the dissociative attachment reaction. The hydrogen concentration results of both models were compared with the experimental results. It was found that the hydrogen concentration results of the simulation model selecting the dissociative attachment reaction were nearly same as that obtained from the experimental results. It was observed that the concentration results dropped by the addition of H- radical into the simulation model with the dissociative attachment reaction when used as a primary reaction of electron water vapour plasmolysis. Furthermore, it was concluded that the dissociative attachment reaction included H- radical controlled the hydrogen production from the detachment electron. The conversion rates were determined for the simulation models and the experimental results. The conversion rate results showed that the simulation model with the dissociative attachment reaction has introduced more acceptable data to the experimental results of the water vapour plasmolysis dissociation reactions pathway.
Acknowledgments
The author would like to thank Prof. Shinji Kambara and Gifu University for their continuous support to this project.
Conflict of interest
The authors declare that they have no conflict of interest that could have appeared to influence the work reported in this paper.









 DownLoad:
DownLoad: